传统的机械产品可靠性研究方法是从电子产品的可靠性研究中演变而来,例如可靠性框图、故障树分析(FTA)、故障模式影响及危害度分析(FMECA)等均首先在电子产品中得到应用。随着科技的不断发展,现代机械产品日趋复杂化、精密化、智能化,传统的可靠性研究方法不再适用于机械部分的可靠性分析要求。从机械系统的工程实际出发,研究人员相继提出了贝叶斯网络、蒙特卡洛仿真、Petri网、通用发生函数等一系列考虑系统结构的复杂性,系统性能的动态性、多态性等特性的可靠性分析方法,多态系统可靠性的研究开始逐渐受到学者们的关注,并在原有的基础上进行了进一步的拓展性研究。CASTET等[1-2]提出了基于数理统计的方法,建立了航天器多状态系统的Petri网分析模型。潘刚等[3-4]考虑系统受到随机冲击造成的不确定性和部件认知的不确定性等情况,分别利用区间通用生成函数和模糊通用生成函数来评估多态系统的可靠性。曹颖赛等[5]针对系统中零部件的故障逻辑关系难以确定的问题,运用广义灰色贝叶斯网络模型进行多状态系统的可靠性分析。以上文献在分析系统多态性时,都假设了多态零部件或多态单元相互独立。Levitin[6]在多态系统可靠性分析中,首次提到了元件性能分配过程中存在的依赖性特点。可靠性研究领域的国际著名学者Zio[7]指出系统状态之间以及组成单元各个状态之间存在的依赖性,是多状态系统建模的困难所在。性能依赖性同失效共因[8]、载荷共享[9]等特性一样,是单元性能相关性的一种外在表现。
本文针对现有多状态系统可靠性分析的不足,提出了一种考虑单元性能依赖特性的可靠性分析方法。首先利用功能层次分解方法得到系统的研究对象——元动作单元,根据元动作单元的多态性,采用非齐次马尔科夫模型建立单元的状态转移率矩阵,并将转移率的大小与依赖特性相关联,然后利用柯尔莫哥洛夫微分方程求得多态单元的稳态概率,用建立多态单元的向量通用发生函数来分析依赖特性对多态系统可靠性的影响,并通过实例证明该理论的有效性。
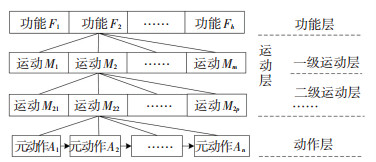
1 多态系统可靠性建模 1.1 元动作单元模型对于结构复杂的机械系统,根据文献[10-11]的研究方法, 可以利用功能(Function)—运动(Motion)—动作(Action)的层次分解方法获得机械系统最底层的研究对象——元动作,FMA分解使得系统的建模和分析过程得到简化。
FMA分解过程可以总结为:首先研究系统要实现的功能,然后将功能分解为各个子系统(部件)的运动,最后将子系统的运动再分解成零件级的动作,即为元动作,如图 1所示。
|
图 1 基于FMA的层次分解模型 Fig. 1 Decomposition model based on FMA |
根据FMA分解方法,系统功能的实现可视为在多个动力源驱动下的一系列元动作完成的。而实现某个元动作的所有相关零件(动力输入件、动力输出件、中间件、支撑件、紧固件)按照装配关系构成的整体称为元动作单元[11]。元动作单元包括移动单元和转动单元两类,移动类单元实现最基本的移动功能,如油缸中活塞移动单元、齿条移动单元等;转动类单元实现最基本的转动功能,如齿轮转动单元、丝杠转动单元等。本文的研究对象就是以元动作单元展开的。
1.2 元动作单元的可靠性分析模型可靠性的定义为产品在规定的时间内和规定的条件下,完成规定功能的能力[12]。当产品为机械系统时,根据FMA分解原理,其规定的功能可分解为系统零部件所要执行的动作,即元动作单元的可靠性可理解为元动作在规定的时间内和规定的条件下,完成规定动作的能力。
一个元动作单元其动作的完成能力可以通过动力输出件的性能参数来反映,从元动作单元的种类来看,其中位移s、速度ν、力σ为移动类单元的参数,角位移θ、角速度ω、力矩τ为转动类单元的参数。在一个维修周期内,外界环境的动态变化和系统功能的复杂性,会使元动作单元呈现多性能参数退化的多态性特征,从而整个系统也会表现出多态性。结合多位专家的知识和丰富的经验,根据不同元动作的服役时间、结构特点以及在系统功能实现上的重要性赋予每个参数不同的权重,定义单元的性能函数f(.),最终得到元动作单元的性能水平值,即
| $ \left\{ {\begin{array}{*{20}{l}} {h(t) = f\left( {{c_1}s(t),{c_2}v(t),{c_3}\sigma (t)} \right),}\\ {q(t) = f\left( {{c_4}\theta (t),{c_5}\omega (t),{c_6}\tau (t)} \right).} \end{array}} \right. $ |
式中:c1, c2, c3表示移动类单元的输出参数相对单元性能水平的权重,c4, c5, c6表示转动类单元的输出参数相对单元性能水平的权重,h(t)、q(t)分别表示移动单元和转动单元在某个时刻的性能水平值。
假设元动作单元的性能阀值为w,在某时刻t, 该单元的性能值为g(t),根据可靠性的定义,其单元的可靠度为
| $ R(t,w) = Pr(g(t) - w \ge 0). $ |
系统的功能由n个元动作实现,n个组成单元与系统存在如下的性能映射关系
| $ \varphi \left[ {\phi \left( {{g_{11}}, \ldots ,{g_{1{K_1}}}} \right), \ldots ,\phi \left( {{g_{n1}}, \ldots ,{g_{n{K_n}}}} \right)} \right] \to \left( {{B_1}, \ldots ,{B_K}} \right). $ |
式中:ϕ(.),φ(.)分别表示单元到子系统,子系统到整机系统的各层次间的物理特性的构型函数,Bi(t)表示系统在某时刻t的性能值,根据系统的性能需求阀值W, 可得系统的可靠度为
| $ {R_B}\left( {t,W} \right) = Pr\left( {{B_i}(t) - W \ge 0} \right). $ | (1) |
元动作单元在一个维修周期里,由外界环境作用以及单元内部的磨损导致其性能水平逐渐劣化,将单元劣化过程中的性能水平值进行离散化处理,假设元动作单元i从最佳性能状态(完全正常)劣化到最差性能状态(完全失效)中间会经历M个性能状态,定义该随机过程{Gi(t), t≥0}为连续时间离散状态马尔科夫过程,Gi(t)={gi1, gi2, ..., gim, ..., giM},其中giM为最佳性能状态,gi1为最差性能状态。采用Markov模型来描述元动作单元性能水平的退化过程,单元i在某时刻t, 由状态m向状态n转移的概率为ηm, ni(t),单元i的状态转移率矩阵如下式所示:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_i}\left( t \right) = \\ \left( {\begin{array}{*{20}{c}} {\eta _{M,M - 1}^i\left( t \right)}&{\eta _{M,M - 2}^i\left( t \right)}& \cdots &{\eta _{M,2}^i\left( t \right)}&{\eta _{M,1}^i\left( t \right)}\\ 0&{\eta _{M - 1,M - 2}^i\left( t \right)}& \cdots &{\eta _{M - 1,2}^i\left( t \right)}&{\eta _{M - 1,1}^i\left( t \right)}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0& \cdots &0&{\eta _{2,1}^i\left( t \right)} \end{array}} \right). \end{array} $ |
已知单元的状态转移率矩阵后,在单元的初始状态确定的情况下,依据Chapman-Kolmogorov公式可求得元动作单元处于不同状态时的稳态概率。求解单元稳态概率的关键在于状态转移率矩阵,本文根据采集的元动作试验数据, 利用统计推断的方法计算单元的初始状态转移率矩阵。
2.2 单元依赖特性分析在系统分解到最底层的元动作层里,由同一个动力源驱动的元动作是上、下游动作的传递过程,上游单元的动作完成能力直接影响到与其相邻的下游单元的动作完成能力。例如蜗轮蜗杆传动,蜗杆转动动作的精度(位移和角速度的综合反映)、力矩等参数的大小直接决定了蜗轮动作的完成能力,即上游单元的性能状态水平决定了下游单元的各个状态性能分布,这种关系称为下游单元对上游单元的依赖性关系。为便于依赖特性的分析,给出以下几个定义:
自立单元i:指元动作单元i的状态性能水平决定相邻下游j的状态性能分布;
依赖单元j:指元动作单元j的状态的性能分布依赖于相邻上游i的状态性能水平;
依赖组:一个依赖单元j与所对应的自立单元i构成一个依赖组。
根据上节分析,设定自立单元i的各状态性能值为Gi(t)={gi1, gi2, ..., gim, ..., giM},i的一个性能值子集对应于与之相邻的依赖单元j的一种状态性能分布。Gi(t)由K个互不相交的子集gik(1≤k≤K)组成,当i的状态性能值gim属于某个子集gik时,单元j的状态性能分布随之确定,依赖单元j的性能值为Gj(t)={gj1, gj2, ..., gjh, ..., gjH},H表示依赖单元j在一个维修周期里的状态总数。当gim∈gik,有
| $ g_{jh}^{i/k} = \left\{ {g_{jc}^{i/k},1 \le c \le {C_{j/k}}} \right\}, $ |
式中:gjhi/k指i的性能值属于子集gik时,j的性能值,Cj/k指j此时的状态数,Cj/k≤H。当自立单元的性能值逐渐退化,落到另一个子区间gik+1时,依赖单元的状态性能分布发生变化。
文献[13-14]在分析系统或单元的状态转移率时,默认状态转移率矩阵的元素值在整个维修周期里是固定值或时间t的固定函数.而文献[15]提到,随着系统工作时间不断累积,系统的状态转移概率是变化的,且在系统处于不同的退化阶段时,其状态转移率的变化特点也是不一致的。基于此,假定存在依赖特性的单元的状态转移率不再是仅与时间t有关的函数值,也更不会是固定值。由依赖特性的定义,当自立单元所处的性能状态越低,对依赖单元造成的影响越大。引入状态转移系数ν, 且
| $ \nu = \frac{{{K_i}}}{{{k_i}\left( {t,m} \right)}}. $ | (2) |
式中:Ki指自立单元i的性能子集总数,ki(t, m)指在某时刻t,自立单元的性能状态值gim所处的性能状态子集数。设依赖单元j的初始状态转移矩阵为Aj(0),则经过一段时间的性能退化之后,依赖单元的状态转移矩阵可表示为
| $ {\mathit{\boldsymbol{A}}_j}(t) = \nu \cdot {\mathit{\boldsymbol{A}}_j}(0). $ |
本文利用通用发生函数在处理多态可靠性问题优势的基础上,提出向量通用发生函数,用以表达具有依赖特性的单元性能状态和对应的状态概率。
根据2.1节的元动作单元多状态分析,一个元动作单元i的性能水平值gmi视为离散型随机变量,其通用发生函数表示为
| $ {u_i}(z) = \sum\limits_{m = 1}^M {p_m^i} {z^{g_m^i}}. $ |
式中:gmi,pmi分别表示元动作单元i处于性能状态m时的性能水平值和处于该状态的概率,M为所有的状态数,z用于区分随机变量的取值和取值概率,本身没有实际含义。
系统性能Q的分布用u函数表示为
| $ \begin{array}{l} {u_Q} = {u_1}(z) \otimes {u_2}(z) \otimes \cdots \otimes {u_n}(z) = \\ \;\;\;\;\;\;\sum\limits_{{m_1} = 1}^{{M_1}} {p_{{m_1}}^1} {z^{g_{{m_1}}^1}}\mathop \otimes \limits_ \times \sum\limits_{{m_2} = 1}^{{M_2}} {p_{{m_2}}^2} {z^{g_{{m_2}}^2}}\mathop \otimes \limits_ \times \cdots \sum\limits_{{m_n} = 1}^{{M_n}} {p_{{m_n}}^n} {z^{g_{{m_n}}^n}} = \\ \;\;\;\;\;\sum\limits_{{m_1} = 1}^{{M_1}} {\sum\limits_{{m_2} = 1}^{{M_2}} \cdots } \sum\limits_{{m_n} = 1}^{{M_n}} {p_{{m_1}}^1} p_{{m_2}}^2 \cdots p_{{m_n}}^n{z^{\phi \left( {g_{{m_1}}^1,g_{{m_2}}^2, \cdots g_{{m_n}}^n} \right)}}. \end{array} $ | (3) |
式中ϕ(gm11, gm22, ..., gmnn)表示在多个元动作单元作用下,上层运动系统或整机功能系统的性能水平值。系统与组成该系统的单元间的相互关系算子ϕ(.)根据系统的结构以及参数的性质不同而具有不同的运算规则,定义如下几个常见的算子
| $ \left\{ {\begin{array}{*{20}{l}} {{\phi _1}\left( {{g_1},{g_2}} \right) = {g_1} + {g_2},}\\ {{\phi _2}\left( {{g_1},{g_2}} \right) = \max \left( {{g_1},{g_2}} \right),}\\ {{\phi _3}\left( {{g_1},{g_2}} \right) = \min \left( {{g_1},{g_2}} \right),}\\ {{\phi _4}\left( {{g_1},{g_2}} \right) = \frac{1}{{{g_1}}} + \frac{1}{{{g_2}}}.} \end{array}} \right. $ | (4) |
根据元动作性能参数的特点,本文计算同一个动力源驱动下的元动作单元相互关系算子ϕ(.)取式(4)中ϕ3(.),即
| $ {u_1}(z)\mathop \otimes \limits_{ser} {u_2}(z) = \sum\limits_{{m_1} = 1}^{{M_1}} {\sum\limits_{{m_2} = 1}^{{M_2}} {p_{{m_1}}^1} } p_{{m_2}}^2{z^{\min \left( {{g_{{m_1}}},{g_{{m_2}}}} \right)}}. $ | (5) |
不同动力源驱动下的子系统之间的相互关系算子取式(4)中ϕ1(.),即
| $ {u_1}(z)\mathop \otimes \limits_{par} {u_2}(z) = \sum\limits_{{m_1} = 1}^{{M_1}} {\sum\limits_{{m_2} = 1}^{{M_2}} {p_{{m_1}}^1} } p_{{m_2}}^2{z^{\left( {{g_{{m_1}}} + {g_{{m_2}}}} \right)}}. $ | (6) |
在一个依赖组中,当自立单元i的性能子集共有K个,根据第2节的分析可知依赖单元j在整个生命周期的状态概率矩阵pj表示为
| $ {\mathit{\boldsymbol{p}}_j} = \left[ {{p_{j1}},{p_{j2}}, \cdots ,{p_{jh}}, \cdots ,{p_{jc/k}}} \right]. $ |
依赖单元j在第h个状态所对应的状态概率可用向量表示为
| $ {\mathit{\boldsymbol{p}}_{jh}} = {\left[ {p_{jh}^{i/1},p_{jh}^{i/2}, \ldots ,p_{jh}^{i/k}, \cdots ,p_{jh}^{i/K}} \right]^{\rm{T}}}. $ |
j的发生函数表示为
| $ {\mathit{\boldsymbol{u}}_j}(z) = \sum\limits_{h = 1}^{{C_{j/k}}} {{\mathit{\boldsymbol{p}}_{jh}}} \cdot {z^{g_h^j}}. $ |
由i和j组成的依赖组的发生函数为
| $ u(i,j,z) = \Omega \left( {{u_i}(z),{\mathit{\boldsymbol{u}}_j}(z)} \right) = \sum\limits_{m = 1}^M {\sum\limits_{h = 1}^H {p_m^i} } p_{jh}^{i/k(m)}{z^{\phi \left( {g_i^m,g_j^h} \right)}}. $ | (7) |
上述讨论的依赖关系是两个单元形成一个依赖组,是一般化的依赖情形.在由多个元动作单元组成的上层运动子系统中,存在更加复杂的依赖关系。本文讨论两种常见情形并给出相应的子系统的发生函数表达式。
情形一:几个单元的状态性能概率分布同时依赖一个单元.
假设有元动作单元a、b、c组成一个运动子系统,b、c的性能状态分布都依赖于a,则可以得到该子系统的发生函数
| $ \begin{array}{l} {u_1}(a,b,c,z) = {\mathit{\Omega }_1}\left( {{u_a}(z),{u_b}(z),{u_c}(z)} \right) = \\ \;\;\;\;\;\;\sum\limits_{{l_1} = 1}^{{N_a}} {\sum\limits_{{l_2} = 1}^{{N_b}} {\sum\limits_{{l_3} = 1}^{{N_c}} {{p_{{l_1}}}} } } \cdot p_{{l_2}}^{a/{k_b}\left( {{l_1}} \right)} \cdot p_{{l_3}}^{a/{k_c}\left( {{l_1}} \right)} \cdot {z^{\phi \left( {g_{{l_1}}^a,g_{{l_2}}^b,g_{{l_3}}^c} \right)}}. \end{array} $ | (8) |
式中:(l1, l2, l3),(Na, Nb, Nc)分别表示单元(a, b, c)的某个状态和最高状态,pl1,pl2a/kb(l1),pl3a/kc(l1)表示a,b,c在对应状态的概率,ϕ(gl1a, gl2b, gl3c)表示在3个单元的综合作用下,子系统的性能值。
情形二:一个元动作单元是上游单元的依赖单元,同时又是下游单元的自立单元。
同样假设单元a、b、c组成一个运动子系统,c的性能值分布依赖于b,b的性能值分布依赖于a,则此时子系统的发生函数表示为
| $ \begin{array}{l} {u_2}(a,b,c,z) = {\mathit{\Omega }_2}\left( {{u_a}(z),{u_b}(z),{u_c}(z)} \right) = \\ \;\;\;\;\;\;\sum\limits_{{l_1} = 1}^{{N_a}} {\sum\limits_{{l_2} = 1}^{{N_b}} {\sum\limits_{{l_3} = 1}^{{N_c}} {{p_{{l_1}}}} } } \cdot p_{{l_2}}^{a/{k_b}\left( {{l_1}} \right)} \cdot p_{{l_3}}^{a/{k_c}\left( {{l_1}} \right)} \cdot {z^{\phi \left( {g_{{l_1}}^a,g_{{l_2}}^b,g_{{l_3}}^c} \right)}}. \end{array} $ |
根据以上讨论,在求得具有依赖特性的依赖组的发生函数后,利用式(3)结合其他相互独立的单元计算整机系统的发生函数,根据系统的性能要求阀值,再利用式(1)求得系统在考虑单元存在性能依赖特性时的可靠度。
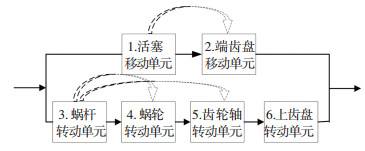
4 算例分析 4.1 元动作单元多态性分析以某企业精密加工中心的一个子系统——端齿盘分度转台为例,转台的分度功能通过转台的升降运动和回转运动实现,升降运动通过活塞移动和端齿盘移动实现,回转运动通过蜗轮蜗杆转动、齿轮轴转动和上齿盘移动实现。通过FMA分解得到动作层对应的元动作单元之后,用串联表示在同一动力源驱动下的单元组,并联表示不同动力源驱动下的单元组,元动作单元层的依赖关系简化为如图 2所示。
|
图 2 元动作单元依赖关系 Fig. 2 Meta action unit dependencies |
元动作单元的性能退化阶段主要通过动力输出件的执行精度来反映,系统实际运行过程中的动作精度通过多类传感器的测量已知。根据实际测量的动作精度范围进行多状态的划分,通常将状态划分为4种,划分原则如表 1所示。
| 表 1 状态类别划分 Tab. 1 State classification |
通过监测元动作单元输出件的动作参数得到实例中6个元动作单元的多状态性能水平值,为简化计算并体现出单元性能退化过程中的不同状态,设定:
| $ {G_1}\left( t \right) = {G_3}\left( t \right) = \left\{ {1,2,3.5,5} \right\}, $ |
| $ {G_2}\left( t \right) = {G_4}\left( t \right) = \left\{ {1,2,4,5} \right\}, $ |
| $ {G_5}\left( t \right) = \left\{ {1.5,2,3.5,5} \right\}, $ |
| $ {G_6}\left( t \right) = \left\{ {1.5,3.5,5} \right\}, $ |
元动作单元1、2初始状态概率分布如表 2所示,p4i(0)为最优性能状态,p1i(0)为最劣性能状态。
| 表 2 元动作单元1, 2的初始状态概率 Tab. 2 Initial state probability of meta action unit 1, 2 |
利用Chapman-Kolmogorov公式建立依赖单元2的多状态概率微分方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{p_4}(t)}}{{{\rm{d}}t}} = - {p_4}(t)\left( {\eta _{4,3}^2 + \eta _{4,2}^2 + \eta _{4,1}^2} \right),}\\ {\frac{{{\rm{d}}{p_3}(t)}}{{{\rm{d}}t}} = {p_4}(t)\eta _{4,3}^2 - {p_3}(t)\left( {\eta _{3,2}^2 + \eta _{3,1}^2} \right),}\\ {\frac{{{\rm{d}}{p_2}(t)}}{{{\rm{d}}t}} = {p_4}(t)\eta _{4,2}^2 + {p_3}(t)\eta _{3,2}^2 - {p_2}(t)\eta _{2,1}^2,}\\ {\frac{{{\rm{d}}{p_1}(t)}}{{{\rm{d}}t}} = {p_4}(t)\eta _{4,1}^2 + {p_3}(t)\eta _{3,1}^2 + {p_2}(t)\eta _{2,1}^2.} \end{array}} \right. $ | (9) |
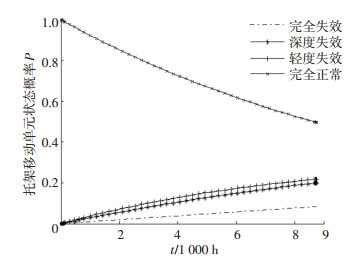
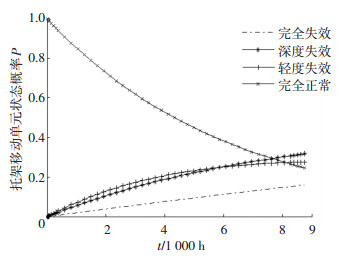
从图 2可知,元动作单元1、2构成一个依赖组。为便于进行依赖特性的分析,设自立单元1的性能子集总数K=2。依据式(2),当3.0≤gm1 < 5.5(k=2)时,依赖单元2的状态转移率系数ν=1;当1.0≤gm1 < 3.0(k=1)时,依赖单元2的状态转移率系数ν=2。依赖单元2在自立单元1处于不同性能子集时的状态转移率见表 3,其状态概率图见图 3、4。
| 表 3 依赖单元2状态转移率 Tab. 3 State transfer probability of dependent unit 2 |
|
图 3 依赖单元2的状态概率图(3.0≤ gm1 < 5.5) Fig. 3 State probability of dependent unit 2(3.0≤gm1 < 5.5) |
|
图 4 依赖单元2的状态概率图(1.0≤ gm1 < 3.0) Fig. 4 State probability of dependent unit 2(1.0≤gm1 < 3.0) |
通过图 3、4自立单元处于不同性能区间时的对比分析可知,在自立单元的性能状态偏高时,其依赖单元的各状态稳态概率曲线更平滑,即在同样的时刻下,依赖单元处于高性能状态的概率更大。在自立单元处于低性能状态时,其依赖单元的失效概率也会增大。
4.2 子系统可靠性分析为分析依赖特性对系统可靠性产生的影响,取端齿盘分度转台子系统的运行时间t=1年,计算各元动作单元的稳态概率。设定各个单元的初始状态性能水平都是从最高性能状态开始劣化的,根据2.1节所述方法,计算各个单元的多状态稳态概率,6个元动作单元的稳态概率值如表 4所示。
| 表 4 各元动作单元稳态概率 Tab. 4 Steady-state probability of each element action unit |
从表中所求的稳态概率可知,在自立单元处于“完全正常”和“轻度失效”时,依赖单元处于“完全正常”和“轻度失效”的概率会大些,反之,当自立单元处于“严重失效”和“完全失效”时,依赖单元处于“严重失效”和“完全失效”的概率也会大些,单元的依赖性通过稳态概率分布得到体现。
将上述的独立单元和依赖组的单元状态性能值通过通用发生函数及改进的发生函数表示如下:
| $ {u_1} = 0.32{z^5} + 0.24{z^{3.5}} + 0.171{z^2} + 0.284{z^1}, $ |
| $ \overrightarrow {{u_2}} = \left( {\begin{array}{*{20}{c}} {0.496}\\ {0.246} \end{array}} \right){z^5} + \left( {\begin{array}{*{20}{c}} {0.218}\\ {0.216} \end{array}} \right){z^4} + \left( {\begin{array}{*{20}{c}} {0.202}\\ {0.377} \end{array}} \right){z^2} + \left( {\begin{array}{*{20}{c}} {0.084}\\ {0.161} \end{array}} \right){z^1}, $ |
| $ {u_3} = 0.32{z^5} + 0.224{z^{3.5}} + 0.171{z^2} + 0.284{z^1}, $ |
| $ \overrightarrow {{u_4}} = \left( {\begin{array}{*{20}{c}} {0.566}\\ {0.32} \end{array}} \right){z^5} + \left( {\begin{array}{*{20}{c}} {0.079}\\ {0.076} \end{array}} \right){z^4} + \left( {\begin{array}{*{20}{c}} {0.249}\\ {0.356} \end{array}} \right){z^2} + \left( {\begin{array}{*{20}{c}} {0.106}\\ {0.248} \end{array}} \right){z^1}, $ |
| $ \overrightarrow {{u_5}} = \left( {\begin{array}{*{20}{l}} {0.518}\\ {0.269} \end{array}} \right){z^5} + \left( {\begin{array}{*{20}{c}} {0.045}\\ {0.044} \end{array}} \right){z^{3.5}} + \left( {\begin{array}{*{20}{c}} {0.188}\\ {0.276} \end{array}} \right){z^2} + \left( {\begin{array}{*{20}{c}} {0.249}\\ {0.411} \end{array}} \right){z^{1.5}}, $ |
| $ {u_6} = 0.717{z^5} + 0.126{z^{3.5}} + 0.157{z^{1.5}}. $ |
根据式(3)、(5)~(8)可以计算各依赖组及独立单元构成的子系统性能状态发生函数:
| $ \begin{array}{l} \overrightarrow {{u_{1,2}}} = {u_1} \otimes \overrightarrow {{u_2}} = 0.159{z^5} + 0.07{z^4} + 0.16{z^{3.5}} + \\ \;\;\;\;\;\;\;\;0.253{z^2} + 0.357{z^1}, \end{array} $ |
| $ \begin{array}{l} \overrightarrow {{u_{3,4,5}}} = {u_3} \otimes \overrightarrow {{u_4}} \otimes \overrightarrow {{u_5}} = 0.094{z^5} + 0.013{z^4} + \\ \;\;\;\;\;\;\;\;\;0.105{z^{3.5}} + 0.255{z^2} + 0.132{z^{1.5}} + \\ \;\;\;\;\;\;\;\;\;0.381{z^1}, \end{array} $ |
最终可计算得到在考虑依赖特性后系统的发生函数为
| $ \begin{array}{l} \;\;\;\;{U_1} = \overrightarrow {{u_{1,2}}} \mathop \otimes \limits_{par} \left( {\overrightarrow {{u_{3,4,5}}} \mathop \otimes \limits_{ser} {u_6}} \right) = \left( {0.159{z^5} + 0.07{z^4} + } \right.\\ \left. {0.16{z^{3.5}} + 0.253{z^2} + 0.357{z^1}} \right)\mathop \otimes \limits_{par} \left( {0.068{z^5} + 0.01{z^4} + } \right.\\ \left. {0.102{z^{3.5}} + 0.215{z^2} + 0.205{z^{1.5}} + 0.381{z^1}} \right) = 0.0108{z^{10}} + \\ 0.0064{z^9} + 0.0271{z^{8.5}} + 0.0007{z^8} + \cdots + 0.0732{z^{2.5}} + \\ 0.1360{z^2}. \end{array} $ |
当不考虑性能依赖时,即系统的各个组成单元相互独立,具体体现在分析过程中只将依赖组中的两个单元做独立不相关处理,即依赖单元的状态转移率矩阵在初步确定后不再改变,其他条件一样,据此计算系统的发生函数为
| $ \begin{array}{l} \;\;\;\;{U_2} = \left( {{u_1}\mathop \otimes \limits_{ser} {u_2}} \right)\mathop \otimes \limits_{par} \left( {{u_3}\mathop \otimes \limits_{ser} {u_4}\mathop \otimes \limits_{ser} {u_5}\mathop \otimes \limits_{ser} {u_6}} \right) = \\ \left( {0.159{z^5} + 0.07{z^4} + 0.16{z^{3.5}} + 0.267{z^2} + 0.344{z^1}} \right)\mathop \otimes \limits_{par} \\ \left( {0.067{z^5} + 0.009{z^4} + 0.089{z^{3.5}} + 0.238{z^2} + 0.234{z^{1.5}} + } \right.\\ \left. {0.36{z^1}} \right) = 0.0106{z^{10}} + 0.0061{z^9} + 0.0249{z^{85}} + 0.0006{z^8} + \\ \cdots + 0.0625{z^{3.5}} + 0.1780{z^3} + 0.0805{z^{2.5}} + 0.1238{z^2}. \end{array} $ |
根据U1、U2和式(1)可以得到两种情形下多态系统可靠度,如图 5所示。
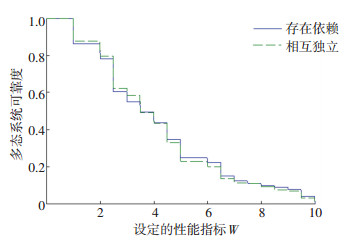
|
图 5 两种情况下的系统多态可靠度 Fig. 5 System multi-state reliability in two cases |
从图 5可以看出,在系统的性能指标值W设定在3.5之前时,考虑了依赖性的系统可靠度比相互独立时的可靠度要低.这是因为在一个维修周期内,随着系统的退化,组成系统的元动作单元由于存在依赖性,当处于低性能状态的自立单元发生失效后会增大其依赖单元状态转移率,即性能水平会同时降低到更低的状态; 而独立的元动作单元之间某一个单元失效并不影响其他单元,最终反映在系统上的结果即有依赖性的系统可靠性降低更多.在性能指标值设定在3.5之后时,考虑了依赖性的系统其可靠度高于相互独立时的可靠度,这是因为在高性能状态,自立单元的高性能状态决定其依赖单元的状态转移率较低,即一个依赖组能同时保持在较高的性能状态。
5 结论1) 利用功能—运动—动作的结构化分解方法,将复杂系统分解至底层元动作,并以元动作单元为研究对象,使得系统层到单元层的结构分析得到简化。
2) 利用非齐次马尔科夫模型描述元动作单元的多态性,并通过设定状态转移系数构建了考虑性能依赖时的元动作单元状态转移矩阵,利用向量通用发生函数建立了对应多态系统的可靠性分析模型,通过对比分析得知依赖特性单元的状态转移率会随着对应自立单元的性能退化而改变。
3) 计算在考虑单元性能依赖下的系统性能水平发生函数,通过与单元相互独立的系统对比分析得知:在单元处于高性能状态时,单元的依赖特性会使系统的可靠性提高; 而在低性能状态时,单元的依赖特性会使系统的可靠性降低。
| [1] |
WAYER J K, CASTET J, SALEH J H. Spacecraft attitude control subsystem: reliability, multi-state analyses, and comparative failure behavior in LEO and GEO[J]. Acta Astronautica, 2013, 85: 83. DOI:10.1016/j.actaastro.2012.12.003 |
| [2] |
KIM S Y, CASTET J, SALEH J H. Spacecraft electrical power subsystem: failure behavior, reliability, and multi-state failure analyses[J]. Reliability Engineering & System Safety, 2012, 98(1): 55. DOI:10.1016/j.ress.2011.10.005 |
| [3] |
潘刚, 尚朝轩, 梁玉英, 等. 随机冲击情况下考虑认知不确定的多态系统可靠性评估[J]. 振动与冲击, 2016(10): 29. PAN Gang, SHANG Chaoxuan, LIANG Yuying, et al. Estimation of interval-valued reliability of multi-state system in consideration of epistemic uncertainty under random shock[J]. Journal of Vibration and Shock, 2016(10): 29. DOI:10.13465/j.cnki.jvs.2016.10.005 |
| [4] |
潘刚, 尚朝轩, 梁玉英, 等. 认知不确定多态系统模糊可靠性评估[J]. 南京航空航天大学学报, 2016, 48(5): 714. PAN Gang, SHANG Chaoxuan, LIANG Yuying, et al. Evaluation on fuzzy reliability of multi-state systems with cognitive uncertainty[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(5): 714. DOI:10.16356/j.1005-2615.2016.05.015 |
| [5] |
曹颖赛, 刘思峰, 方志耕, 等. 多态系统可靠性分析广义灰色贝叶斯网络模型[J]. 系统工程与电子技术, 2018(1): 231. CAO Yingsai, LIU Sifeng, FANG Zhigeng, et al. Generalized grey bayesian network model for reliability analysis of multi-state system[J]. Systems Engineering and Electronics, 2018(1): 231. DOI:10.3969/j.issn.1001-506X.2018.01.33 |
| [6] |
LEVITIN. A universal generating function approach for the analysis of multi-state systems with dependent elements[J]. Reliability Engineering & System Safety, 2004, 84: 285. DOI:10.1016/j.ress.2003.12.002 |
| [7] |
ZIO E. Reliability engineering: old problems and new challenges[J]. Reliability Engineering & System Safety, 2009, 94(2): 125. DOI:10.1016/j.ress.2008.06.002 |
| [8] |
周金宇, 谢里阳. 多状态系统共因失效机理与定量分析[J]. 机械工程学报, 2008, 44(10): 77. ZHOU Jinyu, XIE Liyang. Common failure mechanism and quantitative analysis of multi-state system[J]. Journal of Mechanical Engineering, 2008, 44(10): 77. DOI:10.3901/JME.2008.10.077 |
| [9] |
刘宇, 刘翔宇. 考虑载荷动态分配机制的多状态系统可靠性建模及优化术[J]. 机械工程学报, 2016, 52(6): 197. LIU Yu, LIU Xiangyu. Reliability modeling and optimization of multi-state systems considering dynamic load distribution mechanism[J]. Journal of Mechanical Engineering, 2016, 52(6): 197. DOI:10.3901/JME.2016.06.197 |
| [10] |
RAN Yan, ZHANG Genbao, ZHANG Lian. Quality characteristic association analysis of computer numerical control machine tool based on meta-action assembly unit[J]. Advances in Mechanical Engineering, 2016, 8(1): 1. DOI:10.1177/1687814016629344 |
| [11] |
张根保, 李冬英, 刘佳, 等. 装配可靠性的模块化故障树建模与多维映射[J]. 计算机集成制造系统, 2013, 19(3): 516. ZHANG Genbao, LI Dongying, LIU Jia, et al. Modular fault tree modeling and multidimensional mapping of assembly reliability[J]. Journal of Computer Integrated Manufacturing Systems, 2013, 19(3): 516. DOI:10.13196/j.cims.2013.03.70.zhanggb.001 |
| [12] |
张根保, 何桢, 刘英. 质量管理与可靠性[M]. 北京: 中国科学技术出版社, 2005. ZHANG Genbao, HE Zhen, LIU Ying. Quality Management and Reliability[M]. Beijing: China Science and Technology Press, 2005. |
| [13] |
周丰旭, 李爱平, 谢楠, 等. 基于性能衰退的多态制造系统可靠性分析[J]. 计算机集成制造系统, 2014, 20(6): 1424. ZHOU Fengxu, LI Aiping, XIE Nan, et al. Reliability analysis of multi-manufacturing systems based on performance degradation[J]. Computer Integrated Manufacturing Systems, 2014, 20(6): 1424. DOI:10.13196/j.cims.2014.06.zhoufengxu.1424.8.20140620 |
| [14] |
阚琳洁, 张建国, 王丕东, 等. 基于性能退化和通用发生函数的在轨空间机构系统多状态可靠性分析[J]. 机械工程学报, 2017, 53(11): 20. KAN Linjie, ZHANG Jianguo, WANG Pidong, et al. Multi-state reliability analysis of on-orbit space agency system based on performance degradation and universal generation function[J]. Journal of Mechanical Engineering, 2017, 53(11): 20. DOI:10.3901/JME.2017.11.020 |
| [15] |
何兆民, 王少萍. 基于时变状态转移隐半马尔科夫模型的寿命预测[J]. 湖南大学学报(自然科学版), 2014, 41(8): 47. HE Zhaomin, WANG Shaoping. Life prediction based on time-varying state transition hidden semi-Markov model[J]. Journal of Hunan University(Natural Science), 2014, 41(8): 47. |
 2020, Vol. 52
2020, Vol. 52


