2. 北京理工大学 机械与车辆学院,北京 100081;
3. 北京科技大学 机械工程学院,北京 100083
2. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;
3. School of Mechanic Engineering, University of Science and Technology Beijing, Beijing 100083, China
液力变矩器是一种以油液为工作介质传递能量的传动元件.作为一种典型的柔性叶轮传动装置,液力变矩器以其能容大、功率密度高、自动适应性强、可靠性高等特点广泛应用于各类车辆、船舶、铁路机车、工程机械及风电传动装置中.在对液力变矩器进行高功率密度和轻量化设计时,要充分考虑其叶片和流道的强度及刚度问题.
魏巍等基于流固耦合技术(FSI),联合计算流体动力学和有限元数值模拟,实现了叶片强度的较为准确预测,为高功率密度液力变矩器叶栅系统的工程设计提供了理论依据[1].刘城等提出了基于贝塞尔曲线的液力变矩器叶片造型方法,建立了叶栅设计优化系统,提高了叶栅系统的设计水平[2-4].李新毅等以叶片入出口角为优化参数,采用基于存档的小种群遗传算法对某变矩器的性能进行了优化[5].吕倩等利用ANSYS Mechanical与ANSYS CFX无缝集成的流固耦合平台,通过计算流体动力学和结构静力学确定了叶片的变形情况和应力分布情况,为保证液力变矩器的高效运转提供了准确的理论依据[6].王安麟等通过高精度流固耦合数值方法,发现液力变矩器叶片厚度分布与其流场分布具有强相关性[7].陈凯等以泵轮出口角和导轮进出口角为设计变量,建立了多目标匹配优化模型,使用遗传算法进行了优化,得到了Pareto最优解集[8].吴光强等依据一维束流理论,对液力变矩器的工作性能进行了优化[9].综上所述,国内对液力变矩器的设计、分析和优化的研究多是结合起来进行集成化研究的,目前比较有效的方法是将优化算法与三维设计参数化建模和二次分析平台结合起来,实现高效的分析与设计.然而由传统方法设计出的铸造型变矩器通常较为笨重,仍有结构轻量化的必要.本文为了进一步挖掘液力变矩器结构设计潜力,提升质量功率密度,将轻量化思想引入到液力变矩器的研究中.并且基于Isight,matlab,ansys等软件,采用单向流固耦合方法实现对液力变矩器叶栅系统和内外环进行厚度参数化优化和强度校核,同时探究叶栅厚度参数对液力变矩器变矩能力和原始特性的影响.
1 叶栅系统及内外环参数化建模 1.1 叶栅系统参数化设计液力变矩器弯曲变形较大的叶形对工作性能具有很大的影响.通过对液力变矩器的叶形进行参数化建模来达到直观有效地控制空间扭曲的液力变矩器叶栅系统的目的.首先采用贝塞尔曲线分别对单元骨线和叶片厚度进行近似设计,然后通过对所得到的骨线方程和厚度方程进行坐标变换来获得实际比例的叶片骨线值和厚度值,构造叶片二维形状.在叶片厚度构造过程,入、出口处采用圆弧过渡.
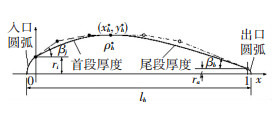
单元厚度造型中较为关键的几何参数为:单元厚度入口厚度半径ri、单元厚度出口厚度半径ro、单元最大厚度半径yh*及其位置xh*、单元厚度峰值处曲率半径ρh*、单元厚度入口处楔角βi、单元厚度出口处楔角βo.如图 1中单元叶片厚度二维示意图所示.以上相关参数采用厚度比例系数进行统一控制,例如对于泵轮厚度变化的调整,可采用泵轮厚度系数:p_thick进行控制.相应的,涡轮厚度系数为t_thick,导轮厚度系数为s_thick.值得注意的是,单元叶片厚度指的是贝塞尔曲线部分弦长为1,加上入、出口圆弧处理后,单元贝塞尔曲线厚度弦长为lh.
|
图 1 单元叶片厚度二维示意图 Fig. 1 Two dimensional schematic diagram of the thickness of a unit blade |
二维叶型构造完成后,采用保形变换法,将二维曲线映射到三维空间,利用三维造型软件进行叶片成形构造.接下来利用成形的叶片和叶轮结构划分单流道流场模型和结构模型,以便于下一步的流场分析和结构校核. 图 2为在各个叶轮厚度系数控制下叶片减薄前后厚度变化示意图.

|
图 2 叶片厚度减薄前后效果图 Fig. 2 Effect map before and after thinning of blade thickness |
液力变矩器内外环厚度的轻量化潜力远远大于叶片.对各个叶轮的内外环进行参数化设计,以探求其厚度变化对其形变,强度和变矩器外特性的影响.这里约定,将叶轮内外环原始厚度时的厚度系数值设为1,将减薄后内环或者外环厚度减到偏移面和边界面相切的状态时的厚度值设为0.则变矩器内外环厚度系数可用以下公式描述:
| $ \begin{array}{l} {\delta _{P{\rm{in}}}} = \frac{{{P_{{\rm{thick\_in}}}} - {P_{{\rm{thick\_inmove}}}}}}{{{P_{{\rm{thick\_in}}}}}}\\ {\delta _{P{\rm{out}}}} = \frac{{{P_{{\rm{thick\_out}}}} - {P_{{\rm{thick\_outmove}}}}}}{{{P_{{\rm{thick\_out}}}}}}\\ {\delta _{T{\rm{in}}}} = \frac{{{T_{{\rm{thick\_in}}}} - {T_{{\rm{thick\_inmove}}}}}}{{{T_{{\rm{thick\_in}}}}}}\\ {\delta _{T{\rm{out}}}} = \frac{{{T_{{\rm{thick\_out}}}} - {T_{{\rm{thick\_outmove}}}}}}{{{T_{{\rm{thick\_out}}}}}}\\ {\delta _{S{\rm{out}}}} = \frac{{{S_{{\rm{thick\_out}}}} - {S_{{\rm{thick\_outmove}}}}}}{{{S_{{\rm{thick\_out}}}}}} \end{array} $ |
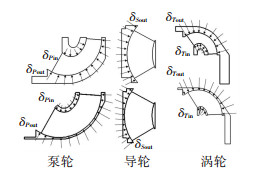
液力变矩器内外环减薄后是由内部开始减薄的,即减薄的同时扩大了流场区域.内环的减薄过程和叶片减薄相似,都是扩大了循环圆的有效区域,而外环的减薄则是直观上放大了循环圆.减薄的过程,同时也是变矩器循环圆的重新设计过程.液力变矩器内外环减薄后简化效果如图 3所示.
|
图 3 液力变矩器内外环厚度减薄前后效果图 Fig. 3 Effect diagram of inner and outer ring thickness of hydraulic torque converter before and after thinning |
流固耦合方法可以用在既涉及固体域求解又涉及流体域求解,而两者又都不能被忽视的问题中.本例中流场对轻量化结构的影响采用单向流固耦合分析,即耦合交界面处的数据传递是单向的.只是把CFD分级计算的结果传递给固体结构分析,但是没有固体结构分析结果传递给流体分析的过程.也就是说,流体分析对结构分析有重大影响,而固体分析的变形对流体变形的影响非常小[10].流固耦合分析要遵循物理守恒定律,对一般流体而言守恒定律可由如下控制方程描述:
质量守恒方程为
| $ \frac{{\partial {\rho _f}v}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}v} \right) = 0, $ |
动量守恒方程为
| $ \frac{{\partial {\rho _f}v}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}v - {\tau _f}} \right) = {f_f}. $ |
式中: t表示时间,ff表示体积力矢量,ρf是流体密度,v是流体速度矢量,τf是剪切力张量,可表示为
| $ {\tau _f} = \left( { - p + \mu \nabla \cdot v} \right)I + 2\mu e. $ |
固体部分的守恒方程可以由牛顿第二定律导出为
| $ {\rho _s}{{\ddot d}_s} = \nabla g{\sigma _s} + {f_s}. $ |
式中:ρs是固体密度,是柯西应力张量;fs是体积力矢量;
同时,流固耦合问题采用分离式解法,即按设定顺序在同一求解器或不同求解器中分别求解流体控制方程和固体控制方程,通过流固交互面把流体域的计算结果传递给固体域.待此时刻的收敛达到要求,进行下一时刻的计算.在流固交界面处,应满足流体与固体应力(τ),位移(d),热流量(q),温度(T)等变量的相等或者守恒,即满足如下4个方程:
| $ \begin{array}{l} {\tau _f}\cdot{n_f} = {\tau _s}\cdot{n_s}, \\ \;\;\;\;{\rm{ }}{d_f} = {d_s}, \\ \;\;\;\;{\rm{ }}{q_f} = {q_s}, \\ \;\;\;\;{\rm{ }}{T_f} = {T_s}. \end{array} $ |
此种求解方法能够最大化地利用已有计算流体力学和计算固体力学的方法和程序,只需对他们做少许修改,从而保持程序的模块化.另外分离解法对内存的需求大幅降低,因而可以用来求解实际的大规模问题.
2.2 周期流道网格生成和流场计算前处理流道壁面条件为无滑移壁面.域交界面的设定主要是泵轮与涡轮、涡轮与导轮和导轮与泵轮之间,存在着不同求解域的数据交互的界面.流场分析中的交互面为泵轮出口面于涡轮入口面、涡轮出口面与导轮入口面、导轮出口面于泵轮入口面.
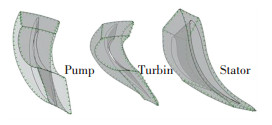
由于采用循环周期边界,每个子求解域都是整个圆周流道的1/Z.其中Z为液力变矩器叶轮的叶片数.3个工作轮的叶片数目不同,也就是循环的周期不同,因此每个周期的周节角不同,在交界面处定义周节角的过渡.工作轮周期流道模型如图 4所示.
|
图 4 工作轮周期流道模型 Fig. 4 Periodic flow channel model of working wheel |
流场求解采用一阶迎风格式,计算精度对结果的准确性有较大的影响,因此在设置计算精度时,压力、流速的均方根值小于10-4,初始迭代次数为600次,在不满足均方根值小于10-4时可以增加迭代次数[11].
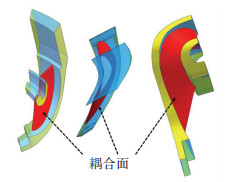
2.3 周期流道网格生成和流场计算前处理单流道变矩器叶片和内外环封闭曲线模型实体化后生成对应的结构校核模型,确保单向流固耦合在流场和结构数据传递时流固耦合面的相互贴合,降低计算误差,以保证流场压力等流场特性数据准确传递.与流场分析一样采用循环周期边界,每个子求解域都是整个叶轮结构的1/Z. 3个工作轮的叶片数目不同,也就是循环的周期不同,需要定义内外环周期面.生成的结构校核模型如图 5所示.
|
图 5 工作轮周期流道结构耦合面 Fig. 5 The coupling surface of the periodic channel structure of a working wheel |
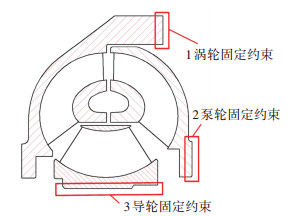
结构计算中对于叶轮的结构约束主要来自于两个方面,其一为周期流道间在循环周期面上的自身结构约束,通过设定周期流道面来模拟整个叶轮的结构特性.其二为实际变矩器整体结构与罩壳、轮毂等固定连接的刚体约束,如图 6所示.图中1处为泵轮与闭锁离合器罩壳固连处,闭锁离合器罩壳视为刚体,所以1处自由度全约束,变形位移为0;图中2处约束为涡轮与涡轮轮毂连接,视为刚体连接;图中3处为导轮与导轮毂固连位置,视为刚体约束.结构校核模型网格化后如图 7所示.
|
图 6 液力变矩器结构约束 Fig. 6 Structural constraints of hydraulic torque converter |

|
图 7 工作轮网格划分 Fig. 7 Grid division of work wheel |
轻量化是汽车行业降低能耗、减少排放的最有效措施之一.其中,结构优化中的尺寸优化和多学科设计优化被作为本次变矩器工作轮厚度优化的主要方法.
叶栅系统参数化后,建立综合叶片及内外环建模、流场分析和结构强度校核的三维优化仿真,其工作流程如图 8所示.

|
图 8 液力变矩器综合优化仿真 Fig. 8 Comprehensive optimization simulation of hydraulic torque converter |
首先,液力变矩器叶栅及内外环三维参数化.基于贝塞尔曲线构造液力变矩器泵轮、涡轮和导轮三维叶形曲线,依据曲线参数化计算方法根据不同的厚度参数生成对应三维叶形.贝塞尔曲线具有端点重合性、逼近性、凸包性、变差减少性和仿射不变性等特性,这些特性使得曲线构造具有明显的几何风格,从而让形状设计更加自然[12-14],该叶片设计方法能够较精确地对原始液力变矩器进行表达[15].分别生成内环与外环封闭曲线,按照指定的厚度参数分别对变矩器入口半径、峰值位置厚度、出口半径进行等比例缩放.并通过实验设计生成多组计算分析叶形组合以进行优化计算.
然后,进行液力变矩器三维流场计算.构造液力变矩器周期流道模型,采用非结构网格进行流场网格划分,稳态流场计算得到对应叶形下的流场特性,并计算液力变矩器原始特性.
最后,液力变矩器单向流固耦合结构强度分析.根据叶形曲线构建叶片三维模型,并与对应生成的叶轮模型布尔运算得到完整叶轮周期三维模型.将叶轮结构模型导入有限元软件中进行非结构四面体网格划分.进行网格划分与前处理后将流场计算得到的流体耦合面上的压力载荷映射传递到对应结构耦合面.并添加约束,求解计算,得到结果.本文通过搭建包含参数化模型的有限元平台,设定优化参数,采用最优拉丁超立方方法对液力变矩器三元件的叶片和内外环进行优化.在每次仿真后提取相应的转矩、转速、最大变形量、最大应力等结果进行综合比较.获取参数改变后对强度和外特性的影响,用以指导以后的变矩器设计工作.
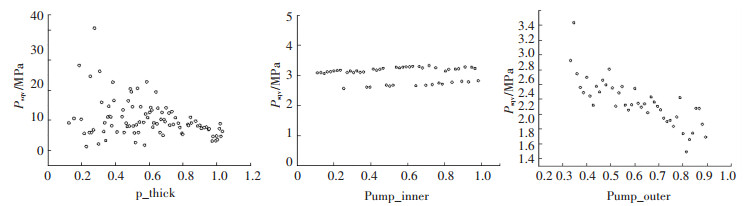
4 液力变矩器优化结果分析 4.1 结构轻量化对强度的影响液力变矩器结构轻量化后,各个部分的变形情况如图 9~图 14所示.泵轮叶片和内环厚度的变化对泵轮工作时的变形影响不大,但是泵轮外环厚度减少时,泵轮在启动工况下所受的应力以及相应产生的应变急剧上升.导轮叶片和外环厚度变化对导轮的形变影响均无明显的变化趋势.和泵轮轻量化对强度的影响规律相反,涡轮的叶片和内环厚度的减小都会导致涡轮在启动工况下所受应力的增加,而涡轮所受应力对其外环变化反而不是很敏感.在轻量化过程中,变矩器所承受的应力始终远远小于最大许用应力.
|
图 9 泵轮厚度参数对强度的影响 Fig. 9 Influence of pump wheel thickness parameters on strength |
|
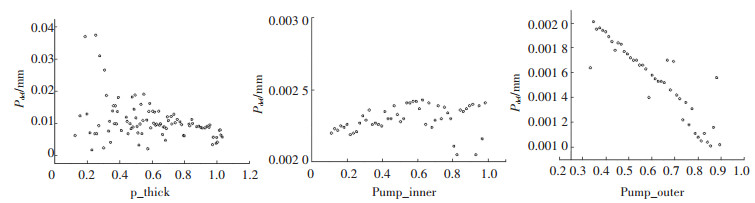
图 10 泵轮厚度参数对变形量的影响 Fig. 10 The influence of the thickness parameters of the pump wheel on the deformation |
|
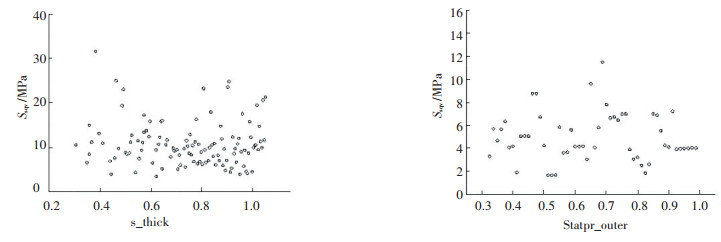
图 11 导轮厚度参数对强度的影响 Fig. 11 The influence of the thickness parameters of the stator wheel on the strength |
|
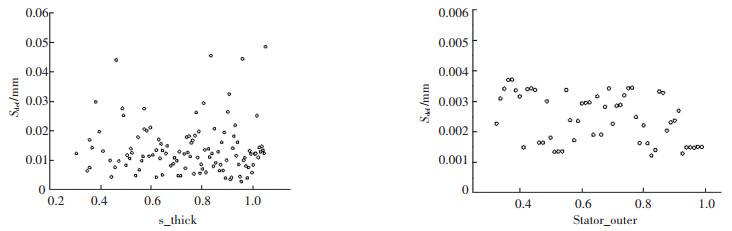
图 12 导轮厚度参数对变形量的影响 Fig. 12 The influence of the thickness parameters of the stator wheel on the strength |
|
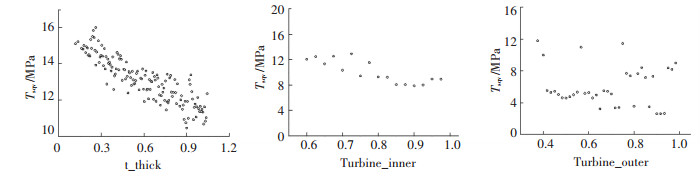
图 13 涡轮厚度参数对强度的影响 Fig. 13 The influence of the thickness of the turbine on the strength |
|
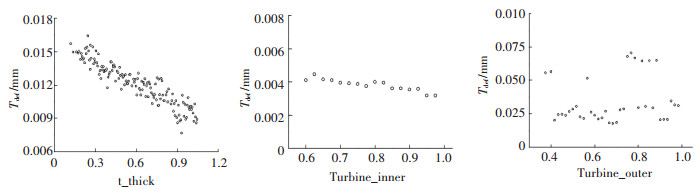
图 14 涡轮厚度参数对变形量的影响 Fig. 14 The influence of the thickness of the turbine on the deformation |
液力变矩器结构轻量化后对起动转矩具有一定的影响.如图 15~图 17所示,在泵轮各个部分厚度减小后,各个工作轮在启动工况下的转矩均有所提升.泵轮叶片厚度减薄后,泵轮转矩处于持续上升状态,速度先急后缓.导轮转矩显示保持稳定,在厚度减到一般后,转矩才开始不断升高.涡轮转矩则是一直比较稳定的上升.泵轮内环厚度减薄后,各个叶轮的转矩先是急剧地升高,在厚度减到50%之后,叶轮转矩基本保持稳定,甚至涡轮和导轮的转矩还有所下降.泵轮外环厚度减薄后,各个叶轮的转矩一直处于上升的趋势.

|
图 15 泵轮叶片厚度参数减小对起动转矩的影响 Fig. 15 Influence of pump impeller blade thickness parameter on starting torque |
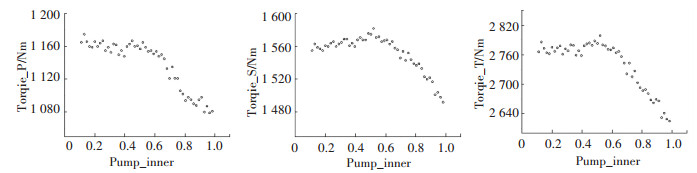
|
图 16 泵轮内环厚度参数减小对起动转矩的影响 Fig. 16 The influence of the inner ring thickness parameter of pump wheel on starting torque |
|
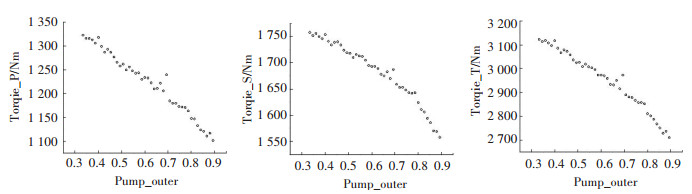
图 17 泵轮外环厚度参数减小对起动转矩的影响 Fig. 17 The influence of the thickness of the outer ring of the pump wheel on the starting torque |
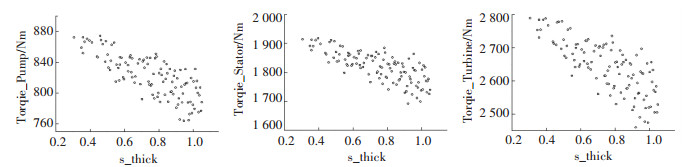
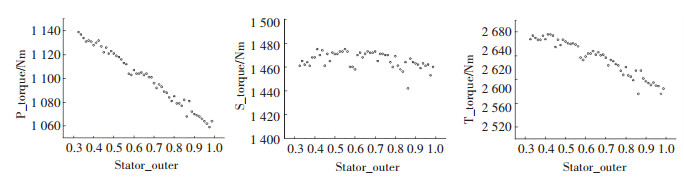
导轮的各个部分厚度按照比例减小之后,工作轮在启动工况下的转矩变化变化有所不同.如图 18~ 图 19所示,在导轮的叶片厚度减小之后,各个工作轮的转矩都处于不断的上升趋势.厚度系数从1.0到0.2, 泵轮、导轮、涡轮转矩分别上升了150 Nm、350 Nm、350 Nm.而在导轮外环厚度减小后,泵轮和涡轮在启动工况下的转矩均处于上升趋势.厚度从1.0到0.3变化过程中,泵轮和导轮的转矩上升幅度分别为100 Nm和200 Nm左右.导轮的转矩只在50 Nm的幅度内波动.在厚度系数为0.5以下后,导轮转矩反而下降.
|
图 18 导轮叶片厚度参数减小对起动转矩的影响 Fig. 18 The influence of stator wheel blade thickness parameter on starting torque |
|
图 19 导轮外环厚度参数减小对起动转矩的影响 Fig. 19 Effect of thickness reduction of stator wheel outer ring on starting torque |
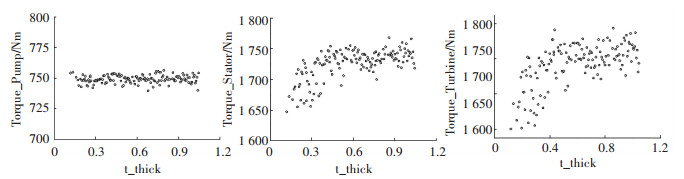
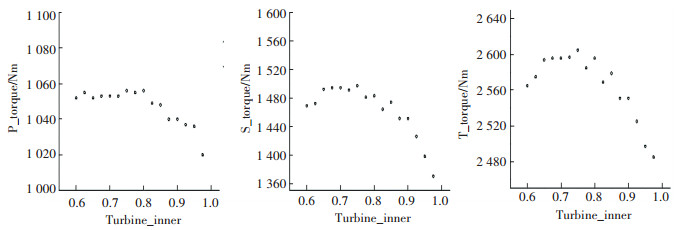
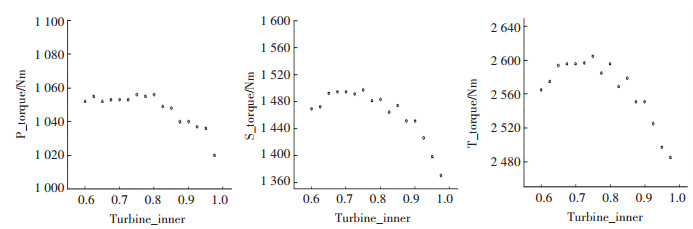
涡轮的各个部分厚度按比例减薄后,工作轮在启动工况下的转矩也产生了相应的变化.在图 20中可见,在涡轮叶片的厚度从1.0减小到0.1时,泵轮在启动工况下的转矩在20 Nm的范围内变化,基本处于稳定状态.导轮和涡轮的转矩随着厚度的减小逐渐下降,并且在0.5厚度以下时的下降趋势比0.5以上时明显的多.如图 21所示,在涡轮内环的厚度减小后,泵轮转矩先是上升,在减到原厚度的0.7以后,保持稳定.而导轮和涡轮的转矩都是先上升,在厚度减到0.7以后开始下降.在图 22中,在涡轮外环的厚度减小以后,泵轮转矩保持稳定,涡轮和导轮的转矩均处于下降的趋势,降幅在200 Nm左右.
|
图 20 涡轮叶片厚度参数减小对起动转矩的影响 Fig. 20 Effect of turbine blade thickness parameter on starting torque |
|
图 21 涡轮内环厚度参数减小对起动转矩的影响 Fig. 21 Effect of turbine inner ring thickness parameter on starting torque |
|
图 22 涡轮外环厚度参数减小对起动转矩的影响 Fig. 22 Effect of thickness reduction of turbine outer ring on starting torque |
液力变矩器循环圆有效直径为400 mm,三叶轮叶片减薄程度均为原来的50%,即减薄系数为0.5,如图 23所示.原始变矩器泵轮、涡轮、导轮的质量分别为17.743kg、8.990 kg、3.636 kg.减薄后叶轮质量分别为11.434 kg、6.597 kg和2.410 kg.减薄程度分别35.56%、26.61%、33.72%.分别设定泵轮转速为1 000 r/min、1 500 r/min和2 000 r/min.涡轮和泵轮的转速比分别为0.9、0.85、0.8、0.75、0.7、0.65、0.6、0.55、0.5、0.4、0.3、0.2、0.1、0.015.其中0.015为模拟变矩器启动工况,保证数据采集的准确性.包箱入口油压0.3~0.5 MPa,出口油压0.2~0.4 MPa.工作油液温度在30~90 ℃变化.

|
图 23 叶片减薄前(左)后(右)变矩器样件 Fig. 23 Blade before thinning (left) rear (right) torque converter sample |
试验后处理2 000 r/min时外特性,并和原型机的实验数据进行对比.
5.2 强度校核仿真对叶片厚度减薄50%的液力变矩器进行单向流固耦合强度校核,3个叶轮的平均应力和平均形变如图 24所示.最大平均应力发生在导轮起动工况下,为14.724 MPa,远小于铸铝合金材料的许用应力.说明减薄后的叶片仍能满足安全要求.

|
图 24 叶片减薄后变矩器强度校核结果 Fig. 24 Checking results of torque converter strength after blade thinning |
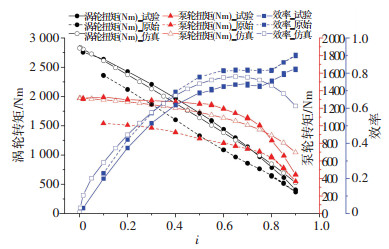
叶片厚度减薄50%后样机2 000 r/min时试验外特性和原样机试验外特性对比较为明显.在图 25中可以看到在变矩器启动工况下,涡轮转矩提升了约220 Nm,比原样机起动转矩提高8.8%,泵轮转矩增加了260 Nm,比原样机提高25.29%.叶片厚度减薄50%的外特性仿真结果与试验较为吻合,并且试验后变矩器无破坏痕迹.验证了减薄仿真的准确性,说明减薄叶片的方式可以明显提高变矩器各个叶轮单位转矩,对设计高功率液力变矩器有一定指导作用.
|
图 25 叶片减薄后变矩器与原样机外特性对比图 Fig. 25 Comparison of external characteristics of torque converter and original sample after blade thinning |
1) 采用单向流固耦合技术和拉丁超立方策略实现了液力变矩器轻量化潜力的探索.结果表明:在0.3~1.0厚度范围内,变矩器可以承受结构大幅度减薄引起的应力增加,而结构减薄导致的流场区域的增加会显著地提高变矩器各叶轮的转矩.
2) 变矩器泵轮外环、导轮内环和涡轮内外环的减薄会使其所承受的转矩呈现出先急剧增加,然后趋于平稳或者开始下降的特征.说明变矩器厚度在减到一定程度后,对提高转矩的效应将变得极小,甚至会出现降低转矩的作用.
3) 厚度减薄50%后的变矩器,仍然满足材料强度的需求并且极大地提高了工作转矩.本文的研究结果对挖掘变矩器的轻量化具有较强的指导意义和参考价值.
| [1] |
魏巍, 闫清东, 朱颜. 液力变矩器叶片流固耦合强度分析[J]. 兵工学报, 2008, 29(10): 1158. WEI Wei, YAN Qingdong, ZHU Yan. Strength analysis of fluid solid interaction field of hydrodynamic torque converter vanes[J]. Acta Armamentarll, 2008, 29(10): 1158. DOI:10.3321/j.issn:1000-1093.2008.10.002 |
| [2] |
刘城.向心涡轮式液力变矩器叶栅系统参数化设计方法研究[D].北京: 北京理工大学, 2015. LIUCheng.Study on parameterized cascade design of radial-turbine torque converter[D].Beijing: Beijing Institute of Technology, 2015. |
| [3] |
刘城, 闫清东, 魏巍. 基于贝塞尔曲线的液力变矩器三维叶片造型方法[J]. 机械工程学报, 2017, 53(10): 201. LIU Cheng, YAN Qingdong, WEI Wei. Three dimensional torque converter blade modelling based on Bezier curves[J]. Journal of Mechanical Engineering, 2017, 53(10): 201. |
| [4] |
刘城, 闫清东, 魏巍. 液力变矩器导轮叶片造型及优化设计[J]. 哈尔滨工业大学学报, 2016, 48(01): 114. LIU Cheng, YAN Qingdong, WEI Wei. Design and optimization of torque converter stator blade[J]. Journal of Harbin Institute of Technology, 2016, 48(01): 114. |
| [5] |
闫清东, 李新毅, 魏巍. 基于多目标优化的液力变矩器叶形角度设计[J]. 华中科技大学学报(自然科学版), 2017, 45(09): 69. YAN Qingdong, LI Xinyi, WEI Wei. Streamline inlet and outlet angles of torque converter blade design based on multi-objective optimization[J]. J.Huazhong Univ.of Sci&Tech.(Natural Science Edition), 2017, 45(09): 69. |
| [6] |
吕倩.基于流固耦合的液力变矩器叶片强度分析与寿命计算[D].南京: 南京航空航天大学, 2014 LÜ Qian.Strength analysis and life calculation of torque converter blades based on fluid-solid interaction[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2014 |
| [7] |
王安麟, 刘伟国, 龙广成. 基于液力变矩器流固耦合的叶片厚度设计方法[J]. 同济大学学报(自然科学版), 2015, 43(04): 599. WANG Anlin, LIU Weiguo, LONG Guangcheng. Design method of blade thickness based on fluid structure interaction of hydrodynamic torque converter[J]. Journal of Tongji University(Natural Science), 2015, 43(04): 599. |
| [8] |
陈凯, 吴光强. 基于遗传算法的液力变矩器与发动机匹配的多目标优化[J]. 汽车工程, 2014(05): 532. CHEN Kai, WU Guangqiang. Genetic algorithm-based multi-objective optimization for the matching of torque convertert with engine[J]. Automotive Engineering, 2014(05): 532. |
| [9] |
WU G Q, WANG L J. Performance optimization of torque converters based on modified 1D flow model[J]. Journal of Donghua Uinversity(English Edition), 2012, 29(5): 380. |
| [10] |
闫清东, 刘博深, 魏巍. 基于动网格的冲焊型液力变矩器流固耦合分析[J]. 华中科技大学学报(自然科版), 2015, 43(12): 37. YAN Qingdong, LIU Boshen, WEI Wei. Fluid structure interaction simulation on torque converter with dynamic mesh[J]. Journal of Huazhong University of Sci.&Tech (Natural Science Edition), 2015, 43(12): 37. |
| [11] |
王福军. 计算流体力学—CFD软件原理[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid mechanics-the principle of CFD software[M]. Beijing: Tinghua Uiversity Press, 2004. |
| [12] |
皮尔, 特莱尔, 赵罡, 等. 非均匀有理B样条[M]. 北京: 清华大学出版社, 2010. PIEGL L, TILLER T, ZHAO Gang. Non uniform rational B-spline[M]. Beijing: Tsinghua University Press, 2010. |
| [13] |
ROGALSKY T, KOCABIYIK S, DERKSEN R. Differential evolution in aerodynamic optimization[J]. Canadian Aeronautics and Space Journal, 2000, 46(4): 183. |
| [14] |
刘荷辉, 虞钢. 自由曲面的二维自适应测量及测球半径的三维补偿[J]. 机械工程学报, 2004, 40(2): 117. LIU Hehui, YU Gang. 2D adaptive measuring for free surface with 3D probe compensation[J]. Chinese Journal of Mechanical Engineering, 2004, 40(2): 117. DOI:10.3321/j.issn:0577-6686.2004.02.025 |
| [15] |
刘城, 闫清东, 魏巍. 基于贝塞尔曲线的液力变矩器三维叶片造型方法[J]. 机械工程学报, 2017, 53(10): 201. LIU Cheng, YAN Qingdong, WEI Wei. Three dimensional torque converter blade modelling based on Bezier curves[J]. Chinese Journal of Mechanical Engineering, 2017, 53(10): 201. |
 2020, Vol. 52
2020, Vol. 52


