2. 广东技术师范大学 机电学院, 广州 510665
2. School of Mechatronic Engineering, Guangdong Polytechnic Normal University, Guangzhou 510641, China
两转一移(2R1T)并联机构因其自由度少、结构简单、制造成本低、适用于多种场合等优势,已引起国内外学者的广泛关注.自Hunt[1]于1983年提出一种构型为3-RPS并联机构以来,2R1T并联机构的构型综合近年来在国内也掀起一股研究热潮[2-9].这类机构目前已成功应用于五轴混联机床的转动中心[10]、姿态调整装置[11]以及坐标测量机[12]等.
速度分析是并联机构运动性能分析和动力学分析的基础,属于微分运动的范畴,常用的分析方法有闭环矢量法、旋量法、影响系数法[13-14]和网络分析法[15]等.前三种方法实质是求解速度映射即雅克比矩阵,一般通过对位置约束方程求导来获得速度映射关系,但在位置约束方程本身就很复杂的情况下,对其进行一阶求导就更加困难.网络分析法以图论为基础,适合多环强耦合并联机构的速度和力分析,对于少自由度并联机构的速度分析通用性不强.
为避开雅克比矩阵和位置导数的求解,本文在文献[9]的基础上,利用Riemann对称空间理论对一种自由度类球面并联机构进行了瞬时速度分析.从机构子链旋量系的对称性出发,建立各子链关节运动的约束,从而简化机构动平台瞬时速度的计算.根据计算和仿真的对比结果来看,角速度误差控制在-0.004~0.006 rad/s以内,线速度误差控制在-0.01~0.015 mm/s以内.采用对称空间理论方法计算瞬时速度用时5.187 s.
1 机构描述及其坐标系建立机构由等半径的动平台和基座以及3个相同的支链组成.在初始位形下,机构的几何简图如图 1所示. 3个支链呈120°均匀分布于基座和动平台之间.与基座相连的转动副记为Bi(i=1, 2, 3),它们的轴线相交于基座中心OB,与动平台相连的转动副记为Di(i=1, 2, 3),它们的轴线相交于动平台中心OD;每条支链上的球副记为Si(i=1, 2, 3),其空间布置为SiOB⊥OBBi, SiOD⊥ODDi, ‖SiOD‖=‖SiOB‖.任意位形下,动平台和基座关于3个球副所组成的平面S1S2S3对称,动平台可以绕对称面内的任意直线发生连续转动,也可以沿两平台中心连线方向进行连续平移. ODS1S2S3OB为一个六面体,平面S1S2S3将此六面体分为上下对称的两部分,OB和OD始终关于S1, S2, S3组成的平面对称.
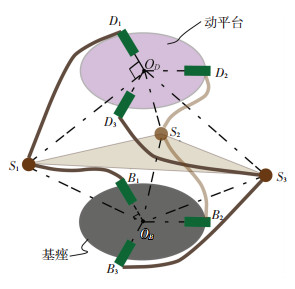
|
图 1 并联机构的几何简图 Fig. 1 Geometric sketch of the parallel mechanism |
建立基坐标系OBxyz(记为{FW})和动坐标系ODuvw(记为{FT}),如图 2所示.初始位形下,基座与动平台平行,各转动副轴线也相互平行. OBOD⊥ S1S2S3交S1S2S3于点M,‖OBM‖=‖ODM‖, ‖OBSi‖=‖ODSi‖=l.
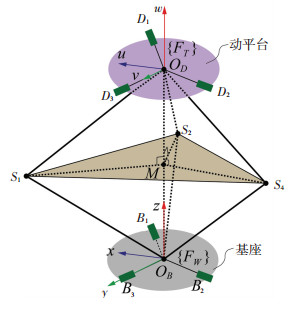
|
图 2 机构坐标系 Fig. 2 Frames of the mechanism |
在基坐标系{FW}中,S1, S2, S3的位置由驱动副Bi的转角αia(i=1, 2, 3)和l决定,可写为
| $ {S_i} = {\mathit{\boldsymbol{R}}_i}{\left[ { - lc{\alpha _{ia}},0,ls{\alpha _{ia}}} \right]^{\rm{T}}}, $ | (1) |
其中
| $ {\mathit{\boldsymbol{R}}_i} = \left[ {\begin{array}{*{20}{c}} {c{\beta _i}}&{ - s{\beta _i}}&0\\ {s{\beta _i}}&{c{\beta _i}}&0\\ 0&0&1 \end{array}} \right],{\beta _i} = \frac{{(6 - 2i){\rm{ \mathsf{ π} }}}}{3},(i = 1,2,3). $ |
对称平面方程ax+by+cz+d=0由各球副的位置坐标确定,满足下式:
| $ \left[ {\begin{array}{*{20}{c}} {{S_1}\left( x \right)}&{{S_1}\left( y \right)}&{{S_1}\left( z \right)}&1\\ {{S_2}\left( x \right)}&{{S_2}\left( y \right)}&{{S_2}\left( z \right)}&1\\ {{S_3}\left( x \right)}&{{S_3}\left( y \right)}&{{S_3}\left( z \right)}&1\\ x&y&z&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} a\\ b\\ c\\ d \end{array}} \right] = 0. $ | (2) |
根据点关于平面对称点的求解原理,容易得到动平台中心OD在{FW}下的位置坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{O_D}}} = - 2ad/A,}\\ {{y_{{O_D}}} = - 2bd/A,}\\ {{z_{{O_D}}} = - 2cd/A.} \end{array}} \right. $ | (3) |
其中,A=a2+b2+c2.展开式(3)即可求得机构的位置正解为
| $ \left\{ \begin{array}{l} {x_{{O_D}}} = \frac{{ - 6l{m_1}{m_4}}}{{m_2^2 + 3m_3^2 + 3m_4^2}},\\ {y_{{o_D}}} = \frac{{ - 2\sqrt 3 l{m_1}{m_2}}}{{m_2^2 + 3m_3^2 + 3m_4^2}},\\ {z_{{O_D}}} = \frac{{ - 6l{m_1}{m_3}}}{{m_2^2 + 3m_3^2 + 3m_4^2}}. \end{array} \right. $ | (4) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{m_1} = {{\rm{c}}_1}{{\rm{c}}_3}{{\rm{s}}_2} + {{\rm{c}}_2}{{\rm{s}}_{13}},}\\ {{m_2} = 2{{\rm{c}}_3}\left( {{{\rm{s}}_1} - {{\rm{s}}_2}} \right) + {{\rm{c}}_2}\left( {{{\rm{s}}_1} - {{\rm{s}}_3}} \right) + {{\rm{c}}_1}\left( {{{\rm{s}}_3} - {{\rm{s}}_2}} \right),}\\ {{m_3} = {{\rm{c}}_2}{{\rm{c}}_3} + {{\rm{c}}_1}\left( {{{\rm{c}}_2} + {{\rm{c}}_3}} \right),}\\ {{m_4} = {{\rm{s}}_{12}} - {{\rm{s}}_3}\left( {{{\rm{c}}_1} + {{\rm{c}}_2}} \right).} \end{array}} \right. $ |
si表示sin αia,ci表示cos αia,s12表示sin(α1a+α2a),s13表示sin(α1a+α3a).
3 瞬时速度分析 3.1 Riemann对称空间理论定义1[16] 设p是Riemann流形M中的一点,如果存在M的一个变换σp:M→M满足下面3个条件:
1) σp是对合的,即σp2=id(id表示恒等变换)但σp≠id;
2) σp是保长变换(即等距变换);
3) p是σp的孤立不动点,即有p的邻域U,使得∀q∈U, σp(q)=pq-1p.
则称M对于p成中心对称,σp叫作关于p的中心对称.
定义2 如果一个Riemann流形M对于M中任意一点p,q都成中心对称,则称M为Riemann对称空间(简称对称空间).
Riemann对称空间的2个典型例子就是欧几里德空间和球体[17].在机构学中存在一种符合Riemann对称的并联机构,它是一类具有对称几何结构支链的并联机构.每条支链可分为相连的两个子支链(C+, C-),如图 3所示.它们的运动副的空间分布满足一种特殊的对称,即可以通过符号相反的一对运动{φ, -φ}使得两个子链重合为一个子链.
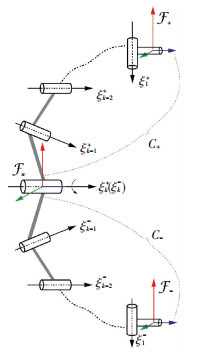
|
图 3 对称并联机构的子支链图 Fig. 3 Riemann symmetric space and equivalent subchains |
如果重合子链的旋量系为ξk, …, ξ1,则原有支链的2个子支链的旋量系为
| $ {\xi _k}(\varphi ), \cdots ,{\xi _1}(\varphi ),{\xi _k}( - \varphi ), \cdots ,{\xi _1}( - \varphi ). $ |
容易得到子链{C++C-}的运动学正解为
| $ f(\alpha ) = {e^{{\xi _1}\left( {{\alpha _1} + {\varphi _1}} \right)}} \cdots {e^{{\xi _k}\left( {{\alpha _k} + {\varphi _k}} \right)}}{e^{{\xi _k}\left( {{\alpha _k} + {\varphi _k}} \right)}} \cdots {e^{{\xi _1}\left( {{\alpha _1} + {\varphi _1}} \right)}} $ |
如果在刚体运动群SE(3)上定义一个反射映射:σp q =pq-1p,则上述子链的正向运动学可以写为
| $ f(\alpha ) = {\sigma _{e{\xi _1}\left( {{\alpha _1} + {\varphi _1}} \right)}}\left( {{\sigma _{e{\xi _2}\left( {{\alpha _2} + {\varphi _2}} \right)}}} \right)\left( { \cdots {\sigma _{e{\xi _k}\left( {{\alpha _k} + {\varphi _k}} \right)}}(e) \cdots } \right). $ |
考虑与f像空间对应的SE(3)的子流形Q.由于f是多个反射的组合,Q必须是SE(3)的对称子空间.
定理1 如果
定理2 如果并联机构的所有支链的约束空间的和正好是TeQ的正交补,则并联机构的任务空间包含Q的关于e的一个邻域.并且每条子链的C+,C-转过的角度正好相反.
本机构任意时刻的运动都可以想象为在一个球体(或椭球体)内进行.动平台与基座始终对称,对称面为过S1, S2, S3的圆面(或椭圆面),如图 4(a)所示.由于球副S可以等效3个转动副R串联,各等效转动副的交点为球副的中心,故将本机构中各支链的球副Si(i=1, 2, 3)局部等效为3个轴线相交于球副中心的转动副R2-, R2+, R3+(R3-),如图 4(b)所示,R2-的轴线沿SiOB方向,R2+的轴线沿SiOD方向,R3-(R3+)的轴线位于对称面S1S2S3内且与连接两平台的转动副轴线同向.这样,机构的每条支链上下两部分可以相互折叠后重合,成为在对称平面里的同一个RRR结构.
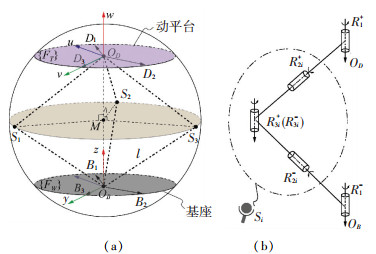
|
图 4 Riemann对称空间及支链等效图 Fig. 4 Riemann symmetric mechanism and equivalent subchains |
至此可以得出结论:本机构是一个具有Riemann对称空间性质的机构,其每条支链经过等效处理后,支链的上下2条子链也是对称的,因此,上子链与动平台的夹角和下子链与基座的夹角相互为负.即转动副Bi, Di的转角关系为:αip=-αia(i=1, 2, 3),其中αia为平面OBBiSi与基座的夹角,αip为平面ODDiSi与动平台的夹角.以B3, D3的转角关系α3p=-α3a为例,如图 5所示.

|
图 5 转动副B3, D3的转角 Fig. 5 Angles of revolute joint B3 and D3 |
构造运动旋量ξi(i=1, 2, 3)与每个关节对应,它表示第i个关节的旋量运动,此时除第i个关节外其他所有关节均固定于αja=0的位置.在研究转动关节时,其运动旋量ξi可表示为
| $ {\mathit{\boldsymbol{\xi }}_i} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_i}}\\ {{\mathit{\boldsymbol{w}}_i} \times {\mathit{\boldsymbol{q}}_i}} \end{array}} \right]_{6 \times 1}}. $ | (5) |
其中,wi∈R3表示旋转轴线上单位矢量,qi∈R3表示轴线上任一点.对移动关节有
| $ {\mathit{\boldsymbol{\xi }}_i} = {\left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{v}}_i}} \end{array}} \right]_{6 \times 1}}. $ | (6) |
下面分别以机构的3种特殊运动为例,推导其运动旋量表达式.
1) 第一种特殊运动:固定S1,S2,让S3自由运动(即锁定α1a, α2a,让α3a做有限转动).此时,机构在初始位形下非奇异,如图 6所示,由于α1a和α2a固定,所以α1p和α2p固定,根据对称性知α1p=-α1a, α2p=-α2a.那么动平台、平面S1D1OD和平面S2D2OD形成一个刚体,动平台将只能绕
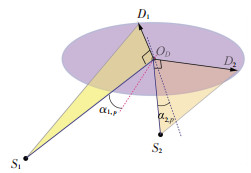
|
图 6 第一种运动:固定S1, S2,让S3自由运动 Fig. 6 Motion pattern Ⅰ: fix S1, S2 and free S3 |
该运动情形下的运动旋量为
| $ {\mathit{\boldsymbol{\xi }}_3} = {\left[ {{{\left( {\frac{{{S_1} - {S_2}}}{{\left\| {{S_1} - {S_2}} \right\|}}} \right)}^{\rm{T}}},{{\left( {{O_D}{S_1} \times \frac{{{S_1} - {S_2}}}{{\left\| {{S_1} - {S_2}} \right\|}}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}. $ | (7) |
2) 第二种特殊运动:固定S1, S3,让S2自由运动(即锁定α1a, α3a,让α2a自由变化).同上面的第一种运动模式类似,由于α1a和α3a固定,则α1p和α3p固定,α1p=-α1a, α3p=-α3a.同理,动平台、平面S1D1OD和平面S3D3OD形成一个刚体,动平台将只能绕
| $ {\mathit{\boldsymbol{\xi }}_2} = {\left[ {{{\left( {\frac{{{S_3} - {S_1}}}{{\left\| {{S_1} - {S_3}} \right\|}}} \right)}^{\rm{T}}},{{\left( {{O_D}{S_3} \times \frac{{{S_3} - {S_1}}}{{\left\| {{S_1} - {S_3}} \right\|}}} \right)}^{\rm{T}}}} \right]^{\rm T}}. $ | (8) |
3) 第三种特殊运动:固定S2, S3,让S1自由运动(即锁定α2a, α3a,让α1a自由变化).同理α2p=-α2a, α3p=-α3a.动平台、平面S2D2OD和平面S3D3OD形成一个刚体,动平台将只能绕
| $ {\mathit{\boldsymbol{\xi }}_1} = {\left[ {{{\left( {\frac{{{S_2} - {S_3}}}{{\left\| {{S_3} - {S_2}} \right\|}}} \right)}^{\rm{T}}},{{\left( {{O_D}{S_2} \times \frac{{{S_2} - {S_3}}}{{\left\| {{S_3} - {S_2}} \right\|}}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}. $ | (9) |
运动旋量系
由于动平台的运动是由3个驱动关节共同作用引起,其运动可以由旋距为零的速度旋量来描述:
| $ \mathit{\boldsymbol{\xi }} = \left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{v}} \end{array}} \right) = \dot \theta \left( {\begin{array}{*{20}{c}} s\\ {r \times s} \end{array}} \right). $ | (10) |
其中,
| $ \mathit{\boldsymbol{\xi }} = {{\dot \alpha }_{1a}}{\mathit{\boldsymbol{\xi }}_1} + {{\dot \alpha }_{2a}}{\mathit{\boldsymbol{\xi }}_2} + {{\dot \alpha }_{3a}}{\mathit{\boldsymbol{\xi }}_3}. $ | (11) |
式中,
选取机构主要参数为:l=100 mm.不失一般性,令驱动关节的角位移分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _{1a}} = \sin ({\rm{ \mathsf{ π} }}t/6),}\\ {{\alpha _{2a}} = \sin ({\rm{ \mathsf{ π} }}t/4),\quad 0 \le t \le 1}\\ {{\alpha _{3a}} = \sin ({\rm{ \mathsf{ π} }}t/3).} \end{array}} \right., $ | (12) |
根据式(1)~(11)对动平台的瞬时速度(包括角速度和线速度)进行ADAMS仿真并与Mathematica计算结果进行对比,结果如图 7所示.由图 7可知,仿真结果与理论计算几乎完全吻合,说明采用对称空间理论分析机构的瞬时速度是正确、可行的.
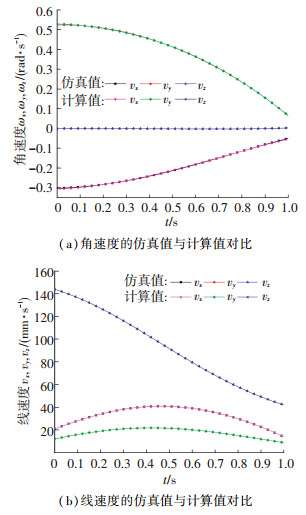
|
图 7 基于对称空间理论的瞬时速度计算与仿真 Fig. 7 Instantaneous velocity computed and simulated by symmetric space theory |
对一种对称结构的3自由度类球面并联机构进行了位置分析.由于位置解析式较为复杂,若通过对其进行一阶求导或推导其雅克比矩阵的方式来获得机构的瞬时速度将是十分困难的事情.为简化计算,利用对称空间理论,从机构子链旋量系的对称性出发,建立各子链关节运动的约束.由于机构有三个驱动关节,每次锁定2个驱动关节,只让1个关节运动,这样就可以得到3种特殊的运动及其运动旋量,这些运动旋量和对应的驱动关节速度的线性组合构成了机构的瞬时速度空间.这个空间的基正好解释了机构的自由度性质为两旋转一平移,物理意义明确,计算方法简单.
| [1] |
HUNT K H. Structural kinematics of in-parallel-actuated robot-arms[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1983, 105(4): 705. DOI:10.1115/1.3258540 |
| [2] |
汪满新, 黄田. 1T2R3自由度并联机构拓扑结构综合[J]. 机械工程学报, 2015, 51(17): 1. WANG M X, HUANG T. Type synthesis of 1T2R 3-DOF parallel mechanism[J]. Journal of Mechanical Engineering, 2015, 51(17): 1. |
| [3] |
杨启志, 訾鹏飞, 曹电锋, 等. 一种基于并联机构的2R-1T运动平台设计[J]. 机械设计与研究, 2012, 28(5): 15. YANG Q Z, ZI P F, CAO D F, et al. Study on a 2R-1T moving platform based on parallel mechanism[J]. Machine Design and Research, 2012, 28(5): 15. DOI:10.3969/j.issn.1006-2343.2012.05.005 |
| [4] |
王飞博, 吴伟峰, 陈祥, 等. 基于运动/力传递特性的1T2R并联机构构型优选[J]. 机械工程学报, 2014, 50(23): 20. WANG F B, WU W F, CHEN X, et al. Optimal type selection of 1T2R parallel mechanisms based on motion/force transmissibility[J]. Journal of Mechanical Engineering, 2014, 50(23): 20. |
| [5] |
付铁, 韩信, 朱涯涯, 等. 基于李群理论的2R1T并联机构构型综合[J]. 北京理工大学学报, 2014, 34(11): 1106. FU T, HAN X, ZHU Y Y, et al. Type synthesis of 2R1T parallel mechanism based on Lie group theory[J]. Transactions of Beijing Institute of Technology, 2014, 34(11): 1106. |
| [6] |
FAN Caixia, LIU Hongzhao, ZHANG Yanbin. Type synthesis of 2T2R, 1T2R and 2R parallel mechanisms[J]. Mechanism and Machine Theory, 2013, 61: 184. DOI:10.1016/j.mechmachtheory.2012.10.006 |
| [7] |
DUAN Zhixiang, YU Jingjun, QU Yufeng, et al. Type synthesis and axodes analysis of a class of special 2R1T parallel mechanisms[C]//Iftomm World Congress. Taiwan: Industrial Technology Research Institute, 2015: 299
|
| [8] |
陈子明, 张扬, 黄坤, 等. 一种无伴随运动的对称两转一移并联机构[J]. 机械工程学报, 2016, 52(3): 9. CHEN Z M, ZHANG Y, HUANG K, et al. Symmetrical 2R1T parallel mechanism without parasitic motion[J]. Journal of Mechanical Engineering, 2016, 52(3): 9. |
| [9] |
张国英, 廖亚军, 梁峰, 等. 一种类球面并联腕部机构及其运动学分析[J]. 机器人, 2017, 39(2): 167. ZHANG Guoying, LIAO Yajun, LIANG Feng, et al. A spheroid parallel wrist mechanism and its Kinematic analysis[J]. Robot, 2017, 39(2): 167. |
| [10] |
于靖军, 裴旭, 宗光华. 机械装置的图谱化创新设计[M]. 北京: 科学出版社, 2014.
|
| [11] |
王永, 姚太克, 周烽, 等. 望远镜副镜的三自由度并联支撑构型研究与运动分析[J]. 光学精密工程, 2013, 21(11): 2860. WANG Yong, YAO Taike, ZHOU Feng, et al. Type synthesis of 3-DOF parallel support system for telescope secondary mirror[J]. Optics and Precision Engineering, 2013, 21(11): 2860. |
| [12] |
LIU Dejun, CHE Rensheng, LI Zifang, et al. Research on the theory and the virtual prototype of 3-DOF parallel-link coordinate-measuring machine[J]. IEEE Transactions on Instrumentation and Measurement, 2003, 52(1): 119. DOI:10.1109/TIM.2003.809487 |
| [13] |
LI Shihua, ZHEN Huang. Instantaneous kinematic characteristics of aspecial 3-UPU parallel manipulator[J]. Chinese Journal of Mechanical Engineering, 2005, 18(3): 376. DOI:10.3901/CJME.2005.03.376 |
| [14] |
淡卜绸, 鲁开讲, 郭旭侠, 等. 基于影响系数法的平面3RRR并联机构运动求解研究[J]. 机械设计与制造, 2016(8): 90. DAN Bochou, LU Kaijiang, GUO Xuxia, et al. Analysis on motion-solving and simulation for planar 3RRR parallel mechanism based on influence coefficient method[J]. Machinery Design & Manufacture, 2016(8): 90. DOI:10.3969/j.issn.1001-3997.2016.08.024 |
| [15] |
黄田, 李江, 曾子平, 等. 空间机构运动学的网络分析方法[J]. 天津大学学报(自然科学与工程技术版), 1995(1): 1. HUANG Tian, LI Jiang, ZENG Ziping, et al. Kinematics of multi-loop spatial kinematic chains using network analysis[J]. Journal of Tianjin University(Natural Science and Engineering Technology Edition), 1995(1): 1. |
| [16] |
孟道骥, 史毅茜. Riemann对称空间[M]. 天津: 南开大学出版社, 2005.
|
| [17] |
OSIPOVA D. Symmetric submanifolds in symmetric spaces[J]. Differential Geometry & Its Applications, 2002, 16(3): 199. |
 2020, Vol. 52
2020, Vol. 52


