2. 兰州理工大学 能源与动力工程学院,兰州 730050;
3. 舜宇光学科技有限公司,浙江 宁波 315400
2. School of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China;
3. Sunny Optical Technology CO., LTD, Noingbo 315400, Zhejiang, China
轴承的运行状态对整台设备的精度、可靠性和寿命都有影响,其性能的退化或失效会影响整机性能,甚至导致设备非计划停机,严重的还会造成巨大的经济损失和人员伤亡[1]. 《国家中长期科学和技术发展规划纲要(2006年-2020年)》列出的16项重大专项中,精密机床、高速机车等重大核心零部件之一就是轴承,它对整个设备制造业的发展起着举足轻重的作用[2].为了预测滚动轴承早期故障,降低因轴承故障导致的损失,就必须要解决故障轴承的振动机理及其振动特性这一基础性问题.因此, 开展滚动轴承故障动力学建模并对其进行分析研究具有重大的工程应用价值和现实意义[3].
在轴承故障诊断研究中,学者们较多地关注轴承的单故障诊断及其振动响应特性[4-8],而对复合故障诱发机理的研究较少.实际运行中,裂纹、凹坑和剥落等轴承故障[7-8]往往同时出现或先后联级发生,将会产生群故障或多点复合故障[3].
为了从机理上研究清楚复合故障所激励的振动响应,学者们建立了动力学模型来模拟和分析内、外圈表面同时存在单点或多点故障(即复合故障)所激励的振动响应. Patel等[9-10]分析了内、外圈表面存在单点和复合故障的深沟球轴承的振动特性,建立了6自由度动力学模型,分别研究了轴承内、外圈表面存在单故障和多故障的振动响应特性;另外针对深沟球轴承复合故障所诱发的振动问题,推导出了两个连续脉冲之间的时间延迟方程. Yaqub等[11]考虑了故障的位置分布对轴承振动特性的影响,建立了一种可模拟复合故障的动力学模型.朱永生等[12]利用Lempel-Ziv量化轴承振动信号特性,建立了一种6自由度动力学模型,探究了复合故障对轴承振动响应的影响.董振振等[13]给出了滚珠与故障区域之间的撞击力计算公式,模拟了多点故障产生的冲击信号之间耦合的现象. Yuan等[14]构建了一种新型轴承系统的多体动力学模型,研究了复合缺陷的演变过程,分析了缺陷演化对振动响应特性的影响. Mohammadi等[15]基于高频共振技术(HFRT),利用包络检波器找出缺陷频率谐波(ADFH),检测轴承的复合缺陷. Koulocheris等[16]将被污染的油脂填充于滚动轴承中,利用振动分析方法来检测轴承的磨损,并验证了该方法能有效识别出复合故障. Tang等[17]提出了一种基于AMCKD诊断复合故障轴承的方法,从复合故障振动信号中分离出与单点故障相关的信号分量,通过对所获得的单故障信号进行调制解调,识别故障类型. Pandya等[18]利用小波分解和希尔伯特变换的自适应算法,从振动信号中提取轴承故障特征分量,研究了复合故障引起的非线性动态响应问题. Singh等[19]提出了一种CNN-CMF-EEMD复合方法,可有效解决轴承元件间复杂的非线性耦合问题,更容易提取和识别轴承复合故障特征.
尽管国内外众多学者已经开展了对复合故障轴承振动响应特性的研究,但轴和轴承座与轴承之间的耦合激励、时变位移激励等因素的存在,使得轴承系统的建模和仿真都相对比较困难,因此国内外许多研究人员仅针对影响轴承振动响应的简化模型进行了研究,并没有综合考虑多个因素对故障轴承振动的共同影响.针对该问题,本文基于内、外圈同时存在单点故障,建立了深沟球轴承-轴承座系统4自由度复合故障动力学模型,考虑轴和轴承座与轴承之间的耦合激励、时变位移激励和滚动体滑动等因素的共同影响,探究因复合故障诱发的力和位移激励响应的机理,并通过实验验证了所建模型的正确性.
1 建立复合故障轴承动力学模型 1.1 深沟球轴承建模假设为简化模型,在考虑模型的主要影响因素基础上,设定以下合理的条件对轴承进行建模假设.
1) 滚动体与滚道之间的接触满足Hertz接触理论,忽略接触界面材料的塑性变形.
2) 忽略滚动体数目奇偶对载荷分布的影响.
3) 滚动体均匀分布,由于转速为中低速,忽略滚动体惯性效应、陀螺运动的影响.
4) 针对轴承的早期缺陷,缺陷深度和宽度尺寸远小于滚动体直径,缺陷边缘的曲率半径远小于滚动体的半径.
1.2 简化模型将滚动体与滚道之间的接触简化为弹簧-阻尼系统.系统简化模型如图 1所示.图中A和B分别代表内圈和外圈故障;内圈和轴之间的接触刚度为Ks,阻尼为Cs;外圈和轴承座之间的接触刚度为Kp,阻尼为Cp;滚动体与滚道间的等效接触刚度为Kio.

|
图 1 简化模型示意图 Fig. 1 Simplified model of rolling bearing |
滚动体与内、外滚道的接触刚度计算公式[20]分别为
| $ {K_{{\rm{in}}}} = \frac{{2\sqrt 2 \left( {\frac{E}{{1 - {\sigma ^2}}}} \right)}}{{3{{\left( {\sum {{\rho _{{\rm{in}}}}} } \right)}^{\frac{1}{2}}}}}{\left( {\frac{1}{{\delta _{{\rm{in}}}^*}}} \right)^{\frac{3}{2}}}, $ | (1) |
| $ {K_{{\rm{ou}}}} = \frac{{2\sqrt 2 \left( {\frac{E}{{1 - {\sigma ^2}}}} \right)}}{{3{{\left( {\sum {{\rho _{{\rm{ou}}}}} } \right)}^{\frac{1}{2}}}}}{\left( {\frac{1}{{\delta _{{\rm{ou}}}^*}}} \right)^{\frac{3}{2}}}. $ | (2) |
式中:E为弹性模量,σ为泊松比,
滚动体与滚道间的等效接触刚度Kio[20]为
| $ {K_{{\rm{io}}}} = \frac{1}{{{{\left( {\frac{1}{{{K_{{\rm{in}}}}\frac{2}{3}}} + \frac{1}{{{K_{{\rm{ou}}}}\frac{2}{3}}}} \right)}^{1.5}}}}. $ | (3) |
通过Pro/E软件建立轴和轴承座的三维模型,将其导入ABAQUS软件中进行有限元分析和计算.轴和轴承内圈之间的接触刚度为Ks,轴承外圈和轴承座之间的接触刚度为KP.
1.4 时变位移时变位移由两部分组成:一部分是由轴承变刚度振动引起的时变径向变形,另一部分是由轴承缺陷引起的时变位移.
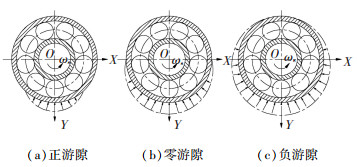
1.4.1 轴承变刚度振动引起的时变径向变形模型中主要考虑深沟球轴承承受径向载荷.承受载荷的滚动体数量会随着滚动体方位角的变化而改变,且由于轴承径向游隙的存在,组件的刚度会发生周期性的变化,轴承会产生变刚度振动.图 2所示为游隙与轴承载荷分布的情况,本文考虑正游隙下轴承承受的径向载荷.
|
图 2 不同游隙下的滚动轴承载荷分布 Fig. 2 Load distribution of rolling bearing under different clearance |
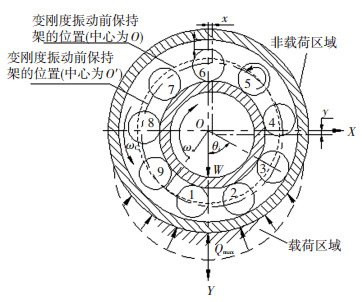
轴承的变刚度振动会引起轴承系统水平方向和竖直方向上位移的变化,如图 3所示,规定向右、向下分别是X、Y轴的正方向,逆时针方向为角度的正方向.保持架的速度为
|
图 3 滚动轴承的变刚度振动 Fig. 3 Varying compliance vibration of rolling bearing |
| $ {w_{\rm{c}}} = \left( {1 - \frac{{{d_{\rm{b}}}}}{{{D_{\rm{m}}}}}} \right)\frac{{{w_{\rm{s}}}}}{2}, $ | (4) |
式中:db是滚动体直径,Dm是轴承节径,ws是轴的转速.
第i个滚动体在时刻t的方位角为
| $ {\theta _i} = \frac{{2{\rm{ \mathsf{ π} }}\left( {i - 1} \right)}}{Z} + {w_{\rm{c}}}t + {\theta _0},\left( {i = 1,2, \ldots ,Z} \right). $ | (5) |
式中:Z是滚动体数量,i是滚动体编号,θ0是编号为1的滚动体相对于Y轴的初始角位置.
根据图 3所示的几何位置关系,得到径向变形δγ为
| $ \begin{array}{l} {\delta _\gamma } = \left( {{x_{\rm{s}}} - {x_{\rm{p}}}} \right)\sin {\theta _i} + \left( {{y_{\rm{s}}} - {y_{\rm{p}}}} \right)\cos {\theta _i} - {C_\gamma },\\ \;\;\;\;\;\;\;\;\;\left( {i = 1,2, \ldots ,Z} \right), \end{array} $ | (6) |
式中:xs和ys是轴的位置坐标,xP和yP是轴承座的位置坐标,Cγ是径向游隙.
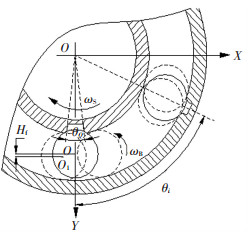
1.4.2 轴承缺陷引起的时变位移轴承故障类型为剥落故障,为了便于计算接触刚度和建立动力学方程,将故障简化为位于滚道中央的长方形的坑.坑的长度为L,宽度为0.1778 mm,深度为0.1778 mm.滚动体从进入缺陷到离开缺陷的过程中会产生附加位移Hf,如图 4、5所示.考虑缺陷尺寸即缺陷长度L远小于滚动体直径db,滚动体与缺陷底部不发生碰撞的情况,则最大附加位移Hmax和附加位移Hf分别如式(7)和式(8)所示:
|
图 4 缺陷引起的时变位移 Fig. 4 Time-varying displacement caused by defects |
| $ {H_{\max }} = \frac{{{d_{\rm{b}}}}}{2} - \sqrt {{{\left( {\frac{{{d_{\rm{b}}}}}{2}} \right)}^2} - {{\left( {\frac{L}{2}} \right)}^2}} , $ | (7) |
式中L是缺陷长度,如图 5(b)所示.
| $ {H_{\rm{f}}} = \left\{ {\begin{array}{*{20}{c}} {{H_{\max }}\sin \left[ {\frac{{\rm{ \mathsf{ π} }}}{{{\theta _q}}}v} \right],0 \le v \le {\theta _q};}\\ {0,{\rm{other}}{\rm{.}}} \end{array}} \right. $ | (8) |
式中:υ=mod(θi, 2π)-φ0, (i=1, 2, ..., Z),θq是缺陷角,φ0是缺陷初始角.
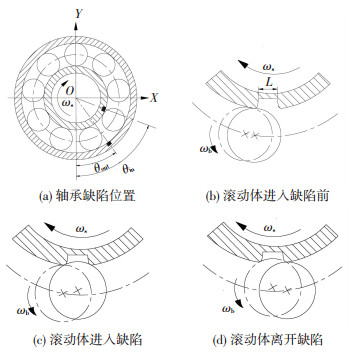
图 5(a)所示为轴承内、外圈故障位置的示意图, 图 5(b)~(d)是以内圈故障为例,滚动体经过缺陷的过程细节图.轴承外圈故障时,滚动体经过缺陷时情况与内圈故障时相似.
|
图 5 缺陷位置和时变位移细节图 Fig. 5 Defect location and time-varying displacement in detail |
由于内圈随主轴一起转动,则内圈故障的缺陷角可以表示为(
| $ \left( {{w_{\rm{s}}}t - \frac{L}{{{D_{\rm{i}}}}}} \right) \le {\theta _i} \le \left( {{w_{\rm{s}}}t + \frac{L}{{{D_{\rm{i}}}}}} \right). $ | (9) |
同理,第i个滚动体位于外圈缺陷区域时应满足
| $ \left( {{\theta _{{\rm{out }}}} - \frac{L}{{{D_{\rm{o}}}}}} \right) \le {\theta _i} \le \left( {{\theta _{{\rm{out }}}} + \frac{L}{{{D_{\rm{o}}}}}} \right), $ | (10) |
式中Do为外滚道直径.
1.5 滚动体的滑动滚动轴承中滚动体的滑动是客观存在的现象,本模型用范围为[0.01 rad, 0.04 rad]的θslip和[-θslip, θslip]上的随机函数Δ来表示轴承运行过程中滚动体的随机滑动特性[21],则第i个滚动体在任意时刻t的方位角为
| $ {\theta _i} = \frac{{2{\rm{ \mathsf{ π} }}\left( {i - 1} \right)}}{Z} + {w_{\rm{c}}}t + {\theta _0} + \left( {\frac{1}{2} - \Delta } \right){\theta _{{\rm{slip}}}}. $ | (11) |
基于Hertz接触理论,滚动轴承点接触载荷-位移关系为[20]
| $ F = K{\delta ^{\frac{3}{2}}}, $ | (12) |
式中K为Hertz接触刚度,δ为径向变形量.
轴承内圈表面有单故障情况下总径向变形可由式(6)变为
| $ \delta = \left( {{x_{\rm{s}}} - {x_{\rm{p}}}} \right)\sin {\theta _i} + \left( {{y_{\rm{s}}} - {y_{\rm{p}}}} \right)\cos {\theta _i} - {C_\gamma } - \beta {H_{\rm{i}}}. $ | (13) |
轴承外圈表面有单故障情况下总径向变形可由式(6)变为
| $ \delta = \left( {{x_{\rm{s}}} - {x_{\rm{p}}}} \right)\sin {\theta _i} + \left( {{y_{\rm{s}}} - {y_{\rm{p}}}} \right)\cos {\theta _i} - {C_\gamma } - \beta {H_{\rm{o}}}. $ | (14) |
轴承表面有复合故障(内、外圈表面各同时含有一个故障)情况下总径向变形可由式(6)变为
| $ \delta = \left( {{x_{\rm{s}}} - {x_{\rm{p}}}} \right)\sin {\theta _i} + \left( {{y_{\rm{s}}} - {y_{\rm{p}}}} \right)\cos {\theta _i} - {C_\gamma } - \beta {H_{{\rm{i}} + {\rm{o}}}}, $ | (15) |
式中:Hi为滚动体经过内圈故障时的附加位移,Ho为滚动体经过外圈故障时的附加位移,Hi+o为滚动体经过复合故障时的附加位移,Hi+o=Hi+Ho.
滚动体与内、外滚道之间的非线性赫兹接触力与滚动体是否位于载荷区域有关.如图 3所示,当滚动体位于非载荷区域时,认为滚动体与滚道不接触,只有当滚动体位于载荷区域时才会受到力的作用.因此引入Dirac函数判断滚动体是否进入载荷区域,只有当δ大于零时滚动体与内、外滚道之间才有Hertz接触力.
根据Hertz接触理论,滚动轴承内、外圈总非线性赫兹接触力F为
| $ F = \sum\limits_{i = 1}^Z {{K_{{\rm{io}}}}} \beta {\delta ^{\frac{3}{2}}}, $ | (16) |
其中,β表示为
| $ \beta = \left\{ {\begin{array}{*{20}{l}} {1,\delta > 0;}\\ {0,\delta \le 0.} \end{array}} \right. $ | (17) |
在水平、竖直方向的分量Fx、Fy分别为
| $ {F_x} = \sum\limits_{i = 1}^Z {{K_{{\rm{io}}}}} \beta {\delta ^{\frac{3}{2}}}\sin {\theta _i}, $ | (18) |
| $ {F_y} = \sum\limits_{i = 1}^Z {{K_{{\rm{io}}}}} \beta {\delta ^{\frac{3}{2}}}\cos {\theta _i}. $ | (19) |
根据牛顿第二定律,建立了复合故障滚动轴承动力学模型,其动力学方程为式(20)~(23).
| $ {M_{\rm{s}}}{{\ddot X}_{\rm{s}}} + {C_{\rm{s}}}{{\dot X}_{\rm{s}}} + {K_{\rm{s}}}{X_{\rm{s}}} + {F_x} = {W_x}, $ | (20) |
| $ {M_{\rm{s}}}{{\ddot Y}_{\rm{s}}} + {C_{\rm{s}}}{Y_{\rm{s}}} + {K_{\rm{s}}}{Y_{\rm{s}}} + {F_y} = {W_y}, $ | (21) |
| $ {M_{\rm{p}}}{{\ddot X}_{\rm{p}}} + {C_{\rm{p}}}{{\dot X}_{\rm{p}}} + {K_{\rm{p}}}{X_{\rm{p}}} - {F_x} = 0, $ | (22) |
| $ {M_{\rm{p}}}{{\ddot Y}_{\rm{p}}} + {C_{\rm{p}}}{{\dot Y}_{\rm{p}}} + {K_{\rm{p}}}{Y_{\rm{p}}} - {F_y} = 0. $ | (23) |
其中,Wx、Wy分别为水平方向和竖直方向上滚动轴承系统的外加载荷.
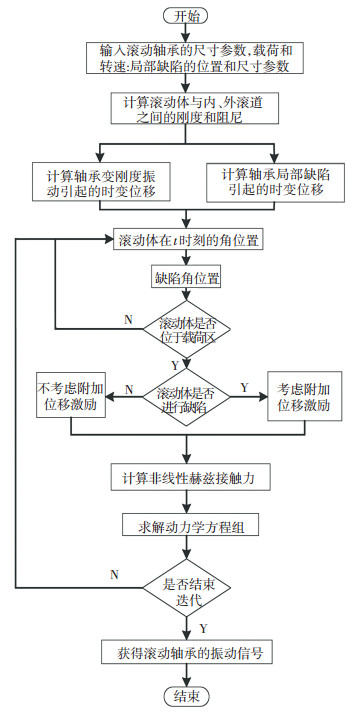
3 模型求解及验证设定X轴和Y轴方向上的初始位移为Xs=10-6 m,Xp=10-6 m和Ys=10-6 m,Yp=10-6 m,初速度为0 m/s,载荷Wx=500 N,Wy=0 N,步长设定为1×10-6.采用龙格库塔方法求解方程(20)~(23), 模型求解过程如图 6所示.
|
图 6 模型求解流程图 Fig. 6 Flow chart of model solution |
采用凯斯西储大学(Case Western Reserve University)的故障轴承实验数据和董振振[13]的实验结果来验证本模型的正确性.
实验所用轴承为SKF 6205深沟球轴承,该轴承具体参数见表 1. 表 2所示为西储大学实验时SKF 6205深沟球轴承在1750 r/min时转频(fs)、内滚道故障频率(fbpi)、外滚道故障频率(fbpo)、滚动体频率(fb)、保持架频率(fc)计算的数值.
| 表 1 SKF 6205深沟球轴承参数 Tab. 1 Parameters of deep groove ball bearing SKF 6205 |
| 表 2 转频、内外圈故障频率、滚动体、保持架故障频率值 Tab. 2 Values of fault frequency for rotating frequency, inner and outer race, ball, and cage in 1750 r/min Hz |
实验和模型研究的轴承故障类型均为剥落故障.对于实验数据采用包络分析的方法得到故障特征频率及相关信息,先通过Protrugram[22]方法得到中心频率和带宽,再利用带通滤波器和低通滤波器将调制的故障信号从原始信号中分离出来,对信号进行平方包络和傅里叶变换,得到解调后信号的时域和频域图.
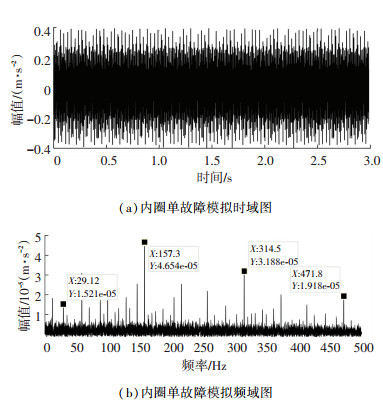
3.1 内圈局部单故障轴承振动响应当主轴转速为1750 r/min,缺陷尺寸为0.5334 mm时,内圈含单故障轴承的模拟和实验振动响应分别如图 7和图 8所示.
|
图 7 轴承内圈单故障模拟时域及频域图 Fig. 7 Simulation time domain and frequency domain of bearing inner race with single fault |
|
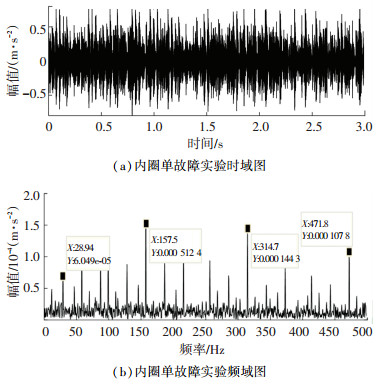
图 8 轴承内圈单故障实验时域及频域图 Fig. 8 Experimental time domain and frequency domain of bearing inner race with single fault |
从图 7和图 8中可以看出,模型仿真信号在时域上存在周期性冲击现象;在频域图上转频29.12 Hz、特征缺陷频率157.3 Hz及其倍频成分清晰可见.实验的内圈故障轴承信号在时域上同样存在明显的周期性冲击现象;在频域上转频28.94 Hz、特征缺陷频率157.5 Hz及其倍频成分清晰可见.比较图 7和图 8中的数据,发现模型仿真数据与实验数据基本吻合,具有较高的准确性,故本模型可用于内圈局部单故障轴承振动响应特性的分析与研究.
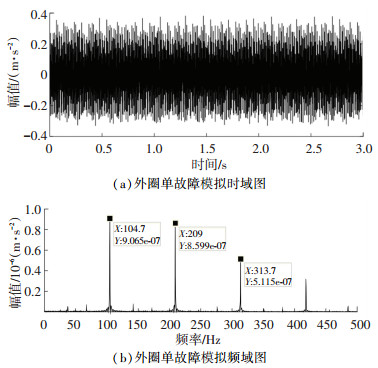
3.2 外圈局部单故障轴承振动响应当主轴转速为1 750 r/min,缺陷尺寸为0.533 4 mm时,外圈含单故障轴承的模拟和实验振动响应分别如图 9和图 10所示.
|
图 9 轴承外圈单故障模拟时域及频域图 Fig. 9 Simulated time domain and frequency domain of bearing outer race with single fault |

|
图 10 轴承外圈单故障实验时域及频域图 Fig. 10 Experimental time domain and frequency domain of bearing outer race with single fault |
从图 9和图 10中可以看出,模型仿真信号在时域上存在较明显的周期性冲击现象;在频域上特征缺陷频率104.7 Hz及其倍频成分清晰可见.试验的外圈故障轴承信号在时域上同样存在较明显的周期性冲击现象;在频域上特征缺陷频率104.8 Hz及其倍频成分清晰可见.比较图 9和图 10中的数据,发现模型仿真数据与试验数据基本吻合,具有较高的准确性,故本模型可用于外圈局部单故障轴承振动响应特性的分析与研究.
从图 7~图 10中可以看出,时域上,模拟和实验的单故障轴承信号都具有周期性冲击现象,内圈与外圈相比其周期性冲击现象更明显,振幅更大.在频域上,模型内圈单故障模拟频域图中转频、故障特征频率及其倍频清晰可见,模型外圈单故障模拟频域图中故障特征频率及其倍频清晰可见;实验内圈单故障频域图中转频、故障特征频率及其倍频和边频带清晰可见,外圈单故障频域图中转频、故障特征频率及其倍频清晰可见.
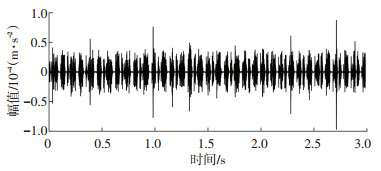
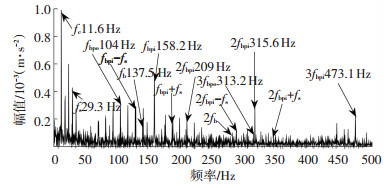
3.3 轴承复合故障轴承振动响应当主轴转速为1750 r/min,缺陷尺寸为0.5334 mm时,内、外圈各同时含一个故障即复合故障时轴承的振动响应,分别如图 11和图 12所示.从图 12中可以看出,轴承复合故障模型模拟频域图中转频、特征缺陷频率及其二倍频、三倍频成分和它们周围的边频带清晰可见.
|
图 11 轴承复合故障模拟时域图 Fig. 11 Simulated time domain of bearing with compound fault |
|
图 12 轴承复合故障模拟频域图 Fig. 12 Simulatied frequency domain of bearing with compound fault |
通过图 12可以看出,本模型模拟的特征频率成分和表 2中得到的理论特征频率数值误差在2%以内,有较好的吻合度.误差产生的原因与预紧力、滚动体滑动等因素有关.
通过观察、对比图 7~图 12,可以清晰地看出滚动轴承内、外圈各包含一个故障(复合故障)时,其频率成分与单故障相比较,其幅值增大,复合故障的振动响应是由内、外圈单故障的振动响应耦合作用的结果,这与董振振的实验结论[13]相一致,如图 13所示,董振振通过实验验证了轴承复合故障信号是单点故障信号耦合作用的结果.故本文所建复合故障滚动轴承动力学模型具有一定的可靠性与正确性.
4 复合故障滚动轴承振动特性分析 4.1 缺陷尺寸对复合故障轴承振动的影响轴承在工作运行中会产生裂纹、点蚀和凹坑等局部缺陷[7-8],且缺陷的尺寸会不断增大,导致轴承产生异常的振动,引起振动频率和幅值的变化.故障的形貌特征与其激励的冲击响应之间有一定的关系,故研究缺陷尺寸对揭示振动特性有重大的意义.
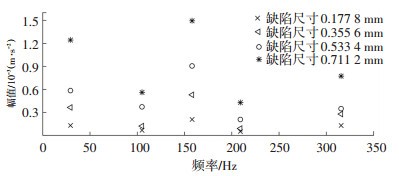
图 14是在轴承转速1 750 r/min,外部载荷500 N的情况下,剥落缺陷尺寸分别为0.177 8、0.355 6、0.533 4、0.711 2 mm的轴承振动响应情况.从图 14中可观察出,随着缺陷尺寸由0.177 8 mm增大到0.711 2 mm时,相对应的故障特征频率及其倍频成分的频率值没有发生改变,但其所对应的加速度幅值呈上升趋势,轴承振动冲击愈加强烈,表现在加速度幅值的增大.这是由于轴承缺陷尺寸增大导致系统内部激励力的增加,表现为振动幅值的增大.
|
图 14 不同缺陷尺寸模拟信号频率幅值趋势图 Fig. 14 Simulated frequency domain under different defect size |
设备在运行过程中,转速的大小对于轴承系统的稳定性有着极大的影响,故研究复合故障轴承在不同转速条件下的振动响应是十分必要的.考虑到在频域上能直观的分析不同转速下振动信号的变化情况,而在时域上观察仅能看到故障信号的冲击现象,故在分析转速对振动的影响时本文仅考虑振动信号在频域上的变化.
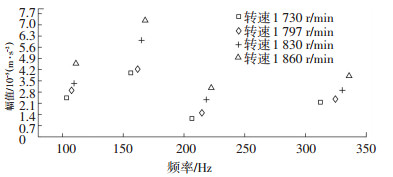
图 15是在缺陷尺寸0.355 6 mm,载荷500 N的情况下,主轴转速分别为1 730、1 797、1 830、1860 r/min时轴承的振动响应情况.由图 15可以观察出,转速的增加会导致内圈的转频、故障特征频率及其倍频成分的频率值增大,对应的加速度幅值呈上升趋势.
|
图 15 不同转速下模拟信号频率幅值趋势图 Fig. 15 Simulated frequency domain under different shaft rotational speed |
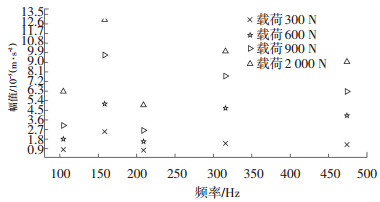
图 16是轴承在转速为1 750 r/min,缺陷尺寸为0.355 6 mm情况下,载荷分别为300、600、900、2 000 N时轴承的振动响应情况.从图 16中可观察出,在一定载荷范围内,随着载荷由300 N增大到2 000 N时,故障特征频率及其倍频成分的频率值没有发生改变,但其所对应的加速度幅值呈上升趋势,表现为轴承振动更加剧烈.
|
图 16 不同载荷下模拟信号频率幅值趋势图 Fig. 16 Simulated frequency domain under different load |
1) 复合故障的振动响应是由内、外圈单故障的振动响应耦合作用的结果,在频谱图中可以明显地分辨出内、外圈故障特征频率及倍频成分,与单故障相比较,其对应的幅值增大.
2) 研究了在不同工况条件下复合故障轴承的振动响应规律,缺陷尺寸增大、转速增高和载荷增强都会使复合故障轴承的振动幅值增大,影响其运行状态,进而加速轴承的失效,降低轴承的使用寿命.
| [1] |
EL-THALJI I, JANTUNEN E. A summary of fault modelling and predictive health monitoring of rolling element bearings[J]. Mechanical Systems & Signal Processing, 2015, 60-61(1): 252. |
| [2] |
王煜, 闫柯, 张进华. 我国高性能滚动轴承基础研究进展[J]. 中国基础科学, 2015, 17(6): 11. WANG Yu, YAN Ke, ZHANG Jinhua. Research progress on the basis of high-performance rolling bearing in China[J]. China Basic Science, 2015, 17(6): 11. |
| [3] |
王国彪, 何正嘉, 陈雪峰, 等. 机械故障诊断基础研究"何去何从"[J]. 机械工程学报, 2013, 49(1): 63. WANG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Future research of mechanical fault diagnosis[J]. Journal of Mechanical Engineering, 2013, 49(1): 63. |
| [4] |
MCFADDEN P D, SMITH J D. Model for the vibration produced by single point defect in a rolling element bearing[J]. Journal of Sound and Vibration, 1984, 96(1): 69. DOI:10.1016/0022-460X(84)90595-9 |
| [5] |
LIU J, SHAO Y. Overview of dynamic modelling and analysis of rolling element bearings with localized and distributed faults[J]. Nonlinear Dynamics, 2018, 93(4): 1765. DOI:10.1007/s11071-018-4314-y |
| [6] |
CUI L, ZHANG Y, ZHANG F, et al. Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis[J]. Journal of Sound and Vibration, 2015, 364(3): 67. |
| [7] |
ASHTEKAR A, SADEGHI F, STACKE L E. Surface defects effects on bearing dynamics[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2010, 224(1): 25. DOI:10.1243/13506501JET578 |
| [8] |
SINGH S, HOWARD C Q, HANSEN C H. An extensive review of vibration modelling of rolling element bearings with localised and extended defects[J]. Journal of Sound and Vibration, 2015, 357(2): 300. |
| [9] |
PATEL V N, TANDON N, PANDEY R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races[J]. Journal of Tribology, 2010, 132(4): 041101-10. DOI:10.1115/1.4002333 |
| [10] |
PATEL V N, TANDON N, PANDEY R K. Vibrations generated by rolling element bearings having multiple local defects on races[J]. Procedia Technology, 2014, 14: 312. DOI:10.1016/j.protcy.2014.08.041 |
| [11] |
YAQUB M F, GONDAL I, KAMRUZZAMAN J. Multiple-points fault signature's dynamics modeling for bearing defect frequencies[C]//Proc.Int.Conf.Contr. 2011: 2729
|
| [12] |
朱永生, 袁幸, 张优云, 等. 滚动轴承复合故障振动建模及Lempel-Ziv复杂度评价[J]. 振动与冲击, 2013, 32(16): 23. ZHU Yongsheng, YUAN Xing, ZHANG Youyun, et al. Modeling of compound fault vibration of rolling bearing and evaluation of Lempel-Ziv complexity[J]. Journal of Vibration and Shock, 2013, 32(16): 23. DOI:10.3969/j.issn.1000-3835.2013.16.005 |
| [13] |
董振振.滚动轴承复合故障机理及振动模型研究[D].哈尔滨: 哈尔滨工业大学, 2015 Dong Zhenzhen. Study on compound fault mechanism and vibration model of rolling bearing[D]. Harbin: Harbin Institute of Technology, 2015 |
| [14] |
YUAN X, ZHU Y S, ZHANG Y Y. Multi-body vibration modelling of ball bearing-rotor system considering single and compound multi-defects[J]. Proceedings of the Institution of Mechanical Engineers Part K-Journal of Multi-body Dynamics, 2014, 228(2): 199. DOI:10.1177/1464419314522372 |
| [15] |
MOHAMMADI A, SAFIZADEH M S. Bearing multiple defects detection based on envelope detector time constant[J]. Journal of Tribology, 2013, 135(1): 011102-11. DOI:10.1115/1.4007806 |
| [16] |
KOULOCHERIS D, STATHIS A, COSTOPOULOS T, et al. Wear and multiple fault diagnosis on rolling bearings using vibration signal analysis[J]. International Journal of Engineering Science Invention, 2014, 3(4): 11. |
| [17] |
TANG G, WANG X, HE Y. Diagnosis of compound faults of rolling bearings through adaptive maximum correlated kurtosis deconvolution[J]. Journal of Mechanical Science & Technology, 2016, 30(1): 43. |
| [18] |
PANDYA D H, UPADHYAYA S H, HARSHA S P. Nonlinear dynamic analysis of high speed bearings due to combined localized defects[J]. Journal of Vibration & Control, 2013, 20(15): 2300. |
| [19] |
SINGH S K, KUMAR S, DWIVEDI J P. Compound fault prediction of rolling bearing using multimedia data[J]. Multimedia Tools & Applications, 2017, 76(18): 1. |
| [20] |
HARRIS T A, KOTZALAS M N. Rolling bearing analysis essential concepts of bearing technology(fifth edition)[M]. Taylor & Francis, 2006.
|
| [21] |
剡昌锋, 康建雄, 苑浩, 等. 考虑弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励动力学建模[J]. 振动与冲击, 2018, 37(5): 56. YAN Changfeng, KANG Jianxiong, YUAN Hao, et al. Dynamics modeling of displacement excitation in rolling element bearing system with local defect bearings under elasto-hydrodynamic lubrication and slipping conditions[J]. Journal of Vibration and Shock, 2018, 37(5): 56. |
| [22] |
FAN Zhiqi. Vibration-based condition monitoring in planetary gearbox via using an internal sensor[D]. Sydney: The University of New South Wales, 2015
|
 2020, Vol. 52
2020, Vol. 52



