2. 吉林大学 汽车仿真与控制国家重点实验室,长春130022
2. State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130022, China
侧窗的清晰度对保证汽车驾驶的安全性和舒适性有着重要作用[1].汽车在大雨中行驶,雨水在侧窗玻璃上积聚形成的水膜或者水流,会严重阻碍驾驶员视野.因此,在汽车设计过程中,控制车身表面的雨水十分重要.
根据污染源的不同,汽车外部水管理主要分为三个研究方面:表面水流、自身溅水污染以及外车溅水污染[2-3].汽车在雨天行驶时,雨水在车身表面的分布和运动情况属于表面水流[4].传统的汽车外部水管理问题在汽车设计的后期才能被发现,难以满足新车型开发周期及成本的需要.国外有学者采用数值模拟的方法解决此类问题[5]. Kenneth J. Karbon等人在计算稳定流场的基础上,运用多相流方法模拟雨水在车身表面的流动状态,并通过实验初步验证了数值模拟的可行性[6-7]. Nicolas Kruse等人在此基础上将DPM模型与欧拉液面模型结合,完善液膜分离模型,考虑壁面的局部湿润条件和液面的局部力平衡,改进气液、气固和液液之间相互作用的计算,提高了计算的准确性[8]. Filipe Fabian Buscariolo等利用VOF方法进行多相流计算,明确雨水从车顶流向水槽的路径,避免乘客开窗时被雨水淋湿[9]. Adrian P. Gaylard等采用格子玻尔兹曼结合多相流的方法模拟水流在A柱和侧窗上的运动状态,预测A柱溢流发生位置,并用实验验证了仿真结果的可靠性[10].以上学者集中于车身表面水流以及A柱溢流现象的研究,缺少对侧窗水相分布影响因素的研究.
本文针对侧窗水污染问题,应用空气动力学知识和多相流理论,将格子玻尔兹曼方法和拉格朗日方法相结合,分析影响侧窗水污染的因素,在此基础上提出有效的控制措施,探讨不同A柱型面对侧窗清晰度的影响,为后续研究提供一定的理论指导.
1 数值计算理论 1.1 格子玻尔兹曼法格子玻尔兹曼方法是建立在分子运动论和统计力学基础上的一种模拟流场的数值方法.相比于传统的CFD方法,格子玻尔兹曼方法从微观的角度获取流体分子的运动信息,描述分子相互碰撞的统计学行为和规律,是宏观连续模型和微观分子动力学模型之间的介观模型[11].该方法将流体看成许多微小粒子,把空间和时间完全离散,通过流体粒子的迁移和碰撞来描述流动现象,碰撞规则遵循质量、动量和能量守恒定律[12].
格子玻尔兹曼模型由离散速度模型、平衡态分布函数以及分布函数的演化方程三个部分组成[13].本文采用的是D3Q19离散速度模型,其速度结构如图 1所示.

|
图 1 D3Q19模型速度结构图 Fig. 1 Velocity structure of D3Q19 model |
格子玻尔兹曼方法描述的流体粒子位于网格点上并沿着其速度方向进行演化.流体粒子的演化可分解为碰撞和迁移两个过程,碰撞过程为
| $ f_\alpha ^*(r, t) - {f_\alpha }(r, t) = - \frac{1}{t}\left[ {{f_\alpha }(r, t) - f_\alpha ^{{\rm{eq}}}(r, t)} \right], $ |
迁移过程为
| $ {f_\alpha }\left( {r + {\xi _\alpha }{\delta _t}, t + {\delta _t}} \right) = f_\alpha ^*(r, t). $ |
式中:f为概率密度分布函数,τ为松弛时间,feq为平衡态分布函数.
对于D3Q19模型,离散速度ξα的计算如下[14]:
| $ {\xi _\alpha } = \left\{ {\begin{array}{*{20}{c}} {(0, 0), \alpha = 0;}\\ {( \pm 1, 0, 0)c, (0, \pm 1, 0), (0, 0 \pm 1)c, \alpha = 1, 2, \ldots , 6;}\\ {( \pm 1, \pm 1, 0)c, ( \pm 1, 0, \pm 1)c, (0, \pm 1, \pm 1)c, \alpha = 7, 8, \ldots , 18.} \end{array}} \right. $ |
平衡态分布函数feq可表示为
| $ {f^{{\rm{eq}}}} = {\omega _\alpha }\rho \left[ {1 + \frac{{{\xi _\alpha } \cdot u}}{{c_s^2}} + \frac{{{{\left( {{\xi _\alpha } \cdot u} \right)}^2}}}{{2c_s^4}} - \frac{{{u^2}}}{{2c_s^2}}} \right]. $ |
其中:cs为格子声速,cs2=c2/3. ωα为权系数,其值为
| $ {\omega _\alpha } = \left\{ {\begin{array}{*{20}{c}} {1/3, \alpha = 0;}\\ {1/18, \alpha = 1, 2, \ldots , 6;}\\ {1/36, \alpha = 7, 8, \ldots , 18.} \end{array}} \right. $ |
模拟侧窗水相分布时,将雨滴定义为球形颗粒,采用拉格朗日离散相模型模拟,利用求解运动方程单独追踪这些颗粒在流场中的运动轨迹[15].单个雨滴颗粒的运动方程为
| $ \begin{array}{*{20}{l}} {{{\rm{m}}_p}\frac{{{\rm{d}}\overline {{{v}_p}} }}{{{\rm{d}}t}} = \frac{1}{2}{\rho _p}{C_D}|\bar v - \overline {{v_p}} {|^2}{\rm{\pi }}{R^2}\frac{{(\bar v - \overline {{v_p}} )}}{{|\bar v - \overline {{v_p}} |}} + {m_p}\bar g,}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\rm{d}}\overline {{v_p}} }}{{{\rm{d}}t}} = \frac{{{C_p}{Re}{\rm{\pi }}R\mu }}{{4{m_p}}}(\bar v - \overline {{v_p}} ) + \bar g.} \end{array} $ |
式中:v为来流速度,vp为颗粒速度,R为雨滴颗粒的半径,mp为粒子的质量,g为重力加速度,μ为流体动力粘度,ρ为流体密度,CD为雨滴阻力系数,Re为相对雷诺数.其中:
| $ \begin{array}{*{20}{c}} {Re = \frac{{2\rho R\left| {\overline v - \overline {{v_p}} } \right|}}{\mu }}\\ {{C_D} = \frac{{24}}{{Re}}\left( {1 + 0.15 \cdot R{e^{0.657}}} \right) + \frac{{0.42}}{{\left( {1 + 42500 \cdot R{e^{ - 1.16}}} \right)}}.} \end{array} $ |
此外,水滴颗粒间也会发生碰撞合并,在数值模拟时,利用O’Rourke的颗粒块模型将一定数量的水滴颗粒作为一个整体代替单个颗粒的碰撞计算,从而有效减少计算量.利用泰勒类比液滴破碎(TAB)模型模拟颗粒破碎,当水滴颗粒的震荡变形过大时,大液滴将会破碎成小液滴[16].
2 试验与仿真为了验证数值仿真方法的精度和可行性,通过风雨耦合试验平台对某实车进行试验,如图 2所示.试验风速50 km/h,淋雨面积为30 m2, 供水量为0.51 m3/h.仿真风速等同试验风速,设置降雨量为17 mm/h,离散相设置与后续计算中设置一致.将仿真计算得到的侧窗区域液膜厚度分布图与试验结果进行了对比,如图 3所示.结果表明侧窗污染区域和沉积趋势与试验结果存在良好的一致性,仿真方法可靠性较高.

|
图 2 风雨耦合实验平台 Fig. 2 Wind and rain coupled experimental platform |

|
图 3 试验与仿真结果对比 Fig. 3 Comparison between test result and computation results |
DrivAer模型是依据宝马3系和奥迪A4建立的标准模型,具有整车细节,相比Ahmed、MIRA、SAE等简化标准模型更具代表性[17].为更好地体现整车几何细节,采用STL格式划分面网格,将网格弦偏差设置为0.012 5 mm,最大网格尺寸设为15 mm.为控制网格总数,节省计算成本,且能捕捉流场细节,保证仿真结果的精确度和可靠性,对计算敏感区域进行加密,共设置10个VR区(加密区),如图 4所示.

|
图 4 VR区示意图 Fig. 4 Schematic diagram of VR region |
最小VR区的网格尺寸为1.25 mm,网格尺寸随VR区依次向外逐倍增加,最终体网格的分布如图 5所示,网格总数共计8397.36万.

|
图 5 体网格示意图 Fig. 5 Schematic diagram of the volume mesh |
离散相参数主要包括离散相喷射口,初始条件,边界条件等,这些参数的正确设置是准确模拟侧窗水污染的必要条件.为真实模拟雨天环境,本文在汽车前方设置雨滴发射器,如图 6所示,雨滴发射器喷射范围需覆盖整车,考虑前方气流分离以及汽车尾涡的影响,其宽度应大于两倍车宽.本文计算工况为大雨,参数设置如下:设置进入流场的雨量为17 mm/h,雨滴颗粒粘度为0.001 Pa·s,表面张力为0.072 8 N/m2,颗粒密度为1 000 kg/m3,并考虑重力影响,g=9.8 m/s2,雨滴颗粒直径分布服从Gaussian分布,粒子最大半径为3 mm,最小为1 mm.雨滴颗粒在求解过程中考虑碰撞、破碎、飞溅,聚合.雨滴的水平初速度为27.78 m/s,等同于车速.其中:
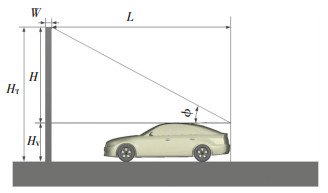
|
图 6 雨滴发射器示意图 Fig. 6 Schematic diagram of the emitter |
| $ {H_{\rm{T}}} = H + {H_{\rm{v}}} = \frac{{L \cdot {V_{\rm{d}}}}}{{{V_{\rm{e}}}}} + {H_{\rm{v}}} $ |
式中:HV为车高;Vd为雨滴竖直方向的最终速度;Ve为车速,即入口的风速.
3.3 边界条件以及求解仿真过程中,针对雷诺数不同的区域,选用不同的计算方法.采用格子玻尔兹曼方法计算自由流区域,采用ABLM边界层模型以及直接模拟方法计算车身近壁面区域,采用非常大涡模拟方法计算尾流区域的小尺寸涡结构[18-19].边界条件如表 1所示.
| 表 1 边界条件设置表 Tab. 1 Boundary condition setting |
水滴与车身表面碰撞时可能会发生粘附、反弹、扩张或者飞溅.粘附、扩张和飞溅都会在车身表面形成液膜,液膜随近壁面气流流动,进而形成水污染.侧窗区域的水污染来自:A柱溢流;来流中夹带的水滴直接撞击侧窗玻璃;后视镜表面脱落的大水滴撞击侧窗玻璃.通过对basic模型计算分析,确定该车的侧窗区域水污染的来源. 图 7为侧窗区域液膜厚度分布,可见basic模型侧窗水污染严重.

|
图 7 液膜厚度分布图 Fig. 7 Distribution of the film thickness |
来流中夹带的雨滴直接撞击车身表面时会形成撞击点,如图 8所示,蓝色点为撞击点.由于A柱附近和侧窗区域存在强烈的涡流,气流在这个区域先分离再附着,雨滴在气流的作用下直接撞击到车窗下方,对驾驶员视野区造成污染较少.

|
图 8 车身表面撞击点示意图 Fig. 8 Schematic diagram of impact point on surface |
图 9为涡速度λ2等值面,能够表达速度在空间上的变化情况,体现大尺度湍流流动.由图 9可知,气流附着在后视镜的迎风面上,在后视镜的边缘产生剪切层分离流动,此处液膜与壁面的接触处会产生液膜流动以及液膜分裂出液滴等复杂物理现象. 图 10为不同时刻后视镜纵向截面上水相分布图,可以发现,随着计算时间的增加,后视镜表面积聚的水膜在强剪切的作用下从后视镜后端边缘脱落,随气流形成环状涡流运动,液滴撞击在侧窗区域后方,并未对驾驶员关键视野区造成影响.

|
图 9 λ2=-50等值面 Fig. 9 Iso suface when λ2=-50 |

|
图 10 后视镜纵向截面水相分布图(Z=0.7 m) Fig. 10 Water phase distribution of mirror longitudinal section(Z=0.7 m) |
液膜的流动取决于表面张力,气流剪切力、壁面摩擦力以及重力之间的平衡关系,其中气流剪切力和重力起主要作用[20].受A柱分离涡结构的影响,近侧窗区域的气流流速明显减小,图 11可知,速度的变化导致车身表面剪切力在5 N/m2的范围内波动. A柱表面剪切力较高,水膜流速较大,挡风玻璃处的水膜在剪切力的推动作用下溢过A柱向侧窗流动,如图 12所示.侧窗区域表面剪切力较小,水膜在重力影响下向下流动,进而影响驾驶员的视野.

|
图 11 表面摩擦力 Fig. 11 Surface friction |

|
图 12 液膜速度 Fig. 12 Film velocity magnitude |
通过上述分析可知,该车型侧窗区域水污染来源于A柱溢流.基于此对basic模型的A柱型面进行分析,如图 13所示,A柱与前挡风玻璃之间的过渡过于平缓,导致水流溢过A柱造成侧窗污染.

|
图 13 basic模型A柱型面 Fig. 13 A-column surface of basic model |
在basic模型的基础上,对A柱型面进行修改,提出了如图 14所示的4种优化方案,其中红色虚线代表basic模型的A柱型面,黑色实线为优化模型的A柱型面.期望获得A柱结构与侧窗水污染面积之间的关系,改善A柱附近流动状态,减少侧窗水污染.

|
图 14 优化方案的A柱型面图 Fig. 14 A-column surface of optimization model |
汽车侧窗区域多为三维复杂曲面,衡量侧窗实际污染面积较为困难,运动图像处理软件,将三维问题转换为二维问题,可有效将侧窗污染面积量化,本文用污染面积像素Rs和区域面积像素Rw的比值Rv来衡量污染程度.
| $ {R_v} = \frac{{{R_s}}}{{{R_w}}} $ |
式中:Rs为侧窗污染区域的像素数,Rw为侧窗区域总像素数.各工况下的污染情况如表 2所示.其中方案2的侧窗水污染面积Rv最小,较basic模型减小了19.2%,车窗视野最好.
| 表 2 水相附着区域面积 Tab. 2 Area of water phase |
各优化方案侧窗区域的液膜厚度分布如图 15所示.与basic模型相比,4种A柱优化型面有效抑制了A柱溢流,减小了侧窗区域水污染面积.为直观分析雨水污染来源,将侧窗区域进行划分为T区、M区和L区,如图 15(a)所示.

|
图 15 各优化方案液膜厚度分布图 Fig. 15 Film thickness distribution of optimization models |
各模型液膜速度图如图 16所示,前挡风玻璃底部水膜速度较低,原因为此处气流分离涡的影响形成速度相对静止区.而前挡风玻璃上方的水膜在高速气流剪切力的作用下向A柱运动,因此A柱交接处水膜速度较大.该模型车顶部缺乏流水槽,汇集在车顶部的水膜在剪切力的作用下流向侧窗,造成T区域水污染.

|
图 16 各优化方案液膜速度图 Fig. 16 Film velocity magnitude of optimization models |
模型4在T区域的污染面积较大,液膜具有向下流动的速度.由图 17可知,相比其他模型,模型4 T区域气流沿着上边梁向侧窗流动,且侧窗区域表面剪切力较小,加之重力的影响作用,因此水膜更易向下流动,损害驾驶员视野.

|
图 17 各优化方案车身表面剪切力及表面流线图 Fig. 17 Surface shear forces and streamlines of optimization model |
车身表面在前挡风玻璃、车顶部与A柱交界处曲率变化较大,水膜在此处汇集,水膜表面张力易受气流剪切力的破坏.从图 18(b)、(c)Z向水相分布图可见,模型2与模型3的水膜在A柱涡的强剪切作用下与车身表面分离,因此M区污染较小.由图 18(a)可见,模型1水膜产生飞溅的同时有一部分会沿着车身表面移动,溢过A柱,造成M区域污染.气流沿模型4A柱型面平滑的流向后方,飞溅现象不明显,A柱型面水膜在气流剪切力的作用下流向侧窗造成M区域污染,如图 16(d)所示.

|
图 18 各优化方案Z向水相分布图(Z=0.97 m) Fig. 18 Water phase distribution of optimization models(Z=0.97 m) |
仅模型4在L区域存在明显侧窗污染,由图 17发现,模型4A柱表面剪切力明显大于其他模型,A柱水膜在高剪切力的作用下向侧窗流动,L区域表面剪切力较小,水膜因重力向下流动,形成L区域污染.
5.3 改进方案对整车阻力的影响为了评估改进方案对整车阻力的影响,对比了basic模型与优化A柱型面后整车阻力系数的的变化,如表 3所示.
| 表 3 不同方案对比 Tab. 3 Comparison of different programs |
由表 3可知,对A柱型面进行优化后,方案1,方案2和方案3的整车阻力系数均有增加,但相对于basic模型,增阻率均在2%之内.方案4阻力系数略微下降,减阻率仅为0.81%.由此可见,A柱型面的改进方案对整车阻力影响较小.
6 结论1) 利用玻尔兹曼与拉格朗日结合的方法对汽车侧窗水污染进行了数值模拟,获得雨水在车身表面的分布以及雨滴在车身表面的撞击点,揭示侧窗水污染产生的机理,为进一步研究提供理论依据.
2) 水膜运动状态主要受剪切力和重力的影响,气流流速和水膜厚度的变化将导致水膜受力失衡,运动流迹改变.
3) 4种A柱改型模型抑制了A柱溢流,减小了侧窗水污染面积,其中模型2作用最显著,侧窗污染面积占38.2%,较basic模型降低了19.2%.
4) 由于本文重点考虑抑制A柱溢流和机理的研究,在A柱型面对噪声影响的方面未兼顾考虑,后续工作中需综合研究.
| [1] |
胡兴军. 汽车空气动力学[M]. 北京: 人民交通出版社, 2014: 89. HU Xingjun. Automotive aerodynamics[M]. BeiJing: China Communication Press, 2014: 89. |
| [2] |
HAGEMEIER T, HARTMANN M, THEVENIN D. Practice of vehicle soiling investigations: A review[J]. International Journal of Multiphase Flow, 2011, 37(8): 860. DOI:10.1016/j.ijmultiphaseflow.2011.05.002 |
| [3] |
ADRIAN P G, KERRY K, DUNCAN A L. Surface contamination of cars: A review[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2017, 231(9): 1160. DOI:10.1177/0954407017695141 |
| [4] |
廖磊.车轮溅水及其对车身表面污染的仿真研究[D].长春: 吉林大学, 2014 LIAO Lei. Numerical research on wheel spray and rela-ted body soiling[D]. Changchun: Jilin University, 2014 |
| [5] |
胡兴军, 姚宏义, 郭鹏, 等. 汽车涉水时轮辐结构对车表水相分布的影响[J]. 哈尔滨工业大学学报, 2017, 49(7): 113. HU Xingjun, YAO Hongyi, GUO Peng, et al. Influence of wheel spokes structure on the distribution of surface water film during the wading of road vehicle[J]. Journal of Harbin Institute of Technology, 2017, 49(7): 113. DOI:10.11918/j.issn.0367-6243.201607124 |
| [6] |
KARBON K J, LONGMAN S E. Automobile exterior water flow analysis using CFD and wind tunnel visualization[R]. SAE Technical Paper, 1998. DOI: https://doi.org/10.4271/980035
|
| [7] |
FOUCART H, BLAIN E. Water-flow simulation on vehicle panels by taking into account the calculated aerodynamic field[R]. SAE Technical Paper, 2005. DOI: https://doi.org/10.4271/2005-01-3572
|
| [8] |
KRUSE N, CHEN K H. Exterior water management using a custom Euler-Lagrange simulation approach[R]. SAE Technical Paper, 2007. DOI: https://doi.org/10.4271/2007-01-0101
|
| [9] |
FILIPE F B, ROBERTO P R, MANTOVANI D, et al. Multiphase Water Flow Simulation of a Vehicle's Roof[R]. Sae Technical Papers, 2014. DOI: https://doi.org/10.4271/2014-36-0256
|
| [10] |
JILESEN J, GAYLARD A, LINDEN T, et al. Update on a-pillar overflow simulation[R]. SAE Technical Paper, 2018. DOI: https://doi.org/10.4271/2018-01-0717
|
| [11] |
CHEN H, CHEN S, MATTHAEUS W H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method[J]. Physical Review A, 1992, 45(8): R5339. DOI: https://doi.org/10.1103/PhysRevA.45.R5339
|
| [12] |
刘耕, 陈涛, 刘震宇. 基于格子-波尔兹曼法的流体能耗求解[J]. 计算力学学报, 2015, 32(3): 378. LIU Geng, CHEN Tao, LIU Zhenyu. Numerical evaluation of viscous energy dissipation of fluid using lattice Boltzmann method[J]. Chinese Journal of Computational Mechanics, 2015, 32(3): 378. |
| [13] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2019. HE Yaling, WANG Yong, LI Qing. Lattice Boltzmann method: theory and applications[M]. Beijing: Science Press, 2019. |
| [14] |
栗怀广.钝体空气动力学的格子玻尔兹曼方法[D].成都: 西南交通大学, 2010 LI Huaiguang. Lattice Boltzmann method for bluff body aerodynamics[D]. Chengdu: Southwest Jiaotong University, 2010 |
| [15] |
MARCHIOLI C, PICCOIOTTO M, SOLDATI A. Influence of gravity and lift on particle velocity statistics and transfer rates in turbulent vertical channel flow[J]. International Journal of Multiphase Flow, 2007, 33(3): 227.DOI: https://doi.org/10.1016/j.ijmultiphaseflow.2006.09.005
|
| [16] |
O'ROURKE P J, AMSDEN A A. A spray/wall interaction submodel for the KIVA-3 wall film model[J]. SAE Transactions, 2000, 281. |
| [17] |
WIESER D, SCHMIDT H J, MULLER S, et al. Experimental comparison of the aerodynamic behavior of fastback and notchback drivAer models[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2014, 7(2014-01-0613): 682. DOI: https://doi.org/10.4271/2014-01-0613
|
| [18] |
LI Y, SHOCK R, ZHANG R, et al. Numerical study of flow past an impulsively started cylinder by the lattice-Boltzmann method[J]. Journal of Fluid Mechanics, 2004, 519: 273. DOI: https://doi.org/10.1017/S0022112004001272
|
| [19] |
DASARATHAN D, JILESEN J, CROTEAU D, et al. CFD water management design for a passenger coach with correlation[R]. SAE Technical Paper, 2016. DOI: https://doi.org/10.4271/2016-01-8155
|
| [20] |
郑梅, 董威, 朱剑鋆, 等. 来流速度对防冰表面溢流水流动换热的影响[J]. 空气动力学学报, 2016, 34(3): 295. ZHENG Mei, DONG Wei, ZHU Jianjun, et al. Influence of free stream velocity on runback water flow and heat transfer on anti-icing surface[J]. Acta Aerodynamica Sinica, 2016, 34(3): 295. DOI:10.7638/kqdlxxb-2015.0219 |
 2020, Vol. 52
2020, Vol. 52


