2. 中国空间技术研究院 通信卫星事业部, 北京100094
2. Institute of Telecommunication Satellite, China Academy of Space Technology, Beijing 100094, China
球头-锥面密封结构易于拆装,且具有良好的密封性能,广泛应用于卫星推进系统的管路连接中,因此,近年来有关其性能的研究开始得到学者们的关注[1-3].周等[3]采用有限元方法计算不同预紧力条件下球面密封结构中密封面间的接触压力及密封宽度,并在此基础上,结合Roth模型建立了分子流状态下球面密封泄漏率计算模型,获得球面密封的泄漏率.韩等[4]采用有限元方法获得不同流体压力作用下球头-锥面间的接触应力及密封宽度,并将上述结果代入基于Roth泄漏模型推导出的考虑应力松弛的泄漏率计算公式中,以计算球头-锥面密封的泄漏率.
应力松弛效应会对材料的性能产生较大影响,进而会对有密封或紧固要求,且长期存放的零部件产生显著影响[5-9].王等[10]采用有限元方法建立了常温下螺栓应力松弛模型,并采用这一模型分析了不同因素影响下螺栓应力随蠕变时间增长的变化规律. Liu等[11]采用试验方法研究了室温环境下钢的蠕变性能,研究结果表明较大的应力、较长的蠕变时间、较低的硬度以及不均匀的微观结构等因素均会增大蠕变应变. Jiang等[12]建立了蒸汽轮机中螺母连接部件的有限元模型,并采用这一模型研究了蠕变效应对螺母连接部件密封性能的影响规律. Mann等[13]建立了螺栓凸缘连接结构的有限元模型,并采用这一模型分析了高温环境下蠕变松弛效应对其性能的影响规律. Silva等[14]采用试验方法研究了提升温度对多种制备方法获得的PTFE垫片蠕变松弛性能的影响. Gordon等[15]采用试验方法分析了新型垫片蠕变松弛的本构模型,并获得填充材料及扭转力等参数对垫片性能的影响规律. Maximov等[16]采用有限元方法分析了室温环境下铝合金材料的蠕变特性,并在此基础上提出了描述残余松弛应力的数学模型,这一模型可以快速确定不同蠕变时间下铝合金材料的残余应力. Mao等[17]采用有限元方法研究了蠕变条件下,凸缘厚度及螺栓预紧力对凸缘密封性能的影响,研究结果表明蠕变效应会对凸缘密封的性能产生显著影响.
以往研究虽然考虑应力松弛效应的影响,但多是在泄漏率计算公式中计入应力松弛效应的影响,而螺母残余预紧应力及球头-锥面间接触应力等参数保持不变的条件下获得的,这必然会对计算结果的精度产生较大的影响.
基于此,本文在球头-锥面有限元模型中计入应力松弛效应的影响,获得螺母残余预紧应力及球头-锥面间接触应力随蠕变时间增长的变化规律,然后基于Roth泄漏模型推导的泄漏率公式计算获得球头-锥面密封泄漏率随蠕变时间增长的变化规律.
1 理论模型球头-锥面密封性能分析主要包含两部分内容:一是建立考虑应力松弛效应的球头-锥面密封性能分析有限元模型;二是基于Roth提出的泄漏模型,推导出适用于球头-锥面密封泄漏性能计算的理论公式.
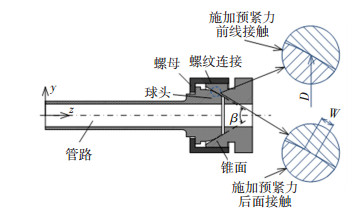
1.1 球头-锥面密封力学分析模型球头-锥面密封结构示意图如图 1所示,其主要由管路、球头、锥面及螺母4部分组成.螺母与锥面之间为螺纹连接,在螺母上施加拧紧力矩时,螺母将球头沿轴向压向锥面,球面与锥面表面初始状态的线接触也会随着球头与锥面间的压缩贴合转变为面接触.两个面的相互挤压使接触面上的微观间歇被填满,实现密封.
|
图 1 球头-锥面密封结构示意图 Fig. 1 Globe-cone sealing schematic |
管路、球头、锥面三个零件均为轴对称结构,螺母一般为正六角结构,本文分析中忽略了螺母边角,并认为螺母对球头的预紧力绕z轴均布.由于球头-锥面密封结构具有周向循环的结构特征,为减少计算工作量以提高工作效率,可以建立如图 2所示的网格模型,模型绕z轴的夹角,即循环特征结构在圆周方向上的尺度为3°,其边界条件具体如下:

|
图 2 球头-锥面密封性能分析有限元模型 Fig. 2 Finite element model for performance analysis of globe-cone sealing |
球头、锥面及螺母截面1处施加循环对称约束;螺母外表面2处及锥面右侧端面3处均施加x、y和z三个方向的位移约束;球头及锥面内表面4处均施加流体压力载荷;管路外表面5处施加y和z方向的位移约束;根据螺纹特点,将与初始预紧力矩对应的预紧力施加在螺母处的截面6上,预紧力方向沿z轴并指向锥面;球头-锥面密封结构整体施加均匀温度载荷.另外,分别在螺母与球头、螺母与锥面、球头与锥面之间建立接触对,并设置相应的摩擦系数.
采用第一阶段应变强化蠕变模型及其理论公式来模拟预紧螺母的应力松弛特性,理论公式为
| $ \dot e = {C_1}{\sigma ^{{C_2}}}{\varepsilon ^{{C_3}}}{e^{ - {C_4}/T}} $ | (1) |
式中:ė为蠕变应变速率;σ为应力;ε为应变;C1、C2、C3、C4均为材料的蠕变参数,分析中[C1, C2, C3, C4]分别取为[5.2×10-29, 7, 0.8, 2][10].
通过上述有限元模型可以求解考虑应力松弛状态下的球头-锥面密封接触平均应力、密封面宽度等参数,并作为泄漏分析的输入.
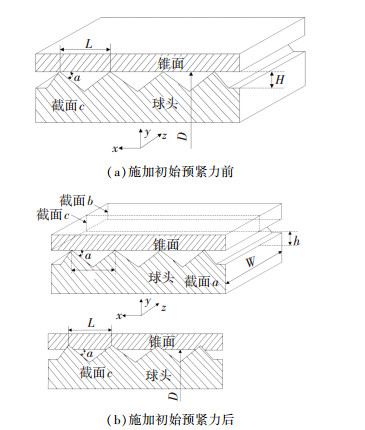
1.2 泄漏模型依据Roth提出的泄漏模型(如图 3所示),可以将球头-锥面间形成的泄漏通道视为由若干横截面积恒定且为等腰三角形并联而成,球头-锥面间总泄漏为所有泄漏通道的叠加.
|
图 3 接触式密封泄漏通道截面示意图 Fig. 3 Shematic of contact sealing leakage section |
在施加初始预紧力前,球头与锥面仅在截面c处接触,D为密封环直径.随着施加预紧力,球头与锥面在z方向上接触区域扩展,在截面a和截面b为接触区域起点,截面a和截面b之间球头与锥面均接触,该泄漏通道的长度即为密封面的宽度W.因球头-锥面密封结构的总漏率小于1×10-6Pa·m3/s,因此泄漏通道间的气体流动可以视为分子流.
单个横截面为等腰三角形的微型柱体流导可以表示为[1]
| $ {C_s} = \frac{2}{3}\sqrt {\frac{{8{\rm{ \mathsf{ π} }}R{\rm{T}}}}{m}} \frac{{K{h^3}}}{{W{\rm{tan}}\alpha (1 + 1/\cos \alpha )}}. $ | (2) |
式中:α为等腰三角形底角;h为实际工作状态下微型漏孔底边上的高;W为密封面的宽度;m为气体分子质量;R为气体常数;T为气体的绝对温度;K为形状修正系数.
对于直径为D的密封环,其密封面上漏孔的个数为
| $ n = \frac{{{\rm{ \mathsf{ π} }}D{\rm{tan}}\alpha }}{{2H}}. $ | (3) |
式中:H为初始状态下微型漏孔底边上的高.
综合式(3)和式(2),可以获得整个密封面的总流导为
| $ C = n{C_s} = \frac{1}{3}\sqrt {\frac{{8{\rm{ \mathsf{ π} }}RT}}{m}} \frac{{KD{h^3}}}{{WH(1 + 1/{\rm{cos}}\alpha )}}. $ |
根据文献[1]
| $ \frac{h}{H} = {\rm{exp}}\left( { - \frac{{{\sigma _m}}}{{{K_s}}}} \right). $ |
式中:σm为密封面上的平均应力;Ks为反映密封面上较软材料密封性能的系数.则总漏率可以表示为
| $ Q = C\Delta p = \frac{1}{3}\sqrt {\frac{{8{\rm{ \mathsf{ π} }}RT}}{m}} \frac{{KD{H^2}}}{{W(1 + 1/{\rm{cos}}\alpha )}}{\rm{exp}}\left( { - \frac{{3{\sigma _m}}}{{{K_s}}}} \right)\Delta p. $ |
Roth指出接触形成的泄漏路径横截面的典型形式是底角α=4°的等腰三角形,此时形状修正系数K=1.7.那么,考虑应力松弛效应条件下的总漏率可以表示为
| $ Q = 1.42\sqrt {\frac{{RT}}{m}} \frac{{D{H^2}}}{W}\exp \left( { - \frac{{3{\sigma _m}}}{{{K_s}}}} \right)\Delta p. $ |
式中:σm为考虑应力松弛效应条件下球头-锥面间的平均应力;D为密封环直径;W为密封面的宽度.其中,σm、D及W均需通过有限元仿真分析获得.上式反映出球头-锥面接头处总漏率受到球头-锥面间接触应力、密封面宽度等的影响,工程实际中球头-锥面密封结构的接触应力、密封面宽度是随着时间变化的,先前工作并未综合考虑这一变化,所以对漏率的计算结果精度存在偏差.
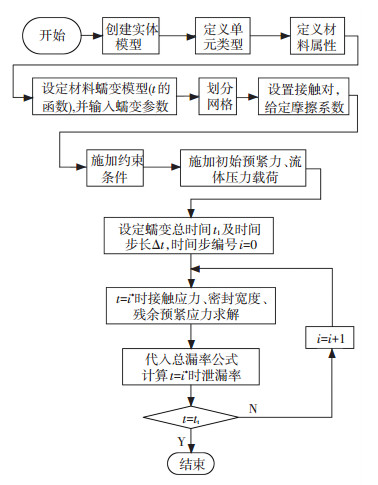
综上,本文中考虑应力松弛效应球头-锥面密封漏率计算流程如图 4所示.
|
图 4 考虑应力松弛效应球头-锥面密封漏率计算流程 Fig. 4 Calculation of globe-cone seal leakage rate considering stress relaxation |
本文球头-锥面密封结构处于常温氦检漏状态,因此,相关参数分别取为:T=293 K;m=4;R=8314.4;H=0.8 μm;Ks=103 MPa.
2 计算结果与讨论 2.1 考虑应力松弛效应与否的球头-锥面密封结构性能对比这部分内容在锥面倾斜角度β=60°、摩擦系数为0.15、螺母预紧力为10.5 kN及流体绝对压力为2 MPa条件下(下同),对比考虑应力松弛效应与否的球头-锥面密封性能的差异.
图 5所示为考虑应力松弛效应与否的球头-锥面密封性能的对比,从图中可以看出,除蠕变时刻为0的情况,不考虑应力松弛效应的球头-锥面密封的残余预紧应力及球头-锥面间的接触应力均大于考虑应力松弛效应的球头-锥面密封的相关性能.这是因为产生了应力松弛现象,即在维持恒定变形的材料中,应力会随蠕变时间的增长而减小.从图中还可以看出,考虑应力松弛效应影响下,球头-锥面密封中螺母残余预紧应力及球头-锥面间的接触应力均会随蠕变时间的增长而减小,产生这种现象的原因同上所述.另外,从图中还可以看出蠕变时间愈长,考虑应力松弛效应与否条件下获得的螺母残余预紧应力及球头-锥面间的接触应力间的差异愈大,这是容易理解的.

|
图 5 考虑应力松弛效应与否的球头-锥面密封性能对比 Fig. 5 Comparison of globe-cone seal performance with and without consideration of stress relaxation |
球头-锥面密封螺母残余预紧应力随蠕变时间的变化规律如图 6所示,从图中可以看出随螺母预紧力的增大,球头-锥面密封螺母残余预紧应力会随之增大,这表明螺母预紧力与其残余预紧应力正相关.从图中还可以看出随蠕变时间的增长,球头-锥面密封的残余预紧应力先急剧减小,然后缓慢减少,这与金属材料的一般蠕变松弛理论是符合的,证明仿真结果是正确的.实际工程中,当螺母残余预紧应力降低至其初始预紧应力的60%时,需对螺母重新进行预紧.

|
图 6 不同初始预紧力下螺母残余预紧应力随蠕变时间的变化 Fig. 6 Nut residual preload force change with increasing creep time under different initial preload force |
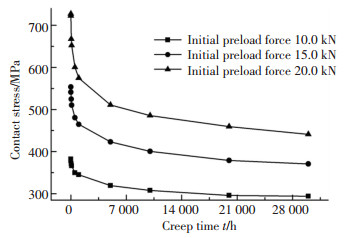
球头-锥面间接触应力随蠕变时间的变化规律如图 7所示,从图中可以看出随螺母初始预紧力的增大,对应蠕变时刻下球头-锥面间的接触应力会随之增大,这表明螺母初始预紧力与球头-锥面间的接触应力是正相关的.产生这种现象的原因在于螺母初始预紧力的增大,会使球头与锥面间产生更大挤压效应,直接表现为球头-锥面间接触应力的增大,这是容易理解的.从图中还可以看出,随蠕变时间的增长,球头-锥面间的接触应力会先急剧减小,尔后缓慢减少,这与金属材料应力松弛理论是一致的.此外,从图中还可以看出,不同螺母初始预紧力条件下的,球头-锥面间的接触应力均显著大于流体压力,表明这一结构及工况下的球头-锥面密封均满足密封性能的要求.
|
图 7 不同初始预紧力下接触应力随蠕变时间的变化 Fig. 7 Contact stress change with increasing creep time under different initial preload force |
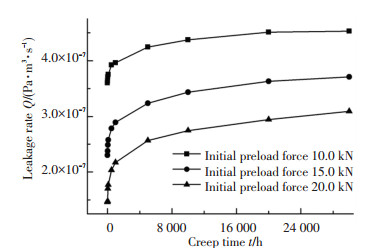
与图 7相对应,图 8所示为泄漏率随时间的变化,从图中可以看出随螺母初始预紧力的增大,对应蠕变时刻下球头-锥面密封的泄漏率会随之减小.从图中还可以看出,随蠕变时间的增长,3种螺母初始预紧力条件下的泄漏率均会随之增大,这是容易理解的.
|
图 8 不同初始预紧力下泄漏率随蠕变时间的变化 Fig. 8 Leakage rate change with increasing creep time under different initial preload force |
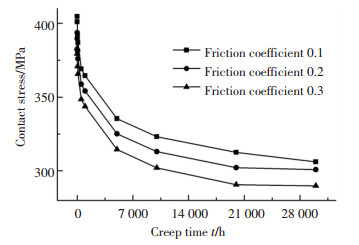
摩擦系数对螺母预紧应力及接触应力的影响如图 9和图 10所示,从图中可以看出,随摩擦系数的增大,对应蠕变时刻下螺母的残余预紧应力会随之降低,产生这种现象的原因在于:接触面松弛过程是两个接触面间缓慢变形、错动及相互适应并逐渐扩展接触面积的过程.虽然初始预紧力相同,但摩擦系数大,则几处接触副接触面之间初始时接触得较“虚”,在后期松弛过程中,接触面间缓慢变形、错动及相互适应并逐渐扩展接触面积的过程发生得越容易,所以摩擦系数越大,残余预紧应力以及接触应力随着时间推移下降得越快.从图中还可以看出,随蠕变时间的增长,螺母残余预紧应力会先急剧减小,尔后缓慢减小,这所呈现的现象是合理的.

|
图 9 不同摩擦系数下残余预紧应力随蠕变时间的变化 Fig. 9 Residual preload force change with increasing creep time under different friction coefficient |
|
图 10 不同摩擦系数下接触应力随蠕变时间的变化 Fig. 10 Contact stress change with increasing creep time under different friction coefficient |
与图 10相对应,图 11所示为泄漏率随蠕变时间的变化.从图中可以看出,随摩擦系数的增大,对应蠕变时刻下球头-锥面密封的泄漏率会随之增大.从图中还可以看出随蠕变时间的增长,不同摩擦系数下的球头-锥面密封的泄漏率均会随之增大.

|
图 11 不同摩擦系数下泄漏率随蠕变时间的变化 Fig. 11 Change of leakage rate with increasing creep time under different friction coefficient |
流体压力对螺母残余预紧应力的影响如图 12所示,从图中可以看出随流体压力的增大,对应蠕变时刻下螺母的残余预紧应力会随之增大,产生这种现象的原因可能与螺母初始预紧力、接触面间的摩擦阻力以及流体压力间复杂的耦合作用有关.

|
图 12 不同流体压力下残余应力随蠕变时间的变化 Fig. 12 Residual preload force change with increasing creep time under different fluid pressure |
流体压力对球头-锥面间接触应力的影响如图 13所示,从图中可以看出随流体压力的增大,对应蠕变时刻下球头-锥面间的接触应力会随之略微增大,产生这种现象的主要原因有两个方面:一是螺母残余预紧应力与球头-锥面间的接触应力正相关,故螺母残余预紧应力的增大是造成球头-锥面间接触应力增大的主要原因之一.二是在流体压力的抬升作用下,球头-锥面间的挤压效果会随流体压力的增大而愈加显著,这是造成球头-锥面间接触应力增大的另一个主要原因.

|
图 13 不同流体压力下接触应力随蠕变时间的变化 Fig. 13 Contact stress change with increasing creep time under different fluid pressure |
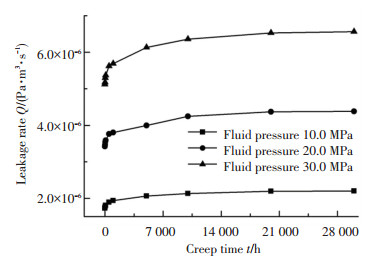
图 14所示为不同流体压力作用下球头-锥面密封的泄漏率随蠕变时间的变化,从图中可以看出随流体压力的增大,对应蠕变时刻下球头-锥面密封的泄漏率均会随之增大,这是容易理解的.从图中还可以看出随蠕变时间的增长,3种流体压力条件下的球头-锥面密封的泄漏率均会随之增大,这与图 13所示的现象是相对应的.
|
图 14 不同流体压力下泄漏率随蠕变时间的变化 Fig. 14 Change of leakage rate with increasing creep time under different fluid pressure |
参照卫星推进系统工程实际设计了一段管路,其中含有球头-锥面接点,并对螺母施加预紧力矩.对管路进行了氦气充压,之后管路处于长期保压状态,在1年中定期采用氦质谱检漏仪的吸枪对球头-锥面的漏率进行漏率测量并记录了结果.检漏的环境条件包括温度18~28 ℃、相对湿度30%~70%,气压为实验室气压,洁净度优于10万级.
在锥面倾斜角度β=60°、流体压力为2 MPa、摩擦系数为0.15及螺母预紧力为10.5 kN条件下,开展考虑应力松弛效应与否的球头-锥面密封泄漏性能的理论分析及试验研究.需要说明的是:试验中每个蠕变时刻点的泄漏率均需测试3次,然后求和取均值.

|
图 15 球头-锥面连接单点检漏包覆示意图 Fig. 15 The leakage rate test of globe-cone sealing |
球头-锥面密封泄漏率的理论结果与试验结果的对比如图 16所示.从图中可以看出随蠕变时间的增长,较之不考虑应力松弛效应和仅考虑球头-锥面应力松弛,考虑综合应力松弛效应下获得的球头-锥面密封的泄漏率与试验结果吻合较好.这表明考虑综合应力松弛效应下获得的球头-锥面密封的泄漏率更加精确.从图中还可以看出随蠕变时间的增长,考虑应力松弛效应的球头-锥面密封的泄漏率会随之增大,这与试验结果所呈现的变化趋势是一致的,而不考虑应力松弛效应的球头-锥面密封的泄漏率始终保持不变,这与试验结果所呈现的变化趋势存在显著差异.这一现象体现出在进行球头-锥面密封性能分析时,考虑应力松弛效应的影响是很有必要的.
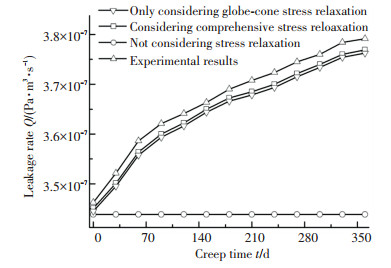
|
图 16 理论结果与试验结果的对比 Fig. 16 Comparison of theoretical experimental results |
1) 对比考虑应力松弛效应与否的球头-锥面密封性能的差异,研究结果表明随着蠕变时间的增长,考虑应力松弛效应与否的球头-锥面密封性能会存在显著的差异.这一研究为具有长期服役要求的球头-锥面密封中多久需要补充螺母初始预紧力提供理论依据.
2) 研究螺母初始预紧力对考虑应力松弛效应的球头-锥面密封性能的影响.结果表明随着螺母初始预紧力的增大,螺母的残余预紧应力及球头-锥面间的接触应力均会随之增大,而其泄漏率会随之减小,这表明螺母初始预紧力的增大会提升球头-锥面密封的性能,但值得注意的是,过大的螺母初始预紧力,可能会对球头-锥面密封结构的实际使用寿命产生不利影响.因此,在满足密封性能的基础上,选择较小的螺母初始预紧力是很有裨益的.
3) 探讨摩擦系数对考虑应力松弛效应的球头-锥面密封性能的影响.结果表明随着摩擦系数的增大,螺母的残余预紧应力及球头-锥面间的接触应力均会随之减小,而其泄漏率会随之增大,这与不同粗糙度下,表面实际接触区域及接触状态存在差异有关.因此,提高加工表面的质量,可以有效提升球头-锥面密封的性能.
4) 分析流体压力对考虑应力松弛效应的球头-锥面密封性能的影响.研究结果表明随着流体压力的增大,螺母的残余预紧应力及泄漏率均会显著增大,而球头-锥面间的接触压力会略微增大.这一研究为超高压流体作用下,螺母初始预紧力等的选取提供理论依据.
5) 开展考虑应力松弛效应与否条件下获得的球头-锥面密封的泄漏率与试验结果的对比.研究结果表明,较之不考虑应力松弛效应,考虑应力松弛效应下获得的球头-锥面密封的泄漏率与试验结果吻合较好,体现出在开展球头-锥面密封性能分析时,考虑应力松弛效应的影响是很有必要的.
| [1] |
王勇, 闫荣鑫. 应力松弛对球头密封结构漏率影响的分析[J]. 航天器环境工程, 2009, 26(5): 455. WANG Yong, YAN Rongxin. Effect of stress relaxation on the leak rate of the orbicular seal joint[J]. Spacecraft Environment Engineering, 2009, 26(5): 455. DOI:10.3969/j.issn.1673-1379.2009.05.012 |
| [2] |
周鑫, 庞贺伟, 闫少光, 等. 球头-锥面连接结构非线性接触分析[J]. 航天器环境工程, 2005, 22(4): 211. ZHOU Xin, PANG Hewei, YAN Shaoguang, et al. Nonlinear contact analysis of globe-cone joint[J]. Spacecraft Environment Engineering, 2005, 22(4): 211. DOI:10.3969/j.issn.1673-1379.2005.04.006 |
| [3] |
周鑫, 庞贺伟, 刘宏阳. 球面密封结构的漏率预估[J]. 宇航学报, 2007, 28(3): 762. ZHOU Xin, PANG Hewei, LIU Hongyang. Leak rate prediction of orbicular seal joint[J]. Journal of Astronautics, 2007, 28(3): 762. DOI:10.3321/j.issn:1000-1328.2007.03.050 |
| [4] |
韩冲, 张勇. 导管连接件球头-锥面结构密封性能研究[J]. 润滑与密封, 2012, 37(10): 105. HAN Chong, ZHANG Yong. Research on sealing property of globe-cone joint for pipeline[J]. Lubrication Engineering, 2012, 37(10): 105. |
| [5] |
刘海波, 吴嘉琨, 王永青. 地脚螺栓蠕变松弛对大型数控机床几何精度衰退的影响[J]. 西安交通大学学报, 2015, 49(9): 14. LIU Haibo, WU Jiakun, WANG Yongqing. Impact of anchor bolts creep relaxation on geometric accuracy decline of large computer numerical control machine tools[J]. Journal of Xi'an Jiaotong University, 2015, 49(9): 14. |
| [6] |
XU Hongfa, WANG Fajun, CHENG Xuexin. Pullout creep properties of grouted soil anchoes[J]. Journal of Central South University of Technology, 2007, 14: 474. |
| [7] |
DELHOMME F, DEBICKI G. Numerical modelling of anchor bolts under pullout and relaxation tests[J]. Construction and Building Materials, 2010, 24(7): 1232. DOI:10.1016/j.conbuildmat.2009.12.015 |
| [8] |
CROCCOLO D, AGOSTINIS M D, VINCENZI N. Failure analysis of bolted joints: effect of friction coefficients in torque-preloading relationship[J]. Engineering Failure Analysis, 2011, 18(1): 364. DOI:10.1016/j.engfailanal.2010.09.015 |
| [9] |
KASSNER M E, SMITH K. Low temperature creep plasticity[J]. Journal of Materials Research and Technology, 2014, 3(3): 280. DOI:10.1016/j.jmrt.2014.06.009 |
| [10] |
王娜, 张博. 预紧螺栓常温应力松弛仿真分析[J]. 太原学院学报, 2016, 34(4): 6. WANG Na, ZHANG Bo. Simulation analysis of the stress relaxation of assembly bolt at room temperature[J]. Journal of Taiyuan College, 2016, 34(4): 6. |
| [11] |
LIU Cheng, LIU Ping, ZHAO Zhenbo, et al. Room temperature creep of a high strength steel[J]. Materials & Design, 2001, 22(4): 325. |
| [12] |
JIANG Puning, WANG W Z, JIAO G C. Analysis of high temperature creep on the nut connection components of a 600MW supercritical steam turbine[C]// Proceedings of ASME Turbo Expo. Copenhagen: ASME, 2012.GT2012-69599
|
| [13] |
MANN J A, HILSABECK J, MCKOON C. et al. Bolted flanged joint creep/relaxation results at high temperatures[C].// Proceedings of the ASME 2014 Pressure Vessels & Piping Conference. Anaheim: ASME, 2014. PVP2014-28261
|
| [14] |
SILVA A C, WERNER F, XAVIER L. The influence of elevated temperature in creep relaxation of various PTFE gaskets production methods[C]. // Proceedings of the ASME 2018 Pressure Vessels and Piping Conference. ASME, 2018. PVP2018-84077
|
| [15] |
GORDON A P, ALBURY J, LOPEZ M, et al. Application of miniaturized experiments for constitutive modeling of creep relaxation of a novel textured gasket product[C]// Proceedings of the ASME 2018 Pressure Vessels and Piping Conference. ASME, 2018. PVP2018-84040
|
| [16] |
MAXIMOV J T, DUNCHEVA G V, ANCHEV A P. An approach to modeling time-dependent creep and residual stress relaxation around cold worked holes in aluminium alloys at room temperature[J]. Engineering Failure Analysis, 2014, 45: 1. DOI:10.1016/j.engfailanal.2014.06.008 |
| [17] |
MAO Jianfeng, WANG Weizhe, LIU Yingzheng, et al. Comparative study of flange-to-seal contact couplings with bolt relaxation under creep condition[J]. Journal of Engineering for Gas Turbines and Power, 2014, 136(7): 1. |
 2020, Vol. 52
2020, Vol. 52


