2. 北京航天动力研究所, 北京 100076
2. Beijing Aerospace Propulsion Institute, Beijing 100076, China
陀螺仪作为惯性平台的重要组成元件,在航天、航海以及国防等领域有着广泛的应用.陀螺马达(图 1)通过转子的高速旋转形成陀螺仪表所需要的稳定的角动量,是陀螺仪表的核心部件.气浮陀螺马达具有精度高,可靠性好,应用技术较为成熟等诸多优点,是我国现阶段在惯性仪表中应用最广泛的陀螺马达[1-4].

|
图 1 动压陀螺马达结构 Fig. 1 Configuration of gyro motor with hydrodynamic gas bearing |
在实际的生产和应用过程中,陀螺马达转子的质量不平衡量、轴承的制造和装配误差以及运行过程中陀螺马达壳体的离心和热变形,都会使轴承性能发生变化,影响陀螺马达的回转精度,产生干扰力矩,进而影响陀螺仪的漂移精度[5-6].因此,陀螺马达转子的回转精度是评价陀螺马达产品质量的重要指标.由于目前尚缺乏对陀螺马达回转精度进行定量评价的体系和标准,本文引入回转元件评价的国际标准ISO 230-7[7],开展对陀螺马达转子的运动误差(Error Motion)和变形的测量分析工作,评估陀螺马达产品的性能,对陀螺马达的产品质量评价以及产品质量检测具有重要指导意义.
1 三点法误差分离技术 1.1 三点法误差分离原理三点法误差分离技术最早由日本学者青木保雄和大园成夫提出[8],用于解决工件圆度测量时的圆度误差与运动误差的分离问题,后经过科研人员的研究与发展,到今天已经成为应用最为普遍,技术最成熟的误差分离方法.其基本原理是将三只传感器沿径向按一定角度布置于被测截面上,利用同步采集的三个传感器信号数据的加权组合来消除转子运动误差[9-12].
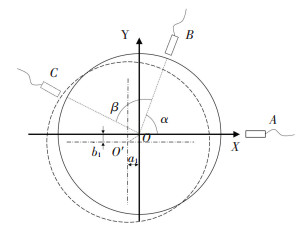
如图 2所示,以A传感器轴线为x轴,以传感器交点为坐标原点建立平面直角坐标系. α, β分别为A、B,B、C传感器轴线的夹角.转子几何中心O′在给定坐标系中的偏心坐标为(a1, b1).运动误差在x,y方向上的分量分别为x(θ),y(θ),转子外壳的圆度误差为r(θ),其中θ为转子当前角度.则各传感器的信号可表示为
| $ \begin{array}{l} A\left( \theta \right) = r\left( \theta \right) + x\left( \theta \right) + {a_1}\cos \theta + {b_1}\sin \theta ,\\ B\left( \theta \right) = r\left( {\theta + \alpha } \right) + x\left( \theta \right)\cos \alpha + y\left( \theta \right)\sin \alpha + \\ \;\;\;\;\;\;\;\;\;\;\;{a_1}\cos \left( {\theta + \alpha } \right) + {b_1}\sin \left( {\theta + \alpha } \right),\\ C\left( \theta \right) = r\left( {\theta + \alpha + \beta } \right) + x\left( \theta \right)\cos \left( {\alpha + \beta } \right) + \\ \;\;\;\;\;\;\;\;\;\;y\left( \theta \right)\sin \left( {\alpha + \beta } \right) + {a_1}\cos \left( {\theta + \alpha + \beta } \right) + \\ \;\;\;\;\;\;\;\;\;\;{b_1}\sin \left( {\theta + \alpha + \beta } \right). \end{array} $ | (1) |
|
图 2 三点法原理 Fig. 2 Principle of three-point method |
取三只信号的加权和,即可消去信号中的运动误差分量,加权系数如式(2)所示[8]:
| $ \left\{ \begin{array}{l} s\left( \theta \right) = {z_1}A\left( \theta \right) + {z_2}B\left( \theta \right) + {z_3}{\rm{C}}\left( \theta \right),\\ {z_1} = 1,\\ {z_2} = \frac{{ - \sin \left( {\alpha + \beta } \right)}}{{\sin \beta }},\\ {z_3} = \frac{{\sin \alpha }}{{\sin \beta }}. \end{array} \right. $ | (2) |
取加权信号的离散傅里叶变换:
| $ \begin{array}{l} S\left( k \right) = {\rm{DFT}}\left( {s\left( \theta \right)} \right) = R\left( k \right) \times W\left( k \right),\\ W\left( k \right) = {z_1} + {z_2}{{\rm{e}}^{ - {\rm{j}}k\alpha }} + {z_3}{{\rm{e}}^{ - {\rm{j}}k\left( {\alpha + \beta } \right)}}. \end{array} $ | (3) |
由式(3)可得圆度误差r(θ)的表达式为
| $ r\left( \theta \right) = {\rm{IDFT}}\left( {\frac{{S(k)}}{{W(k)}}} \right),\left( {W\left( k \right) \ne 0} \right) $ | (4) |
由于W(1)=0,因此上式中在进行离散傅里叶逆变换时,无法得到原信号的一次谐波分量,而一次谐波分量主要为偏心误差,因此得到的圆度误差中也去除了偏心误差的干扰.
在傅里叶逆变换过程中要求所关心的谐波次数k(k≠1)范围内,要求W(k)≠0,否则该次谐波被抑制,导致分离的圆度误差失真.
1.2 偏心误差与运动误差分离马达运动误差可由式(5)表示.要得到运动误差,需在分离得出圆度误差r(θ)的基础上,在剩余信号中将偏心误差分量分离出去.
| $ \left\{ \begin{array}{l} x\left( \theta \right) = A\left( \theta \right) - r\left( \theta \right) - \left( {{a_1}\cos \theta + {b_1}\sin \theta } \right),\\ y\left( \theta \right) = \frac{{B\left( \theta \right) - r\left( {\theta + \alpha } \right) - x\left( \theta \right)\cos \alpha }}{{\sin \alpha }} - \\ \;\;\;\;\;\;\;\;\;\left( {{b_1}\cos \theta - {a_1}\sin \theta } \right). \end{array} \right. $ | (5) |
将式(1)代入式(5),化简后可得到
| $ {a_1}\cos \theta + {b_1}\sin \theta + x\left( \theta \right) = A\left( \theta \right) - r\left( \theta \right), $ | (6) |
| $ \begin{array}{l} - {a_1}\sin \theta + {b_1}\cos \theta + y\left( \theta \right) = \\ \frac{{B\left( \theta \right) - r\left( {\theta + \alpha } \right) - \left[ {A\left( \theta \right) - r\left( \theta \right)} \right]\cos \alpha }}{{\sin \alpha }}. \end{array} $ | (7) |
针对式(6)和式(7),令(6)×sin θ-(7)×cos θ,得到
| $ \begin{array}{l} {a_1}\sin \left( {2\theta } \right) - {b_1}\cos \left( {2\theta } \right) = \left[ {A\left( \theta \right) - r\left( \theta \right)} \right]\sin \theta - \\ \frac{{B\left( \theta \right) - \cos \alpha \left[ {A\left( \theta \right) - r\left( \theta \right)} \right] - r\left( {\theta + \alpha } \right)}}{{\sin \alpha }}\cos \theta . \end{array} $ | (8) |
对式(8)两端分别乘以sin(2θ)/π和cos(2θ)/π在整个测量周期[0, 2π]上积分即可得到(a1, b1),即
| $ \begin{array}{l} {a_1} = \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^{2{\rm{ \mathsf{ π} }}} {\left[ {\left( {A\left( \theta \right) - r\left( \theta \right)} \right)\sin \theta - } \right.} \\ \;\;\;\;\;\;\;\frac{{B\left( \theta \right) - \cos \alpha \left( {A\left( \theta \right) - r\left( \theta \right)} \right) - r\left( {\theta + \alpha } \right)}}{{\sin \alpha }} \cdot \\ \;\;\;\;\;\;\;\left. {\cos \theta } \right]\sin \left( {2\theta } \right){\rm{d}}\theta ,\\ {b_1} = \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^{2{\rm{ \mathsf{ π} }}} {\left[ {\left( {A\left( \theta \right) - r\left( \theta \right)} \right)\sin \theta - } \right.} \\ \;\;\;\;\;\;\frac{{B\left( \theta \right) - \cos \alpha \left( {A\left( \theta \right) - r\left( \theta \right)} \right) - r\left( {\theta + \alpha } \right)}}{{\sin \alpha }} \cdot \\ \;\;\;\;\;\;\left. {\cos \theta } \right]\sin \left( {2\theta } \right){\rm{d}}\theta . \end{array} $ | (9) |
将(a1, b1)代入式(5)即可得到去除偏心的运动误差信号.
1.3 径向变形量计算由式(1)、(2)知,给定系数z1,z2,z3满足以下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {{z_1} + {z_2}\cos \alpha + {z_3}\cos \left( {\alpha + \beta } \right) = 0,}\\ {{z_2}\sin \alpha + {z_3}\sin \left( {\alpha + \beta } \right) = 0.} \end{array}} \right. $ | (10) |
不考虑转子的径向变形,三支传感器示数变化量ΔhA,ΔhB,ΔhC有以下关系:
| $ {z_1}\Delta {h_A} + {z_2}\Delta {h_B} + {z_3}\Delta {h_C} = 0. $ | (11) |
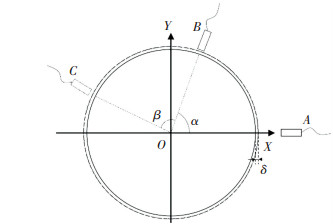
假设转子径向变形量δ,如图 3所示.传感器示数的实际变化量Δh′可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {{h'}_A} = \Delta {h_A} + \delta ,}\\ {\Delta {{h'}_B} = \Delta {h_B} + \delta ,}\\ {\Delta {{h'}_C} = \Delta {h_C} + \delta .} \end{array}} \right. $ | (12) |
|
图 3 膨胀量分离原理图 Fig. 3 Schematic of expansion test |
联立式(11)、(12)得到径向变形量δ:
| $ \delta = \frac{{{z_1}\Delta {{h'}_A} + {z_2}\Delta {{h'}_B} + {z_3}\Delta {{h'}_C}}}{{{z_1} + {z_2} + {z_3}}}. $ | (13) |
为验证回转精度测试系统中误差分离的准确性,对模拟信号进行了误差分离仿真.按表 1所示的数据生成圆度和运动误差的仿真信号,以α=106.875,β=63.28,生成A、B、C三支传感器的仿真波形信号.将圆度信号,x方向(传感器A的轴线方向),y方向运动误差信号分离结果分别与原信号进行对比,对比结果如图 4和表 2所示.
| 表 1 仿真信号 Tab. 1 Simulation signal |

|
图 4 信号分离结果对比 Fig. 4 Comparison of signal separation results |
| 表 2 分离误差 Tab. 2 Segregation errors |
由表 2结果得知,在当前给定参数下,圆度和运动误差的分离结果与原始仿真信号对比,最大误差不超过0.3%,因此,基于三点法误差分离技术从混合信号中提取运动误差是可信的.
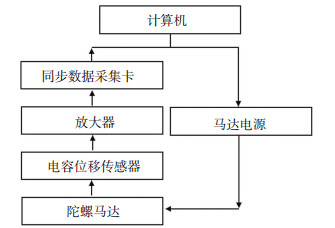
3 实验与分析 3.1 实验系统搭建测试过程中,将马达固定于工装框架上,在马达转子径向布置三只高精度电容传感器, 如图 5所示.由于传感器量程较小,设计了传感器微调装置.传感器信号采用NI同步数据采集系统对传感器信号进行采集.实验系统组成如图 6所示.

|
图 5 实验装置 Fig. 5 Experimental device |
|
图 6 测试系统组成 Fig. 6 Diagram of test system |
测试时,在陀螺马达起动阶段设置采样频率为500 kS/s;当陀螺马达到达同步转速后,固定每周采样点数N=200,重设采集系统的采样频率:
| $ {{f'}_s} = \frac{{N\omega }}{{2{\rm{ \mathsf{ π} }}}} $ | (14) |
同步采集记录三支传感器信号,记录长度为512圈.使用Butterworth低通滤波器,滤波频率为5 000 Hz,进行数据分析.马达转速ω可根据短时傅里叶变换较为精确地提取[13].
3.2 传感器角度在线测量两传感器之间夹角受工装制造和传感器安装误差影响[14-15],一般很难精确确定.本文根据传感器信号的相关函数进行在线求取,以A,B两只传感器为例:
| $ {R_{AB}}\left( m \right) = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {A\left( n \right)B\left( {n + m} \right)} $ | (15) |
当RAB(m)为两传感器信号的互相关函数,当RAB(m)取得最大值时,此时m对应的时间即是传感器B相对于传感器A的时延,对应的角度即A,B两传感器之间的角度差:
| $ \alpha = \frac{{2{\rm{ \mathsf{ π} }}{f_S}m}}{\omega } $ | (16) |
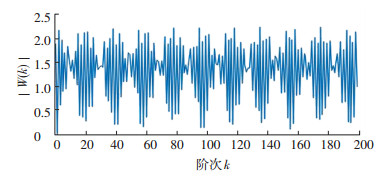
依据式(16)可以精确测得传感器之间的夹角,如表 3所示.根据传感器角度和每周采样点数N,计算测试系统权函数|W(k)|,如图 7所示.从图 7可以看出,200阶谐波内,除一次谐波外,不存在其他谐波抑制.
| 表 3 实验参数 Tab. 3 Experimental parameters |
|
图 7 测试系统权系数 Fig. 7 Weight function of experimental device |
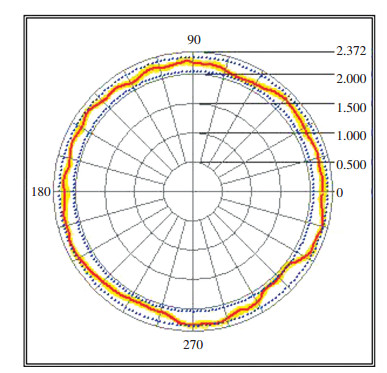
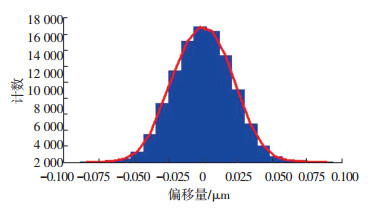
对某型号气浮动压陀螺马达进行测试.得到马达圆度误差、运动误差如图 8~10所示,分离结果如表 4所示.在传感器信号中,圆度误差和偏心误差占主要成分,这也说明了要研究马达转子的运动误差时进行误差分离的必要性.同步误差是异步误差1.65倍,表明该马达转子系统中,同步误差是影响回转精度主要因素,需考虑从提高转子动平衡等级、轴承制造装配精度等方面来提高转子回转精度.

|
图 8 马达圆度测试结果 Fig. 8 Roundness error of gyro motor |
|
图 9 马达运动误差 Fig. 9 Error motion of gyro motor |
|
图 10 马达异步运动误差分布直方图 Fig. 10 Histogram of radial ASEM distribution |
| 表 4 误差分离结果 Tab. 4 Error separation results |
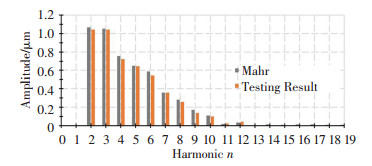
为验证马达圆度分离结果的准确性,将其与圆度仪的测量结果进行对比. 图 11比较了两种方法所得圆度的各次谐波分量,可以看出圆度分离结果与圆度仪测量结果的频谱符合良好;圆度仪检测得到马达外圆轮廓圆度为6.448 μm,与本实验中通过误差分离得到的圆度6.403 μm仅相差35 nm.实验结果不仅验证了圆度误差分离的准确性,也保证了运动误差的真实性.
|
图 11 马达圆度误差频谱对比 Fig. 11 Comparison of roundness error's spectrogram |
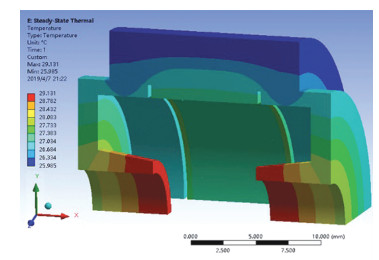
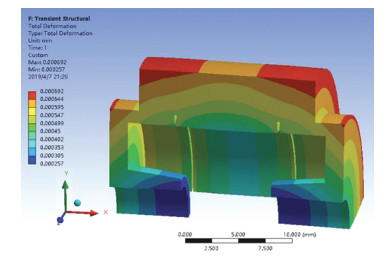
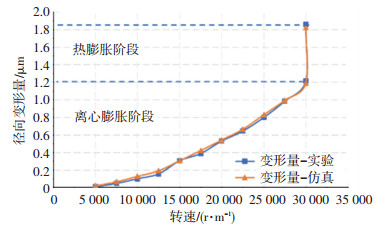
根据式(13)可以得到马达转动时的径向变形量,其中包括离心变形和热膨胀变形.在起动过程中,径向变形量随转速升高而快速变大,由于起动时间较短,电机发热引起的转子热变形可忽略不计,因此,此时的径向形变量主要是由转子离心变形引起的.达到稳定运转后,径向变形随运转时间缓慢上升并逐渐趋于平缓,这一阶段的径向变形主要为电机发热引起的热变形. 图 12所示为某柱形陀螺马达外壳离心和热变形有限元仿真模型,仿真参数如表 5所示. 图 13~14给出了该马达运行时的温度分布及热变形. 图 15给出了不同转速下离心变形和热变形测试结果与有限元计算结果的比较,可以看出两者吻合度良好,说明理论分析与实际测量具有较好的一致性.

|
图 12 马达外壳径变形的有限元模型 Fig. 12 Finite element model of motor deformation simulation |
| 表 5 有限元仿真参数 Tab. 5 Finite element simulation parameters |
|
图 13 马达运行时外壳温度分布 Fig. 13 Temperature distribution of motor during operation |
|
图 14 马达外壳径向热变形云图 Fig. 14 Radial thermal deformation of motor |
|
图 15 马达外壳径向变形比较 Fig. 15 Comparison of radial deformation of motor |
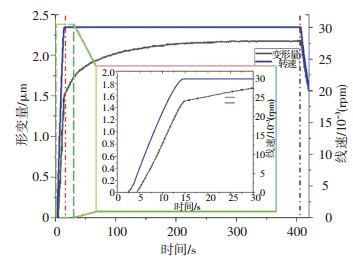
图 16所示为马达从起动到稳定再到降速过程中径向变形量与转速随时间变化的关系.从图中可以看出,马达在起动后约12 s达到30 000 r/m的稳定转速,此时马达外壳离心变形量为1.512 μm.当马达到达稳定运转后,径向变形缓慢增加直到热平衡为止,在实验时间内径向热变形为0.644 μm.因此,该马达起动后离心变形和热膨胀变之和为2.156 μm,并以离心变形为主,约占总变形量的70%.马达外壳径向变形会改变气浮轴承的间隙和形状,从而影响马达轴承的刚度和运动误差,因此从结构设计的角度应该提高马达外壳结构刚度,尽量减小马达的离心变形.
|
图 16 马达转子径向变形 Fig. 16 Measured radial expansion of rotor |
1) 基于三点法误差分离技术,搭建了陀螺马达径向运动误差测量实验系统,从仿真和实验两方面验证了测量结果的准确性,为在生产中对陀螺马达回转精度进行定量评价提供了有益的探索.
2) 提出了马达转子变形量的测量方法和流程,使用该方法可以测量出马达起动后壳体的总变形量,并能区分出离心变形和热变形,对评价马达壳体刚度以及由此引起的马达轴承气膜刚度和回转精度变化具有重要作用.
3) 提出了一种传感器之间夹角的在线检测方法,为提高测试分离精度提供了保证.
| [1] |
王巍. 惯性技术研究现状及发展趋势[J]. 自动化学报, 2013, 39(6): 723. WANG Wei. Status and development trend of inertial technology[J]. Acta Automatica Sinica, 2013, 39(6): 723. |
| [2] |
刘智平, 吴丽丽. 陀螺发展简史[J]. 电子设计工程, 2012, 20(7): 66. LIU Zhiping, WU Lili. Development history of gyroscope[J]. Electronic Design Engineering, 2012, 20(7): 66. DOI:10.3969/j.issn.1674-6236.2012.07.023 |
| [3] |
李新刚, 袁建平. 微机械陀螺的发展现状[J]. 力学进展, 2003, 33(3): 289. LI Xingang, YUAN Jianping. Developemnt status of MEMS gyroscope[J]. Advances in Mechanics, 2003, 33(3): 289. DOI:10.3321/j.issn:1000-0992.2003.03.001 |
| [4] |
王京峰, 刘景林, 许卫刚. 动压气体轴承陀螺电机技术发展综述[J]. 微电机, 2016, 49(3): 91. WANG Jingfeng, LIU Jinglin, XV Weigang. Development and application of technology of dynamic hydrodynamic gas bearing gyroscope motor[J]. Micromotors, 2016, 49(3): 91. |
| [5] |
陆元九. 惯性器件(上)[M]. 北京: 中国宇航出版社, 1993. LU Yuanjiu. Inertial device (Volume Ⅰ)[M]. Beijing: China Aerospace Publishing House, 1993. |
| [6] |
刘晶石.气浮陀螺仪干扰力矩影响因素研究[D].哈尔滨: 哈尔滨工业大学, 2011 LIU Jingshi. Research on influencing factors of interference torque of gas-floated gyroscope[D]. Harbin: Harbin Institute of Technology, 2011 http://d.wanfangdata.com.cn/Thesis/D264230 |
| [7] |
ISO 230-7: 2015(E)[S]
|
| [8] |
AOKI Y, OZONO S. On a new method of roundness measurement based on the three-point method[J]. JSPE, 1966, 12: 27. |
| [9] |
李庆华, 母德强, 李振华. 三点法轴径圆度误差精度分析[J]. 长春大学学报, 2003, 13(6): 1. LI Qinghua, MU Deqiang, LI Zhenhua. An analysis of round tolerance error accuracy of crooked axis diameter of 3-point method[J]. Journal of Changchun Uniersity, 2003, 13(6): 1. DOI:10.3969/j.issn.1009-3907-B.2003.06.001 |
| [10] |
雷贤卿, 李言, 周彦伟, 等. 3点法圆度误差分离技术的新算法[J]. 兵工学报, 2007, 28(1): 73. LEI Xianqing, LI Yan, ZHOU Yanwei, et al. A new matrix algorithm of three-point method roundness error separation technique[J]. Acta Armamentarii, 2007, 28(1): 73. |
| [11] |
梅雪松. 机床主轴高精度动平衡技术[M]. 北京: 科学出版社, 2015. MEI Xuesong. High Precision dynamic balancing technology for machine tool spindle[M]. Beijing: Science Press, 2015. |
| [12] |
周继昆, 张荣, 凌明祥. 基于三点法的机床主轴回转误差在线测试技术研究[J]. 计算机测量与控制, 2018, 26(3): 58. ZHOU Jikun, ZHANG Rong, LING Mingxiang. Study on the online test of spindle's radial error of machine tool base on three pint method[J]. Computer Measurement & Control, 2018, 26(3): 58. |
| [13] |
李安, 覃方君, 金云翔.基于自相关-短时傅里叶的陀螺电机转速提取方法[C]//中国仪器仪表学会第八届全国信息获取与处理学术会议论文集.威海: 中国仪器仪表学会, 2010: 530 LI An, QIN Fangjun, JIN Yunxiang. Determination method of gyroscope motor speed using autocorrelation-short time fourier transform[C]//The 8th National Conference on Information Acquisition and Processing. Weihai: China Instrument and Control Society, 2010: 530 |
| [14] |
张宇华, 王晓琳, 张国雄, 等. 提高三点法测量精度的研究[J]. 北京理工大学学报, 1999, 19(2): 157. ZHANG Yuhua, WANG Xiaolin, ZHANG Guoxiong, et al. A study on improving the accuracy for roundness and spindle motion error measurements with three-point method[J]. Journal of Beijing Institute of Technology, 1999, 19(2): 157. DOI:10.3969/j.issn.1001-0645.1999.02.006 |
| [15] |
韩正桐, 洪迈生, 李自军. 三点法圆度误差分离及演化形式与精度分析[J]. 上海交通大学学报, 2002, 36(9): 1225. HAN Zhengtong, HONG Maisheng, LI Zijun. Three-point method and its variation for roundness error separation and accuracy analysis[J]. Journal of Shanghai Jiaotong University, 2002, 36(9): 1225. DOI:10.3321/j.issn:1006-2467.2002.09.002 |
 2020, Vol. 52
2020, Vol. 52


