在机械产品的生命周期中,精度设计与控制是决定产品最终质量的关键因素之一[1].精度是机械产品的一个关键质量特性.其中,对于精密或者超精密数控机床而言,其运动精度又是影响机床精度的关键因素.长期以来,我国机床企业传统的精度设计主要依赖于经验,没有定量的理论值可以参考.为使数控机床精度设计有定量的理论数值供参考,提高数控机床的精度,对机床精度映射的研究就显得至关重要.
对于运动精度的研究,Pezeshki等[2]、Ibaraki等[3]、Fan等[4]根据运动学理论建立了数控机床运动学模型,对数控机床运动误差进行了识别.郭世杰等[5]、余永维等[6]对机床运动误差进行了快速识别与测量.张学波等[7]提出一种基于冗余阵元回波数据的运动误差补偿方法,对声呐系统的运动误差进行补偿.雷楠南[8]对磨齿机数控系统进行了螺距误差补偿,提高了机床精度.对于精度等质量特性映射的研究,王美清等[9]、安相华等[10]对客户需求进行映射,得到基于客户需求的精度等质量特性.
分析上述文献可知,首先现有对于运动精度的研究[2-8]主要是在机床制造生产出来后对其运动精度的识别、测量及运动误差补偿,无法得到可以供机床精度设计阶段参考的运动精度理论数值.其次,现有对于精度映射的研究[9-10]主要集中在设计过程中用户需求与精度等质量特性之间的映射关系.研究的内容主要是用户需求向整机或者部件映射,其映射的最小单元是整机或部件,不能为更小单元(零件)的设计提供设计依据.
针对上述问题,本文从运动角度对数控机床的运动精度进行分析,提出了基于元动作单元的运动精度映射模型.首先,采用“功能-运动-动作”的结构化分解方法得到元动作单元;其次,利用多体系统理论并结合元动作分解树,描述了数控机床拓扑结构,进而运用旋量理论建立了数控机床运动误差模型;再次,为使数控机床空间运动误差表达更具有几何意义,运用螺旋理论建立了空间运动误差螺旋模型,形式化表达了空间运动误差;然后,以制造成本、空间运动误差螺旋螺距为设计准则,构建了运动精度映射模型;最后,利用NSGA-Ⅱ遗传算法进行映射求解,得到映射结果.
1 基于多体系统理论的数控机床拓扑结构分析数控机床运动精度首先需要对数控机床结构进行准确描述,准确、完整的数控机床结构数学模型是进行数控机床相关工作的基础,因此建立准确的数控机床结构数学模型是进行运动精度分析的前提.本文利用多体系统理论并结合元动作单元分解树,从运动的角度出发对数控机床拓扑结构进行描述,为建立数控机床精度模型提供基础.
1.1 基于多体系统理论的数控机床元动作分解多体系统理论是建立在传统坐标变换理论基础上的,它对复杂的机械系统有很强的概括能力和独特的系统描述方法.多体系统是指多个物体通过一定方式相互连接构成的系统,系统中的物体可以是刚体也可以是柔性体,是分析和研究复杂机械系统的最优模式[11].
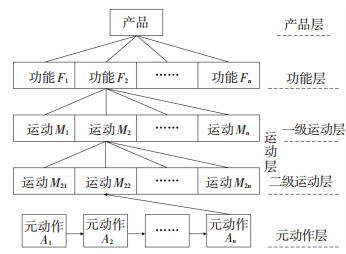
对数控机床的运动精度进行分析,需要从运动的角度对机床进行结构化分解,传统的以零部件为最小单元且只考虑零部件之间连接关系的结构化分解方法对于分析运动精度是不适用的.因此,从运动角度出发,结合多体系统的思想,考虑机床通过最小的动作来实现其功能的过程,可以通过“功能(Function)-运(Motion)-动作(Action)”的分解方法对其进行结构化分解[12].结构化分解模型如图 1所示.
|
图 1 FMA结构化分解模型 Fig. 1 FMA structural decomposition model |
由图 1可知,机电产品要实现整机的运动功能需要相应的部件子功能去实现,部件子功能的实现依靠相应的运动,运动的实现又依靠相应的动作,即“功能-运动-动作,FMA”.在此,把机械产品中传递运动和动力的最基本的运动形式,称为元动作(Meta-action, MA);把实现某一个元动作的所有零件按照结构关系构成的整体,称为元动作单元(Meta-action Unit, MU).将元动作单元看作多体系统中的一个体,即可从运动的角度对数控机床的结构进行描述.
元动作单元通常包括移动单元和转动单元两种,例如油缸中活塞移动单元,齿轮转动单元.对一个元动作单元而言通常包含动力输入件、支撑件、中间件、动力输出件和紧固件五大基本要素.其中动力输出件定义如下[13]:元动作单元中向下游元动作单元输出运动和动力的零件.例如蜗杆转动元动作单元中的蜗杆.
1.2 数控机床拓扑结构拓扑结构是对多体系统本质的高度提炼和概括,是研究多体系统的依据和基础,对多系统拓扑结构描述,是多体系统理论的基本问题[14].根据多体系统理论,将一个元动作单元看作一个体,各元动作单元之间只有单自由度的相对运动,约束类型为移动或转动,因此数控机床拓扑结构如图 2所示.

|
图 2 基于多体系统和元动作单元的数控机床拓扑结构 Fig. 2 CNC machine tool topology based on multi-body system and meta-action units |
如图 2所示,在多体系统中,在惯性体B0(一般数控机床惯性体为床身)和所有元动作单元上均建立与其固定联接的右手直角笛卡尔三维坐标系,这些坐标系称为广义坐标系.其中,广义坐标系中惯性体上的坐标系称为惯性参考坐标系,各个元动作单元坐标系称为子坐标系或动坐标系,每个坐标系中的三个正交基按右手定则分别设为X、Y、Z轴.由于元动作单元的动力输出件(简称输出件)的作用是向下游元动作单元输出动力和运动,所以元动作单元的运动精度很大程度取决于输出件的运动精度.因此元动作单元动坐标系一般建立在动力输出件上.建立多体系统坐标系后,对于各元动作单元之间的相对运动分析就可以转换为对各动坐标系之间的相对运动分析.
2 基于旋量理论的数控机床运动误差建模 2.1 旋量理论在三维欧式空间R3中设S为参考坐标系,T为固定在刚体上的物体坐标系,刚体相对于参考坐标系的位置和姿态(位姿)可由下式描述[15]:
| $ {\rm{SE}}\left( 3 \right) = \left\{ {\left( {\mathit{\boldsymbol{R}},\mathit{\boldsymbol{t}}} \right)\;\;\;\mathit{\boldsymbol{R}} \in {\rm{SO}}\left( 3 \right),t \in {{\bf{R}}^3}} \right\}. $ | (1) |
式中:SE(3)为特殊欧式群;R为3×3姿态旋转矩阵;t为位置向量;SE(3)为特殊正交群.
根据欧拉旋转定理,对于刚体的每一个旋转运动,都有一个旋转矩阵R(R∈SO(3))与之对应,设ω表示旋转轴方向的单位矢量,θ为转角,则R可写成ω和θ的函数:
| $ \mathit{\boldsymbol{R}} = {{\rm{e}}^{\theta \mathit{\boldsymbol{\hat \omega }}}}, $ | (2) |
其中
| $ \mathit{\boldsymbol{\hat \omega }} = \left( {\begin{array}{*{20}{c}} 0&{ - {\omega _z}}&{{\omega _y}}\\ {{\omega _z}}&0&{ - {\omega _x}}\\ { - {\omega _y}}&{{\omega _x}}&0 \end{array}} \right). $ |
根据指数映射关系,可得
| $ {{\rm{e}}^{\theta \mathit{\boldsymbol{\hat \omega }}}} = \mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\hat \omega }}\sin \theta + {{\mathit{\boldsymbol{\hat \omega }}}^2}\left( {1 - \cos \theta } \right). $ | (3) |
根据Chasles定理[16],任意刚体运动都可以通过螺旋运动即通过绕某轴的转动与沿该轴移动的复合运动实现.也就是说刚体运动与螺旋运动是等价的.因此刚体运动变换可以用旋量指数积形式表示为
| $ \mathit{\boldsymbol{g}} = \left( {\begin{array}{*{20}{c}} {{{\rm{e}}^{\theta \mathit{\boldsymbol{\hat \omega }}}}}&{\left( {\mathit{\boldsymbol{E}} - {{\rm{e}}^{\theta \mathit{\boldsymbol{\hat \omega }}}}\left( {\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{v}}} \right)} \right) + \theta \mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{v}}}\\ 0&1 \end{array}} \right). $ | (4) |
式中:ω表示螺旋轴方向的单位矢量;υ表示沿螺旋轴移动的位移矢量;θ表示转角.将式中的υ和θ分别用移动误差矢量和转动误差代替即可得到运动误差变换矩阵.
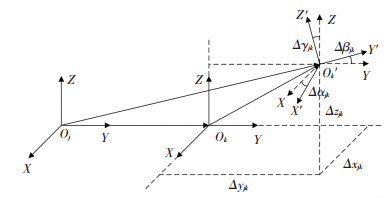
2.2 相邻元动作单元运动误差矩阵当某一元动作单元相对于其相邻元动作单元的某一轴运动时,会在六个自由度方向上产生六项运动误差,其几何意义如图 3所示.
|
图 3 相邻元动作单元相对运动示意图 Fig. 3 Schematic diagram of relative motion of meta-action units |
图 3中:Ok表示元动作单元k相对于其相邻元动作单元j的理论位置;Ok′表示元动作单元k相对于相邻元动作单元j的实际位置;Δxjk、Δyjk、Δzjk分别为沿X、Y、Z轴的移动误差;Δαjk、Δβjk、Δγjk为绕X、Y、Z轴的转动误差.
根据图 3的相邻元动作单元相对运动示意图,将元动作单元k从Ok运动到Ok′这一运动过程称为误差运动.因此可以把误差运动分解为X、Y、Z三个方向上的螺旋运动. X方向螺旋运动描述为:绕X轴转动Δαjk与沿X轴移动Δxjk的复合运动. Y方向螺旋运动描述为:绕Y轴转动Δβjk与沿Y轴移动Δyjk的复合运动. Z方向螺旋运动描述为:绕Z轴转动Δγjk与沿Z轴移动Δzjk的复合运动.应用旋量理论可分别求出三个螺旋运动的运动误差矩阵,最后综合三个螺旋运动误差矩阵即可得到相邻元动作单元的运动误差矩阵.以X方向螺旋运动为例:螺旋轴方向(X)的单位矢量ω=(1 0 0)T;转角θ=Δαjk;沿X轴移动的位移矢量υ=(Δxjk 0 0);反对称矩阵
| $ \mathit{\boldsymbol{\hat \omega }} = \left( {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&{ - 1}\\ 0&1&0 \end{array}} \right). $ |
将ω、θ、υ、
| $ {\mathit{\boldsymbol{g}}_X} = \left( {\begin{array}{*{20}{c}} 1&0&0&{\Delta {x_{jk}}\Delta {\alpha _{jk}}}\\ 0&{\cos \Delta {\alpha _{jk}}}&{ - \sin \Delta {\alpha _{jk}}}&0\\ 0&{\sin \Delta {\alpha _{jk}}}&{\cos \Delta {\alpha _{jk}}}&0\\ 0&0&0&1 \end{array}} \right). $ | (5) |
同理可得到Y、Z方向螺旋运动的运动误差矩阵:
| $ {\mathit{\boldsymbol{g}}_Y} = \left( {\begin{array}{*{20}{c}} {\cos \Delta {\beta _{jk}}}&0&{\sin \Delta {\beta _{jk}}}&0\\ 0&1&0&{\Delta {y_{jk}}\Delta {\beta _{jk}}}\\ { - \sin \Delta {\beta _{jk}}}&0&{\cos \Delta {\beta _{jk}}}&0\\ 0&0&0&1 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{g}}_Z} = \left( {\begin{array}{*{20}{c}} {\cos \Delta {\gamma _{jk}}}&{ - \sin \Delta {\gamma _{jk}}}&0&0\\ {\sin \Delta {\gamma _{jk}}}&{\cos \Delta {\gamma _{jk}}}&0&0\\ 0&0&1&{\Delta {z_{jk}}\Delta {\gamma _{jk}}}\\ 0&0&0&1 \end{array}} \right). $ |
相邻元动作单元运动误差矩阵为三个方向螺旋运动误差矩阵相乘,当Δαjk、Δβjk、Δγjk较小时,忽略高阶无穷小,相邻元动作单元误差矩阵为
| $ \begin{array}{l} {\mathit{\boldsymbol{g}}_{jk}} = {\mathit{\boldsymbol{g}}_X}{\mathit{\boldsymbol{g}}_Y}{\mathit{\boldsymbol{g}}_Z} = \\ \;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} 1&{ - \Delta {\gamma _{jk}}}&{\Delta {\beta _{jk}}}&{\Delta {x_{jk}}\Delta {\alpha _{jk}}}\\ {\Delta {\gamma _{jk}}}&1&{ - \Delta {\alpha _{jk}}}&{\Delta {y_{jk}}\Delta {\beta _{jk}}}\\ { - \Delta {\beta _{jk}}}&{\Delta {\alpha _{jk}}}&1&{\Delta {z_{jk}}\Delta {\gamma _{jk}}}\\ 0&0&0&1 \end{array}} \right). \end{array} $ | (6) |
将相互联系且按一定顺序排列的能够实现一定运动功能的元动作单元组合定义为元动作单元链.由FMA分解树以及元动作单元链定义可以知道,数控机床完成某功能运动是由不同的元动作单元链综合作用而实现的.因此,数控机床整机的误差是由各条元动作单元链的误差累积形成.对于某一条元动作单元链而言,其误差又是由组成单元链的各个元动作单元的误差累计形成.在此将元动作单元链空间运动误差定义为组成某一条元动作单元链所有元动作单元运动误差的综合.显然,数控机床空间运动误差可以定义为元动作单元链空间运动误差的综合. 图 4是元动作单元链空间运动误差形成过程.其中:R0为惯性参考坐标系,R1、Rk、Rk+1、Rq-1、Rq为元动作单元理想位置坐标系,R1'、Rk'、Rk+1'、Rq-1'、Rq'为元动作单元实际位置坐标系,Ei为第i条元动作单元链的空间运动误差矩阵.

|
图 4 元动作单元链空间运动误差形成过程 Fig. 4 Meta-motion unit chain space motion error formation process |
利用式(6)的运动误差矩阵描述元动作单元链中相邻元动作单元之间的相对运动关系,定义元动作单元链空间运动误差矩阵为元动作单元链中各相邻元动作单元的运动误差矩阵相乘.则Ei为
| $ {\mathit{\boldsymbol{E}}_i} = {\mathit{\boldsymbol{g}}_{01}}{\mathit{\boldsymbol{g}}_{12}} \cdots {\mathit{\boldsymbol{g}}_{q - 2,q - 1}}{\mathit{\boldsymbol{g}}_{q - 1,q}}. $ | (7) |
数控机床整机误差是由各条元动作单元链的运动误差综合累积而成,定义整机空间运动误差矩阵为各条元动作单元链元的运动误差矩阵相乘,当Δαjk、Δβjk、Δγjk较小时,忽略高阶无穷小,整机误差特征矩阵简化形式如下:
| $ \mathit{\boldsymbol{E}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{E}}_i}} = \left( {\begin{array}{*{20}{c}} 1&{\Delta \gamma }&{\Delta \beta }&{\Delta x\Delta \alpha }\\ {\Delta \gamma }&1&{ - \Delta \alpha }&{\Delta y\Delta \beta }\\ { - \Delta \beta }&{\Delta \alpha }&1&{\Delta z\Delta \gamma }\\ 0&0&0&1 \end{array}} \right). $ | (8) |
式中:n为元动作单元链数目;Δx、Δy、Δz表示整机误差沿参考坐标系的X、Y、Z轴的移动误差分量;Δα、Δβ、Δγ表示整机误差沿参考坐标系的X、Y、Z轴的转动误差分量.由式(8)可以看出,空间运动误差由六个分量组成,但是在实际中对于精度的衡量指标并没有分为六个分量,往往是六个分量的综合.例如机床加工精度为0.002 mm,0.002 mm这个数值并不表示加工精度的某个分量的值,而是表示由六个分量误差综合作用后形成的最终误差.因此为了使空间运动误差更具有几何意义,利用螺旋理论来综合空间运动误差的六个分量.
根据文献[17]中关于螺旋理论的定义可知,螺旋是指绕特定轴线的转动和沿改轴线的移动的合成运动,空间中任意运动都可以合成为一个螺旋运动.该轴线称为螺旋轴线,且利用Plücker坐标表示单位螺旋如下:
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {\vec s}\\ {\vec r \times \vec s + h\vec s} \end{array}} \right] = {\left( {{s_1},{s_2},{s_3},{s_4},{s_5},{s_6}} \right)^{\rm{T}}}. $ | (9) |
式中:s1、s2、s3分别表示绕X、Y、Z轴的转动分量和s4、s5、s6沿X、Y、Z轴的移动分量;
| $ h = \frac{{{s_1}{s_4} + {s_2}{s_5} + {s_3}{s_6}}}{{\sqrt {s_1^2 + s_2^2 + s_3^2} }}, $ | (10) |
| $ m = \sqrt {s_1^2 + s_2^2 + s_3^2} . $ | (11) |
根据式(8)~(11),空间运动误差螺旋定义为
| $ {h_E} = \frac{{\Delta \alpha \times \Delta x + \Delta \beta \times \Delta y + \Delta \gamma \times \Delta z}}{{\sqrt {{{\left( {\Delta \alpha } \right)}^2} + {{\left( {\Delta \beta } \right)}^2} + {{\left( {\Delta \gamma } \right)}^2}} }}, $ | (12) |
| $ {m_E} = \sqrt {{{\left( {\Delta \alpha } \right)}^2} + {{\left( {\Delta \beta } \right)}^2} + {{\left( {\Delta \gamma } \right)}^2}} . $ | (13) |
其中,mE表示空间运动误差螺旋大小,SE表示空间运动误差单位螺旋矢量,hE表示空间运动误差螺旋螺距.一般情况下可以用hE作为空间运动误差的综合值.
3 数控机床运动精度映射模型精度与零部件的制造成本之间存在一定的关系:零部件精度越高,越能满足设计要求,但是制造成本较高;零部件精度越低,制造成本越低,但生产出的产品质量越差[18].因此,在对精度质量特性进行映射时,必须考虑成本问题.
3.1 运动精度映射模型 3.1.1 运动精度-成本函数在设计阶段,通常还不能定出成本数值,因此一般不可能建立制造成本的精确数值,但是可以定性或相似的估计.根据文献[19]提出的成本估计模型,精度成本函数近似计算模型如下:
| $ \min f\left( x \right) = {\rm{Cos}}{{\rm{t}}_\Sigma } = \sum\limits_{i = 1}^n {a{{\rm{e}}^{ - {x_i}/b}}} , $ | (14) |
其中,a,b为待定常数,一般根据各个企业的经验取值;xi为第i个元动作单元的运动精度值,由公式(12)计算;n为元动作单元的个数.
3.1.2 运动精度映射模型设数控机床预定的精度值为ΔE,为不使机床精度超过预定的值,一般情况下要让机床空间运动误差螺旋大小mE小于预定的精度值,即约束条件为
| $ {m_E} \le \Delta E. $ | (15) |
精度映射问题可以看作是满足产品性能要求且制造成本最低的多目标优化问题.根据式(12)~(15),以空间运动误差螺旋大小为约束,以空间运动误差螺距最小和制造成本最低为目标,构建运动精度多目标优化映射模型如下:
以F=[f1 f2]T为优化目标:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{Minimize}}\;{f_1} = \frac{{\Delta \alpha \times \Delta x + \Delta \beta \times \Delta y + \Delta \gamma \times \Delta z}}{{\sqrt {{{\left( {\Delta \alpha } \right)}^2} + {{\left( {\Delta \beta } \right)}^2} + {{\left( {\Delta \gamma } \right)}^2}} }},}\\ {{\rm{Minimize}}\;{f_2} = {\rm{Cos}}{{\rm{t}}_\Sigma } = \sum\limits_{i = 1}^n {a{{\rm{e}}^{ - {x_i}/b}}} ,}\\ {{\rm{s}}.{\rm{t}}.\;\;{m_E} = \sqrt {{{\left( {\Delta \alpha } \right)}^2} + {{\left( {\Delta \beta } \right)}^2} + {{\left( {\Delta \gamma } \right)}^2}} \le \Delta E.}\\ {0 \le {x_i},1 \le i \le n.} \end{array}} \right. $ | (16) |
式中:f1、f2为优化目标;mE为约束条件;xi为设计变量,即各个元动作单元的运动精度值;n为设计变量数.
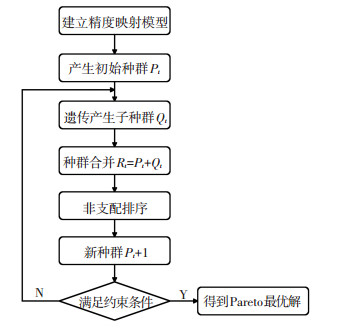
3.2 基于NSGA-Ⅱ算法的精度映射方法为解决上述多目标优化问题,采用NSGA-Ⅱ算法进行运动精度映射求解. NSGA-Ⅱ是由K.Ded和S.Agrawala[20]提出,是非支配排序遗传算法NSGA的改良版.映射方法步骤如下:
1) 建立数控机床运动精度映射模型.以根据公式(16)以空间运动误差螺旋大小为约束,以空间运动误差螺距最小和制造成本最低为目标,构建运动精度多目标优化映射模型.
2) 初始化种群.随机初始化个体数为N的种群Pt,并将所有各体按非支配关系排序且计算适应度值.
3) 利用遗传操作选择、交叉和变异产生新种群Qt.
4) 对种群Pt和种群Qt进行合并得到种群Rt.
5) 非支配排序.采用快速非劣排序算法将种群Rt中的各体划分成不同的非劣级别.
6) 产生新种群Pt+1.
7) 判断是否满足遗传算法约束条件,若满足则退出算法,并得到Pareto最优解;否则继续执行步骤3).计算流程如图 5所示.
|
图 5 遗传算法中精度映射计算流程图 Fig. 5 Flow chart of precision mapping calculation in genetic algorithm |
以国产某机床厂设计生产的某型号精密卧式加工中心为例,说明运动精度映射过程.由于卧式加工中心分解后得到的元动作单元数目较多,限于篇幅原因,这里只以托盘交换架为例,说明映射过程.托盘交换架的功能是交换已加工工件和待加工工件的位置,其运动精度的大小直接影响工件的加工位置,进而影响整机加工精度,其回转部分结构如图 6所示.

|
图 6 托盘交换架回转部分结构图 Fig. 6 Swivel part structure of pallet exchange frame |
根据图 6托盘交换架回转部分结构,按照元动作单元获取步骤对托盘交换架进行分解, 得到液压电磁阀阀门开合、回转油缸活塞移动、齿条移动、齿轮转动、托架转动5个元动作单元.由于液压电磁阀阀门开合运动对托盘交换架的运动精度影响较小,因此这里不作讨论.交换架回转运动单元结构化分解如图 7所示,其元动作单元链如图 8所示.

|
图 7 交换架回转运动单元结构化分解 Fig. 7 Structured decomposition of exchange frame rotary motion unit |

|
图 8 元动作单元链 Fig. 8 Chain of meta-motion unit |
根据式(8)空间运动误差模型,以元动作单元的运动精度(如活塞移动元动作单元的移动精度、齿轮转动元动作单元的转动精度)为设计变量,最小化制造成本和最小化空间运动误差螺距为目标函数,空间运动误差螺旋大小为约束构建精度质量特性映射模型.
1) 运动精度设计变量.由图 6托盘交换架回转部分结构图可知,相邻元动作单元之间只有单自由度的相对运动,因此设计变量为
| $ \begin{array}{l} X = \left( {\Delta _x^{01},\Delta _y^{01},\Delta _z^{01},\Delta _\alpha ^{01},\Delta _\beta ^{01},\Delta _\gamma ^{01},\Delta _x^{12},\Delta _y^{12},\Delta _z^{12},} \right.\\ \;\;\;\;\;\;\;\Delta _\alpha ^{12},\Delta _\beta ^{12},\Delta _\gamma ^{12},\Delta _x^{23},\Delta _y^{23},\Delta _z^{23},\Delta _\alpha ^{23},\Delta _\beta ^{23},\Delta _\gamma ^{23},\\ \;\;\;\;\;\;\;\left. {\Delta _x^{34},\Delta _y^{34},\Delta _z^{34},\Delta _\alpha ^{34},\Delta _\beta ^{34},\Delta _\gamma ^{34}} \right) = \left( {{x_1},{x_2},{x_3},{x_4},} \right.\\ \;\;\;\;\;\;\;{x_5},{x_6},{x_7},{x_8},{x_9},{x_{10}},{x_{11}},{x_{12}},{x_{13}},{x_{14}},{x_{15}},{x_{16}},\\ \;\;\;\;\;\;\;\left. {{x_{17}},{x_{18}},{x_{19}},{x_{20}},{x_{21}},{x_{22}},{x_{23}},{x_{24}}} \right). \end{array} $ |
根据公式(6)、(7),求得空间运动误差矩阵为:
| $ \begin{array}{l} \mathit{\boldsymbol{E}} = {\mathit{\boldsymbol{g}}_{01}}{\mathit{\boldsymbol{g}}_{12}}{\mathit{\boldsymbol{g}}_{23}}{\mathit{\boldsymbol{g}}_{34}} = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} 1&{ - {x_6}}&{{x_5}}&{{x_1}{x_4}}\\ {{x_6}}&1&{ - {x_4}}&{{x_2}{x_5}}\\ { - {x_5}}&{{x_4}}&1&{{x_3}{x_6}}\\ 0&0&0&1 \end{array}} \right] \times \\ \;\;\;\left[ {\begin{array}{*{20}{c}} 1&{ - {x_{12}}}&{{x_{11}}}&{{x_7}{x_{10}}}\\ {{x_{12}}}&1&{ - {x_{10}}}&{{x_8}{x_{11}}}\\ { - {x_{11}}}&{{x_{10}}}&1&{{x_9}{x_{12}}}\\ 0&0&0&1 \end{array}} \right] \times \\ \;\;\;\left[ {\begin{array}{*{20}{c}} 1&{ - {x_{18}}}&{{x_{17}}}&{{x_{13}}{x_{16}}}\\ {{x_{18}}}&1&{ - {x_{16}}}&{{x_{14}}{x_{17}}}\\ { - {x_{17}}}&{{x_{16}}}&1&{{x_{15}}{x_{18}}}\\ 0&0&0&1 \end{array}} \right] \times \\ \;\;\;\left[ {\begin{array}{*{20}{c}} 1&{ - {x_{24}}}&{{x_{23}}}&{{x_{19}}{x_{22}}}\\ {{x_{24}}}&1&{ - {x_{22}}}&{{x_{20}}{x_{23}}}\\ { - {x_{23}}}&{{x_{22}}}&1&{{x_{21}}{x_{24}}}\\ 0&0&0&1 \end{array}} \right]. \end{array} $ |
为减小篇幅,定义:
| $ {t_x} = {x_1}{x_4} + {x_7}{x_{10}} + {x_{13}}{x_{16}} + {x_{19}}{x_{22}}, $ |
| $ {t_y} = {x_2}{x_5} + {x_8}{x_{11}} + {x_{14}}{x_{17}} + {x_{20}}{x_{23}}, $ |
| $ {t_y} = {x_3}{x_6} + {x_9}{x_{12}} + {x_{15}}{x_{18}} + {x_{21}}{x_{24}}, $ |
| $ {t_\alpha } = {x_4} + {x_{10}} + {x_{16}} + {x_{22}}, $ |
| $ {t_\beta } = {x_5} + {x_{11}} + {x_{17}} + {x_{23}}, $ |
| $ {t_\gamma } = {x_6} + {x_{12}} + {x_{18}} + {x_{24}}. $ |
忽略高阶无穷小,求得的最终的空间运动误差矩阵为
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{r}} 1&{ - {t_\gamma }}&{{t_\beta }}&{{t_x}}\\ {{t_\gamma }}&1&{ - {t_\alpha }}&{{t_y}}\\ { - {t_\beta }}&{{t_\alpha }}&1&{{t_z}}\\ 0&0&0&1 \end{array}} \right] $ |
2) 根据公式(12)、(14),运动精度映射目标函数为
| $ {f_1} = \frac{{{t_x} + {t_y} + {t_z}}}{{\sqrt {{{\left( {{t_\alpha }} \right)}^2} + {{\left( {{t_\beta }} \right)}^2} + {{\left( {{t_\gamma }} \right)}^2}} }}. $ |
根据该机床厂的经验,咨询该厂相关设计人员,式(14)中的a、b分别取值为1.2和1.6,则精度成本函数为
| $ \begin{array}{l} {f_2} = {\rm{Cos}}{{\rm{t}}_\Sigma } = \sum\limits_{i = 1}^4 {{\rm{M}}{{\rm{C}}_i}} = {\rm{M}}{{\rm{C}}_1} + {\rm{M}}{{\rm{C}}_2} + {\rm{M}}{{\rm{C}}_3} + {\rm{M}}{{\rm{C}}_4} = \\ \;\;\;\;1.2{{\rm{e}}^{ - \frac{{{x_1}{x_4} + {x_2}{x_5} + {x_3}{x_6}}}{{{{\left( {{x_4}} \right)}^2} + {{\left( {{x_5}} \right)}^2} + {{\left( {{x_6}} \right)}^2}}}}} + 1.2{{\rm{e}}^{ - \frac{{{x_7}{x_{10}} + {x_8}{x_{11}} + {x_9}{x_{12}}}}{{1.6\sqrt {{{\left( {{x_{10}}} \right)}^2} + {{\left( {{x_{11}}} \right)}^2} + {{\left( {{x_{12}}} \right)}^2}} }}}} + \\ \;\;\;\;1.2{{\rm{e}}^{ - \frac{{{x_{13}}{x_{16}} + {x_{14}}{x_{17}} + {x_{15}}{x_{18}}}}{{1.6\sqrt {{{\left( {{x_{16}}} \right)}^2} + {{\left( {{x_{17}}} \right)}^2} + {{\left( {{x_{18}}} \right)}^2}} }}}} + 1.2{{\rm{e}}^{ - \frac{{{x_{19}}{x_{22}} + {x_{20}}{x_{23}} + {x_{21}}{x_{24}}}}{{1.6\sqrt {{{\left( {{x_{22}}} \right)}^2} + {{\left( {{x_{23}}} \right)}^2} + {{\left( {{x_{24}}} \right)}^2}} }}}}. \end{array} $ |
3) 加工中心精度预定值为ΔE=0.005 mm.由公式(15)、(16)精度映射数学模型为
| $ \left\{ {\begin{array}{*{20}{c}} {{x_i},1 \le i \le 24,}\\ {\min {f_1}\left( X \right),}\\ {\min {f_2}\left( X \right),}\\ {{\rm{s}}.{\rm{t}}.\;\;0 < {x_i} < 0.005,}\\ {g\left( X \right) = {m_E} - 0.005 \le 0.} \end{array}} \right. $ |
建立好精度映射模型后,运用Isight软件并结合MATLAB的NSGA-Ⅱ算法进行精度映射求解,NSGA-Ⅱ算法参数设置如下:种群数pop=16,进化代数gen=30,交叉率Pc=0.9,变异率Pm=0.1,交叉操作分配率mu=20,变异操作分配率mum=20.映射求解结果如图 8所示.
经过NSGA-Ⅱ算法得到481组结果,其中绿色区表示最优解,其他颜色区域表示非最优解.根据绿色区的最优解,利用公式(12)对每个元动作单元的精度进行螺旋综合,得到元动作单元的映射精度值,如表 1所示.由表 1可知,精度质量特性映射结果为:回转油缸活塞移动元动作单元A1的移动精度为0.003 38 mm,齿条移动元动作单元A2的移动精度为0.002 07 mm,齿轮转动元动作单元A3的回转精度为0.002 75 mm,托架转动元动作单元A4的回转精度为0.003 96 mm.根据映射结果,设计人员可以把上述映射结果作为元动作单元的设计输入,合理安排设计要求对元动作单元进行设计.

|
图 9 映射求解结果 Fig. 9 Mapping solution result |
| 表 1 映射结果 Tab. 1 Mapping result |
1) 从运动角度出发对数控机床进行结构化分解得到元动作单元分解树,结合多体系统理论并利用旋量理论建立了数控机床误差模型,并运用螺旋理论对空间运动误差进行了综合.
2) 建立了运动精度映射模型,使用Isight和MATLAB软件结合NSGA-Ⅱ遗传算法进行运动精度映射求解.
3) 以某国产加工中心为例求解得到元动作单元的运动精度值,验证了映射模型的有效性和可行性,并为设计人员提供了设计参考.
| [1] |
孛朝旺, 杨志宏, 王林博, 等.尺寸工程技术综述与展望[J].计算机集成制造系统, 2014, 20(3): 464 BO Chaowang, YANG Zhihong, et al. Review and outlook of dimensional engineering[J]. Computer Integrated Manufacturing Systems, 2014, 20(3): 464 http://www.cqvip.com/QK/97749X/201403/49173673.html |
| [2] |
PEZESHKI M, AREZOO B. Kinematic errors identification of three-axis machine tools based on machined work pieces[J]. Precision Engineering, 2016, 43: 493. DOI:10.1016/j.precisioneng.2015.09.018 |
| [3] |
IBARAKI S, SAWADA M, MASTUBARA A. Machining tests to identify kinematic errors on five-axis machine tools[J]. Precision Engineering, 2010, 34: 387. DOI:10.1016/j.precisioneng.2009.09.007 |
| [4] |
FAN Jinwei, TAO Haohao, WU Changjun. Kinematic errors prediction for multi-axis machine tools' guideways based on tolerance[J]. International Journal of Advanced Manufacturing Technology, 2018, 98(5): 1131. |
| [5] |
郭世杰, 姜歌东, 梅雪松. 摆头转台型五轴机床旋转轴运动误差测量与辨识[J]. 农业机械学报, 2019, 50(2): 402. GUO Shijie, JIANG Gedong, MEI Xuesong. Motionerror measurement and identification of rotary axis of five-axis machine tool[J]. Transactions of the Chinese Society of Agricultural Machinery, 2019, 50(2): 402. |
| [6] |
余永维, 杜柳青. 深度学习框架下数控机床运动误差溯因方法[J]. 仪器仪表学报, 2019, 40(1): 28. YU Yongwei, DU Liuqing. Motion error tracing of NC machine tools based on deep learning framework[J]. Chinese Journal of Scientific Instrument, 2019, 40(1): 28. |
| [7] |
张学波, 方标, 应文威. 多子阵合成孔径声呐系统中的侧摆运动误差补偿[J]. 电讯技术, 2018, 58(2): 138. ZHANG Xuebo, FANG Biao, YING Wenwei. Motioncompensation of sway error for multireceiver synthetic aperture sonar system[J]. Telecommunication Engineering, 2018, 58(2): 138. DOI:10.3969/j.issn.1001-893x.2018.02.004 |
| [8] |
雷楠南. 基于螺距误差补偿提高YK7350数控磨齿机的运动精度[J]. 无锡职业技术学院学报, 2018, 17(5): 30. LEI Nannan. Improving the motion accuracy of YK7350 CNC gear grinding machine based on pitch error compensation[J]. Journal of Wuxi Institute of Technology, 2018, 17(5): 30. |
| [9] |
王美清, 唐晓青. 产品设计中的用户需求与产品质量特映射方法研究[J]. 机械工程学报, 2004, 40(5): 136. WANG Meiqing, TANG Xiaoqing. Mapping customer requirements to produce quality characteristics[J]. Chinese Journal of Mechanical Engineering, 2004, 40(5): 136. DOI:10.3321/j.issn:0577-6686.2004.05.028 |
| [10] |
安相华, 冯毅雄, 谭建荣. 基于DEMATEL和Choquet积分的质量特性映射方法[J]. 计算机集成制造系统, 2011, 17(9): 1887. AN Xianghua, FENG Yixiong, TAN Jianrong. Quality characteristics mapping method based on DEMATEL and Choquet integral[J]. Computer Integrated Manufacturing Systems, 2011, 17(9): 1887. |
| [11] |
HUSTON R. L. Multibody dynamics-model and analysis methods[J]. Appl. Mech. Rev, 1991, 44(3): 109. DOI:10.1115/1.3119496 |
| [12] |
鞠萍华, 黄广全, 冉琰, 等. 基于运动单元故障建模的装配可靠性控制技术[J]. 中南大学学报, 2018, 49(9): 2197. JU Pinghua, HUANG Guangquan, RAN Yan, et al. Reliability control method of assembly process of products based on motion unit fault model[J]. Journal of Central South University, 2018, 49(9): 2197. |
| [13] |
姚梦生.数控机床典型元动作单元可靠性分析技术研究[D].重庆: 重庆大学, 2018 YAO Mengsheng. Research on reliability analysis technology of typical meta-action units of NC machine tools[D]. Chongqing: Chongqing University, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10611-1018852954.htm |
| [14] |
康方, 范晋伟. 用于精度分配的数控机床误差建模[J]. 机械制造, 2007, 45(4): 9. KANG Fang, FAN Jinwei. Error modeling of CNC machine tools for accuracy distribution[J]. Machinery, 2007, 45(4): 9. DOI:10.3969/j.issn.1000-4998.2007.04.003 |
| [15] |
李丽, 房立金, 王国勋. 基于螺旋理论的6R串联工业机器人奇异位形分析[J]. 组合机床与自动化加工技术, 2017(12): 1. LI Li, FANG Lijin, WANG Guoxun. Singularity analysis of 6R series industrial robot based on screw theory[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2017(12): 1. |
| [16] |
SELIG J. Geometrical foundations of robotics[M]. Singapore: World Scientific Publishing Co., Inc., 2000.
|
| [17] |
黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2014. HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Higher space institution[M]. Beijing: Higher Education Press, 2014. |
| [18] |
赵廷明, 刘德顺, 张俊, 等. 面向多质量特征的产品质量损失成本模型及其应用[J]. 中南大学学报(自然科学版), 2012, 43(5): 1753. ZHAO Yanming, LIU Deshun, ZHANG Jun, et al. Quality loss cost model and its application to products with multi-quality characteristics[J]. Journal of Central South University: Science and Technology, 2012, 43(5): 1753. |
| [19] |
WIKDE D, PRENTICE E, Minimum exponential cost allocation of sure-fit tolerance ASME Paper USA 1975, 75-DET-93
|
| [20] |
DEB K, PRATAP A, AGARWAL S, et al. A first and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions. On Evolutionary Computation, 2002, 6(2): 182. DOI:10.1109/4235.996017 |
 2020, Vol. 52
2020, Vol. 52


