涡旋压缩机与其他类型的压缩机相比,具有结构紧凑、高效节能、可靠性高、微振低噪等诸多优点,已广泛应用于制冷、空调、涡旋增压器和涡旋膨胀机等领域[1-3].它是依靠一对啮合的动静涡旋齿之间所形成的密闭容积由大到小的周期性变化,来实现对工作介质的吸入、压缩和排放的.构成涡旋齿的型线决定了涡旋压缩机的几何特性、加工性能和磨损,进而最终影响涡旋压缩机的容积效率和机械效率[4-5],所以有关涡旋齿型线的研究成为一个热点.
根据涡旋齿齿廓的形状,可将型线划分为三大类,分别为等壁厚涡旋齿型线、渐变壁厚涡旋齿型线和变壁厚涡旋齿型线.等壁厚涡旋齿型线因数学描述简单、加工比较方便而得到广泛应用[6-7],它可由基圆渐开线、线段渐开线、正多边形渐开线等曲线构成;渐变壁厚涡旋齿型线可由变径基圆渐开线、阿基米德螺旋线和代数螺线等曲线构成,它的优势在于其齿厚的变化规律与其工作腔内介质压力的变化规律相一致,所以其性能较高[8-11].当涡旋压缩机需要较大压缩比时,采用前两种涡旋齿型线会导致型线圈数增加,泄漏线的长度增加,进而对涡旋压缩机产生不利影响.为克服上述缺陷,相关学者提出了用组合曲线来构造变壁厚涡旋齿型线的思路[12-13],从而用较少的圈数实现了大压缩比的要求.由上述分析可知,在理论上,能构成三大类涡旋齿型线的曲线类型众多,但每种曲线都有各自的特点和相应的表征方式.在以往对型线的研究中,只是针对每一种具体曲线展开讨论,给出其复杂的计算公式,这种研究方法将造成型线过分依赖于具体的型线表征方式,导致一种型线对应一种模型的局面,使建模不断重复.与此同时,因建立的模型针对性过强,致使得到的结论不具有普遍性和通用性.为解决上述问题,近年来又提出了通用型线的理论[14-15],这在一定程度上减少了重复建模的次数,提高了设计效率,但该理论并不完善,尚有待进一步研究.
涡旋齿型线传统设计方法是根据已知型线的特点,先选定型线类型,然后进行性能分析.这种方法存在的缺点是未充分考虑涡旋压缩机在实际工程应用中几何性能倾向性的问题,致使设计出的涡旋齿型线不能满足设计要求.为克服涡旋齿型线传统设计中存在的弊端,本文基于微分几何理论[16],在构成涡旋齿型线的曲线上依附一个Frenet标架,让其跟着曲线一起运动,通过Frenet标架的运动状态来刻画该曲线的形状特征,进而建立以曲率和Frenet标架为参数的涡旋齿型线的通用几何模型,实现对涡旋齿型线的准确描述,并以考虑涡旋压缩机工程应用为设计目标,来构造出众多符合设计要求的涡旋齿型线.
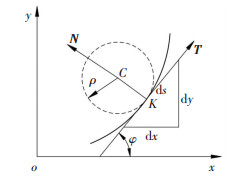
1 涡旋齿型线的通用几何模型图 1是任意涡旋型线的微分几何关系示意图.图中:ρ为曲率半径;C为曲率中心;φ为型线切向角参数;K为型线切点,T为单位切向量;N为单位法向量;dx为横坐标轴增量;dy为纵坐标轴增量;ds为弧长增量.
|
图 1 涡旋型线的微分几何关系 Fig. 1 Differential geometric relations of scroll profile |
在平面E2的右手笛卡尔直角坐标系下,曲线r=r(s)可以表示为
| $ \mathit{\boldsymbol{r}} = \mathit{\boldsymbol{r}}\left( s \right) = \left( {x\left( s \right),y\left( s \right)} \right), $ | (1) |
其中s是弧长参数.
记任意涡旋型线的切线与x轴正向的夹角为φ=φ(s),则在切点处的单位切向量和单位法向量分别为
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{T}}\left( s \right) = \left( {\cos \varphi \left( s \right),\sin \varphi \left( s \right)} \right), $ | (2) |
| $ \mathit{\boldsymbol{N}} = \mathit{\boldsymbol{N}}\left( s \right) = \left( { - \sin \varphi \left( s \right),\cos \varphi \left( s \right)} \right), $ | (3) |
根据微分几何关系,见图 1,易得
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}x}}{{{\rm{d}}s}} = \cos \varphi \left( s \right),}\\ {\frac{{{\rm{dy}}}}{{{\rm{d}}s}} = \sin \varphi \left( s \right).} \end{array}} \right. $ | (4) |
且涡旋型线在切点处的曲率半径为
| $ \rho \left( \varphi \right) = \frac{{{\rm{d}}s}}{{{\rm{d}}\varphi }}. $ | (5) |
由于T(s)为单位向量场,故有T(s)⊥T′(s),所以T′(s)是N(s)的倍数,设为
| $ \mathit{\boldsymbol{T'}}\left( s \right) = {\mathit{\boldsymbol{\kappa }}_r}\left( s \right)\mathit{\boldsymbol{N}}\left( s \right), $ | (6) |
因此
| $ {\mathit{\boldsymbol{\kappa }}_r}\left( s \right) = \mathit{\boldsymbol{T'}}\left( s \right) \cdot \mathit{\boldsymbol{N}}\left( s \right) = \left| {\begin{array}{*{20}{l}} {x'\left( s \right)}&{y'\left( s \right)}\\ {x''\left( s \right)}&{y''\left( s \right)} \end{array}} \right|, $ | (7) |
式中κr为平面曲线的曲率.故有
| $ {\mathit{\boldsymbol{\kappa }}_r}\left( s \right) = \frac{{{\rm{d}}\varphi \left( s \right)}}{{{\rm{d}}s}}. $ | (8) |
综合以上各式,得到平面曲线的Frenet标架{r(s); T(s), N(s)}沿涡旋齿型线运动的公式为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}\mathit{\boldsymbol{r}}}}{{{\rm{d}}s}} = \mathit{\boldsymbol{T}}\left( s \right),}\\ {\frac{d}{{{\rm{d}}s}}\left( {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{T}}\left( s \right)}\\ {\mathit{\boldsymbol{N}}\left( s \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{{k_r}\left( s \right)}\\ { - {k_r}\left( s \right)}&0 \end{array}} \right)\left( {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{T}}\left( s \right)}\\ {\mathit{\boldsymbol{N}}\left( s \right)} \end{array}} \right).} \end{array}} \right. $ | (9) |
结合式(5)与式(9),并代入初值(x0(φ0), y0(φ0)),便得到任意涡旋齿型线的母线方程为
| $ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} x\left( \varphi \right) = {x_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {\rho \left( \varphi \right)\cos \varphi \left( s \right){\rm{d}}\varphi } ,\\ y(\varphi ) = {y_0}\left( {{\varphi _0}} \right) + \int_0^\varphi \rho (\varphi )\sin \varphi (s){\rm{d}}\varphi , \end{array} \right.}\\ {\left( {\varphi \in \left[ {0,{\varphi _{\max }}} \right]} \right)} \end{array} $ | (10) |
式中φmax为母线的最大切向角.
根据泰勒级数,任意函数曲线的数学表达式都可表示为切向角φ的函数形式,并且只要该函数是关于φ的递增函数,就可以通过此函数来表示任意满足啮合条件的涡旋型线.因此将式(10)中的曲率半径函数表征为
| $ \begin{array}{l} \rho \left( \varphi \right) = {a_0} + {a_1}\varphi + {a_2}{\varphi ^2} + \cdots = \sum\limits_{i = 0}^n {{a_i}} {\varphi ^i}.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 0,1,2, \cdots ,n} \right) \end{array} $ |
式中:ai称为型线的控制系数,i称为曲线的阶次.当i=0时称为零次曲线,型线方程表示的曲线是圆或者圆弧,可用来对涡旋齿型线的齿头部分进行修正;当i=1时称为一次曲线,型线方程表示的曲线是圆渐开线,可构成等壁厚涡旋齿型线;当i≥2时称为高次曲线,型线方程表示的曲线是变径基圆渐开线,可构成渐变壁厚涡旋齿型线.
若要构造变壁厚的涡旋齿型线,可将曲率半径函数ρ(φ)表征为分段函数的形式,只要在各连接点处满足曲线连续性和光滑性的条件即可.由此可见,当曲率半径函数ρ(φ)不分段时,能构成等壁厚和渐变壁厚的涡旋齿型线;当ρ(φ)分段时,又能构造出变壁厚的涡旋齿型线.通过曲率半径函数ρ(φ)的不同表征形式,不但将涡旋压缩机中的三大类涡旋齿型线统一纳入到一个函数方程中,而且通过调整曲率半径函数式中的控制系数就能对涡旋齿型线的特性进行优化和控制.
母线方程确定后,根据法向等距曲线的特点[17],确定动、静涡旋的内外壁型线方程.
动涡旋外壁型线方程为
| $ \left\{ \begin{array}{l} {x_{oo}} = {x_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {\left( {\rho \left( \varphi \right) - \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \cos \varphi \left( s \right){\rm{d}}\varphi ,\\ {y_{oo}} = {y_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {\left( {\rho \left( \varphi \right) - \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \sin \varphi \left( s \right){\rm{d}}\varphi . \end{array} \right. $ |
静涡旋内壁型线方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{fi}} = {x_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {\left( {\rho (\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \cos \varphi (s){\rm{d}}\varphi ,}\\ {{y_{fi}} = {y_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {\left( {\rho (\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \sin \varphi (s){\rm{d}}\varphi .} \end{array}} \right. $ |
动涡旋内壁型线方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{oi}} = - {x_0}\left( {{\varphi _0}} \right) - \int_0^\varphi {\left( {\rho (\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \cos \varphi (s){\rm{d}}\varphi ,}\\ {{y_{oi}} = - {y_0}\left( {{\varphi _0}} \right) - \int_0^\varphi {\left( {\rho (\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \sin \varphi (s){\rm{d}}\varphi .} \end{array}} \right. $ |
静涡旋外壁型线方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{fo}} = - {x_0}\left( {{\varphi _0}} \right) - \int_0^\varphi {\left( {\rho (\varphi ) - \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \cos \varphi (s){\rm{d}}\varphi ,}\\ {{y_{fo}} = - {y_0}\left( {{\varphi _0}} \right) - \int_0^\varphi {\left( {\rho (\varphi ) - \frac{{{R_{{\rm{or}}}}}}{2}} \right)} \sin \varphi (s){\rm{d}}\varphi .} \end{array}} \right. $ |
式中Ror为回转半径.
为计算方便,取初值x0(φ0)=a1,y0(φ0)=0,根据上述涡旋型线方程,得到的动静涡旋啮合如图 2所示.

|
图 2 动静涡旋啮合 Fig. 2 Meshing of the fixed and orbiting scroll |
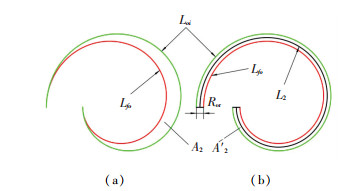
动、静涡旋相互啮合时,能够形成多对封闭的工作腔,如图 2所示,从内到外依次称为第一压缩腔(又称排气腔)、第二和第三压缩腔,分别用编号①、②、③来表示,各个工作腔的容积随着曲轴转角θ的变化而变化.如图 3(a)所示,以动涡旋的内壁面与静涡旋的外壁面所围成的第二压缩腔为例,易得单一月牙形腔体的面积A2为动涡旋内壁型线Loi所组成的面积与静涡旋外壁型线Lfo所组成的面积之差.根据法向等距线法,对涡旋型线进行平动,如图 3(b)所示,则
| $ {A_2} = {{A'}_2} = {L_2}{R_{{\rm{or}}}}, $ |
|
图 3 第二压缩腔轴向投影面积 Fig. 3 Axial projection area of the second compression chamber |
其中
| $ {L_2} = \int_{2{\rm{ \mathsf{ π} }} - \theta }^{4{\rm{ \mathsf{ π} }} - \theta } \rho \left( \varphi \right){\rm{d}}\varphi , $ |
所以第二压缩腔腔体面积为
| $ {A_2}(\theta ) = 2{R_{{\rm{or}}}}\int_{2{\rm{ \mathsf{ π} }} - \theta }^{4{\rm{ \mathsf{ π} }} - \theta } \rho (\varphi ){\rm{d}}\varphi , $ |
由此可得,涡旋压缩机除排气腔以外的任一对压缩腔容积的通用计算式为
| $ {V_N}(\theta ) = 2h{R_{{\rm{or}}}}\int_{2(N - 1){\rm{ \mathsf{ π} }} - \theta }^{2N{\rm{ \mathsf{ π} }} - \theta } \rho (\varphi ){\rm{d}}\varphi .\;\;\;\;(N = 2,3, \cdots ) $ |
式中:N为压缩腔编号,h为涡旋齿高度.
对于排气腔,它的容积与开始排气角及型线最初一段的修正情况有关,本文采用对称双圆弧修正的方法对齿头进行修正[18].根据曲轴转角θ的变化,可将排气腔容积的计算划分为两个阶段.
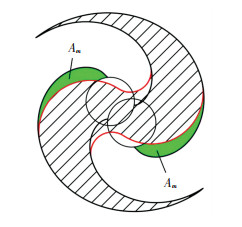
在第一阶段,排气腔是由圆渐开线和修正圆弧组成,如图 4所示.工作腔的容积为
| $ \begin{array}{l} {V_{11}}(\theta ) = \\ \;\;h\left\{ {\frac{1}{3}a_1^2\left[ \begin{array}{l} {\left( {\theta + \frac{{\rm{ \mathsf{ π} }}}{2} - \partial } \right)^3} - {\left( {\theta - \frac{{\rm{ \mathsf{ π} }}}{2} + \partial } \right)^3} + \\ {\left( {\phi + {\rm{ \mathsf{ π} }} + \partial } \right)^3} - {\left( {\phi + {\rm{ \mathsf{ π} }} - \partial } \right)^3} \end{array} \right] - } \right.\\ \;\;\left. {a_1^2\left( {{\rm{ \mathsf{ π} }} - 4\partial } \right) - 2{A_m}} \right\}, \end{array} $ |
|
图 4 由圆渐开线和圆弧组成的排气腔 Fig. 4 The discharge chamber consisting of circle involutes and circular arcs |
其中
| $ \begin{array}{l} {A_m} = \frac{1}{6}a_1^2\left[ {{{\left( {\phi + {\rm{ \mathsf{ π} }} + \partial } \right)}^3} - {{\left( {\phi + \partial } \right)}^3}} \right] + \\ \;\;\;\;\;\;\;\;\frac{{\rm{ \mathsf{ π} }}}{2}a_1^2 - \frac{\lambda }{2}\left( {R_d^2 - R_x^2} \right). \end{array} $ |
式中:ϕ为修正展角,ə为渐开线发生角,λ为修正圆弧中心角,Rd为修正大圆弧半径,Rx为修正小圆弧半径,γ为修正角.
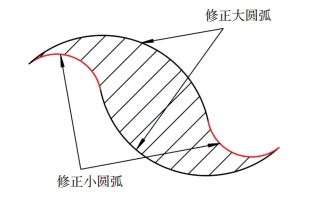
在第二阶段,排气腔完全由修正圆弧组成,如图 5所示.工作腔容积为
| $ {V_{12}}(\theta ) = h\left( {R_d^2 - R_x^2} \right)[(\theta - \gamma ) - \sin (\theta - \gamma )]. $ |
|
图 5 仅有圆弧组成的排气腔 Fig. 5 The discharge chamber consisting of only circular arcs |
为了研究控制系数对涡旋齿型线几何性能的影响,建立两者之间的映射关系,特引入4个能表征涡旋齿型线几何性能的指标,即压缩比、涡盘圆周大径、体积利用系数和涡旋齿齿厚.
3.1 压缩比| $ \nu = {\left( {\frac{{{V_3}(0)}}{{{V_{11}}\left( {{\theta ^*}} \right)}}} \right)^\kappa }. $ |
式中:V3(0)为曲轴转角θ=0时,第三压缩腔的容积; θ*为开始排气角,θ*=2π-γ; κ为气体的等熵指数,取κ=1.21.
3.2 涡盘圆周大径考虑到涡旋压缩机在实际应用中,有尺寸空间限制这一因素,特引入涡盘圆周大径D这一性能指标,如图 2所示.
| $ D = 2{\left\{ {{{\left[ {{x_{oo}}\left( {{\varphi _{\max }} + {\rm{ \mathsf{ π} }}} \right) + {R_{{\rm{or}}}}} \right]}^2} + {{\left( {{y_{oo}}\left( {{\varphi _{\max }} + {\rm{ \mathsf{ π} }}} \right)} \right)}^2}} \right\}^{1/2}}. $ |
为了定量表征涡旋压缩机尺寸结构的大小以及紧凑程度,引入体积利用系数这一性能指标,定义为
| $ \gamma = \frac{{4{V_3}(0)}}{{{\rm{ \mathsf{ π} }}{D^2}h}}. $ |
齿厚t是涡旋压缩机设计、动力学、热力学研究和强度计算中的一个重要几何量,所以其大小的选择对于涡旋压缩机的正常运转至关重要.涡旋齿齿厚t的计算公式定义为
| $ t = \left[ {\rho (\varphi + 2{\rm{ \mathsf{ π} }}) - \rho (\varphi ) - 2{R_{{\rm{or}}}}} \right]/2. $ |
为了建立控制系数与性能指标的映射关系,并探究每项控制系数变化所代表的具体意义,分别讨论了每个控制系数单独变化时其对性能指标的影响.本文以前两项控制系数为研究对象,并且对控制系数的讨论都是在回转半径Ror和涡旋齿高h确定的条件下进行的,因为回转半径Ror和涡旋齿高h是两个重要的几何参数,取值过大或过小均会对涡旋压缩机的性能产生不利的影响.回转半径Ror的大小会影响动静涡旋的啮合,Ror取值不恰当,会使动静涡旋相互干涉而无法正常啮合.而涡旋齿高h的大小与轴向泄漏线长度、涡旋体加工时的难易程度相关,若h过大,会使涡旋体的加工难度增加,不利于保证涡旋体的形位精度;若h过小,又会增加压缩腔轴向间隙的泄漏线长度,不利于提高涡旋压缩机的容积效率.基于以上分析,本文参照文献[19],取回转半径Ror=1.84 mm,涡旋齿高h=25 mm.
当控制系数a1保持不变,a0逐渐增大时,得到的计算结果如表 1中的第1至第3组数据所示.结果表明:在a1不变的条件下,随着a0的逐渐变大,涡盘圆周大径D在变大,压缩比ν和体积利用系数γ在变小,而涡旋齿齿厚t却保持不变;当控制系数a0的值不变,a1取值逐渐变大时,其计算结果如表 1中的第3至第5组数据所示.由结果可知:随着a1的逐渐增大,压缩比ν、涡盘圆周大径D及涡旋齿齿厚t均在变大,只有体积利用系数γ在减小.从表 1中还可以得出,任何控制系数ai的单独变大都会使涡盘圆周大径D增大,也都会使体积利用系数减小.
| 表 1 控制系数ai变化时的性能指标值 Tab. 1 Performance index values with the change of control coefficient ai |
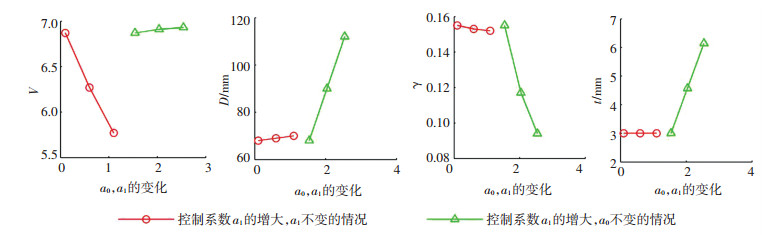
通过探讨前两项控制系数变化对涡旋齿型线性能指标的影响,建立了控制系数与性能指标的映射关系,如表 2所示.利用表 2中的映射关系,得到了控制系数与各项性能指标的变化趋势图,如图 6所示.运用该变化趋势图可优选出一系列满足设计要求的控制系数,进而构造出涡旋齿型线.
| 表 2 控制系数与涡旋齿型线性能指标的映射关系 Tab. 2 Mapping relation between control coefficients and performance indexes of scroll wrap profiles |
|
图 6 控制系数与性能指标的变化趋势图 Fig. 6 Change trend graphs of control coefficients and performance indexes |
对于涡旋压缩机而言,压缩比和体积利用系数无疑是两个非常重要的性能指标,它们对于提高压缩性能,改善整个空压系统工作性能的影响关系较大.所以在以往的研究中,对这两个性能指标特别重视,在一味地追求压缩比或体积利用系数的最大值.但同时也忽略了另外两个形象直观、便于测量的指标,即涡盘圆周大径D和涡旋齿齿厚t.
对于涡盘圆周大径D而言,它的大小受空间尺寸的限制.在达到同样大小的压缩比或体积利用系数的条件下,D的尺寸可以有多种.如当涡旋压缩机被用于轿车等空间有限的地方时,虽然压缩比或体积利用系数达到了设计要求,但若D的尺寸过大或过小都将导致涡旋压缩机无法正确安装.
对于涡旋齿齿厚t而言,它的大小主要根据涡旋齿工作时受力状况而定,以保证强度和刚度为前提.若t过小,则涡旋齿的强度和刚度会降低,加工中容易变形;若t过大,则涡旋盘的整体尺寸会增大,涡旋齿的质量也会过大,导致传热性能变差.当涡旋齿顶部要求设置密封槽时,t在取值时还要将密封槽与密封条的加工工艺考虑在内.由此可见,涡旋齿齿厚大小的选择对涡旋压缩机性能的改善是极其关键的.
因此,本文分别讨论了在涡盘圆周大径D与涡旋齿齿厚t恒定的前提下,利用控制系数与性能指标的映射关系,来优选满足要求的控制系数,进而构造出性能优良的涡旋齿型线.
利用映射关系,寻找满足涡盘圆周大径D的控制系数.例如,在a0=0.10,a1=1.54时,得到的D=68 mm,若此时需要D=80 mm的外形尺寸,由映射关系可知,可分别增大a0或a1的值,把a0值增大至a0=6.10来达到要求,也可把a1值增大到a1=1.81来满足要求,即在涡盘圆周大径D确定的前提下,控制系数a0或a1的取值是在参照表 1的基础上,依据映射关系,会计算得到一系列满足要求的控制系数.如表 3所示,仅仅是满足要求的其中的五组控制系数.由表 3可知,在保证涡盘圆周大径D一定的条件下,第3组的压缩比最大,但其体积利用系数又较小;第1组的体积利用系数最大,但其压缩比和齿厚却是最小的.所以在选择控制系数时,应根据涡旋压缩机的实际需求合理选择,若需要较大的压缩比,则选择第3组的控制系数来构造涡旋齿型线;若需要较大的体积利用系数,就选择第1组的控制系数来构造涡旋齿型线.
| 表 3 D=80 mm,改变控制系数ai时的性能指标值 Tab. 3 Performance index values with the change of control coefficient ai when D=80 mm |
同样利用映射关系来寻找满足涡旋齿齿厚t的控制系数.例如,在a0=0.10,a1=1.54时,得到的t=3.00 mm,若需要t=4.00 mm的齿厚,可增大控制系数a1的值,即把a1值增大至a1=1.86来达到要求.即在涡旋齿齿厚t确定的条件下,根据表 1并结合表 2中的映射关系,可计算得到控制系数若干.由表 2可知,虽然齿厚t不受控制系数a0的影响,但a0取较小值时,可以增大压缩比和体积利用系数.如表 4所示,是满足涡旋齿齿厚t=4.00 mm要求的其中的五组控制系数.
| 表 4 t=4.00 mm,改变控制系数ai时的性能指标值 Tab. 4 Performance index values whith the change of control coefficient ai when t=4.00 mm |
由表 4可知,在保证涡旋齿齿厚t一定的前提下,第1组的压缩比和体积利用系数最大,而涡盘圆周大径D却最小;第5组的压缩比和体积利用系数又是最小的,但涡盘圆周大径D又是最大的.因此在优选控制系数时,要综合考虑各个性能指标,若需要较大的压缩比或体积利用系数,则选择第1组的控制系数来构造涡旋齿型线;若需要较大的涡盘圆周大径,则选择第5组的控制系数来构造涡旋齿型线.
6 结论1) 利用微分几何中的Frenet标架,建立了涡旋齿型线的通用几何模型,将等壁厚涡旋齿型线、渐变壁厚涡旋齿型线和变壁厚涡旋齿型线集成在一个函数方程中,并且将对型线几何性能的研究转化为对控制系数的研究,设计人员可更加专注于控制系数选取对涡旋压缩机性能影响的研究.
2) 建立了控制系数与涡旋齿型线性能指标的映射关系,通过该映射关系,不但可以有效避免控制系数取值的盲目性,而且还可以构造出众多符合设计要求的涡旋齿型线.
3) 突破了涡旋齿型线设计中只注重压缩比或体积利用系数等条件的限制,以考虑实际需求为抓手,依据设计需求的倾向性,利用映射关系来构造出综合性能优良的涡旋齿型线.
| [1] |
LIU Yicai, XIA Yubo, YAN Peng, et al. Structural dynamic analysis of the orbiting scroll wrap in the scroll compressor[J]. Frontiers in Energy, 2013, 7(1): 19. DOI:10.1007/s11708-012-0223-9 |
| [2] |
IVLEVV I, MISYURIN S Y. Calculated and experimental characteristics of a scroll machine operating in the air motor mode[J]. Doklady Physics, 2017, 62(1): 42. DOI:10.1134/S1028335817010116 |
| [3] |
QIU K, THOMAS M, DOUGLAS M. Investigation of a scroll expander driven by compressed air and its potential applications to ORC[J]. Applied Thermal Engineering, 2018, 135: 109. DOI:10.1016/j.applthermaleng.2018.01.118 |
| [4] |
程哲铭, 欧阳新萍, 雷蓉. 涡旋式压缩机涡旋型线的研究综述与前景[J]. 流体机械, 2015, 43(1): 51. CHEN Zheming, OUYANG Xinping, LEI Rong. Overview and prospect of the research on profile of scroll compressor[J]. Fluid Machinery, 2015, 43(1): 51. DOI:10.3969/j.issn.1005-0329.2015.01.011 |
| [5] |
CHEN Y, HALM N P, GROLL E A, et al. Mathematical modeling of scroll compressor. part Ⅰ: compression process modeling[J]. International Journal of Refrigeration, 2002, 25(6): 731. DOI:10.1016/S0140-7007(01)00071-8 |
| [6] |
王立存, 李世六, 明勇, 等. 涡旋压缩机型线耦合机理动态性研究[J]. 哈尔滨工业大学学报, 2009, 41(7): 187. WANG Licun, LI Shiliu, MING Yong, et al. Dynamics of joggling principle for scroll profiles of scroll compressor[J]. Journal of Harbin Institute of Technology, 2009, 41(7): 187. DOI:10.3321/j.issn:0367-6234.2009.07.043 |
| [7] |
陈进, 张永栋, 宋立权, 等. 基于多目标遗传算法的涡旋型线形状优化[J]. 机械工程学报, 2005, 41(1): 172. CHEN Jin, ZHANG Yongdong, SONG Liquan, et al. Profile optimization of scrolls based on multiobjective genetic algorithms[J]. Chinese Journal of Mechanical Engineering, 2005, 41(1): 172. DOI:10.3321/j.issn:0577-6686.2005.01.034 |
| [8] |
刘强, 曹晨燕, 王君, 等. 涡旋压缩机新型渐变壁厚涡旋齿的设计和工作特性研究[J]. 流体机械, 2018, 46(12): 18. LIU Qiang, CAO Chenyan, WANG Jun, et al. Design and performance study of a novel tapered thickness wrap for scroll compressors[J]. Fluid Machinery, 2018, 46(12): 18. DOI:10.3969/j.issn.1005-0329.2018.12.004 |
| [9] |
LIU Yangguang, TANG Yuehju, CHANG Yuchoung, et al. Optimum design of scroll profiles created from involute of circle with variable radii by using finite element analysis[J]. Mechanism and Machine Theory, 2012, 55(55): 1. DOI:10.1016/j.mechmachtheory.2012.04.002 |
| [10] |
王君, 刘强, 曹晨燕, 等. 涡旋压缩机全啮合渐变壁厚涡旋齿的设计与分析[J]. 工程热物理学报, 2018, 39(8): 1713. WANG Jun, LIU Qiang, CAO Chenyan, et al. Design and analysis of completely meshing profile of tapered thickness wrap for scroll compressors[J]. Journal of Engineering Thermophysics, 2018, 39(8): 1713. |
| [11] |
SHAFFER B R, GROLL E A. Variable wall thickness scroll geometry modeling with use of a control volume approach[J]. International Journal of Refrigeration, 2013, 36(7): 1809. DOI:10.1016/j.ijrefrig.2013.08.003 |
| [12] |
刘涛, 侯富勇, 李传恒. 三段基圆渐开线涡旋型线的多目标遗传算法优化[J]. 流体机械, 2015, 43(8): 32. LIU Tao, HOU Fuyong, LI Chuanheng. Multi-objective genetic algorithm based optimization of scroll wraps with three involutes of circle[J]. Fluid Machinery, 2015, 43(8): 32. DOI:10.3969/j.issn.1005-0329.2015.08.007 |
| [13] |
彭斌, 孙迎. 变截面涡旋压缩机数学模型及试验研究[J]. 机械工程学报, 2015, 51(14): 185. PENG Bin, SUN Ying. Investigation of mathematical modeling and experiment for variable thickness scroll compressor[J]. Journal of Mechanical Engineering, 2015, 51(14): 185. DOI:10.3901/JME.2015.14.185 |
| [14] |
陈进, 王立存, 李世六. 通用涡旋型线理论研究与深入分析[J]. 机械工程学报, 2006, 42(5): 11. CHEN Jin, WANG Licun, LI Shiliu. Study and profound analysis on general profile theory of scrolls[J]. Chinese Journal of Mechanical Engineering, 2006, 42(5): 11. DOI:10.3321/j.issn:0577-6686.2006.05.003 |
| [15] |
王立存, 张国进, 王旭东, 等. 基于向量方法的通用涡旋型线生成研究[J]. 机械科学与技术, 2015, 34(7): 1035. WANG Licun, ZHANG Guojin, WANG Xudong, et al. Generation of general scroll profiles based on vector method[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(7): 1035. |
| [16] |
马力. 简明微分几何[M]. 北京: 清华大学出版社, 2004. MA Li. Simple differential geometry[M]. Beijing: Tsinghua University Press, 2004. |
| [17] |
刘涛, 邬再新, 刘振全. 法向等距线法生成涡旋压缩机型线的研究[J]. 机械工程学报, 2004, 40(6): 55. LIU Tao, WU Zaixin, LIU Zhenquan. Study on generating profile with nomal-equidistant-curve method for scroll compressor[J]. Chinese Journal of Mechanical Engineering, 2004, 40(6): 55. DOI:10.3321/j.issn:0577-6686.2004.06.011 |
| [18] |
王君, 刘振全. 涡旋压缩机渐开线类型的双圆弧修正[J]. 机械工程学报, 2005, 41(9): 202. WANG Jun, LIU Zhenquan. Modification to involute type profile using twin-circular arcs for scroll compressor[J]. Chinese Journal of Mechanical Engineering, 2005, 41(9): 202. DOI:10.3321/j.issn:0577-6686.2005.09.039 |
| [19] |
王立存, 陈进. 基于多学科设计优化的通用涡旋型线形状优化[J]. 华中科技大学学报(自然科学版), 2008, 36(3): 12. WANG Licun, CHEN Jin. Shape optimization of general scroll profiles based on multidisciplinary design optimization[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2008, 36(3): 12. DOI:10.3321/j.issn:1671-4512.2008.03.004 |
 2020, Vol. 52
2020, Vol. 52


