2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
静态破碎剂是一种黑色或灰色的粉状化学制剂,通常以游离氧化钙(f-CaO)为主要成分,与水反应体积膨胀可达2~3倍,对于岩石或混凝土等脆性材料可产生良好的破碎效果.静态破碎技术作为一种新型的拆除方法,具有无声、安全、操作简单、绿色环保等特点,已经引起广泛关注.
许兰保等[1]用直径分别为32、38、48、58和72 mm的钢管测量了静态破碎剂在1 h内的短期膨胀压应力,发现孔径越大短期膨胀压应力越大.姜楠等[2]则用直径为40和100 mm的钢管探究了静态破碎剂对两种孔径钢管内壁的膨胀压应力,发现直径100 mm钢管中部的膨胀压应力为直径40 mm钢管中部膨胀压应力的3倍左右,可达97 MPa.谢益盛等[3]采用直径为30、40、50和60 mm的钢管进行试验,发现随着孔径的增大,轴向应变与径向应变的比值逐渐增大.武世亮等[4]探究了孔径对静态破碎剂喷孔的影响,发现孔径越大,破碎剂温度上升速率越大,越易喷孔.Gambatese[5]在强度为20.7 MPa的素混凝土中预留了直径为3.18、4.76和6.35 mm的孔,并灌入静态破碎剂浆体,发现当孔深达到孔径的6至12倍,孔距为孔径的4至10倍时,混凝土开裂.Huynh等[6]通过试验探究发现,布孔合理且试件高度或厚度不大于1 m时,钻孔深度为高度或厚度的70%,可将待破碎体破碎.冯彧雷[7]建议破碎岩石时根据实际情况及破碎需要调整钻孔深度,钻孔位于节理面等易裂处或基岩等坚固部位时,孔深应分别减小或增大5%.
以往研究主要集中于孔径对静态破碎剂的破碎效果的影响,缺乏对孔深、孔的约束程度的影响的研究及膨胀压应力沿钻孔深度方向的分布的研究.因此,开展孔径、孔深、约束程度对膨胀压应力影响的试验,考察膨胀压应力沿孔深的分布,对促进静态破碎技术的发展具有重要意义.
1 试验概况采用中华人民共和国建材行业标准JC 506—2008《无声破碎剂》提供的“电阻应变片法”[8]测量静态破碎剂径向膨胀压应力,并对该方法进行改进:在将钢管装入防水PE塑料袋的基础上,用704硅橡胶将应变片覆盖以提供更佳的防水能力,在钢管表面粘贴热电偶以监测钢管表面的温度变化、修正温度应变的影响.本试验所用的应变片为邢台金志传感元件厂生产的BX120-5AA,具体试验装置及测点布置见图 1,测点分别布置在距离管口、管底50 mm处及钢管中部.本试验所用的无缝钢管从哈尔滨古铁市场购置,材质为45号钢.图 1中200、150、100 mm分别对应钢管G-1至G-5、钢管G-6及钢管G-7.钢管编号和具体参数见表 1.
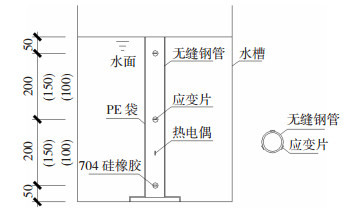
|
图 1 试验装置及测点布置(mm) Fig. 1 Arrangement of test equipment and measuring points (mm) |
| 表 1 钢管参数 Tab. 1 Parameters of steel pipes |
本试验采用三种静态破碎剂,分别为:施必达(大连)公司生产的S-611无声爆破剂,三强建材集团有限公司生产的三顺高效静态膨胀剂,飞鹰膨胀剂厂生产的飞鹰无声高效岩石膨胀剂.
本试验静态破碎剂的水灰比为1:3(质量比).由于工程中为防止破碎剂浆体自孔底流出,常不将孔钻通,为模拟工程实践,本试验过程中管口不做封堵措施,钢管底部焊接6 mm厚钢板封堵.试验于房间内进行,水槽内水温为17 ℃.
钢管上中下3处各设3个测点,每处取相应3个测点的应变平均值,结合弹性力学中的理论公式,求解静态破碎剂产生的径向膨胀压应力[9]:
| $ P = \frac{{{\varepsilon _\theta }E({b^2} - {a^2})}}{{2{a^2}}} = \frac{{{\varepsilon _\theta }E}}{2}({K^2} - 1), $ | (1) |
式中:P为静态破碎剂产生的径向膨胀压应力,MPa;εθ为钢管外壁环向拉应变;E为钢管弹性模量,210 GPa;a为钢管内径,mm;b为钢管外径,mm;K为钢管外径b与内径a的比值.
2 试验结果与分析 2.1 膨胀压应力沿孔深方向的分布由于在混凝土柱墩的静态破碎过程中时常会发生少量粉末状静态破碎剂自孔口溢出的现象[10],认为静态破碎剂产生的膨胀压应力在钻孔内分布不均匀,钻孔中部和下部的膨胀压应力大于钻孔上部.利用钢管高度模拟钻孔深度,测量距管口、管底各50 mm处及管中部的应变,基于实测数据按式(1)得到膨胀压应力时程曲线,见图 2.图中G-n-A表示钢管编号为G-n,管内装有飞鹰静态破碎剂;G-n-B表示钢管编号为G-n,管内装有三顺静态破碎剂;G-n-C表示钢管编号为G-n,管内装有施必达静态破碎剂.由于设备断电,管G-7-B仅有前20 h的试验数据.
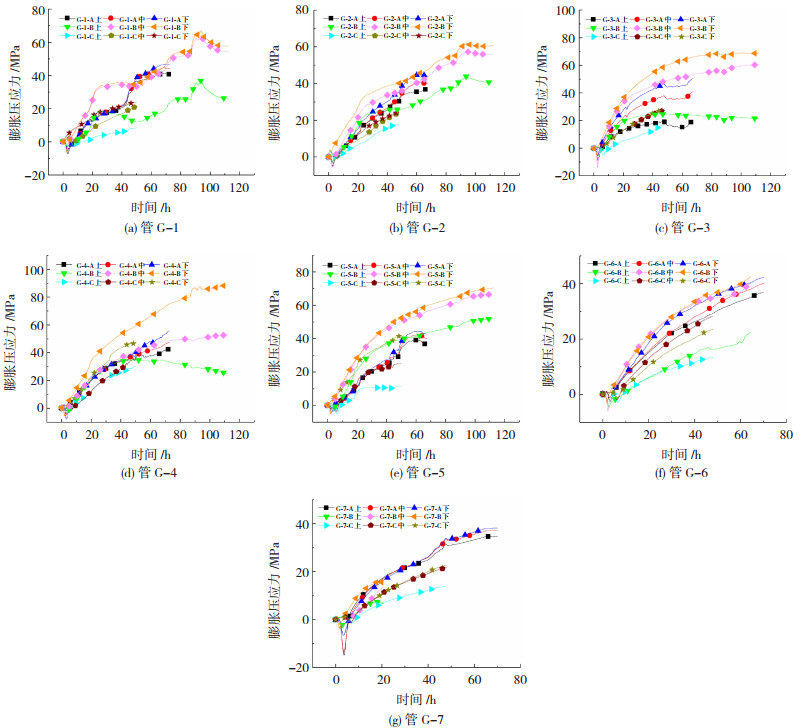
|
图 2 静态破碎剂膨胀压应力时程曲线 |
分析上述21根钢管的膨胀压应力时程曲线可发现:钢管中下部的膨胀压应力始终大于钢管上部的膨胀压应力;除G-6-C外,钢管下部膨胀压应力均大于中部膨胀压应力.此外,除G-4-B、G-2-A、G-4-A、G-4-C、G-5-C五根管之外,钢管中部膨胀压应力均与下部膨胀压应力相接近.这是因为:1)随着静态破碎剂与水反应发生体积膨胀,使无缝钢管对破碎剂柱体会产生摩阻力,水硬性物质所提供的黏结力与无缝钢管所提供的摩阻力两者合力随距管口距离的减小而不断减小,当两者的合力小于静态破碎剂静态破碎剂向上膨胀的膨胀压应力时,静态破碎剂会产生向上的膨胀,致使径向膨胀压应力释放;2)静置后管中静态破碎剂逐渐下沉,管口发生泌水现象,使管底破碎剂药量变相增加,水灰比减小,产生的径向膨胀压应力变大;3)根据圣维南原理,距钢管底端端板距离越远的位置,受端板约束影响越小.
分别取三种静态破碎剂20、40、60 h的钢管上部、中部、下部三个位置对应的径向膨胀压应力,并计算钢管下部与钢管上部、中部两个位置膨胀压应力的差值.膨胀压应力数值及计算结果见表 2~4.
| 表 2 三种静态破碎剂20 h径向膨胀压应力 Tab. 2 Radial expansion compressive stress of three static crushing agents at 20 h |
| 表 3 三种静态破碎剂40 h径向膨胀压应力 Tab. 3 Radial expansion compressive stress of three static crushing agents at 40 h |
| 表 4 三种静态破碎剂60 h径向膨胀压应力 Tab. 4 Radial expansion compressive stress of three static crushing agents at 60 h |
观察钢管下部与上部、中部径向膨胀压应力的差值可以发现:钢管下部和上部径向膨胀压应力的差值及下部和中部的差值随着时间增长逐渐增大,且孔径越大,钢管下部和上部的径向膨胀压应力差值越大,最大可达39.84 MPa.这是因为随着孔径增大,静态破碎剂产生的轴向膨胀压应力逐渐增大[11],水硬性物质所产生的黏结作用相对减弱,管中破碎剂有向上膨胀的趋势,使得管口破碎剂溢出.孔径越大,溢出的破碎剂越多,破碎剂溢出致使钢管上部所受摩阻力减少,膨胀压应力向轴向释放,因此获得的径向膨胀压应力远小于底部径向膨胀压应力.管口破碎剂溢出情况见图 3.

|
图 3 管口破碎剂溢出情况 Fig. 3 Overflow of static crushing agent at nozzle |
为避免破碎剂溢出对测量结果产生影响,对钢管上部的测点数据不做具体分析.由于钢管下部测点距离管底50 mm,根据圣维南原理,除钢管G-2及G-3外,其他钢管底部焊接的钢板对下部测点影响较小.因此,研究孔径、孔深及约束程度对径向膨胀压力的影响时以钢管中部数据为主,底部数据为辅.
2.2 孔径对径向膨胀压应力的影响利用钢管内径模拟孔径,三种静态破碎剂的试验结果见图 4.
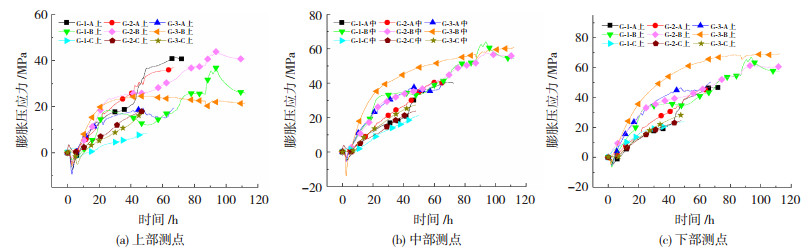
|
图 4 三种破碎剂不同孔径的膨胀压应力时程曲线 Fig. 4 Time-history curves of expansion compressive stress with different hole diameters of three types of crushing agents |
由图 4可看出A破碎剂G-3-A管下部50 h左右膨胀压应力已经发展平缓,发展平缓阶段所达到的膨胀压应力为44.71 MPa,而G-1-A、G-2-A管下部依然处于膨胀压应力缓慢发展阶段.B破碎剂G-1-B管、G-2-B管、G-3-B管下部达到发展膨胀压应力发展平缓阶段的时间分别为105、100、90 h,发展平缓阶段所达到的膨胀压应力分别为57.55、60.51、68.34 MPa.C破碎剂的膨胀压应力在50 h内并未达到发展平缓阶段,三个管膨胀压应力都在缓慢发展,45 h时钢管G-1-C、G-2-C、G-3-C下部所能达到的膨胀压应力分别为27.40、23.68、23.04 MPa.由此可见,大孔径钢管内的破碎剂会先于小孔径钢管内的破碎剂达到最大径向膨胀压应力,这种情况发生的原因是孔径大,静态破碎剂质量大,水化反应产生的热量大于热量的传递与消耗,热量的积聚和上升进一步催化水化反应,致使大孔径试件先达到最大径向膨胀压应力.
三种破碎剂的径向膨胀压应力-孔径的关系见图 5.
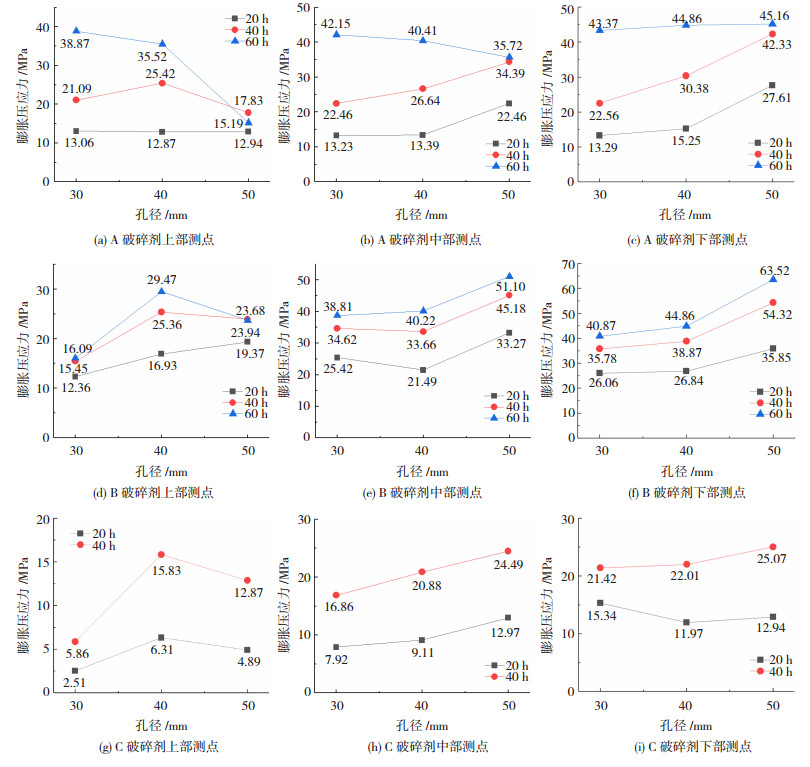
|
图 5 三种破碎剂膨胀压应力与孔径关系曲线 Fig. 5 Relation curves between expansion compressive stress and hole diameters of three types of crushing agents |
由图 5可看出,除三种破碎剂上部,C破碎剂下部20 h,B破碎剂中部20 h、40 h及A破碎剂中部60 h的膨胀压应力外,径向膨胀压应力随着钢管内径的增大而增大.且孔径由40 mm到50 mm对径向膨胀压应力的提升比孔径由30 mm到40 mm的提升大.因此,孔径越大,静态破碎剂水化反应速度越快,达到最大径向膨胀压应力的时间越短,产生的径向膨胀压应力值也越大.此外,钢管内径在30 mm至50 mm之间变化时,钢管内径每增加10 mm,径向膨胀压应力可增加1~18 MPa.因此在实际工程中扩大孔径是提高破碎效率的有效手段,但孔径也不宜过大,孔径过大将发生喷孔现象.
2.3 孔深对径向膨胀压应力的影响利用钢管高度模拟孔深,三种静态破碎剂的试验结果见图 6.
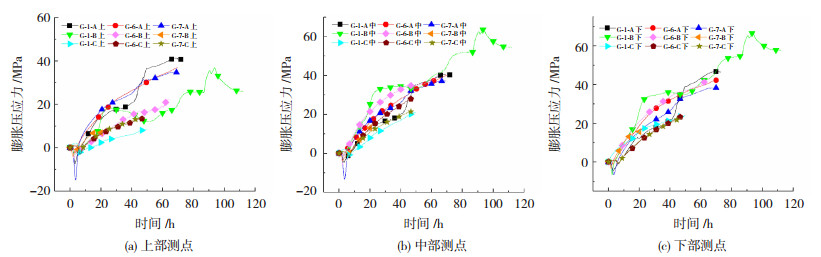
|
图 6 三种破碎剂不同孔深的膨胀压应力时程曲线 Fig. 6 Time-history curves of expansion compressive stress with different hole depths of three types of crushing agents |
由图 6可看出,孔深对静态破碎剂径向膨胀压应力的上升速度影响不大.取图 6中20、40、60 h对应的膨胀压应力,绘制三种破碎剂的径向膨胀压应力与孔深的关系见图 7.
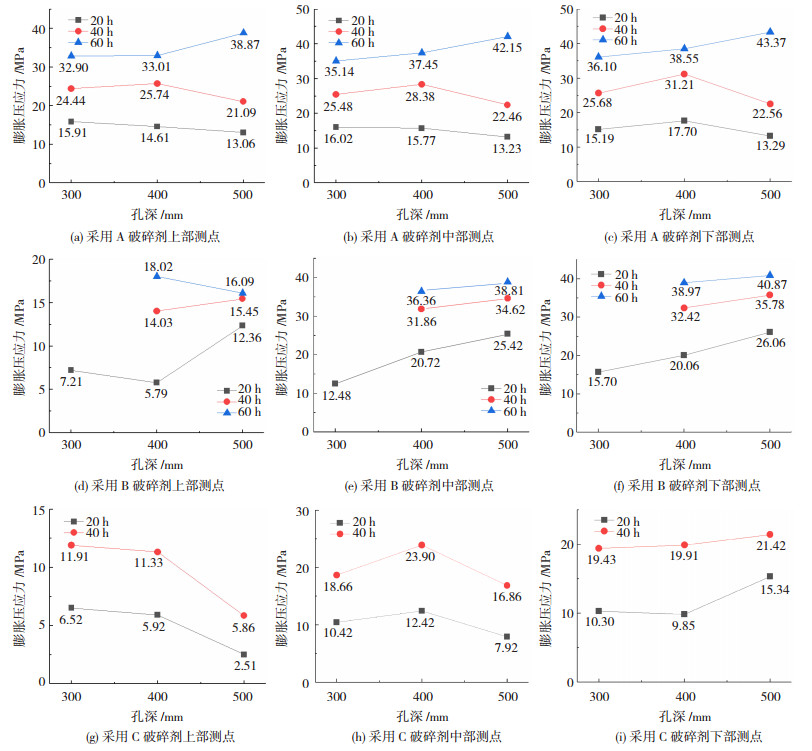
|
图 7 三种破碎剂膨胀压应力与孔深关系曲线 Fig. 7 Relation curves between expansion compressive stress and hole depths of three types of crushing agents |
由图 7可知,除三种破碎剂上部,A破碎剂中部20 h、40 h,A破碎剂下部20 h、40 h及C破碎剂中部20 h、40 h的膨胀压应力外,径向膨胀压应力随着钢管高度的增加而增大.这是因为钢管底部破碎剂的轴向膨胀受到破碎剂自重、水硬性物质所提供的黏结力和无缝钢管所提供摩阻力三者合力的限制.随着钢管高度的增加,三者合力也逐渐增大,对底部破碎剂轴向变形的约束增强,故其径向膨胀压应力有所增加.此外,钢管高度在300 mm至500 mm之间变化时,钢管高度每增加100 mm,径向膨胀压应力增加1~5 MPa.因此,从成本效益及破碎剂破碎能力利用率方面考虑,实际工程应用中孔深不宜过大,结合Huynh等[6]和冯彧雷等[7]的建议,孔深取至待破碎深度的70%~90%即可.
2.4 约束程度对径向膨胀压应力的影响利用钢管混凝土中的套箍指标来表示钢管对于孔内静态破碎剂约束程度的大小,套箍系数为
| $ \zeta = \frac{{{A_{\rm{s}}}{f_{\rm{y}}}}}{{{A_{\rm{j}}}{f_{\rm{j}}}}}, $ | (2) |
式中:ζ为静态破碎剂弹性柱体的套箍系数;As为钢管的截面面积,mm2;fy为钢管的抗拉强度实测值,MPa;Aj为钢管内静态破碎剂的横截面面积,mm2;fj为钢管内静态破碎剂的抗压强度实测值,MPa.
因为本文fy/fj为定值,故可用As/Aj代表钢管对管内静态破碎剂的约束程度.试验外界条件保持不变,钢管G-1、G-4、G-5参数见表 1,试验结果见图 8.由图 8可看出,约束程度对静态破碎剂径向膨胀压应力的上升速度影响不大.取图 8中20、40、60 h对应的膨胀压应力,以时间(T)为x轴、约束程度(λ)为y轴、膨胀压应力(P)为z轴,绘制三种破碎剂关系曲线见图 9.
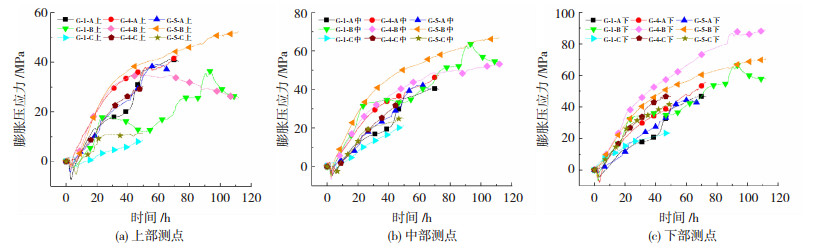
|
图 8 三种破碎剂不同约束程度的膨胀压应力时程曲线 Fig. 8 Time-history curves of expansion compressive stress with different constraint degrees of three types of crushing agents |
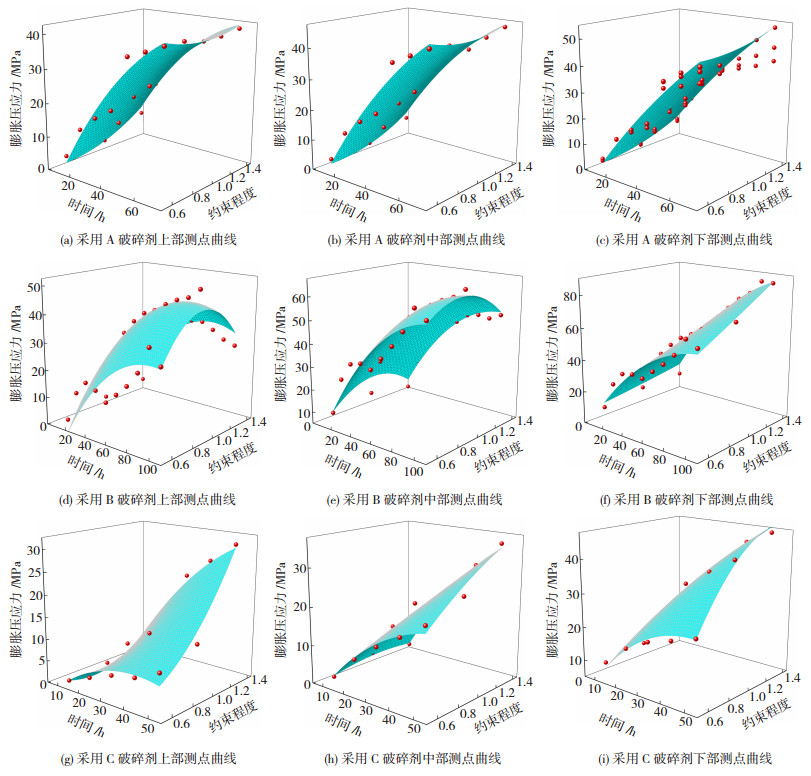
|
图 9 膨胀压应力与约束程度和时间关系曲线 Fig. 9 Relation curves between expansion compressive stress, constraint degree, and time |
经拟合得到图 9中膨胀压应力与约束程度及时间的数学关系表达式见式(3)~(11).
| $ \begin{array}{*{20}{l}} {P = - 5.84 + 1.26T - 14.72\lambda - 0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} 8{T^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 15.15{\lambda ^2} - 0.208T\lambda ,} \end{array} $ | (3) |
曲线的拟合优度R2=0.968.
| $ \begin{array}{*{20}{l}} {P = - 3.77 + 1.24T - 19.57\lambda - 0.004{\kern 1pt} {\kern 1pt} {\kern 1pt} 8{T^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 16.84{\lambda ^2} - 0.178T\lambda ,} \end{array} $ | (4) |
曲线的拟合优度R2=0.976.
| $ \begin{array}{*{20}{l}} {P = - 4.30 + 1.02T - 13.01\lambda - 0.002{\kern 1pt} {\kern 1pt} {\kern 1pt} 8{T^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 12.40{\lambda ^2} - 0.050T\lambda ,} \end{array} $ | (5) |
曲线的拟合优度R2=0.983.
| $ \begin{array}{*{20}{l}} {P = - 101.76 + 1.01T + 205.76\lambda - 0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{T^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 93.85{\lambda ^2} - 0.176T\lambda ,} \end{array} $ | (6) |
曲线的拟合优度R2=0.842.
| $ \begin{array}{*{20}{l}} {P = - 52.34 + 1.12T + 123.50\lambda - 0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{T^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 61.38{\lambda ^2} - 0.087T\lambda ,} \end{array} $ | (7) |
曲线的拟合优度R2=0.948.
| $ \begin{array}{l} P = - 0.61 + 0.85T + 4.07\lambda - 0.004{\kern 1pt} {\kern 1pt} {\kern 1pt} 9{T^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2.095{\lambda ^2} + 0.311T\lambda , \end{array} $ | (8) |
曲线的拟合优度R2=0.968.
| $ \begin{array}{l} P = 13.18 + 0.17T - 43.03\lambda - 0.006{\kern 1pt} {\kern 1pt} {\kern 1pt} 9{T^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 22.30{\lambda ^2} + 0.633T\lambda , \end{array} $ | (9) |
曲线的拟合优度R2=0.969.
| $ \begin{array}{*{20}{l}} {P = - 11.05 + 0.63T + 12.28\lambda - 0.007{\kern 1pt} {\kern 1pt} {\kern 1pt} 8{T^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 7.83{\lambda ^2} + 0.462T\lambda ,} \end{array} $ | (10) |
曲线的拟合优度R2=0.984.
| $ \begin{array}{*{20}{l}} {P = - 27.14 + 0.59T + 63.49\lambda - 0.011{\kern 1pt} {\kern 1pt} {\kern 1pt} 2{T^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 35.92{\lambda ^2} + 0.800T\lambda ,} \end{array} $ | (11) |
曲线的拟合优度R2=0.991.
从图 9能够看出B、C破碎剂已经较为明显地到达了径向膨胀压应力发展平缓阶段,A破碎剂的G-4-A却还有一定的膨胀力上升趋势,且随着约束程度的增大,径向膨胀压应力也随之增大.这是因为约束越强,对钢管内静态破碎剂的变形限制越强,静态破碎剂产生的径向膨胀压应力越大.约束程度在0.6~1.4区间,约束程度每增加0.4,产生的膨胀压应力增加4~10 MPa.
3 结论1) 静态破碎剂产生的径向膨胀压应力沿孔深方向并非均匀分布,一般钻孔中下部的膨胀压应力大于钻孔上部,而钻孔中部的膨胀压应力与下部接近.
2) 根据“钢管混凝土套箍理论”,定义钢管截面面积与静态破碎剂截面面积的比值为约束程度.当孔深、约束程度和破碎剂种类一定时,孔径越大,产生的径向膨胀压应力越大,钻孔底部与上部的径向膨胀压应力差值越大;当孔径、约束程度和破碎剂种类一定时,孔深越大,静态破碎剂产生的径向膨胀压应力越大;当孔径、孔深和破碎剂种类一定时,约束程度越大,静态破碎剂产生的径向膨胀压应力越大.
3) 当孔深、约束程度和破碎剂种类一定时,孔径越大,静态破碎剂水化反应速度越快,达到最大径向膨胀压应力的时间越短.孔深和约束程度对径向膨胀压应力的发展速度影响不大.
| [1] |
许兰保, 倪红娟. 静态破碎剂的性能试验研究[J]. 四川建材, 2013(5): 84. XU Lanbao, NI Hongjuan. Experimental study on performance of static breaker[J]. Sichuan Building Materials, 2013(5): 84. |
| [2] |
姜楠, 徐全军, 龙源, 等. 大孔径静态破碎膨胀压力特性及布孔参数分析[J]. 爆炸与冲击, 2015, 35(4): 471. JIANG Nan, XU Quanjun, LONG Yuan, et al. Expansive pressure characteristic and borehole parameter analysis on large scale borehole soundless cracking[J]. Explosion and Shock Waves, 2015, 35(4): 471. |
| [3] |
谢益盛, 杨光辉, 黄小朋. 静态破碎剂膨胀压应力学性能试验研究[J]. 煤矿安全, 2019, 50(3): 12. XIE Yisheng, YANG Guanghui, HUANG Xiaopeng. Experimental research on mechanical properties of static breaking agents[J]. Safety in Coal Mines, 2019, 50(3): 12. DOI:10.13347/j.cnki.mkaq.2019.03.003 |
| [4] |
武世亮, 翟成, 向贤伟, 等. 钻孔内静态破碎剂喷孔实验研究[J]. 煤炭技术, 2015, 34(9): 145. WU Shiliang, ZHAI Cheng, XIANG Xianwei, et al. Experimental study on jet orifice of static cracking agent in drilling hole[J]. Coal Technology, 2015, 34(9): 145. DOI:10.13301/j.cnki.ct.2015.09.056 |
| [5] |
GAMBATESE J A. Controlled concrete demolition using expansive cracking agents[J]. Journal of Construction Engineering and Management, 2003, 129: 98. DOI:10.1061/(ASCE)0733-9364(2003)129:1(98) |
| [6] |
HUYNH M P, LAEFER D. Expansive cement and soundless chemical demolition agents: State-of-technology review[C]// Proceedings of the 11th Conference on Science and Technology. Ho Chi Minh City: [s.n.], 2009
|
| [7] |
冯彧雷.静态破碎剂的膨胀压力测试试验与应用[D].淮南: 安徽理工大学, 2010 FENG Yulei. Experimental research and apply on the soundless cracking agent[D]. Huainan: Anhui University of Science & Technology, 2010 |
| [8] |
中华人民共和国建材行业标准(无声破碎剂): JC 506—2008[S].北京: 中国建材工业出版社, 2008 Standard for building materials industry of the People's Republic of China (Soundless cracking agent): JC 506—2008[S]. Beijing: China Building Materials Press, 2008 |
| [9] |
GHOLINEJAD M, ARSHADNEJAD S H. An experimental approach to determine the hole-pressure under expansion load[J]. Journal of the Southern African Institute of Mining and Metallurgy, 2012, 112: 631. |
| [10] |
徐笠博.静态破碎剂比选及混凝土构件静态破碎试验研究[D].哈尔滨: 哈尔滨工业大学, 2019 XU Libo. Comparison and selection of static crushing agents and static crushing test of concrete components[D]. Harbin: Harbin Institute of Technology, 2019 |
| [11] |
戴星航, 张凤鹏, 邱兆国, 等. 静态破碎剂的轴向膨胀力学性能实验研究[J]. 东北大学学报(自然科学版), 2016, 37(2): 251. DAI Xinghang, ZHANG Fengpeng, QIU Zhaoguo, et al. Experimental study on axial swelling mechanical properties of static cracking agent[J]. Journal of Northeastern University (Natural Science), 2016, 37(2): 251. |
 2020, Vol. 52
2020, Vol. 52


