2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
K型圆钢管相贯节点是空间格构式结构中一类常用的节点形式,1970年Easttwood等[1]提出了采用容许应力法设计钢管相贯节点承载力的设计方法;1986年牧野熊二等[2]对X、T、Y、K四种平面节点进行研究,率先提出K型节点压弯承载力计算公式.经过各国学者[3-4]的深入研究,K型相贯节点目前已发展较为成熟,中国现行GB 50017─2017《钢结构设计标准》和DL/T 5254─2010《架空输电线路钢管塔设计技术规定》中均给出了无加劲K型相贯焊节点承载力计算方法.在特高压直流线路大跨越工程中,有加劲的圆管相贯焊节点被普遍采用,见图 1.但该类节点的设计均未考虑加劲板的有利影响,从而低估节点的承载能力,设计分析中往往需要通过增加腹杆截面来满足节点承载力要求,造成材料浪费.因此,各国学者开始针对各种加劲后的节点力学性能开展研究.张巧珍等[5]对插板加强的K型节点进行有限元分析;吴亮秦等[6]对垫板加强N形圆钢管相贯节点进行了静力性能试验研究;潘奕康[7]分别对单板加强和贯通加劲板强化下的小管径K型节点进行了试验及模拟分析,研究了3种加劲形式对小直径圆管相贯节点受力性能的影响,提出了加劲高度、厚度等参数变化对节点失效模式的影响规律;宋启明[8]采用外加劲肋加固圆钢管节点,并研究其静力性能;Nassiraei等[9-10]对采用模拟环口板强化的T、Y、X型节点的力学性能进行了分析.上述对于相贯加劲节点的研究成果极大地推动了其应用和发展.

|
图 1 大跨越输电塔形式及连接节点 Fig. 1 Types and connecting joints of long-span transmission towers |
然而大跨越输电塔中所采用的钢管尺寸一般较大,目前的研究成果尚未覆盖这一范畴,而针对大尺寸-纵板加劲相贯焊节点的研究相对较少.本文基于上述背景,对大管径的纵板加劲K型相贯节点的极限承载能力进行研究,便于为工程应用提供设计参考.
1 节点数值有限元模型及几何参数 1.1 有限元模型有限元模型的精细化和基本假设将直接影响计算结果,为此参考文献[7]和工程实例,取图 2(a)所示的计算简图对节点静力性能进行研究;取支管长度为6倍的支管外径,弦管长度为8倍的弦管外径.本文使用有限元分析软件ABAQUS,K型节点的有限元模型所用单元为C3D8R,支杆约束端部、加载端部与弦杆约束端部均采用刚性端板,约束条件及加载形式,见图 2(a),为与规范协调,支管加载仅考虑一拉一压受力状态,对于支管同拉同压的一些状态未在计算范畴.模型几何尺寸取自溪洛渡-浙西湘江大跨越输电塔的实际节点尺寸.本文综合考虑计算精度与效率,经试算确定:对主支管及加劲板相贯区域,网格尺寸不大于1倍弦管壁厚;对弦管两侧外伸部分等非重点研究区域,网格尺寸采用2倍弦管壁厚,网格划分见图 2(b).
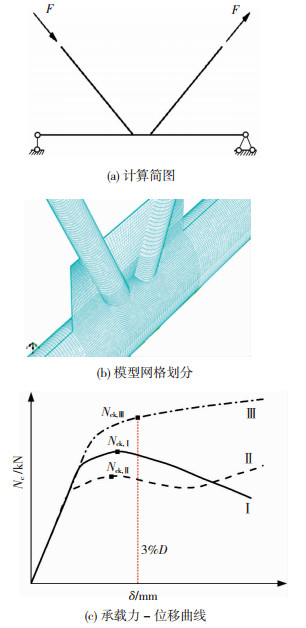
|
图 2 K型节点有限元分析模型 Fig. 2 Finite element model of K-type joint |
相贯节点主要有图 2(c)所示3种典型荷载-位移曲线.图中横坐标δ为相贯处弦管管壁沿管径方向的凹陷变形,纵坐标为支管端轴向压力Nc,即节点抗压承载力.根据Lu等[3]的承载力判别准则,通过图中极限承载力-位移曲线,采用峰值点和弦管弹塑性变形(3%D)两者中较小荷载值判定节点抗压承载力,D为弦管外径尺寸.
1.2 主要分析参数K型节点模型各参数见图 3.影响K型节点承载力的主要参数为:支管间隙a;支弦管夹角θ;管径比β=Di/D;支弦管厚度比τ=ti/t;弦管径厚比γ=D/t;加劲板长度L;加劲板厚度因子τm=ts/ti;加劲板高度因子η=h/D;弦管轴压系数n=N/(A·fy).D、t分别为弦管外径和壁厚,Di、ti分别为支管外径和壁厚,A为弦管横截面积.分别分析上述参数对节点静力性能的影响.
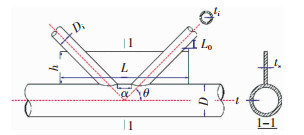
|
图 3 K型节点模型参数 Fig. 3 Model parameters of K-type joint |
文献[7]共开展了2组10个加劲相贯节点的试验研究,考虑了3种加劲形式,2类支管管径变化.为验证有限元分析方法的准确性,本文选取了其中纵板通常加劲的试件A-4[7]作为验证目标进行对比分析,选取节点的尺寸如下:弦管尺寸Φ140×2.94 mm,长度1 450 mm,屈服强度344 MPa,极限抗拉强度428 MPa;支管尺寸Φ 60×2.86 mm,长度400 mm,屈服强度327 MPa,极限抗拉强度370 MPa;加劲板尺寸100 mm×2.86 mm,屈服强度304 MPa,极限抗拉强度404 MPa.计算中采用双折线等向强化弹塑性模型,弹性模量2.06×105 MPa,折线段切线模量为弹模的1.6%,极限强度对应的应变值为0.02,泊松比0.3.约束方式为约束弦管一端和此端同侧支管端部的平动自由度,在另一支管端部施加轴向压力.
图 4为文献[7]试验与本文模拟结果对比图:两条曲线吻合程度较好,弦管管壁在弦管处发生凹陷,受压支管在加劲板上边缘处存在局部屈曲,支管整体变形较大,节点试验与模拟的失效模式一致,说明本文加劲节点模型的建立方式和分析结果是合理的.
2 典型算例分析选取典型尺寸节点,保持D=450 mm、θ=45°、τ=0.67、γ=37.5、L0=100 mm、τm=1.00不变,加劲板高度因子η为0、0.33、0.67、1.00,对各节点抗压性能进行分析.图 5为在不同加劲下,K型节点达到抗压承载力时节点的变形及应力分布.可以看出,未加劲(η=0)节点支管受压时,支管与弦管相贯处的弦管上应力集中比较明显,随着外力的不断增大,弦管管壁出现明显塑性区,发生凹陷变形;增加加劲板后,弦管管壁承载能力增强,节点破坏时弦管变形变小,而支管上出现局部屈曲,当η达到1.0时,节点失效模式为支管整体屈曲,弦管凹陷变形较小,由此可见,加劲板会影响节点失效模式,使节点破坏为支管整体屈曲,这也是相贯节点设计所期望的破坏模式,可以保证强节点弱构件的原则.

|
图 5 节点应力分布及变形(MPa) Fig. 5 Stress distribution and deformation of joints (MPa) |
各节点几何参数对K型节点抗压性能的影响主要表现为9个方面.
3.1 支管间隙a(50~200 mm)影响对于未加劲节点,在拉、压支管共同作用下,弦管管壁产生反向位移,形成应力张拉场,面内应力将增加面外的刚度,限制节点变形.a减小,张拉效应增强,两支管作用在垂直于弦管轴向的分力相互抵消,因此节点承载力增加.分别对比a=50 mm和a=200 mm两类节点的失效模式,发现a=50 mm节点的拉、压支管的内部应力更大,节点抗压承载力也高于a=200 mm的节点,符合上述分析.
当采用加劲板后,加劲板一方面对弦管管壁起到强化作用,使张拉场的作用更加明显;另一方面,加劲板作为拉、压支管间的又一传力路径,相当于拉压支管间的“腹板”,进而提高了节点的抗压承载力.当加劲板具有足够强度后,加劲板将成为拉、压支管间的主要传力路径,减少了弦管管壁所承担的荷载,从而会削弱支管间隙a对极限承载力NcK的影响.
图 6分别为β取0.25和0.49时,抗压承载力随a的变化曲线.无加劲节点主要为弦管管壁发生塑性凹陷破坏;采用加劲板后,弦管管壁的凹陷程度减弱,加劲板和支管管壁均出现明显塑性区.η为0时,a越小,K型节点承载力越高;但随着η值增大,图 6曲线变化幅度逐渐减小;当η值达到0.67以后,节点承载力不再随支管间距而发生增减.因此可知,节点间隙a变化会影响节点的承载力,而采用加劲板后会减弱节点间隙a对节点承载力的影响,减弱的程度取决于加劲板的几何尺寸.另一方面,对比a=50 mm和a=200 mm两节点加劲板上塑性区的开展情况发现,a=200 mm节点加劲板塑性区要大于a=50 mm的节点,说明增大支管间隙,加劲板会承担更多的受压支管传递的荷载.
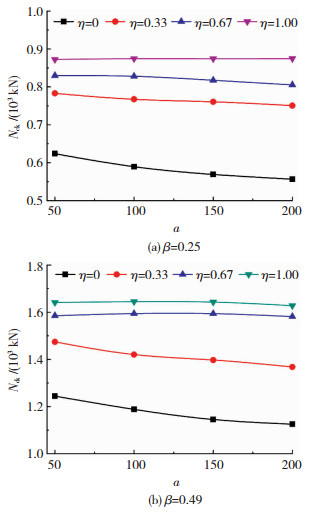
|
图 6 支管间隙a对节点抗压承载力影响 Fig. 6 Effect of a on compressive bearing capacity of joints |
支弦管夹角θ对节点抗压承载力影响见图 7,对于未加劲节点,θ从45°增加到60°,节点的抗压承载力降低18.3%;而采用加劲板后,θ从45°增加到60°,η为0.33、0.67、1.00各加劲节点承载力分别降低17.4%、15.7%、7%,可见加劲板会减弱θ对节点抗压承载力的影响,且加劲板尺寸越大,即强度越高,减弱的效果越显著.另一方面,当η由0增加到1.0时,θ为45°、50°、55°、60°的节点承载力分别增长40.81%、47.10%、53.43%、60.31%,可见同尺寸加劲板对θ较大的K型节点强化作用更明显.
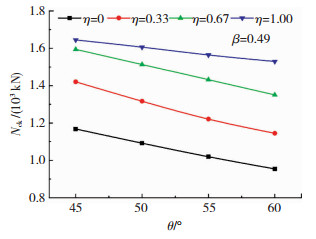
|
图 7 θ对节点抗压承载力影响 Fig. 7 Effect of θ on compressive bearing capacity of joints |
为进一步研究节点的受力性能,定义节点支管利用效率Uef为
| $ {U_{{\rm{ef}}}} = \frac{{{N_{{\rm{eK}}}}}}{{{A_{\rm{L}}}{f_{\rm{y}}}}}, $ | (1) |
式中A1为受压支管横截面积,NcK为节点极限抗压承载力.
表 1为不同夹角的K型节点的支管利用效率,可以看出,当η≤0.67,θ增加5°,Uef降低5%左右,变化较大;当η达到1.0,θ增加5°,Uef减小量在2%以内,说明加劲尺寸增大,会减弱支弦管夹角θ对NcK的影响.
| 表 1 不同θ下的节点利用效率 Tab. 1 Joint utilization efficiency with different θ |
图 8所示为不同β值下节点失效模式:β=0.25时,由于支管管径过小,当其在相贯处进入塑性时,弦管管壁变形还在弹性范围内,故此时节点的破坏模式为支管的塑性屈曲,伴随发生弦管管壁的轻微局部凹陷;当采用加劲板后,塑性失效位置上移至加劲板上边缘与支管相接处,破坏模式为支管的局部屈曲,加劲板上出现少量塑性区域.β=0.49的节点失效时,弦管管壁发生局部凹陷,支管在相贯区域发生塑性变形;采用加劲板后,加劲板强化了弦管管壁的承载能力,节点失效时,支管的塑性区域增大,弦管的局部凹陷量减小,加劲板出现屈曲.β=0.72时,此时支、弦管的相贯面积增加,支管自身承载能力也显著增加,节点失效时,表现为弦管管壁出现大面积的凹陷区域;采用加劲板后,弦管的塑性失效区域增大,支管沿加劲板焊缝发生塑性屈曲.可见,支管施加的荷载,通过加劲板向弦管传递时,作用区域会沿加劲板与弦管管壁的相贯区域发生扩散,增大弦管管壁的受力区域,使弦管的受力更加均匀.

|
图 8 β对节点抗压承载力影响 Fig. 8 Effect of β on compressive bearing capacity of joints |
从构造上可看出,相贯节点的支弦管管径比β不宜过大,否则会在相贯面最外侧使支管形成尖端,易产生应力集中等问题.
3.4 支弦管厚度比τ(0.5~1.33)影响如图 9所示,支弦管厚度比越大,节点抗压承载力越高.对于未加劲节点,当支弦管厚度比τ < 0.5时,由于支管的管壁过薄,其承载能力明显弱于弦管管壁的承载能力,故节点破坏主要为支管发生整体屈曲,表现在荷载-位移曲线中即曲线达到峰值点后快速下落;当τ增加到0.5时,节点破坏模式转变为弦管管壁发生塑性凹陷,同时支管屈曲.当τ继续增加时,节点破坏时弦管凹陷程度进一步增加,而支管塑性区减小,当τ>1.0时,节点破坏为弦管管壁凹陷,支管未出现塑性区,此时节点承载力主要由弦管的承载能力决定,表现在荷载-位移曲线中为曲线达到峰值点后平稳有限的下滑.
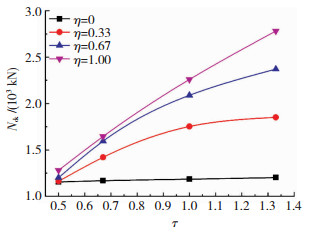
|
图 9 τ对节点抗压承载力影响 Fig. 9 Effect of τ on compressive bearing capacity of joints |
对于加劲节点,当τ≤0.67时,节点失效模式表现为支管屈曲,弦管未出现塑性凹陷;当0.67 < τ≤1.33时,失效模式为弦管凹陷,支管局部屈曲;当τ>1.33时,支管塑性区消失.可见,加劲板会强化弦管管壁的承载能力,减小节点失效时的弦管变形,使塑性区在支管上出现,实现“强节点弱构件”设计,具体形式见图 10.

|
图 10 不同τ下K节点失效模式 Fig. 10 Failure modes of K-type joints with different τ |
弦管壁厚t增大,γ减小,弦管的承载能力提高,弦管对支管的约束增强,NcK提高,其规律见图 11.另外,根据控制变量原则,当γ=D/t减小时,t增大,而保持τ、τm不变,则ts、ti均会增大,在破坏模式未发生较大变化的情况下,节点抗压承载力将会显著提高.因此,当其他参数不变时,减小γ使节点承载力显著提高是主支管壁厚和加劲板厚度增大的结果.
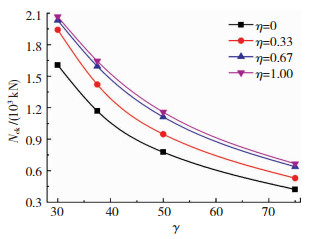
|
图 11 γ对节点抗压承载力影响 Fig. 11 Effect of γ on compressive bearing capacity of joints |
在不同管径比β下,均发现加劲板长度对节点抗压承载力影响较小,见图 12.加劲板受力的主要范围集中在与主支管相连及其邻近区域,其余部位的应力水平均较低.但在工程实际中,加劲板要留有足够外伸长度,便于焊接施工;另外,输电塔中的加劲板外伸多是直接焊接至法兰板边缘.因此,分析时,加劲板外伸长度L0取100 mm,不再另外考虑加劲板长度的影响.
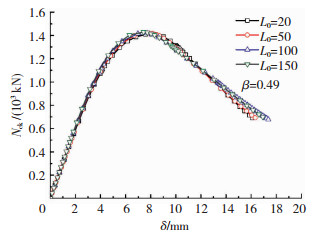
|
图 12 不同L0节点荷载-位移曲线 Fig. 12 Load-displacement curves of specimen with L0 |
当τm < 0.75时,K型节点的承载力随加劲板厚度的增加而增大,两者为线性增长关系;当τm>1.0时,节点承载力不再随着加劲板厚度增加而增大.而τm与承载力呈线性关系的临界点与η有关,该临界点随着η增加而降低,见图 13.对于η=0.17和η=0.33两种情况下,当τm >1.0以后,节点承载力会出现下降趋势,原因可能为加劲板高度较小,与支管相贯面积较小,当加劲板过厚时,支管与加劲板相焊处发生应力集中,导致节点抗压承载力略有下降.在设计中,为防止在较大荷载作用下,加劲板发生屈曲,加劲板厚度因子不宜小于0.5,也不宜大于1.0,过大的加劲板厚度会增加用钢量和结构自重,所以,应合理取定加劲板厚度.
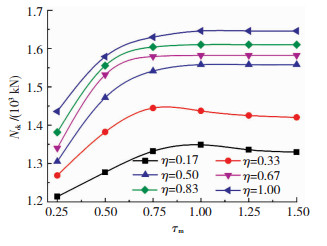
|
图 13 τm对节点抗压承载力影响 Fig. 13 Effect of τm on compressive bearing capacity of joints |
当η较小时,节点抗压承载力呈线性增长;当抗压承载力接近支管强度时,增长减慢,变化曲线见图 14.
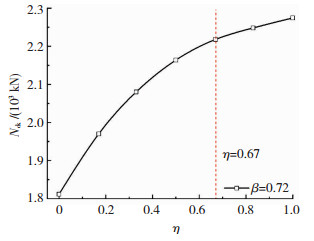
|
图 14 η对节点抗压承载力影响 Fig. 14 Effect of η on compressive bearing capacity of joints |
增大K型节点弦管两端的轴压,会使节点的抗压承载力降低,见图 15.轴压系数增加0.2,节点抗压承载力下降5%~7%,且轴压越大,下降比例越大.对于加劲节点,随着η值的不断提升,轴压力的影响不断减弱,η达到1.0时,轴压系数增加0.2会导致节点承载力下降3%,显然加劲作用较强,此时轴压变化对节点抗压承载力影响较小.

|
图 15 n对节点抗压承载力影响 Fig. 15 Effect of n on compressive bearing capacity of joints |
综合加劲高度和厚度分析结果,对于采用不同尺寸加劲板的K型节点,其失效模式的转变如下:当τm < 0.25且η < 0.17时,加劲作用不明显,节点破坏形式与无加劲节点相同(图 16(a));当0.25 < τm < 0.50且0.17 < η < 0.33时,节点破坏模式表现为弦管管壁凹陷,加劲板出现贯通塑性区,支管存在局部塑性区(图 17(b));当0.50 < τm < 1.00且0.33 < η < 1.00时,加劲板具有足够的强度,节点破坏时,支弦管均出现明显凹陷区,加劲板屈曲(图 17(c));当τm>1.00且η>1.00时,继续增加加劲板尺寸,加劲板强度已能完全承受支管的荷载,弦管表面的凹陷程度会进一步减轻,节点失效表现为支管整体屈曲,加劲板出现少量塑性区,而弦管变形很小(图 17(d)).另外,当τm < 0.25而η>0.67时,加劲板过于薄柔会发生明显的弯矩变形,设计时应予以避免.
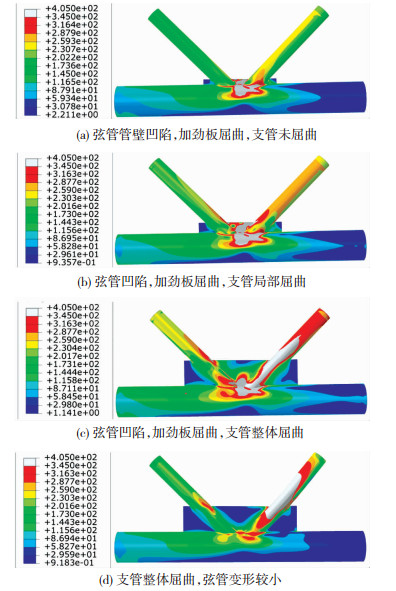
|
图 16 加劲节点失效模式示意 Fig. 16 Failure modes of stiffened joints |

|
图 17 抗压承载力随τm和η变化等值线 Fig. 17 Effect of τm and η on compressive bearing capacity of joints |
节点的失效模式受加劲板高度和厚度的共同影响,图 17给出K型节点抗压承载力在τm和η变化时的等值线图,图 18为NcK随τm×η的变化情况.当τm× η≤0.15时,节点抗压承载力处于区域Ⅰ内,其失效模式与未加劲节点基本相同,主要为弦管塑性凹陷失效;当0.15 < τm×η≤0.50时,节点抗压承载力处于区域Ⅱ内,其失效模式为弦管凹陷,伴随支管局部屈曲;当τm×η>0.50时,节点抗压承载力处于区域Ⅲ内,失效模式转变为支管的整体屈曲,加劲作用明显.在区域Ⅰ、Ⅱ内,节点承载力呈线性增长趋势,区域Ⅲ内曲线趋于平缓,承载力变化范围在5%以内.综上所述,为充分发挥加劲作用,建议取τm×η不小于0.50,但过大的加劲板会增加结构重量,因此建议取τm×η不大于1.
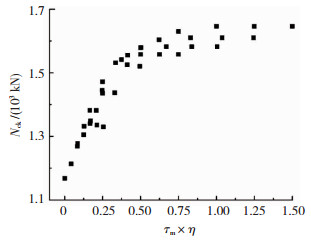
|
图 18 抗压承载力随τm×η分布 Fig. 18 Effect of τm× η on compressive bearing capacity of joints |
为便于简化计算纵板加劲相贯节点的承载力设计值,对上述参数拟合分析,以无量纲参数Nc/Nc,0为因变量,考虑的影响参数有a、θ、β、τ、γ、τm、η、n,回归中采用无量纲化参数,并结合模拟结果,最终采用a/D、sin θ、β、τ、γ、τm、η、n为自变量,最终经过试算对比,确定回归方程形式:
| $ \frac{{{N_{\rm{c}}}}}{{{N_{{\rm{c}}, 0}}}} = {\left[ {{{\left( {\frac{a}{D}} \right)}^{{C_{{\rm{Nl}}}}}}{{(\sin \theta )}^{{c_{{\rm{N}}2}}}}{\beta ^{{C_{{\rm{N}}3}}}}{\tau ^{{C_{{\rm{N}}4}}}}{\gamma ^{{C_{{\rm{NS}}}}}}{{\left( {{{\rm{e}}^{{\tau _{\rm{m}}}}}} \right)}^{{C_{{\rm{N}}6}}}}{{\left( {{{\rm{e}}^\eta }} \right)}^{{C_{{\rm{N}}7}}}}{{\left( {{{\rm{e}}^n}} \right)}^{{C_{{\rm{N}}8}}}}{{\rm{e}}^{{C_{{\rm{N}}9}}}}} \right]^{{\tau _{\rm{m}}}\eta }}, $ | (2) |
进行置信度为95%的多元线性回归,得
| $ \frac{{{N_{\rm{c}}}}}{{{N_{{\rm{c}}, 0}}}} = {\left[ {{{\left( {\frac{a}{D}} \right)}^{0.09}}{{(\sin \theta )}^{0.13}}{\beta ^{ - 0.15}}{\tau ^{0.82}}{\gamma ^{0.18}}{{\rm{e}}^{ - 0.59{\tau _{\rm{m}}}}}{{\rm{e}}^{ - 0.44\eta }}{{\rm{e}}^{0.4n}}{{\rm{e}}^{1.12}}} \right]^{{\tau _{\rm{m}}}\eta }}, $ | (3) |
式(3)通过各项检验,令ψsK, N=Nc/Nc, 0并代入GB 50017—2017的K型节点设计公式(符号参见规程13.3.2 -10)中,可得K型纵板加劲节点的承载力:
| $ {N_{{\rm{cK}}}} = {\psi _{\rm{n}}}{\psi _{\rm{d}}}{\psi _{\rm{a}}}{\psi _{{\rm{sK}}, {\rm{N}}}}\frac{{11.51}}{{\sin \theta }}{\left( {\frac{D}{t}} \right)^{0.2}}{t^2}f. $ | (4) |
进一步验证式回归结果的准确性,将式(4)的计算承载力Nc, MRM和有限元模拟的承载力Nc, FEM进行对比,见图 19.图中横坐标轴为有限元分析所得节点极限承载力Nc, FEM,纵坐标轴为采用回归公式所得计算承载力Nc, MRM,可以看出,点(Nc, FEM, Nc, MRM)主要分布在直线Nc, FEM=Nc, MRM临近区域,可见公式拟合程度较好.为了更加明显地对结果进行统计计算,选取无量纲参数Nc, MRM /Nc, FEM统计,其均值为1.004,方差为0.0020.
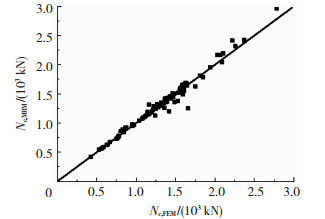
|
图 19 数值分析与简化公式结果比较 Fig. 19 Comparison between results of numerical analysis and simplified formula |
1) 纵向加劲方式可以明显提高K型间隙相贯节点的支管在节点处的抗压承载力.
2) 随着加劲板尺寸的增大,K型加劲节点的失效模式由弦管表面的塑性凹陷失效逐渐过渡到支管的整体屈曲破坏.纵板加劲相贯节点支管的整体屈曲破坏为节点预期的失效模式,可保证“强节点弱构件”的原则理念.
3) 对K型加劲节点进行参数分析发现:支管间距与弦管外径比a/D、支弦管夹角θ、支弦管厚度比τ、弦管径厚比γ、加劲板厚度因子τm、加劲板高度因子η、轴压系数n与加劲板对节点抗压承载力的强化因子ψsK, N呈正相关,而支弦管管径比β则呈负相关.
4) 弦管承受轴向压力作用时,K型节点的极限承载力均会降低,且轴压越大降幅越大,而加劲板可分担部分轴压,减缓节点承载力的降幅.
5) 增加纵向加劲板的高度和厚度可明显提高节点抗压承载力,但加劲板达到一定尺寸后节点承载力增长减缓,分析时发现对于K型节点,加劲板高度和厚度的合理取值范围为τm在0.75~1.00,η在0.33~0.67,且τm·η范围在0.5~1.0为宜;加劲长度对节点承载力的影响很小,设计时满足焊接等方面的尺寸要求即可.
6) 根据模拟分析,完成了纵板加劲节点设计方式的修正.
| [1] |
EASTTWOOD W, WOOD A A. Welded joints in tubular structures involving rectangular sections[C]//Conference on Joints in Structures, Session A Paper 2. Sheffield: University of Sheffield, England, 1970
|
| [2] |
牧野雄二, 黒羽啓明, 山本昇.軸力と面內曲げモーメントを受ける鋼管K継手[C]//日本建築学会大会学術講演梗概集.北海道: 日本建築学会, 1986: 919
|
| [3] |
LU L H, DE WINKEL G D, YU Y, et al. Deformation limit for the ultimate strength of hollow section joints[J]. Tubular Structures VI, 1994, 25: 341. |
| [4] |
高艳林. K型圆钢管相贯节点套管加强及承载力研究[D].兰州: 兰州交通大学, 2012 GAO Yanlin. Research on circular tubular K-joints casing to strengthen and bearing capacity[D]. Lanzhou: Lanzhou Jiaotong University, 2012 |
| [5] |
张巧珍, 周洪彬, 张明莉. 插板加强K型间隙圆钢管相贯节点的极限承载能力非线性有限元分析[J]. 钢结构, 2006, 21(1): 54. ZHANG Qiaozhen, ZHOU Hongbin, ZHANG Mingli. Nonlinear finite element analysis of the ultimate bearing capacity of reinforced circular tubular gapped K-joints with a flashboard[J]. Steel Structure, 2006, 21(1): 54. DOI:10.3969/j.issn.1007-9963.2006.01.016 |
| [6] |
吴亮秦, 李自林, 韩庆华. 垫板加强N形圆钢管相贯节点静力性能试验研究[J]. 建筑结构学报, 2010, 31(10): 83. WU Liangqin, LI Zilin, HAN Qinghua. Experimental study on static behavior of plate reinforced tubular N-joints[J]. Journal of Building Structures, 2010, 31(10): 83. |
| [7] |
潘奕康.纵向板加强平面K型圆管间隙节点静力工作性能的试验研究[D].哈尔滨: 哈尔滨工业大学, 2013 PAN Yikang. Experimental investigations on static behavior of uniplanar gapped K-type CHS joints reinforced with longitudinal plates[D]. Harbin: Harbin Institute of Technology, 2013 |
| [8] |
宋启明.采用外加劲肋加固圆钢管节点的研究[D].北京: 北京建筑大学, 2016 SONG Qiming. Study on strength of CHS joints reinforced by external stiffeners[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2016 |
| [9] |
NASSIRAEI H, LOTFOLLAHI-YAGHIN M A, AHMADI H, et al. Static strength of doubler plate reinforced tubular T/Y-joints under in-plane bending load[J]. Journal of Constructional Steel Research, 2017, 136: 49. DOI:10.1016/j.jcsr.2017.05.009 |
| [10] |
NASSIRAEI H, MOJTAHEDI A, LOTFOLLAHI-YAGHIN M A. Static strength of X-joints reinforced with collar plates subjected to brace tensile loading[J]. Ocean Engineering, 2018, 161: 227. DOI:10.1016/j.oceaneng.2018.05.017 |
 2020, Vol. 52
2020, Vol. 52



