砌体结构因施工工艺传统、造价较低等特点在村镇及较小城市地区应用广泛.因此,砌体结构的抗震能力评价研究具有重要的理论和工程意义.将砌体结构等效为分别考虑砌块和砂浆性能的精细化模型,其建模过程复杂,计算效率过低,很难实现结构整体的地震易损性分析.近年来,研究者尝试建立砌体结构的适度简化模型并进行动力分析.郑山锁等[1]利用能较好反映结构基本动力特性的三弹簧单元简化模型建立了砌体结构模型,但该模型参数较多且参数对腐蚀次数不同的墙体不具有普适性;郑淏等[2]在传统等效框架简化模型基础上,采用同时考虑轴向弯曲和剪切变形的纤维截面模拟砌体墙的墙柱和墙梁,但该方法对墙柱、墙梁及刚性区域的界定尚需进一步明确.
等效斜撑模型是由Polyakov[3]基于填充墙框架结构试验提出的.最初的单等效斜撑模型简单,但不能反映填充墙与框架间的应力相互关系,之后发展出的多斜撑模型能部分反映上述关系[4],但构成更加复杂.此外,等效斜撑宽度的计算一直是研究的难点,1966年,Smith[5]最先引入反映填充墙材料与框架材料刚度比的特征参数来计算等效斜撑宽度,之后陆续有学者[6-7]对等效斜撑宽度计算公式进行修正和提出不同的等效斜撑面积计算公式.然而,等效斜撑模型能否适用于砌体结构尚需进行深入探究.
根据以上研究现状,本文基于OpenSEES软件提出了砌体结构(包括满布墙体、开门、窗洞口)的等效斜撑建模方法.在模型正确性得到验证的基础上,建立了三层砌体结构的等效斜撑模型.引入能量损伤指数作为工程需求参数,与传统的最大层间位移角作为工程需求参数一起综合评价结构的抗震性能.同时,本文分别建立了仅考虑横墙砌体结构模型(横墙模型)和同时考虑纵横墙砌体结构模型(完全模型),对比了两种模型的地震易损性曲线差异,为建模精度要求提供了建议.
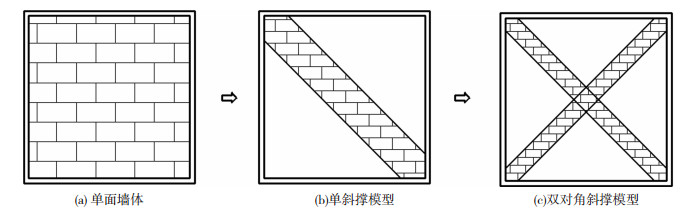
1 等效斜撑模型原理及计算Polyakov[3]认为在侧向水平力作用下框架中填充墙的作用如同1根只承受压力的斜撑杆,因此提出等效斜撑模型的概念,见图 1.目前该方法已在框架结构的填充墙抗震性能分析中得到广泛应用.然而,在地震动往复作用下,单方向斜撑杆不能充分描述墙框之间的相互作用,因此可将单斜撑模型转化成图 1(c)所示的双对角斜撑模型.在双对角斜撑模型中,每根斜撑杆的宽度可取单斜撑模型宽度的一半[8].
|
图 1 等效斜撑 Fig. 1 Equivalent diagonal brace |
根据Holmes[9]的研究,等效斜撑杆的材料和厚度可与框架填充墙的参数一致.在斜撑杆宽度取值的研究中,研究者给出了多种计算公式,本文选取Saneinejad等[10]提出的公式确定不开洞时单对角斜撑模型的斜撑杆宽度,该公式也是FEMA273建议采用的斜撑宽度计算公式,具体形式为
| $ \left\{ {\begin{array}{*{20}{l}} {w = 0.175{{(\lambda H)}^{ - 0.4}}\sqrt {{H^2} + {L^2}} ,}\\ {\lambda = {{\left( {\frac{{{E_{\rm{w}}}{t_{\rm{w}}}\sin 2\theta }}{{4{E_{\rm{c}}}{I_{\rm{c}}}{H_{{\rm{in}}}}}}} \right)}^{\frac{1}{4}}}.} \end{array}} \right. $ | (1) |
式中:w表示斜撑杆宽度,λ表示相对刚度系数,H表示框架层高,L表示框架梁长,Ew表示填充墙材料的弹性模量,tw表示填充墙厚度,θ表示斜撑与水平梁的夹角,Ec表示框架材料的弹性模量,Ic表示柱正交荷载方向的惯性矩,Hin表示填充墙的高度.
值得注意的是,上述等效斜撑模型一般均应用于框架填充墙的模拟,其能否在砌体结构中应用尚需进一步验证,本文将研究采用等效斜撑模型模拟无洞口砌体结构和开有门洞或窗洞的砌体结构的可行性和准确性.
2 等效斜撑模型在砌体结构分析中的应用 2.1 无洞口砌体结构等效斜撑建模首先研究采用等效斜撑模型模拟无洞口砌体结构的可行性.由于式(1)充分考虑了砌体墙高宽比、构造柱圈梁与砌体墙相对强度等因素,因此,本文仍采用该公式计算无洞口砌体结构对应的等效斜撑杆宽度.
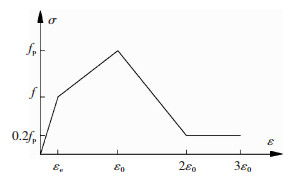
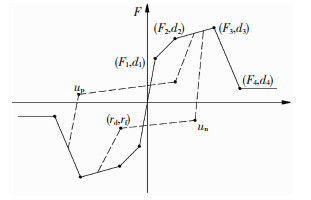
采用有限元软件OpenSEES建立砌体结构模型.构造柱和圈梁采用最常用的Nonlinear beamcolumn单元进行模拟,取5个积分点,不考虑P-Δ效应.截面采用纤维截面,混凝土采用不考虑受拉的Concrete01本构关系,考虑箍筋对核心区混凝土的约束作用.钢筋采用Steel02材料,等效斜撑杆采用Truss单元.文献[11]结合中国砌体结构设计规范建立了图 2所示的四段直线式砌体应力应变曲线,其中fp为峰值应力,ε0为峰值应力对应应变.由于OpenSEES中的Pinching4材料受拉区及受压区本构关系(图 3)与上述砌体本构模型相似,且其滞回规则明确易调,其中骨架曲线参数参考试验滞回曲线进行取值,up、un为卸载结束时的荷载值,rf为再加载开始点的荷载值,rd为再加载开始点变形值.因此,本文采用Pinching4材料作为斜撑杆材料进行模拟.
|
图 2 砌体本构模型 Fig. 2 Masonry constitutive model |
|
图 3 Pinching4材料本构关系及滞回规则 Fig. 3 Constitutive relation and hysteresis rule of Pinching4 material |
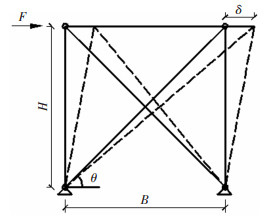
首先验证无洞口砌体结构等效斜撑建模及计算方法,结合文献[1]中试件WR-1的试验结果进行分析和比较该试件尺寸为1 480 mm×831 mm,构造柱尺寸为120 mm×120 mm,圈梁尺寸为120 mm×150 mm,砂浆强度为12.68 MPa,砖强度为16.37 MPa,弹性模量为5 030 MPa.等效斜撑厚度取为墙厚,宽度按式(1)计算为174 mm.由于在地震动作用下砌体墙的破坏通常表现为出现交叉斜裂缝,因此建模时采用图 4所示的双对角斜撑模型,每根斜撑杆宽度各取计算宽度的一半,即87 mm.峰值应力取砌体轴心抗压强度平均值,可由砌体结构设计规范[12]中公式计算得出,即
| $ {f_{\rm{m}}} = {k_{\rm{L}}}f_1^\alpha \left( {1 + 0.07{f_2}} \right){k_2}, $ | (2) |
|
图 4 等效斜撑布置 Fig. 4 Equivalent diagonal brace arrangement |
式中:fm为砌体轴心抗压强度平均值,f1为块体抗压强度平均值,f2为砂浆抗压强度平均值,当f2≥1时k2=1,k1为砌体种类和砌筑方法等因素对砌体抗压强度的影响系数,α为回归参数.最终求得峰值应力为5.957 MPa,峰值应变取为0.003.其他材料参数取值见表 1.
| 表 1 部分Pinching4材料参数取值 Tab. 1 Values of some Pinching4 material parameters |
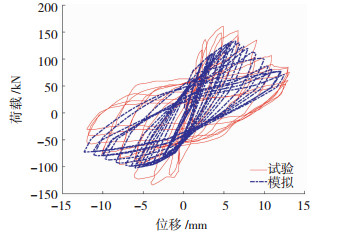
有限元模型的结果和原试验结果见图 5,可见采用Pinching4材料模拟的砌体结构滞回曲线与试验滞回曲线吻合较好,除极限荷载较试验值略低外,基本可准确反映砌体结构的初始刚度、强度和刚度退化性能.
|
图 5 无开洞砌体结构模拟结果 Fig. 5 Simulated results of masonry structures without openings |
对于开洞砌体结构,仍采用上述双对角斜撑建模方式.斜撑宽度的计算首先把开洞墙体划分为多个墙段,将每个墙段刚度进行叠加后得到开洞墙体理论刚度,之后对理论刚度适当修正,代入墙体刚度与等效斜撑宽度换算公式得到斜撑宽度.具体推导过程如下文所述.
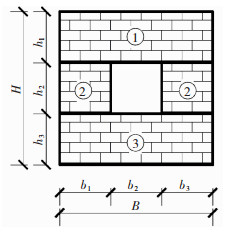
参考文献[13]的分析方法,将带洞口墙体划分为图 6所示的多个墙段,每个墙段按式(3)计算墙体抗侧刚度后叠加,得到开窗洞墙体理论刚度计算公式.
| $ {{k_{\rm{s}}} = \frac{{{G_{\rm{w}}}A}}{{\xi {H_{\rm{w}}}}},} $ | (3) |
| $ {{k_{\rm{c}}} = \frac{{{G_{\rm{w}}}B{t_{\rm{w}}}\left( {{b_1} + {b_3}} \right)}}{{\xi \left[ {\left( {{h_1} + {h_3}} \right)\left( {{b_1} + {b_3}} \right) + {h_2}B} \right]}}.} $ | (4) |
|
图 6 开洞口墙体划分 Fig. 6 Wall division of opening |
式中:ks为单个墙段的初始抗侧刚度;kc为开窗洞墙体理论刚度;Gw为墙体材料的剪切模量,一般取Gw=0.4Ew;A为墙体水平向截面面积;ξ为应变不均匀系数,对矩形截面,ξ=1.2;Hw为墙体高度.
采用力学公式推导的得到的弹性刚度kc与墙体实测开裂刚度kw相差较大,根据文献[13-14]中统计的砌体墙试验数据及研究成果中实测开裂刚度kw与弹性刚度kc的比值,结合常见开洞率,本文建议取kw=0.2 kc.
李常青[15]按图 4的计算简图,通过结构力学的分析方法,确定了简图中等效斜撑的截面宽度与填充墙的侧向刚度换算公式为
| $ w = \frac{{{k_{\rm{w}}}{B_{\rm{w}}}}}{{2{t_{\rm{w}}}{E_{\rm{w}}}{{\cos }^3}\theta }}, $ | (5) |
式中:w为单个对角斜撑的宽度,kw为墙体侧向刚度,Bw为墙体宽度,tw为墙体厚度,Ew为墙体材料的弹性模量,θ为等效斜撑杆与水平方向的夹角.
本文将式(4)的理论刚度按上述比例调整后,代入式(5)得到开窗洞等效斜撑截面宽度公式:
| $ {W_{\rm{c}}} = \frac{{\left( {{b_1} + {b_3}} \right){{\left( {{H^2} + {B^2}} \right)}^{3/2}}}}{{30B\left[ {\left( {{h_1} + {h_3}} \right)\left( {{b_1} + {b_3}} \right) + {h_2}B} \right]}}. $ | (6) |
令h3=0,可得开门洞等效斜撑截面宽度计算公式:
| $ {W_{\rm{m}}} = \frac{{\left( {{b_1} + {b_3}} \right){{\left( {{H^2} + {B^2}} \right)}^{3/2}}}}{{30B\left[ {{h_1}\left( {{b_1} + {b_3}} \right) + {h_2}B} \right]}}. $ | (7) |
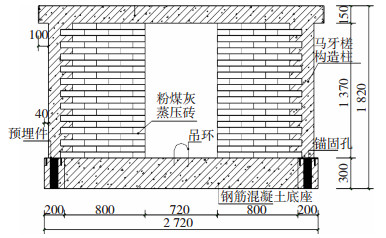
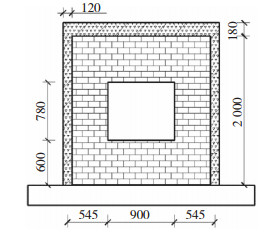
基于上述开洞砌体结构等效斜撑计算公式,对文献[16]中开门洞砌体结构(试件WA3,构造见图 7)和文献[17]中开窗洞砌体结构(试件W1,构造见图 9)进行有限元模拟.按式(6)计算得开窗洞斜撑宽度为74 mm,按式(7)计算得开门洞斜撑宽度为75 mm,Pinching4材料参数同表 1.
|
图 7 开门洞砌体结构WA3(mm) Fig. 7 Masonry structure WA3 with door openings (mm) |
|
图 9 开窗洞砌体结构W1(mm) Fig. 9 Masonry structure W1 with window openings (mm) |
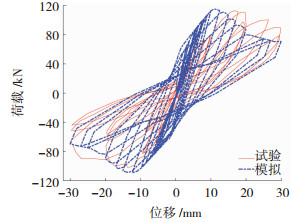
模拟结果见图 8、10,可见有限元分析结果在滞回特征和极限荷载等方面与试验结果非常接近,采用上述开门窗洞砌体结构等效斜撑杆宽度计算公式及建模方法能够较好的模拟开洞砌体结构的强度及力学性能.
|
图 8 开门洞砌体结构模拟结果 Fig. 8 Simulated results of masonry structure with door openings |

|
图 10 开窗洞砌体结构模拟结果 Fig. 10 Simulated results of masonry structure with window openings |
增量动力分析方法(IDA)是将某一地震动幅值按比例依次增大,对结构进行多次非线性时程反应分析,然后提取损伤参数(DM)和地震动参数(IM),将DM和IM分布进行统计,从而获得从弹性到最终整体动力失稳的全反应过程.结构地震易损性是指结构在不同水平地震作用下,发生不同程度破坏的概率,即结构的地震需求参数超过结构本身能力参数的概率,多用结构的超越概率来衡量.本文对算例砌体结构的分析中IM取PGA,DM取为最大层间位移角和能量损伤指数.
3.1 地震动记录的选择不同的分析地震波对结构的非线性动力时程分析影响很大,与底部剪力法或振型分解反应谱法的结构差别有时可达到数倍乃至10倍之多[18].使得增量动力分析方法具有很大的随机性,因此在选取地震记录时,应该尽量合理,以得到理想的分析结果.在选取地震记录时主要考虑了以下参数:地震设防烈度、地震强度等级、震中距、场地土类别等.本文基于美国ATC-63(2008)报告[19]及中国现行建筑抗震设计规范[20],确定了如下的选波原则:1)所选地震震级应大于6.5级;2)地震波的PGA尽量大于0.2 g,PGV尽量大于15 cm/s;3)震中距大于10 km;4)多组时程波的平均地震影响系数曲线与振型分解反应谱法所用的地震影响系数曲线相比,在对应于结构主要振型的周期点上相差不大于20%.
文献[21]的研究表明,当采用一个合适有效的地震动强度指标时,10到20条地震记录通常能足够精确的评估出结构的地震需求.基于以上原则,本文选取满足要求的12条地震波进行增量动力分析,地震波名称参见文献[22],本文另补充了Chi-Chi波及Kobe波.
3.2 砌体结构地震易损性分析方法对算例结构的IDA数据取自然对数后进行回归拟合,得到结构损失参数DM与地震动参数IM之间的回归方程:
| $ \ln \left( {{\rm{DM}}} \right) = A + B\ln \left( {{\rm{IM}}} \right), $ | (8) |
式中A和B可由线性回归拟合结果直接得到,将A和B的值代入下式:
| $ {P_{\rm{f}}} = \phi \left( {\frac{{\ln \left( {{{\rm{e}}^4}{{({\rm{PGA}})}^B}/C} \right)}}{{\sqrt {\sigma _{\rm{C}}^2 + \sigma _{\rm{D}}^2} }}} \right), $ | (9) |
式中Pf表示失效概率,根据文献[23]
传统砌体结构地震易损性分析中DM多取为最大层间位移角,本文在砌体结构地震易损性分析中引入能量损伤指数为DM,对比两项指标下结构地震易损性曲线的差异.在较小的外力作用下,结构或构件只发生弹性变形,若此时撤去外力结构可恢复至初始状态且不发生损伤.若外力作用较强,结构或构件将发生屈服破坏,转化的能量以塑性变形能为主,且随着力的增加产生更严重的损伤.如果提高结构的承载力令其不发生屈服,即确保结构处于理想弹性状态,则损伤仍不会发生.可见,损伤的形式和程度与结构理想弹性变形能和实际弹塑性变形能之间的差异密切相关,可用该差值表征损伤特征.本文采用文献[24]中动力下耗能差率损伤模型计算结构能量损伤指数时程:
| $ \begin{array}{l} {D_{\rm{F}}}(t) = \frac{{{E_{\rm{E}}}(t) - {E_{\rm{F}}}(t)}}{{{E_{\rm{E}}}(t)}} = \\ 1 - \frac{{\sum\limits_{i = b}^n {\left| {{F_{\rm{F}}}(i){u_{\rm{F}}}(i)} \right|} }}{{\sum\limits_{i = b}^n {\left| {{F_{\rm{E}}}(i){u_{\rm{E}}}(i)} \right|} }}, \end{array} $ | (10) |
式中:FF(i)和FE(i)分别为i时刻弹塑性状态下和理想弹性状态下的基底剪力,uF(i)和uE(i)分别为i时刻弹塑性状态下和理想弹性状态下的顶部位移,b为结构首次进入屈服状态时对应的时间点,n为从时间点b至现时t的时间步长数.
在做砌体结构增量动力分析时,同时提取结构底部剪力和顶点位移,得到每条波下不同地震峰值能量损伤指数时程曲线,能量损伤指数数值上随地震动和响应的随机性和往复性发生一定范围的波动,且严格介于0~1.基于能量损伤指数生成结构易损性曲线时,本文取损伤曲线末端中较稳定的数值作为等效损伤值进行计算.提取不同记录各峰值地震动下的能量损伤指数作为IDA数据,按式(8)、(9)进行计算分析,也可得到结构地震易损性曲线.
4 砌体结构算例分析依据上述建模方式,采用OpenSEES建立四川省都江堰市某三层砌体结构宿舍楼模型,具体工况为:抗震设防烈度为8度,设计地震分组为第二组,设计基本地震加速度值0.20 g.建筑场地类别为Ⅱ类,建筑安全等级二级,设计使用年限50 a.
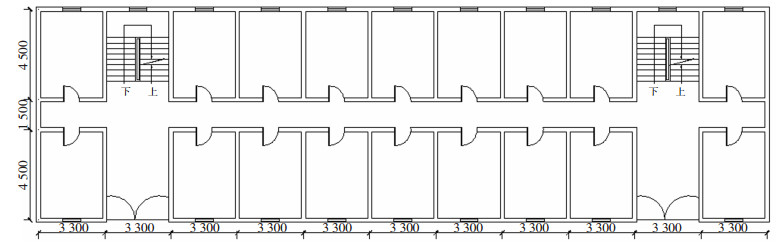
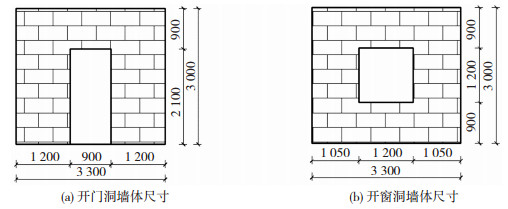
楼面及楼板均为现浇钢筋混凝土板,厚度120 mm,墙体厚度统一为240 mm,层高均为3 000 mm,所有纵横墙交接处均设置构造柱圈梁,尺寸均为240 mm×240 mm,砌体墙采用MU15烧结普通砖与M5水泥砂浆砌筑,构造柱圈梁混凝土等级为C20.不上人屋面活荷载标准值为0.5 kN/m2,楼面及走廊活荷载标准值为2.0 kN/m2,雪压标准值为0.25 kN/m2,楼屋面恒荷载取为4.0 kN/m2.结构平面布置见图 11,门窗洞口尺寸见图 12.
|
图 11 结构平面布置(mm) Fig. 11 Structural plane layout (mm) |
|
图 12 门窗洞口尺寸图(mm) Fig. 12 Dimensions of door and window openings (mm) |
采用Nonlinear beamcolumn单元及Concrete01、Steel02材料模拟圈梁构造柱,Truss单元及Pinching4材料模拟砌体墙等效斜撑杆,实体墙、开窗墙和开门洞等效斜撑宽度依据砌体墙尺寸图按式(1)、(6)、(7)计算得出,由上述方法建立砌体结构模型进行地震易损性分析.
对于砌体结构,若所有的砌体墙均采用等效斜撑模型来模拟,其建模和计算工作量均较大,可以考虑适当简化建模.因此,本文分别建立了同时考虑纵横墙砌体结构模型(完全模型)和仅考虑横墙砌体结构模型(横墙模型),从最大层间位移角和能量损伤指数两个方面分析了横墙在砌体结构地震易损性分析中所占比重,探究了用横墙模型代替完全模型是否可行.
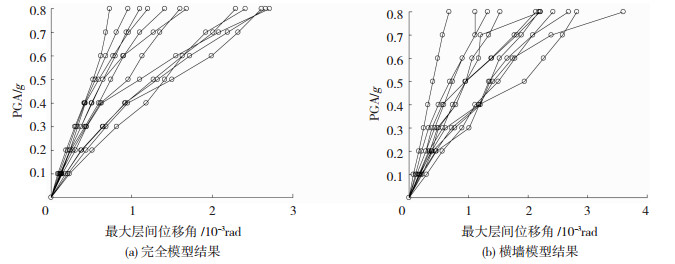
对结构进行IDA分析时,采用二维加载地震波方式,依次输入12条地震记录,对每条记录进行等步长调幅,调幅步长取为0.1 g,并由0.1 g逐步增加至0.8 g.由计算结果绘制算例结构的IDA曲线见图 13.
|
图 13 IDA曲线 Fig. 13 IDA curves |
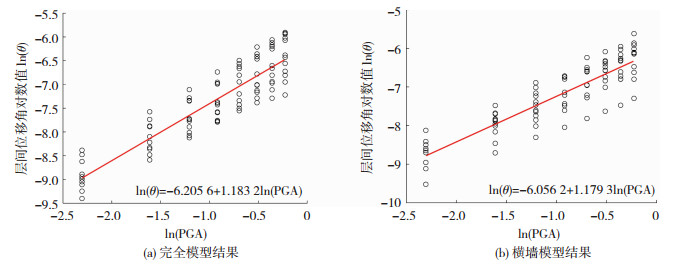
对算例结构的IDA数据取自然对数后进行回归拟合,图 14为算例砌体结构线性拟合分析结果.
|
图 14 线性回归分析 Fig. 14 Linear regression analysis |
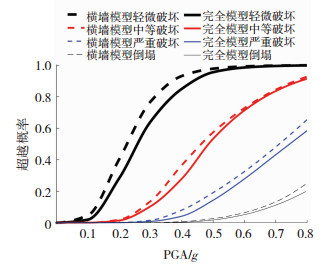
对于C为结构各极限状态时的最大层间位移角限值的情况,根据已有研究[22-25]及砌体结构设计规范的要求,并基于IDA曲线确定了完全模型及横墙模型不同损伤状态下的最大层间位移角范围,见表 2.取某一破坏状态下的θmax值,代入不同的PGA值,由式(9)得到算例砌体结构在各破坏状态下的易损性曲线数据,易损性曲线见图 15.结果表明当以最大层间位移角为损伤参数时,横墙模型与完全模型的易损性曲线比较接近,横墙模型的易损性上浮比例不足10%,可认为砌体结构抗震能力主要由横墙提供,开洞纵墙提供的抗震能力较小.
| 表 2 不同破坏等级对应限值 Tab. 2 Limits of different failure levels |
|
图 15 是否考虑开洞纵墙砌体结构地震易损性曲线对比 Fig. 15 Comparison of seismic fragility curves of longitudinal wall masonry structures with or without openings |
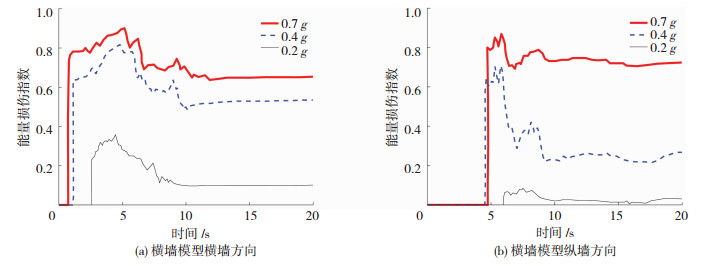
在做砌体结构增量动力分析时,提取结构底部剪力和顶点位移,并按式(10)计算获得不同峰值地震动下的能量损伤指数,限于篇幅只给出了一条典型地震波下横墙模型纵轴向及横轴向的结果,见图 16.
|
图 16 不同地震峰值能量损伤指数曲线对比 Fig. 16 Comparison of damage index curves of different earthquakes |
由图 16可知,当结构整体发生屈服后,能量损伤指数随随地震动和响应的随机性和峰值增大而不断波动和加剧,且严格介于0~1.在地震后期由于地震动幅值的逐渐减小以及结构刚度的回弹,损伤指数呈现适当下降.从图 16(b)的结果表明横墙模型在两个方向均出现了较明显的损伤,不考虑纵墙的抗震作用将高估结构的损伤程度.此外,与基于位移的损伤评价相比,基于能量的损伤评价是更全面而准确的.
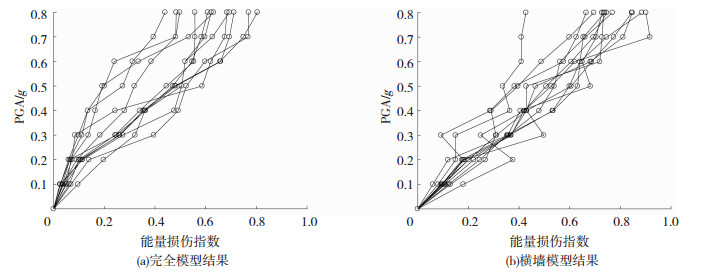
提取算例模型在每条波不同幅值下末段中较为稳定的能量损伤指数数值,得到能量损伤指数下的IDA曲线见图 17.
|
图 17 IDA曲线 Fig. 17 IDA curves |
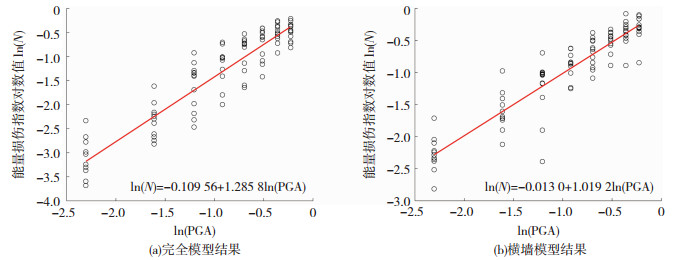
对算例结构的能量损伤指数IDA数据取自然对数后进行回归拟合,得出两个算例结构模型线性拟合结果见图 18.
|
图 18 线性回归分析 Fig. 18 Linear regression analysis |
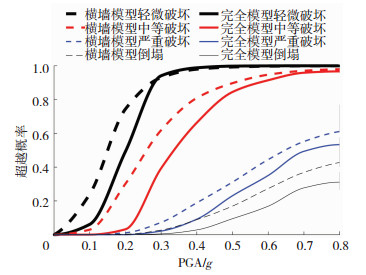
参考已有研究成果并结合能量损伤指数特点,定义对应结构不同破坏等级损伤性能指标限值见表 2.在式(9)中代入不同的限值及PGA值得到两个算例结构的地震易损性曲线数据,绘制易损性曲线见图 19.
|
图 19 是否考虑开洞纵墙砌体结构地震易损性曲线对比 Fig. 19 Comparison of seismic fragility curves of longitudinal wall masonry structures with or without openings |
通过分析可认为采用耗能差率为损伤指标得到的结构地震易损性曲线与结构破坏状态、特征和发展趋势吻合,能够更准确地反映结构的损伤程度和演变趋势,更适合应用于砌体抗震易损性分析.以弹塑性耗能差率作为损伤参数时,横墙模型与完全模型的地震易损性曲线差异较大,横墙模型的易损性值最大上浮比例达到了65%,这一方面是由于弹塑性耗能差能明显表征和区分不同模型的损伤程度和演变趋势,另一方面也表明虽然横墙在砌体结构的抗震中仍具有至关重要的作用,但开洞纵墙的作用不容忽视,而基于位移的损伤参数并不能充分反映这一事实.综上,采用横墙模型计算效率较高,但将高估结构的损伤程度和抗震易损性,偏于保守;当对地震易损性精度要求较高时,宜采用完全模型.对于具体结构,应根据精度需求、建模能力和计算效率选择适合的建模方案.
5 结论本文将等效斜撑模型应用于砌体结构,提出了适用于实体墙、开窗墙和开门洞墙的斜撑宽度计算方法,通过有限元分析和试验数据的对比验证了上述方法的准确性和实用性.分别将层间位移角和弹塑性耗能差作为损伤参数进行了砌体结构的地震易损性分析,得到的结论主要包括:
1) 本文采用的Pinching4材料和等效斜撑宽度计算方法建立的砌体结构模型能够较准确地模拟实体墙及开门窗洞口砌体结构的强度及滞回耗能性能.
2) 从砌体结构IDA曲线可以看出,砌体结构脆性大,在地震动峰值加速度小于0.4 g时,基本处于弹性状态,之后刚度开始下降,随着峰值加速度的增大,刚度下降明显;能量损伤指数分析结果显示,随着地震动幅值增加,能量损伤指数逐步提高,且严格介于0~1,模型强轴、弱轴方向均存在不同程度的损伤.
3) 从砌体结构地震易损性曲线可以看出,在以最大层间位移角为损伤参数时,有无开洞纵墙对结构地震易损性曲线影响不大,并没有充分体现纵墙的抗震作用;在以能量指数为损伤参数时,能够体现开洞纵墙的作用和影响.因此,在建立砌体结构模型时不宜忽视开洞纵墙的作用,应根据具体需求建立适宜精度的有限元模型.
| [1] |
郑山锁, 程明超, 马德龙, 等. 酸雨环境下砌体结构地震易损性研究[J]. 地震工程学报, 2016, 38(1): 79. ZHENG Shansuo, CHENG Mingchao, MA Delong, et al. Seismic fragility of masonry structures under acid rain[J]. Journal of Seismic Engineering, 2016, 38(1): 79. DOI:10.3969/j.issn.1000-0844.2016.1.0079 |
| [2] |
郑淏, 郑山锁, 牛丽华. 基于等效框架模型的砌体结构抗震模拟及验证[J]. 世界地震工程, 2019, 35(1): 138. ZHENG Hao, ZHENG Shansuo, NIU Lihua. Seismic simulation and verification of masonry structure based on equivalent frame model[J]. World Seismic Engineering, 2019, 35(1): 138. |
| [3] |
POLYAKOV S V. An investigation into the strength and stiffness of masonry infilling[M]. Moscow: Masonry in Framed Buildings, 1957.
|
| [4] |
EL-DAKHAKHNI W W, ELGAALY M, HAMID A A. Three-strut model for concrete masonry-infilled steel frames[J]. Journal of Structural Engineering, 2003, 129(2): 179. DOI:10.1061/(ASCE)0733-9445(2003)129:2(177) |
| [5] |
SMITH B S. Model test results of vertical and horizontal loading of infilled frames[J]. ACI Journal Proceedings, 1968, 65(8): 618. |
| [6] |
FLANAGAN R D, BENNETT R M. In-plane behavior of structural clay tile infilled frames[J]. Journal of Structural Engineering, 1999, 125(6): 590. DOI:10.1061/(ASCE)0733-9445(1999)125:6(590) |
| [7] |
KLINGNER R E, BERTERO V V. Earthquake resistance of infilled frames[J]. Journal of the Structural Division, 1976, 104(6): 973. |
| [8] |
郑文豪.钢框架结构地震易损性分析[D].北京: 北京工业大学, 2017 ZHENG Wenhao. Seismic fragility analysis of steel frame structures[D]. Beijing: Beijing University of Technology, 2017 |
| [9] |
HOLMES M. Steel frames with brickwork and concrete infilling[J]. ICE Proceedings, 1961, 19(4): 473. DOI:10.1680/iicep.196-1.11305 |
| [10] |
SANEINEJAD A, HOBBS B. Inelastic design of infilled frames[J]. Journal of Structural Engineering, 1995, 121(4): 634. DOI:10.1061/(ASCE)0733-9445(1995)121:4(634) |
| [11] |
施楚贤. 砌体结构理论与设计[M]. 北京: 中国建筑工业出版社, 2003. SHI Chuxian. Masonry structure theory and design[M]. Beijing: China Construction Industry Publishing House, 2003. |
| [12] |
砌体结构设计规范: GB 50003—2011[S].北京: 中国建筑工业出版社, 2011 Code for design of masonry structures: GB 50003—2011[S]. Beijing: China Construction Industry Publishing House, 2011 |
| [13] |
唐斌.开洞填充墙对混凝土框架结构抗震性能影响分析[D].南昌: 南昌航空大学, 2018 TANG Bin. Analysis of the influence of filling wall with openings on seismic performance of concrete frame structures[D]. Nanchang: Nanchang Hangkong University, 2018 |
| [14] |
MOHAMMADI M, NIKFAR F. Strength and stiffness of masonry infilled frames with central openings based on experimental results[J]. Journal of Structural Engineering, 2013, 139(6): 974. DOI:10.1061/(ASCE)ST.1943-541X.0000717 |
| [15] |
李常青.填充墙框架结构动力模型修正研究[D].长沙: 湖南大学, 2004 LI Changqing. Study on modification of dynamic model of filled wall frame structures[D]. Changsha: Hunan University, 2004.DOI: 10.7666/d.y667623 |
| [16] |
张宏.带洞口约束梁柱粉煤灰蒸压砖承重墙、粉煤灰砌块自承重墙抗震性能的试验研究[D].扬州: 扬州大学, 2007 ZHANG Hong. Experimental study on seismic behavior of fly ash autoclaved brick bearing wall and fly ash block bearing wall with hole restraint[D]. Yangzhou: Yangzhou University, 2007.DOI: 10.7666/d.y1102788 |
| [17] |
彭少民, 张祥顺, 管克俭, 等. 碳纤维布加固带窗洞砌体结构试验研究[J]. 河南科学, 2002(6): 693. PENG Shaomin, ZHANG Xiangshun, GUAN Kejian, et al. The experimental study of the brick wall with a window strengthened by carbon fiber sheet[J]. Henan Science, 2002(6): 693. DOI:10.3969/j.issn.1004-3918.2002.06.021 |
| [18] |
邓军, 唐家祥. 时程分析法输入地震记录的选择与实例[J]. 工业建筑, 2000(8): 9. DENG Jun, TANG Jiaxiang. Selection and example of input seismic records by time history analysis[J]. Industrial Architecture, 2000(8): 9. DOI:10.3321/j.issn:1000-8993.2000.08.003 |
| [19] |
Quantification of building seismic performance factors: ATC-63[S]. America: FEMA, 2008
|
| [20] |
建筑抗震设计规范: GB 50011—2010(2016年版)[S].北京: 中国建筑工业出版社, 2016 Code for seismic design of buildings: GB 50011—2010 (2016 Edition)[S]. Beijing: China Construction Industry Publishing House, 2016 |
| [21] |
LUCO N, CORNELL C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions[J]. Earthquake Spectra, 2007, 23(2): 357. DOI:10.1193/1.2723158 |
| [22] |
赵杰超.考虑墙体开洞影响的砌体结构房屋地震易损性研究[D].长沙: 湖南大学, 2013 ZHAO Jiechao. Research on seismic vulnerability of masonry structures considering the effect of wall opening[D]. Changsha: Hunan University, 2013.DOI: 10.7666/d.Y2356330 |
| [23] |
SCHNEIDER P J, SCHAUER B A. HAZUS—its development and its future[J]. Natural Hazards Review, 2006, 7(2): 43. |
| [24] |
何浩祥, 陈奎, 范少勇. 基于弹塑性耗能差率的地震损伤评估模型及分析方法[J]. 振动工程学报, 2018, 31(3): 385. HE Haoxiang, CHEN Kui, FAN Shaoyong. Seismic damage assessment model and analysis method based on elastic-plastic energy dissipation difference rate[J]. Journal of Vibration Engineering, 2018, 31(3): 385. DOI:10.16385/j.cnki.issn.1004-4523.2018.03.003 |
| [25] |
RIAHI Z. Backbone model for confined masonry walls for performance-based seismic design[J]. Journal of Structural Engineering, 2009, 135(6): 649. |
 2020, Vol. 52
2020, Vol. 52


