2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
当前,中国以50 a超越概率10%的地震危险性水平进行抗震设防,是一种基于“一致危险(uniform hazard)”的抗震设防思想.由于地震危险性存在地区差异,工程结构抗地震倒塌能力也存在不确定性,因此按一致危险性设防的地震动参数不一定能够保证抗震设防水平具有一致的倒塌概率(即倒塌风险),从而导致各地的地震风险水平差异较大.因此,抗震设防水准的决策应该从只考虑地震危险性的“一致危险”原则向同时考虑地震危险性区域差异和工程结构抗倒塌能力不确定性的“一致风险(uniform risk)”原则转变[1-2].
2007年,Luco等[3]提出了“风险导向地震动(risk-targeted ground motion, RTGM)”.2009年,FEMA P750[4]引入了风险导向地震动的定义,并编制了相应的区划图,规定以50 a倒塌概率1%进行抗震设防,从而完成了抗震设防从“一致危险”向“一致风险”的转换.2010年,ASCE/SEI 7-10[5]进行修订时也采用了风险导向地震动,并将地震易损性的对数标准差从0.8降为了0.6.2015年,FEMA P1050[6]对风险导向最大考虑地震区划图进行了进一步的修订.印度尼西亚于2010年完成了风险导向地震动参数区划图的编制,并于2012年基于一致风险设计思想对抗震设计规范进行了修订[7-8].此外,法国[9-10]、加拿大[11]、意大利[12]、罗马尼亚[13]、沙特阿拉伯[14]等国家的学者也对风险导向地震动进行了大量研究.
中国在风险导向地震动方面的研究相对比较薄弱.张晓梅[15]对基于抗倒塌设防目标的设计地震动区划进行了研究,认为以防倒塌为设防目标的地震动参数是更为合理的用于抗震设计的地震动参数.陈鲲等[16-17]基于GB 18306—2001《中国地震动参数区划图》以及ATC-63对一般工程结构抗倒塌能力不确定性的研究成果,初步获得了中国具有一致倒塌风险的峰值地面加速度图.
中国GB 50011—2010《建筑抗震设计规范》[18]仅对少数重要的建筑结构进行抗倒塌计算,GB 18306—2015《中国地震动参数区划图》[19]部分实现了抗倒塌的设防目标,但是还未能提供设计用的风险导向地震动参数.
本文作者在文献[1]中提出了风险导向地震设防水平决策的解析方法,并计算了中国巨震、大震、中震、小震的风险导向地震动参数PGA值.但是,通过解析方法得到的风险导向地震动参数是全国范围的,并不适用于具体场地的地震动设防水平决策.本文基于场地相关的概率地震危险性分析,采用风险积分方法对风险导向地震设防水平进行决策分析,以期为具体场地提供抗震设计用风险导向地震动参数.为此,本文以西安地区为例,将地震危险性函数与结构易损性函数进行耦合,采用风险积分方法得到西安地区6个计算控制点的风险导向地震动参数、风险系数以及风险导向的巨震和大震与中震地震动参数的比值,并研究结构易损性对数标准差对计算结果的影响.
1 基于场地相关概率地震危险性分析的风险导向地震动参数确定方法根据结构可靠度理论的概率干涉法[20],风险积分有两种表达形式.第一种表达式为
| $ {v_0} = \int_0^\infty {{F_{\rm{R}}}} (x)|{\rm{d}}{H_{\rm{A}}}(x)|, $ | (1) |
式中:v0为年目标倒塌风险;HA(x)为地震危险性函数,通过概率地震危险性分析得到;x为地震动强度;FR(x)为结构的地震易损性函数,通常假设结构的地震易损性服从对数正态分布:
| $ {F_{\rm{R}}}(x) = \Phi \left[ {\frac{{{\rm{ln}}(x/{m_{\rm{R}}})}}{{{\beta _{\rm{R}}}}}} \right], $ | (2) |
式中:mR为地震易损性的中位值;βR为地震易损性的对数标准差,综合反映地震动记录之间的差异以及建造质量、材料特性、非结构构件等差异造成的建筑结构抗倒塌能力的不确定性.
| $ {v_{{\rm{fT}}}} = 1 - {(1 - {v_0})^T}. $ | (3) |
对于没有场地相关概率地震危险性结果的一般场地,本文作者根据GB 50011—2010《建筑抗震设计规范》中提供的不同抗震设防烈度的地震动参数,在文献[1]中提出了基于式(1)~(3)确定风险导向地震动参数的决策方法.
对于有场地相关概率地震危险性分析结果的工程场地,本文采用风险积分的第二种表达式确定风险导向地震动参数:
| $ {v_0} = \int_0^\infty {{H_{\rm{A}}}} (x){\rm{d}}{F_{\rm{R}}}(x) = \int_0^\infty {{H_{\rm{A}}}} (x){f_{\rm{R}}}(x){\rm{d}}x, $ | (4) |
式中fR(x)为结构地震易损性的概率密度函数,对于对数正态分布,fR(x)为
| $ {f_{\rm{R}}}(x) = \frac{1}{{\sqrt {2\pi } {\beta _{\rm{R}}}x}}{\rm{exp}}\left\{ { - \frac{1}{2}{{\left[ {\frac{{{\rm{ln}}x - {\rm{ln}}{m_{\rm{R}}}}}{{{\beta _{\rm{R}}}}}} \right]}^2}} \right\}, $ | (5) |
若已知HA(x),在给定vfT和βR的情况下,根据式(3)~(5),求解式(4)所示的积分方程,即可得到mR.
得到mR之后,若分别给定巨震(very rare earthquake, VRE)、大震(maximum considered earthquake, MCE)和中震(design basis earthquake, DBE)的目标条件倒塌概率pdV、pdM和pdD,则根据式(2),即可得到各级设防水平的风险导向地震动参数:
| $ {\rm{PG}}{{\rm{A}}_{{\rm{RV}}}} = {m_{\rm{R}}}{\rm{exp}}[{\beta _{\rm{R}}}{\Phi ^{ - 1}}({p_{{\rm{dV}}}})], $ | (6) |
| $ {{\rm{PG}}{{\rm{A}}_{{\rm{RM}}}} = {m_{\rm{R}}}{\rm{exp}}[{\beta _{\rm{R}}}{\Phi ^{ - 1}}({p_{{\rm{dM}}}})],} $ | (7) |
| $ {{\rm{PG}}{{\rm{A}}_{{\rm{RD}}}} = {m_{\rm{R}}}{\rm{exp}}[{\beta _{\rm{R}}}{\Phi ^{ - 1}}({p_{{\rm{dD}}}})].} $ | (8) |
式中PGARV、PGARM、PGARD分别为巨震、大震、中震的风险导向地震动参数.
若根据本文作者在文献[1]的建议,取pdV=50%,则根据式(6)可知PGARV=mR.
对于给定的HA(x),式(4)很难直接进行求解,本文采用数值积分方法予以求解
| $ {v_0} = \sum\limits_{{x_i} = 0}^\infty H ({x_i})f({x_i})\Delta {x_i}. $ | (9) |
风险积分的数值积分求解过程示意见图 1.
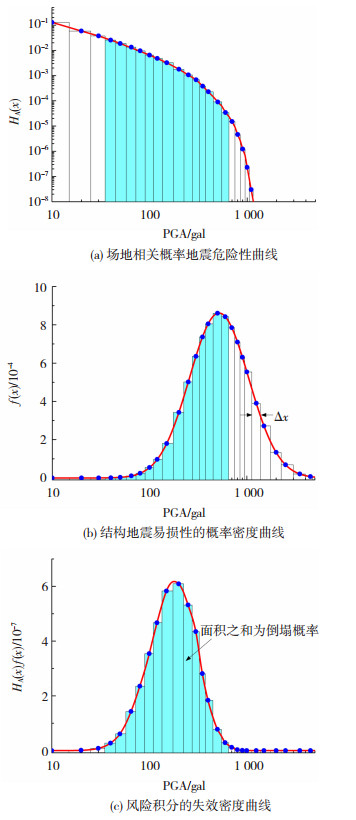
|
图 1 风险积分的数值积分分解过程示意 Fig. 1 Numerical integration deaggregation process of risk integral |
由图 1可知,风险积分同时考虑了地震危险性以及结构易损性,最终通过求和(或积分)得到倒塌概率.确定风险导向地震动参数的流程图见图 2.
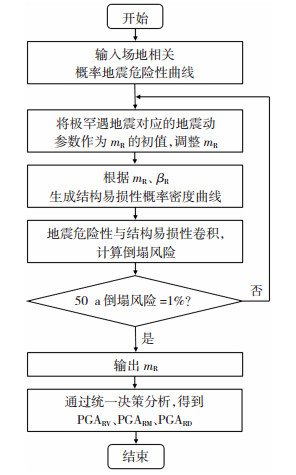
|
图 2 确定风险导向地震动参数的流程图 Fig. 2 Flowchart for determination of risk-targeted ground motion parameters |
参照ASCE/SEI 7-10,本文将PGARM与相应的非风险导向大震地震动参数PGAM之比定义为风险系数Rc:
| $ {R_{\rm{c}}} = {\rm{PG}}{{\rm{A}}_{{\rm{RM}}}}/{\rm{PG}}{{\rm{A}}_{\rm{M}}}. $ | (10) |
参照GB 18306—2015《中国地震动参数区划图》,本文将PGARV和PGARM分别与PGARD的比值定义为比例关系K1和K2:
| $ {{K_1} = {\rm{PG}}{{\rm{A}}_{{\rm{RV}}}}/{\rm{PG}}{{\rm{A}}_{{\rm{RD}}}},} $ | (11) |
| $ {{K_2} = {\rm{PG}}{{\rm{A}}_{{\rm{RM}}}}/{\rm{PG}}{{\rm{A}}_{{\rm{RD}}}}.} $ | (12) |
概率地震危险性分析是确定风险导向地震动参数的过程中至关重要的一步,在本课题组庞健[21]、吕大刚等[22]对西安地区的概率地震危险性分析研究的基础上,基于庞健开发的ArcGIS Engine概率地震危险性分析平台,采用离散算法对场点的概率地震危险性进行分析.
《西安市地震小区划项目技术报告》[23](以下简称“西安报告”)提供的各地震带的4级以上地震年平均发生率λ0、震级-频度关系中的b值以及震级上限muz见表 1.
| 表 1 地震带年平均发生率、b值和震级上限[23] Tab. 1 Annual mean occurrence rate, b value, and upper magnitude limit for each seismic belt[23] |
将地震统计区的震级域离散为多个震级档,各地震统计区的震级分布P(mj)为
| $ \begin{array}{*{20}{l}} {P({m_j}) = }\\ {\frac{{2{\rm{exp}}[ - b{\rm{ln}}10({m_j} - {m_0})]}}{{1 - {\rm{exp}}[ - b{\rm{ln}}10({m_{{\rm{uz}}}} - {m_0})]}}{\rm{sinh}}\left( {\frac{{b{\rm{ln}}10}}{2}\Delta m} \right),} \end{array} $ | (13) |
式中:mj为各震级档的中心值;m0为起算震级,取4级;Δm为各震级档的震级间隔;sinh为双曲正弦函数.
各震级档的地震年平均发生率λmj为
| $ {\lambda _{{m_j}}} = P({m_j}){\lambda _0}, $ | (14) |
λmj的计算结果见表 2.
| 表 2 各震级档地震年平均发生率 Tab. 2 Annual mean occurrence rate for each magnitude interval |
西安市地震局提供的各潜在震源区的地震活动性参数见表 3.
| 表 3 主要潜在震源区的地震活动性参数[23] Tab. 3 Seismic activity parameters for major potential seismic source zones[23] |
考虑到地震动加速度的震级饱和与距离饱和,地震动参数X采用以下衰减关系模型:
| $ {\rm{lg}}(X) = {c_1} + {c_2}M + {c_3}{M^2} + {c_4}{\rm{lg}}(R + {c_5}{\rm{exp}}({c_6}M)) + \varepsilon , $ | (15) |
式中:M为面波震级;R为震中距;c1、c2、c3、c4、c5、c6为回归系数,具体取值见表 4;ε表征回归分析中的不确定性,一般假设服从对数正态分布,均值为0,标准差为σ.
| 表 4 西安地区地震动衰减关系系数[23] Tab. 4 Coefficients of ground motion attenuation relations in Xi'an region[23] |
假设地震的发生符合齐次泊松过程,根据全概率公式可得,工程场点处的X不小于给定值x的概率P(X≥x)为
| $ {H_{\rm{A}}}(x) = P(X \ge x) = 1 - {\rm{exp}}[ - \sum\limits_{k = 1}^{{N_{\rm{z}}}} {\sum\limits_{j = 1}^{{N_{\rm{m}}}} {\sum\limits_{i = 1}^{{N_{{\rm{ks}}}}} {\int {\int {\int P } } } } } (X \ge x|E({m_j},{r_{{{(y,z)}_{{k_i}}}}},\theta )){f_\theta }{\lambda _{k,{m_j}}}\frac{{{f_{{k_i},{m_i}}}}}{{{S_{{k_i}}}}}{\rm{d}}y{\rm{d}}z{\rm{d}}\theta ]. $ | (16) |
式中:Nz为地震统计区的个数;Nm为震级档的个数;Nks为第k个地震统计区内潜在震源区的个数;P(X≥x|E(mj, r(y, z)ki, θ))为第k个地震统计区内(y, z)位置处发生一次第mj档地震,工程场点处给定的x被超越的条件概率;fθ为方向性函数;λk, mj为第k个地震统计区内第mj档地震的年平均发生率;fki, mj为空间分布函数,表示第k个地震统计区内第i个潜在震源区第mj档地震发生的概率;Ski为第k个地震统计区内第i个潜在震源区的面积.
西安报告[23]考虑到地震环境对小区划场地的影响,选取了13个计算控制点,其分布见图 3.
选取计算控制点P1、P4、P9、P10、P12、P13进行概率地震危险性分析,其坐标见表 5.
本文采用离散算法对计算控制点进行概率地震危险性分析,将各潜在震源区离散成大小为2 km×2 km的栅格并当作点源处理,分别计算每个栅格对计算控制点的地震动参数超越概率.西安报告采用CPSHA90算法对各计算控制点进行地震危险性分析计算,得到各计算控制点50 a超越概率63%、10%和2%的基岩峰值加速度.以计算控制点P9、P12为例,离散算法计算结果与CPSHA90算法计算结果的对比见图 4.

|
图 4 基岩峰值加速度超越概率对比 Fig. 4 Comparison of exceeding probability for peak ground acceleration |
从图 4可以看出,基于离散算法得到的50 a不同超越概率水平的基岩峰值加速度与基于CPSHA90算法得到的结果相近,所以,可以基于离散算法得到的超越概率曲线通过风险积分确定风险导向地震动参数.
3 西安地区风险导向地震动参数的确定本文以丙类建筑中的钢筋混凝土框架结构为研究背景,基于西安地区不同计算控制点的地震危险性曲线,根据文献[1]的研究,βR取0.6,3个设防水准的目标条件倒塌概率分别取pdV=50%、pdM=10%、pdD=0.2%,计算得到了西安地区各计算控制点的PGARV、PGARM和PGARD,并在此基础上计算了Rc以及K1、K2.以计算控制点P12为例,风险导向地震动参数的计算过程见图 5.
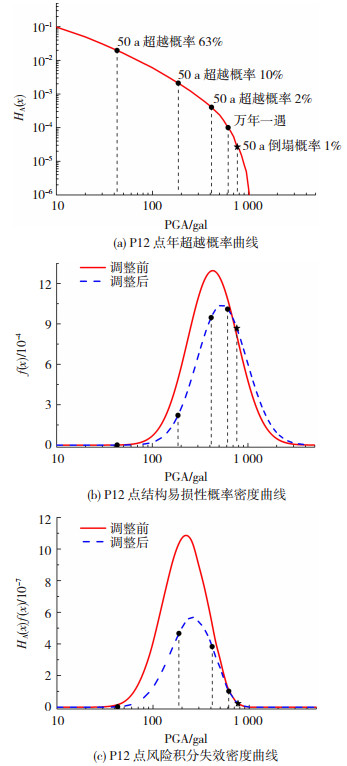
|
图 5 风险积分分解过程 Fig. 5 Risk integral deaggregation process |
图 5(c)中红色实线下面包围的面积是mR调整前对应的年倒塌概率,为3.42×10-4(相当于50 a倒塌概率1.70%),此时的倒塌概率高于目标倒塌风险,需要提高mR的值来调整风险积分失效密度曲线包围的面积,使其等于2.0×10-4(相当于50 a倒塌概率1%),从而确定风险导向地震动参数.图 5(b)和图 5(c)中蓝色虚线对应的mR=766.00 gal.将mR代入式(6)~(8)进行统一决策分析可得P12点的风险导向地震动参数分别为PGARV=766.00 gal、PGARM=355.05 gal、PGARD=136.22 gal,进一步可得Rc=0.86、K1=5.62、K2=2.61.
由图 5可知,50 a超越概率63%对应的地震动强度对倒塌概率的贡献很小;50 a超越概率10%和2%对应的地震动强度对倒塌概率的贡献较大;万年一遇对应的地震动强度对倒塌概率的贡献较小.
各计算控制点的风险导向地震动参数计算结果见表 6.
| 表 6 各计算控制点的计算结果 Tab. 6 Calculation results of each control point |
从表 6可看出,随着PGAM的增大,PGARM逐渐增大,相应的Rc有逐渐减小的趋势.由于PGARV、PGARM、PGARD是通过mR统一决策分析得到的,所以,对于不同的计算控制点,K1和K2是不变的.
本文对计算控制点P9、P12的风险导向地震动参数计算过程进行了对比分析, 见图 6.
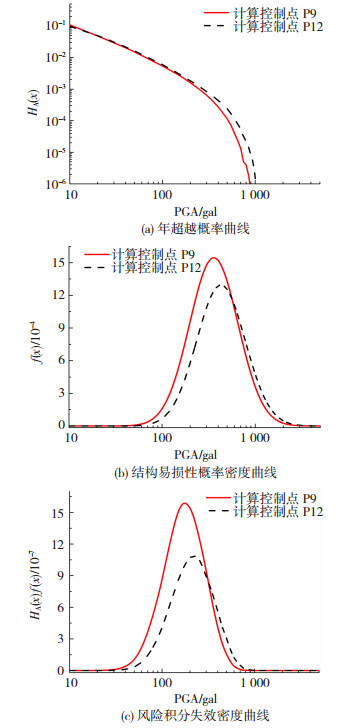
|
图 6 风险积分分解过程对比 Fig. 6 Comparison of risk integral deaggregation processes |
通过图 6对比可以发现,计算控制点P9的年超越概率曲线略低于计算控制点P12,但是经过风险积分计算得到的P9点的年倒塌概率(3.94×10-4)反而高于P12点的年倒塌概率(3.42×10-4).这是因为倒塌风险不仅与地震危险性有关,也与结构易损性有关.因此,位于地震危险性水平较低地区但是抗倒塌能力较弱的建筑结构,其在地震作用下的倒塌概率可能高于地震危险性水平较高地区抗倒塌能力较强的建筑结构.
本文对风险导向地震动参数的研究为探索性研究,要想更精细化地确定风险导向地震动参数,需要对建筑结构的倒塌易损性进行深入研究,以确定不同结构类型、不同建造质量的建筑结构的地震易损性参数.而且,结构易损性是区域性指标,地震危险性计算的则是计算控制点的概率,如何将危险性与易损性更好地结合也有待进一步研究.
4 西安地区风险导向地震动参数的影响分析上节是在假设vfT=1.0%、βR=0.6、pdV=50%、pdM=10%、pdD=0.2%的情况下得到的风险导向地震动参数计算结果.本节进一步研究这些决策参数对风险导向地震动参数的影响规律.
本文作者在文献[2]中对适用于中国的风险导向地震动决策参数vfT、βR、pdV、pdM、pdD进行了分析,得出的4种方案见表 7.本节基于表 7中的取值,对西安地区不同计算控制点的风险导向地震动参数进行了决策分析,计算结果见表 8.
| 表 7 风险导向地震动决策参数反推结果[2] Tab. 7 Inversion results of risk-targeted decision parameters of seismic ground motions[2] |
| 表 8 不同方案各计算控制点的计算结果 Tab. 8 Calculation results of each control point in different cases |
GB 50011—2010《建筑抗震设计规范》[18]中规定:西安(未央、莲湖、碑林、灞桥、雁塔)的抗震设防烈度为8度,设计基本地震加速度值为0.20 g;西安(长安)的抗震设防烈度为7度,设计基本地震加速度值为0.15 g.结合表 5中各计算控制点的所属区可知,计算控制点P1、P4、P9、P10、P12的设计基本地震加速度为0.20 g,计算控制点P13的设计基本地震加速度为0.15 g.GB 18306—2015《中国地震动参数区划图》[19](以下简称“区划图”)中给出的不同设防水平的地震动峰值加速度见表 9.
结合表 8、表 9可以看出,对于计算控制点P1、P4、P9、P10、P12,不同方案得到的各计算控制点的PGARV、PGARM、PGARD大都小于区划图给出的地震动峰值加速度;对于计算控制点P13,不同方案得到的各级设防水平的PGARV、PGARM、PGARD均大于区划图中的地震动强度.不同方案各计算控制点计算得到的Rc均小于1,这表明风险导向大震的地震动参数小于地震危险性曲线上50 a超越概率2%对应的地震动参数.以上分析说明依据区划图提供的地震动参数进行抗震设防对大多数场点来说是偏于保守的.区划图[19]中指出:罕遇地震的地震动强度宜按基本地震所对应地震动强度的1.6~2.3倍确定,极罕遇地震的地震动强度宜按基本地震所对应地震动强度的2.7~3.2倍确定.各方案计算得到的K1值分别为2.83、3.00、2.90、2.88,K2值分别为1.86、1.94、1.86、1.91,K1和K2的取值都在区划图建议的范围内.本文在计算过程中发现,mR调整前各方案对应的倒塌概率范围分别是0.76%~0.91%、0.95%~1.24%、1.58%~2.26%、1.58%~2.26%,所以本文认为方案4中vfT取0.4%偏低.对比不同方案的倒塌概率范围可知,方案1对应的倒塌概率偏低,所以本文认为方案1中βR取0.3偏低.经综合分析,本文认为对于中国规范和区划图,在西安地区,取vfT=1.0%、βR=0.4、pdV=50%、pdM=10%、pdD=0.2%或vfT=1.0%、βR=0.6、pdV=30%、pdM=10%、pdD=1.0%是合理的.
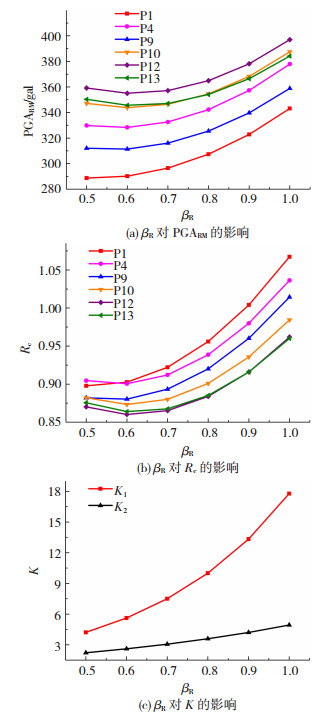
在上述研究基础上,分别取βR=0.5、0.6、0.7、0.8、0.9、1.0,vfT=1.0%、pdV=50%、pdM=10%、pdD=0.2%,通过参数影响分析研究了βR对PGARM、Rc以及K1和K2的影响程度,见图 7.
|
图 7 参数影响分析 Fig. 7 Parameter effect analysis |
由图 7可知,随着βR的增大,PGARM、Rc、K1和K2总体上都逐渐增大.其中,PGARM和Rc的相对增长率(同一曲线中相邻两点A、B纵坐标之差的绝对值与A点纵坐标的比值)逐渐增大,这说明结构倒塌能力的不确定性越大,对PGARM和Rc的影响越大;K1和K2的相对增长率均为常数,这说明βR逐渐增大时对K1和K2的影响是不变的.由于Rc为PGARM与PGAM的比值,而对于同一计算控制点,PGAM相同,所以,图 7(a)中PGARM-βR曲线与图 7(b)中Rc-βR曲线的相对增长率相同.图 7(c)中K1-βR曲线的相对增长率大于K2-βR曲线,两者都大于图 7(a)和图 7(b)中相应曲线的相对增长率.因此,βR对K1和K2的影响比对PGARM和Rc的影响大,βR对K1影响最大.
5 结论本文在对西安地区的计算控制点进行概率地震危险性分析的基础上,基于地震动决策参数已有的分析结果以及反推结果,采用风险积分的方法对西安地区的风险导向地震动参数进行了决策分析,得到了各计算控制点的PGARV、PGARM和PGARD,并计算了Rc、K1和K2;然后分别取βR=0.5、0.6、0.7、0.8、0.9、1.0,通过参数影响分析研究了βR对PGARM、Rc以及K1和K2的影响,得到以下结论:
1) 小震对应的地震动强度对倒塌概率的贡献很小,中震和大震对应的地震动强度对倒塌概率的贡献都较大,巨震对应的地震动强度对倒塌概率的贡献较小.
2) 风险积分同时考虑了场地的地震危险性和结构的地震易损性,对于同一地震动强度,地震危险性曲线中年超越概率高的计算控制点,其倒塌概率并不一定高;换言之,对于不同的计算控制点,倒塌概率并不会随着极罕遇地震所对应地震动强度的增加而增加.
3) 对于中国规范和区划图,在西安地区,取vfT=1.0%、βR=0.4、pdV=50%、pdM=10%、pdD=0.2%或vfT=1.0%、βR=0.6、pdV=30%、pdM=10%、pdD=1.0%是合理的.
4) PGARM、Rc、K1和K2总体上都随着βR的增大而增大;βR越大,对PGARM和Rc的影响越大;βR增大时对K1和K2的影响不变.K1和K2比PGARM和Rc对βR敏感,其中,K1对βR最敏感.
| [1] |
吕大刚, 周洲, 王丛, 等. 考虑巨震的四级地震设防水平一致风险导向定义与决策分析[J]. 土木工程学报, 2018, 51(11): 47. LÜ Dagang, ZHOU Zhou, WANG Cong, et al. Uniform risk-targeted definitions and decision-making of four seismic design levels considering very rare earthquake[J]. China Civil Engineering Journal, 2018, 51(11): 47. |
| [2] |
王丛, 吕大刚. 基于抗震规范和地震动区划图的风险导向地震动决策参数分析[J]. 建筑结构学报, 2020, 41(8): 26. WANG Cong, LÜ Dagang. Analysis of risk-targeted decision parameters of seismic ground motions based on seismic design code and ground motion zonation map of China[J]. Journal of Building Structures, 2020, 41(8): 26. DOI:10.14006/j.jzjgxb.2018.0703 |
| [3] |
LUCO N, ELLINGWOOD B R, HAMBURGER R O, et al. Risk-targeted versus current seismic design maps for the conterminous United States[C]// SEAOC 2007 Convention Proceedings. Sacramento, California: Structural Engineers Association of California, 2007: 6
|
| [4] |
Federal Emergency Management Agency (FEMA). NEHRP recommended provisions for seismic regulations for new buildings and other structures: FEMA P750[R]. Washington DC: FEMA, 2009
|
| [5] |
American Society of Civil Engineers (ASCE). Minimum design loads for buildings and other structures: ASCE/SEI 7—10[S]. New York: Structural Engineering Institute, ASCE, 2010
|
| [6] |
Federal Emergency Management Agency (FEMA). NEHRP recommended provisions for seismic regulations for new buildings and other structures: FEMA P1050[R]. Washington DC: FEMA, 2015
|
| [7] |
SENGARA I W, MASYHUR I, SIDI I D, et al. Development of earthquake risk-targeted ground motions for Indonesian earthquake resistance building code SNI 1726—2012[C]// Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12). Vancouver, Canada: University of British Columbia, 2015: 5
|
| [8] |
SENGARA I W, SIDI I D, MULIA A, et al. Development of risk coefficient for input to new Indonesian seismic building codes[J]. Journal of Engineering Technology, 2016, 48(1): 61. DOI:10.5614/j.eng.technol.sci.2016.48.1.5 |
| [9] |
DOUGLAS J, ULRICH T, NEGULESCU C. Risk-targeted seismic design maps for mainland France[J]. Natural Hazards, 2013(65): 2010. DOI:10.1007/s11069-012-0460-6 |
| [10] |
ULRICH T, DOUGLAS J, NEGULESCU C. Seismic risk maps for Eurocode—8 designed buildings[C]// Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology (2ECEES). Istanbul, Turkey: Turkish Earthquake Foundation Earthquake Engineering Committee and Prime Ministry, 2014: 2
|
| [11] |
ALLEN T I, ADAMS J, HALCHUK S. The seismic hazard model for Canada: past, present and future[C]// Proceedings of the 10th Pacific Conference on Earthquake Engineering, Building an Earthquake-Resilient Pacific. Sydney, Australia: Seismology Research Centre, 2015: 6
|
| [12] |
ZANINI M A, HOFER L, FALESCHINI F, et al. The seismic risk map of Italy[C]// Proceedings of the 6th International Workshop on Design in Civil and Environmental Engineering (DCEE). Cagliari, Italy: University of Cagliari, 2017: 5
|
| [13] |
VACAREANU R, PAVEL F, CRACIUN I, et al. Risk-targeted maps for Romania[J]. Journal of Seismology, 2018, 22(3): 412. DOI:10.1007/s10950-017-9713-x |
| [14] |
SOKOLOV V, ZAHRAN H M. Seismic hazard analysis for development of risk-targeted ground-motion maps in the western Saudi Arabia[C]// Proceedings of the 16th European Conference on Earthquake Engineering (ECEE). Thessaloniki, Greece: Aristotle University, 2018: 10
|
| [15] |
张晓梅.基于抗倒塌设防目标的设计地震动区划研究[D].北京: 中国地震局地球物理研究所, 2000: 28
|
| [16] |
陈鲲.针对大地震设防的地震动参数确定方法研究[D].北京: 中国地震局地球物理研究所, 2013: 94
|
| [17] |
陈鲲, 高孟潭. 中国大陆地区一般建设工程抗地震倒塌风险研究[J]. 建筑结构学报, 2015, 36(1): 27. CHEN Kun, GAO Mengtan. Controlling seismic collapse risk of general construction projects in China mainland[J]. Journal of Building Structures, 2015, 36(1): 27. DOI:10.14006/j.jzjgxb.2015.01.003 |
| [18] |
建筑抗震设计规范: GB 50011—2010[S].北京: 中国建筑工业出版社, 2010
|
| [19] |
中国地震动参数区划图: GB 18306—2015[S].北京: 中国标准出版社, 2015
|
| [20] |
MELCHERS R E, BECK A T. Structural reliability analysis and prediction[M]. Chichester: John Wiley and Sons, 2018: 14.
|
| [21] |
庞健.基于ArcGIS的西安地区地震危险性分析系统研究与开发[D].哈尔滨: 哈尔滨工业大学, 2015: 83
|
| [22] |
吕大刚, 刘亭亭, 李思雨, 等. 概率地震危险性分析、分解与设定地震及其在西安地区的应用[J]. 地震工程与工程振动, 2018, 38(5): 17. LÜ Dagang, LIU Tingting, LI Siyu, et al. Probabilistic seismic hazard analysis, deaggregation and scenario earthquakes with applications to Xi'an region[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(5): 17. |
| [23] |
西安大地地震工程勘察中心.西安市地震小区划项目技术报告[R].西安: 西安市地震局, 2011
|
| [24] |
贾晓琳.基于随机有限断层模型的西安地区概率地震危险性分析[D].哈尔滨: 哈尔滨工业大学, 2016: 59
|
 2020, Vol. 52
2020, Vol. 52



