高强钢板组合螺栓由开设丝孔的高强钢板和常规高强螺栓组成.钢板钻孔攻丝后替代螺母,中心丝孔与螺栓配合,四周孔设置构造螺栓,形成一种新的连接副.安装时先将钢板置于钢管柱内,高强螺栓穿钢管柱壁板并拧入钢板丝孔,完成连接.
目前研究多集中在自成型锚固单边螺栓,关于这种高强钢板组合螺栓研究较少.Wang等[1]方管柱单边螺栓连接试件进行拉伸试验,提出一种用于预测极限强度和屈服强度的分析模型.传统单边螺栓存在锚固不足的缺陷[2],为提高单边螺栓抗拔能力,Yao等[3]提出带扩大端单边螺栓,Pokharel等[4]提出双头锚定单边螺栓,抗拉试验表明混凝土强度对锚固效果影响显著[5-6].何明胜等[7]提出将钢板帖焊于钢管柱外侧,钻孔攻丝后再与高强螺栓连接,存在钢板变形和螺纹脱扣的问题,原因可能是钢板抗拉强度与螺栓不匹配.丁娟等[8]提出当加大钢板厚度并降低螺栓强度等级时,钢板螺纹脱扣现象消失并能达到刚接.吴琼尧等[9]建立了螺栓球节点有限元精细化模型,考虑了螺纹啮合传力,但未能模拟螺栓连接破坏现象.陈绍蕃[10]建议高强螺栓抗拉承载力为螺栓有效拉力的0.7倍,但需试验验证.刘秀丽等[11]通过数值模拟提出考虑撬力的高强螺栓抗拉承载力计算公式.田振山等[12]以最后一圈螺纹牙被剪断建立螺栓拉力极限承载力公式,但是以压力加载且假设两板之间受力连续,有待验证.
为深入研究这种螺栓的抗拉性能和螺栓连接的破坏机理,采用ABAQUS有限元软件对M16、M20、M24、M27、M30五种高强钢板组合螺栓进行抗拉数值模拟,探讨不同板厚和高强螺栓直径对连接副力学性能影响规律.通过极限承载力、变形能力、应力云图分析,获得高强钢板与螺栓的最优配合参数,并通过理论分析,推导抗拉承载力计算公式.
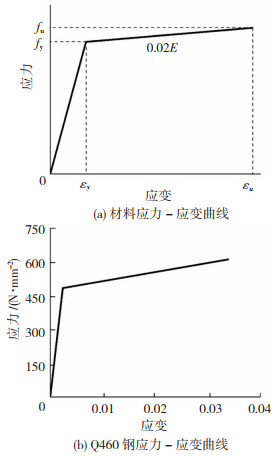
1 模拟方案设计64组高强钢板组合螺栓试件,选取Q345B、45号钢、Q460C和Q690D共4种钢材和10.9级M16、M20、M24、M27、M30共5种高强螺栓进行组合,钢板厚度按“略薄、标准、略厚”的原则选取[13],试件编号见表 1,其中45-M16-16表示钢材牌号为45号钢,螺栓为M16,钢板厚度为16 mm,以此类推.采用双折线本构模型,切线模量为0.02倍的初始弹性模量[9],材料参数见表 2,部分材料本构关系见图 1.
| 表 1 试件编号 Tab. 1 Specimens numbering |
| 表 2 材料参数 Tab. 2 Materials parameters |
|
图 1 材料本构关系 Fig. 1 Constitutive relations of materials |
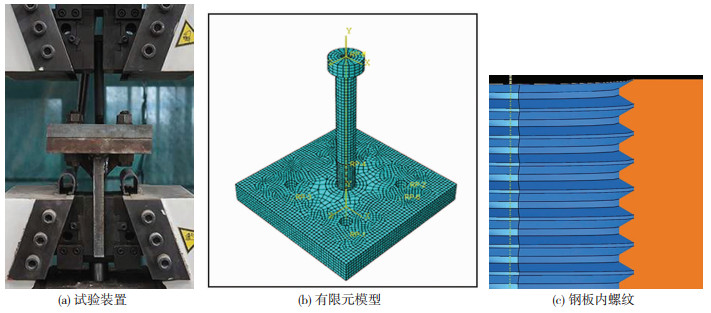
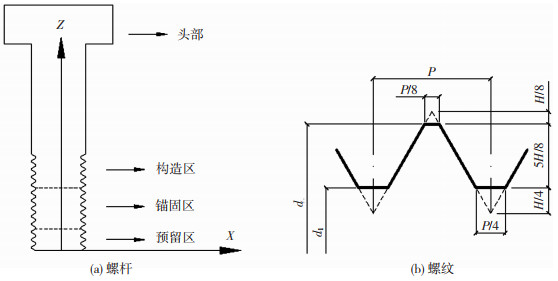
高强钢板组合螺栓试件及试验装置[14]见图 2(a),用构造螺栓将钢板固定于T型连接件,将10.9级高强螺栓旋入攻丝孔内并穿出钢板外露2~3个丝扣,螺杆和T型件分别在万能试验机的上下夹头处夹紧,完成安装.通过ABAQUS建模分析,试件精细化模型及网格划分见图 2(b),螺纹模型见图 2(c).螺栓螺纹尺寸[15]见图 3,细部几何尺寸见表 3.采用围绕中心轴旋转360°的平面齿形螺纹替代螺旋上升螺纹,二者最大计算误差仅1%,可以接受[16].
|
图 2 试验装置及有限元模型 Fig. 2 Experimental setup and finite element model |
|
图 3 螺栓示意 Fig. 3 Schematic diagram of bolts |
| 表 3 螺纹参数 Tab. 3 Threads parameters |
隐式方法ABAQUS/Standard分析程序中,材料的退化和失效常常导致严重的收敛困难,螺栓的受拉过程是材料失效的过程,材料刚度能够退化并且一直降低到零,在这段过程中单元从模型中被完全除掉.为真实模拟破坏过程,采用显式动力学进行求解.有限元建模装配时统一将螺栓穿出钢板外露2个丝扣,模型采用8节点缩减积分实体单元C3D8R.螺栓螺纹与钢板螺纹采用通用接触[17],切向采用罚摩擦公式,法向设置为硬接触.采用柔性损伤准则,断裂应变取材料本构模型的极限应变,见图 1(a).钢板构造螺栓几何中心处取耦合点完全固定,螺栓头部设置成刚体见图 3(a),采用位移控制加载,最大位移20 mm.
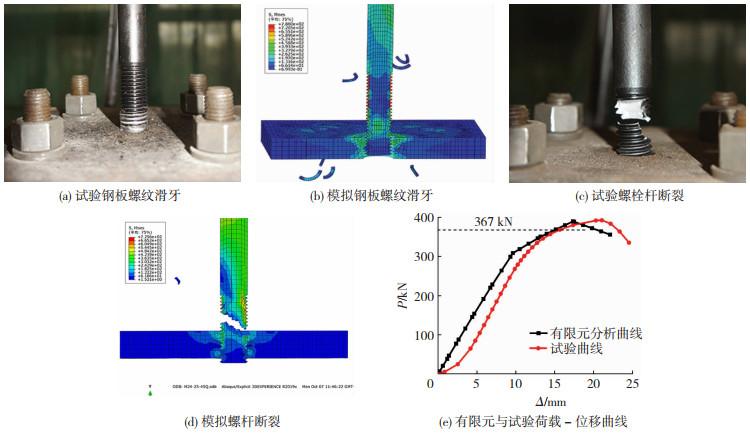
2.2 模型验证为验证有限元模型,选取45-M24-20和45-M24-25两组试件与本组试验结果对比,有限元试件极限承载力Pe和试验试件极限承载力Ps[14]的对比结果见表 4,最大误差为5.73%;有限元试件45-M24-20发生钢板滑牙破坏、45-M24-25发生螺杆拉断破坏,与试验结果吻合, 见图 4.选取45-M24-25试件的试验与有限元模拟值得到的荷载-位移曲线进行对比见图 4(e).加载初期试验值小于有限元分析值,后期两者数值基本吻合.原因是试验试件有偏心,加载初期板件和夹具之间有缝隙.以上证明有限元模型准确,可进行参数化分析.
| 表 4 有限元与试验极限承载力对比 Tab. 4 Comparison of finite element and experimental ultimate capacity |
|
图 4 试验结果与模拟结果对比 Fig. 4 Comparison of experimental and simulation results |
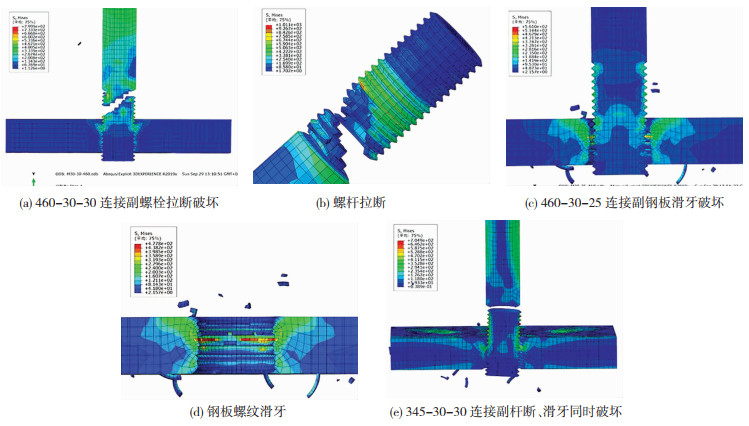
高强钢板组合螺栓连接副有3种破坏模式见图 4.第一种是钢板板厚足够厚时螺杆拉断破坏,一般为斜45°破坏面见图 5(a)、(b),螺栓拉断前存在明显变形,钢板螺纹完好,延性破坏.第二种是钢板板厚不足时钢板螺纹滑牙破坏见图 5(c)、(d),构件破坏为钢板出现面外凸起变形,螺杆未被拉断,螺栓螺纹完好,脆性破坏.第三种为螺杆拉断和钢板滑牙破坏同时发生,即钢板螺纹和螺栓螺纹均达到极限状态,是前两种破坏的临界状态,见图 5(e).
|
图 5 钢板组合螺栓抗拉模拟破坏现象 Fig. 5 Failure modes of steel plate composite bolts in tensile simulation |
各试件极限承载力分析见表 5.拾取钢板任意一个构造螺栓几何中心耦合点,取反作用力最大值的4倍为有限元极限承载力Pmax,Pn为螺栓最小拉力荷载Pn=As×σb min,As为螺纹的应力截面积,σb min为最小抗拉强度,本文所用10.9级高强螺栓σb min取1 040 N/mm2,Pb为螺栓极限荷载[18].钢板组合螺栓抗拉承载力Pb =Aeftb,其中Ae为螺栓有效面积,ftb为螺栓极限抗拉强度.S代表钢板螺纹滑牙破坏,F代表螺杆拉断破坏,SF代表两者同时发生.由表 5可知,Q345B、45号钢、Q460C、Q690D试件Pmax /Pb螺杆拉断最小值分别为88.12%、90.09%、90.92%、97.60%,均大于70%,可知当钢板厚度符合抗滑牙条件时,高强螺栓抗拉承载力设计值Ne可取螺栓有效拉力的0.7倍.螺纹承载力随着钢板抗拉强度的提高而提高.
| 表 5 有限元计算结果对比 Tab. 5 Comparison of finite element calculation results |
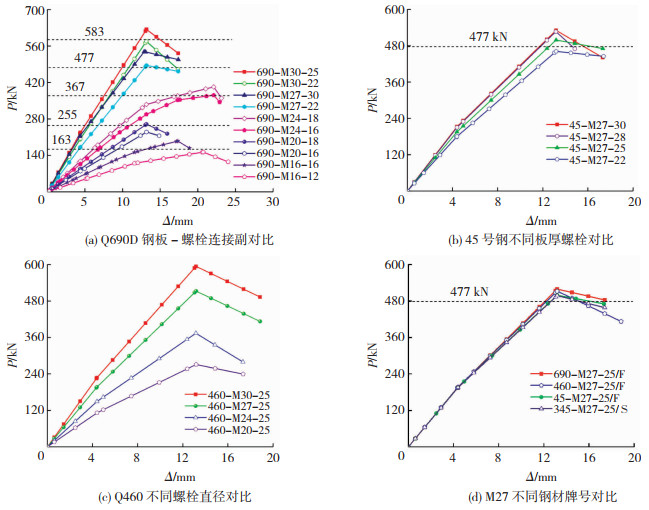
分析Q690D荷载-位移(P-Δ)曲线.由图 6(a)可知,试件发生螺杆拉断破坏时,连接副的抗拉极限承载力均大于Pn,表明连接副锚固可靠;试件发生钢板螺纹滑牙破坏时,部分构件的极限抗拉承载力小于Pn.由图 6(b)可知,随着板厚的增加,构件的极限抗拉承载力明显上升,构件由钢板滑牙的脆性破坏变成螺杆拉断的延性破坏,但当连接副为螺杆拉断破坏时,增加板厚并不能显著提升连接副极限承载力,原因是螺杆已达到受拉极限状态.由图 6(c)可知,随着螺栓直径的增加Pmax显著提升,原因是在发生螺杆拉断破坏时,材料相同的螺栓直径大的试件有着更大的拉伸区域.由图 6(d)可知,Q690D和Q460C的破坏模式与45号钢一致,发生螺杆拉断破坏,Pmax均大于45号钢,且前者较后者无明显提升,而Q345B则发生滑牙破坏,由表 5可知,若增大板厚,发生螺杆拉断破坏.图中水平线为不同螺栓的Pn值.
|
图 6 钢板组合螺栓P-Δ曲线 Fig. 6 P-Δ curves of steel plate composite bolts |
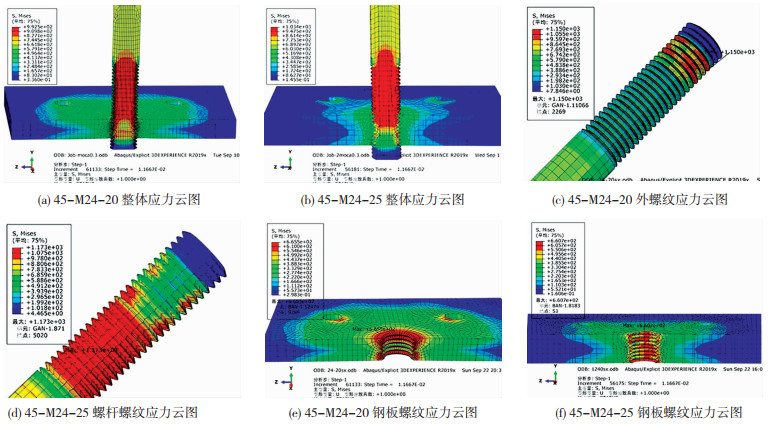
以45-M24-20钢板螺纹滑牙破坏和45-M24-25螺杆拉断破坏两种连接副为例,对比分析其应力云图.便于分析,将螺栓螺纹化分为3个区域:螺栓穿出钢板外露区域螺纹为预留区,钢板锚固区域螺纹为锚固区,其余区域螺纹为构造区(图 3(a)).45-M24-20和45-M24-25连接副破坏时的整体应力云图见图 7(a)、(b).由图 7(c)、(d)可知,试件45-M24-20锚固区域的应力值最大,为1 150 MPa;试件45-M24-25螺杆区域除钢板外露丝扣均进入极限状态,螺杆构造区大部分螺纹应力值已超过其材料的屈服强度1 040 MPa,最大值为1 173 MPa位于构造区,而锚固区应力值则相对较小.由图 7(e)、(f)可知,两试件最大应力值均位于第一扣处,分别为665.5、660.7 MPa,与文献[19-20]中螺纹荷载分布规律一致.
|
图 7 钢板组合螺栓模拟云图 Fig. 7 Simulation nephogram of steel plate composite bolts |
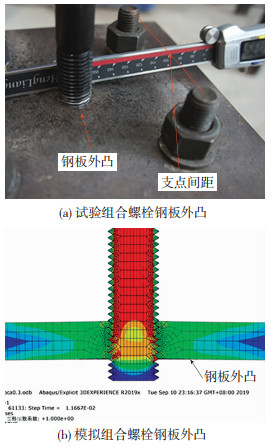
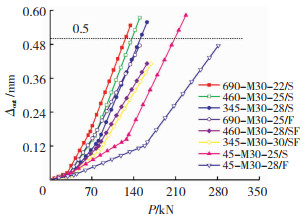
试验和有限元模拟中均发现,当试件发生滑牙破坏时,钢板有明显的面外凸起现象见图 8.以M30螺栓为例,外凸变形量Δout与荷载P的关系曲线见图 9.由图可知,当试件发生钢板螺纹滑牙破坏时,外凸变形较大,Δout均大于0.5 mm,取同侧构造螺栓间距为支点间距lb见图 8(a),最大凸起量Δout与支点间距lb的比值大于1/200;试件当发生另外两种破坏时,钢板凸起现象不明显,Δout/lb均小于1/200.
|
图 8 组合螺栓钢板外凸变形对比 Fig. 8 Comparison of out-of-plane deformation of steel plate composite bolts |
|
图 9 钢板组合螺栓P-Δout曲线 Fig. 9 P-Δout curves of steel plate composite bolts |
钢板厚度是影响破坏模式主要因素.当钢板较薄时,在拉力的作用下,钢板螺纹受剪外凸,最终在螺杆受拉屈服之前发生钢板螺纹受剪屈服破坏;钢板较厚时,发生螺杆受拉屈服破坏.两种破坏模式中螺杆和钢板的最大应力值及钢板最大应力值所作用位置无明显差异,钢板螺纹滑牙破坏时,钢板螺纹产生了大面积塑性变形,失去承载能力,螺杆被拔出;螺杆拉断破坏时,螺杆预留区螺纹出现大面积塑性变形,先于钢板螺纹屈服,螺杆被拉断.
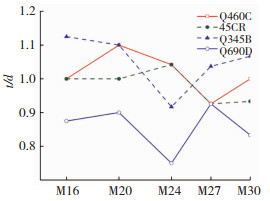
钢板组合螺栓承载力与钢板厚度的关系见图 10,图中采用钢板厚度t与螺栓直径d的比值,即厚径比t/d作为变量进行分析,厚度取保证不发生滑牙破坏所需要的最小板厚.由图可知,Q345B板厚不宜低于1.15 d,Q460C钢不宜低于1.10 d,Q690D钢不宜低于0.95 d;Q460C与螺母常用材质45号钢最为接近.
|
图 10 钢板组合螺栓承载力与钢板厚度关系曲线 Fig. 10 Fig.10 Relation between tensile capacity of steel plate composite bolts and steel plate thickness |
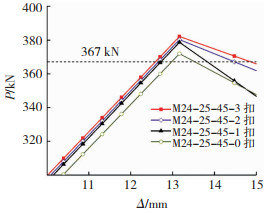
探究外露丝扣数量对承载力的影响,选取45-M24-25试件,使得螺杆依次拧出0扣到3扣共4组,分析对比各组试件Pmax值,见表 6和图 11,发现当螺杆拧出钢板2~3扣时其抗拉承载力较平齐时提升2%左右,对承载力影响很小.
| 表 6 拧出0~3扣螺纹抗拉承载力分析 Tab. 6 Analysis on tensile capacity of 0-3 threads |
|
图 11 钢板组合螺栓P-Δ曲线 Fig. 11 P-Δ curves of steel plate composite bolts |
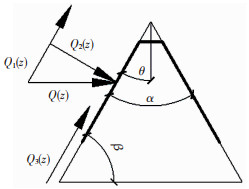
将螺纹牙简化成楔形体[21]进行受力分析,螺纹牙体受力见图 12.坐标轴见图 3(a),其中Q(z)为z截面螺杆拉力或者螺母压力,将Q(z)分解为平行于斜面的应力Q1(z)和垂直于斜面的应力Q2(z),以及由Q(z)引起的摩擦应力Q3(z).本文在计算螺纹牙表面应力分布时进行如下假设:螺纹牙的变形在弹性范围内且钢板螺纹与螺栓螺纹变形量相等,螺纹牙为三角形,螺纹牙牙面荷载不考虑应力集中.
|
图 12 螺纹牙体受力图 Fig. 12 Screw thread body force |
则:
| $ {Q_1}\left( z \right) = Q(z){\rm{sin}}\beta , $ |
| $ {Q_2}\left( z \right) = Q\left( z \right){\rm{cos}}\beta , $ |
| $ {Q_3}\left( z \right) = \mu Q\left( z \right){\rm{sin}}\beta . $ |
根据应力叠加和第三强度理论及文献[13]得:
| $ \begin{array}{l} {\sigma _1} - {\sigma _3} = \sqrt {{{({\sigma _x} - {\sigma _y})}^2} + 4\tau _x^2} = {\sqrt {{{({\sigma _{正r}} + {\sigma _{正\theta = 0}} + {\sigma _{切r}} + {\sigma _{切\theta = 0}} + {\sigma _{摩r}} + {\sigma _{摩\theta = 0}})}^2} + 4({\tau _{切\theta = 0}} + {\tau _{摩\theta = 0}})^2} },\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\sigma _1} - {\sigma _3} = Q\left( z \right)\omega \le \left[ \sigma \right],\\ \omega = \\ \sqrt {{{\left[ {{\rm{sin}}\beta \left( {\frac{{3{\rm{sin}}\beta }}{{4({\rm{sin}}\alpha - \alpha {\rm{cos}}\alpha )}} - 2} \right) + \frac{{\mu {\rm{sin}}\beta + {\rm{cos}}\beta }}{{{\rm{sin}}2\alpha }} - \frac{{({\rm{cos}}2\alpha - 1)({\rm{cos}}\beta + \mu {\rm{sin}}\beta )[({\rm{cos}}2\alpha - 1) + 2\alpha {\rm{sin}}2\alpha ]}}{{{\rm{sin}}2\alpha (1 - \alpha {\rm{sin}}2\alpha - {\rm{cos}}2\alpha )}}} \right]}^2} + 4{{[{\rm{cos}}\beta + 1]}^2}.} \end{array} $ |
式中:α为螺纹牙体的顶角,β为螺纹牙体的底角,μ为螺杆螺纹牙与螺帽螺纹牙之间的摩擦系数,r为螺纹牙顶和牙底圆弧半径,[σ]为螺纹牙的抗拉屈服强度.
根据螺栓变形协调条件,在轴力的作用下,螺杆和螺母的总变形量是相等的,用沿着螺纹长度上轴向力分布密度来表明各螺圈间荷载的分布[22]:
| $ Q\left( z \right) = \frac{{{\rm{d}}Q\left( z \right)}}{{{\rm{d}}z}}. $ | (1) |
求其微分方程考虑其边界条件,式(1)的解有如下形式:
| $ q\left( z \right) = \frac{{Qm}}{{{\rm{sh}}\left( {mH} \right)}}{\rm{ch}}\left( {mz} \right). $ |
前三圈螺纹牙体被剪断时承载力:
| $ Q\left( z \right) = \frac{{2{\rm{sin}}\frac{\alpha }{2}\int_0^{3P} {q\left( z \right){\rm{d}}z} }}{{P{\rm{cos}}\frac{\alpha }{2}}}\xi , $ |
式中:P为螺距;钢板钻孔攻丝代替螺母时螺纹牙接触面的应力不均匀分布系数
前三圈螺纹共承受70%荷载[22].此类螺栓,一般α=β=60°,μ=0.5,则ω=3.521.当钢板为Q345B和Q690D时m取0.019 9,Q460C和45号钢时m取0.022,可得
| $ Q \le 0.172{\rm{ }}2\frac{{\left[ \sigma \right]P{{\rm{e}}^{m(t - 3P)}}}}{\xi }. $ | (2) |
螺栓连接副承载力对比分析见表 7,可知所提出的高强钢板组合螺栓抗拉承载力公式计算值与有限元结果吻合良好,可为钢板组合螺栓的设计提供参考.
| 表 7 螺栓抗拉承载力对比 Tab. 7 Comparison of tensile capacity of bolts |
1) 建立带有螺纹的高强钢板螺栓连接副精细化模型,与本组试验对比表明,模型能反映高强螺栓和高强钢板之间的啮合传力规律、受力性能和破坏模式.
2) 钢板较薄时,钢板螺纹受剪并向外凸起,凸起量大于支点间距的1/200,螺栓拔出,试件发生钢板螺纹滑牙破坏,螺杆最大应力值位于锚固区;钢板较厚时,发生螺杆拉断破坏,螺杆最大应力值位于构造区,两种破坏模式中钢板的最大应力及位置无明显差异,均位于钢板螺纹第一扣处.
3) 为保证钢板组合螺栓不发生钢板滑牙破坏,建议Q345B、Q460C、Q690D的钢板厚度不宜低于1.15 d、1.10 d、0.95 d,d为螺栓直径.这3种钢材均可作为45号钢的替代材料.
4) 高强钢板组合螺栓满足不发生滑牙的厚径比时,可按极限抗拉承载力的70%作为该连接副的拉力设计值.所提出的高强钢板组合螺栓抗拉承载力公式计算值与有限元结果吻合良好,可为钢板组合螺栓的设计提供参考.
| [1] |
WANG Zhiyu, WANG Qingyuan. Yield and ultimate strengths determination of a blind bolted endplate connection to square hollow section column[J]. Engineering Structures, 2016, 111: 345. DOI:10.1016/j.engstruct.2015.11.058 |
| [2] |
KOROL R M, GHOBARAH A, MOURAD S. Blind bolting W-shape beams to HSS columns[J]. Journal of Structural Engineering, 1993, 119(12): 3463. DOI:10.1061/(ASCE)0733-9445(1993)119:12(3463) |
| [3] |
YAO Huang, GOLDSWORTHY H, GAD E. Experimental and numerical investigation of the tensile behavior of blind-bolted T-stub connections to concrete-filled circular columns[J]. Journal of Structural Engineering, 2008, 134(2): 198. DOI:10.1061/(ASCE)0733-9445(2008)134:2(198) |
| [4] |
POKHAREL T, GOLDSWORTHY H M, GAD E F. Tensile behaviour of double headed anchored blind bolt in concrete filled square hollow section under cyclic loading[J]. Construction and Building Materials, 2019, 200: 146. DOI:10.1016/j.conbuildmat.2018.12.089 |
| [5] |
PITRAKKOS T, TIZANI W. Experimental behaviour of a novel anchored blind-bolt in tension[J]. Engineering Structures, 2013, 49(2): 905. DOI:10.1016/j.engstruct.2012.12.023 |
| [6] |
AGHESHLUI H, GOLDSWORTHY H, GAD E, et al. Tensile behavior of groups of anchored blind bolts within concrete-filled steel square hollow sections[J]. Journal of Structural Engineering, 2016, 142(2): 04015125. DOI:10.1061/(ASCE)ST.1943-541X.0001388 |
| [7] |
何明胜, 李志强, 贺泽峰. 新型单边螺栓承载力试验研究[J]. 兰州理工大学学报, 2016, 42(2): 118. HE Mingsheng, LI Zhiqiang, HE Zefeng. Experimental investigation of bearing capacity of new type unilateral bolts[J]. Journal of Lanzhou University of Technology, 2016, 42(2): 118. DOI:10.13295/j.cnki.jlut.2016.02.024 |
| [8] |
丁娟, 杨彬, 李瑞锋, 等. 采用钢板攻丝高强螺栓法兰连接的装配式钢框架柱受力性能研究[J]. 建筑结构学报, 2016, 37(8): 143. DING Juan, YANG Bin, LI Ruifeng, et al. Research on mechanical behavior of prefabricated steel frame columns using high-strength bolted flange connection with tapping steel plate[J]. Journal of Building Structures, 2016, 37(8): 143. DOI:10.14006/j.jzjgxb.2016.08.017 |
| [9] |
吴琼尧, 王化杰, 钱宏亮, 等. 拧入缺陷对螺栓球节点受力性能影响[J]. 哈尔滨工业大学学报, 2017, 49(12): 53. WU Qiongyao, WANG Huajie, QIAN Hongliang, et al. Study on influence caused by bolt connection defect on mechanical properties of bolt ball joint[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 53. DOI:10.11918/j.issn.0367-6234.201703115 |
| [10] |
陈绍蕃. 论高强度螺栓连接的分类和抗拉连接的计算[J]. 建筑钢结构进展, 2014, 16(3): 1. CHEN Shaofan. On the classification of high-strength bolt connections and the calculation of connection subject to tension[J]. Progress in Steel Building Structures, 2014, 16(3): 1. DOI:10.13969/j.cnki.cn31-1893.2014.03.002 |
| [11] |
刘秀丽, 王燕. 外伸端板高强度螺栓抗拉连接设计方法研究[J]. 建筑钢结构进展, 2013, 15(1): 29. LIU Xiuli, WANG Yan. Study on the design method of high strength bolts of extended end-plate tensile connections[J]. Progress in Steel Building Structures, 2013, 15(1): 29. |
| [12] |
田振山, 何明胜, 郭坤, 等. 新型螺栓受力特性理论分析[J]. 建筑钢结构进展, 2014, 16(1): 1. TIAN Zhenshan, HE Mingsheng, GUO Kun, et al. Theoretical analysis of mechanical characteristics for a new-type bolt[J]. Progress in Steel Building Structures, 2014, 16(1): 1. DOI:10.13969/j.cnki.cn31-1893.2014.01.001 |
| [13] |
钢结构用高强度大六角头螺母: GB/T 1229—2006[S].北京: 中国标准出版社, 2006 High strength large hexagon nuts for steel structures: GB/T 1229—2006[S]. Beijing: China Standards Press, 2006 |
| [14] |
段留省, 周天华, 苏明周. 高强钢板-螺栓连接副抗拉性能试验研究[J]. 西安建筑科技大学(自然科学版), 2019, 51(5): 704. DUAN Liusheng, ZHOU Tianhua, SU Mingzhou. Experimental study on tensile performance of the high strength steel plate-bolt assemblies[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2019, 51(5): 704. DOI:10.15986/j.1006-7930.2019.05.014 |
| [15] |
普通螺纹基本尺寸: GB/T 196—2003[S].北京: 中国建筑工业出版社, 2003 General purpose metric screw threads—basic dimensions: GB/T 196—2003[S]. Beijing: China Architecture & Building Press, 2003 |
| [16] |
刘丽君.螺栓球节点网架用高强螺栓的疲劳影响因素及缺口效应分析[D].太原: 太原理工大学, 2003 LIU Lijun. Analysis on fatigue influencing factors and notch effect of high strength bolt used in grid structure with bolt-sphere joints[D]. Taiyuan: Taiyuan University of Technology, 2003 http://cdmd.cnki.com.cn/Article/CDMD-10112-2003094217.htm |
| [17] |
WANG Zhiyu, TIZANI W, WANG Qingyuan. Strength and initial stiffness of a blind-bolt connection based on the T-stub model[J]. Engineering Structures, 2010, 32(9): 2505. DOI:10.1016/j.engstruct.2010.04.005 |
| [18] |
紧固件机械性能螺栓、螺钉和螺柱: GB/T 3098.1—2010[S].北京: 中国标准出版社, 2011 Mechanical properties of fasteners bolts, screws and studs: GB/T 3098.1—2010[S]. Beijing: China Standards Press, 2011 |
| [19] |
陈海平, 曾攀, 方刚, 等. 螺纹副承载的分布规律[J]. 机械工程学报, 2010, 46(9): 171. CHEN Haiping, ZENG Pan, FANG Gang, et al. Load distribution of bolted joint[J]. Journal of Mechanical Engineering, 2010, 46(9): 171. DOI:10.3901/JME.2010.09.171 |
| [20] |
ZHAO Hua. A numerical method for load distribution in threaded connections[J]. Journal of Mechanical Design, 1996, 118(2): 274. DOI:10.1115/1.2826880 |
| [21] |
王光钦. 弹性力学[M]. 北京: 中国铁道出版社, 2008: 89. WANG Guangqin. Elastic mechanics[M]. Beijing: China Railway Press, 2008: 89. |
| [22] |
(苏)比尔格尔, (苏)绍尔苏比, (苏)约西列维奇.机械零件强度计算手册[M].姚兆生, 译.北京: 机械工业出版社, 1987: 60 БИРГЕР ИA, ШОРРБФ, ИОССИЛЕВИЦГБ. Mechanical parts strength calculations manual[M]. YAO Zhaosheng, trans. Beijing: China Machine Press, 1987: 60 |
 2020, Vol. 52
2020, Vol. 52


