2. 通信网信息传输与分发技术重点实验室, 石家庄 050081;
3. 专用通信系统教育部工程研究中心, 哈尔滨 150001
2. Key Laboratory of Communication Network Information Transmission and Distribution Technology, Shijiazhuang 050081, China;
3. Dedicated Communication System Engineering Research Center of the Ministry of Education, Harbin 150001, China
基于4项加权分数傅里叶变换(4-Weighted Fractional Fourier Transform,4-WFRFT)的经典混合载波(Hybrid Carrier,HC)系统[1-2],因其可以融合传统单载波(Single Carrier,SC)系统和多载波(Multi-Carrier,MC)系统的优势,在对抗信道衰落[3]、窄带干扰抑制[4]、变换域均衡[5]、带外辐射抑制[6]、峰均比抑制[7]、对抗载波频率偏移[8]以及物理层安全[9]等方面受到广泛关注.经典HC系统之所以能够在双弥散信道下获得优于传统SC和MC系统的误码性能,是因为其信号能量在时频平面上的分布更加均匀[10].但由于受到4-WFRFT约束条件的限制,这种时频能量分布的均匀性与理想的完全均匀分布还存在一定的差距.针对这一问题,文献[11]通过对约束条件的放松,提出广义加权分数傅里叶变换(Generalized Weighted Fractional Fourier Transform, GWFRFT).与4-WFRFT相比,GWFRFT在信号设计方面具有更高的自由度,可以设计出一些传统HC框架下无法实现的信号形式.而文献[11]也正是利用这一点,设计出时频能量分布更为均匀的4分量等功率HC信号,进一步提升HC系统在双弥散信道下的误码性能.
受此启发,如果能利用GWFRFT在信号设计方面的灵活性,设计出在时域或频域中能量分布更加均匀的信号,将有可能进一步提高通信系统抗时间/频率选择性抗衰落的性能.正是基于这一思路,本文提出一种基于GWFRFT的两分量组合信号设计方案,在不改变载波体制的前提下,提升SC和MC系统的抗衰落性能.
1 4-WFRFT与GWFRFT基本理论经典HC系统的数学机理来自4-WFRFT.对于离散复信号x(n),其4-WFRFT定义为
| $ \begin{array}{*{20}{l}} {F_\omega ^\alpha [x(n)] = {\omega _0}(\alpha )x(n) + {\omega _1}(\alpha )X(n) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\omega _2}(\alpha )x( - n) + {\omega _3}(\alpha )X( - n).} \end{array} $ | (1) |
式中ωl(α)为加权系数,l=0, 1, 2, 3.4个加权系数的具体形式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _0}(\alpha ) = (1 + {{\rm{e}}^{{\rm{i}}\pi \alpha /2}} + {{\rm{e}}^{{\rm{i}}\pi \alpha }} + {{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4,}\\ {{\omega _1}(\alpha ) = (1 - {\rm{i}}{{\rm{e}}^{{\rm{i}}\pi \alpha /2}} - {{\rm{e}}^{{\rm{i}}\pi \alpha }} + {\rm{i}}{{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4,}\\ {{\omega _2}(\alpha ) = (1 - {{\rm{e}}^{{\rm{i}}\pi \alpha /2}} + {{\rm{e}}^{{\rm{i}}\pi \alpha }} - {{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4,}\\ {{\omega _3}(\alpha ) = (1 + {\rm{i}}{{\rm{e}}^{{\rm{i}}\pi \alpha /2}} - {{\rm{e}}^{{\rm{i}}\pi \alpha }} - {\rm{i}}{{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4.} \end{array}} \right. $ | (2) |
式中i、e分别为虚数单位和自然对数的底,π为圆周率.x(n)和x(-n)分别为时域分量和时域反转分量,X(n)和X(-n)分别为频域分量和频域反转分量,X(n)是x(n)经归一化离散傅里叶变换而得,其具体定义形式为
| $ X(k) = \frac{1}{{\sqrt N }}\sum\limits_{n = 0}^{N - 1} x (n){{\rm{e}}^{ - {\rm{i}}\frac{{2\pi }}{N}kn}}. $ | (3) |
由上述定义可知,4-WFRFT的加权系数完全由参数α决定,这种强约束关系制约了信号设计的灵活性.
为了提高HC信号设计的自由度,GWFRFT在保持原有加权形式不变化的情况下,重新定义加权系数,将参数由单一的参数α扩展为θ0、θ1、θ2和θ3 4个角度参数.基于4个角度参数的GWFRFT的正、逆变换的加权系数表达式分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _0^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {{\rm{e}}^{{\theta _1}{\rm{i}}}} + {{\rm{e}}^{{\theta _2}{\rm{i}}}} + {{\rm{e}}^{{\theta _3}{\rm{i}}}})/4,}\\ {\omega _1^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}} - {{\rm{e}}^{{\theta _2}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{{\theta _3}{\rm{i}}}})/4,}\\ {\omega _2^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {{\rm{e}}^{{\theta _1}{\rm{i}}}} + {{\rm{e}}^{{\theta _2}{\rm{i}}}} - {{\rm{e}}^{{\theta _3}{\rm{i}}}})/4,}\\ {\omega _3^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}} - {{\rm{e}}^{{\theta _2}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{{\theta _3}{\rm{i}}}})/4.} \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _0^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} + {{\rm{e}}^{ - {\theta _1}{\rm{i}}}} + {{\rm{e}}^{ - {\theta _2}{\rm{i}}}} + {{\rm{e}}^{ - {\theta _3}{\rm{i}}}})/4,}\\ {\omega _1^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{ - {\theta _1}{\rm{i}}}} - {{\rm{e}}^{ - {\theta _2}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{ - {\theta _3}{\rm{i}}}})/4,}\\ {\omega _2^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} - {{\rm{e}}^{ - {\theta _1}{\rm{i}}}} + {{\rm{e}}^{ - {\theta _2}{\rm{i}}}} - {{\rm{e}}^{ - {\theta _3}{\rm{i}}}})/4,}\\ {{\omega _3} = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{ - {\theta _1}{\rm{i}}}} - {{\rm{e}}^{ - {\theta _2}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{ - {\theta _3}{\rm{i}}}})/4.} \end{array}} \right. $ | (5) |
当参数θl=πlα/2, (l=0, 1, 2, 3)时,GWFRFT回退为4-WFRFT,而当θl取其他值时,基于GWFRFT的广义混合载波(Generalized Hybrid Carrier,GHC)系统可以获得经典HC系统无法实现的信号形式.
2 基于GWFRFT的两分量组合信号设计方案 2.1 两分量组合信号可行性分析及系统模型为了不改变载波体制,4个分量中应只保留两项时域分量或两项频域分量.在4-WFRFT框架下,对于只保留两个时域分量的情况,式(2)中两个频域分量的加权系数应为0,即:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _1}(\alpha ) = (1 - {\rm{i}}{{\rm{e}}^{{\rm{i}}\pi \alpha /2}} - {{\rm{e}}^{{\rm{i}}\pi \alpha }} + {\rm{i}}{{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4 = 0,}\\ {{\omega _3}(\alpha ) = (1 + {\rm{i}}{{\rm{e}}^{{\rm{i}}\pi \alpha /2}} - {{\rm{e}}^{{\rm{i}}\pi \alpha }} - {\rm{i}}{{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4 = 0.} \end{array}} \right. $ | (6) |
对方程组中两式相加可得eiπα=1.在变换阶数的主值区间α∈[0, 4)内,式(6)的解为α=0和α=2.
当α=0时,4-WFRFT中两个时域分量的加权系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _0}(0) = 1,}\\ {{\omega _2}(0) = 0.} \end{array}} \right. $ | (7) |
当α=2时,4-WFRFT中两个时域分量的加权系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _0}(2) = 0,}\\ {{\omega _2}(2) = 1.} \end{array}} \right. $ | (8) |
此时系统回退为只包含一个时域分量的SC体制.同理,对于只保留两个频域分量的情况,两个时域分量的加权系数为0,应满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _0}(\alpha ) = (1 + {{\rm{e}}^{{\rm{i}}\pi \alpha /2}} + {{\rm{e}}^{{\rm{i}}\pi \alpha }} + {{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4 = 0,}\\ {{\omega _2}(\alpha ) = (1 - {{\rm{e}}^{{\rm{i}}\pi \alpha /2}} + {{\rm{e}}^{{\rm{i}}\pi \alpha }} - {{\rm{e}}^{3{\rm{i}}\pi \alpha /2}})/4 = 0.} \end{array}} \right. $ | (9) |
式(9)的解依然为α=0和α=2.此时系统回退为只包含一个频域分量的传统MC体制.可见,经典HC系统无法实现两个分量组合的信号形式.
根据GWFRFT的定义,GHC信号包含4个分量,其中ω0+项和ω2+项等价于SC系统的时域信号,而ω1+项和ω3+项等价于MC系统的频域信号.要实现两时域分量信号的组合形式,需要令两频域分量的加权系数为0,即:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _1^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}} - {{\rm{e}}^{{\theta _2}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{{\theta _3}{\rm{i}}}})/4 = 0,}\\ {\omega _3^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}} - {{\rm{e}}^{{\theta _2}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{{\theta _3}{\rm{i}}}})/4 = 0.} \end{array}} \right. $ | (10) |
此时,角度参数的关系需满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\rm{e}}^{{\theta _0}{\rm{i}}}} = {{\rm{e}}^{{\theta _2}{\rm{i}}}},}\\ {{{\rm{e}}^{{\theta _1}{\rm{i}}}} = {{\rm{e}}^{{\theta _3}{\rm{i}}}}.} \end{array}} \right. $ | (11) |
由于角度参数θl以2π为周期,当θl∈[0, 2π)时,式(10)的解为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _0} = {\theta _2},}\\ {{\theta _1} = {\theta _3}.} \end{array}} \right. $ | (12) |
将式(12)代入式(4)和(5),则两项时域的正、逆变换的加权系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _0^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {{\rm{e}}^{{\theta _1}{\rm{i}}}})/2,\omega _2^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {{\rm{e}}^{{\theta _1}{\rm{i}}}})/2;}\\ {\omega _0^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} + {{\rm{e}}^{ - {\theta _1}{\rm{i}}}})/2,\omega _2^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} - {{\rm{e}}^{ - {\theta _1}{\rm{i}}}})/2.} \end{array}} \right. $ | (13) |
同理,对于只包含两项频域分量组合的情况,要使两项时域分量的加权系数ω0+和ω2+为0,满足:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _0^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {{\rm{e}}^{{\theta _1}{\rm{i}}}} + {{\rm{e}}^{{\theta _2}{\rm{i}}}} + {{\rm{e}}^{{\theta _3}{\rm{i}}}})/4 = 0,}\\ {\omega _2^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {{\rm{e}}^{{\theta _1}{\rm{i}}}} + {{\rm{e}}^{{\theta _2}{\rm{i}}}} - {{\rm{e}}^{{\theta _3}{\rm{i}}}})/4 = 0.} \end{array}} \right. $ | (14) |
此时,角度参数的关系需满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\rm{e}}^{{\theta _0}{\rm{i}}}} = - {{\rm{e}}^{{\theta _2}{\rm{i}}}},}\\ {{{\rm{e}}^{{\theta _1}{\rm{i}}}} = - {{\rm{e}}^{{\theta _3}{\rm{i}}}}.} \end{array}} \right. $ | (15) |
则式(14)的解为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _0} = {\theta _2} \pm \pi ,}\\ {{\theta _1} = {\theta _3} \pm \pi .} \end{array}} \right. $ | (16) |
对应的正、逆变换加权系数分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _1^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}})/2,\omega _3^ + = ({{\rm{e}}^{{\theta _0}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{{\theta _1}{\rm{i}}}})/2;}\\ {\omega _1^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} - {\rm{i}}{{\rm{e}}^{ - {\theta _1}{\rm{i}}}})/2,\omega _3^ - = ({{\rm{e}}^{ - {\theta _0}{\rm{i}}}} + {\rm{i}}{{\rm{e}}^{ - {\theta _1}{\rm{i}}}})/2.} \end{array}} \right. $ | (17) |
可见,GHC系统可以在不改变载波体制的情况下,实现两分量组合信号结构.
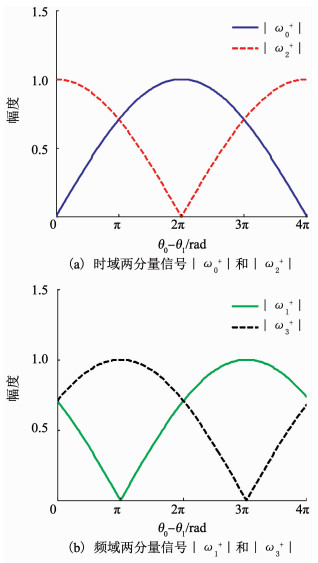
图 1分别给出时域两分量组合信号和频域两分量组合信号中两个分量信号所对应的加权系数模值随θ0-θ1的变化情况.
|
图 1 两分量组合信号加权系数模值随θ0-θ1的变化规律 Fig. 1 Variation of weighting coefficient module value with θ0-θ1 in double-component combined signal |
可见随着θ0-θ1的变化两个加权参数的模值在0~1之间连续变化,这说明GHC系统不仅可以实现两分量信号形式,还可以实现分量功率的任意比例能量分配.
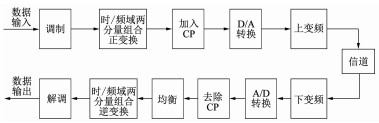
基于GWFRFT的两分量信号形式的通信系统结构如图 2所示.当选用时域两分量组合信号时,如果|ω0+|=1且|ω2+|=0,此系统将退化为传统SC系统;在其他情况下,该系统的信号由两项时域分量叠加而成,因而称其为时域广义混合载波(GHCT)系统,此系统仍然属于SC系统.而当选用频域两分量组合信号时,如果|ω1+|=0且|ω3+|=1,此系统等价于传统MC系统;而在其他情况下,该系统的信号由两项频域分量叠加而成,因而称其为频域广义混合载波(GHCF)系统,此系统仍然属于MC系统.由此可见,本方案所提出的信号形式可以与传统的SC体制和MC体制完全兼容.
|
图 2 两分量组合信号系统实现框图 Fig. 2 Implementation diagram of double-component combination signal system |
在经典HC系统中,时频能量的功率比例直接影响系统的误码性能[12].在两分量组合信号中,如何对两分量的功率进行分配同样是一个需要研究的问题.
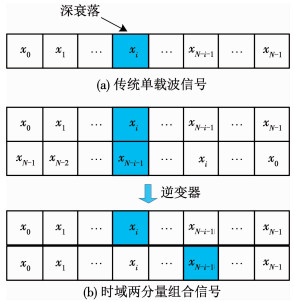
以时间选择性衰落信道为例,图 3给出时域深衰落对SC信号和时域两分量组合信号影响的示意图.
|
图 3 时域深衰落对SC和GHC时域两分量组合信号的影响 Fig. 3 Influence of time-domain deep fading on SC and GHC time-domain double-component combination signal |
假设传统SC信号的第i比特位置受深衰落影响,则该比特的信噪比显著降低,从而造成接收机错判.对信号进行基于GWFRFT的时域两分量设计后,原来第i比特的能量分散到第一个分量的第i比特和第二个分量的第N-i-1比特处;对于相同位置的深衰,接收端经广义加权逆变换后,未受深衰落的另一个分量会对深衰落比特进行能量补偿.如果这种补偿的能量足够多,使得该比特处的信噪比仍然保持在接收机灵敏度范围以上,则能被接收机正确解调.显然,这种补偿特性效果的好坏与两个分量的功率分配直接相关.若两个分量的功率分配明显不均,则大功率分量遭遇深衰落时,小功率分量的补偿效果有限;而当两分量等功率时,可得到最好的补偿效果.由于时域与频域之间具有对偶性质,在频率选择性衰落信道中,对于只包含频域分量与频域反转分量的频域两分量组合信号,也应当在两分量等功率分配时获得最优的误码性能.
除了从两分量相互补偿的角度理解之外,两分量组合信号抗衰落机理还可以从分集增益的角度进行解释.仍然以两时域组合信号为例,由于两时域分量组合信号的特殊形式,每一个符号的能量被分散到两个不同的时隙进行传输.而两个时隙同时出现深衰落的概率要比单一时隙出现深衰落的概率小得多,因而两时域分量组合信号中符号遭遇深衰落的概率也远远低于传统SC信号,从而可以获得一定的分集增益.而从图 3给出的结构可以看出,变换前后码块的长度也不发生改变.可见,本文所提的两分量组合信号只是以一定的复杂度为代价换取分集增益,而并没有占用额外的时间和频率资源.
2.3 半码块反转优化设计从补偿特性的角度和分集增益的角度均可以很好地解释两分量组合信号取得性能优势的机理.但无论从哪种角度理解,取得这种性能优势的大前提都是同一符号在两分量中经历的衰落具有独立性.从补偿特性角度上看,如果同一符号在两分量中经历的衰落完全相同,则逆变换后的符号能量与SC系统完全一致,并不会体现出补偿特性的优势.而从分集增益角度看,完全相同的衰落也并不会带来分集增益.因而,为了尽可能地挖掘两分量组合信号的性能优势,应当尽量增大两分量中相同符号衰落的独立性.
在时间选择性衰落信道中,同一符号在不同分量中所经历衰落的独立性由其在两分量中所处位置的时间间隔与信道相干时间之间的关系决定.当时间间隔大于相干时间时,二者衰落相互独立,反之则不独立.类似地,在频率选择性衰落信道中,同一符号在不同分量中所经历衰落的独立性由其在两分量中对应频点的频率差与信道相干带宽之间的关系决定.当频率差大于相干带宽时,二者衰落相互独立,反之则不独立.
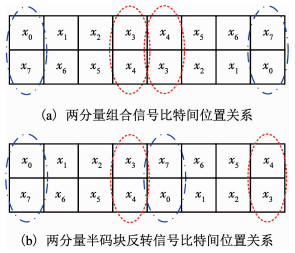
而根据两个分量组合信号的结构特点,处在码块不同位置的符号,在经过两分量组合变换后,其两部分对应的时间/频率间隔的大小存在很大的差异.以一个码块长度为8的时域两分量信号为例,其信号的比特位置关系如图 4(a)所示.对于位于码块两端的符号x0和x7而言,其在时域分量和时域反转分量中所在位置的时间间隔为7个时隙,而对于位于码块中间的符号x3和x4而言,其在时域分量和时域反转分量中所在位置的时间间隔仅仅为1个时隙.如果信道相干时间为4个符号周期,此时码块边缘的符号x0, x1, x6, x7由于在两个分量中经历的衰落相互独立,因而可以获得有效的分集增益,而位于码块中间4个符号,由于在两个分量中经历的衰落具有相关性,无法获得完全的分集增益效果.
|
图 4 时域两分量组合信号半码块反转前后的比特位置关系示意 Fig. 4 Bit position relationship of time-domain double-component combined signals without and with half-block inversion |
为了使得码块中间位置的符号也能获得完全的分集增益,可以对时域两分量信号的后一半码块进行反转,得到带有半码块反转过程的时域两分量组合信号,其信号比特间的位置关系如图 4(b)所示.仍然假设相邻的4个符号经历的衰落具有相关性,经过半码块反转的两分量组合信号中,每一个符号在时域分量和时域反转分量中的位置间隔均为半个码块的长度,大于相干时间.此时码块中的所有符号均可以获得分集增益.在实际系统中,只需设置适当的码块长度,使码块长度的一半大于相干时间,即可利用半码块反转方案进一步提升系统抗衰落性能.而在接收端只要对接收到的信号再进行一次半码块反转,然后进行广义加权傅里叶逆变换即可.
2.4 两分量组合信号及半码块反转优化方案的实现过程根据上文的分析,对于两分量组合信号而言,当两分量等功率分配时,系统可获得最优的误码性能.对于时域两分量组合信号,如果信号的总功率为1,则两个等功率分量的功率应均为0.5,此时相应的加权系数的模值应均为2/2,因而有:
| $ \left\{ {\begin{array}{*{20}{l}} {|\omega _0^ + | = \frac{1}{2}|{{\rm{e}}^{{\theta _0}{\rm{i}}}} + {{\rm{e}}^{{\theta _1}{\rm{i}}}}| = \frac{1}{2}|{{\rm{e}}^{{\theta _0}{\rm{i}}}}||1 + {{\rm{e}}^{({\theta _1} - {\theta _0}){\rm{i}}}}| = \frac{{\sqrt 2 }}{2},}\\ {|\omega _2^ + | = \frac{1}{2}|{{\rm{e}}^{{\theta _0}{\rm{i}}}} - {{\rm{e}}^{{\theta _1}{\rm{i}}}}| = \frac{1}{2}|{{\rm{e}}^{{\theta _0}{\rm{i}}}}||1 - {{\rm{e}}^{({\theta _1} - {\theta _0}){\rm{i}}}}| = \frac{{\sqrt 2 }}{2}.} \end{array}} \right. $ | (18) |
根据式(18),解得θ1-θ0=±π/2,对应的加权系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _0^ + = \frac{{1 \pm {\rm{i}}}}{2}{{\rm{e}}^{{\theta _0}{\rm{i}}}},}\\ {\omega _2^ + = \frac{{1 \mp {\rm{i}}}}{2}{{\rm{e}}^{{\theta _0}{\rm{i}}}}.} \end{array}} \right. $ | (19) |
与之相对应的两时域分量组合信号的数学表达式为
| $ F_T^ + [x(n)] = \omega _0^ + X(n) + \omega _2^ + X( - n). $ | (20) |
同理,对于频域两分量组合信号,中间参量应满足θ1-θ0=±π,此时的频域分量与频域反转分量的加权系数的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega _1^ + = \frac{{1 \pm {\rm{i}}}}{2}{{\rm{e}}^{{\theta _0}{\rm{i}}}},}\\ {\omega _3^ + = \frac{{1 \mp {\rm{i}}}}{2}{{\rm{e}}^{{\theta _0}{\rm{i}}}}.} \end{array}} \right. $ | (21) |
与之相对应的两频域分量组合信号的数学表达式为
| $ F_F^ + [x(n)] = \omega _1^ + X(n) + \omega _3^ + X( - n). $ | (22) |
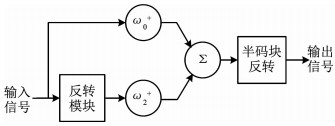
根据式(20)和(22),可知GHC系统可以实现两分量等功率分配.对于GHCT系统,在分量等功率分配的基础上,引入半码块反转优化,可得优化后的GHCT系统称为带有半码块反转的时域广义混合载波(ReGHCT)系统,ReGHCT信号生成过程如图 5所示.该生成结构较为简单:先将输入的原始信号分为两路,第一路作为时间分量直接与加权系数ω0+相乘;另一路先经过反转模块得到时间反转分量,再与加权系数ω1+相乘;两路分量经过加法器后得到两分量组合信号,再通过半码块反转模块得到输出信号.
|
图 5 ReGHCT信号生成框图 Fig. 5 Generation diagram of ReGHCT signal |
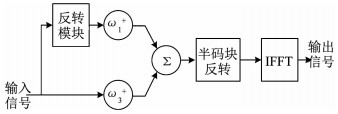
类似地,对于GHCF系统,半码块反转方案同样可以提高同一符号在不同频域分量内所经历衰落的独立性.从机理上讲,对于频域信号的半码块反转,应当是对映射到后一半子载波上的符号顺序进行反转.而对于GHCF信号,其IFFT变换之前的信号恰好对应映射到每个子载波上的符号,因而可以直接在子载波映射之前完成半码块反转操作.带有半码块反转优化的GHCF系统称为带有半码块反转的频域广义混合载波(ReGHCF)系统,ReGHCF信号生成过程如图 6所示.
|
图 6 反转频域两分量组合信号生成框图 Fig. 6 Generation diagram of ReGHCF signal |
由图 5、6给出的信号生成框图可以看出,ReGHCT信号和ReGHCF信号的实现过程主要是由反转模块、半码块反转模块、加法器、复数乘法器模块和快速傅里叶变换(Fast Fourier Transform, FFT)模块组成.因而,这两种信号实现的复杂度由各个模块的实现复杂度之和决定.
在实际系统中,通常采用复数乘法的次数来度量实现复杂度.对于反转模块和半码块反转模块而言,在硬件实现过程中只需要对寄存器倒序寻址或对后半码块倒序寻址,即可实现反转,并不需要复数乘法计算,因而该模块的复杂度可以忽略.而相对于乘法过程,加法器的复杂度也常被忽略.对于FFT模块,其实现的复杂度为O(NlogN).对于复数乘法器模块,显然每一次运算产生的复杂度为1.那么,反转两分量GHC信号实现的复杂度实际上是由FFT模块和复数乘法器模块的复杂度之和决定.
基于上述分析,ReGHCT信号和ReGHCF信号的实现复杂度,如表 1所示.可以看出,ReGHCT信号和ReGHCF信号的实现复杂度分别为O(2N)和O(NlogN+2N).也就是说,GHCT和GHCF与传统的SC系统和MC系统的复杂度相比均在同一数量级.
| 表 1 ReGHCT和ReGHCF信号实现复杂度 Tab. 1 Implementation complexity of ReGHCT and ReGHCF signal |
由于信号的频谱与信号的时域波形之间具有傅里叶变换关系,因而想要研究GHC信号频谱特性首先要对其时域波形进行研究.
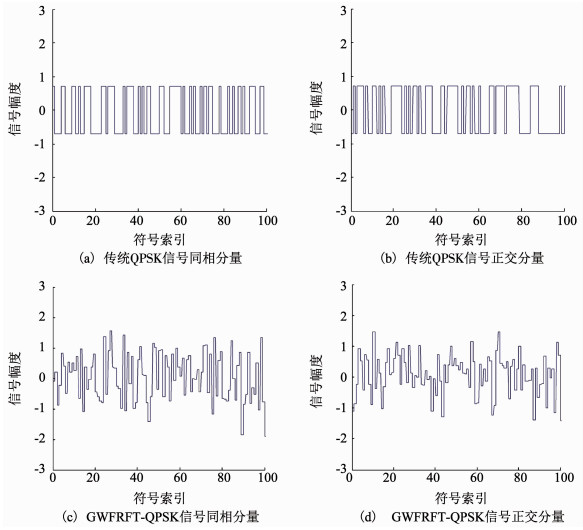
图 7给出传统QPSK信号和经过GWFRFT变换的QPSK信号(GWFRFT-QPSK)的同相分量及正交分量时域波形对比.其中GWFRFT-QPSK的4个角度参数为θ0=0.2π,θ1=0.35π,θ2=0.2π,θ3=0.35π.由图 7可见,无论是同相分量还是正交分量,两分量GWFRFT-QPSK信号与传统QPSK信号的码元宽度相同,唯一区别在于前者的信号幅度不再是两种正负电平的变化,而呈现为多电平变化的波形.
|
图 7 QPSK信号与GWFRFT-QPSK信号时域波形 Fig. 7 Time-domain waveforms of QPSK signal and GWFRFT-QPSK signal |
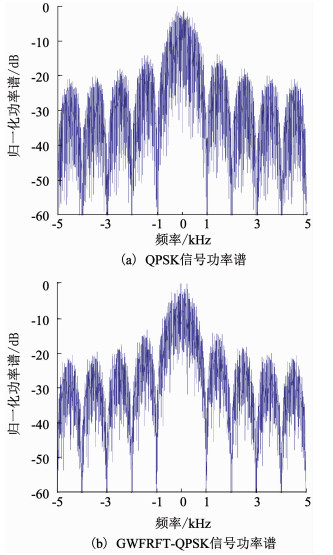
图 8为QPSK信号和GWFRFT-QPSK基带信号的归一化功率谱.其中码元长度为1 024,符号速率为1 kHz.由图 8可见,两种信号的归一化功率谱包络在频率上的过零点位置和包络形状基本一致;这也表明传统的QPSK信号经过GWFRFT后生成的两分量组合信号不会展宽系统带宽,也就是说两分量组合信号的生成不会占用额外的频谱资源.
|
图 8 QPSK信号与GWFRFT-QPSK信号归一化功率谱 Fig. 8 Normalized power spectrum of QPSK signal and GWFRFT-QPSK signal |
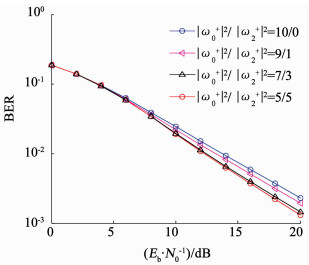
为了验证所提方案的有效性,本节对两分量组合信号的误码性能进行仿真.仿真中时域选择性衰落信道采用单径Jakes信道模型,采样间隔Ts=1×10-4 s,最大多普勒频移fd=50 Hz;频域选择性衰落信道由3条具有不同时延的单径Jakes信道组成,三径信道的多径时延分别为[0,1,2]Ts,各径的平均功率服从复指数分布,均值为[3.0, 5.1, 7.3]dB.两分量组合信号码块长度为256 bit,采用QPSK调制方式和MMSE均衡.图 9、10分别给出时域/频域选择性衰落信道下,GHCT/GHCF信号不同分量功率分配方案下的误码率比较.
|
图 9 GHCT系统分量功率分配与误码率关系 Fig. 9 Power allocation in GHCT system versus BER |
|
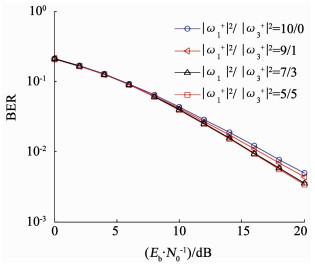
图 10 GHCF系统分量功率分配与误码率关系 Fig. 10 Power allocation in GHCF system versus BER |
在图 9中,|ω0+|2/|ω2+|2为时间分量和时间反转分量的能量比值,比值10/0为信号所有能量均赋给时域分量,此时系统等价于传统SC系统,两分量能量比值从9/1,7/3逐渐变化到5/5为时域分量和时域反转分量能量分配渐趋均匀的过程,比值5/5为两时域分量等功率分配的情况.从图 9中可以看出,在时域选择性衰落信道下,两时域分量组合信号方案可以有效提升SC系统的误码性能,且当两分量等功率分配时,对系统误码性能的提升最大;当误码率为2×10-3时,与传统SC系统相比,等功率分配的GHCT系统可以获得约1.5 dB的性能提升.
在图 10中,频率分量与频率反转分量的能量比值仍然从全部赋予频率分量向均匀分配逐渐变化;比值10/0为信号所有能量均赋给频率分量,此时系统等价于传统MC系统,比值5/5为两频域分量等功率分配的情况.与时域情况类似,当两频域分量等功率分配时,系统可以获得最佳的抗频域选择性衰落的性能;在所给信道条件下,当误码率为4×10-3时,与传统MC系统相比,等功率分配的频域GHCF系统可以获得约1.5 dB的性能提升.
可见,与传统SC系统和MC系统相比,两分量组合GHC信号(包括GHCT及GHCF信号)方案可以在不占用额外时间和频谱资源,且不改变载波体制的前提下,以同一数量级的微小复杂度提升换取传统SC系统和MC系统抗衰落性能的有效提升.
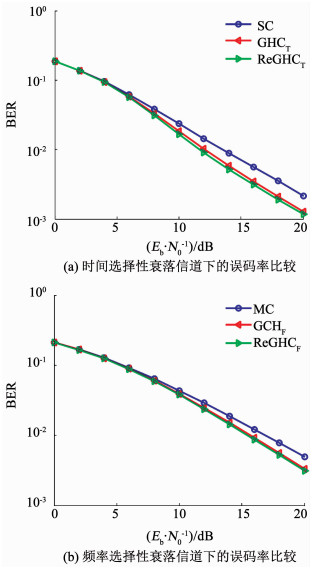
图 11验证了半码块反转过程对系统性能的提升情况.图 11(a)比较时间选择性衰落信道下传统SC系统、GHCT系统以及ReGHCT系统的误码率.图 11(b)比较频率选择性衰落信道下传统MC系统、GHCF系统以及ReGHCF系统的误码率.可以看出,经过半码块反转后的两分量组合GHC信号可以在可以在GHCT/GHCF系统的基础上获得额外的性能提升.
|
图 11 时/频选择性衰落信道下3种系统的误码率比较 Fig. 11 BER comparison among the three systems in time/frequency selective fading channel |
1) 结合GHC系统生成信号的高灵活性,提出一种基于GWFRFT的两分量组合抗衰落技术,在不改变载波体制的情况下,提升传统SC和MC系统的抗衰落能力.
2) 在两分量组合GHC信号形式下,对两个分量的功率分配比例进行优化,得出当两分量等功率分配时,系统抗衰落性能最佳的结论,同时给出两分量组合GHC信号生成方法.
3) 在分量等功率分配的基础上提出半码块反转优化方案,该方案可以使得码块中间部分符号在两分量中经历的衰落更加独立,从而进一步提升两分量组合信号的抗衰落性能.
4) 仿真表明:在时间和频率选择性衰落信道下,相比于传统SC或MC信号,两分量组合GHC信号可以在不占用额外时间和频谱资源的前提下,以很小的复杂度为代价换取系统抗衰落性能的有效提升.而基于分量功率分配和半码块反转的优化可以使得这种性能提升的效果更加显著.
综上所述,本文在时间选择性衰落信道或频率选择性衰落信道下对两分量组合GHC信号进行设计,并验证了该信号比传统SC和MC信号具有更好的抗衰落性能;然而,在更为复杂的信道场景下,基于GWFRFT理论的信号结构设计方法和时频分量能量分配准则也具有潜在的性能优势,这部分内容将作为接下来的研究方向.
| [1] |
RAN Qiwen, YEUNG D S, TSANG E C, et al. General multifractional Fourier transform method based on the generalized permutation matrix group[J]. IEEE Transactions on Signal Processing, 2004, 53(1): 83. DOI:10.1109/tsp.2004.837397 |
| [2] |
陈青, 孙海信. 加权分数傅里叶变换在混合系统中的应用[J]. 哈尔滨工业大学学报, 2016, 48(5): 100. CHEN Qing, SUN Haixin. Application of weighted fractional Fourier transform in hybrid system[J]. Journal of Harbin Institute of Technology, 2016, 48(5): 100. DOI:10.11918/j.issn.0367-6234.2016.05.016 |
| [3] |
MEI Lin, SHA Xuejun, RAN Qiwen, et al. Research on the application of 4-weighted fractional Fourier transform in communication system[J]. Science China: Information Sciences, 2010, 53(6): 1251. DOI:10.1007/s11432-010-0073-1 |
| [4] |
MEI Lin, ZHANG Qinyu, SHA Xuejun, et al. WFRFT precoding for narrowband interference suppression in DFT-based block transmission systems[J]. IEEE Communications Letters, 2013, 17(10): 1916. DOI:10.1109/LCOMM.2013.090213.131126 |
| [5] |
WANG Kun, SHA Xuejun, MEI Lin, et al. Performance analysis of hybrid carrier system with MMSE equalization over doubly-dispersive channels[J]. IEEE Communications Letters, 2012, 16(7): 1048. DOI:10.1109/lcomm.2012.050112.120414 |
| [6] |
WANG Zhenduo, MEI Lin, WANG Xiaolu, et al. On the performance of hybrid carrier system with spectrum precoding based on WFRFT[J]. EURASIP Journal on Wireless Communications & Networking, 2017(1): 102. DOI:10.1186/s13638-017-0890-7 |
| [7] |
KIM H, JUNG I, PARK Y, et al. Time spread-windowed OFDM for spectral efficiency improvement[J]. IEEE Wireless Communications Letters, 2018, 7(5): 696. DOI:10.1109/LWC.2018.2812150 |
| [8] |
WANG Zhenduo, MEI Lin, WANG Xiaolu, et al. BER analysis of hybrid carrier system based on WFRFT with carrier frequency offset[J]. Electronics Letters, 2015, 51(21): 1708. DOI:10.1049/el.2015.1027 |
| [9] |
FANG Xiaojie, ZHANG Ning, ZHANG Shan, et al. On physical layer security: Weighted Fractional fourier transform based user cooperation[J]. IEEE Transactions on Wireless Communications, 2017, 16(8): 5498. DOI:10.1109/twc.2017.2712158 |
| [10] |
HUI Yongtao, ZHAO Tong, LI Bingbing. 4-weighted fractional Fourier transform over doubly selective channels and optimal order selecting algorithm[J]. Electronics Letters, 2015, 51(2): 177. DOI:10.1049/el.2014.2268 |
| [11] |
MA Cong, SHA Xuejun, MEI Lin, et al. An equal component power-based generalized hybrid carrier system[J]. IEEE Communications Letters, 2018, 23(2): 378. DOI:10.1109/LCOMM.2018.2887382 |
| [12] |
LIM B, KO Y. SIR analysis of OFDM and GFDM waveforms with timing offset, CFO, and phase noise[J]. IEEE Transactions on Wireless Communications, 2017, 16(10): 6979. DOI:10.1109/TWC.2017.2736998 |
| [13] |
刘晨, 沙学军, 张文彬, 等. 积分判决的高效协同信号调制解调方法[J]. 哈尔滨工业大学学报, 2015, 47(3): 29. LIU Chen, SHA Xuejun, ZHANG Wenbin, et al. An efficient signal modulation and demodulation method based on integral judgments[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 29. DOI:10.11918/j.issn.0367-6234.2015.03.005 |
 2020, Vol. 52
2020, Vol. 52


