2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
智能移动终端和互联网的快速发展导致视频数据呈指数级增长,为了有效地分析和利用海量的视频数据,对连续视频中指定的目标对象进行实时处理逐渐成为迫切需求.视频目标跟踪作为计算机视觉领域重要的研究方向之一,在基于海量视频的目标识别、安全监控、远程医疗、无人机驾驶等场景中具有广阔的应用前景[1-3].
国内外学者对基于视频序列的目标跟踪开展了大量的研究;根据被处理对象,目标跟踪可分为多目标跟踪和单目标跟踪,前者主要关注多个目标之间关联性研究,而后者主要研究指定的单个目标的运动状态;但二者面临一些共同的难点,例如:运动过程中目标被遮挡、背景环境干扰以及光线强度变化等.针对单目标跟踪,一些具有代表性的方法被相继提出;其中,基于检测的跟踪方法得到广泛地应用和研究,它将目标跟踪视为二分类问题,使用预训练的分类网络,对每帧视频图像中目标物体和背景进行区分,实现对目标的跟踪表现.在基于检测的跟踪方法中,准确的目标表征对跟踪结果至关重要,一些人工设计的特征被用于视觉目标跟踪中;Henriques等提出了高速核化相关滤波器(Kernelized Correlation Filters,KCF)跟踪算法[4],使用方向梯度直方图(Histogram of Oriented Gradient,HOG)特征对目标进行表征,通过多通道快速扩展使得相关滤波器对目标特征进行提取,快速确定目标坐标位置;但在目标尺度快速变化的场景中表现并不理想.为了克服KCF中循环矩阵导致的边界效应问题,Danelljan等[5]对网络代价函数施加空间正则化项以抑制背景区域响应,结合HOG特征、灰阶(greyscale)特征以及颜色(Color Name,CN)特征对目标物体进行表征;在线更新过程中通过迭代高斯赛德尔(Gauss-Seidel)方法加速网络收敛过程.陈东岳等提出了一种基于多特征的融合的跟踪算法[6],使用BWH算法融合了照度不变性特征和基于LBP纹理特征,该算法对目标被遮挡场景下有一定鲁棒性,但未能对目标框尺寸进行自动调节,导致在目标消失场景中表现不佳.
近年来,随着深度卷积网络(Convolutional Neural Network,CNN)在图像分类任务中取得了优良的表现[7],深度学习逐渐被应用于计算机视觉的各个领域[8-10];经过大量数据训练后的CNN能够自动地提取物体的深度卷积特征,这些特征相比于人工选取的特征更具有通用性、判别性以及丰富的语义信息;因此,一些基于深度特征和CNN的跟踪算法被相继提出.Danelljan等使用深度卷积网络第一层特征代替人工选取的HOG和CN特征[11],提升了网络在跟踪任务中的鲁棒性.Wang等提出结构化输出的深度跟踪网络[12],通过离线训练的CNN预测视频帧中像素概率图以确定目标位置,并对跟踪网络进行定期微调,提高算法在目标旋转、光照变化场景中的适应性和鲁棒性;上述基于CNN跟踪算法取得较高的跟踪准确度,但网络的在线更新增加了算法的计算复杂度;此外,单目标跟踪任务中,要求跟踪算法根据初始帧中给定的运动物体在随后每帧视频中进行唯一性匹配,由此可视为给定目标模板寻找最大相似度图像区域.基于上述思想,文献[13-14]使用了孪生神经网络(Siamese Neural Network,SNN)作为跟踪框架,该结构由两个特征映射子网络构成,通过度量学习衡量目标模板与输入样本间特征的相似度关系;相比于基于CNN的跟踪算法,基于SNN的跟踪算法在未对目标模板和网络参数进行在线更新的情况下,能够取得准确跟踪精度,同时达到了实时的跟踪速度.然而由于上述基于深度学习的跟踪网络训练通常以全监督的方式进行,在训练过程中需要海量的标签数据,因此在有限的数据集中,网络易发生过拟合现象而导致目标漂移;部分学者基于大规模数据集,采用密集采样策略生成大量训练样本(图 1);但获得的样本缺乏多样性,并未涵盖跟踪过程中目标物体受遮挡以及形变情况,无法对目标变化进行准确表征.

|
图 1 密集采样策略示例 Fig. 1 Examples of dense sampling |
综上所述,为了缓解基于深度学习的目标跟踪算法训练数据不足以及样本缺乏多样性,跟踪缺乏实时性的问题,本文基于SNN跟踪算法,对离线训练数据和训练方式提出改进,同时提高了跟踪算法的实时性.基于大规模数据集,首先使用无监督学习的变分自编码器(Variational Autoencoder,VAE)和负样本挖掘策略生成大量的困难样本,以满足网络对多样性训练数据的需求;然后使用概率三元组损失对网络进行训练,挖掘目标模板、正负样本之间的潜在关系;对比实验表明:该算法在保持实时性的情况下,能够对跟踪过程中目标形态变化、相似语义干扰物、目标被遮挡情况以及快速运动导致的图像模糊有较好的鲁棒性.
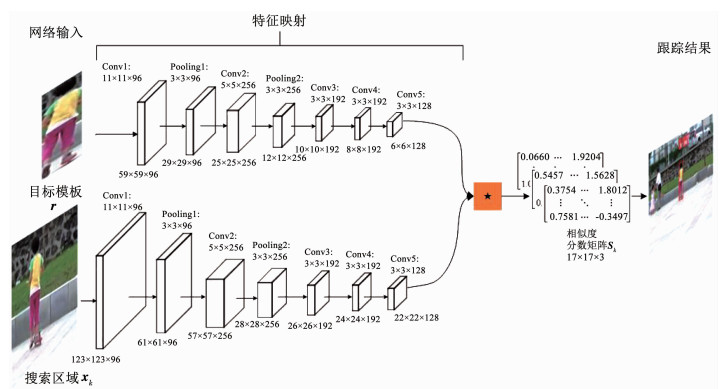
1 基于SNN的单目标跟踪算法Bertinetto等结合CNN提出了一种端到端的全卷积孪生网络(Fully-Convolutional Siamese Networks,SiamFC)跟踪框架[13],网络的模型结构如图 2所示.该网络利用两个CNN构建特征映射网络,分别提取模板和搜索区域深度卷积特征;然后在互相关层集成目标和搜索区域的深度特征图得到相似度分数图,图中最大分数值的区域为目标当前时刻的位置.基于SNN的单目标跟踪网络拥有轻量级网络架构,因此能够对目标物体进行实时定位.在视频第一帧时,对目标模板r进行特征映射,生成并保存模板的特征向量f(r),该操作仅在初始帧时进行;在跟踪过程中,基于上一帧目标状态,提出候选搜索窗口,并进行特征映射.
|
图 2 基于SNN的单目标跟踪网络架构 Fig. 2 Architecture of single target tracking based on SNN |
得到搜索区域内图像特征向量f(xk),通过下式度量目标模板和搜索窗口相似度分数sk
| $ {\mathit{\boldsymbol{s}}_k}\left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{x}}_k}} \right) = g\left( {f\left( \mathit{\boldsymbol{r}} \right), f\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right). $ | (1) |
式中f(·)为特征映射,g(·)为互相关操作.本文使用文献[13]中互卷积计算二者相似度,由此式(1)可等效为
| $ {\mathit{\boldsymbol{s}}_k}\left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{x}}_k}} \right) = f\left( \mathit{\boldsymbol{r}} \right) \cdot f\left( {{\mathit{\boldsymbol{x}}_k}} \right) + \mathit{\boldsymbol{b}}. $ | (2) |
式中: b为网络偏置项.上式得到相似度分数矩阵中,通过下式取得最大分数值的区域映射到视频图像中对应区域,即为目标物体在当前时刻的位置x *
| $ {\mathit{\boldsymbol{x}}^*} = \mathop {\arg \;\max \mathit{\boldsymbol{s}}}\limits_{{\mathit{\boldsymbol{x}}_k}} \left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{x}}_k}} \right). $ | (3) |
该算法对目标快速运动场景有较好的鲁棒性,对于网络参数没有进行在线调整;相较于基于CNN跟踪算法,SiamFC算法在跟踪阶段计算复杂度更低,达到了实时的跟踪速度;但是由于使用固定尺度更新目标框,导致对多尺度变化目标的跟踪准确度略显不足;并且在出现相似语义干扰项场景中常常出现目标漂移的情况.
2 基于SNN的单目标跟踪算法的改进本文基于SiamFC跟踪网络,针对该网络离线训练过程进行改进及优化,满足SNN单目标跟踪网络对训练样本量需求同时提高网络在线跟踪时的鲁棒性和跟踪准确度.首先,使用VAE网络对训练图片进行降维编码,通过在低维隐空间采样重构目标样本,生成大量包含多样性的困难正样本,构建离线训练数据集;其次,将原始的二元逻辑损失替换为概率三元组损失函数,挖掘目标样本和正负实例的潜在联系,提高网络对目标和干扰项的判别能力.
2.1 VAE网络生成正样本在目标跟踪领域中,与测试数据拥有相同分布情况的训练数据集相对匮乏,因此样本生成网络被应用于生成大量相似的样本数据;另外,由于基于SiamFC的跟踪算法并未执行网络参数的在线更新,对于目标的形态剧烈变化缺乏鲁棒性,因此不增加额外时间开销的情况下,本文在离线训练阶段,通过深度生成网络产生丰富的样本数据,使SiamFC跟踪算法能够获得跟踪任务中目标的多样性表征.
基于深度学习的生成网络主要包含VAE[15]和生成对抗网络(Generative Adversarial Networks,GANs)[16].其中VAE算法能够准确地提取高维非线性样本特征,在训练过程中实现对数据在样本空间中随机分布情况的近似学习;因此VAE被广泛应用在计算机视觉领域中,文献[17]利用VAE网络对输入图像进行分析,通过对隐藏层中特征分布情况进行采样,生成输入图像的分类标签和标题描述;Waker等提出了条件变分自编码器(Conditional Variational Autoencoder,CVAE)[18]通过隐藏变量对图像中信息进行编码,推断静态图像中目标物体可能的轨迹分布,预测目标的运动趋势.
在跟踪网络训练过程中,由于图像样本均位于高维空间,因此通常通过在高维流形空间中沿一定方向对目标数据信息进行遍历以此生成样本数据,但高维流形建模复杂度较高,直接在高维流形空间上执行遍历操作较困难.因此在离线训练阶段,本文使用VAE网络能够学习高维流形空间和低维空间即隐藏空间之间的特征映射关系和目标样本的流形分布情况,通过简化遍历操作解码重构生成正样本训练数据;并且VAE网络生成的数据样本更加可控,能够避免图像失真情况,在保留原始样本特征部分相似性的同时,呈现出目标样本丰富的多样性表征;生成的多样性样本涵盖了跟踪任务中目标物体的变化趋势,能够提升SiamFC跟踪算法对运动过程中目标变化的鲁棒性.
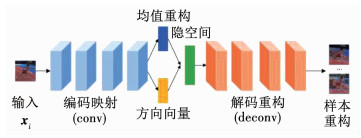
文中VAE网络架构如图 3所示:首先从视频图像中截取目标物体的RGB图像作为网络输入,其尺寸大小为64×64×3,随后经过4层的卷积神经网络提取样本特征激活值,每一层卷积都使用上一层输出激活值作为本层的输入,如下式
|
图 3 VAE网络结构 Fig. 3 Structure of VAE |
| $ \mathit{\boldsymbol{a}}_m^l = f\left( {\sum\limits_n {\mathit{\boldsymbol{W}}_{mn}^l * \mathit{\boldsymbol{a}}_n^{l - 1} + \mathit{\boldsymbol{b}}_m^l} } \right). $ | (4) |
式中:aml和anl-1分别为l层第m个通道输出的特征矩阵和l-1层第n个通道的输出特征矩阵,Wmnl和bml分别表示相应的第m个输出通道的卷积权重矩阵和偏置项,其初始值通过高斯分布随机初始化,*代表卷积操作.在每一次卷积操作后对特征响应值施加批量规范化(Batch Normalization,BN)操作,使得每一层卷积输入保持相同分布情况,加快网络训练收敛速度和网络稳定性;隐空间和中间全连接层的维度分别为2和512,最后通过4层解卷积层对目标样本进行重构并采用tanh函数激活响应值生成多样性训练样本.
给定样本集X={xi}i=1N,通过对xi进行建模,产生相似的重构样本.在上述随机过程中引入了连续随机隐变量z,VAE通过编码部分将输入图像xi映射为概率后验分布pθ(z|xi),经过隐空间和解码重构图像分布pθ(xi|z),对重构分布进行采样获得重构样本Ii;其中真实后验分布pθ(z|xi)通过贝叶斯定理定义
| $ {p_\theta }\left( {\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_i}} \right) = \frac{{{p_\theta }\left( {{\mathit{\boldsymbol{x}}_i}|\mathit{\boldsymbol{z}}} \right){p_\theta }\left( \mathit{\boldsymbol{z}} \right)}}{{{p_\theta }\left( {{\mathit{\boldsymbol{x}}_i}} \right)}}. $ | (5) |
然而通过上式难以直接计算,VAE中可以通过使用变分构建qφ(z | xi)近似pθ(z | xi),因此对该生成网络的训练可视为最小化qφ(z | xi)和pθ(z | xi)两者的距离,也即最大化每个训练样本xi变分下界,定义为
| $ \begin{array}{*{20}{c}} {L({\mathit{\boldsymbol{x}}_i},\mathit{\boldsymbol{\varphi }},\mathit{\boldsymbol{\theta }}) = - {\rm{KL}}(\left. {{q_\varphi }(\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_i})} \right\|{p_\theta }(\mathit{\boldsymbol{z}})) + }\\ {{{\rm{E}}_{{q_\varphi }(\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_i})}}[{\rm{log}}{p_\theta }({\mathit{\boldsymbol{x}}_i}|\mathit{\boldsymbol{z}})].} \end{array} $ | (6) |
式中:pθ(z)为隐变量概率分布,φ和θ分别为隐空间变分参数和编码解码模块参数,等式右侧第一部分表示计算qφ(z | xi)和pθ(z | xi)的KL散度(Kullback-Leibler Divergence),衡量二者分布相似情况,最后一项为关于近似后验qφ(z | xi)的期望重构损失.通过反向传播算法最优化式(6)以求得各参数权值,令pθ(z)和qφ(z | xi)服从高斯分布,便利网络训练;因此,式(6)中KL散度项可解析表示为
| $ - {\rm{KL}} = \frac{1}{2}\sum\limits_{d = 1}^D {\left( {1 + \log \left( {\sigma _d^2} \right) - \mu _d^2 - \sigma _d^2} \right)} . $ | (7) |
式中:D为隐变量z的维度大小,均值μ和σ为网络编码部分关于输入样本xi和变分参数φ的输出.由于z为隐空间中随机变量,为了实现反向传播梯度优化,对式(6)中重构损失项使用重参数技巧(reparametrization trick),并将式(7)带入式(6)中,代价函数可近似为
| $ \begin{array}{l} L\left( {{\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{\varphi }}, \mathit{\boldsymbol{\theta }}} \right) \approx \frac{1}{2}\sum\limits_{d = 1}^D {\left( {1 + \log \left( {\sigma _d^2} \right) - \mu _d^2 - \sigma _d^2} \right)} + \\ \frac{1}{L}\sum\limits_{l = 1}^L {\log {p_\theta }} \left( {{\mathit{\boldsymbol{x}}_i}|{\mathit{\boldsymbol{z}}_{i, l}}} \right) \end{array} $ | (8) |
式中:引入εl~N(0, 1),利用zi, l=μi+σi☉εl确定z实现反向传播计算.在解码部分中,通过伯努利交叉熵(Bernoullicross-entropy)损失计算log pθ(xi|zi, l).
通过上述训练过程,VAE中参数φ、θ的权值以及qφ(z|xi)得以确定.利用上述预训练的VAE网络生成多样性正样本数据,部分生成结果在参数设置中进行了展示;将正样本数据集Zp={I1, …, Ii, …, IM}结合负样本数据集Zn={O1, …, Oj, …, OH},构建训练样本数据集Z=Zp∪Zn训练目标跟踪网络.
2.2 概率三元组损失训练SNN跟踪网络文献[13]中使用的二元逻辑损失函数仅利用了模板和样本间联系;本文利用概率三元组损失对跟踪网络进行离线训练,不仅可以进一步挖掘范例、正实例和负实例之间的潜在关系,而且在每次训练迭代时包含了更多的训练元素.
2.2.1 二元逻辑损失在原始的SiamFC目标跟踪网络中,每段训练视频二元逻辑损失函数定义为
| $ {L_{\rm{b}}} = \sum\limits_{{\mathit{\boldsymbol{x}}_t} \in \mathit{\boldsymbol{Z}}} {{\mathit{\boldsymbol{w}}_t}} {\rm{log}}(1 + {\rm{exp}}( - {y_t},{\mathit{\boldsymbol{s}}_t}(\mathit{\boldsymbol{r}},{\mathit{\boldsymbol{x}}_t}))). $ | (9) |
式中:yt∈{+1, -1}为每个样本的真实标签值,通过式(2)计算得到st∈S为每个模板-样本对(r, xt)的相似度分数,wt为每个样本实例xt的平衡权重,以保持不同数量正负样本对损失函数拥有同样的影响,其取值定义为
| $ {\mathit{\boldsymbol{w}}_t} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{2M}},{y_t} = 1;}\\ {\frac{1}{{2H}},{y_t} = - 1.} \end{array}} \right. $ | (10) |
且满足
| $ \sum\nolimits_{{\mathit{\boldsymbol{x}}_t} \in \mathit{\boldsymbol{Z}}} {{\mathit{\boldsymbol{w}}_t}} = 1,{\mathit{\boldsymbol{w}}_t} > 0. $ | (11) |
式(9)中每次迭代时输入一个模板-样本对,因此每段训练视频中,网络损失由M+H个训练样本损失构成.
2.2.2 概率三元组损失本文将所有模板-样本对分数S划分为正样本相似度分数集Sp={sp1, …, spi, …, spM}和负样本相似度分数集Sn={sn1, …, snj, …, snH},分别使用模板-正样本对(r, Zp)和模板-负样本对(r, Zn)作为输入利用式(2)求得.
将每组正负分数对(spi, snj)作为输入,通过softmax函数定义三元组样本匹配概率
| $ p({\mathit{\boldsymbol{s}}_{{\rm{p}}i}},{\mathit{\boldsymbol{s}}_{{\rm{n}}j}}) = \frac{{{\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{p}}i}})}}{{{\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{p}}i}}) + {\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{n}}j}})}}. $ | (12) |
训练目的是最大化所有相似度分数对组合的联合概率,跟踪网络的损失函数定义如下
| $ {L_{\rm{t}}} = - \frac{1}{{MH}}\sum\limits_i^M {\sum\limits_j^H {{\rm{log}}} } p({\mathit{\boldsymbol{s}}_{{\rm{p}}i}},{\mathit{\boldsymbol{s}}_{{\rm{n}}j}}). $ | (13) |
式中:
| $ \begin{array}{*{20}{l}} {{L_{\rm{t}}} = - \frac{1}{{MH}}\sum\limits_i^M {\sum\limits_j^H {{\rm{log}}} } \frac{{{\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{p}}i}})}}{{{\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{p}}i}}) + {\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{n}}j}})}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{MH}}\sum\limits_i^M {\sum\limits_j^H {{\rm{log}}} } (1 + {\rm{exp}}({\mathit{\boldsymbol{s}}_{{\rm{n}}j}} - {\mathit{\boldsymbol{s}}_{{\rm{p}}i}})).} \end{array} $ | (14) |
通过最小化上述损失函数,得到跟踪网络中特征映射网络的权值.由于式(12)中样本匹配概率p(spi, snj)的计算同时涉及到模板r、正样本数据Zp以及负样本数据Zn三种变量,因此将式(14)称为概率三元组损失.由式(14)看出,概率三元组损失由M×H个正负分数对组合组成,与二元逻辑损失相比,概率三元组损失涵盖更丰富的样本组合方式,并且能够同时挖掘模板、正样本、负样本的潜在关系;在训练过程中,式(9)中二元逻辑损失函数关于正负样本产生的梯度分别为
| $ \frac{{\partial {L_{\rm{b}}}}}{{\partial \mathit{\boldsymbol{s}}}} = \left\{ {\begin{array}{*{20}{l}} { - \frac{1}{{2(1 + {\rm{exp}}({\mathit{\boldsymbol{s}}_{\rm{p}}}))}},\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{s}}_{\rm{p}}};}\\ {\frac{1}{{2(1 + {\rm{exp}}( - {\mathit{\boldsymbol{s}}_{\rm{n}}}))}},\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{s}}_{\rm{n}}}.} \end{array}} \right. $ | (15) |
本文使用的概率三元组损失的梯度则可表示为
| $ \frac{{\partial {L_{\rm{t}}}}}{{\partial \mathit{\boldsymbol{s}}}} = \left\{ {\begin{array}{*{20}{c}} { - \frac{1}{{1 + {\rm{exp}}({\mathit{\boldsymbol{s}}_{\rm{p}}} - {\mathit{\boldsymbol{s}}_{\rm{n}}})}},\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{s}}_{\rm{p}}};}\\ {\frac{1}{{1 + {\rm{exp}}({\mathit{\boldsymbol{s}}_{\rm{p}}} - {\mathit{\boldsymbol{s}}_{\rm{n}}})}},\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{s}}_{\rm{n}}}.} \end{array}} \right. $ | (16) |
通过对比上述两式不难发现,在反向传播过程中,概率三元组损失函数涵盖了正样本-模板对和负样本-模板对,能够同时考虑正负样本对梯度变化的影响;并且在网络训练中没有引入额外的样本特征,唯一增加的时间开销来自于概率三元组损失计算,且仅出现在离线训练阶段,在线跟踪过程没有产生额外的计算负担.
3 实验与分析本文实验在以下平台实现:CPU为Intel(R)Xeon(R)E5-2643 @ 3.40 GHz,16 GB RAM,GPU为NVIDIA GTX1080Ti,程序代码基于PyTorch深度学习环境下使用Python语言编写.
3.1 参数设置离线训练阶段,在ILSVRC15视频目标检测数据集(Object Detection from Video, VID)[19]中选取16段视频序列作为跟踪网络的训练数据;针对选取的每一段视频,训练一个对应的VAE样本生成网络用以生成困难正样本数据;本文使用Root Mean Square prop(RMSprop)对VAE网络的训练过程进行优化,减小梯度下降时振荡幅度,加快网络训练时的收敛速度;学习率设置为10-3,迭代104次.样本生成阶段,综合跟踪网络对训练数据的需求以及视频中目标运动变化的频率,将每帧原始样本和生成数据比例设置为1: 5,图 4展示了VAE网络生成的部分正样本示例,红色矩形框中图像表示对应视频片段的原始样本.与原图像相比,经过重构后生成的正样本呈现示出目标物体潜在的运动形态和运动趋势;同时从图中可以看出,生成的样本图像分辨率较低,这使得训练后的跟踪网络对目标快速运动和视频采集设备导致图像模糊情况有较高的鲁棒性,从而增强算法在低分辨率环境下的跟踪表现;在随后的实验结果及分析中,上述观点得到了验证.

|
图 4 重构训练样本示例 Fig. 4 Examples of reconstructed training samples |
训练SNN跟踪网络时,通过N(0, 0.01)高斯分布对权重初始化;然后利用随机梯度下降(Stochastic Gradient Descent,SGD)算法最小化式(14)概率三元组损失得到网络的最优权值;训练视频序列中,每帧片段包含正样本|M|=13,负样本|H|=256;初始学习率设为10-2,随训练次数增加逐渐衰减至10-5,训练经过50次迭代.
3.2 实验数据为了验证改进后跟踪网络的性能表现,从目标跟踪公共数据集OTB100[20]上选取了几段比较有代表性的视频序列,每段视频帧数从81~1 500帧不等,从320×240至800×336多种图像分辨率,包含了多个复杂的跟踪难点,视频详情见表 1.
| 表 1 实验视频序列详情 Tab. 1 Details of video sequences in the experiment |
为了评估算法在实验数据集上的表现情况,本文使用了中心像素点误差和文献[20]提出的跟踪成功率作为评价指标;前者计算预测目标框的中心坐标与真实值的欧氏距离,反映了跟踪算法的定位准确度;后者是通过计算预测值和真实目标框交并比(Intersection over Union,IoU)进行衡量,定义如下
| $ {o_{\rm{s}}} = \frac{{|{\mathit{\boldsymbol{l}}_{\rm{t}}} \cap {\mathit{\boldsymbol{l}}_{\rm{g}}}|}}{{|{\mathit{\boldsymbol{l}}_{\rm{t}}} \cup {\mathit{\boldsymbol{l}}_{\rm{g}}}|}}. $ | (17) |
式中:lt和lg分别为预测目标框和真实值目标框,∪和∩分别计算两个目标框内相并和相交部分,|·|用于统计像素个数,os为二者的重叠率.当os大于0.5时,表示算法在当前帧上实现了成功跟踪;统计成功跟踪帧数占全部视频帧的比例即为算法的成功跟踪率.
3.3 实验结果展示及分析本文选取了几种具有代表性的跟踪算法与所提出的改进算法进行对比实验,包括SiamFC算法[13]、基于SNN的相关滤波器(CFNet)算法[14]、KCF算法[4]、空间正则化判别相关滤波器(Spatially Regularized Discriminative Correlation Filters,SRDCF)算法[5];其中前两者和本文算法均使用了SNN作为跟踪阶段的网络架构,CFNet算法在SiamFC网络中结合相关滤波层构建非对称SNN跟踪网络,实现了对底层深度特征表示的优化.KCF和SRDCF算法则是基于相关滤波器的单目标跟踪网络;其中SRDCF算法通过施加空间正则化分量缓解了相关滤波跟踪网络中的边界效应问题.
本小节中,选取实验视频序列其中两段的跟踪结果进行展示,绘制5种算法的中心误差曲线和目标框重叠率曲线,并对算法的跟踪表现进行分析.
3.3.1 关键帧跟踪结果及分析选取展示的第一段视频为“ClifBar”,由472帧的黑白图像组成.从图 5中可以看出:目标物体处于相似背景下,且为图像,并伴随快速运动导致的图像模糊,对跟踪算法的鲁棒性有较高的要求.在第80帧时,目标正从右侧向左侧快速移动,KCF和CFNet算法开始出现目标漂移的现象,这是由于上述两种算法对快速运动导致图像模糊处理能力不足;第230帧时,由于目标平面内旋转以及快速左右位移,目标物体发生较大的尺度变化,SiamFC算法陷入局部最优值,预测的目标框转移到背景中;在五种算法中,SRDCF通过空间正则化抑制背景噪音,和本文算法始终保持对目标物体的准确定位,直到视频最后.说明本文算法对于快速运动以及导致的画面模糊、目标尺度变化现象有较强的鲁棒性.

|
图 5 ClifBar视频跟踪结果 Fig. 5 Tracking results of video sequence ClifBar |
图 6展示的“Skiing”视频序列,包含的主要跟踪难点在于目标人物始终处于旋转的运动模式中,形态变化剧烈,在部分片段中背景信息比较复杂.根据跟踪结果可以看出,由于目标向内旋转,外观发生剧烈变化,KCF和SRDCF算法在第7帧时发生明显的漂移现象,并持续陷入局部区域,随后丢失目标直到视频结束;与上述算法相似,由于目标运动过程中快速的形态变化,SiamFC算法在第12帧时未能保持对目标准确定位,逐渐漂移至画面右侧,最终导致跟踪失败;本文算法和CFNet算法能够对目标多种形态进行准确表征,有效判别背景干扰物和目标,保持对视频中目标的连续跟踪,表现出对目标快速运动、旋转导致的外表剧烈变化以及复杂背景干扰的鲁棒性.

|
图 6 Skiing视频跟踪结果 Fig. 6 Tracking results of video sequence Skiing |
此外,对本文算法在上述两段视频中关键帧跟踪网络产生的响应图进行绘制,展示于图 7中.从图中可以看出,在“ClifBar”序列中,目标进行多种尺度变化,并伴随部分相似的背景干扰;而第二段视频序列中,目标物体持续旋转和快速移动,外形和尺度不断发生变化,同样在部分帧中出现复杂背景的干扰;本文算法能够对目标产生较大的相似度响应值,背景和干扰物部分取得较低分数,说明该算法对目标和背景有较好的处理能力,验证了该算法上述视频中关键片段的跟踪结果.

|
图 7 两段视频关键帧响应 Fig. 7 Response of key frames on ClifBar and Skiing |
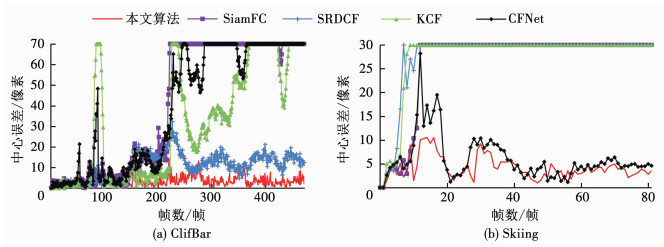
为了进一步对比5种算法在上述两段视频中的表现,逐帧绘制了算法的中心误差曲线和目标框重叠率曲线,如图 8和图 9所示.在ClifBar和Skiing两段视频中,当中心误差分别超过阈值像素时,预测的目标框已完全远离目标,因此将中心误差曲线上限设置为对应的最大阈值70和30像素.
|
图 8 中心误差曲线 Fig. 8 Center error curves of two video sequences |
|
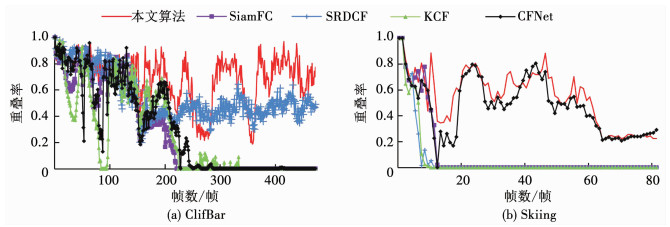
图 9 重叠率曲线 Fig. 9 Overlap rate curves of two video sequences |
从图 8及图 9中可以看出,相比于其他4种算法,本文算法在两段视频上均保持最低中心误差值和最高目标框重叠率,并且曲线波动最小,说明该跟踪算法能够实现稳定且准确的跟踪表现.在第一段视频中,SRDCF算法在前期保持了较低的中心误差;然而在第230帧时目标频繁左右移动出现模糊情况,导致SRDCF算法误差值增大,在重叠率曲线(图 9(a))上相应部分也反映了同样的现象;另外3种算法曲线振动幅度较大,相继丢失目标.“Skiing”序列中,由于目标旋转运动以及嘈杂背景干扰,SiamFC、SRDCF和KCF算法均未能对目标持续定位,在第10帧后丢失了目标导致跟踪失败;CFNet算法由于对背景干扰处理能力不足,跟踪曲线出现较大波动;本文算法在复杂背景干扰下目标快速运动导致的模糊、形态变化场景中都保持了较好的跟踪表现.
由于以上两段视频中,算法表现存在一定的随机性,因此对算法在所有实验视频上跟踪表现进行统计,表 2展示了各算法成功跟踪率和平均跟踪速度.本文算法在保持实时跟踪速度的同时在其中9段视频上都实现了最优跟踪表现;在较困难的“Ironman”和“Matrix”两段视频上,相比于SiamFC算法成功跟踪率提高了25%和68%,并且在SiamFC算法表现较差的序列上,也完成了准确的跟踪;此外,KCF算法在所有视频序列上实现最快平均速度,但其跟踪表现远远落后于本文算法.综上所述,本文算法利用SNN学习多样性样本,提高了网络对于目标物体多形态的表征能力;同时使用概率三元组损失函数,挖掘正负样本潜在关系,提高网络的判别能力和鲁棒性.
| 表 2 成功跟踪率及平均跟踪速度 Tab. 2 Success rate and average tracking speed of tracking algorithms |
本文对基于SNN单目标跟踪网络算法进行优化.利用VAE对原始训练样本进行编码重构生成困难正样本,构建训练数据集;与传统密集采样策略相比,本文算法从采样多样性角度增加了正样本数据,使跟踪网络学习丰富的样本表征;并缓解了深度跟踪网络训练数据不足的问题.在离线训练阶段,使用了概率三元组损失函数代替传统的二元逻辑损失,通过深入挖掘正负样本的潜在关系,提高了跟踪网络对目标和背景干扰物体的判别能力.实验结果表明,相比于核化相关滤波器、空间正则化、传统的SNN等跟踪算法,本文提出的优化算法在目标被遮挡及尺度变化、目标快速运动、目标旋转、画面模糊、复杂背景情况下有更好的鲁棒性和定位准确度,并保持了实时的跟踪表现.
| [1] |
LAURENSE V A, GOH J Y, GERDES J C. Path-tracking for autonomous vehicles at the limit of friction[C]//Proceedings of 2017 American Control Conference (ACC). Seattle: IEEE, 2017: 5586. DOI: 10.23919/ACC.2017.7963824
|
| [2] |
SIVANANTHAM S, PAUL N N, IYER R S. Object tracking algorithm implementation for security applications[J]. Far East Journal of Electronics and Communications, 2016, 16(1): 1. DOI:10.17654/EC016010001 |
| [3] |
ONATE J M B, CHIPANTASI D J M, ERAZO N R V. Tracking objects using artificial neural networks and wireless connection for robotics[J]. Journal of Telecommunication, Electronic and Computer Engineering (JTEC), 2017, 9(1/2/3): 161. |
| [4] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 37(3): 583. DOI:10.1109/TPAMI.2014.2345390 |
| [5] |
DANELLJAN M, HAGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 4310. DOI: 10.1109/ICCV.2015.490
|
| [6] |
陈东岳, 陈宗文, 桑永嘉. 基于多特征在线模板更新的鲁棒目标跟踪算法[J]. 哈尔滨工业大学学报, 2014, 46(7): 87. CHEN Dongyue, CHEN Zongwen, SANG Yongjia. Robust object tracking based on online update of multi-feature template[J]. Journal of Harbin Institute of Technology, 2014, 46(7): 87. DOI:10.11918/j.issn.0367-6234.2014.07.015 |
| [7] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84. DOI:10.1145/3065386 |
| [8] |
ZHANG Kaipeng, ZANG Zhanpeng, LI Zhifeng, et al. Joint face detection and alignment using multitask cascaded convolutional networks[J]. IEEE Signal Processing Letters, 2016, 23(10): 1499. DOI:10.1109/LSP.2016.2603342 |
| [9] |
HE Kaiming, GKIOXARI G, DOLLAR P, et al. Mask R-CNN[C]//Proceedings of 2017 IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017: 2980. DOI: 10.1109/ICCV.2017.322
|
| [10] |
DAI Jifeng, HE Kaiming, LI Yi, et al. Instance-sensitive fully convolutional networks[C]//Proceedings of European Conference on Computer Vision. Cham: Springer, 2016: 534. DOI: 10.1007/978-3-319-46466-4_32
|
| [11] |
DANELLJAN M, HAGER G, KHAN F S, et al. Convolutional features for correlation filter based visual tracking[C]//Proceedings of 2015 IEEE International Conference on Computer Vision Workshop (ICCVW). Santiago, Chile: IEEE, 2016: 621. DOI: 10.1109/ICCVW.2015.84
|
| [12] |
WANG Naiyan, LI Siyi, GUPTA A, et al. Transferring rich feature hierarchies for robust visual tracking[EB/OL].(2015-04-23)[2019-05-11].https://arxiv.org/pdf/1501.04587v2.pdf
|
| [13] |
BERTINETTO L, VALMADRE J, HENRIQUES J F, et al. Fully-convolutional siamese networks for object tracking[M]//Computer Vision-ECCV 2016 Workshops. Cham: Springer, 2016: 850. DOI: 10.1007/978-3-319-48881-3_56
|
| [14] |
VALMADRE J, BERTINETTO L, HENRIQUES J F, et al. End-to-end representation learning for correlation filter based tracking[C]// Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017: 5000. DOI: 10.1109/CVPR.2017.531
|
| [15] |
KINGMA D P, WELLING M. Auto-encoding variational Bayes[EB/OL]. (2014-05-01)[2019-05-11]. https://arxiv.org/pdf/1312.6114.pdf
|
| [16] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Proceedings of International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2014: 2672
|
| [17] |
PU Yunchen, GAN Zhe, HENAO R, et al. Variational autoencoder for deep learning of images, labels and captions[C]//Proceedings of Advances in Neural Information Processing Systems. New York: Curran Associates Inc., 2016: 2352
|
| [18] |
WAKER J, DOERSCH C, GUPTA A, et al. An uncertain future: forecasting from static images using variational autoencoders[C]//Proceedings of European Conference on Computer Vision. Cham: Springer, 2016: 835. DOI: 10.1007/978-3-319-46478-7_51
|
| [19] |
RUSSAKOVSKY O, DENG Jia, SU Hao, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211. DOI:10.1007/s11263-015-0816-y |
| [20] |
WU Yi, LIM J, YANG M. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834. DOI:10.1109/TPAMI.2014.2388226 |
 2020, Vol. 52
2020, Vol. 52


