移动机器人集动态决策与规划、行为控制与执行等多种功能于一体,能在恶劣环境、危险环境、灾难环境中代替人类以更低的成本完成许多重要工作.因此,在军事、工业等众多领域具有广泛的应用,一直是广大科研工作者的研究热点.
移动机器人主要包括履带式、蛇形式、腿式、跳跃式、复合式和轮式等.与其他类型的移动机器人相比,尽管轮式移动机器人的运动稳定性受路况影响较大,但其具有承载大、驱动和控制较方便、自重轻、行走速度快、机构简单、工作效率高、机动灵活、运动噪声低等多种优点,因此成为本文及诸多学者的研究对象.然而,作为一种典型的非完整系统,轮式移动机器人的轨迹跟踪控制问题迄今仍然被很多人关注.早期的轨迹跟踪控制方法主要集中在针对运动学方程提供虚拟控制器使机器人能够渐近跟踪给定的参考轨迹,如反演控制[1]、滑模控制[2]、预测控制等[3-4].随后,许多工作将这些非线性控制方法与其他方法相结合,同时考虑机器人的动力学模型,提出了一些具有鲁棒性和实用性的机器人轨迹跟踪控制方法,如与自适应补偿相结合的研究工作[5-6]、与神经动力学优化方法相结合的研究工作[7]以及与其他方法相结合的研究工作[8-11].此外,随着人工智能理论的发展,还涌现出了一些新的轨迹跟踪控制方法,如基于机器学习、神经网络、模糊控制设计的轨迹跟踪控制方法[12-13],基于视觉伺服的轨迹跟踪控制方法[14-15],基于多体动力学的保辛瞬时最优控制方法[16]等.
与以上文献的研究重点不同,本文主要研究如何利用预演信息克服机器人响应能力的有限性,以保证机器人快速跟踪给定的参考轨迹.事实上,已有的大量研究亦表明:合理利用预演信息设计控制器能够有效地改善控制系统的性能如暂态性能、闭环性能等,该事实在文献[17-22]中都有详细的阐述与证明;另一方面,大自然及人类社会有许多成熟的利用预演控制的实际系统,比如,文献[18]曾提到,司机如果能利用更多的前方路况及时调整车速及车子的前进方向,就能够提供更安全、舒适的驾驶.基于此,再考虑到轨迹跟踪问题中轮式移动机器人参考轨迹已知的特点,本文提出一种基于预演控制策略的轮式移动机器人轨迹跟踪控制方法.不同于其他控制方法,由于该控制策略有效地利用了当前及将来的参考信息,因而能够达到更好的轨迹跟踪效果.
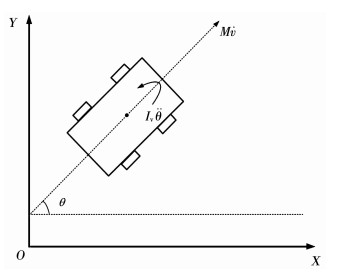
1 轮式移动机器人的动力学模型假设绝对坐标系XOY固定在平面内,轮式移动机器人的运动示意如图 1所示.其后轮为随动轮,仅用于支撑车体,无导向作用.两个前轮为独立驱动轮,各采用一台直流伺服电机驱动.当两个前轮被输入不同的驱动电压时,它们将产生速度差,继而可调整机器人前进的方向及轨迹.
|
图 1 轮式移动机器人的运动示意 Fig. 1 Schematic diagram of movement of a wheeled mobile robot |
首先,为方便阅读,我们在表 1中定义移动机器人建模所涉及到的相关参数和变量.其中,下标l和r被用于区别左右轮的同一参数或变量.
| 表 1 轮式移动机器人变量和参数的定义 Tab. 1 Definition of wheeled mobile robot variables and parameters |
根据表 1定义的机器人参数与变量,在轮式移动机器人的质心与几何中心重合的前提下,根据力矩平衡原理、牛顿第二运动定律以及双轮驱动轮式移动机器人的速度调节原理,推导出如下的轮式移动机器人的动力学模型:
| $ {\dot v = {a_1}v + {b_1}({u_{\rm{r}}} + {u_1}),} $ | (1) |
| $ {\dot \omega = {a_2}\omega + {b_2}({u_{\rm{r}}} - {u_1}).} $ | (2) |
其中:
| $ \begin{array}{*{20}{l}} {{a_1} = - \frac{{2c}}{{M{r^2} + 2{I_{\rm{ \mathsf{ ω} }}}}},{a_2} = - \frac{{2c{L^2}}}{{{I_{\rm{v}}}{r^2} + 2{I_{\rm{ \mathsf{ ω} }}}{L^2}}},}\\ {{b_1} = \frac{{kr}}{{M{r^2} + 2{I_{\rm{ \mathsf{ ω} }}}}},{b_2} = \frac{{krL}}{{{I_{\rm{v}}}{r^2} + 2{I_{\rm{ \mathsf{ ω} }}}{L^2}}}.} \end{array} $ |
定义如下变量
| $ {\mathit{\boldsymbol{x}}_1} = {\left[ {\begin{array}{*{20}{l}} v&\omega \end{array}} \right]^{\rm{T}}},{\mathit{\boldsymbol{u}}_1} = {\left[ {\begin{array}{*{20}{l}} {{u_{\rm{r}}}}&{{u_1}} \end{array}} \right]^{\rm{T}}}. $ |
则轮式移动机器人的动力学方程(1)、(2)可表示成:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{B}}_1}{\mathit{\boldsymbol{u}}_1},}\\ {{\mathit{\boldsymbol{y}}_1} = \mathit{\boldsymbol{x}}\mathit{\boldsymbol{.}}} \end{array}} \right. $ | (3) |
式(3)中
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&0\\ 0&{{a_2}} \end{array}} \right],{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{b_1}}&{{b_1}}\\ {{b_2}}&{ - {b_2}} \end{array}} \right]. $ |
获得了轮式移动机器人的动力学方程,只是完成了预演控制跟踪的第一步.考虑到轮式移动机器人对预演控制跟踪策略的执行问题,系统(3)被离散化成:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\bar x}}(k + 1) = \mathit{\boldsymbol{A}}{\kern 1pt} \mathit{\boldsymbol{\bar x}}(k) + \mathit{\boldsymbol{Bu}}(k),}\\ {\mathit{\boldsymbol{\bar y}}(k) = \mathit{\boldsymbol{\bar x}}(k).} \end{array}} \right. $ | (4) |
这里,为了减少并简化符号,连续时间系统(3)与离散时间系统(4)使用了相似的符号.式(4)中的x(k), u(k), y(k)分别表示连续时间系统(3)的状态x1、控制u1和输出y1在kT时刻的采样值,T是采样周期,系统参数
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{I}} + T{\mathit{\boldsymbol{A}}_1},\mathit{\boldsymbol{B}} = T{\mathit{\boldsymbol{B}}_1}. $ |
式中I是维数相容的单位阵.
关于轮式移动机器人动力学方程(3)的推导,本文假设了轮式移动机器人的质心与几何中心重合.事实上,质心与几何中心不重合并不会影响动力学方程(3)的线性特性.
2 轮式移动机器人的运动学模型为了进行轮式移动机器人的轨迹跟踪,有必要给出轮式移动机器人的运动学方程.
记[x(t) y(t)θ]T为t时刻轮式移动机器人的位姿,(x(t), y(t))为t时刻轮式移动机器人的几何中心在笛卡尔坐标系XOY中的坐标,θ是轮式移动机器人的航向角.依然考虑轮式移动机器人的质心与几何中心重合的情况,假设轮式移动机器人侧向不打滑,即其不能沿着驱动轮轴线的方向运动,故机器人沿驱动轮轴线方向的速度为零,满足纯滚动无滑动的非完整约束
| $ \dot x{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - \dot y(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta = 0. $ | (5) |
根据约束条件(5),轮式移动机器人的运动学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x(t) = v{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ,}\\ {\dot y(t) = v{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ,}\\ {\dot \theta (t) = \omega .} \end{array}} \right. $ | (6) |
相似地,对于轮式移动机器人的质心与几何中心不重合的情况,轮式移动机器人的约束条件和运动学模型也可以根据坐标转换关系建立,所不同的是,约束方程和运动学方程都引入了与质心和几何中心之间距离相关的项,该项的引入亦不影响本文预演追踪策略的执行.至此,双轮驱动轮式移动机器人的建模完成.
3 轮式移动机器人的轨迹跟踪控制基于运动学模型,轮式移动机器人的轨迹跟踪问题可叙述为:寻找控制器u使轮式移动机器人的轨迹[x(t) y(t) θ]T跟踪预先给定的参考轨迹[xr(t) yr(t) θr]T.
为方便理解,将参考轨迹看成一个虚拟的轮式移动机器人的轨迹.令vr与θr分别为虚拟轮式移动机器人的线速度和方位角,则其运动学模型为:
| $ \begin{array}{l} {{\dot x}_{\rm{r}}}(t) = {v_{\rm{r}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{\rm{r}}},\\ \begin{array}{*{20}{c}} {{\kern 1pt} {y_{\rm{r}}}(t) = {v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _r},}\\ {{{\dot \theta }_{\rm{r}}}(t) = {\omega _{\rm{r}}}.} \end{array} \end{array} $ |
假设 1 虚拟轮式移动机器人的线速度vr和角速度ωr不同时为零,即被跟踪的虚拟轮式移动机器人始终处于移动或转动状态.
下面首先根据运动学模型提供能够保证轮式移动机器人跟踪参考轨迹的虚拟控制器.其次,以虚拟控制器为桥梁,将参考轨迹转化成可利用的预演信息,建立预演信息的离散线性模型,方便预演控制器的设计与执行.
3.1 轮式移动机器人的虚拟控制器根据运动学模型(6), 轮式移动机器人的轨迹跟踪误差模型为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot e}_x}}\\ {{{\dot e}_y}}\\ {{{\dot e}_\theta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&0\\ { - \rm{sin} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{r}}} - x}\\ {{y_{\rm{r}}} - y}\\ {{\theta _{\rm{r}}} - \theta } \end{array}} \right], $ |
进一步的推导表明,轨迹跟踪误差满足如下方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_x} = \omega {e_y} - v + {v_{\rm{r}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {e_\theta },}\\ {{{\dot e}_y} = - \omega {e_x} + {v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta },}\\ {{{\dot e}_\theta } = {\omega _{\rm{r}}} - \omega .} \end{array}} \right. $ | (7) |
为寻找虚拟控制器,轮式移动机器人的轨迹跟踪问题此时可重述为:对于较小的初始轨迹误差,寻找有界的虚拟控制器[v ω]T, 使得
| $ {{\rm{li}}{{\rm{m}}_{t \to \infty }}({e_x},{e_y},{e_\theta }) = (0,0,0),} $ | (8) |
| $ {{\rm{li}}{{\rm{m}}_{t \to \infty }}(v,\omega ) = ({v_{\rm{r}}},{\omega _{\rm{r}}}),} $ | (9) |
同时成立.
结合轮式移动机器人的误差方程(7), 选择
| $ V(t) = \frac{1}{2}(e_x^2 + e_y^2 + e_\theta ^2), $ |
作为时变系统(7)的一个候选Lyapunov函数.不难推出,
| $ V = - {e_x}(v - {v_{\rm{r}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {e_\theta }) + {e_y}{v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta } + {e_\theta }({\omega _{\rm{r}}} - \omega ), $ |
选择具有可调参数k1与k2的虚拟非线性状态反馈控制律:
| $ \left[ {\begin{array}{*{20}{l}} v\\ \omega \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_{\rm{r}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {e_\theta } + {k_1}{e_x}}\\ {{\omega _{\rm{r}}} + {e_y}{v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta }/{e_\theta } + {k_2}{e_\theta }} \end{array}} \right], $ | (10) |
只要k1与k2>0同时成立,
下面证明在虚拟控制器(10)的调节下,轨迹跟踪误差闭环系统解的渐近稳定性.将虚拟控制器(10)代入轨迹跟踪误差系统(7)可得闭环系统:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_x} = ({\omega _{\rm{r}}} + {e_y}{v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta }/{e_\theta } + {k_2}{e_\theta }){e_y} - {k_1}{e_x},}\\ {{{\dot e}_y} = ({\omega _{\rm{r}}} + {e_y}{v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta }/{e_\theta } + {k_2}{e_\theta }){e_x} + {v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta },}\\ {{{\dot e}_\theta } = - {e_y}{v_{\rm{r}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {e_\theta }/{e_\theta } - {k_2}{e_\theta },} \end{array}} \right. $ | (11) |
考虑系统(11)相关的不变集合
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S = \{ ({e_x},{e_y},{e_\theta })|\dot V(t) = 0\} = \{ ({e_x},{e_y},{e_\theta })|{e_x} = \\ 0,{e_\theta } = 0\} , \end{array} $ |
当ex=0, eθ=0时,根据式(11)可推得:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_y} = 0,}\\ {{e_y}{\omega _{\rm{r}}} = 0,}\\ {{e_y}{v_{\rm{r}}} = 0.} \end{array}} \right. $ | (12) |
联合假设1与式(12)可得,ey=0.这意味着不变集合S中仅包含零点.根据文献[23],闭环跟踪误差系统(11)在零点渐近稳定,故式(8)成立.再结合式(10),可推得式(9)亦成立.
注 1 若考虑虚拟机器人的线速度和角速度同时为零的情况,可参考文献[11],引入如下的变量
| $ {e_\rho } = {e_\theta } + {\rm{arcsin}}(\frac{{k(t){e_y}}}{{\sqrt {1 + e_x^2 + e_y^2} }}), $ |
以克服轮式移动机器人的欠驱动特性[24]带来的控制器设计困难,其中,k(t)=λ1vr, λ1为大于零的常数,满足λ1|vr|max≤1,|vr|max为|vr|的极大值.本文重点强调使用预演信息设计控制器使机器人快速跟踪给定轨迹,因而未对这类情况进行深入讨论.
3.2 虚拟控制器的离散线性模型由于轮式移动机器人的参考轨迹即虚拟机器人的轨迹可能是各种不同类型的曲线,结合式(10)则意味着:机器人的虚拟控制器可能是不同类型的曲线.因此,在设计预演控制器之前,本文先为虚拟控制器建立统一的状态空间模型.
令yd(k)是虚拟控制器(10)在k时刻的采样值,则虚拟控制器可建模成
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{\rm{d}}}(k + 1) = {\mathit{\boldsymbol{A}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}}(k) + {\mathit{\boldsymbol{B}}_{\rm{d}}}{\mathit{\boldsymbol{w}}_{\rm{d}}}(k),}\\ {{\mathit{\boldsymbol{y}}_{\rm{d}}}(k) = {\mathit{\boldsymbol{C}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}}(k).} \end{array} $ | (13) |
其中,wd(k)可理解为虚拟控制系统的外部输入,wd(k)=yd(k+Np); Np是给定的正整数,能够表示对将来虚拟控制信息的使用量,即使用了多少将来的虚拟控制信息,称为预演窗口宽度或预演长度; 系数矩阵
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0& \cdots &0\\ 0&0&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0& \cdots & \cdots & \cdots &1\\ 0& \cdots & \cdots & \cdots &0 \end{array}} \right],{\mathit{\boldsymbol{B}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ \vdots \\ 1 \end{array}} \right],\\ {\mathit{\boldsymbol{C}}_{\rm{d}}} = {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ \vdots \\ 1 \end{array}} \right]^{\rm{T}}},{\mathit{\boldsymbol{x}}_{\rm{d}}}(k) = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_{\rm{d}}}(k)}\\ {{\mathit{\boldsymbol{y}}_{\rm{d}}}(k + 1)}\\ {{\mathit{\boldsymbol{y}}_{\rm{d}}}(k + 2)}\\ \vdots \\ {{\mathit{\boldsymbol{y}}_{\rm{d}}}(k + {N_{\rm{p}}} - 1)} \end{array}} \right]^{\rm{T}}}. \end{array} $ |
观察该模型的状态xd(k),不难发现,其中不仅包含当前时刻虚拟控制器的信息yd(k),也包含将来时刻的虚拟控制器信息yd(k+1), yd(k+2), …, yd(k+Np-1).这对虚拟控制器可提前离线计算的移动舞台机器人是可行的.该模型的建立,为利用将来的虚拟控制器信息设计预演控制器铺平了道路.
注 2 Np越大,意味着可利用越多将来的虚拟控制器信息设计控制器.尽管如此,也应意识到:Np并非越大越好.这是因为:一方面,离当前时刻越久远的将来虚拟控制信息,设计控制器时它的增益实际上越小,因而对跟踪控制效果的贡献也相对越小;另一方面,轮式移动机器人处理器的处理能力也将制约预演控制器的跟踪性能.利用的将来虚拟控制信息越多,意味着虚拟控制器的模型(13)维度越高,这将给后续控制增益的求解带来越高的运算代价.
注 3 由于虚拟控制器可能是任意曲线,因此,本文为虚拟控制器建立离散线性模型的方法可以推广建立任意已知信号的离散线性模型.
3.3 最优预演控制器的设计至此,轮式移动机器人轨迹跟踪的控制问题实际上转化成了虚拟速度的跟踪问题.为了使跟踪误差尽可能小,本文设计了一个最优预演控制器,以最小化下面的代价函数
| $ J = \frac{1}{2}\mathop \sum \limits_{k = 0}^\infty [{\mathit{\boldsymbol{e}}^{\rm{T}}}(k)\mathit{\boldsymbol{Qe}}(k) + {\mathit{\boldsymbol{u}}^{\rm{T}}}(k)\mathit{\boldsymbol{Ru}}(k)]. $ | (14) |
在代价函数(14)中,
| $ \mathit{\boldsymbol{e}}(k) = \mathit{\boldsymbol{\bar y}}(k) - {\mathit{\boldsymbol{y}}_{\rm{d}}}(k). $ | (15) |
回顾前文可知:yd(k)是根据给定的参考轨迹生成的虚拟速度向量,y(k)是轮式移动机器人的实际速度输出向量.从(15)可知,e (k)是轮式移动机器人的速度跟踪误差. Q, R分别是速度跟踪误差和控制输入的加权矩阵.为了保证问题有唯一解,本文选择Q半正定矩阵,R正定矩阵.
基于虚拟控制器的状态空间模型,前述利用预演信息设计控制器的轮式移动机器人最优追踪问题将被重述成一个线性二次调节问题.该问题受到如下线性状态空间方程的约束
| $ {\mathit{\boldsymbol{x}}_{\rm{a}}}(k + 1) = {\mathit{\boldsymbol{A}}_{\rm{a}}}{\mathit{\boldsymbol{x}}_{\rm{a}}}(k) + {\mathit{\boldsymbol{B}}_{\rm{a}}}\mathit{\boldsymbol{u}}(k) + {\mathit{\boldsymbol{B}}_{{\rm{da}}}}{\mathit{\boldsymbol{w}}_{\rm{d}}}(k), $ | (16) |
其中:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_{\rm{a}}}(k) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar x}}(k)}\\ {{\mathit{\boldsymbol{x}}_{\rm{d}}}(k)} \end{array}} \right],{\mathit{\boldsymbol{A}}_{\rm{a}}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&{{\mathit{\boldsymbol{A}}_{\rm{d}}}} \end{array}} \right],}\\ {{\mathit{\boldsymbol{B}}_{\rm{a}}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{B}}\\ 0 \end{array}} \right],{\mathit{\boldsymbol{B}}_{{\rm{da}}}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{B}}_{\rm{d}}}} \end{array}} \right].} \end{array} $ |
根据式(4)、(15)以及(16),跟踪误差亦可以表示成
| $ \mathit{\boldsymbol{e}}(k) = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{C}}&{ - {\mathit{\boldsymbol{C}}_{\rm{d}}}} \end{array}} \right]{\mathit{\boldsymbol{x}}_{\rm{d}}}(k) = {\mathit{\boldsymbol{C}}_{\rm{a}}}{\mathit{\boldsymbol{x}}_{\rm{a}}}(k), $ |
因此,跟踪性能(13)也可以重新表述成
| $ J = \frac{1}{2}\mathop \sum \limits_{k = 0}^\infty [\mathit{\boldsymbol{x}}_{\rm{a}}^{\rm{T}}(k){\mathit{\boldsymbol{Q}}_{\rm{a}}}{\mathit{\boldsymbol{x}}_{\rm{a}}}(k) + {\mathit{\boldsymbol{u}}^{\rm{T}}}(k)\mathit{\boldsymbol{Ru}}(k)], $ | (17) |
其中,Qa= CaTQCa.
至此,预演跟踪控制问题转化成了一个针对系统(16)的二次调节问题.与一般的线性二次调节问题不同,观察(16)不难发现:该问题受到的系统约束具有已知输入wd(k).下面我们给出该问题的解.
定理 1 考虑系统(16),能够使代价函数(17)最小的最优预演控制器如下:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}}(k) = - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{x}}_{\rm{a}}}(k) - \mathit{\boldsymbol{Nr}}(k) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - [{\mathit{\boldsymbol{K}}_1}\quad {\mathit{\boldsymbol{K}}_2}]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}(k)}\\ {{\mathit{\boldsymbol{x}}_{\rm{d}}}(k)} \end{array}} \right] - \mathit{\boldsymbol{Nr}}(k),} \end{array} $ | (18) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{K}} = {{(\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{B}}_{\rm{a}}} + \mathit{\boldsymbol{R}})}^{ - 1}}\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{A}}_{\rm{a}}},}\\ {\mathit{\boldsymbol{N}} = {{(\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{B}}_{\rm{a}}} + \mathit{\boldsymbol{R}})}^{ - 1}}\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}},}\\ {\mathit{\boldsymbol{r}}(k) = - (\mathit{\boldsymbol{A}}_{\rm{a}}^{\rm{T}} - \mathit{\boldsymbol{K}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}})\mathit{\boldsymbol{r}}(k + 1) - \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{B}}_{{\rm{da}}}}{\mathit{\boldsymbol{w}}_{\rm{d}}}(k).} \end{array}} \right. $ | (19) |
S满足如下的代数Riccati方程,
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{A}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{A}}_{\rm{a}}} + {\mathit{\boldsymbol{Q}}_{\rm{a}}} - \mathit{\boldsymbol{A}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{B}}_{\rm{a}}}{(\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{B}}_{\rm{a}}} + \mathit{\boldsymbol{R}})^{ - 1}}\mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{A}}_{\rm{a}}}. $ |
证明 与无已知输入的标准线性二次调节问题的最优解的推导类似,上述结果可根据极大值原理和繁复的代数运算推出.不同之处在于:这种情况下,由极大值原理产生的最优状态及伴随状态之间呈仿射关系而非线性关系.因此,详细的证明此处不再赘述.
观察(18)可以发现:最优的控制器不仅跟xa(k)有关,还跟r(k)有关.根据(19),r(k)包含了未来所有已知输入,即它包含了所有的wd(s), s≥k,等价于r(k)包含了所有的yd(s), s≥k+Np.
一方面,由于矩阵AaT-KaTBaT的所有特征根都在单位圆盘内,由此可知,与当前时刻相隔越久远的将来已知输入,对当前的r(k)贡献越小以致可以忽略不计.
另一方面,由于轮式移动机器人的处理器能力有限,使用太多的将来虚拟控制可能使跟踪效果得不偿失.为此,可以在最优跟踪性能和处理速度之间进行一个权衡,将控制器(18)修改为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}}(k) = - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{x}}_{\rm{a}}}(k) = }\\ { - \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{K}}_1}}&{{\mathit{\boldsymbol{K}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}(k)}\\ {{\mathit{\boldsymbol{x}}_{\rm{d}}}(k)} \end{array}} \right].} \end{array} $ | (20) |
结合(16)来观察(20), 不难发现,xa(k)中不仅包含当前时刻的虚拟控制信息,也包含了k+1, k+2, …, k+Np-1时刻的虚拟控制信息.
注 4 控制器(18)与(20)不是直接、显式地利用将来的参考轨迹,而是以虚拟控制器为桥梁,通过使用将来的虚拟控制信息,把将来的参考轨迹充分利用起来.
4 数值仿真为了验证本文所提预演控制算法的有效性, 本文对两轮驱动轮式移动机器人进行了轨迹跟踪仿真研究,观察了最优预演控制策略驱动下的轮式移动机器人的实际跟踪效果.
仿真实验中,轮式移动机器人的主要物理参数取值为:M=50 kg, r=0.125 m, c=0.05 kg · m2/s, Iv=10 kg · m2, Iω=0.05 kg · m2, L=0.5 m.先后以直线、圆、类正弦三类典型曲线为参考轨迹,验证了本文所提跟踪策略的有效性.为了节省空间,下文仅展示对类正弦曲线的跟踪效果图.
设轮式移动机器人的初始位姿误差为(-0.3, 0.4, -π/10),待跟踪轨迹由参考速度vr=1 m/s, ωr=2cos(πt/2)rad/s及θr=4sin(πt/2)/πrad生成.
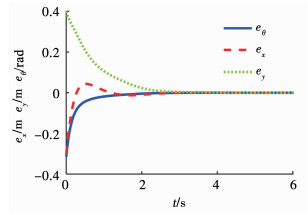
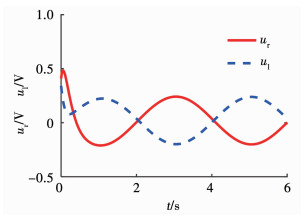
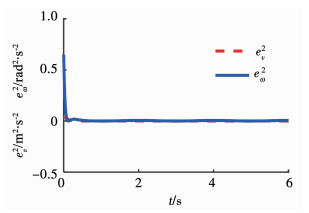
1) 如图 2所示,在虚拟控制器(10)的作用下,轮式移动机器人的轨迹跟踪误差在3 s左右收敛到了零.在实际控制器(18)(如图 3所示)的调节下,图 4中机器人的线速度和角速度仅需大约1 s就快速地跟踪了虚拟控制器(10),这保证了实际控制器(18)驱动下的轮式移动机器人也能在3 s内跟踪到参考轨迹(如图 5).对比图 2与图 5可知:研究虚拟控制器与研究实际控制器有本质区别;同时也表明本文所提出的最优预演跟踪策略基本能够保证实际控制器与虚拟控制器有相同的追踪效果.
|
图 2 虚拟控制器产生的轨迹跟踪误差 Fig. 2 Trajectory tracking errors generated by virtual controller |
|
图 3 实际控制器 Fig. 3 Actual controller |
|
图 4 线速度与角速度的跟踪误差 Fig. 4 Linear and angular velocity tracking errors |

|
图 5 实际控制器驱动下的轨迹跟踪误差 Fig. 5 Trajectory tracking errors generated by actual controller |
2) 考虑到线性时不变的机器人动力学模型过于理想,讨论当机器人的系统参数随机变化时,本文所提跟踪策略的调节效果.因为轮胎与地面的摩擦系数c、电机与传动机构的驱动增益k往往会随工作环境及工况的变化而变化,本文通过数值实验展示这两个参数的随机变化对机器人跟踪误差的影响.
以下考虑参数c和k受到强弱两种干扰后,本文所提出的控制策略的跟踪效果.假设参数c和k均受到方差为σ的乘性随机噪声w的干扰,即干扰后的摩擦系数和增益分别为(1+w)c和(1+w)k.
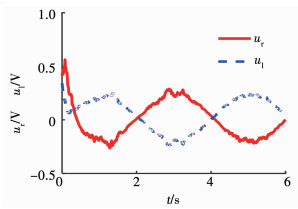
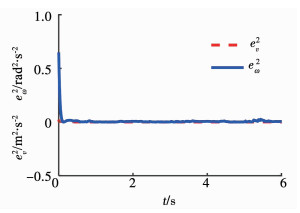
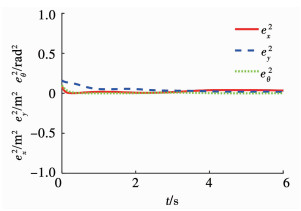
2.1)当σ=0.5时,实际控制器(18)如图 6所示,在该控制器作用下,机器人的线速度和角速度的跟踪误差如图 7所示,机器人的实际轨迹跟踪误差如图 8所示.
|
图 6 实际控制器 Fig. 6 Actual controller |
|
图 7 线速度与角速度跟踪误差 Fig. 7 Linear and angular velocity tracking errors |
|
图 8 实际控制器驱动下的轨迹跟踪误差 Fig. 8 Trajectory tracking errors generated by actual controller |
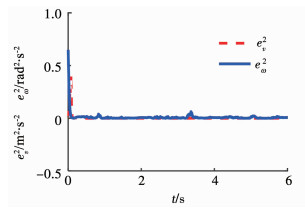
2.2)当σ=1时,实际控制器(18)如图 9所示,在该控制器的作用下,机器人的线速度和角速度跟踪误差如图 10所示,机器人的实际轨迹跟踪误差如图 11所示.

|
图 9 实际控制器 Fig. 9 Actual controller |
|
图 10 线速度与角速度的跟踪误差 Fig. 10 Linear and angular velocity tracking errors |
|
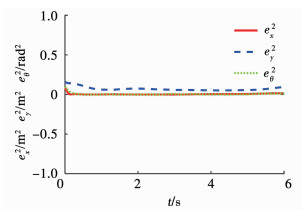
图 11 实际控制器驱动下的轨迹跟踪误差 Fig. 11 Trajectory tracking errors generated by actual controller |
将情况1)与情况2.1)、情况2.2)的实验结果比较可知,当动力学系统参数受到的随机干扰较小(即随机干扰的方差σ=0.5)时,无论跟踪时间还是跟踪误差,都与参数无扰动时基本一致.随着随机干扰的增强(即随机干扰的方差σ=1),速度与轨迹跟踪误差都明显增大,由图 11可见,实际跟踪轨迹有更明显的纵向偏差.这说明该控制策略具有对参数c和k的小扰动不敏感的优点.
5 结论1) 围绕如何充分利用已知的将来参考轨迹设计控制器使轮式移动机器人有效跟踪参考轨迹的问题, 本文提出了最优预演控制跟踪策略,该策略将包含当前及将来参考轨迹及参考速度的信息于当前时刻用于机器人轨迹跟踪,为机器人提供了足够的处理及响应时间,因而能够保证机器人快速有效地进行轨迹跟踪;
2) 基于运动学模型提出了一个轮式移动机器人的虚拟控制器,建立了该虚拟控制器的离散线性状态空间模型,为利用将来的参考信息设计跟踪策略做好了准备,该思路可以用于建立任意已知信号的离散线性状态空间模型;
3) 基于虚拟控制器的离散线性模型及离散化的轮式移动机器人动力学模型,将速度跟踪问题等价转化成一个特殊的、具有已知输入项的线性系统最优二次调节问题,利用极大值原理予以解决;
4) 以类正弦曲线为参考轨迹进行数值实验,考虑了机器人参数的随机扰动对本文所提控制器对跟踪效果的影响,验证了本文所提算法的有效性.
| [1] |
KANELLAKOPOULOS I, KOKOTOVIC P V, MORSE A S. Systematic design of adaptive controllers for feedback linearizable systems[J]. IEEE Transactions on Automatic Control, 1991, 36(11): 1241. DOI:10.1109/9.100933 |
| [2] |
LEVANT A. Principles of 2-sliding mode design[J]. Automatica, 2007, 43(4): 576. DOI:10.1016/j.automatica.2006.10.008 |
| [3] |
GU Dongbing, HU Huosheng. Receding horizon tracking control of wheeled mobile robots[J]. IEEE Transactions on Control Systems Technology, 2006, 14(4): 743. DOI:10.1109/TCST.2006.872512 |
| [4] |
何德峰, 郭晓慧, 姬超超, 等. 基于CLF的移动舞台机器人轨迹跟踪预测控制[J]. 浙江工业大学学报, 2018, 46(5): 487. HE Defeng, GUO Xiaohui, JI Chaochao, et al. Trajectory tracking and predict control of mobile stage robot based on CLF[J]. Journal of Zhejiang University of Technology, 2018, 46(5): 487. |
| [5] |
SUN Weichao, TANG Songyuan, GAO Huijun, et al. Two time-scale tracking control of nonholonomic wheeled mobile robots[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6): 2059. DOI:10.1109/TCST.2016.2519282 |
| [6] |
MATRAJ I, AL-DURRA A, HARYONO A, et al. Trajectory tracking control of skid-steered mobile robot based on adaptive second order sliding mode control[J]. Control Engineering Practice, 2018, 72: 167. DOI:10.1016/j.conengprac.2017.11.009 |
| [7] |
LI Zhijun, DENG Jun, LU Renquan, et al. Trajectory-tracking control of mobile robot systems incorporating neural-dynamic optimized model predictive approach[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 46(6): 740. DOI:10.1109/TSMC.2015.2465352 |
| [8] |
LI Zhijun, YANG Chenguang, SU Chunyi, et al. Vision-based model predictive control for steering of a nonholonomic mobile robot[J]. IEEE Transactions on Control Systems Technology, 2016, 24(2): 553. DOI:10.1109/TCST.2015.2454484 |
| [9] |
XIN Linjie, WANG Qinglin, SHE Jinhua, et al. Robust adaptive tracking control of wheeled mobile robots[J]. Robotics and Autonomous Systems, 2016, 78: 36. DOI:10.1016/j.robot.2016.01.002 |
| [10] |
YANG Hongjiu, FAN Xiaozhao, SHI Peng, et al. Nonlinear control for tracking and obstacle avoidance of a wheeled mobile robot with nonholonomic constraint[J]. IEEE Transactions on Control Systems Technology, 2015, 24(2): 741. DOI:10.1109/TCST.2015.2457877 |
| [11] |
HUANG Jiangshuai, WEN Changyun, WANG Wei, et al. Adaptive output feedback tracking control of a nonholonomic mobile robot[J]. Automatica, 2014, 50(3): 821. DOI:10.1016/j.automatica.2013.12.036 |
| [12] |
ANTONELLI G, CHIAVERINI S, FUSCO G. A fuzzy-logic-based approach for mobile robot path tracking[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(2): 211. DOI:10.1109/TFUZZ.2006.879998 |
| [13] |
HOU Zengguang, ZOU Anmin, CHENG Long, et al. Adaptive control of an electrically driven nonholonomic mobile robot via backstepping and fuzzy approach[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 803. DOI:10.1109/TCST.2009.2012516 |
| [14] |
ZHANG Kaixiang, CHEN Jian, LI Yang, et al. Visual tracking and depth estimation of mobile robots without desired velocity information[J]. IEEE Transactions on Cybernetics, 2020, 50(1): 361. DOI:10.1109/TCYB.2018.2869623 |
| [15] |
CHEN Jian, JIA Bingxi, ZHANG Kaixiang. Trifocal tensor-based adaptive visual trajectory tracking control of mobile robots[J]. IEEE Transactions on Cybernetics, 2017, 47(11): 3784. DOI:10.1109/TCYB.2016.2582210 |
| [16] |
PENG Haijun, LI Fei, LIU Jinguo, et al. A symplectic instantaneous optimal control for robot trajectory tracking with differential-algebraic equation models[J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 3819. DOI:10.1109/TIE.2019.2916390 |
| [17] |
WU Jiang, LIAO Fucheng, TOMIZUKA M. Optimal preview control for a linear continuous-time stochastic control system in finite-time horizon[J]. International Journal of Systems Science, 2017, 48(1): 129. DOI:10.1080/00207721.2016.1160456 |
| [18] |
TOMIZUKA M. Optimal continuous finite preview problem[J]. IEEE Transactions on Automatic Control, 1975, 20(3): 362. DOI:10.1109/TAC.1975.1100962 |
| [19] |
KOJIMA A, ISHIJIMA S. Formulas on preview and delayed H∞ control[J]. IEEE Transactions on Automatic Control, 2006, 51(12): 1920. DOI:10.1109/TAC.2006.886485 |
| [20] |
TADMOR G, MIRKIN L. H∞ control and estimation with preview-part I: Matrix ARE solutions in continuous time[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 19. DOI:10.1109/TAC.2004.840460 |
| [21] |
TADMOR G, MIRKIN L. H∞ control and estimation with preview-part Ⅱ: Fixed-size ARE solutions in discrete time[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 29. DOI:10.1109/TAC.2004.840465 |
| [22] |
王宏霞. H∞预演控制问题研究[D].哈尔滨: 哈尔滨工业大学, 2009 WANG Hongxia. H∞ preview control problem[D]. Harbin: Harbin Institute of Technology, 2009 |
| [23] |
HASSAN K K. Nonlinear systems[M]. 3rd ed. New Jersey: Prentice Hall, 2002: 129.
|
| [24] |
BROCKETT R W. Asymptotic stability and feedback stabilization[J]. Differential Geometric Control Theory, 1983, 27: 181. |
 2020, Vol. 52
2020, Vol. 52


