2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
小孔扩张问题在土体原位测试、压桩实践、压密注浆等方面得到了广泛应用,国内外学者进行了大量的研究[1-13].另一方面小孔收缩问题在大量的工程实践中存在,比如石油钻井、桩基钻孔、隧道开挖掘进等,由于土体卸荷引起的钻孔失稳、桩孔缩径、隧道沉降等严重影响了工程安全.已有文献就球形孔或者柱形孔的小孔收缩问题进行研究[14-27].Houlsby等[14-15]对砂土中的旁压仪采用小孔扩张和收缩理论进行了分析;Yu等[16-17]通过小孔收缩理论得到小孔在正常固结土或剪胀性土中的卸荷收缩解,采用的屈服准则为完全弹塑性的Tresca准则、Mohr-Coulomb屈服准则以及修正剑桥模型,并未就中间主应力的具体影响给出详细的解析解;Chen等[18-20]采用小孔收缩理论结合临界状态的修正剑桥模型、边界面模型等系统研究了排水和不排水条件下的井壁稳定性问题, 并给出了严格的解析解;Mo等[21]在小孔收缩中运用余海岁提出的统一临界状态模型CASM[32]分析了隧道周边土体的行为;Vrakas等[22-23]在研究隧道沉降问题时给出了考虑3个主应力的严格解析解,详细阐述了孔壁压力与孔壁位移的解析解,但参数较多且采用大量的数值计算.杨砚宗[24]采用Mohr-Coulomb准则获取了考虑应变软化和剪胀性的不同卸荷压力下孔壁收缩解析解,但仍未就中间主应力对卸荷压力和缩孔的影响进行阐述.统一强度理论体系下的屈服准则能考虑中间主应力影响[12-13, 27-28, 31],可用于研究考虑3个主应力状态的小孔收缩问题.范文等[25]基于统一强度理论考虑材料软化和剪胀的特性分析了有压隧洞的围岩压力、围岩应力、围岩位移及围岩所处状态的判别;龚辉等[26]运用统一强度理论得到了桩孔临界失稳压力的解析解.
但对不同程度中主应力(主要表现为中主剪应力及相应面上的主应力)如何具体影响卸荷缩孔关系并未有阐述,而且对于全应力空间条件和某指定卸荷程度下缩孔半径的变化,没有相应的近似解可供预测采用,因此,着重利用统一强度屈服准则引入卸荷因子和缩孔系数的概念,得到可描述不同中主应力影响的的卸荷缩孔关系近似解析式,并就统一强度理论参数、土体参数对卸荷和缩孔关系的影响因素进行分析,得到的解析公式能对柱孔开挖卸荷过程中一定卸荷程度下的缩孔和塑性变形进行量化预测,用于指导隧道支护和开挖、桩基开挖卸荷后的承载特性以及钻井稳定性分析的具体实践.
1 问题的提出及力学模型、屈服准则的建立 1.1 问题的提出及力学模型的建立隧道开挖、油井和桩基钻孔的开挖卸荷过程可以简化为柱形孔收缩的平面应变问题[17, 29].如图 1所示,设原位初始应力p0,初始半径为a0.假定p从p0逐步降低,孔壁发生卸荷,缩孔半径变为a,当卸荷至土体屈服强度py时,孔壁处开始产生弹性-塑性边界面.随着p进一步减小,塑性区逐步扩大,在孔周边形成a≤r≤R的塑性区.
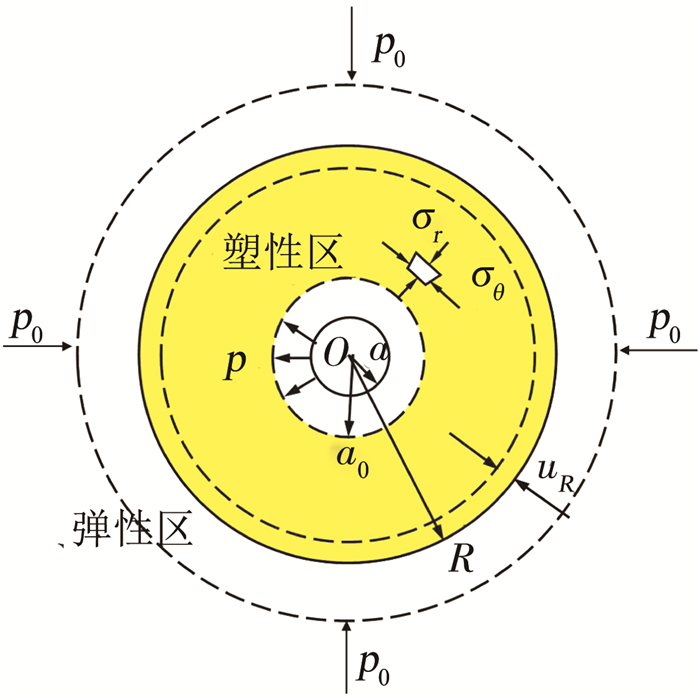
|
图 1 土体开挖卸荷的圆孔收缩示意 Fig. 1 Schematic diagram of cavity contraction under soil excavation unloading |
柱形孔收缩的平面应变解析解的推导,需要满足以下假定:
1) 土体初始应力场是均匀的、各向同性的;
2) 孔壁压力逐步卸荷过程中,远场应力一直保持为初始应力;
3) 土体假定为理想弹塑性体,并满足统一强度理论屈服准则;
4) 在整个卸荷缩孔过程中,出平面方向始终保持为中主应力方向;
5) 弹性区的应变很小且塑性区的弹性应变可以忽略.
定义卸荷因子为λrel,缩孔系数为λcon,其表达式分别为
| $ {{\lambda }_{\text{rel}}}=\frac{p}{{{p}_{0}}}, $ | (1) |
| $ {{\lambda }_{\text{con}}}=\frac{a}{{{a}_{0}}}. $ | (2) |
为研究方便,受力分析符号以应力、应变受压为正,受拉为负.孔周边土体的平衡微分方程、弹性阶段的物理方程和几何方程分别满足:
| $ \frac{\partial {{\sigma }_{r}}}{\partial r}+\frac{{{\sigma }_{r}}-{{\sigma }_{\theta }}}{r}=0, $ | (3) |
| $ {{\varepsilon }_{r}}=\frac{1-{{\nu }^{2}}}{E}\left( {{\sigma }_{r}}-\frac{\nu }{1-\nu }{{\sigma }_{\theta }} \right), $ | (4a) |
| $ {{\varepsilon }_{\theta }}=\frac{1-{{\nu }^{2}}}{E}\left( {{\sigma }_{\theta }}-\frac{\nu }{1-\nu }{{\sigma }_{r}} \right), $ | (4b) |
| $ {{\varepsilon }_{r}}=-\frac{\text{d}{{u}_{r}}}{\text{d}r},{{\varepsilon }_{\theta }}=-\frac{{{u}_{r}}}{r}. $ | (5) |
式中:σr为径向正应力, σθ为环向正应力, ur为半径为r点处的径向位移, ν为泊松比, E为杨氏模量.
应力边界条件满足:
| $ {{\sigma }_{r(r=a)}}=p, $ | (6a) |
| $ {{\sigma }_{r(r=\infty )}}={{p}_{0}}. $ | (6b) |
统一强度理论下的屈服函数[31]需满足:
| $ \begin{matrix} F={{\sigma }_{1}}-\frac{\alpha }{1+b}(b{{\sigma }_{2}}+{{\sigma }_{3}})={{\sigma }_{\text{t}}}, \\ {{\sigma }_{2}}\le \frac{{{\sigma }_{1}}+\alpha {{\sigma }_{3}}}{1+\alpha }, \\ \end{matrix} $ | (7a) |
| $ \begin{matrix} {{F}^{\prime }}=\frac{1}{1+b}({{\sigma }_{1}}+b{{\sigma }_{2}})-\alpha {{\sigma }_{3}}={{\sigma }_{\text{t}}}, \\ {{\sigma }_{2}}\ge \frac{{{\sigma }_{1}}+\alpha {{\sigma }_{3}}}{1+\alpha }. \\ \end{matrix} $ | (7b) |
其中
统一强度理论参数b为反映中间主剪应力以及相应面上的主应力对材料破坏程度影响的系数,称为中间主应力影响系数;σ1, σ2, σ3分别为最大主应力、中主应力以及最小主应力;φ0为土体摩擦角,c0为黏聚力,两参数可由三轴试验得到.
与前述研究问题受力符号定义原则相同,将式(7)改写为
| $ \begin{matrix} {{F}^{\prime }}=\alpha {{\sigma }_{1}}-\frac{1}{1+b}(b{{\sigma }_{2}}+{{\sigma }_{3}})={{\sigma }_{\text{t}}}, \\ {{\sigma }_{2}}\le \frac{{{\sigma }_{3}}+\alpha {{\sigma }_{1}}}{1+\alpha }, \\ \end{matrix} $ | (8a) |
| $ \begin{matrix} F=\frac{\alpha }{1+b}({{\sigma }_{1}}+b{{\sigma }_{2}})-{{\sigma }_{3}}={{\sigma }_{\text{t}}}, \\ {{\sigma }_{2}}\ge \frac{{{\sigma }_{3}}+\alpha {{\sigma }_{1}}}{1+\alpha }, \\ \end{matrix} $ | (8b) |
且满足
| $ {{\sigma }_{2}}=\frac{m}{2}({{\sigma }_{1}}+{{\sigma }_{3}}). $ | (9) |
其中m为统一强度理论下表征中间主应力影响程度的参数, 平面应变问题中,在弹性状态下m=2ν < 1, 在塑性状态下m接近1[31],因此,在塑性状态下:
| $ \begin{array}{*{35}{l}} {{\sigma }_{2}}=\frac{m}{2}({{\sigma }_{1}}+{{\sigma }_{3}})\approx \frac{1}{2}({{\sigma }_{1}}+{{\sigma }_{3}})\ge \\ \frac{1}{2}({{\sigma }_{1}}+{{\sigma }_{3}})+\frac{\text{sin}{{\varphi }_{0}}}{2}({{\sigma }_{3}}-{{\sigma }_{1}}). \\ \end{array} $ | (10) |
将式(7)的α代入式(8b)条件中发现
| $ \frac{{{\sigma _3} + \alpha {\sigma _1}}}{{1 + \alpha }} = \frac{1}{2}({\sigma _1} + {\sigma _3}) + \frac{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0}}}{2}({\sigma _3} - {\sigma _1}) \le {\sigma _2}. $ | (11) |
式(8b)即为满足问题的屈服函数.将式(7)的α, σt代入式(8b)中,整理得
| $ \begin{array}{*{20}{l}} {F = {\sigma _1} - \frac{{2(1 + b)(1 + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0}) - bm(1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0})}}{{(2 + bm)(1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0})}}{\sigma _3} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{4(1 + b)c{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0}}}{{(2 + bm)(1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0})}} = 0.} \end{array} $ | (12) |
小孔卸荷收缩塑性状态下,一般地,最大主应力为σθ, 最小主应力为σr[17], 均采用总应力形式,在平面应变塑性状态下,将(12)整理为
| $ F = {\sigma _\theta } - \zeta {\sigma _r} - {\sigma _0} = 0. $ | (13) |
其中
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\zeta = \frac{{1 + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{t}}}}}{{1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{t}}}}},}\\ {{\sigma _0} = \frac{{2{c_{\rm{t}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{t}}}}}{{1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{t}}}}},} \end{array}\\ {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{t}}} = \frac{{2(1 + b){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0}}}{{2(1 + b) - b(1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0})}},\\ {c_{\rm{t}}} = \frac{{2(1 + b){c_0}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0}}}{{2(1 + b) - b(1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _0})}}\frac{1}{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _t}}}. \end{array} \right. $ | (14) |
当孔周土体处于弹性状态时,联立式(3)~(6)容易求得孔周土体应力与位移的弹性解为
| $ \left\{ \begin{array}{l} {\sigma _r} = {p_0} + (p - {p_0}){\left( {\frac{a}{r}} \right)^2},\\ {\sigma _\theta } = {p_0} - (p - {p_0}){\left( {\frac{a}{r}} \right)^2}. \end{array} \right. $ | (15) |
| $ {u_r} = \frac{{p - {p_0}}}{{2G}}{\left( {\frac{a}{r}} \right)^2}r. $ | (16) |
随着小孔压力p逐步降低,当小孔壁首次达到屈服强度时,孔壁开始屈服,此时初始屈服压力为py.将式(15)代入屈服方程式(13)中,得
| $ {p_{\rm{y}}} = {\sigma _r}{|_{r = a}} = \frac{{2{p_0} - {\sigma _0}}}{{1 + \zeta }}. $ | (17) |
孔壁发生初始屈服后,p进一步降低,将会在小孔壁周边区域产生a≤r≤R的塑性区,在塑性区外是弹性区,弹性区的应力及位移应满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _r} = {p_0} + ({p_{\rm{y}}} - {p_0}){{\left( {\frac{R}{r}} \right)}^2},}\\ {{\sigma _\theta } = {p_0} - ({p_{\rm{y}}} - {p_0}){{\left( {\frac{R}{r}} \right)}^2},} \end{array}} \right.r \ge R, $ | (18) |
| $ {u_r} = \frac{{{p_{\rm{y}}} - {p_0}}}{{2G}}{\left( {\frac{R}{r}} \right)^2}r. $ | (19) |
塑性区应力需满足平衡方程和屈服方程,将式(13)代入式(3), 得
| $ {\frac{{\partial {\sigma _r}}}{{\partial r}} + \frac{{{\sigma _r} - (\zeta {\sigma _r} + {\sigma _0})}}{r} = 0.} $ | (20) |
积分得
| $ {{\sigma _r} = \frac{{{{(Kr)}^{\zeta - 1}} - {\sigma _0}}}{{\zeta - 1}}.} $ | (21) |
K为积分常数,将式(6a)、(17)分别代入式(21), 得
| $ K = \frac{{{{[p(\zeta - 1) + {\sigma _0}]}^{\frac{1}{{\zeta - 1}}}}}}{a} = \frac{{{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}^{\frac{1}{{\zeta - 1}}}}}}{R}. $ | (22) |
将式(21)代入式(20), 并代入屈服方程(12), 得塑性区应力解:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _r} = {{\left( {\frac{r}{R}} \right)}^{\zeta - 1}}\frac{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}},}\\ {{\sigma _\theta } = \frac{\zeta }{{\zeta - 1}}{{\left( {\frac{r}{R}} \right)}^{\zeta - 1}}\frac{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}},} \end{array}\quad a \le r < R,} \right. $ | (23a) |
或
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _r} = {{\left( {\frac{r}{a}} \right)}^{\zeta - 1}} \cdot \frac{{[p(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}},}\\ {{\sigma _\theta } = \frac{\zeta }{{\zeta - 1}}{{\left( {\frac{r}{a}} \right)}^{\zeta - 1}} \cdot \frac{{[p(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}},} \end{array}\quad a \le r < R.} \right. $ | (23b) |
式(18)、(23)即为整个孔周土体的弹塑性应力表达式.
Mair等[33]在预测隧道周围地层运动时给出了轴对称条件下卸载柱形孔周半径为r的塑性区超孔隙水压力公式为
| $ \Delta u = {s_{\rm{u}}}\left( {1 - \frac{{{p_0} - p}}{{{s_{\rm{u}}}}} + 2{\rm{ln}}\frac{r}{a}} \right),a \le r \le R. $ | (24a) |
其中su为不排水抗剪强度.
应注意该公式的局限性,其是预测公式且仅在塑性区有效,从而塑性区的有效应力可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma ^\prime }_r = {{\left( {\frac{r}{R}} \right)}^{\zeta - 1}} \cdot \frac{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}} - \Delta u,}\\ {{\sigma ^\prime }_\theta = \frac{\zeta }{{\zeta - 1}}{{\left( {\frac{r}{R}} \right)}^{\zeta - 1}} \cdot \frac{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}}{{\zeta - 1}} - \frac{{{\sigma _0}}}{{\zeta - 1}} - \Delta u.} \end{array}} \right. $ | (24b) |
将式(22)进行整理,得到孔压与塑性区半径、扩孔半径的关系:
| $ \frac{R}{a} = \frac{{{{[{p_{\rm{y}}}(\zeta - 1) + {\sigma _0}]}^{\frac{1}{{\zeta - 1}}}}}}{{{{[p(\zeta - 1) + {\sigma _0}]}^{\frac{1}{{\zeta - 1}}}}}}. $ | (25) |
将式(17)代入(25), 得
| $ \frac{R}{a} = {[\frac{{{C_1}}}{{p(\zeta - 1) + {\sigma _0}}}]^{\frac{1}{{\zeta - 1}}}}. $ | (26) |
其中
将式(17)代入式(19),并令r=R, 得弹塑性边界的位移为
| $ {u_R} = {u_r}{|_{r = R}} = R - {R_0} = \frac{{(1 - \zeta ){p_0} - {\sigma _0}}}{{2G(1 + \zeta )}}R. $ | (27) |
其中R0为收缩前弹塑性边界.
对不可压缩、不排水的土体或干土,考虑卸荷前后土体体积保持不变,得到卸荷收缩前后的任意点(r0, r)有以下关系:
| $ r_0^2 - {r^2} = R_0^2 - {R^2}. $ | (28) |
在半径为r处,满足
| $ {u_r} = r - {r_0}. $ | (29) |
联立式(27)、(28)、(29), 得
| $ {u_r} = r - \sqrt {{r^2} + u_R^2 - 2{u_R}R} . $ | (30) |
式(30)即为塑性区的弹塑性位移表达式.
联立式(26)、(27)、(28)得
| $ {\left( {\frac{{{r_0}}}{r}} \right)^2} = 1 + {C_2}{[\frac{{{C_1}}}{{p(\zeta - 1) + {\sigma _0}}}]^{\frac{2}{{\zeta - 1}}}}\frac{{{a^2}}}{{{r^2}}}. $ | (31) |
其中
| $ {\left( {\frac{{{a_0}}}{a}} \right)^2} = 1 + {C_2}{[\frac{{{C_1}}}{{p(\zeta - 1) + {\sigma _0}}}]^{\frac{2}{{\zeta - 1}}}}. $ | (32) |
将式(32)改写为以下两种形式:
| $ p = \frac{{{C_3}}}{{{{\left[ {{{\left( {\frac{{{a_0}}}{a}} \right)}^2} - 1} \right]}^{\frac{{\zeta - 1}}{2}}}}} - \frac{{{\sigma _0}}}{{\zeta - 1}}. $ | (33) |
| $ a = \frac{{{a_0}}}{{\sqrt {1 + {{\left( {\frac{{{C_3}}}{{p(\zeta - 1) + {\sigma _0}}}} \right)}^{\frac{2}{{\zeta - 1}}}}} }}. $ | (34) |
此二式即为卸荷压力、初始半径、缩孔半径之间的关系.其中
| $ \begin{array}{*{20}{l}} {{C_3} = C_2^{\frac{{\zeta - 1}}{2}}{C_1} = {{\left[ {{{\left( {1 - \frac{{(1 - \zeta ){p_0} - {\sigma _0}}}{{2G(1 + \zeta )}}} \right)}^2} - 1} \right]}^{\frac{{\zeta - 1}}{2}}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\frac{{2{p_0} - {\sigma _0}}}{{\zeta + 1}}(\zeta - 1) + {\sigma _0}} \right].} \end{array} $ | (35) |
引入初始定义的卸荷因子λrel和缩孔系数λcon,并依据Yu等[17]采用的正则化方法,将卸荷缩孔关系进行无量纲表达:
| $ {{\delta _1} = \frac{{{\sigma _0}}}{{{p_0}}},} $ | (36a) |
| $ {{\delta _2} = \frac{G}{{{p_0}}}.} $ | (36b) |
将式(36)代入式(33)、(34)得
| $ {\lambda _{{\rm{rel}}}} = \frac{{{C^\prime }_3}}{{{{\left[ {{{\left( {\frac{1}{{{\lambda _{{\rm{con}}}}}}} \right)}^2} - 1} \right]}^{\frac{{\zeta - 1}}{2}}}}} - \frac{{{\delta _1}}}{{(\zeta - 1)}}, $ | (37a) |
| $ {\lambda _{{\rm{con}}}} = \frac{1}{{\sqrt {1 + {{\left( {\frac{{{C^\prime }_3}}{{{\lambda _{{\rm{rel}}}}(\zeta - 1) + {\delta _1}}}} \right)}^{\frac{2}{{\zeta - 1}}}}} }}. $ | (37b) |
其中
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{C^\prime }_3 = C_2^{\frac{{\zeta - 1}}{2}}{C^\prime }_1 = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left[ {{{\left( {1 - \frac{{1 - \zeta }}{{2(1 + \zeta ){\delta _2}}} + \frac{{{\delta _1}}}{{2(1 + \zeta ){\delta _2}}}} \right)}^2} - 1} \right]}^{\frac{{\zeta - 1}}{2}}} \times } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\frac{{2(\zeta - 1 + {\delta _1})}}{{\zeta + 1}}} \right]. \end{array} $ | (38) |
文献[27-28, 30-31]证实了考虑统一强度理论得到的力学参数受中间主应力影响系数b的影响,且该参数可由试验得到.采用同Yu等[17]相似的正则化方法无量纲化后,对本文提出的考虑中间主应力影响参数b的小孔卸荷收缩解进行了参数化分析,并同Yu的解答进行了对比;考察了土体刚度指标δ2、黏聚力和内摩擦角对于采用统一屈服准则的完全卸荷时的孔周位移、缩孔效应的影响.
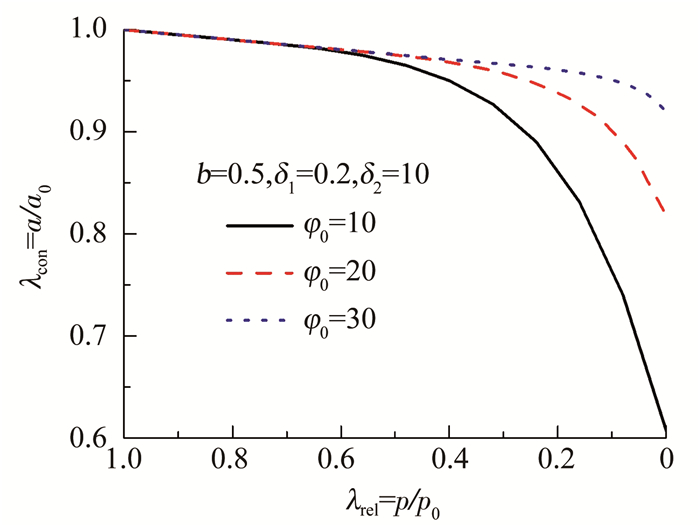
3.1 中间主应力影响参数b对卸荷因子与缩孔系数的影响图 2显示,随着中间主应力影响参数b的增大,缩孔系数逐渐减小,完全卸荷时,b=1时的缩孔系数较不考虑中主应力影响情况增大约5%,表明不考虑中间主应力影响的Mohr-coulomb准则(Yu解[17])得到的卸荷产生的缩孔效应解析解相对保守.
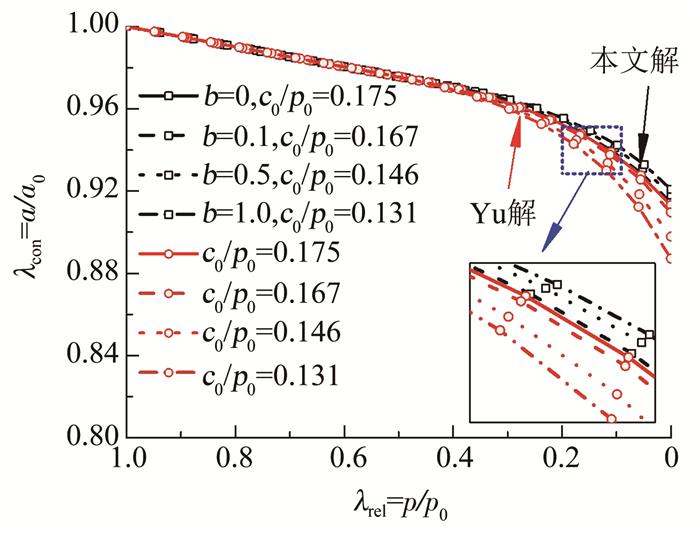
|
图 2 不同b值时的卸荷缩孔曲线 Fig. 2 Unloading-contraction curves with different b |
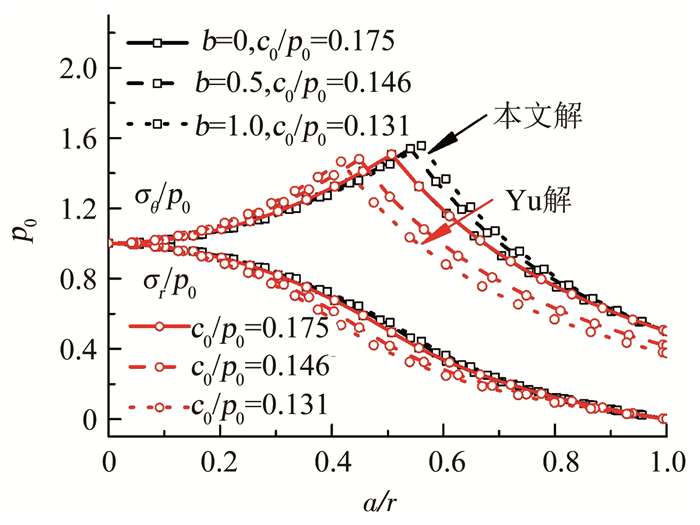
图 3表明,中间主应力会减缓塑性区的出现,且b值越大,塑性区越小,b=1相较b=0时,屈服时的临界卸荷因子由0.49减小为0.43,其本质表现为初始屈服卸荷压力的减小改善了塑性变形.图 4显示,b值越大,孔周位移越小.图 5描述了孔周不同距离处径向应力与环向应力随b值的变化.相较本文解与Yu解在位移上的较大不同,考虑中主应力影响的径向应力与采用Mohr-Coulomb准则的径向应力基本相同,峰值环向应力也基本相同,只是由于采用b值,考虑了不同中主应力的影响,从而推迟了峰值环向应力的出现,使峰值环向应力出现的位置向孔壁靠近.
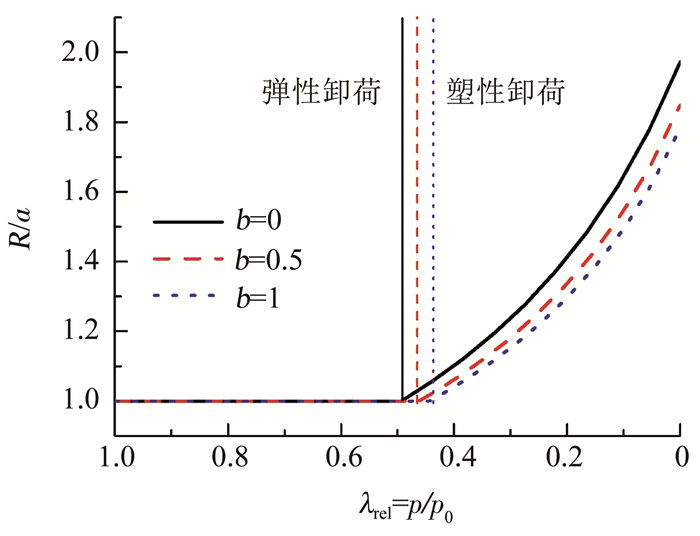
|
图 3 不同b值时塑性半径随卸荷变化 Fig. 3 Unloading-plastic radius curves with different b |
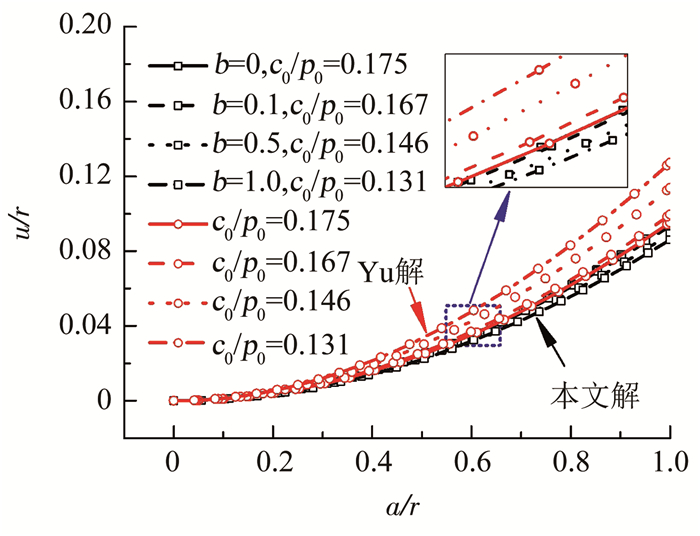
|
图 4 不同b值时的孔周位移场变化 Fig. 4 Displacement field around cavity variation with different b |
|
图 5 不同b值时孔周应力场变化 Fig. 5 Stress field around cavity variation with different b |
Yu解受黏聚力变化影响较大,黏聚力越小时,其塑性区迅速向左移动,表明塑性区迅速增大,而本文解变化较小,可以理解为未考虑中间主应力影响的Yu解更为保守.
3.3 土体刚度指数对缩孔系数的影响Yu等[17]引入了式(36b)的土体刚度指数δ2将土体剪切刚度正则化,研究土体刚度对缩孔的影响.表 1~3列出了孔壁完全卸荷时土体刚度指数与缩孔系数的对应关系.当δ2=10时,土体刚度较小,黏聚力为0.334p0,b由0.1增大为1时,缩孔系数维持在0.946,基本保持不变;而当b=0.1, 黏聚力保持为0.334p0,而δ2由10增大到50时,缩孔系数由0.945增大到0.988.而且,δ2=10,随着黏聚力减小,缩孔系数由0.946减小至0.795,变化幅度为16%;δ2=50时,缩孔系数由0.988减小为0.947,变化幅度仅为4.1%.这表明刚度越大,中间主应力效应越大,缩孔效应越小;刚度较大时,中间主应力效应对缩孔的影响较小,土体刚度对缩孔有至关重要的减弱效应,此时,b的影响较土体刚度的影响很小.
| 表 1 完全卸荷时不同δ2、c0值的缩孔系数 Tab. 1 Contraction coefficients of different δ2 and c0 under complete unloading |
| 表 2 完全卸荷时不同δ2、c0值的缩孔系数 Tab. 2 Contraction coefficients of different δ2 and c0 under complete unloading |
| 表 3 完全卸荷时不同δ2、c0值的缩孔系数 Tab. 3 Contraction coefficients of different δ2 and c0 under complete unloading |
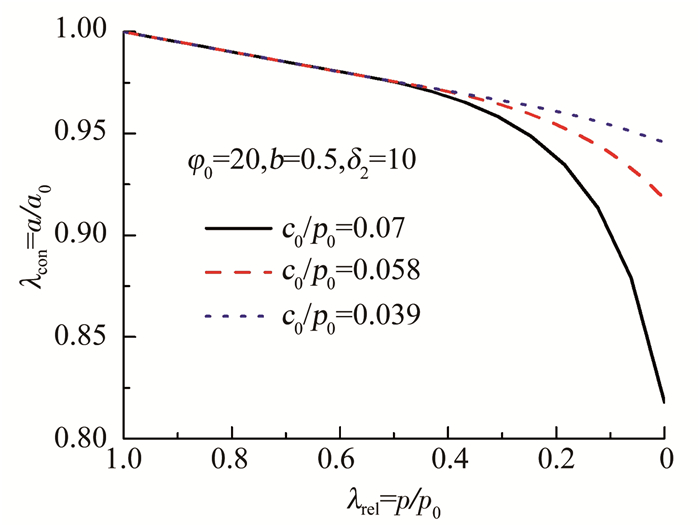
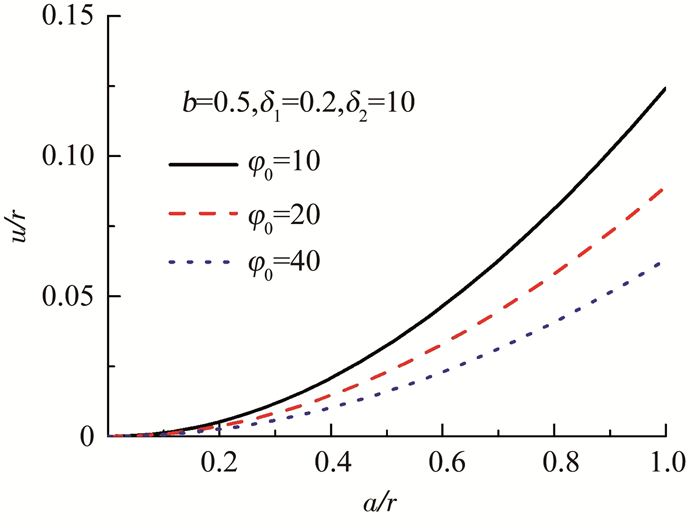
如图 6,7所示,在较软的土体中(δ2较小)时,φ0, c0的增大,均可有效减小卸荷引起的缩孔效应;图 8,9表明,φ0, c0的增大,有助于减小孔周位移,推迟大变形在近孔壁周围的出现.这与砂土的孔壁稳定性很差而硬塑性黏性土的孔壁稳定性较好的实际状况相符.
|
图 6 不同φ0时的孔壁卸荷缩孔曲线 Fig. 6 Unloading-contraction curves of cavity wall under different φ0 |
|
图 7 不同c0时的孔壁卸荷缩孔曲线 Fig. 7 Unloading-contraction curves of cavity wall under different c0 |
|
图 8 不同φ0时的孔周位移 Fig. 8 Displacement field around cavity under different φ0 |

|
图 9 不同c0值时的孔周位移 Fig. 9 Displacement field around cavity under different c0 |
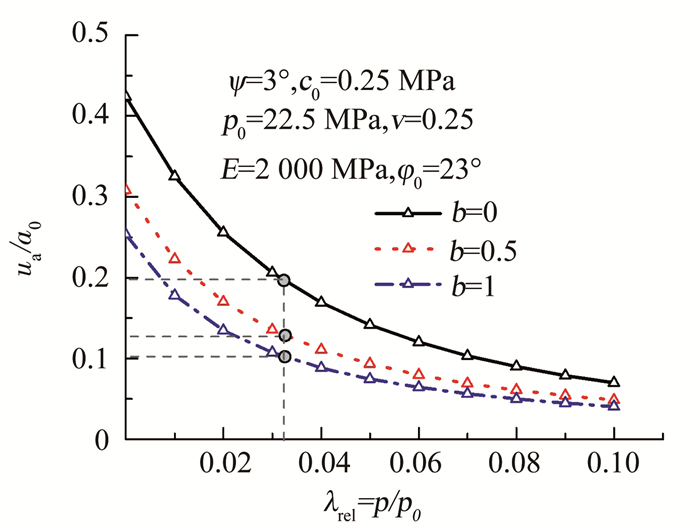
为描述中主应力系数在工程实践中的具体影响,以文献[34]中Gotthard Base隧道开挖为例说明.土体具体参数为:弹性模量E=2 000 MPa, 泊松比ν=0.25,原位初始应力为p0=22.5 MPa,黏聚力为0.25 MPa,摩擦角为23°,剪胀角ψ=3°.
图 10为对应不同b时孔壁位移随卸荷变化关系.对于设计要求的隧道支护压力σp=0.75 MPa, 对应的卸荷因子λrel为0.033, 对应要求实现的隧道半径a=5 m.当b=0,0.5,1时,根据公式a=a0-ua,可得到a0分别为6.25,5.7,5.55 m.其对应单位长度的超开挖量为44.2,23.5,18.2 m3.考虑不同程度的中主应力,造成土方超开挖可能超过一倍的影响.由此可见, 中主应力对于隧道设计与施工具有重要的影响,在隧道支护设计与施工中考虑土体中主应力的影响是必要的.
|
图 10 不同b时的孔壁位移随卸荷变化关系 Fig. 10 Relation between cavity wall displacement and unloading with different b |
1) 推导得到了基于统一强度理论的考虑中主应力影响系数b的无量纲化的柱孔卸荷收缩公式(33)、(34)或(37)、(38),通过该式可对指定卸荷程度下的柱孔缩孔系数进行定量预测.
2) 采用考虑不同中间主应力效应得到的柱孔收缩解较Mohr-Coulomb准则大,说明不考虑中主应力影响的解答偏于保守,其本质为:b的增大,减小了初始屈服卸荷压力,推迟了临界弹塑性区峰值环向应力的出现,降低了孔周塑性区扩展.
3) 中间主应力影响参数b越大,卸荷缩孔效应越小;中间主应力影响参数对孔周径向位移的影响不可忽略;孔周径向应力受其影响较小而环向应力影响较大,b越大,推动峰值环向应力逐渐向孔壁移动,表明中主应力有利于减小孔周塑性区.
4) 土体刚度对卸荷与缩孔关系的影响很大,而且当刚度较大时,中间主应力影响系数b对卸荷缩孔的影响相对减小.
| [1] |
CHADWICK P. The quasi-static expansion of a spherical cavity in metals and ideal soils[J]. Quarterly Journal of Mechanics & Applied Mathematics, 1959, 12(1): 52. |
| [2] |
COLLINS I F, PENDER M J, WANG Yan. Cavity expansion in sands under drained loading conditions[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1992, 16(1): 3. DOI:10.1002/nag.1610160103 |
| [3] |
COLLINS I F, STIMPSON J R. Similarity solutions for drained and undrained cavity expansions in soils[J]. Géotechnique, 1994, 44(1): 21. DOI:10.1680/geot.1994.44.1.21 |
| [4] |
YU H S, HOULSBY G T. Finitecavity expansion in dilatant soils: Loading analysis[J]. Géotechnique, 1991, 41(2): 173. DOI:10.1680/geot.1991.41.2.173 |
| [5] |
CAO L F, TEH C I, CHANG M F. Undrained cavity expansion in modified Cam clay I: Theoretical analysis[J]. Géotechnique, 2001, 51(4): 323. DOI:10.1680/geot.51.4.323.39395 |
| [6] |
CAO Laifa, TEH C I, CHANG Mingfang. Analysis of undrained cavity expansion in elasto-plastic soils with non-linear elasticity[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(1): 25. DOI:10.1002/nag.189 |
| [7] |
LI Jingpei, LI Lin, SUN Dean, et al. Analysis of undrained cylindrical cavity expansion considering three-dimensional strength of soils[J]. International Journal of Geomechanics, 2016, 16(5): 04016017. DOI:10.1061/(asce)gm.1943-5622.0000650 |
| [8] |
LI Lin, LI Jingpei, SUN Dean, et al. Unified solution to drained expansion of a spherical cavity in clay and sand[J]. International Journal of Geomechanics, 2017, 17(8): 04017028. DOI:10.1061/(asce)gm.1943-5622.0000909 |
| [9] |
ZHAO C F, FEI Y, ZHAO C, et al. Analysis ofexpanded radius and internal expanding pressure for undrained cylindrical cavity expansion[J]. International Journal of Geomechanics, 2018, 18(2): 04017139. DOI:10.1061/(ASCE)GM.1943-5622.0001058 |
| [10] |
綦春明, 莫斌, 聂春龙, 等. 饱和土体柱形扩孔时大变形不排水统一解析解[J]. 岩石力学与工程学报, 2009, 28(4): 827. QI Chunming, MO Bin, NIE Chunlong, et al. Unified analytical solutions for cylindrical cavity expansion in saturated soil under large deformation and undrained conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 827. DOI:10.3321/j.issn:1000-6915.2009.04.023 |
| [11] |
赵春风, 贾尚华, 赵程. 基于统一强度准则的柱孔扩张问题及扩孔孔径分析[J]. 同济大学学报(自然科学版), 2015, 43(11): 1634. ZHAO Chunfeng, JIA Shanghua, ZHAO Cheng. Theoretical analysis of expansion and expanded radius of cylindrical cavity based on unified strength criterion[J]. Journal of Tongji University (Natural Science), 2015, 43(11): 1634. DOI:10.11908/j.issn.0253-374x.2015.11.004 |
| [12] |
蒋明镜, 沈珠江. 考虑材料应变软化的柱形孔扩张问题[J]. 岩土工程学报, 1995, 17(4): 10. JIANG Mingjing, SHEN Zhujiang. Expansion of cylindrical cavity of materials with strain-softening behaviour[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(4): 10. DOI:10.3321/j.issn:1000-4548.1995.04.003 |
| [13] |
蒋明镜, 沈珠江. 岩土类软化材料的柱形孔扩张统一解问题[J]. 岩土力学, 1996, 17(1): 1. JIANG Mingjing, SHEN Zhujiang. Unified solution to expansion of cylindrical cavity for geomaterials with strain-softening behavior[J]. Rock and Soil Mechanics, 1996, 17(1): 1. |
| [14] |
HOULSBY G, CLARKE B, WROTH C.Analysis of the unloading of a pressuremeter in sand[C]//BRIAUD J, AUDIBERT J. The Pressuremeter and Its Marine Applications: Second International Symposium. West Conshohocken, PA: ASTM International, 1985: 245. DOI: 10.1520/STP19290S
|
| [15] |
YU H S. Interpretation of pressuremeter unloading tests in sands[J]. Géotechnique, 1996, 46(1): 17. DOI:10.1680/geot.1996.46.1.17 |
| [16] |
YU H S, HOULSBY G T. A large strain analytical solution for cavity contraction in dilation soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(11): 793. DOI:10.1002/nag.1610191104 |
| [17] |
YU H S, ROWE R K. Plasticity solutions for soil behavior around contracting cavities and tunnels[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 1245. DOI:10.1002/(sici)1096-9853(199910) |
| [18] |
CHEN S. Analytical and numerical analyses of wellbore drilled in elastoplastic porousformations[D]. Ann Arbor: The University of Oklahoma, 2012
|
| [19] |
CHEN S L, ABOUSLEIMAN Y N. Drained and undrained analyses of cylindrical cavity contractions by bounding surfaceplasticity[J]. Canadian Geotechnical Journal, 2016, 53(9): 1398. DOI:10.1139/cgj-2015-0605 |
| [20] |
CHEN S L, ABOUSLEIMAN Y N, MURALEETHARA K K. Closed-form elastoplastic solution for the wellbore problem in strain hardening/softening rock formations[J]. International Journal of Geomechanics, 2012, 12(4): 494. DOI:10.1061/(ASCE)GM.1943-5622.0000157 |
| [21] |
MO Pinqiang, YU Haisui. Undrained cavity-contraction analysis for prediction of soil behavior around tunnels[J]. International Journal of Geomechanics, 2017, 17(5): 04016121. DOI:10.1061/(asce)gm.1943-5622.0000816 |
| [22] |
VRAKAS A, ANAGNOSTOU G. A finite strain closed-form solution for the elastoplastic ground response curve intunnelling[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(11): 1131. DOI:10.1002/nag.2250 |
| [23] |
VRAKAS A, ANAGNOSTOU G. Finite strain elastoplastic solutions for the undrained ground response curve intunnelling[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(7): 738. DOI:10.1002/nag.2335 |
| [24] |
杨砚宗.砂土考虑卸荷效应的钻孔灌注桩试验与理论研究[D].上海: 同济大学, 2011 YANG Yanzong. Study on the test and method of bored pile in sand with unloading[D]. Shanghai: Tongji University, 2011 |
| [25] |
范文, 俞茂宏, 陈立伟, 等. 考虑材料剪胀及软化的有压隧洞弹塑性分析的解析解[J]. 工程力学, 2004, 21(5): 16. FAN Wen, YU Maohong, CHEN Liwei, et al. An analytical solution of elastoplastic pressure tunnel considering material softening and dilatancy[J]. Engineering Mechanics, 2004, 21(5): 16. DOI:10.3969/j.issn.1000-4750.2004.05.008 |
| [26] |
龚辉, 赵春风. 基于统一强度理论桩孔稳定性分析[J]. 沈阳建筑大学学报(自然科学版), 2011, 27(2): 237. GONG Hui, ZHAO Chunfeng. Stability analysis of borehole based on unified strength theory[J]. Journal of Shenyang Jianzhu University (Natural Science), 2011, 27(2): 237. |
| [27] |
俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1. YU Maohong. Unified strength theory for geomaterials and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1. DOI:10.3321/j.issn:1000-4548.1994.02.001 |
| [28] |
赵春风, 杨砚宗, 张常光, 等. 考虑中主应力的常用破坏规则适用性研究[J]. 岩石力学与工程学报, 2011, 30(2): 327. ZHAO Chunfeng, YANG Yanzong, ZHANG Changguang, et al. Investigation on applicability of common failure criteria considering intermediate principal stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 327. |
| [29] |
YU Haisui.岩土介质小孔扩张理论[M].周国庆, 赵光思, 梁恒昌, 等, 译.北京: 科学出版社, 2013 YU Haisui. Cavity expansion method in geomechanics[M]. ZHOU Guoqing, ZHAO Guangsi, LIANG Hengchang, et al, translate. Beijing: Science Press, 2013 |
| [30] |
石修松, 程展林. 堆石料平面应变条件下统一强度理论参数研究[J]. 岩石力学与工程学报, 2011, 30(11): 2244. SHI Xiusong, CHENG Zhanlin. Unified strength theory parameters of rockfill material in plane strain state[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2244. |
| [31] |
YU Maohong. Unified strength theory and its applications[M]. Berlin Heidelberg: Springer-Verlag, 2004
|
| [32] |
YU Haisui.岩土塑性理论[M].周国庆, 刘恩龙, 商翔宇, 译.北京: 科学出版社, 2018 YU Haisui. Plasticity and geomechanics[M]. ZHOU Guoqing, LIU Enlong, SHANG Xiangyu, translate. Beijing: Science Press, 2018 |
| [33] |
MAIR R J, TAYLOR R N. Prediction of clay behavior around tunnels using plasticity solutions[C]//Proceedings of the WROTH Memorial Symposium. Predictive Soil Mechanics. London: Thomas Telford, 1993: 449
|
| [34] |
VRAKAS A, ANAGNOSTOU G. A simple equation for obtaining finite strain solutions from small strain analyses of tunnels with very largeconvergences[J]. Géotechnique, 2015, 65(11): 936. DOI:10.1680/jgeot.15.P.036 |
 2020, Vol. 52
2020, Vol. 52


