2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
压密注浆是指用稠度较大的浆液注入土体,通过对周围土体的挤压来加固土体的方式,压密注浆最早由Graf[1]于1969年首先提出,并对其工艺进行了详细的描述,主要应用于沉降建筑物的抬升、桩基承载力提高、土石坝的加固和隧洞掘进时地层位移的控制等方面[2].
对于压密注浆问题,国内外已有很多学者从试验、理论和数值等方面展开了较为深入的研究.Brown[3]、Younis等[4]也通过室内试验和现场试验等研究了压密注浆的适用性以及浆液对土体的影响; El-Kelesh等[5]通过现场试验对桩的压密注浆加固效果进行分析,研究了土体特性、浆液注入顺序、置换比等对压密注浆效果的影响,发现浆液注入顺序对桩压密注浆效果产生很大影响; Seo等[6]通过一系列试验研究了4种不同花岗岩残积土压密注浆效果对抗拔锚索抗拔承载力的影响,并通过圆孔扩张理论对试验结果进行对比研究,发现压密注浆提高抗拔承载力主要通过孔扩张进行压密土体、残余应力作用以及对土体剪胀角的影响; Nichols等[7]通过室内模型试验得出压密注浆浆液在土体中形成的浆泡呈现圆柱形和泪珠形两种并且将浆泡直径与注浆管的直径进行比值无量纲化,从而建立了其与浆液上返高度之间的关系; 张忠苗等[8]通过室内模型试验研究了黏土中压密注浆浆液扩散机理,发现黏土注浆中存在压滤效应并且贯穿于整个注浆过程,压密注浆形成的浆泡大小随着浆液水灰比的增大而减小; 邹金峰等[9]基于能量分析法和孔扩张理论研究了土体中压密注浆的极限注浆压力,发现球形扩孔得出的注浆压力比柱形扩孔的注浆压力要小得多; 张忠苗[10]、邹健等[11]采用球形和柱形孔扩张理论对黏土中压密注浆进行了分析,引入有效应力比并考虑了浆液压滤效应对压密注浆的影响,计算结果发现要比未考虑浆液压滤效应更准确; 叶飞等[12]利用球孔扩张理论,通过对压密注浆浆液扩散扩张过程的力学分析,建立了盾构壁后压密注浆的力学模型,分析了浆体扩张对管片衬砌产生压力效应的影响因素主要是注浆压力、土体弹性模量、黏聚力和内摩擦角; 曾胜等[13]利用球形扩孔过程中的能量和体变守恒原理推导出压密注浆极限注浆压力求解的理论方程组并得出了压密注浆的极限注浆压力; Ivanetich等[14]通过数值方法研究了浆液特性对浆泡形成的影响; Wang等[15]通过有限元数值分析方法研究了压密注浆浆体径向扩张和对地表土体隆起的影响,并通过与现场试验和理论解析结果进行对比验证了结果的合理性,发现压密注浆效果受控于浆体上方圆锥体重量和土的剪切强度.
现有的研究很少涉及压密注浆在土体中存在卸荷情况条件下对土体以及结构物等力学特性影响研究,而在实际工程中经常会涉及土体中存在卸荷工况条件下注浆的情况,比如隧道拱顶注浆(衬砌背后注浆)的加固过程[12]等.为此,采用理论分析的方法,基于球孔扩张理论,在假定后注浆为压密注浆模式下呈球形扩散方式的基础上,通过土体弹性模量折减值来考虑不同卸荷程度对土体压密注浆效应的影响,分析得出不同卸荷程度下压密注浆极限注浆压力、浆体扩张率、塑性区扩张率、径向和环向应力沿径向分布以及径向位移沿径向的分布关系,得出考虑土体卸荷效应影响的压密注浆模型,为实际工程中压密注浆实践提供一定的理论指导.
1 压密注浆模型 1.1 基本假定为便于研究,结合已有有关压密注浆的研究[12],对黏土中压密注浆球孔扩散做如下假定:
1) 忽略浆液在土体交界面处的渗透效应,认为注浆过程中仅存在浆液对土体的压密效应;
2) 忽略浆液沿结构物表面的扩散运动,注浆体在土体中呈球形扩散,压密注浆过程相当于在土体中扩张一个半径为Ru的球形浆体,如图 1所示,p为注浆压力,R0为球形浆体的初始半径,Rp为土体塑性区最大半径;

|
图 1 压密注浆模型 Fig. 1 Model of compaction grouting |
3) 土体在初始状态下为均质各向同性体;
4) 土体在受到浆体扩张挤压后发生弹塑性变形,且变形在应力施加后立刻发生;
5) 浆液和土颗粒不可压缩;
6) 忽略重力对土体压缩的影响.
1.2 理论推导根据球对称问题的平衡微分方程为
| $ \frac{{{\rm{d}}{\sigma _{\rm{r}}}}}{{{\rm{d}}r}} + 2\frac{{{\sigma _{\rm{r}}} - {\sigma _\theta }}}{r} = 0. $ | (1) |
式中σr和σθ分别表示径向和切向正应力.
几何方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _{\rm{r}}} = - \frac{{{\rm{d}}{u_{\rm{r}}}}}{{{\rm{d}}r}},}\\ {{\varepsilon _\theta } = - \frac{{{u_{\rm{r}}}}}{r}.} \end{array}} \right. $ | (2) |
式中:ur为土体的径向位移,εr和εθ分别表示径向应变和切向应变.
物理方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _{\rm{r}}} = \frac{{{\sigma _{\rm{r}}} - 2v{\sigma _\theta }}}{E},}\\ {{\varepsilon _\theta } = \frac{{(1 - v){\sigma _\theta } - v{\sigma _{\rm{r}}}}}{E}.} \end{array}} \right. $ | (3) |
式中υ和E分别表示泊松比和土体弹性模量.
应力边界条件为
| $ {\sigma _r}{|_{r = {R_{\rm{u}}}}} = p,{\sigma _{\rm{r}}}{|_{r \to \infty }} = {p_0}. $ | (4) |
式中:p和p0分别表示注浆压力和初始静压力,Ru为浆体半径.
当注浆压力较小时,浆体周围土体全部处于弹性状态,根据弹性理论,联立式(1)~(3)并考虑边界条件式(4)可得弹性区应力场和位移场为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{r}}} = {p_0} + (p - {p_0}) \cdot {{\left( {\frac{{{R_{\rm{u}}}}}{r}} \right)}^3},}\\ {{\sigma _\theta } = {p_0} - \frac{{(p - {p_0})}}{2} \cdot {{\left( {\frac{{{R_{\rm{u}}}}}{r}} \right)}^3},}\\ {{u_r} = \frac{{(1 + v)(p - {p_0})r}}{{2E}} \cdot {{\left( {\frac{{{R_{\rm{u}}}}}{r}} \right)}^3},} \end{array}} \right. $ | (5) |
随着注浆压力的持续增大,注浆体边缘土体逐渐进入塑性屈服状态.塑性变形阶段采用Mohr-Coulomb准则,其屈服函数表达式为
| $ F = ({\sigma _{\rm{r}}} - {\sigma _\theta }) - ({\sigma _{\rm{r}}} + {\sigma _\theta }){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi - 2c{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi = 0. $ | (6) |
式中c和φ分别为土体的黏聚力和内摩擦角.将式(6)简化为如下形式:
| $ {{\sigma _{\rm{r}}} - \alpha {\sigma _\theta } = Y,} $ | (7) |
其中
| $ {\alpha = \frac{{1 + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }},Y = \frac{{2c{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{1 - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }},} $ | (8) |
当p=py时,浆体边缘土体首先出现屈服,根据屈服准则式(6)和式(5)得土体进入塑性状态的临界压力为
| $ {p_y} = \frac{{2[Y + (\alpha - 1){p_0}]}}{{2 + \alpha }} + {p_0}. $ | (9) |
随着注浆压力p的进一步增大,当p>py时,在孔壁周围土体内会形成一个半径为Rp的塑性区,塑性区外为弹性区,弹性区和塑性区的交界面为Sc,交界面Sc上的土体径向正应力为py.分别用Rp和py代替式(5)中的Ru和p,可得弹性区域De={r|r≥Rp, p>py}的应力场和位移场为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{r}}} = {p_0} + ({p_y} - {p_0}) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3},}\\ {{\sigma _\theta } = {p_0} - \frac{{({p_y} - {p_0})}}{2} \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3},}\\ {{u_{\rm{r}}} = \frac{{(1 + v)({p_y} - {p_0})r}}{{2E}} \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3}.} \end{array}} \right. $ | (10) |
联立式(1)和(6)得塑性区(Ru<r<Rp)的应力分量为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{r}}} = \frac{Y}{{1 - \alpha }} + A \cdot {r^{\frac{{2(1 - \alpha )}}{\alpha }}},}\\ {{\sigma _\theta } = \frac{Y}{{1 - \alpha }} + \frac{A}{\alpha } \cdot {r^{\frac{{2(1 - \alpha )}}{\alpha }}}.} \end{array}} \right. $ | (11) |
式中A为待定常数.
利用塑性区应力边界条件σr|r=Ru=p,σr|r=Rp=py,可得积分常数A为
| $ A = \left( {p - \frac{Y}{{1 - \alpha }}} \right) \cdot R_{\rm{u}}^{\frac{{2(\alpha - 1)}}{\alpha }} = \left( {{p_y} - \frac{Y}{{1 - \alpha }}} \right) \cdot R_{\rm{p}}^{\frac{{2(\alpha - 1)}}{\alpha }}. $ | (12) |
则塑性区径向、环向应力为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{r}}} = \frac{Y}{{1 - \alpha }} + \left( {{p_y} - \frac{Y}{{1 - \alpha }}} \right) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^{\frac{{2(\alpha - 1)}}{\alpha }}},}\\ {{\sigma _\theta } = \frac{Y}{{1 - \alpha }} + \frac{1}{\alpha } \cdot \left( {{p_y} - \frac{Y}{{1 - \alpha }}} \right) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^{\frac{{2(\alpha - 1)}}{\alpha }}}.} \end{array}} \right. $ | (13) |
由式(12)可得塑性区外半径Rp与当前注浆体半径Ru和注浆压力p之间的关系为
| $ \beta = \frac{{{R_{\rm{p}}}}}{{{R_{\rm{u}}}}} = {\left[ {\frac{{(\alpha - 1)p + Y}}{{(\alpha - 1){p_y} + Y}}} \right]^{\frac{\alpha }{{2(\alpha - 1)}}}}. $ | (14) |
将r=Rp代入式(10)可得弹塑性边界位移为
| $ {u_{{\rm{rp}}}} = \frac{{(1 + v)({p_y} - {p_0})}}{{2E}}{R_{\rm{p}}} = \delta {R_{\rm{p}}}. $ | (15) |
在孔内壁作用均匀分布压力p(p>p0)时,孔周围土体产生的弹塑性体积变化应该等于孔的体积变化[17],假定某一离小孔中心初始距离为r0的点,在进入塑性区后,离小孔中心的距离变为r,即
| $ \chi \frac{{4\pi }}{3}(R_{\rm{u}}^3 - R_0^3) = \chi \frac{{4\pi }}{3}({r^3} - r_0^3) + \varDelta . $ | (16) |
式中:χ定义为考虑结构物表面曲率变化对浆液球形扩散的影响系数,χ的取值为(0,1],当土体中不存在结构物表面影响时,浆液呈完整球形扩散,χ取为1,当存在结构物表面曲率影响时,χ取值范围为(0, 1),χ具体取值对后续球孔扩张应力位移分析无影响; Δ为塑性区的体积变形.相关研究认为[16-17],Δ受剪胀等因素的影响,可以忽略.在弹塑性边界,有
| $ {R_{\rm{u}}^3 - R_0^3 = R_{\rm{p}}^3 - {{({R_{\rm{p}}} - {u_{{\rm{rp}}}})}^3},} $ | (17) |
| $ {1 - {{\left( {\frac{{{R_0}}}{{{R_{\rm{u}}}}}} \right)}^3} = {{\left( {\frac{{{R_{\rm{p}}}}}{{{R_{\rm{u}}}}}} \right)}^3}({\delta ^3} - 3{\delta ^2} + 3\delta ).} $ | (18) |
则浆体扩张率为
| $ \xi = \frac{{{R_{\rm{u}}}}}{{{R_0}}} = \frac{1}{{\sqrt[3]{{1 - {{\left( {\frac{{{R_{\rm{p}}}}}{{{R_{\rm{u}}}}}} \right)}^3}({\delta ^3} - 3{\delta ^2} + 3\delta )}}}}. $ | (19) |
塑性区扩张率为
| $ \zeta = \frac{{{R_{\rm{p}}}}}{{{R_0}}} = \beta \cdot \xi . $ | (20) |
对于塑性区位移的求解,设小孔周围土体某一离小孔中心初始距离为r0的点,在进入塑性区后,离小孔中心的距离变为r,若令该点的位移为ur,则有
| $ {u_{\rm{r}}} = r - {r_0}. $ | (21) |
对上式进行变换,有
| $ {r_0} = r - {u_{\rm{r}}}. $ | (22) |
如前文所述,若塑性区的体积变形可忽略,则有
| $ \chi \frac{4}{3}\pi {({R_{\rm{p}}} - {u_{{r_{\rm{p}}}}})^3} - \chi \frac{4}{3}\pi r_0^3 = \chi \frac{4}{3}\pi R_{\rm{p}}^3 - \chi \frac{4}{3}\pi {r^3}. $ | (23) |
联立式(22)和(23)有
| $ {u_{\rm{r}}} = r - \sqrt[3]{{{r^3} - 3R_{\rm{p}}^2{u_{{r_{\rm{p}}}}} + 3{R_{\rm{p}}}u_{{r_{\rm{p}}}}^2 - u_{{r_{\rm{p}}}}^3}}. $ | (24) |
联立式(14)和(18)可得注浆压力表达式为
| $ \begin{array}{l} p = \frac{{[(\alpha - 1){p_y} + Y]{{\left[ {1 - {{\left( {\frac{{{R_0}}}{{{R_u}}}} \right)}^3}} \right]}^{\frac{{2(\alpha - 1)}}{{3\alpha }}}}}}{{\alpha - 1}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {\frac{1}{{{\delta ^3} - 3{\delta ^2} + 3\delta }}} \right)^{\frac{{2(\alpha - 1)}}{{3\alpha }}}} - \frac{Y}{{\alpha - 1}}. \end{array} $ | (25) |
对于初始孔径R0不为0,扩孔后注浆体半径Ru→∞,则极限注浆压力为
| $ \begin{array}{*{20}{c}} {{p_{\rm{u}}} = \mathop {{\rm{lim}}}\limits_{{R_{\rm{u}}} \to \infty } p = \frac{{[(\alpha - 1){p_y} + Y]}}{{\alpha - 1}} \times }\\ {{{\left( {\frac{1}{{{\delta ^3} - 3{\delta ^2} + 3\delta }}} \right)}^{\frac{{2(\alpha - 1)}}{{3\alpha }}}} - \frac{Y}{{\alpha - 1}}.} \end{array} $ | (26) |
根据上述分析,可得到小孔周围土体弹塑性状态下的应力场和位移场的解析解如下:
| $ {\sigma _{\rm{r}}} = \left\{ {\begin{array}{*{20}{l}} {{p_0} + ({p_y} - {p_0}) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3},r \ge {R_{\rm{p}}},}\\ {\frac{Y}{{1 - \alpha }} + \left( {{p_y} - \frac{Y}{{1 - \alpha }}} \right) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^{\frac{{2(\alpha - 1)}}{\alpha }}},{R_{\rm{u}}} \le r < {R_{\rm{p}}}.} \end{array}} \right. $ | (27) |
| $ {\sigma _\theta }{\sigma _\theta } = \left\{ {\begin{array}{*{20}{l}} {{p_0} - \frac{{({p_y} - {p_0})}}{2} \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3},r \ge {R_{\rm{p}}},}\\ {\frac{Y}{{1 - \alpha }} + \frac{1}{\alpha } \cdot \left( {{p_y} - \frac{Y}{{1 - \alpha }}} \right) \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^{\frac{{2(\alpha - 1)}}{\alpha }}},{R_{\rm{u}}} \le r < {R_{\rm{p}}}.} \end{array}} \right. $ | (28) |
| $ {u_{\rm{r}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{(1 + v)({p_y} - {p_0})r}}{{2E}} \cdot {{\left( {\frac{{{R_{\rm{p}}}}}{r}} \right)}^3},r \ge {R_{\rm{p}}},}\\ {r - \sqrt[3]{{{r^3} - 3R_{\rm{p}}^2{u_{{\rm{rp}}}} + 3{R_{\rm{p}}}u_{{\rm{rp}}}^2 - u_{{\rm{rp}}}^3}},{R_{\rm{u}}} \le r < {R_{\rm{p}}}.} \end{array}} \right. $ | (29) |
在实际工程注浆过程中,存在土体卸荷效应的影响,如隧道拱顶注浆(衬砌背后注浆)的加固过程[12],即会产生应力释放.在土体应力释放过程中,土体弹性模量减小,因此,在考虑隧道拱顶注浆(衬砌背后注浆)加固过程存在的卸荷效应时,上文推导的理论公式中,弹性模量应是土体原始弹性模量的折减值.根据文献[18]给出的对软黏土初始弹性模量的估算公式:
| $ {E_i} = {C_0}\eta {s_{\rm{u}}}. $ | (30) |
式中:su为不排水抗剪强度; C0和η为无量纲系数,可根据土体的超固结比ROC和塑性指数Ip查图 2得到.
超固结比ROC的计算式为
| $ {R_{{\rm{OC}}}} = \frac{{{P_{\rm{c}}}}}{{{P_{{\rm{ul}}}}}}. $ | (31) |
式中:Pc为先期固结压力,Pul为当前压力.在考虑卸荷效应时,若引入卸荷比[19]
| $ \varsigma = \frac{{{P_{\rm{c}}} - {P_{{\rm{ul}}}}}}{{{P_{\rm{c}}}}}. $ | (32) |
则式(30)可转化为
| $ {R_{{\rm{OC}}}} = \frac{{{P_{\rm{c}}}}}{{{P_{{\rm{ul}}}}}} = \frac{1}{{1 - \varsigma }}. $ | (33) |
联立式(30)~(33)即可得出不同卸荷程度下的土体初始弹性模量折减值.
3 参数确定与模型适用性的讨论 3.1 参数确定从模型的推导过程可以看出,与压密注浆浆体扩散过程有关的参数有:初始静压力p0、注浆压力p、球形浆体初始半径R0、黏聚力c、内摩擦角φ、泊松比ν.浆体初始半径R0应与注浆孔半径相等,注浆压力p可通过注浆泵上的压力表测得,土体的特性参数可通过试验得到.
3.2模型适用性
本文模型适用于渗透系数较小的软黏土地层中,以及存在卸荷情况下软黏土中进行压密注浆,不适用于渗透系数较大的砂性土地层.本文模型未考虑浆液特性对压密注浆效果的影响.
4 实例分析采用文献[20]提供的黏土物理特性参数对模型进行分析,黏聚力c=10 kPa,不排水抗剪强度su=15.2 kPa,内摩擦角φ=12.5°,泊松比ν=0.35,初始静压力p0=100 kPa,塑性指数Ip=29.9%,C0=800,卸荷比取=0, 0.2, 0.4, 0.5, 0.6, 0.7, 0.8和0.9进行系统研究,对应的系数η=1, 0.98, 0.94, 0.88, 0.8, 0.69, 0.47和0.2,从而可以换算出不同卸荷比下土体弹性模量分别为12.16, 11.92, 11.43, 10.70, 9.73, 8.39, 5.72, 2.43 MPa.
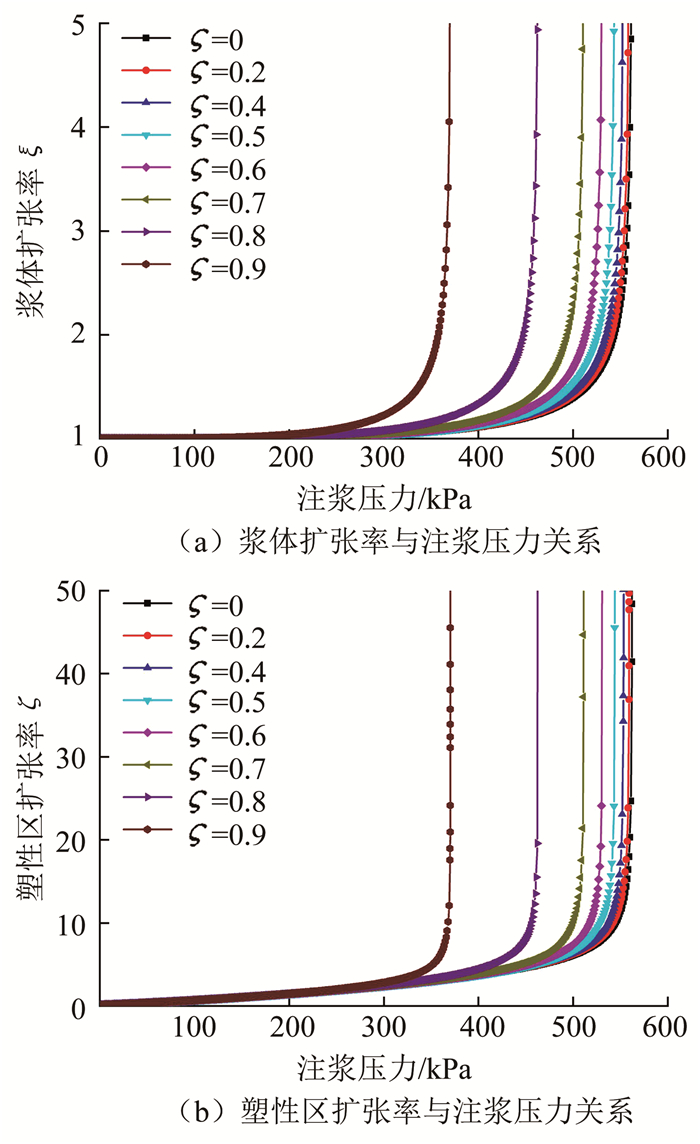
4.1 不同卸荷程度下球形浆体和土体塑性区扩张率按照给定的卸荷比换算出超固结比ROC带入式(30)~(33)计算出折减后土体弹性模量值,并将上述土体参数代入式(19)和(20),得出图 3不同卸荷程度下球形浆体和土体塑性区扩张率随注浆压力的变化曲线.可以看出,注浆压力对球形浆体扩张率和土体塑性区扩张率的影响明显.浆体扩张率和土体塑性区扩张率在初始阶段均随注浆压力的增大而增大,并且增大的速率随注浆压力的增大不断提高.当注浆压力超过一定值后,浆体和土体塑性区扩张率趋于无穷大,此时注浆压力值即可做为压密注浆的极限注浆压力.不同卸荷工况下的极限注浆压力如表 1所示.
|
图 3 不同卸荷比下浆体扩张率和土体塑性区扩张率与注浆压力关系 Fig. 3 Relation between expansion rates and grouting pressure under different unloading ratios |
| 表 1 不同卸荷比下极限注浆压力 Tab. 1 Ultimate grouting pressure under different unloading ratios |
分析表 1可知,达到压密注浆的极限注浆压力随着卸荷程度的增大而减小,且这种减小随卸荷程度的改变呈非线性,当卸荷比小于0.7时,压密注浆极限注浆压力随卸荷比的减小改变不明显,当卸荷比大于0.7时,压密注浆极限注浆压力明显减小,并且减小幅度随着卸荷程度的增大而快速增长.因此,在实际注浆过程中,当土体中存在卸荷效应,要达到压密注浆效果所需的注浆压力时,需考虑此时土体卸荷程度的大小进而分析采用合适的注浆压力.
4.2 不同卸荷程度下塑性区半径与浆体扩散半径关系图 4给出了不同卸荷程度下塑性区半径与浆体扩散半径关系曲线,可以看出,塑性区半径随着浆体扩散半径的增大而增大,增大速率逐渐变大并最后趋于稳定,即二者最后呈现线性增长关系.不同卸荷比条件下,塑性区半径随浆体扩散半径的稳定增长速率随卸荷比的增大而非线性减小,即卸荷程度越大,塑性区半径随浆体扩散半径增长的速率越低; 当卸荷比小于0.7时,土体中卸荷程度的改变对塑性区半径随浆体扩散半径的增长速率影响很小; 当卸荷比大于0.7时,土体中卸荷程度的改变对塑性区半径随浆体扩散半径的增长速率影响较为显著.

|
图 4 塑性区半径与浆体扩散半径关系 Fig. 4 Relation between plastic zone radius Rp and grout diffusion radius Ru |
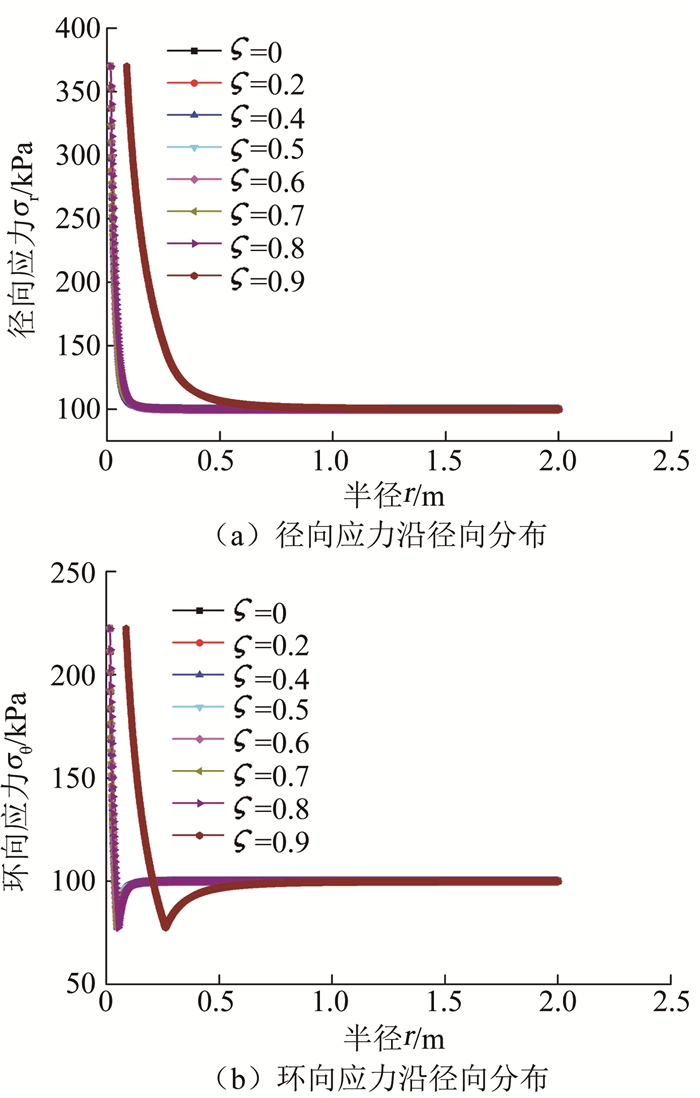
图 5给出了注浆压力370 kPa不同卸荷程度下注浆体周围土体径向和环向应力沿径向的分布关系曲线,可以看出,同一注浆压力下,当卸荷比小于0.8时,不同卸荷程度下注浆体周围土体的径向应力和环向应力沿径向分布基本一致,当卸荷比大于0.8时,注浆体周围同一位置处的土体径向应力明显高于卸荷比小于0.8时的应力.不同卸荷比条件下的环向应力均呈现沿半径方向先增大后减小的规律,且当卸荷比小于0.8时,最小环向应力均在同一位置出现,当卸荷比大于0.8时,最小环向应力出现位置距注浆孔距离较卸荷比小于0.8情况下大.不同卸荷比条件下最小环向应力大小基本一致,约为78 kPa.径向应力和环向应力均随着径向距离的增大而逐渐趋于稳定,即趋向于初始静压力100 kPa.
|
图 5 注浆压力370 kPa不同卸荷比下土体径向和环向应力沿径向分布 Fig. 5 Stress distributions along radial direction with grouting pressure of 370 kPa under different unloading ratios |
图 6给出了同一注浆量(注浆体半径0.5 m)不同卸荷程度下注浆体周围土体径向和环向应力沿径向的分布关系曲线.可以看出,当注浆量相同时,不同卸荷程度下注浆体周围土体径向应力沿径向逐渐趋于稳定,稳定径向应力为初始静压力100 kPa,并且随着卸荷程度的增大,达到稳定径向应力的径向距离逐渐减小; 同一位置处的径向应力随着卸荷程度的增大而减小; 对于环向应力,同样呈现沿着径向先减小后增大最后趋于稳定即初始静压力值100 kPa; 达到最小环向应力值以及稳定环向应力的径向距离随着卸荷程度的增大而减小,并且不同卸荷程度下最小环向应力值相等,即最小环向应力值不随卸荷程度的改变而变化.

|
图 6 同一注浆量不同卸荷比下土体径向和环向应力沿径向分布 Fig. 6 Stress distributions along radial direction with same grouting volume under different unloading ratios |
根据环向应力计算公式(28)可知,最小环向应力出现在r=Rp情况下,即弹塑性界面处.在弹性区一侧,由于柱孔扩孔使环向应力逐渐减小,在弹塑性界面处环向应力达到最小; 对于塑性区一侧,所有土体都满足屈服准则,环向应力和径向应力呈正比,随径向应力的变化而变化,因此,也在弹塑性界面处最小[17].此时最小环向应力为
| $ {\sigma _\theta } = {p_0} = \frac{{({p_y} - {p_0})}}{2}. $ | (34) |
从该最小环向应力表达式可以看出,最小环向应力σθ只与土体初始静压力p0和土体进入塑性状态的临界压力py有关,与卸荷程度大小无关.因此,最小环向应力值不随卸荷程度的改变而变化.
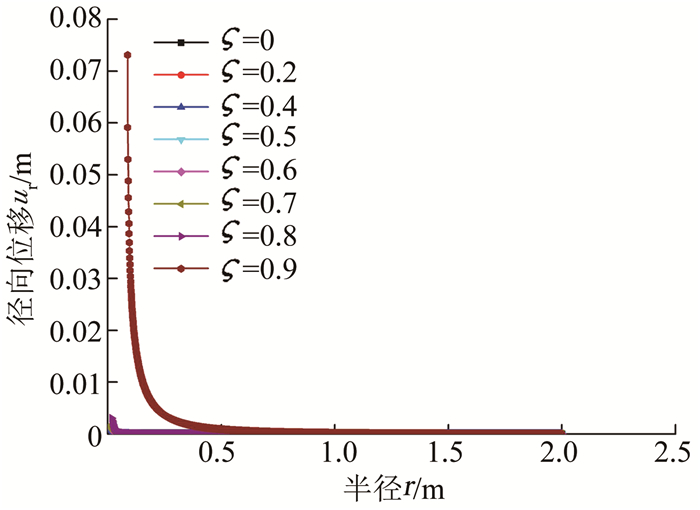
4.4 不同卸荷程度下径向位移沿径向分布关系图 7给出了注浆压力370 kPa不同卸荷程度下径向位移沿径向的分布关系曲线,可以看出,同一注浆压力下注浆体周围不同卸荷程度下土体径向位移沿着半径方向逐渐趋于稳定值0;当卸荷比小于0.8时,径向位移沿半径方向分布基本一致,当卸荷比大于0.8时,径向位移沿半径方向分布明显区别于卸荷比小于0.8时情况,具体表现为:在达到稳定值之前,同一位置处的土体径向位移,卸荷比大于0.8情况下土体的径向位移远大于卸荷比小于0.8时的情况; 卸荷比小于0.8时土体径向位移沿半径方向达到稳定值的位置基本一致并且小于卸荷比大于0.8时的径向距离.
|
图 7 注浆压力370 kPa不同卸荷比下土体径向位移沿径向分布 Fig. 7 Radial displacement distributions along radial direction with grouting pressure of 370 kPa under different unloading ratios |
图 8给出了同一注浆量(注浆体半径0.5 m)不同卸荷程度下径向位移沿径向的分布关系曲线.可以看出,同一注浆量下周围不同卸荷程度下土体径向位移沿着半径方向同样逐渐趋于稳定值0,但达到稳定值的位置要远大于相同注浆压力下的情况; 不同卸荷程度下的土体径向位移沿半径方向的分布一致,即同一注浆量下的土体径向位移沿半径方向的分布不受卸荷程度的影响.

|
图 8 同一注浆量不同卸荷比下土体径向位移沿径向分布 Fig. 8 Radial displacement distributions along radial direction with same grouting volume under different unloading ratio |
由不同卸荷比下对应的土体弹性模量折减值可以看出,当土体卸荷比为0.8和0.9时,对应的土体弹性模量明显小于其他卸荷比下对应的土体弹性模量,卸荷比0~0.6内的土体弹性模量折减值变化不大,而土体弹性模量越小在同一压力下对应的变形量则相应越大.因此,在同一注浆压力下,卸荷比大于0.8时对应的土体径向位移沿半径方向分布区别于卸荷比小于0.8时的情况.而在同一注浆量下,由于最终形成的球形浆体体积一致,不同土体卸荷程度下对应的土体径向位移沿半径方向分布区别不明显.
4.5 不同注浆量下径向、环向应力和径向位移沿径向分布关系为了分析卸荷工况下不同注浆量对土体内部应力和位移分布的影响,图 9给出了卸荷比0.5不同注浆量下注浆体周围土体径向和环向应力沿径向的分布关系曲线,可以看出,当卸荷比相同时,不同注浆量下注浆体周围土体径向应力沿径向逐渐趋于稳定,稳定径向应力为初始静压力100 kPa,并且随注浆量的增大,达到稳定径向应力的径向距离逐渐增大; 同一位置处的径向应力随注浆量的增大而增大; 对于环向应力,同样呈现沿着径向先减小后增大最后趋于稳定值即初始静压力值100 kPa; 达到最小环向应力值以及稳定环向应力的径向距离随注浆量的增大而增大,并且不同注浆量下最小环向应力值亦相等,即最小环向应力值不随注浆量的改变而变化.

|
图 9 卸荷比0.5不同注浆量下土体径向和环向应力沿径向分布 Fig. 9 Stress distributions along radial direction under unloading ratio of 0.5 with different grouting volumes |
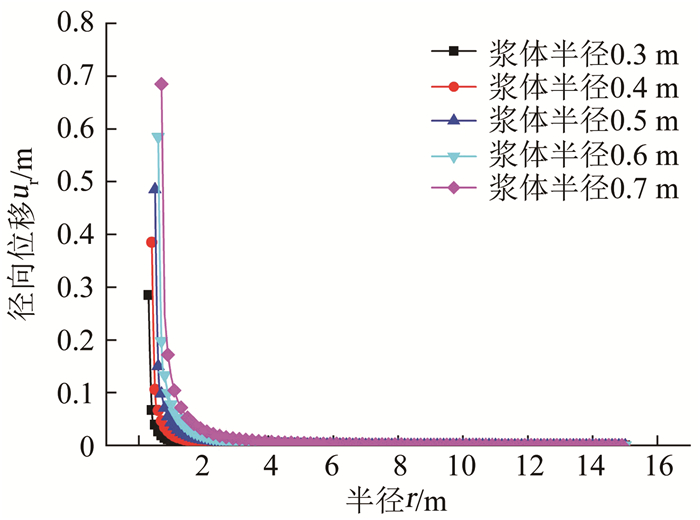
图 10给出了卸荷比0.5不同注浆量下径向位移沿径向的分布关系曲线,可以看出,同一卸荷比不同注浆量下土体径向位移沿着半径方向同样逐渐趋于稳定值0,达到稳定值的径向距离随注浆量的增大而增大.
|
图 10 卸荷比0.5不同注浆量下土体径向位移沿径向分布 Fig. 10 Radial displacement distributions along radial direction under unloading ratio of 0.5 with different grouting volumes |
1) 当卸荷比小于0.7时,压密注浆极限注浆压力以及土体塑性区半径随浆体扩散半径的增长速率受卸荷程度改变的影响较小,当卸荷比大于0.7时,压密注浆极限注浆压力以及塑性区半径随浆体扩散半径的增长速率则随卸荷程度的增大而快速减小.因此在实际工程注浆中,要实现压密注浆效果,必须考虑实际工况下可能存在的土体卸荷工况以及卸荷程度的大小.
2) 同一注浆压力下,当卸荷比小于0.8时,注浆体周围土体的径向应力、环向应力以及径向位移沿径向分布基本一致,当卸荷比大于0.8时,注浆体周围同一位置处的土体径向应力以及径向位移明显高于卸荷比小于0.8时的情况.
3) 同一注浆量下,相同位置处的径向应力、达到最小环向应力、稳定环向应力和径向应力的径向距离均随着卸荷程度的增大而减小,但是土体径向位移分布不受卸荷程度的影响; 最小环向应力大小不受卸荷程度的影响但出现位置受其影响.
4) 同一卸荷比下,相同位置处的径向应力、达到最小环向应力、稳定环向应力、稳定径向应力以及稳定径向位移对应的径向距离均随着注浆量的增大而增大,但最小环向应力值不随注浆量的改变而变化.
| [1] |
GRAF E D. Compaction grouting technique and observations[J]. Journal of Geotechnical Engineering Division, ASCE, 1969, 95(5): 1151. |
| [2] |
罗长军. 紫山灰坝迎灰坡裂缝成因分析及灌浆防治对策[J]. 岩土力学, 2004, 25(4): 666. LUO Changjun. Cause analysis of crack formation on the ash-ward slope of Zishan dam and measures of prevention and cure with grouting[J]. Rock and Soil Mechanics, 2004, 25(4): 666. DOI:10.16285/j.rsm.2004.04.038 |
| [3] |
BROWN D R, WARNER J. Compaction grouting[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(8): 589. DOI:10.1016/0148-9062(74)91742-2 |
| [4] |
YOUNIS M A. Small scale physical modeling of compaction grouting[D]. College Park, MD: University of Maryland, College Park, 1994
|
| [5] |
EL-KELESH A M, MATSUI T, TOKIDA K I. Field investigation into effectiveness of compaction grouting[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(4): 451. DOI:10.1061/(asce)gt.1943-5606.0000540 |
| [6] |
SEO H J, JEONG K H, CHOI H, et al. Pullout resistance increase of soil nailing induced by pressurized grouting[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(5): 604. DOI:10.1061/(ASCE)GT.1943-5606.0000622 |
| [7] |
NICHOLS S C, GOODINGS D J. Physical model testing of compaction grouting in cohesionless soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(9): 848. DOI:10.1061/(ASCE)1090-0241(2000)126:9(848) |
| [8] |
张忠苗, 邹健, 贺静漪, 等. 黏土中压密注浆及劈裂注浆室内模拟试验分析[J]. 岩土工程学报, 2009, 31(12): 1818. ZHANG Zhongmiao, ZOU Jian, HE Jingyi, et al. Laboratory tests on compaction grouting and fracture grouting of clay[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1818. DOI:10.3321/j.issn:1000-4548.2009.12.003 |
| [9] |
邹金锋, 李亮, 杨小礼, 等. 压密注浆的能量分析方法[J]. 岩土力学, 2006, 27(3): 475. ZOU Jinfeng, LI Liang, YANG Xiaoli, et al. Method of energy analysis for compaction grouting[J]. Rock and Soil Mechanics, 2006, 27(3): 475. DOI:10.3969/j.issn.1000-7598.2006.03.028 |
| [10] |
张忠苗, 邹健, 何景愈, 等. 考虑压滤效应下饱和黏土压密注浆柱扩张理论[J]. 浙江大学学报(工学版), 2011, 45(11): 1980. ZHANG Zhongmiao, ZOU Jian, HE Jingyu, et al. Cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(11): 1980. DOI:10.3785/j.issn.1008-973X.2011.11.015 |
| [11] |
邹健, 张忠苗. 考虑压滤效应饱和黏土压密注浆球孔扩张理论[J]. 哈尔滨工业大学学报, 2011, 43(12): 119. ZOU Jian, ZHANG Zhongmiao. Spherical cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Harbin Institute of Technology, 2011, 43(12): 119. |
| [12] |
叶飞, 陈治, 苟长飞, 等. 基于球孔扩张的盾构隧道壁后注浆压密模型[J]. 交通运输工程学报, 2014(1): 35. YE Fei, CHEN Zhi, GOU Changfei, et al. Back-filled grouting compaction model of shield tunnel based on spherical cavity expansion[J]. Journal of Traffic and Transportation Engineering, 2014(1): 35. DOI:10.3969/j.issn.1671-1637.2014.01.007 |
| [13] |
曾胜, 赵健, 邹金锋. 压密注浆极限注浆压力研究[J]. 哈尔滨工业大学学报, 2008, 40(7): 1173. ZENG Sheng, ZHAO Jian, ZOU Jinfeng. Research of limit grouting pressure in compaction grouting[J]. Journal of Harbin Institute of Technology, 2008, 40(7): 1173. DOI:10.3321/j.issn:0367-6234.2008.07.039 |
| [14] |
IVANETICH K B, BORDEN R H. Shear strength and consolidation properties of compaction grout[R]. Raleigh, NC: North Carolina State University, 1996
|
| [15] |
WANG Dongyuan, XING Xiaoman, QU Huihong, et al. Simulated radial expansion and heave caused by compaction grouting in noncohesive soils[J]. International Journal of Geomechanics, 2015, 15(4): 04014069. DOI:10.1061/(ASCE)GM.1943-5622.0000333 |
| [16] |
ZHAO C F, FEI Y, ZHAO C, et al. Analysis of expanded radius and internal expanding pressure for undrained cylindrical cavity expansion[J]. International Journal of Geomechanics, 2018, 18(2): 04017139. DOI:10.1061/(ASCE)GM.1943-5622.0001058 |
| [17] |
贾尚华, 赵春风, 赵程. 砂土中柱孔扩张问题的扩孔压力与扩孔半径分析[J]. 岩石力学与工程学报, 2015, 34(1): 182. JIA Shanghua, ZHAO Chunfeng, ZHAO Cheng. Analysis of expanded radius and internal expanding pressure of cylindrical hole[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 182. DOI:10.13722/j.cnki.jrme.2015.01.020 |
| [18] |
贾堤, 石峰, 郑刚, 等. 深基坑工程数值模拟土体弹性模量取值的探讨[J]. 岩土工程学报, 2008, 增刊1: 155. JIA Di, SHI Feng, ZHENG Gang, et al. Elastic modulus of soil used in numerical simulation of deep foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2008, 增刊1(S1): 155. |
| [19] |
赵春风, 吴悦, 赵程, 等. 考虑卸荷效应的砂土-混凝土接触面剪切特性影响研究[J]. 岩石力学与工程学报, 2018, 37(4): 1020. ZHAO Chunfeng, WU Yue, ZHAO Cheng, et al. Effect of unloading on shear behavior of interface between sand and concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 1020. DOI:10.13722/j.cnki.jrme.2017.1399 |
| [20] |
周秋娟.软土卸荷力学特性及软弱地层中基坑稳定性研究[D].广州: 暨南大学, 2009 ZHOU Qiujuan. Research on mechanical characteristics of soft soil under unloading and stability of foundation on weak underground[D]. Guangzhou: Jinan University, 2009 |
 2020, Vol. 52
2020, Vol. 52



