土木、水利、交通等工程中存在着大量的土与结构相互作用问题,合理地描述土与结构接触面的力学特性,对于正确地评价土与结构相互作用具有重要意义.为探讨土与结构接触面的变形和强度特性,国内外学者进行了大量的试验研究[1-9],建立了不同的本构模型[10-22].张嘎等[3-4]进行了粗粒土与混凝土接触面及粗粒土与钢板接触面的单调与循环剪切试验,研究了接触面的变形与强度特性; 侯文峻[6]和冯大阔等[7]通过粗粒土与钢板接触面的单调和循环剪切试验,研究了不同法向应力下接触面的剪应力-剪切位移、法向位移-剪切位移关系的变化规律; 朱俊高等[8]对土-混凝土接触面以及土-泥皮-混凝土接触面的变形与强度特性进行了单剪试验研究; 张冬霁等[11]在分析接触面变形及破坏机理的基础上,不考虑切向与法向作用的耦合影响,建立了接触面双曲线本构模型; 张嘎等[12-13]在粗粒土与结构面剪切试验的基础上,建立了能够统一描述软化、剪胀与剪缩的损伤模型; 彭凯等[16]利用塑性状态方程取代传统屈服面,采用分段函数建立了能考虑应变软化的接触面弹塑性本构模型; 刘京茂等[17-18]在广义塑性模型的框架内,把Liu等[14-15]提出的二维接触面模型发展成一个状态相关的三维弹塑性接触面模型,使模型可以用一组参数较好地反映在不同围压和不同密度条件下接触面的单调和循环剪切三维变形特性.路德春等[19]基于土与结构接触面变形特性分析,将接触面土体的剪切滑动面与单元体三维应力状态下的八面体面相对应,通过土的三维弹塑性模型在八面体面上的剪切应力-应变关系,建立了接触面土体剪应力-应变关系; Saberi等[21-22]提出了状态相关的二维接触面弹塑性模型,并对不同土与结构接触面的单调和循环剪切试验进行了模拟验证.
以上模型适用于单向剪切或正交两向剪切的接触面问题.为了能处理任意方向剪切以及加载过程中剪切方向可变的接触面问题,本文利用塑性滑移理论,将土与结构接触面的宏观变形与宏观法向变形和剪切面内不同方向的虚拟微观剪切变形之间建立联系; 通过虚功原理,在粒状土的状态相关和边界面弹塑性理论框架内建立一个粗粒土与结构接触面的多重剪切边界面模型; 对不同土与结构接触面的单调与循环剪切试验进行数值模拟与比较,以验证模型的有效性.
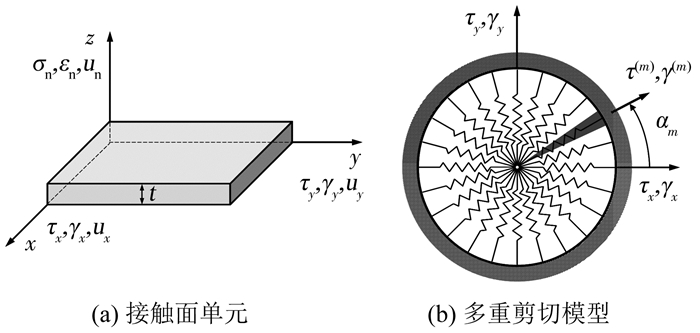
1 本构模型 1.1 多重剪切模型框架土与结构接触面受到外部荷载作用时土体内部颗粒相互摩擦与挤压,变形复杂.如图 1(a)所示,取一个厚度为t的接触面单元,应力和应变矢量分别定义为
| $ {\rm{d}}\mathit{\boldsymbol{\sigma }} = {\rm{d}}{\sigma _{\rm{n}}}{\mathit{\boldsymbol{n}}^{(0)}} + \frac{1}{M}\sum\limits_{m = 1}^M {\rm{d}} {\tau ^{(m)}}{\mathit{\boldsymbol{n}}^{(m)}}. $ | (1) |
|
图 1 多重剪切模型示意 Fig. 1 Illustration of multi-shear model |
式中:
试验与微观力学数值分析表明,应力水平和孔隙率会对粗粒土的力学特性产生较大影响.根据Been等[23]的研究,这种影响可用状态参数ψ来考虑,定义为
| $ \psi = e - {e_{\rm{c}}}. $ | (2) |
式中e和ec分别为粗粒土的孔隙比和临界状态孔隙比.孔隙比增量定义为
| $ {e_{\rm{c}}} = {e_\Gamma } - {\lambda _{\rm{c}}}{\rm{ln}}({\sigma _{\rm{n}}}/{p_{\rm{a}}}). $ | (3) |
式中:eΓ和λc为与临界状态相关的材料参数,pa为标准大气压.
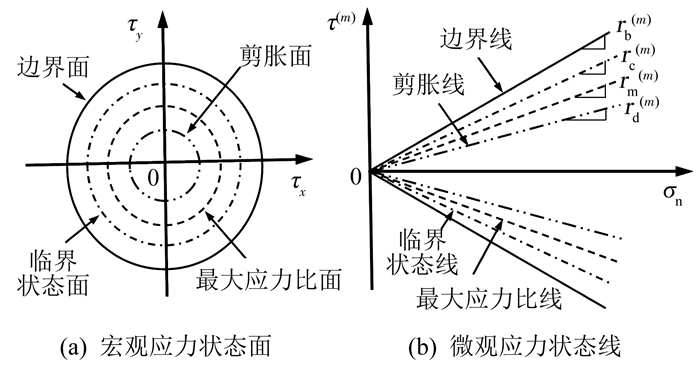
1.3 宏微观应力-应变关系如图 2(a)所示,在宏观应力空间中定义4个应力状态面,即边界面、临界状态面、剪胀面和最大应力比面.其中,边界面限制接触面所能达到的极限应力状态,接触面的应力状态不能在边界面外; 临界状态面表示接触面的应力已达到临界状态; 剪胀面控制接触面的剪胀剪缩,当应力状态位于剪胀面内时接触面发生剪缩,位于剪胀面外时接触面发生剪胀; 最大应力比面为历史最大屈服面,用于反映应力比历史对接触面变形的影响.4个应力状态面方程可表示为
| $ {f_i} = \sqrt {\tau _x^2 + \tau _y^2} - {M_i}{\sigma _{\rm{n}}} = 0,i = {\rm{b,c,d,m}}{\rm{.}} $ | (4) |
|
图 2 宏微观应力状态 Fig. 2 Macro and micro stress states |
式中:fb、fc、fd和fm分别代表宏观应力空间中的边界面、临界状态面、剪胀面和最大应力比面; Mb、Mc、Md和Mm分别为边界、临界状态、剪胀和最大应力比参数.宏观应力比定义为
| $ {{M_{\rm{b}}} = {M_{\rm{c}}}{\rm{exp}}(\langle - {n_{\rm{b}}}\psi \rangle ),} $ | (5) |
| $ {{M_{\rm{d}}} = {M_{\rm{c}}}{\rm{exp}}({n_{\rm{d}}}\psi ).} $ | (6) |
式中:nb和nd为模型参数,反映Mb和Md随状态参数ψ的变化; 〈x〉代表当x < 0时〈x〉=0,当x>0时〈x〉=x.
与宏观应力状态面类似,在微观剪应力-法向应力平面中定义4个微观应力状态线,即边界线、临界状态线、剪胀线和最大应力比线,见图 2(b).各状态线的定义与宏观应力状态面类似,4个应力状态线方程可表示为
| $ f_i^{(m)} = {\tau ^{(m)}} - r_i^{(m)}{\sigma _{\rm{n}}} = 0,i = {\rm{b,c,d,m}}{\rm{.}} $ | (7) |
式中:fb(m)、fc(m)、fd(m)和fm(m)分别代表第m个微观剪切机构的微观边界线、临界状态线、剪胀线和最大应力比线.rb(m)、rc(m)、rd(m)和rm(m)分别为第m个微观剪切机构的微观边界、临界状态、剪胀和最大应力比参数.第m个微观剪切机构的微观应力比定义为r(m)=τ(m)/σn.rm(m)取微观应力比r(m)的历史最大值,rb(m)、rc(m)和rd(m)与相应宏观应力比参数的关系可表示为
| $ r_i^{(m)} = \frac{{M{M_i}}}{{\sum\limits_{m = 1}^M | {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _m}|}},i = {\rm{b,c,d}}. $ | (8) |
宏观法向应变与法向应力的关系可表示为
| $ {\rm{d}}{\varepsilon _{\rm{n}}} - {\rm{d}}{\varepsilon _{{\rm{nd}}}} = \frac{{{\rm{d}}{\sigma _{\rm{n}}}}}{K}. $ | (9) |
式中:εnd为由剪胀引起的法向应变, K为法向模量,可表示为
| $ K = {\left( {\frac{1}{{{K_{\rm{e}}}}} + \frac{1}{{{K_{\rm{p}}}}}h({\sigma _{\rm{n}}} - {\sigma _{{\rm{nm}}}})\frac{{\langle {\rm{d}}{\sigma _{\rm{n}}}\rangle }}{{|{\rm{d}}{\sigma _{\rm{n}}}|}}} \right)^{ - 1}}. $ | (10) |
式中:Ke为法向弹性模量,Kp为法向塑性模量,h(x)为阶梯函数,σnm为最大法向应力.
| $ {K_{\rm{e}}} = \frac{{1 + e}}{\kappa }{p_{\rm{a}}}{\left( {\frac{{{\sigma _{\rm{n}}}}}{{{p_{\rm{a}}}}}} \right)^{0.5}}. $ | (11) |
式中:κ为与法向膨胀相关的材料参数,可表示为
| $ {K_{\rm{p}}} = \frac{{1 + e}}{{\lambda - \kappa }}{p_{\rm{a}}}{\left( {\frac{{{\sigma _{\rm{n}}}}}{{{p_{\rm{a}}}}}} \right)^{0.5}}\left( {\frac{{{M_{\rm{c}}}}}{{{M_{\rm{c}}} - R}}} \right). $ | (12) |
式中:λ为与法向压缩相关的材料参数,可表示为
由剪胀引起的宏观法向应变增量dεnd等于所有由剪胀引起的微观法向应变增量之和,即
| $ {\rm{d}}{\varepsilon _{{\rm{nd}}}} = \frac{1}{M}\sum\limits_{m = 1}^M {\rm{d}} \varepsilon _{{\rm{nd}}}^{(m)}. $ | (13) |
式中εnd(m)为由剪胀引起的第m个微观剪切机构的法向应变.根据张嘎等[3-4]对土与结构接触面的单调和循环剪切试验研究,由剪胀引起的微观法向应变增量可表示为
| $ {\rm{d}}\varepsilon _{{\rm{nd}}}^{(m)} = {d_1}( \pm r_{\rm{d}}^{(m)} - {r^{(m)}}){\rm{d}}\gamma _{\rm{p}}^{(m)}. $ | (14) |
式中:d1为模型参数; γp(m)为第m个微观剪切机构的微观塑性剪应变; ±:在dγp(m)>0时取正,在dγp(m) < 0时取负.为了更好地模拟循环加载过程中的剪胀与剪缩,式(8)中的微观剪胀应力比修正为
| $ r_{\rm{d}}^{(m)} = \frac{{M{M_{\rm{c}}}}}{{\sum\limits_{m = 1}^M | {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{m}}}|}}{\rm{exp}}\left( {\frac{{{n_{\rm{d}}}\psi }}{{1 + {{(\gamma _{{\rm{pcr}}}^{(m)})}^{{d_2}}}}}} \right). $ | (15) |
式中:d2为模型参数,
微观剪应变增量可分为弹性和塑性两部分,即
| $ {\rm{d}}{\gamma ^{(m)}} = {\rm{d}}\gamma _{\rm{e}}^{(m)} + {\rm{d}}\gamma _{\rm{p}}^{(m)}. $ | (16) |
式中γe(m)为第m个微观剪切机构的微观弹性剪应变.根据边界面弹塑性理论[24-26],微观弹性剪应变和微观塑性剪应变的增量可分别表示为
| $ {\rm{d}}\gamma _{\rm{e}}^{(m)} = \frac{1}{{G_{\rm{e}}^{(m)}}}{\rm{d}}{\tau ^{(m)}}. $ | (17) |
| $ \begin{array}{*{20}{l}} {{\rm{d}}\gamma _{\rm{p}}^{(m)} = \frac{1}{{G_{\rm{p}}^{(m)}}}{\sigma _n}{\rm{d}}{r^{(m)}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{H_{\rm{p}}^{(m)}}}h({\sigma _{\rm{n}}} - {\sigma _{{\rm{nm}}}})\frac{{\langle {\rm{d}}{\sigma _{\rm{n}}}\rangle }}{{|{\rm{d}}{\sigma _{\rm{n}}}|}}{r^{(m)}}{\rm{d}}{\sigma _{\rm{n}}}.} \end{array} $ | (18) |
式中:Ge(m)为第m个微观剪切机构的微观弹性剪切模量,Gp(m)为与微观应力比相关的第m个微观剪切机构的微观塑性剪切模量,Hp(m)为与法向应力相关的第m个微观剪切机构的微观塑性剪切模量.
宏微观弹性剪切模量的关系可表示为
| $ G_{\rm{e}}^{(m)} = \frac{{M{G_{\rm{e}}}}}{{\sum\limits_{m = 1}^M {{\rm{co}}{{\rm{s}}^2}} {\alpha _{\rm{m}}}}}. $ | (19) |
式中Ge为宏观弹性剪切模量,可取为[27]
| $ {G_{\rm{e}}} = {G_0}\frac{{{{(2.97 - e)}^2}}}{{1 + e}}{p_{\rm{a}}}{\left( {\frac{{{\sigma _{\rm{n}}}}}{{{p_{\rm{a}}}}}} \right)^{0.5}}. $ | (20) |
式中G0为材料参数.
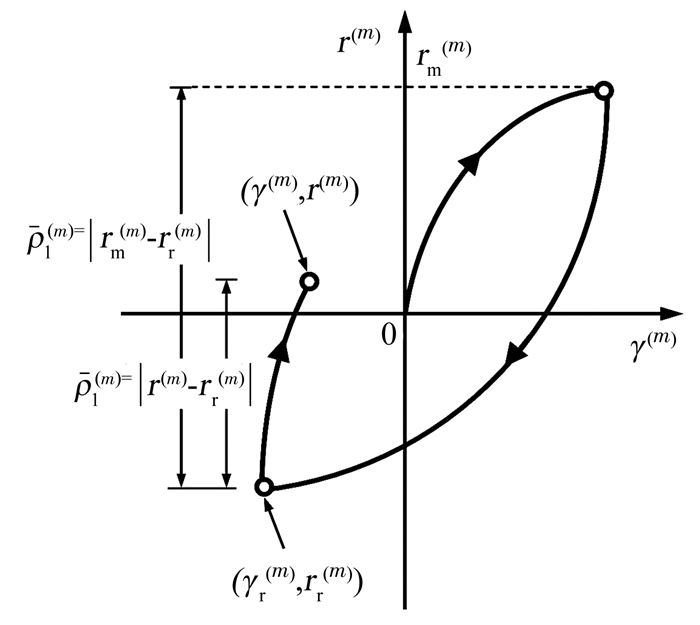
| $ G_{\rm{p}}^{(m)} = {h_1}G_{\rm{e}}^{(m)}\left( {\frac{{r_{\rm{b}}^{(m)}\bar \rho _1^{(m)}}}{{r_{\rm{m}}^{(m)}\rho _1^{(m)}}} - 1} \right). $ | (21) |
式中:h1为模型参数;
|
图 3 微观应力比映射规则 Fig. 3 Mapping rule of micro stress ratio |
| $ H_{\rm{p}}^{(m)} = {h_2}G_{\rm{e}}^{(m)}\frac{{r_{\rm{c}}^{(m)}{{\bar \rho }_2}}}{{{r^{(m)}}{\rho _2}}}. $ | (22) |
式中:h2为模型参数;
根据微观应力比的定义,利用式(16)~(18),微观剪应力可表示为
| $ {\rm{d}}{\tau ^{(m)}} = {G^{(m)}}{\rm{d}}{\gamma ^{(m)}} + (1 - {G^{(m)}}/{H^{(m)}}){r^{(m)}}{\rm{d}}{\sigma _{\rm{n}}}. $ | (23) |
式中
| $ {G^{(m)}} = {\left( {\frac{1}{{G_{\rm{e}}^{(m)}}} + \frac{1}{{G_{\rm{p}}^{(m)}}}} \right)^{ - 1}}, $ | (24) |
| $ {H^{(m)}} = {\left( {\frac{1}{{G_{\rm{e}}^{(m)}}} + \frac{1}{{H_{\rm{p}}^{(m)}}}h({\sigma _{\rm{n}}} - {\sigma _{{\rm{nm}}}})\frac{{\langle {\rm{d}}{\sigma _{\rm{n}}}\rangle }}{{|{\rm{d}}{\sigma _{\rm{n}}}|}}} \right)^{ - 1}}. $ | (25) |
从式(13)、(14)、(16)~(18)和(23),可得
| $ \begin{array}{*{20}{l}} {{\rm{d}}{\varepsilon _{{\rm{nd}}}} = \frac{1}{M}\sum\limits_{m = 1}^M {d_{\rm{r}}^{(m)}} \{ (1 - \frac{{{G^{(m)}}}}{{G_{\rm{e}}^{(m)}}}){\rm{d}}{\gamma ^{(m)}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{G_{\rm{e}}^{(m)}}}\left( {1 - \frac{{{G^{(m)}}}}{{{H^{(m)}}}}} \right){r^{(m)}}{\rm{d}}{\sigma _{\rm{n}}}\} .} \end{array} $ | (26) |
式中
式(26)代入式(9)可得
| $ {\rm{d}}{\sigma _{\rm{n}}} = {K_1}\{ {\rm{d}}{\varepsilon _{\rm{n}}} - \frac{1}{M}\sum\limits_{m = 1}^M {d_{\rm{r}}^{(m)}} \left( {1 - \frac{{{G^{(m)}}}}{{G_{\rm{e}}^{(m)}}}} \right){\rm{d}}{\gamma ^{(m)}}\} . $ | (27) |
式中
| $ {K_1} = \frac{{KM}}{{M - K\sum\limits_{m = 1}^M {d_{\rm{r}}^{(m)}} (1 - {G^{(m)}}/{H^{(m)}})/G_{\rm{e}}^{(m)}}}. $ | (28) |
利用式(1)、(23)和(27),宏观应力-应变增量关系可表示为
| $ {\rm{d}}\mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{D}}{\rm{d}}\mathit{\boldsymbol{\varepsilon }}. $ | (29) |
式中D为弹塑性应力-应变刚度矩阵,表示为
| $ \mathit{\boldsymbol{D}} = {K_1}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{n}}^{{\rm{(0)T}}}} + \frac{1}{M}\sum\limits_{m = 1}^M {( - {Q^{(m)}}\mathit{\boldsymbol{A}} + {G^{(m)}}{\mathit{\boldsymbol{n}}^{(m)}})} {\mathit{\boldsymbol{n}}^{(m){\rm{T}}}}. $ | (30) |
式中
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{n}}^{(0)}} + \frac{1}{M}\sum\limits_{m = 1}^M {{r^{(m)}}} (1 - {G^{(m)}}/{H^{(m)}}){\mathit{\boldsymbol{n}}^{(m)}}, $ | (31) |
| $ {Q^{(m)}} = {K_1}d_{\rm{r}}^{(m)}(1 - {G^{(m)}}/G_{\rm{e}}^{(m)}). $ | (32) |
本模型共计12个参数,分别为:弹性模量参数G0和κ0; 临界状态参数Mc、eΓ和λc; 塑性模量参数h1、h2、nb和λ0; 剪胀参数d1、d2和nd.各参数可按以下方法确定:G0由剪应力-剪切位移曲线的初始斜率计算得出; λ0和κ0分别由法向应力-法向位移关系的加载曲线和卸载曲线求得,κ0也可以用法向弹性模量与弹性剪切模量的线性关系和泊松比计算得出; Mc、eΓ和λc由处于临界状态下的剪应力-剪切位移、法向应力-法向位移关系确定; nb由式(5)求得,其中Mb和ψ分别取应力比达到最大值时的应力比值和ψ值; nd由式(6)求得,其中Md和ψ分别取相变状态时的应力比值和ψ值; h1、h2、d1和d2可用试错法,对剪应力-剪切位移、法向应力-法向位移等关系的试验结果进行模拟计算予以确定.
3 模型验证利用建立的多重剪切边界面模型,对破碎砾石料与混凝土接触面的二维单调和循环剪切试验[3-4, 12-13]以及破碎堆石料与钢板接触面的二维和三维单调剪切试验[6]进行模拟计算.破碎砾石料试样的平均粒径和初始孔隙比分别为10 mm和0.271,接触面厚度可取为100 mm(10倍平均粒径[28]).破碎堆石料试样的平均粒径和初始孔隙比分别为7.5 mm和0.467,接触面厚度可取为75 mm.利用上节所述方法和试验数据确定模型参数值,结果如表 1所示,其中λ0=2κ0.
| 表 1 模型参数 Tab. 1 Model parameters |
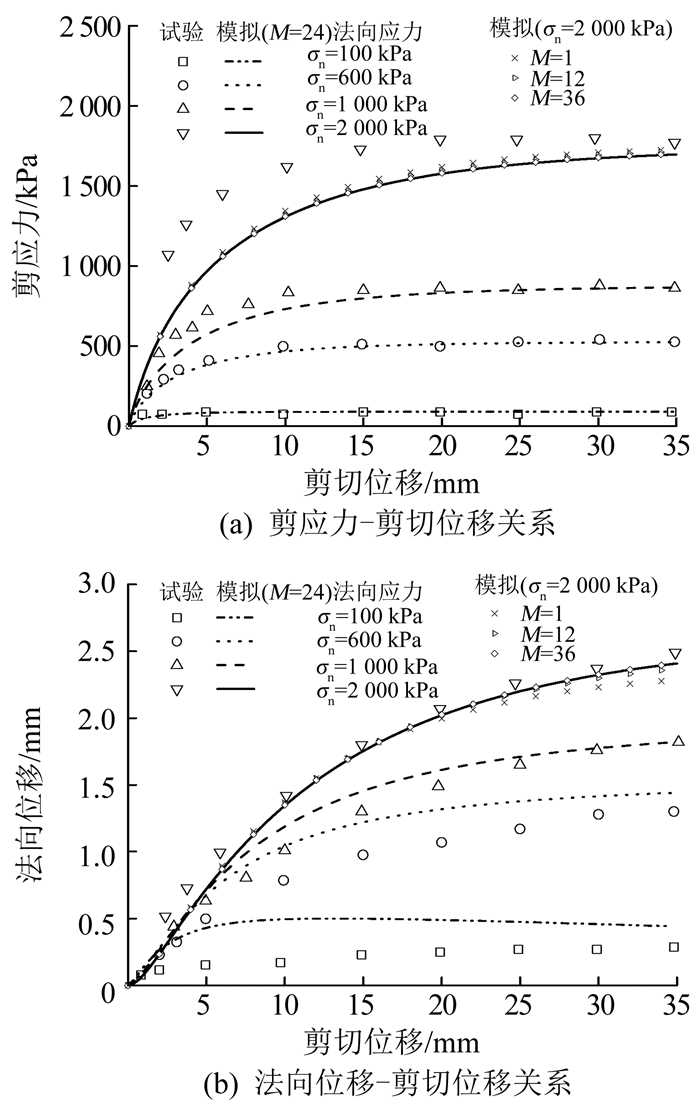
图 4为破碎砾石料-混凝土接触面在100,600,1 000和2 000 kPa法向应力作用下二维单调剪切的试验结果[13]和模型预测.可以看出,模型可以较好地反映不同法向应力作用下的接触面剪切变形和法向变形行为.为了探讨M对计算结果的影响,图 4中列出了法向应力为2 000 kPa、M取不同值时的模拟结果.可以看出,M为24和36时,两者的计算结果几乎相同,因此,本文取24.
|
图 4 砾石料-混凝土接触面二维单调剪切试验模拟 Fig. 4 Simulation of 2D monotonic shear test for gravel-concrete interfaces |
图 5,6分别为破碎砾石料-混凝土接触面在600和2 000 kPa法向应力作用下二维循环剪切的试验结果[13]和模型预测.从两图可以看出,模型预测与试验结果吻合较好,模型不仅较好地模拟了剪应力-剪切位移的循环变化规律,而且合理地描述了法向变形的循环累积压缩行为,即法向位移随循环次数的增加而增大,但其增长速率随循环次数的增加而减小.
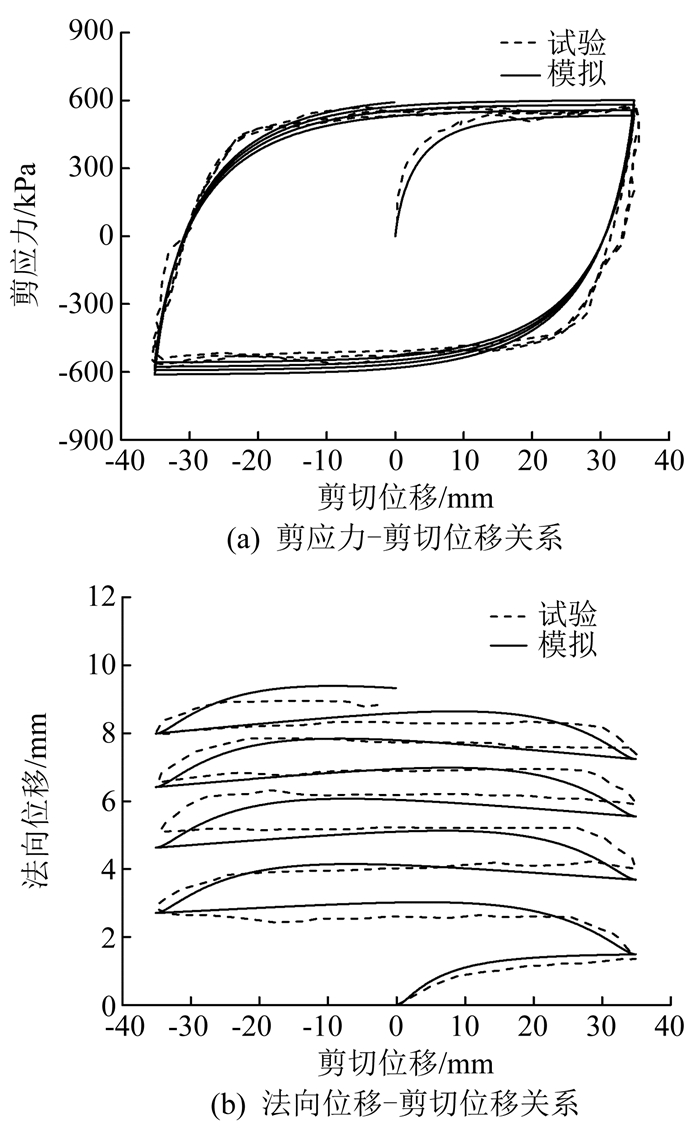
|
图 5 法向应力600 kPa作用下砾石料-混凝土接触面二维循环剪切试验模拟 Fig. 5 Simulation of 2D cyclic shear test for gravel-concrete interfaces at σn=600 kPa |
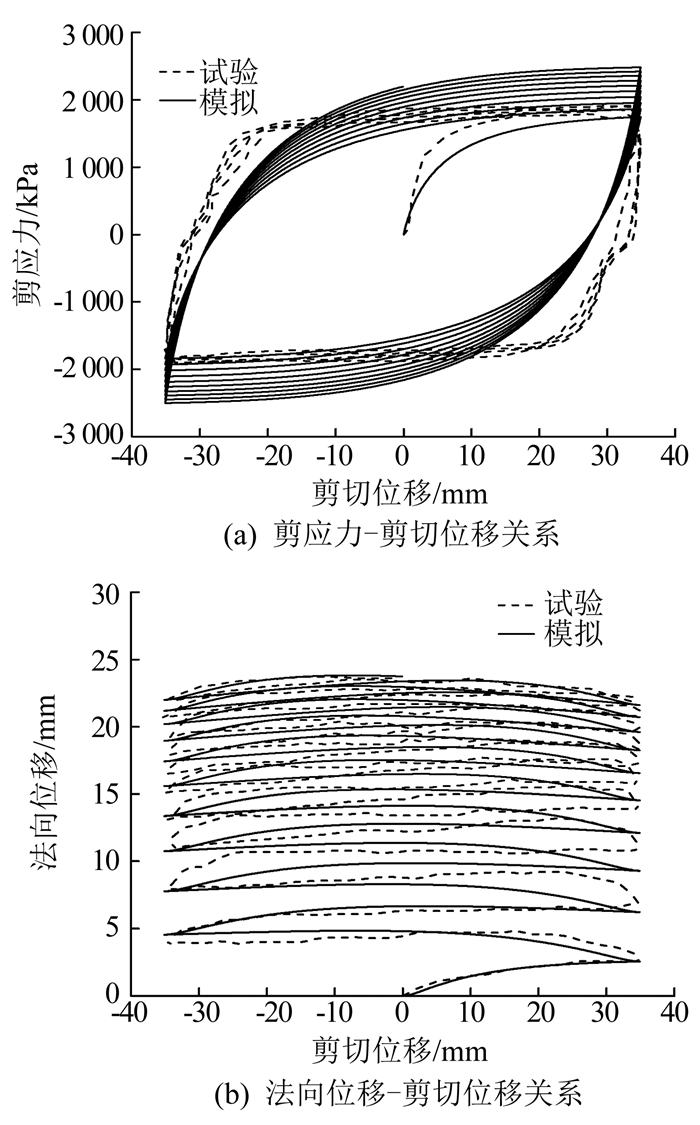
|
图 6 法向应力2 000 kPa作用下砾石料-混凝土接触面二维循环剪切试验模拟 Fig. 6 Simulation of 2D cyclic shear test for gravel-concrete interfaces at σn=2 000 kPa |
图 7为破碎堆石料-钢板接触面在200,400,700和1 000 kPa法向应力作用下二维单调剪切的试验结果[6]和模型预测.可以看出,接触面剪切变形和法向变形的预测值与试验结果吻合较好,模型较准确地描述了低法向应力下以剪胀为主、高法向应力下以剪缩为主的剪胀特性.
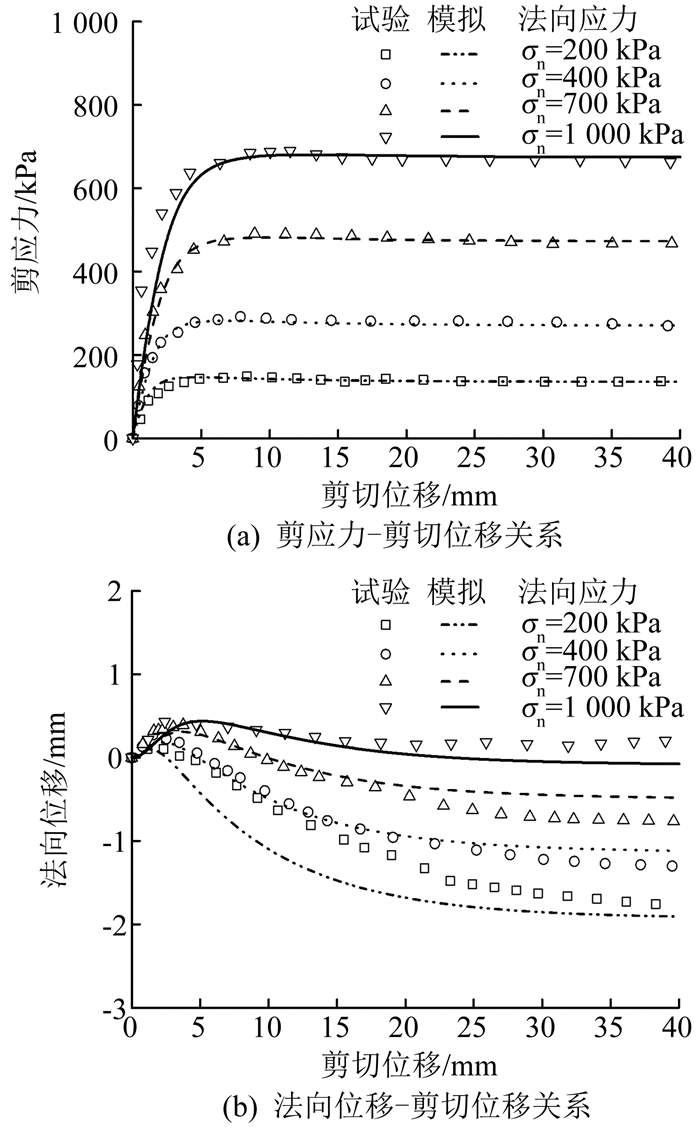
|
图 7 堆石料-钢板接触面二维单调剪切试验模拟 Fig. 7 Simulation of 2D monotonic shear test for rockfill-steel interfaces |
图 8为破碎堆石料-钢板接触面在400 kPa法向应力作用下双向单调剪切的试验结果[6]和模型预测.图 8(a)为双向剪切的应力控制条件,剪切角定义为θ=arctan(τy/τx).图 8(b)~8(f)分别为剪切角等于60°时的Y向剪切位移- X向剪切位移、X向剪应力- X向剪切位移、Y向剪应力- Y向剪切位移、法向位移- X向剪切位移和法向位移- Y向剪切位移关系的试验结果和模型预测,图 8(g)和8(h)分别为0°、30°、60°和90°剪切角下总剪应力-总剪切位移和法向位移-总剪切位移关系的试验结果和模型预测.从这些图可以看出,模型预测与试验结果比较接近,表明本模型可以合理地描述双向剪切条件下各向剪应力-剪切位移、法向位移-剪切位移、总剪应力-总剪切位移和法向位移-总剪切位移关系的变化规律,较好地反映了接触面的三维非线性力学行为.

|
图 8 堆石料-钢板接触面三维单调剪切试验模拟 Fig. 8 Simulation of 3D monotonic shear test for rockfill-steel interfaces |
1) 提出了一个粗粒土与结构接触面的多重剪切边界面模型.本模型把接触面的宏观变形分解为一个宏观法向变形和剪切面内一系列不同方向分布的相互独立虚拟微观剪切变形.通过对不同方向一维力学行为的叠加,可以模拟任意方向剪切以及加载过程中剪切方向可变的三维接触面问题.
2) 在模型中引入状态参数,以考虑法向应力和密度对接触面力学行为的综合影响,使模型既符合粗粒土的临界状态理论,又能用一组材料参数来模拟接触面在不同状态下的剪胀与剪缩特性.
3) 使用本模型对不同粗粒土与结构接触面在二维或三维应力条件下的单调和循环剪切试验进行了模拟计算.通过与试验结果的比较表明,模型能够反映法向和剪切方向的耦合效应,较准确地模拟接触面的非线性力学行为.
| [1] |
EVGIN E, FAKHARIAN K. Effect of stress paths on the behavior of sand-steel interfaces[J]. Canadian Geotechnical Journal, 1996, 33(6): 853. DOI:10.1139/t96-116-336 |
| [2] |
胡黎明, 濮家骝. 土与结构物接触面物理力学特性试验研究[J]. 岩土工程学报, 2001, 23(4): 431. HU Liming, PU Jialiu. Experimental study on mechanical characteristics of soil-structure interface[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 431. |
| [3] |
张嘎, 张建民. 粗粒土与结构接触面单调力学特性的试验研究[J]. 岩土工程学报, 2004, 26(1): 21. ZHANG Ga, ZHANG Jianmin. Experimental study on monotonic behavior of interface between soil and structure[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 21. |
| [4] |
张嘎, 张建民. 循环荷载作用下粗粒土与结构接触面变形特性的试验研究[J]. 岩土工程学报, 2004, 26(2): 254. ZHANG Ga, ZHANG Jianmin. Experimental study on cyclic behavior of interface between soil and structure[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(2): 254. |
| [5] |
周小文, 龚壁卫, 丁红顺, 等. 砾石垫层-混凝土接触面力学特性单剪试验研究[J]. 岩土工程学报, 2005, 27(8): 876. ZHOU Xiaowen, GONG Biwei, DING Hongshun, et al. Large-scale simple shear test on mechanical properties of interface between concrete face and gravel underlayer[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(8): 876. |
| [6] |
侯文峻.土与结构接触面三维静动力变形规律与本构模型研究[D].北京: 清华大学, 2008 HOU Wenjun. Research on monotonic and cyclic behavior and constitutive model of three-dimensional soil-structure interface[D]. Beijing: Tsinghua University, 2008 |
| [7] |
冯大阔, 张嘎, 张建民, 等. 常刚度条件下粗粒土与结构接触面三维力学特性试验研究[J]. 岩土工程学报, 2009, 31(10): 1571. FENG Dakuo, ZHANG Ga, ZHANG Jianmin, et al. Experimental study on 3D cyclic behavior of soil-structure interface under constant normal stiffness condition[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1571. |
| [8] |
朱俊高, SHAKIRR R, 杨有莲, 等. 土-混凝土接触面特性环剪单剪试验比较研究[J]. 岩土力学, 2011, 32(3): 692. ZHU Jungao, SHAKIR R R, YANG Youlian, et al. Comparison of behaviors of soil-concrete interface from ring-shear and simple shear tests[J]. Rock and Soil Mechanics, 2011, 32(3): 692. |
| [9] |
袁运涛, 施建勇. 土与结构界面位移特性静动力单剪试验研究[J]. 岩土力学, 2011, 32(6): 1707. YUAN Yuntao, SHI Jianyong. Study of displacement behavior of interface between soil and structure by static and dynamic simple shear tests[J]. Rock and Soil Mechanics, 2011, 32(6): 1707. |
| [10] |
殷宗泽, 朱泓, 许国华. 土与结构材料接触面的变形及其数学模拟[J]. 岩土工程学报, 1994, 16(3): 14. YIN Zongze, ZHU Hong, XU Guohua. Numerical simulation of the deformation in the interface between soil and structural material[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 14. |
| [11] |
张冬霁, 卢廷浩. 一种土与结构接触面模型的建立与应用[J]. 岩土工程学报, 1998, 20(6): 62. ZHANG Dongji, LU Tinghao. Establishment and application of an interface model between soil and structure[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(6): 62. |
| [12] |
张嘎, 张建民. 粗粒土与结构接触面统一本构模型及试验验证[J]. 岩土工程学报, 2005, 27(10): 1175. ZHANG Ga, ZHANG Jianmin. Unified modeling of soil-structure interface and its test confirmation[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(10): 1175. |
| [13] |
ZHANG Ga, ZHANG Jianmin. Unified modeling of monotonic and cyclic behavior of interface between structure and gravelly soil[J]. Soils and Foundations, 2008, 48(2): 231. DOI:10.3208/sandf.48.231 |
| [14] |
LIU Huabei, SONG Erxiang, LING H I. Constitutive modeling of soil-structure interface through the concept of critical state soil mechanics[J]. Mechanics Research Communications, 2006, 33(4): 515. DOI:10.1016/j.mechrescom.2006.01.002 |
| [15] |
LIU Huabei, LING H I. Constitutive description of interface behavior including cyclic loading and particle breakage within the framework of critical state soil mechanics[J]. International Journal of Numerical and Analytical Methods in Geomechanics, 2008, 32(12): 1495. DOI:10.1002/nag.682 |
| [16] |
彭凯, 朱俊高, 冯树荣, 等. 考虑剪胀与软化的接触面弹塑性模型[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3978. PENG Kai, ZHU Jungao, FENG Shurong, et al. Elasto-plastic constitutive model of interface incorporating strain softening and dilatancy[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3978. |
| [17] |
LIU Jingmao, ZOU Degao, KONG Xianjing. A three-dimensional state-dependent model of soil-structure interface for monotonic and cyclic loadings[J]. Computers and Geotechnics, 2014, 61: 166. DOI:10.1016/j.compgeo.2014.05.012 |
| [18] |
刘京茂, 孔宪京, 邹德高. 接触面模型对面板与垫层间接触变形及面板应力的影响[J]. 岩土工程学报, 2015, 37(4): 700. LIU Jingmao, KONG Xianjing, ZOU Degao. Effects of interface models on deformation of interface between slab and cushion layer and slab stress of concrete faced rock fill dam[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 700. |
| [19] |
路德春, 罗磊, 王欣, 等. 土与结构接触面土体软/硬化本构模型及数值实现[J]. 工程力学, 2017, 34(7): 41. LU Dechun, LUO Lei, WANG Xin, et al. Softening/hardening constitutive model for soil-structure interface and numerical implementation[J]. Engineering Mechanics, 2017, 34(7): 41. |
| [20] |
STUTZ H, MASIN D, WUTTKE F. Enhancement of a hypoplastic model for granular soil-structure interface behaviour[J]. Acta Geotechnica, 2016, 11(6): 1249. DOI:10.1007/s11440-016-0440-1 |
| [21] |
SABERI M, ANNAN C D, KONRAD J M, et al. A critical state two-surface plasticity model for gravelly soil-structure interfaces under monotonic and cyclic loading[J]. Computers and Geotechnics, 2017, 80: 71. DOI:10.1016/j.compgeo.2016.06.011 |
| [22] |
SABERI M, ANNAN C D, KONRAD J M. Constitutive modeling of gravelly soil-structure interface considering particle breakage[J]. Journal of Engineering Mechanics, 2017, 143(8). DOI:10.1061/(ASCE)EM.1943-7889.0001246 |
| [23] |
BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99. DOI:10.1680/geot.1985.35.2.99 |
| [24] |
LI X S. A sand model with state-dependent dilatancy[J]. Géotechnique, 2002, 52(3): 173. DOI:10.1680/geot.2002.52.3.173 |
| [25] |
WANG Z L, DAFALIAS Y F, SHEN C K. Bounding surface hypoplasticity model for sand[J]. Journal of Engineering Mechanics, 1990, 116(5). DOI:10.1061/(ASCE)0733-9399(1990)116:5(983) |
| [26] |
FANG H L, ZHENG H, ZHENG Jun. Micromechanics-based multimechanism bounding surface model for sands[J]. International Journal of Plasticity, 2017, 90: 242. DOI:10.1016/j.ijplas.2017.01.011 |
| [27] |
RICHART F E, HALL J R, WOODS R D. Vibrations of soils and foundations[M]. Englewood Cliffs, NJ: Prentice-Hall, 1970
|
| [28] |
WANG Jianfeng, GUTIERREZ M S, DOVE J E. Numerical studies of shear banding in interface shear tests using a new strain calculation method[J]. International Journal of Numerical and Analytical Methods in Geomechanics, 2007, 31(12): 1349. DOI:10.1002/nag.589 |
 2020, Vol. 52
2020, Vol. 52



