纵向成层土与桩基相互作用体系耦合振动特性研究一直都是岩土工程领域的热点问题[1-2].桩周土体在桩基施工过程中会产生沿桩基径向的不均匀性[3],而此种径向非均质效应对桩基纵向振动特性的影响也受到国内外学者的广泛关注.
Novak等[4]利用滞回阻尼模型考虑土体黏性,并采用平面应变理论建立了存在单层内部扰动区域的桩身-土体动力相互作用模型,初步分析了土体径向非均质效应对桩身纵向振动特性的影响.在此基础上,EI Naggar[5]为更合理地考虑桩周土的径向不均匀性,将内部区域进一步划分为多个圈层,分析了施工扰动效应对桩基纵向振动特性的影响.王奎华等[6-7]指出EI Naggar模型与实测曲线存在较大差别,Wang等[8-9]基于此对EI Naggar模型进行修正,土体材料采用滞回阻尼模型,提出了较为严格的平面应变径向多圈层模型,进行了桩顶振动特性频域解析和时域半解析研究.
以上研究对象均为实心桩,然而管桩由于存在桩芯土,与实心桩振动特性必然存在一定差异性.刘汉龙等[10]基于桩身三维模型,忽略土体对管桩的约束作用,研究了管桩桩身平截面假定对桩顶动力响应的影响深度.丁选明等[11]在此基础上将桩周土及桩芯土对管桩的作用简化为弹簧-阻尼器模型,分析了桩顶速度反射曲线的影响因素.此外,丁选明等[12]利用简化的平面应变模型考虑土体作用,郑长杰等[13]基于三维轴对称模型,Zheng等[14]考虑土体真三维波动效应,对均质黏弹性地基中管桩纵向振动频域特性进行理论研究.为考虑管桩在施工过程中引起土体径向非均质效应,Li等[15]考虑土层复杂非均匀特性,采用滞回阻尼模型,对管桩-土耦合纵向振动特性进行解析研究.
综上,考虑管桩施工扰动引起径向非均质性的研究较少,且在考虑此种效应时土体材料阻尼均采用滞回阻尼模型(与频率及应变速率无关),其在解决非谐和激振问题时不考虑土体材料阻尼随频率及应变速率的变化会在概念上引起矛盾,此时采用黏性阻尼模型[16-17]更为合理.崔春义等[18]基于黏性阻尼土体模型,考虑土层径向非均质效应,对考虑施工扰动效应的管桩-土耦合纵向振动特性进行研究.因土体天然沉积作用使得其沿纵向成层分布,且桩基施工过程中的扰动会引起土体的径向非均质,为考虑土体这种复杂非均质特性,同时避免土体滞回阻尼模型在应用非谐和激振问题时产生的矛盾,提出一种基于土体黏性阻尼的双向非均质土体-管桩动力相互作用模型,通过解析方法求解了管桩桩顶受任意荷载作用下的纵向振动特性,为管桩抗振防振设计提供理论指导.
1 桩土动力相互作用模型 1.1 力学简化模型根据土体纵向成层特性,将桩周土-管桩-桩芯土相互作用体系分成m个层段,各层段自桩身底部依次编号为1, 2, …, i, …, m,厚度为l1, l2, …, li, …, lm,顶部埋深为h1, h2, …,hi,…,hm.管桩面积、弹性模量、密度、内径和外径分别为AiP、EiP、ρiP、ri0和ri1,桩底支承阻尼系数和刚度系数分别为δp和kp.第i层段桩芯土密度、剪切模量和黏性阻尼系数分别为ρi0、Gi0和ηi0.第i层段桩周土体厚度为bi的内部扰动区域划分为n个径向圈层,其中第j圈层桩周土的密度、剪切模量和黏性阻尼系数分别为ρij、Gij和ηij,其值按式(1)和式(2)确定:
| $ {G_{ij}}(r) = \left\{ {\begin{array}{*{20}{c}} {{G_{i1}},}&{r = {r_{i1}},}\\ {{G_{i(n + 1)}} \times {f_i}(r),}&{{r_{i1}} < r < {r_{i(n + 1)}},}\\ {{G_{i(n + 1)}},}&{r \ge {r_{i(n + 1)}},} \end{array}} \right. $ | (1) |
| $ {\eta _{ij}}(r) = \left\{ {\begin{array}{*{20}{c}} {{\eta _{i1}},}&{r = {r_{i1}},}\\ {{\eta _{i(n + 1)}} \times {f_i}(r),}&{{r_{i1}} < r < {r_{i(n + 1)}},}\\ {{\eta _{i(n + 1)}},}&{r \ge {r_{i(n + 1)}}.} \end{array}} \right. $ | (2) |
式中fi(r)为二次函数形式[8].
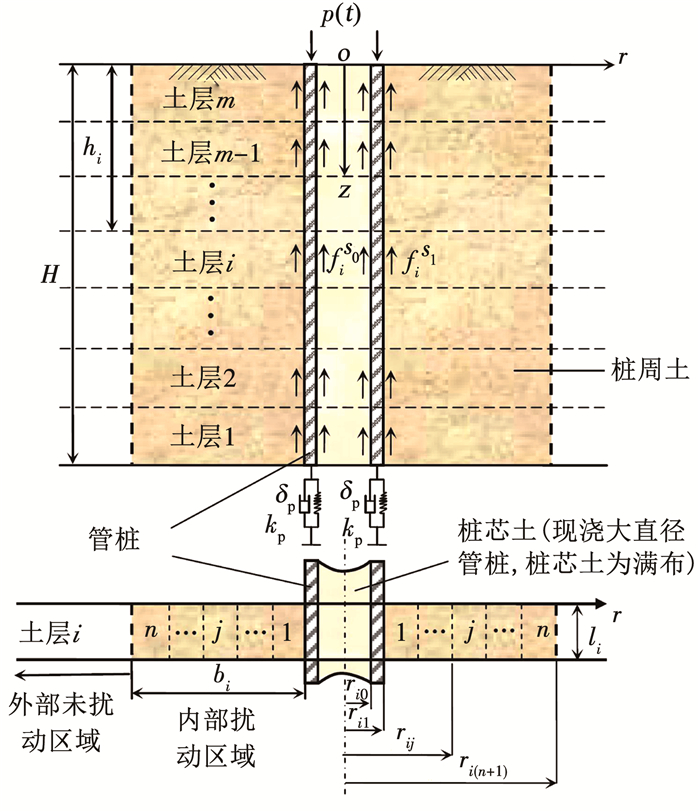
桩土耦合振动体系力学简化模型如图 1所示.本文基本假定参照文献[16]相关描述.
|
图 1 桩土动力相互作用模型 Fig. 1 Dynamic interaction model for pile-soil system |
平面应变条件下基于土体黏性阻尼模型的桩周土和桩芯土纵向振动控制方程为
| $ \begin{array}{*{20}{c}} {{G_{ij}}\frac{{{\partial ^2}w_{ij}^1(r,t)}}{{\partial {r^2}}} + {\eta _{ij}}\frac{{{\partial ^3}w_{ij}^1(r,t)}}{{\partial t\partial {r^2}}} + \frac{{{G_{ij}}}}{r}\frac{{{\partial ^2}w_{ij}^1(r,t)}}{{\partial {t^2}}} + }\\ {\frac{{{\eta _{ij}}}}{r}\frac{{{\partial ^3}w_{ij}^1(r,t)}}{{\partial t\partial r}} = {\rho _{ij}}\frac{{{\partial ^2}w_{ij}^1(r,t)}}{{\partial {t^2}}},} \end{array} $ | (3) |
| $ \begin{array}{*{20}{c}} {{G_{i0}}\frac{{{\partial ^2}w_i^0(r,t)}}{{\partial {r^2}}} + {\eta _{i0}}\frac{{{\partial ^3}w_i^0(r,t)}}{{\partial t\partial {r^2}}} + \frac{{{G_{i0}}}}{r}\frac{{\partial w_i^0(r,t)}}{{\partial r}} + }\\ {\frac{{{\eta _{i0}}}}{r}\frac{{{\partial ^3}w_i^0(r,t)}}{{\partial t\partial r}} = {\rho _{i0}}\frac{{{\partial ^2}w_i^0(r,t)}}{{\partial {t^2}}},} \end{array} $ | (4) |
式中wi0、wij1分别为桩芯和桩周土体位移.
设第i层段桩身位移为wip,则桩身纵向振动方程为
| $ \frac{{{\partial ^2}w_i^p}}{{\partial {z^2}}} - \frac{{2\pi {r_{i1}}f_i^{{S_1}}}}{{E_i^PA_i^P}} - \frac{{2\pi {r_{i0}}f_i^{{S_0}}}}{{E_i^PA_i^P}} = \frac{{\rho _i^P}}{{E_i^P}}\frac{{{\partial ^2}w_i^p}}{{\partial {t^2}}}, $ | (5) |
式中fiS0、fiS1分别为第i层段桩芯土和桩周土对桩身产生的切应力.
桩芯土边界条件为
| $ {\mathop {{\rm{lim}}}\limits_{r \to 0} w_i^0(r,t) = {\rm{ 有限值 }},} $ | (6) |
| $ {w_i^0({r_{i0}},t) = w_i^p({r_{i0}},t),} $ | (7) |
| $ {f_i^{{S_0}} = \tau _i^{{S_0}}({r_{i0}}).} $ | (8) |
桩周土边界条件为
| $ {\mathop {{\rm{lim}}}\limits_{r \to \infty } w_{i(n + 1)}^1(r,t) = 0,} $ | (9) |
| $ {w_i^1({r_{i1}},t) = w_i^p({r_{i1}},t),} $ | (10) |
| $ f_i^{{S_1}} = \tau _i^{{S_1}}({r_{i1}}). $ | (11) |
桩身边界条件为
| $ {{{\left. {E_m^PA_m^P\frac{{\partial w_m^P}}{{\partial z}}} \right|}_{z = 0}} = - p(t),} $ | (12) |
| $ {E_1^P\frac{{\partial w_1^P}}{{\partial z}} + {{\left. {({k_{\rm{p}}}w_1^P + {\delta _{\rm{p}}}\frac{{\partial w_1^P}}{{\partial t}})} \right|}_{z = H}} = 0.} $ | (13) |
对方程(3)进行Laplace变换得
| $ \begin{array}{l} {G_{ij}}\frac{{{\partial ^2}}}{{\partial {r^2}}}W_{ij}^1(r,s) + {\eta _{ij}}s\frac{{{\partial ^2}}}{{\partial {r^2}}}W_{ij}^1(r,s) + \frac{{{G_{ij}}}}{r}\frac{\partial }{{\partial r}}W_{ij}^1(r,s) + \\ \frac{{{\eta _{ij}}s}}{r}\frac{\partial }{{\partial r}}W_{ij}^1(r,s) = {\rho _{ij}}{s^2}W_{ij}^1(r,s), \end{array} $ | (14) |
式中Wij1(r, s)为wij1(r, t)的Laplace变换.
进一步对式(14)进行整理可得
| $ \frac{{{\partial ^2}}}{{\partial {r^2}}}W_{ij}^1 + \frac{1}{r}\frac{\partial }{{\partial r}}W_{ij}^1 = {(q_{ij}^{{S_1}})^2}W_{ij}^1, $ | (15) |
式中
求解可得方程(15)的通解为
| $ W_{ij}^1 = A_{ij}^1{K_0}(q_{ij}^1r) + B_{ij}^1{I_0}(q_{ij}^1r). $ | (16) |
式中:I0(qij1r)、K0(qij1r)分别为零阶第一类、第二类修正Bessel函数,Aij1、Bij1为待定系数.
进一步利用桩周土体边界条件及各圈层的连续条件可得土层剪切刚度递推公式为
| $ FF_{ij}^1 = 2\pi {r_{ij}}({G_{ij}} + {\eta _{ij}}s)q_{ij}^1\frac{{C_{ij}^1 + M_{ij}^1FF_{i(j + 1)}^1}}{{D_{ij}^1 + N_{ij}^1FF_{i(j + 1)}^1}}. $ | (17) |
式中:FFij1、FFi(n+1)1分别为第i层段j圈层中外边界(r=ri(j+1))和内边界(r=rij)处的剪切刚度.
| $ \begin{array}{*{20}{l}} {C_{ij}^1 = 2\pi {r_{i(j + 1)}}({G_{ij}} + {\eta _{ij}}s)q_{ij}^1[{I_1}(q_{ij}^1{r_{i(j + 1)}}){K_1}(q_{ij}^1{r_{ij}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_1}(q_{ij}^1{r_{i(j + 1)}}){I_1}(q_{ij}^1{r_{ij}})],} \end{array} $ |
| $ \begin{array}{*{20}{l}} {D_{ij}^1 = 2\pi {r_{i(j + 1)}}({G_{ij}} + {\eta _{ij}}s)q_{ij}^1[{I_1}(q_{ij}^1{r_{i(j + 1)}}){K_0}(q_{ij}^1{r_{ij}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_1}(q_{ij}^1{r_{i(j + 1)}}){I_0}(q_{ij}^1{r_{ij}})],} \end{array} $ |
| $ {M_{ij}^1 = {K_0}(q_{ij}^1{r_{i(j + 1)}}){I_1}(q_{ij}^1{r_{ij}}) + {K_1}(q_{ij}^1{r_{ij}}){I_0}(q_{ij}^1{r_{i(j + 1)}}),} $ |
| $ {N_{ij}^1 = - {K_0}(q_{ij}^1{r_{i(j + 1)}}){I_0}(q_{ij}^1{r_{ij}}) + {K_0}(q_{ij}^1{r_{ij}}){I_0}(q_{ij}^1{r_{i(j + 1)}}).} $ |
对方程(4)进行Laplace变换可得
| $ \begin{array}{*{20}{l}} {{G_{i0}}\frac{{{\partial ^2}}}{{\partial {r^2}}}W_i^0(r,s) + {\eta _{i0}}s\frac{{{\partial ^2}}}{{\partial {r^2}}}W_i^0(r,s) + \frac{{{G_{i0}}\partial }}{r}\frac{\partial }{{\partial r}}W_i^0(r,s) + }\\ {\frac{{{\eta _{i0}}s}}{r}\frac{\partial }{{\partial r}}W_i^0(r,s) = {\rho _{i0}}{s^2}W_i^0(r,s),} \end{array} $ | (18) |
式中Wi0(r, s)为wi0(r, t)的Laplace变换.
进一步对式(18)进行整理可得
| $ \frac{{{\partial ^2}}}{{\partial {r^2}}}W_i^0 + \frac{1}{r}\frac{\partial }{{\partial r}}W_i^0 = {(q_i^0)^2}W_i^0, $ | (19) |
式中
对方程(19)进行求解并利用桩芯土体边界条件可得管桩内壁受到桩芯土体的剪切刚度为
| $ \begin{array}{*{20}{l}} {FF_i^0 = - \frac{{2\pi {r_{i0}}\tau _i^{{S_0}}({r_0})}}{{W_i^P}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2\pi {r_{i0}}q_i^0({G_{i0}} + {\eta _{i0}}s)\frac{{{I_1}(q_i^0{r_{i0}})}}{{{I_0}(q_i^0{r_{i0}})}}.} \end{array} $ | (20) |
对式(5)进行Laplace变换,并将由式(17)递推所得FFi11和式(20)计算所得FFi0代入可得
| $ \frac{{{\partial ^2}W_i^P}}{{\partial {z^2}}} - \alpha _i^2W_i^P = 0. $ | (21) |
式中:
求解可得方程(21)的通解为
| $ W_i^P = M_i^P{{\rm{e}}^{{{\bar \alpha }_i}z/{l_i}}} + N_i^P{{\rm{e}}^{ - {{\bar \alpha }_i}z/{l_i}}}. $ | (22) |
式中:
进一步利用阻抗函数传递性可得管桩桩顶动力阻抗函数
| $ Z_m^P{|_{z = {h_m} = 0}} = \frac{{ - E_m^PA_m^P{{\bar \alpha }_m}({\beta _m} - 1)}}{{{l_m}({\beta _m} + 1)}} = \frac{{ - E_m^PA_m^P}}{{{l_m}}}Z_m^{{P^\prime }}. $ | (23) |
式中:
参照文献[6]取径向圈层数n=20,纵向层段取m=5,如无特殊说明,管桩具体参数取值如下:ri0=0.38 m,ri1=0.50 m,ρiP=2 500 kg/m3,EiP=25 GPa,H=6 m,kp=1 000 kN/m3,δp=100 kN/m3.桩周各圈层土体相关参数按如下方式取值:
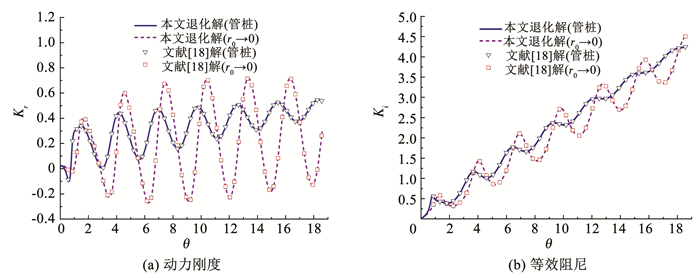
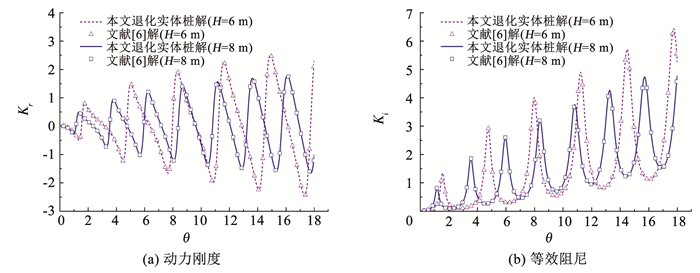
为了验证本文所提模型及相关解析解答的合理性,分别将本文推导所得桩顶动力阻抗解析解答退化到土体纵向均质和实体桩情况,与文献[18]和文献[6]已有解进行对比,如图 2和3所示.图中
|
图 2 本文解析解退化与已有解[18]对比验证 Fig. 2 Comparison of the proposed analytical solution with the solution in Ref.[18] |
|
图 3 本文解析解退化与已有解[6]对比验证 Fig. 3 Comparison of the proposed analytical solution with Wang's solution in Ref.[6] |
桩周土纵向成层特性对桩顶动力阻抗影响如图 4所示.假设桩周存在一个参数不同的某纵向夹层,厚度为1 m,距桩顶距离为3.8 m.定义λ为该夹层土体剪切波速与其余土层剪切波速的比值,λ < 1为软弱夹层,λ>1为硬夹层.由图 4可知,软硬夹层的存在仅对一定低频范围内的振动幅值有较明显影响,其对共振频率的影响则相对较小.剪切波速比越小(大),夹层越软(硬),共振频率处对应的动力阻抗振幅水平越高(低).当夹层剪切波速比为1.8时,动力阻抗共振幅值减小约25%,当夹层剪切波速比为0.6时,动力阻抗共振幅值增大约19%.

|
图 4 纵向软、硬夹层对桩顶复刚度曲线的影响 Fig. 4 Effect of vertical soft and hard interlayer on complex stiffness curves of pile head |
众所周知,不同深度范围施工扰动引起的桩周土径向软化程度亦不同.桩周土纵向第i层段施工扰动系数qi随施工软化程度、硬化程度工况变化如表 1所示(i=1, 2, …, 5).
| 表 1 桩周各层段施工软化程度和硬化程度工况 Tab. 1 Soil softening and hardening degree due to construction disturbance |
图 5,6分别为施工扰动引起管桩桩周土径向软(硬)化程度对桩顶复刚度曲线的影响.综合图 5,6和表 1可知,桩周土软(硬)化程度对管桩桩顶复刚度曲线的共振幅值及共振频率均有显著影响.具体地,桩顶动力阻抗曲线的振动幅值和共振频率均随土体径向软化程度的增强而增大,随土体径向硬化程度的增强而降低.当桩周土软化到未扰动土的60%时,桩顶动力阻抗曲线共振幅值增大约38%;

|
图 5 桩周土软化程度对桩顶复刚度曲线的影响 Fig. 5 Effect of softening degree of pile surrounding soil on complex stiffness curves of pile head |

|
图 6 桩周土硬化程度对桩顶复刚度曲线的影响 Fig. 6 Effect of hardening degree of pile surrounding soil on complex stiffness curves of pile head |
当桩周土比未扰动土硬60%时,桩顶动力阻抗曲线共振幅值减小约17%.说明在对管桩纵向振动特性进行分析时,不考虑桩周土体的软化和硬化效应计算所得桩顶纵向振动特性存在较大误差,将对管桩抗振防振设计产生不利影响.
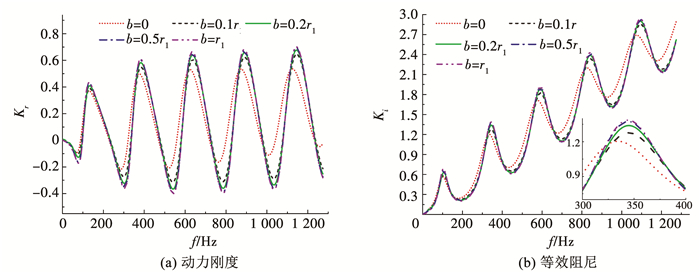
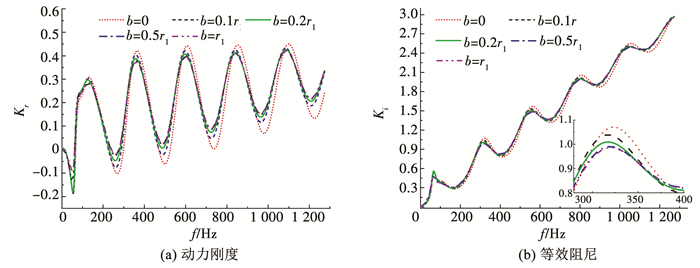
施工扰动范围对桩顶动力阻抗的影响如图 7,8所示.综合两图可以发现,施工扰动范围仅对动力阻抗曲线振动幅值有明显影响,对共振频率的影响可忽略.振动幅值随施工扰动引起土体软(硬)化范围的增大而升高(减小).另外,即使桩周土体扰动范围很小(0.1r1=0.05 m),管桩施工仅影响桩身附近几厘米厚度范围内土体性质,其对桩顶动力阻抗特性的影响同样不可忽略,这就说明考虑施工扰动效应的影响对管桩纵向振动特性进行研究的必要性.
|
图 7 桩周土体软化范围对桩顶复刚度曲线的影响(软化工况S1) Fig. 7 Effect of softening range of pile surrounding soil on complex stiffness curves of pile head (softening condition S1) |
|
图 8 桩周土体硬化范围对桩顶复刚度曲线的影响(硬化工况H4) Fig. 8 Effect of hardening range of pile surrounding soil on complex stiffness curves of pile head (hardening condition H4) |
1) 纵向软硬夹层对一定低频区间内动力阻抗曲线振幅水平影响显著.夹层越软(硬),共振频率处对应的动力阻抗曲线振幅水平越高(低).当夹层剪切波速比为1.8时,动力阻抗共振幅值减小约25%,当夹层剪切波速比为0.6时,动力阻抗共振幅值增大约19%.
2) 桩周土软(硬)化程度对管桩桩顶复刚度曲线的共振幅值及共振频率均有显著影响,当桩周土软化到未扰动土的60%时,桩顶动力阻抗曲线共振幅值增大约38%;当桩周土比未扰动土硬60%时,桩顶动力阻抗曲线共振幅值减小约17%.说明在对管桩纵向振动特性进行分析时,不考虑桩周土体的软化和硬化效应计算所得桩顶纵向振动特性存在较大误差,将对管桩抗振防振设计产生不利影响.
3) 施工扰动土体软(硬)化范围主要影响管桩桩顶复刚度曲线的共振幅值,即使桩周土体扰动范围很小(0.1r1=0.05 m),管桩施工仅影响桩身附近几厘米厚度范围内土体性质,其对桩顶动力阻抗特性的影响同样不可忽略,这就说明考虑施工扰动效应的影响对管桩纵向振动特性进行研究的必要性.
| [1] |
崔春义, 孟坤, 武亚军, 等. 考虑竖向波动效应的径向非均质黏性阻尼土中管桩纵向振动响应研究[J]. 岩土工程学报, 2018, 40(8): 1433. CUI Chunyi, MENG Kun, WU Yajun, et al. Dynamic response of vertical vibration of pipe piles in soils with radial inhomogeneousity and viscous damping considering vertical wave effect[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1433. DOI:10.11779/CJGE201808008 |
| [2] |
CUI Chunyi, MENG Kun, WU Yajun, et al. Dynamic response of pipe pile embedded in layered visco-elastic media with radial inhomogeneity under vertical excitation[J]. Geomechanics and Engineering, 2018, 16(6): 609. DOI:10.12989/gae.2018.16.6.609 |
| [3] |
WU Wenbing, JIANG Guosheng, DOU Bin, et al. Vertical dynamic impedance of tapered pile considering compacting effect[J]. Mathematical Problems in Engineering, 2013(2): 1. DOI:10.1155/2013/304856 |
| [4] |
NOVAK M, HAN Y C. Impedances of soil layer with boundary zone[J]. Journal of Geotechnical Engineering, 1990, 116(6): 1008. DOI:10.1061/(asce)0733-9410(1990)116:6(1008) |
| [5] |
EI NAGGAR M H. Vertical and torsional soil reactions for radially inhomogeneous soil layer[J]. Structural Engineering & Mechanics, 2000, 10(4): 299. DOI:10.12989/sem.2000.10.4.299 |
| [6] |
王奎华, 杨冬英, 张智卿. 基于复刚度传递多圈层平面应变模型的桩动力响应研究[J]. 岩石力学与工程学报, 2008, 27(4): 825. WANG Kuihua, YANG Dongying, ZHANG Zhiqing. Study on dynamic response of pile based on complex stiffness transfer model of radial multizone plane strain[J]. Chinese Journal of Rock Mechanics & Engineering, 2008, 27(4): 825. DOI:10.3321/j.issn:1000-6915.2008.04.024 |
| [7] |
杨冬英, 王奎华. 任意圈层径向非均质土中桩的纵向振动特性[J]. 力学学报, 2009, 41(2): 243. YANG Dongying, WANG Kuihua. Vertical vibration of pile in radially inhomogeneous soil layers[J]. Chinese Journal of Theoretical & Applied Mechanics, 2009, 41(2): 243. DOI:10.6052/0459-1879-2009-2-2007-186 |
| [8] |
WANG Kuihua, YANG Dongying, ZHANG Zhiqing, et al. A new approach for vertical impedance in radially inhomogeneous soil layer[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2012, 36(6): 697. DOI:10.1002/nag.1024 |
| [9] |
WANG Kuihua, YANG Dongying, ZHANG Zhiqing, et al. Vertical dynamic response of pile in a radially heterogeneous soil layer[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2009, 33(8): 1039. DOI:10.1002/nag.755 |
| [10] |
刘汉龙, 丁选明. 现浇薄壁管桩在低应变瞬态集中荷载作用下的动力响应解析解[J]. 岩土工程学报, 2007, 29(11): 1611. LIU Hanlong, DING Xuanming. Analytical solution of dynamic response of cast-in-situ concrete thin-wall pipe piles under transient concentrated load with low strain[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1611. DOI:10.3321/j.issn:1000-4548.2007.11.003 |
| [11] |
丁选明, 刘汉龙. 低应变下变阻抗薄壁管桩动力响应频域解析解[J]. 岩土力学, 2009, 30(6): 1793. DING Xuanming, LIU Hanlong. Analytical solution in frequency domain of dynamic response of thin-wall pipe piles with variable wave impedance under low strain transient concentrated load[J]. Rock & Soil Mechanics, 2009, 30(6): 1793. DOI:10.3969/j.issn.1000-7598.2009.06.046 |
| [12] |
丁选明, 陈磊. 粘弹性地基中管桩的纵向振动特性研究[J]. 长江科学院院报, 2009, 26(3): 32. DING Xuanming, CHEN Lei. Study on vertical vibration characteristics of pipe piles in viscoelastic soil[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(3): 32. DOI:10.3969/j.issn.1001-5485.2009.03.009 |
| [13] |
郑长杰, 丁选明, 黄旭, 等. 滞回阻尼土中大直径管桩纵向振动响应解析解[J]. 岩石力学与工程学报, 2014(增刊1): 3284. ZHENG Changjie, DING Xuanming, HUANG Xu, et al. Analytical solution of vertical vibration response of large diameter pipe pile in hysteretic damping soil[J]. Chinese Journal of Rock Mechanics & Engineering, 2014(S1): 3284. |
| [14] |
ZHENG Changjie, DING Xuanming, SUN Yifei. Vertical vibration of a pipe pile in viscoelastic soil considering the three-dimensional wave effect of soil[J]. International Journal of Geomechanics, 2015, 16(1): 1. DOI:10.1061/(asce)gm.1943-5622.0000529 |
| [15] |
LI Zhenya, WANG Kuihua, WU Wenbing, et al. Vertical vibration of a large-diameter pipe pile considering the radial inhomogeneity of soil caused by the construction disturbance effect[J]. Computers & Geotechnics, 2017, 85: 90. DOI:10.1016/j.compgeo.2016.12.016 |
| [16] |
胡昌斌, 王奎华, 谢康和. 桩与黏性阻尼土耦合纵向振动时桩顶时域响应研究[J]. 振动工程学报, 2004, 17(1): 72. HU Changbin, WANG Kuihua, XIE Kanghe. Time domain axial response of dynamically loaded pile in viscous damping soil layer[J]. Journal of Vibration Engineering, 2004, 17(1): 72. DOI:10.3969/j.issn.1004-4523.2004.01.016 |
| [17] |
廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002. LIAO Zhenpeng. Introduction to engineering wave theory[M]. Beijing: Science Press, 2002. |
| [18] |
崔春义, 孟坤, 武亚军, 等. 径向非均质黏性阻尼土中管桩纵向振动特性[J]. 哈尔滨工业大学学报, 2019, 51(2): 136. CUI Chunyi, MENG Kun, WU Yajun, et al. Dynamic impedance of vertical vibration of pipe pile embedded in radially inhomogeneous viscoelastic soil[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 136. DOI:10.11918/j.issn.03676234.201801140 |
 2020, Vol. 52
2020, Vol. 52


