弹体对地质材料的侵彻属于冲击动力学研究的一个主要内容, 其实验和理论研究已有三百多年的历史.因其在军事方面有着广泛的应用, 目前仍是一个非常热门的研究领域.当今, 随着侵彻深度和爆炸规模大的精确制导武器的迅速发展, 无论是防护结构计算理论与防护技术, 还是制导武器战斗部研制均亟需解决岩石中侵彻局部破坏效应问题.
随着现代科学技术的飞速发展, 现代常规武器的性能日臻完善.对于深埋地下的重要防护工程, 实施单次打击并不能将其一次性摧毁, 故考虑对同一目标实施多弹重复打击.而且, 信息与制导技术的广泛应用使常规武器的精确多弹重复打击成为可能.迄今, 国内外学者对单次打击岩石及混凝土的相关问题开展大量研究.杨刚等[1]基于三维FEM-SPH自适应耦合算法模拟了子弹侵彻混凝土靶跳飞问题, 指出作用于子弹的不对称阻力所产生的力矩是子弹跳飞的根本原因; Wan等[2]通过钢管约束混凝土(STCC)目标的典型损伤模式, 分析了冲击位置、约束钢管直径和厚度对STCC靶材抗穿透性能的影响; 刘峥等[3]基于AUTODYN开展了钨杆弹对成层式防护结构的超高速打击数值计算分析, 得到了结构的破坏特征和能量分配情况; 王海兵等[4-6]通过弹丸侵彻花岗岩和石灰岩靶板实验, 分析了靶板裂纹长度、侵彻深度及靶板的破坏类型; 宋春明等[7-8]对超高速弹体侵彻岩石靶板进行研究, 认为弹体对岩石靶板的侵彻机制随撞击速度的增加发生“刚体侵彻→半流体侵彻→流体侵彻”的转变; 王明洋等[9-10]通过分析侵爆近区岩石介质的动态可压缩性行为, 创造性地构建了流体弹塑性内摩擦侵彻理论模型, 并基于界定超高速侵彻速度内涵范围及钻地弹固体侵彻、拟流体侵彻和流体侵彻的最小动能阈值, 系统地提出了超高速动能弹打击侵深、成坑及地冲安全厚度的计算方法.Gomez等[11-13]对多弹重复打击破坏效应实验及数值模拟分别进行了一些研究, 但多以侵爆为主.考虑到侵爆耦合及各个过程的复杂性, 用控制变量法分析单一因素对重复打击破坏效应的影响则较为困难.目前, 国内外在多弹重复打击破坏效应方面的公开研究成果很少, 可能归结于这类实验研究危险较大、成本高, 且往往只能获得被打击目标破坏后的最终响应结果及部分测点信息.
基于上述研究现状, 本文将多弹重复侵彻过程及其动力响应作为研究重点.根据已有实验数据和理论推导, 初步确定出花岗岩的Johnson-Homquist(JH-2)材料模型与拉伸断裂软化模型耦合模型的相关参数.通过模拟花岗岩单次侵彻试验验证并优化已确定的参数.最后, 将优化后的模型参数用于描述花岗岩的动力响应, 运用非线性动力分析软件AUTODYN[14]并基于FEM-SPH耦合法对花岗岩多弹重复侵彻过程进行模拟, 力求得出对防护工程设计与建设有参考价值的结论.
1 花岗岩损伤本构模型非线性动力分析软件AUTODYN是由美国世纪动力公司研发的, 已成为国际上爆炸力学、高速冲击碰撞领域研究最著名数值模拟软件之一[14], 为模拟高速碰撞问题提供了丰富的材料模型, 如岩石、混凝土、金属和陶瓷等.材料模型通常由两部分组成[15]:1)强度模型, 可利用强度模型通过塑性理论确定材料的畸变响应; 2)状态方程(EOS), 可通过EOS描述材料的体积响应.本文引入JH系列模型中JH-2模型[16], 并将其与拉伸断裂软化模型相耦合[18], 用以模拟花岗岩靶板内高应力区塑性压缩和剪切破坏效应以及低应力区靶板在主拉伸应力作用下产生的损伤和裂纹扩展.其耦合机理详见文献[4, 17], 此处不再赘述.
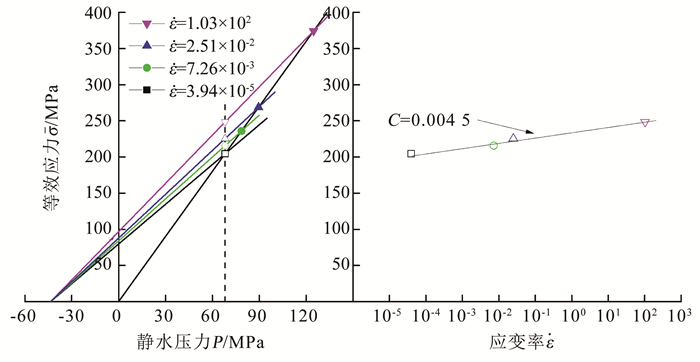
1.1 模型介绍 1.1.1 强度模型JH-2模型的应力和损伤是压力和其他变量的分析函数, 允许以更系统的方式对常数进行参数变化; 当损伤开始累积时, JH-2模型材料开始软化, 允许材料在塑性应变增加的情况下逐渐软化(JH-1模型在材料完全破坏前不会软化, 而在完全破坏时软化立即发生).JH-2材料强度模型描述如图 1(a)所示.可以看出, JH-2材料模型强度是完整强度、断裂强度、应变速率和损伤的平滑变化函数.强度的归一化等效应力可表述为[16]

|
图 1 JH-2材料模型 Fig. 1 JH-2 material model |
| $ {\bar \sigma ^*} = \bar \sigma _{\rm{I}}^* - D(\bar \sigma _{\rm{I}}^* - \bar \sigma _{\rm{F}}^*). $ | (1) |
式中:D为材料损伤因子(0≤D≤1);σI*为完整材料(D=0)的归一化等效应力; σF*为完全破坏材料(D=1)的归一化等效应力.归一化等效应力(σ*, σI*, σF*)可统一表述为σ*=σ/σHEL, σ为实际等效应力, σHEL为Hugoniot弹性极限下的等效应力.
完整材料和完全破坏材料的归一化等效应力表述为[16]
| $ {\sigma _{\rm{I}}^* = A{{({P^*} + {T^*})}^N}(1 + C{\rm{ln}}{{\dot \varepsilon }^*}),} $ | (2) |
| $ {\sigma _{\rm{F}}^* = B{{({P^*})}^M}(1 + C{\rm{ln}}{{\dot \varepsilon }^*}).} $ | (3) |
式中:P*为归一化静水压力, P*=P/PHEL; T*为归一化最大静拉伸应力, T*=TMax/PHEL.其中, P、TMax分别为实际静水压力和岩石材料所能承受的最大静拉伸应力, PHEL为Hugoniot弹性极限下的压力.归一化应变率
损伤因子D是岩石材料从完整到破裂强度的过渡, 损伤演化表达式为[16]
| $ {D = \sum {\frac{{\Delta {\varepsilon _{\rm{p}}}}}{{\varepsilon _{\rm{p}}^{\rm{f}}}},} } $ | (4) |
| $ {\varepsilon _{\rm{p}}^{\rm{f}} = {D_1}{{({P^*} + {T^*})}^{{D_2}}}.} $ | (5) |
式中:Δεp为一个积分循环内的等效塑性应变; εpf为岩石材料在恒定压力P作用下的等效塑性断裂应变, 见图 1(b); D1、D2为损伤参数; P*、T*定义如前所述.
1.1.2 状态方程为了表征岩石类材料在高压冲击下的非线性变形特征, 材料发生损伤前的静水压力与体积应变关系用三次多项式状态方程描述为[16]
| $ P = {K_1}\mu + {K_2}{\mu ^2} + {K_3}{\mu ^3}. $ | (6) |
式中:K1为体积模量, K2、K3为压力常数; 体积应变μ=ρ/ρ0-1, ρ0为初始密度; 当μ < 0, 岩石受拉伸应力作用, 此时P=K1μ.当材料损伤开始累积(D>0)时, 体积膨胀, 静水压力附加一个压力增量ΔP, 即[16]
| $ P = {K_1}\mu + {K_2}{\mu ^2} + {K_3}{\mu ^3} + \Delta P. $ | (7) |
式中:0≤ΔP≤ΔPMax, ΔP在D=0和D=1时分别取到两端点值, 如图 1(c)所示.
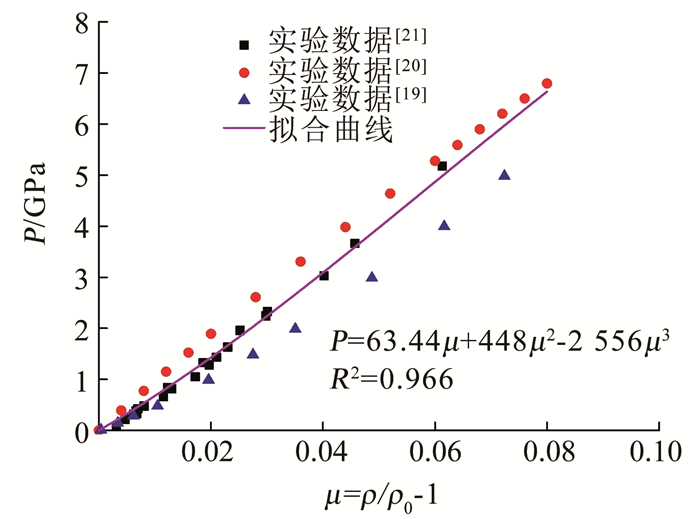
1.2 参数确定 1.2.1 状态方程参数确定花岗岩基本物理力学参数[18]:初始密度ρ0=2 657 kg/m3, 泊松比ν =0.29, 弹性模量E=80 GPa.则剪切模量G=E/2(1+ν)=30.01 GPa, 体积模量K1=E/3(1-2ν)=63.49 GPa.确定岩石P-μ关系所需的高压数据可通过平板试验获得, 如图 2所示.利用式(7)拟合花岗岩不同体积应变率下静水压力[19-20]及花岗岩Hugoniot实验数据[21]可得K1=63.44 GPa, K2=448 GPa, K3=-2 556 GPa.
|
图 2 P-μ关系 Fig. 2 Relation between P and μ |
Hugoniot弹性极限是用于确定材料完整强度的重要参数, 包含了压力和偏应力分量, 其定义为
| $ {L_{{\rm{HE}}}} = {P_{{\rm{HEL}}}} + \frac{2}{3}{\bar \sigma _{{\rm{HEL}}}}. $ | (8) |
式中:花岗岩弹性极限LHE取值为4.5 GPa[4]; PHEL、σHEL定义如前所述, σHEL取为剪切强度2倍[18].联立方程(6)和(8)得[16, 22]
| $ {L_{{\rm{HE}}}} = {K_1}{\mu _{{\rm{HEL}}}} + {K_2}\mu _{{\rm{HEL}}}^2 + {K_3}\mu _{{\rm{HEL}}}^3 + \frac{4}{3}G\frac{{{\mu _{{\rm{HEL}}}}}}{{{\mu _{{\rm{HEL}}}} + 1}}. $ | (9) |
式中:μHEL为LHE下体积应变, 由已知参数LHE、G、K1、K2、K3解得μHEL= 0.038 69, PHEL=2.96 GPa, σHEL=2.31 GPa.
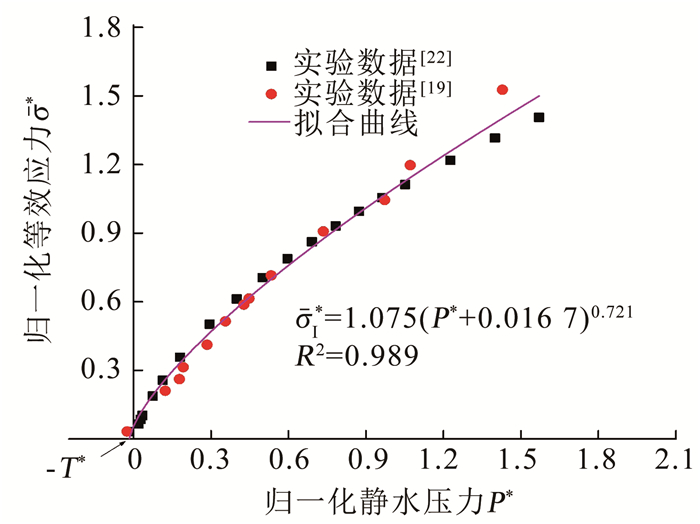
1) D=0时, 完整岩石材料强度在不考虑应变率影响的情况下, 由三轴压缩实验结果[19]经式(2)拟合得常数A=1.075, N=0.721, 如图 3所示.由拟合方程解得曲线与横坐标交点P*=-T*=-0.016 7, 则最大静拉伸应力T=-T*·PHEL=-49.43 MPa.
|
图 3 完整材料等效应力 Fig. 3 Equivalent stress of intact material |
2) 由于缺乏岩石破坏后残余强度的信息, 常数B被认为是常数A的1/3[22], 即B=A/3=0.358;并且常数M被假定为与常数N相同, 则M=N=0.721.此外, 采用25%σHEL的归一化强度作为最大断裂强度σFMax*[22].
3) 应变率影响系数C由材料静态单轴抗压强度和霍普金森单轴冲击实验得到的不同应变率下的抗压强度计算得到.如图 4所示, 不同应变率下单轴均值压应力由实心符号表示, 且根据定义其必定在斜率k=3.0的σ-P直线上, 见图 4左半部分.首先, 从最大拉应力T出发, 分别作通过各实心符号表示的数据点的直线, 所作各直线间斜率的变化反映应变率效应; 再作平行于纵轴且通过最低应变率直线与σ-P直线交点的直线(如图中虚线所示), 并与其他直线相交, 将数据标准化为不同应变率同一静水压力下的强度来量化效果(由空心符号表示), 从而消除静水压力的影响来隔离应变率效应[23].空心符号表示的压应力为对应的应变率函数, 经拟合归一化强度与归一化应变率自然对数对应的数据点得到斜率C=0.004 5, 如图 4右半部分所示.
1.2.3 损伤参数确定岩石材料从未损伤强度到完全破坏强度的过渡由损伤因子D描述.完全破坏脆性材料的塑性应变量非常小且不可能直接测量, 导致无法求解损伤参数D1、D2.相反, 可通过数值模拟试算调整以达到可接受的破坏效果获得可靠的D1、D2的值.模拟中暂取初始损伤参数D1=0.005, D2=0.7[4].
1.2.4 拉伸断裂软化模型参数确定在拉伸断裂软化模型中, 主拉伸失效应力Tf为35 MPa[4]; 而在AUTODYN中拉伸断裂软化模型只涉及一个参数, 即断裂能Gf, 默认值Gf=70 J/m2[4].
2 损伤常数优化及模型参数验证 2.1 SPH算法原理在爆炸与冲击问题的数值模拟中, 材料的高应变率、大变形及失效破坏均要求数值算法能合理描述边界畸变、裂纹扩展等, 同时必然对网格精度及计算成本提出较高要求.对于Lagrange算法, 大变形的网格畸变会使得时间步长过小而导致计算困难甚至终止; 对于Euler算法, 其很难精确捕捉固体材料的变形响应; 而ALE(Arbitrary Lagrange-Euler)算法也存在着因网格不协调导致的Euler物质非物理穿透问题[25].为克服上述各种缺陷, 一种无网格算法——光滑粒子流体动力学方法(SPH)被提出[26], 用于模拟天体物理、连续体结构的解体、碎裂及固体的层裂、脆性断裂等问题, 并逐步解决了可变光滑长度、人工黏性、零能模式、边界处理与多物质界面等相关技术问题.
SPH法通过核函数W(x-x′, h)逼近支持域Ω内任意点的场变量函数f(x), 实现连续体离散成一系列具有质量、坐标、速度与内能等的粒子[25].任意场变量函数f(x)近似值表达式为
| $ \prod\nolimits_{}^h {f(x)} = \int\limits_\varOmega {f({x^\prime })} W(x - {x^\prime },h){\rm{d}}{x^\prime }. $ | (10) |
式中:h为光滑长度, x为质点位置.
在由Monaghan[27]提出的B-Spline光滑函数或插值核心函数邻域内, 如图 5所示, 粒子i的某个变量可以通过粒子集j的加权求和得到

|
图 5 二维粒子邻域与核函数 Fig. 5 Neighborhood and kernel function of 2D particles |
| $ \prod\nolimits_{}^h {f({x_i})} = \sum\limits_{j = 1}^L {{\varPsi _j}} f({x_j})W({x_i} - {x_j},h). $ | (11) |
式中:Ψj=mj/ρj为与粒子j相关的体积, mj、ρj分别为粒子集j的质量与密度(j=1, 2, 3, …, L).
2.2 数值模拟验证分析为得到完整可靠的JH-2与拉伸断裂相耦合模型参数, 采用上述初步确定的状态方程和部分强度模型参数, 利用AUTODYN模拟卵形弹丸冲击花岗岩靶板实验[29].首先, 将数值计算的损伤效果与实验结果进行对比; 然后, 通过数值调整法分析花岗岩在弹丸冲击后的损伤状态, 从而得到可接受的损伤效果及损伤参数D1、D2.为了增加可比性, 二维数值模型中卵形弹丸和靶板尺寸与实验相同, 如图 6所示.

|
图 6 靶板与弹丸尺寸示意 Fig. 6 Schematic diagrams of target plate and ogive-nose projectile |
卵形弹丸射弹头型系数CRH=3.0, 材料为4340钢, 采用Johnson-Cook材料模型描述, 相关参数均采用AUTODYN材料库中参数; 花岗岩靶板材料采用JH-2模型与拉伸断裂软化模型描述, 并在靶板两端施加固定约束.卵形弹丸采用Lagrange算法, 花岗岩靶板采用SPH算法, 通过AUTODYN中的FEM-SPH耦合法实现靶板冲击过程.
一个完整冲击过程中弹丸速度与加速度变化规律如图 7所示.弹丸初始弹速为279 m/s, 在弹丸侵彻开坑阶段, 侵彻深度在2倍弹径范围内(0<z≤4a), 卵形弹头前形成高压区, 阻力Fz[29](Fz=cz, c为常数)呈线性增大, 弹速快速降低.则由牛顿第二定律可知弹丸的减速度亦逐渐增大, 在t=0.12 ms时达最大值-8.2×105 m/s2.此时, 径向裂纹已向外小范围扩展且锥形冲塞雏形萌生, 至其完全形成, 靶板对弹丸的约束阻力逐渐减小至0, 从而弹丸减速度亦逐渐减小至0, 而弹丸保持恒定速度99 m/s不变.

|
图 7 弹丸速度与减速度曲线 Fig. 7 Projectile velocity and deceleration curve |
数值模拟所得花岗岩靶板在卵形弹丸冲击下的最终损伤形态与实验结果对比如图 8所示, 可见弹丸冲击初始阶段, 在迎冲面着弹点附近花岗岩的损伤由剪切应力引起的剪切损伤为主导; 随着冲击波向前传播, 损伤的产生机理为主拉应力, 裂纹通过拉伸应变萌生并向外扩展, 最终在花岗岩体中形成径向拉伸裂纹.将由数值模拟所得的靶板迎冲面弹坑张角α和直径Df及迎冲背面锥形冲击塞高度H和最大直径Dr的值与相应的实验值列于表 1.可以看出, 相关变量的模拟值与实验值相比, 其误差绝对值均在10%以内.同时, 通过图 8中花岗岩靶板裂纹区分布情况对比可知, 模拟所得结果与实验结果基本一致, 说明本文模拟方法能够较好地重现实验中花岗岩真实破坏状态, 亦证明了采用JH-2模型与拉伸断裂软化模型相结合模拟花岗岩靶板侵彻的合理性及模型参数的可靠性.基于上述分析, JH-2材料模型与拉伸断裂软化模型参数列于表 2.
| 表 1 损伤靶板相关变量的模拟值与实验值误差分析 Tab. 1 Analysis of simulated and experimental values of relevant variables of damage target |
| 表 2 JH-2模型与拉伸断裂软化模型参数 Tab. 2 Parameters of JH-2 model and tensile fracture softening model |
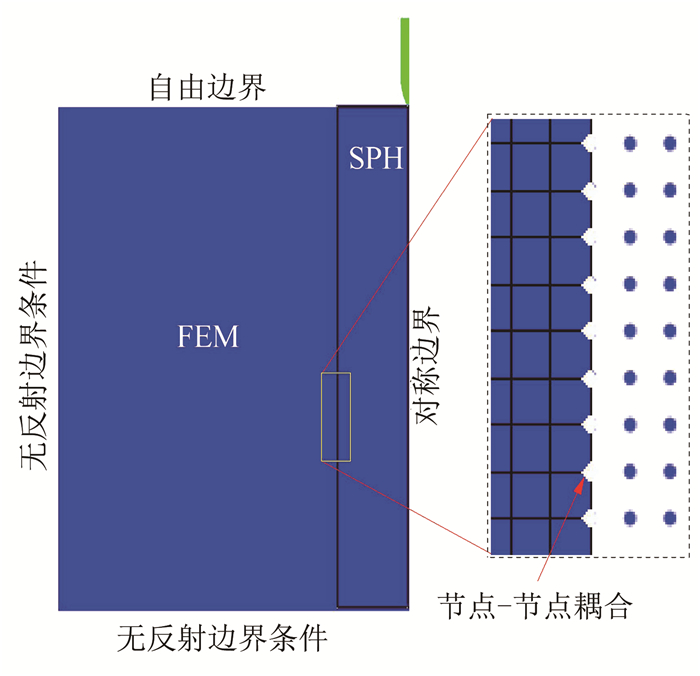
为得出花岗岩在弹丸重复冲击下的相关规律, 用弹径为30 mm, CHR=3.0, 长径比为4.7的弹体冲击直径为1 500 mm, 高为800 mm的花岗岩靶板, 待前次弹体速度出现负值, 或弹体有回弹趋势, 则停止计算, 并重新赋予弹体相同弹速, 实现重复侵彻.弹体材料用4340钢, 参数与2.2节所用材料相同; 花岗岩用JH-2模型与拉伸断裂软化模型耦合模型, 并采用表 1中参数.考虑模型尺寸较大, 为节约计算时间并提高计算效率, 靶板径向0~150 mm范围采用SPH光滑粒子算法, 150~750 mm范围用FEM算法, 并将SPH粒子与FEM单元用共节点连接, 如图 9所示, 与节点到中面节点以及任意节点到面节点两种耦合方式相比[26], FEM-SPH采用共节点耦合, 其界面处相关变量的连续性更好.为消除反射波影响, 靶板模型左侧面及底面设为无反射边界(即透射边界), 用以模拟半无限靶板侵彻.
|
图 9 数值模型及FEM-SPH耦合方式 Fig. 9 Numerical model and FEM-SPH coupling mode |
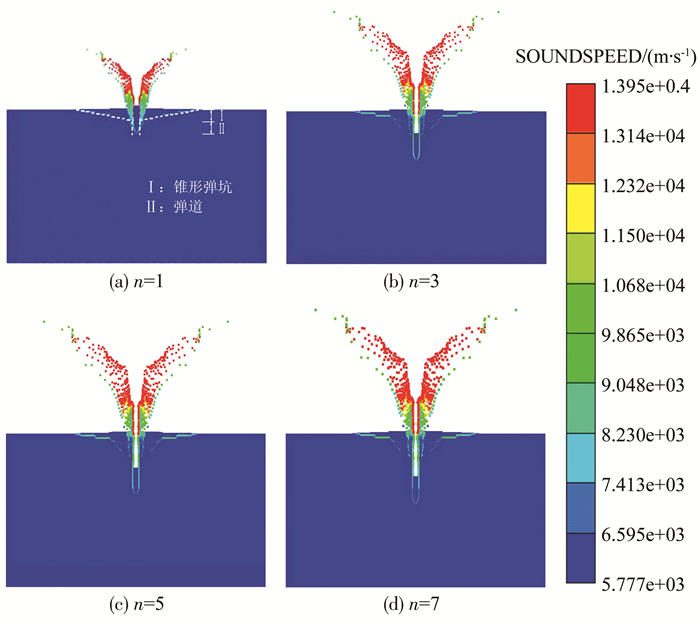
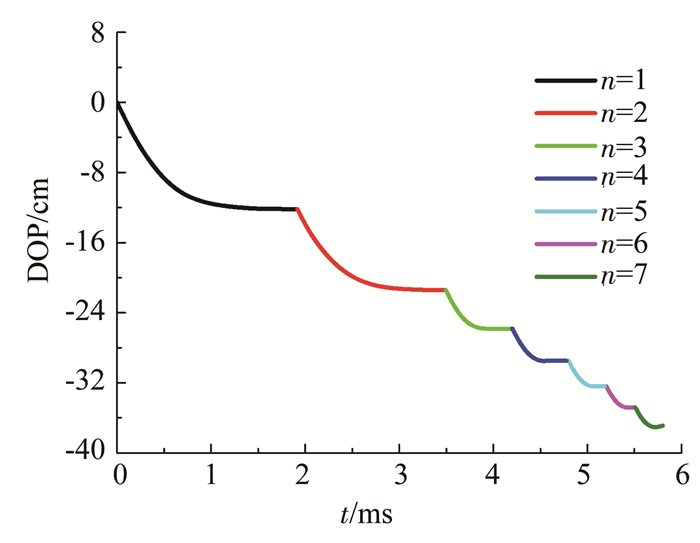
以不同弹速Vs(220, 270, 320, 370及420 m/s)重复侵彻花岗岩靶板, 每个弹速重复侵彻7次.以弹速Vs=220 m/s为例, 数值模拟所得部分重复侵彻过程如图 10所示.弹体第一次冲击花岗岩靶板的破坏情况如图 10(a)所示, 迎冲面整体呈“锥形开坑区+隧道区”组合的破坏形态.介于初次形成的弹道及其对后续侵彻弹体的横向约束作用, 后续各侵彻过程相对稳定, 即随冲击次数的增加, 虽然锥形弹坑直径有一定增加, 但变化范围不大; 由图 10(b)~10(d)可知, 与初次侵彻相比, 后续侵彻各锥形弹坑与弹道交界点, 即弹坑底部到自由面距离的增幅基本一致, 对迎冲面的影响不大.同时, 由弹速Vs=220 m/s重复侵彻7次条件下连续侵彻深度时程曲线可知, 如图 11所示, 初次侵彻为关键的开坑阶段, 其侵彻深度及历时最大; 随侵彻次数n的增加, 相对侵彻深度及相应的历时逐渐减小, 并渐趋于稳定值, 亦说明后续侵彻过程处在一个相对稳定侵彻阶段.
|
图 10 弹速Vs=220 m/s重复侵彻过程 Fig. 10 Repeated penetration process at Vs=220 m/s |
|
图 11 弹速Vs=220 m/s重复侵彻深度时程曲线 Fig. 11 Time history curve of repeated penetration depth at Vs=220 m/s |
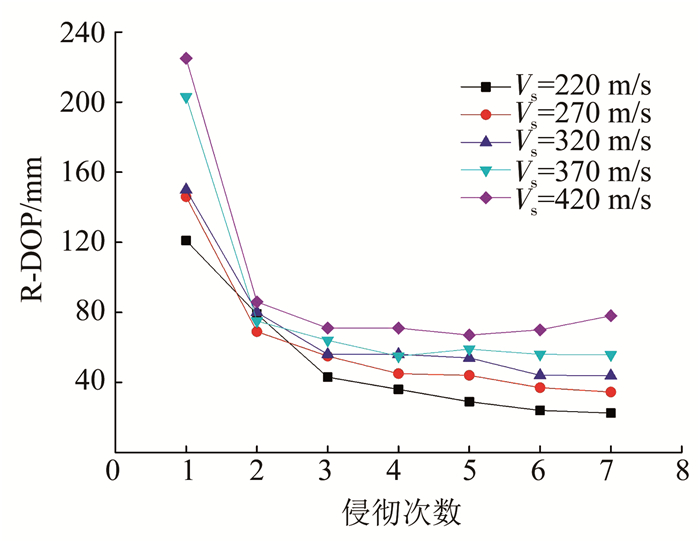
图 12为相对侵彻深度(relative depth of penetration, R-DOP)随冲击次数变化的规律曲线图.可以看出, 不同弹速下相对侵彻深度随冲击次数的增加逐渐减小, 且n=1时的相对侵彻深度与后续相比相差较大, 从n=2时起, 这种变化关系较为平缓, 弹体呈现为较稳定的侵彻.整体上相同冲击次数下(除n=2外)弹速越高相对侵彻深度越大, 仅当n=2时, 相对侵彻深度变化不大, 稳定在80 mm左右.相对侵彻深度随冲击次数逐渐减小的原因在于所形成的隧道区对后续各弹体的横向约束作用; 加之隧道区内壁密度增大及弹体与隧道区内壁存在摩擦作用使得弹体动能耗散, 且冲击次数越大, 弹体所经历的隧道区越长, 以上作用越大.
|
图 12 相对侵彻深度与冲击次数关系 Fig. 12 Relation between relative R-DOP and impact times |
从侵彻深度与冲击次数变化规律上看, 不同弹速下侵彻深度整体上随冲击次数的增加逐渐增大, 如图 13所示.弹速较低时, 如220 m/s≤Vs≤320 m/s, 在重复侵彻次数n < 4时, 侵彻深度变化率变化较大, 表现出较为明显的非线性关系; 而在重复侵彻次数n≥4时, 侵彻深度变化率变化不大, 线性关系明显; 弹速较高时, 如370 m/s≤Vs≤420 m/s, 侵彻深度与冲击次数整体呈较强的线性相关关系.由上述可知, 在所讨论速度范围内, 当弹体重复冲击次数越大或重复冲击的速度越高时, 侵彻深度与冲击次数线性关系越明显, 相对侵彻深度值越稳定, 即弹体侵彻花岗岩靶板的过程越稳定.

|
图 13 侵彻深度与冲击次数关系 Fig. 13 Relation between DOP and impact times |
Forrestal等[30]给出经典的卵形弹丸单次冲击靶板的侵彻深度公式:
| $ {P = \frac{{{m^\prime }}}{{2\pi {a^2}\rho {N^*}}}{\rm{ln}}\left( {1 + \frac{{{N^*}\rho V_1^2}}{{S{f_{\rm{c}}}}}} \right) + z,} $ | (12) |
| $ {V_1^2 = \frac{{{m^\prime }V_{\rm{s}}^2 - 4\pi {a^3}S{f_{\rm{c}}}}}{{{m^\prime } + 4\pi {a^3}{N^*}\rho }}.} $ | (13) |
式中:m′、a为射弹的质量(kg)和半径(m); ρ为靶板密度(kg/m3); N为CRH(曲径比Ψ)的函数, N*=(8Ψ-1)/(24Ψ2); S为材料强度修正因子, S=82.6(fc×10-6)-0.544, fc为靶板材料单轴抗压强度, Pa; z为单次侵彻中锥形弹坑底部与所形成的弹道过渡点深度(m), 取z=4a.
Gomez等[11]认为:弹体以同等弹速第2次射击靶板的同一目标点, 此时靶板初始条件与第1次冲击相比已发生变化, 其通过重复侵彻实验反演出不同弹速相同冲击次数下材料强度修正因子S给出重复侵彻深度计算方法.花岗岩靶板无侧限抗压强度fc被冲击后在整个响应区内并非均匀性变化, 如在迎冲面临近空腔[7]的粉碎区内花岗岩无侧限抗压强度变化最大, 几乎已无抗冲击能力, 而在弹性区及未扰动区内无侧限抗压强度基本没变.由此可见, Gomez通过反演S将材料强度整体修正的做法有不足之处.本文以经典的Forrestal公式作为不同弹速下重复侵彻的初始侵彻深度值, 记为P0, 并通过定义相对侵彻系数函数φ(n)给出重复侵彻深度的表达式:
| $ {P(n,{V_{\rm{s}}}) = \varphi (n){P_0},n = 1,2,3, \cdots ,7,} $ | (14) |
| $ {\varphi (n) = \frac{{{\rm{DO}}{{\rm{P}}_n}}}{{{\rm{DO}}{{\rm{P}}_{\rm{1}}}}},n = 1,2,3, \cdots ,7.} $ | (15) |
式中:DOPn为第n次侵彻深度, 取n=1时其为第1次侵彻深度.
式(14)显示P(n, Vs)仅在因式P0项中涉及因子S, 且为材料初始因子S0, 避免了将靶板材料损伤后因子S均质化问题.考虑到花岗岩材料的非均匀性使得初始因子S0存在一定差异, 由不同弹速下初始侵彻深度, 通过式(12)、(13)解得均值S0=3.226, 使P0仅为速度Vs函数, 记为P0(Vs), 则式(14)变为
| $ P(n,{V_{\rm{s}}}) = \varphi (n){P_0}({V_{\rm{s}}}). $ | (16) |
将不同弹速下随冲击次数变化的靶板侵彻深度(DOPn)按式(15)进行归一化处理, 如图 14所示.相对侵彻系数φ(n)与侵彻次数的关系采用如下表达式

|
图 14 相对侵彻系数 Fig. 14 Relative penetration coefficient |
| $ \varphi (n) = {A^*} + {B^*} \cdot {{\rm{e}}^{{k^*} \cdot n}}. $ | (17) |
式中:A*、B*和k*为相关常数.通过拟合数据得A*=4.696, B*=-4.192, k*=-0.126.拟合公式的可决系数R2=0.986, 说明拟合效果很好.
由上表述, 联立式(12)、(13), (16)、(17)得关于速度Vs与冲击次数n的重复侵彻深度表达式:
| $ \begin{array}{*{20}{l}} {P(n,{V_{\rm{s}}}) = (4.696 - 4.192{{\rm{e}}^{ - 0.126n}}){P_0}({V_{\rm{s}}}),}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n = 1,2,3, \cdots ,7.} \end{array} $ | (18) |
式中:各参数含义与前述相同; P0(Vs)由式(12)、(13)计算可得, 并在式(13)中取S=S0.
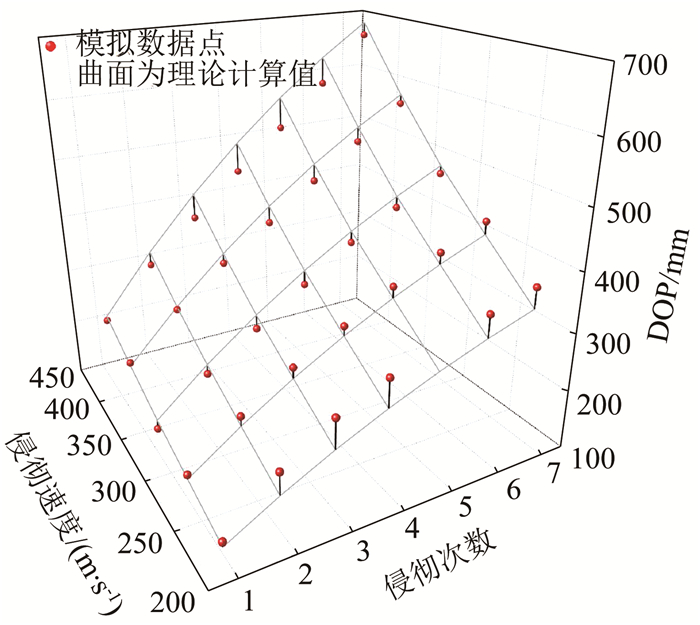
将按式(18)计算值作为理论计算值, 以曲面形式绘于图 15中, 并与数值模拟获取的数据(图中实心圆点)形成对比.为合理显示理论计算值与数值模拟结果之间偏离度的大小, 其偏离度用模拟数据点到理论计算曲面的垂线段表示, 垂线段越长, 则模拟数据点到目标值的偏离度越大; 反之, 偏离度越小, 以此来验证式(18)的合理性.由图 15可知, 该式能较准确地预测花岗岩重复侵彻深度.
|
图 15 侵彻深度随冲击次数和弹速变化关系 Fig. 15 Variations of DOP with impact times and velocity |
基于FEM-SPH耦合算法, 在220 m/s≤Vs≤420 m/s弹速下, 对花岗岩多弹重复侵彻问题进行了数值研究, 得如下主要结论:
1) 拉伸断裂软化模型与JH-2模型相耦合, 可实现JH-2模型模拟靶板内低应力区在主拉伸应力作用下径向裂纹的产生与发展, 且确定的材料模型参数能较准确模拟岩石靶板破坏形态.
2) 多弹重复侵彻岩石靶板, 靶板自由边界对初始侵彻破坏形态的影响较大, 在迎冲面呈“锥形开坑区+隧道区”破坏形态, 隧道区对弹体的横向约束使后续各侵彻过程处在一个相对稳定侵彻阶段.
3) 不同弹速下侵彻深度随冲击次数的增大而增大, 而相对侵彻深度则减小; 当弹体重复冲击次数越多或侵彻速度越高, 弹体侵彻花岗岩靶板越稳定.
4) 基于所提出的相对侵彻系数函数给出重复侵彻深度计算式P(n, Vs), 能较准确描述侵彻深度随冲击次数与冲击弹速变化的规律.
弹体侵彻花岗岩是个复杂的过程, 本文探讨了刚性侵彻条件下重复侵彻深度的变化规律, 对于半流体侵彻及流体侵彻条件下的超高速重复侵彻深度的变化规律尚需进一步研究.
| [1] |
杨刚, 梁超, 刘平, 等. 基于三维FE-SPH自适应耦合算法的子弹侵彻混凝土靶跳飞问题模拟[J]. 工程力学, 2013, 30(9): 276. YANG Gang, LIANG Chao, LIU Ping, et al. Numerical simulation of ricochet problem of projectile penetrating into concrete target based on 3D FE-SPH adaptive coupling algorithm[J]. Engineering Mechanics, 2013, 30(9): 276. DOI:10.6052/j.issn.1000-4750.2012.05.0315 |
| [2] |
WAN F, JIANG Z G, TAN Q H, et al. Response of steel-tube-confined concrete targets to projectile impact[J]. International Journal of Impact Engineering, 2016, 94: 50. DOI:10.1016/j.ijimpeng.2016.03.012 |
| [3] |
刘铮, 程怡豪, 邱艳宇, 等. 成层式防护结构抗超高速侵彻的数值分析[J]. 爆炸与冲击, 2018, 38(6): 1317. LIU Zheng, CHENG Yihao, QIU Yanyu, et al. Numerical analysis on hypervelocity penetration into layered protective structure[J]. Explosion Andshock Waves, 2018, 38(6): 1317. DOI:10.11883/bzycj-2017-0181 |
| [4] |
王海兵, 寿列枫, 张建鑫, 等. 弹丸撞击下花岗岩靶破坏效应实验与数值分析[J]. 岩石力学与工程学报, 2014, 33(2): 366. WANG Haibing, SHOU Liefeng, ZHANG Jianxin, et al. Experiments and numerical analysis of destructive effects of granite target under impact of projectile[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 366. DOI:10.3969/j.issn.1000-6915.2014.02.018 |
| [5] |
沈俊, 徐翔云, 何翔, 等. 弹体高速侵彻岩石效应试验研究[J]. 岩石力学与工程学报, 2010, 29(增刊2): 4207. SHEN Jun, XU Xiangyun, HE Xiang, et al. Experimental study of effect of rock targets penetratedby high-velocity projectiles[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 4207. |
| [6] |
ANTOUN T H, GLENN L A, WALTON O R, et al. Simulation of hypervelocity penetration in limestone[J]. International Journal of Impact Engineering, 2006, 33: 45. DOI:10.1016/j.ijimpeng.2006.09.009 |
| [7] |
宋春明, 李干, 王明洋, 等. 不同速度段弹体侵彻岩石靶体的理论分析[J]. 爆炸与冲击, 2018, 38(2): 250. SONG Chunming, LI Gan, WANG Mingyang, et al. Theoretical analysis of projectiles penetrating into rock targets at different velocities[J]. Explosion and Shock Waves, 2018, 38(2): 250. DOI:10.11883/bzycj-2017-0198 |
| [8] |
李干, 宋春明, 邱艳宇, 等. 超高速弹对花岗岩侵彻深度逆减现象的理论与实验研究[J]. 岩石力学与工程学报, 2018, 37(1): 60. LI Gan, SONG Chunming, QIU Yanyu, et al. Theoretical and experimental studies on the phenomenon of penetration depth reverse reduction in the penetration of granite by hyper-velocity projectiles[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 60. DOI:10.13722/j.cnki.jrme.2017.0584 |
| [9] |
王明洋, 邱艳宇, 李杰, 等. 超高速长杆弹对岩石侵彻、地冲击效应理论与实验研究[J]. 岩石力学与工程学报, 2018, 37(3): 564. WANG Mingyang, QIU Yanyu, LI Jie, et al. Theoretical and experimental study on penetration in rock and ground impact effects of long rod projectiles of hyper speed[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 564. DOI:10.13722/j.cnki.jrme.2017.1348 |
| [10] |
王明洋, 李杰, 李海波, 等. 岩石的动态压缩行为与超高速动能弹毁伤效应计算[J]. 爆炸与冲击, 2018, 38(6): 1200. WANG Mingyang, LI Jie, LI Haibo, et al. Dynamic compression behavior of rock and simulation of damage effects of hypervelocity kinetic energy bomb[J]. Explosion and Shock Waves, 2018, 38(6): 1200. DOI:10.11883/bzycj-2018-0173 |
| [11] |
GOMEZ J T, SHUKLA A. Multiple impact penetration of semi-infinite concrete[J]. International Journal of Impact Engineering, 2001, 25: 965. DOI:10.1016/S0734-743X(01)00029-X |
| [12] |
ANTOUN T H, LOMOV I N, GLENN L A. Simulation of the penetration of a sequence of bombs into granitic rock[J]. International Journal of Impact Engineering, 2003, 29: 81. DOI:10.1016/ijimpeng.2003.09.006 |
| [13] |
邓国强, 杨秀敏. 工程岩体中多弹重复打击效应的数值模拟分析[J]. 爆炸与冲击, 2014, 34(3): 361. DENG Guoqiang, YANG Xiumin. Numerical simulation of the effect of multiply EPW into engineering rock[J]. Explosion and Shock Waves, 2014, 34(3): 361. DOI:10.3969/j.issn.1001-1455.2014.03.016 |
| [14] |
门建兵, 蒋建伟, 王树有. 爆炸冲击数值模拟技术基础[M]. 北京: 北京理工大学出版社, 2015: 4.
|
| [15] |
李世民, 李晓军, 郭彦朋. 基于AUTODYN对弹丸高速碰撞靶体的数值模拟[J]. 系统仿真学报, 2013, 25(4): 621. LI Shimin, LI Xiaojun, GUO Yanpeng. Numerical simulation of projectile high-velocity impacting target with AUTODYN[J]. Journal of System Simulation, 2013, 25(4): 621. DOI:10.16182/j.cnki.joss.2013.04.001 |
| [16] |
JOHNSON G R, HOLMQUIST T J. An improved computational constitutive model for brittle materials[C]//Proceedings of the Aip Conference. 1994, 309: 981. DOI: 10.1063/1.46199
|
| [17] |
CLEGG R A, HAYHURST C J. Numerical modeling of the compressive and tensile response of brittle materials under high pressure dynamic loading[R]. New York: American Institute of Physics, 1999: 1. DOI: 10.1063/1.1303483
|
| [18] |
AI H A, AHRENS T J. Simulation of dynamic response of granite: A numerical approach of shock-induced damage beneath impact craters[J]. International Journal of Impact Engineering, 2006, 33: 1. DOI:10.1016/j.ijimpeng.2006.09.046 |
| [19] |
SCHOCK R N, HEARD H C, STEPHENS D R. Stress-strain behavior of a granodiorite and two graywackes on compression to 20 kilobars[J]. Journal of Geophysical Research, 1973, 78(26): 5922. DOI:10.1029/JB078i026p05922 |
| [20] |
BRACE W F, RILEY D K. Uniaxial deformation of 15 rocks to 30 kb[J]. International Journal of Rock Mechanics and Mining Sciences, 1972, 9: 271. DOI:10.1016/0148-9062(72)90028-9 |
| [21] |
王占江, 张德志, 张向荣, 等. 蓝田花岗岩冲击压缩特性的实验研究[J]. 岩石力学与工程学报, 2003, 22(5): 797. WANG Zhanjang, ZHANG Dezhi, ZHANG Xiangrong, et al. Testing study on shock compression for lantian granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5): 797. DOI:10.3321/j.issn:1000-6915.2003.05.020 |
| [22] |
DEHGHAN BANADAKI M M, MOHANTY B. Numerical simulation of stress wave induced fractures in rock[J]. International Journal of Impact Engineering, 2012, 40/41: 16. DOI:10.1016/j.ijimpeng.2011.08.010 |
| [23] |
HOLMQUIST T J, TEMPLETON D W, BISHNOI K D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications[J]. International Journal of Impact Engineering, 2001, 25: 211. DOI:10.1016/s0734-743x(00)00046-4 |
| [24] |
宫凤强, 王进, 李夕兵. 岩石压缩特性的率效应与动态增强因子统一模型[J]. 岩石力学与工程学报, 2018, 37(7): 1586. GONG Fengqiang, WANG Jin, LI Xibing. The rate effect of compression characteristics and a unified model of dynamic increasing factor for rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(7): 1586. DOI:10.13722/j.cnki.jrme.2017.1239 |
| [25] |
杨秀敏. 爆炸冲击现象数值模拟[M]. 合肥: 中国科技大学出版社, 2010: 258.
|
| [26] |
KIM Y, YOO J, LEE M. Optimal design of spaced plates under hypervelocity impact[J]. Journal of Mechanical Science and Technology, 2012, 26(5): 1567. DOI:10.1007/s12206-012-0327-5 |
| [27] |
MONAGHAN J J. Particle methods for hydrodynamics[J]. Computer Physics Report, 1985, 3: 71. DOI:10.1016/0167-7977(85)90010-3 |
| [28] |
MONAGHAN J J. Smoothed particle hydrodynamics[J]. Annual Review of Astroncomical and Atrophysics, 1992, 30: 543. DOI:10.1088/0034-4885/68/8/R01 |
| [29] |
ZHOU Y X, ZHAO J. Advances in rock dynamics and applications[M]. London: Taylor & Francis Group, 2011: 143.
|
| [30] |
FORRESTAL M J, ALTAN B S, CARGILE D, et al. An empirical equation for penetration depth of ogive-nose projectile into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4): 395. DOI:10.1016/0734-743X(94)80024-4 |
 2020, Vol. 52
2020, Vol. 52