2. 中山大学 土木工程学院,广东 珠海 519082
2. School of Civil Engineering, Sun Yat-sen University, Zhuhai 519082, Guangdong, China
自从波特兰水泥发明以来,水泥基材料广泛应用于各类结构工程领域.在隧道和管道修复方面,发展了许多新型材料修复方法[1].多数学者认为应用砂浆修复结构只能改变结构的抗渗防腐性能,并认为其对结构加固的贡献较小.但随着国内外高强高性能砂浆的研发及应用[2],水泥砂浆喷涂也作为一种非开挖修复方法应用到实际工程中.
国内外较多学者研究了水泥砂浆修复地埋结构的相关课题,研究表明,叠合结构的理论承载力是相同情况下复合结构承载力的2倍.Mcalpine[3]认为水泥砂浆内衬与既有管道的自然黏结面就能满足协调变形条件,Zhao等[4]则提出了与之完全相反的观点,而Shi等[5]通过试验研究发现自然黏结面在大荷载作用下将发生分离,失去协调变形的能力.刘德军等[6]统计了109条隧道的破坏模式,其中张拉破坏和剪切破坏占比达30.27%,进一步说明应用水泥砂浆内衬法结构性修复钢筋混凝土管时,内衬与既有管道能否协调变形(也即能否形成叠合结构)及判断标准的确定,是工程设计施工中必须考虑的关键问题.另一方面,在内衬的设计研究中,Kang等[7]给出了由最大环向拉应力决定内衬壁厚设计公式.但其设计公式直接由直梁的模型推导,存在一定的误差; Dym等[8]认为内衬的基本设计控制因素为内衬层的环向拉应力及开裂裂缝宽度.其将环状内衬用两端固支拱模型代替,忽略了内衬与管-土界面的相互作用.
总体而言,迄今国内外对钢筋混凝土叠合结构的力学性能进行了较多的研究,但仍存在以下问题:已有的叠合结构抗弯性能研究几乎都是针对叠合直梁、叠合板,鲜有对叠合曲梁的分析研究; 相关的研究表明,叠合面抗剪强度取决于叠合面的粗糙程度、配筋率、混凝土强度等级以及剪跨比等因素,但对内衬叠合结构协调变形评判机制的研究较少.本文将“管道-内衬”体系简化为叠合曲梁模型,通过分析界面的黏结张拉应力与剪切应力,建立了界面协调变形判据,参考一些学者的试验模型和试验结果,验证了判据的合理性.在此基础上,对相关参数进行了分析研究,得到了简化公式.最终建立了基于界面黏结张拉强度及抗剪强度的砂浆/混凝土内衬管道修复壁厚设计模型.
1 叠合曲梁应力模型刘鸿文[9]给出了矩形截面单曲梁弯曲的径向张拉应力和剪切应力解析式.Ugural等[10]提出了多种材料的应力计算方法——变形截面法; Yang等[11]给出了复合梁弯曲的应力计算模型,并应用变截面法得到了两种不同材料直梁各截面的弯曲应力计算式.本文对上述学者的研究模型进行分析改善及进一步推导,建立了叠合曲梁的弯曲应力计算解析式.
本文所指的叠合梁(结构)为一次受力叠合结构; 复合梁(结构)为界面之间无黏结、无剪切作用的独立受力梁.
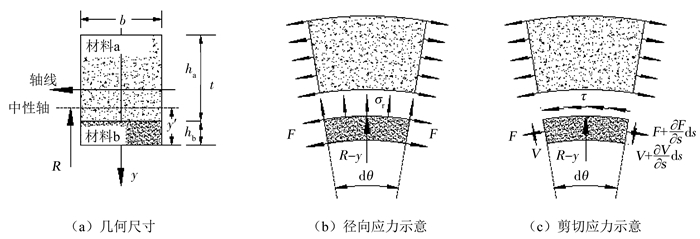
1.1 截面正应力在曲梁平面弯曲的情况下,应用平面假设建立梁纵向纤维的应变关系,其界面相关参数如图 1(a)所示.
|
图 1 叠合曲梁应力分析 Fig. 1 Stress analysis of composite curved beam |
忽略纵向纤维间应力对应变的影响,根据胡克定律可以得到曲梁横截面上的正应力分布规律,考虑到由于曲梁模量不同造成上下部分的内力差异,得到上下梁的正应力计算公式,即
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{{\rm{sa}}}} = \frac{{N{E_{\rm{a}}}}}{{{E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}}}} - \frac{{M{E_{\rm{a}}}}}{{({E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}})r}} + \frac{{M{E_{\rm{a}}}}}{{{E_{\rm{a}}}{J_{{\rm{za}}}} + {E_{\rm{b}}}{J_{{\rm{zb}}}}}} \cdot \frac{y}{{1 - y/r}},{y^\prime } - {h_{\rm{a}}} - {h_{\rm{b}}} \le y \le {y^\prime } - {h_{\rm{b}}},}\\ {{\sigma _{{\rm{sb}}}} = \frac{{N{E_{\rm{b}}}}}{{{E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}}}} - \frac{{M{E_{\rm{b}}}}}{{({E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}})r}} + \frac{{M{E_{\rm{b}}}}}{{{E_{\rm{a}}}{J_{{\rm{za}}}} + {E_{\rm{b}}}{J_{{\rm{zb}}}}}} \cdot \frac{y}{{1 - y/r}},{y^\prime } - {h_{\rm{b}}} \le y \le {y^\prime }.} \end{array}} \right. $ | (1) |
式中:N为轴力,M为弯矩,y为与叠合曲梁截面中性轴的距离,r为叠合曲梁半径,Aa、Ab分别为界面上、下侧截面面积,Jza、Jzb分别为上下曲梁惯性矩,ha、hb分别为上下曲梁厚度,y′为叠合梁截面等效中性轴.
当上下材料相同,即Ea=Eb时,式(1)转化为弯曲单梁的正应力计算公式; 当r→∞时,进一步转化为直梁的弯曲正应力计算公式.
1.2 界面径向应力材料力学理论假设直梁在纯弯曲时,各纵向纤维之间不存在应力.图 1(b)中给出了叠合曲梁下侧微段的受力模型,根据材料b中距曲梁截面等效中性轴为y的微元体在y方向的静力平衡方程,即可得到叠合曲梁界面下侧的径向应力,即
| $ \begin{array}{*{20}{l}} {{\sigma _{\rm{r}}} = \frac{1}{{b(r - y)}}\left[ {\left( {\frac{{N{E_{\rm{b}}}}}{{{E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}}}} - \frac{{M{E_{\rm{b}}}}}{{({E_{\rm{a}}}{A_{\rm{a}}} + {E_{\rm{b}}}{A_{\rm{b}}})r}}} \right){{\bar A}_{\rm{b}}} + } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{M{E_{\rm{b}}}}}{{{E_{\rm{a}}}{J_{{\rm{za}}}} + {E_{\rm{b}}}{J_{{\rm{zb}}}}}} \cdot {{\bar K}_{{\rm{zb}}}}} \right],{y^\prime } - {h_{\rm{b}}} \le y \le {y^\prime }.} \end{array} $ | (2) |
式中:b为计算宽度,通常取单位1;Kzb为与静矩相同的几何量; Ab为计算截面面积.
令y=y′-hb, 即为叠合材料界面处的径向应力.当上下材料相同时,式(2)退化为弯曲单梁的界面径向应力计算公式.
1.3 界面剪切应力曲梁界面的剪切应力可根据图 1(c)建立叠合梁下侧微段的平衡微分方程获得.与界面相切的内力V为积分方程,需要应用叠合直梁的剪切应力解析式进行近似计算,将之代入平衡方程后可得
| $ {\tau ^\prime } = \frac{{rV}}{{b(r - y)}}\left( {\frac{{{E_{\rm{b}}}{{\bar K}_{{\rm{zb}}}}}}{{{E_{\rm{a}}}{J_{{\rm{za}}}} + {E_{\rm{b}}}{J_{{\rm{zb}}}}}} - \frac{1}{r} \cdot \frac{{3E_{\rm{a}}^2h_{\rm{a}}^3 + 4E_{\rm{a}}^2h_{\rm{a}}^2{h_{\rm{b}}} + 3{E_{\rm{a}}}{E_{\rm{b}}}h_{\rm{a}}^2{h_{\rm{b}}} + 5{E_{\rm{a}}}{E_{\rm{b}}}{h_{\rm{a}}}h_{\rm{b}}^2 + E_{\rm{b}}^2h_{\rm{b}}^3}}{{{E_{\rm{a}}}{h_{\rm{a}}}{h_{\rm{b}}}({E_{\rm{a}}}{h_{\rm{a}}} + {E_{\rm{b}}}{h_{\rm{b}}}){k_1}}}} \right). $ | (3) |
叠合直梁的剪切应力可通过变截面法建立微元体沿轴向受力的平衡方程获得,即
| $ \overline {{\tau ^\prime }} = \frac{{3V}}{{2b}}\frac{{{{({E_{\rm{a}}}h_{\rm{a}}^2 + 2{E_{\rm{a}}}{h_{\rm{a}}}{h_{\rm{b}}} + {E_{\rm{b}}}h_{\rm{b}}^2)}^2} - 4{{({E_{\rm{a}}}{h_{\rm{a}}} + {E_{\rm{b}}}{h_{\rm{b}}})}^2} \cdot {y^2}}}{{{E_{\rm{b}}}{h_{\rm{a}}}h_{\rm{b}}^3({E_{\rm{a}}}{h_{\rm{a}}} + {E_{\rm{b}}}{h_{\rm{b}}}){k_1}}}, $ | (4) |
其中
令y=y′-hb, 所得值即为下端界面的剪切应力τ′, 叠合梁剪切应力界面处存在突变,这是由于假定剪切应力沿界面的宽度方向均匀分布引起的.根据力的平衡原理,界面的实际剪切应力应为式(3)、(4)乘相应的模量比.
2 叠合曲梁受力模型判断标准 2.1 界面黏结张拉强度针对不同混凝土/砂浆材料组合,设置C25、C35混凝土材料为基底层,M25水泥砂浆及MS-10 000高性能砂浆作为修复层,进行了立方体试样的劈拉强度试验,结果如表 1所示.
| 表 1 不同材料组合立方体劈拉强度 Tab. 1 Cube split tensile strength of different material combinations |
赵志方等[12]对新老混凝土黏结抗拉性能的试验研究表明,混凝土轴拉强度与劈拉强度之间存在变异系数m,对于整体混凝土,m取0.81~0.85,对于人工凿毛的界面m取0.87~0.93.
经过对比后,按照本文进行的试验,取试验的最小值,即取水泥砂浆C35混凝土组别的试验值为准.考虑变异系数后,取黏结抗拉强度为0.73 MPa,根据CECS 143—2002[13]承载力极限状态设计给出的各分项系数取值范围进行试算,可得K的范围在1.68~2.50,本文取安全系数2.
2.2 界面抗剪强度GB50010—2015《混凝土结构设计规范》给出不配箍筋叠合板叠合面的抗剪强度标准值取0.6 MPa; JTG TJ22—2008《公路桥梁加固设计规范》中规定配置箍筋的叠合面,混凝土纯剪切强度设计值取抗压强度设计值的0.12倍; 对于不配置钢筋的叠合面,混凝土纯剪切强度设计值取0.45 MPa.
本文按照上述的最小抗剪强度标准值0.6 MPa作为标准,当取管道的裂缝荷载计算时,计算结果应乘以1.5的安全系数.
2.3 叠合曲梁协调变形条件修复后管道结构能否协调变形,即结构受力模型的判断标准分别是界面的抗剪强度与界面剪切应力、界面黏结张拉强度和径向张拉应力的大小关系,当抗力大于荷载时形成叠合结构,否则形成复合结构.其判据为
| $ K \cdot S < R. $ | (5) |
式中:K为综合安全系数,由各向分项系数决定; S为荷载; R为抗力.
3 试验验证及参数研究为验证模型的合理性,引用Shi等[5]应用砂浆修复既有管道的试验数据.并根据GB/T 11836—2009《钢筋混凝土排水管》钢筋混凝土管的标准设计条件,按照Ⅱ级管标准,对材料模量、埋管直径、内衬厚度等参数进行了分析.
3.1 1 000 mm管道修复模型验证Shi等[5]的试验研究中,既有管道为DN1 000 mm加筋混凝土管材,混凝土抗拉强度为4.41 MPa,弹性模量Ea为31 950 MPa,考虑到管材的腐蚀缺陷,原壁厚由100 mm减至82 mm; 修复用砂浆的抗拉强度为2.93 MPa,弹性模量Eb=8 900 MPa,修复后内衬壁厚为50 mm.试验中测得的3次破坏荷载分别为105.1,117.2及131.9 kN/m,平均值为118.1 kN/m.
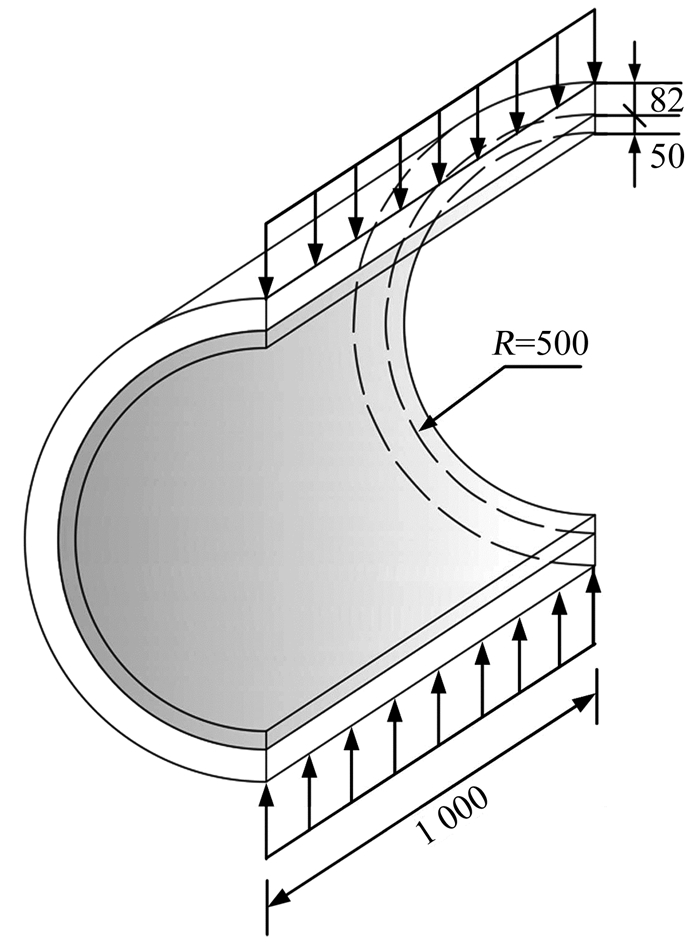
可将试验中的管道(受力模式见图 2)简化成圆环模型来分析集中荷载作用下的内力,内力值表达式如式(6)~(8).
|
图 2 管道-内衬结构尺寸及受力模式(mm) Fig. 2 Pipe-lining structure dimensions and force patterns(mm) |
| $ {M = \frac{{PR}}{\pi } \cdot \left( {1 - \frac{\pi }{2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha } \right),} $ | (6) |
| $ {V = \frac{P}{2}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha ,} $ | (7) |
| $ {N = \frac{P}{2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha .} $ | (8) |
式中:M为弯矩, V为剪力, N为轴力, α为自管顶开始旋转到计算截面的角度, P为集中荷载.
假设破坏荷载大约为裂缝荷载的1.5倍,裂缝荷载Pc取78.7 kN/m.为揭示理论模型中界面开裂的过程,取荷载值P分别为0.25Pc、0.5Pc、Pc和Pb(破坏荷载值)进行分析,并将式(6)~(8)代入式(2)、(4)中获得界面应力,计算结果如表 2所示.
| 表 2 不同集中力作用下的界面应力 Tab. 2 Interface stress under different concentrated force MPa |
计算表明,在集中荷载加载至0.25Pc~0.5Pc时,管顶处的叠合作用已经逐步失效; 荷载增加到裂缝荷载Pc时,叠合界面未失效的区域分布于起拱线67.5°~110°、247.5°~290°; 继续加载至破坏荷载Pb时,未失效区域进一步收窄,如图 3所示.可见,用上述材料喷涂50 mm,内衬与既有管道无法形成叠合结构,在加载至裂缝荷载之前内衬与既有管道之间的界面已经由于剪切作用失效.管道加载试验的结果也表明,在“管道-内衬”结构产生裂缝之前,管道局部内衬界面已经裂开,由叠合结构转化为复合结构,如图 4所示.

|
图 3 叠合界面随荷载变化的失效过程 Fig. 3 Failure process of composite interface with increasing load P |

|
图 4 修复后的管道试件在荷载达到Pc前脱离[5] Fig. 4 Repaired pipe sample breaks away before the crack load reaches Pc[5] |
根据上述分析获得的初步结果,以GB/T 11836—2009给出的钢筋混凝土管标准条件,分析应用高性能砂浆(初始弹性模量Eb=37 500 MPa、抗压强度80 MPa、抗拉强度8 MPa)对管道进行修复后材料模量、埋管直径、内衬厚度等因素对界面应力分布的影响.
3.2 材料弹性模量对界面应力的影响通过对不同材料模量比η所对应的界面剪切应力随β变化情况的分析,发现η < 1.5时,界面的剪切应力随管径的变化较小; η>1.5时,界面的剪切应力随着管径的增大差异变大.通常混凝土和水泥砂浆这两种修复材料与钢筋混凝土既有管道材料之间η < 1.5,一些新型的玻纤树脂内衬及碳纤维塑料内衬与原管材的η可高达10.
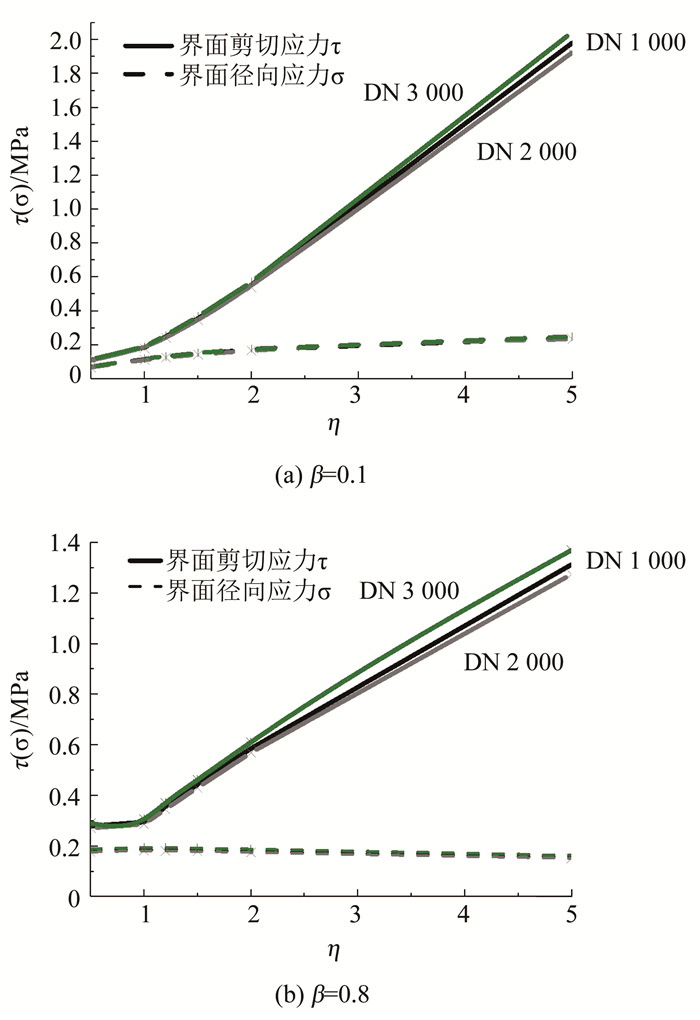
图 5(a)、5(b)分别是β为0.1及0.8时界面应力随η的变化情况.分析表明,界面的径向应力在β=0.1时随着η的增加而增加,在β=0.8时随着η的增加而降低.随着β的增加,界面剪切应力成为内衬壁厚设计的控制因素.同时也说明,当修复材料与原管材料的弹性模量比值较大时(如用玻纤树脂及碳纤维塑料内衬修复既有管道),如果使修复后的“管道-内衬”体系协调变形,必须大幅度增加两种材料界面的抗剪强度.
|
图 5 界面应力与材料模量比间的关系 Fig. 5 Relation between interface stress and material modulus ratio |
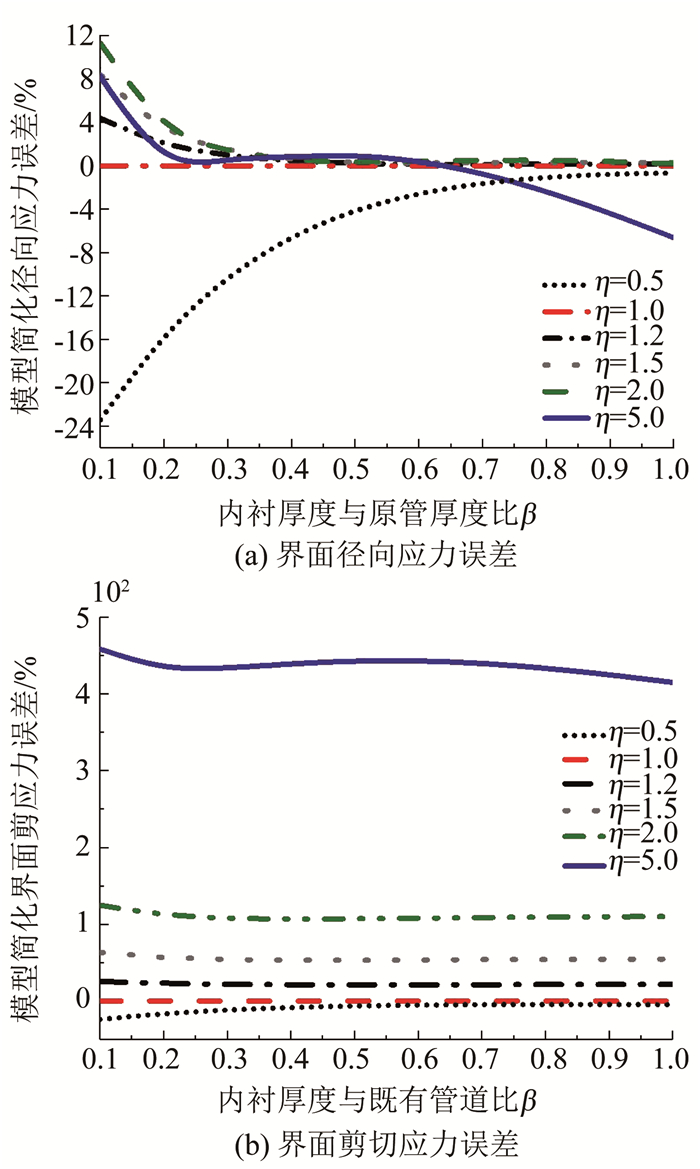
另外,单曲梁和叠合曲梁的差异主要是由于材料模量的变化引起的,分析结果表明,叠合曲梁受力模型计算值在η < 1时小于单曲梁计算值,η>1时大于单曲梁的计算值,即按单曲梁模型计算可能导致不安全的设计; 从图 6发现,剪切应力的差值可达到按单梁模型计算值的460%,径向应力的差值小于24%.随着模量比的增大以及水泥砂浆内衬壁厚的降低,两者计算的差异越来越大.
|
图 6 叠合曲梁模型简化误差 Fig. 6 Simplified error of composite curved beam model |
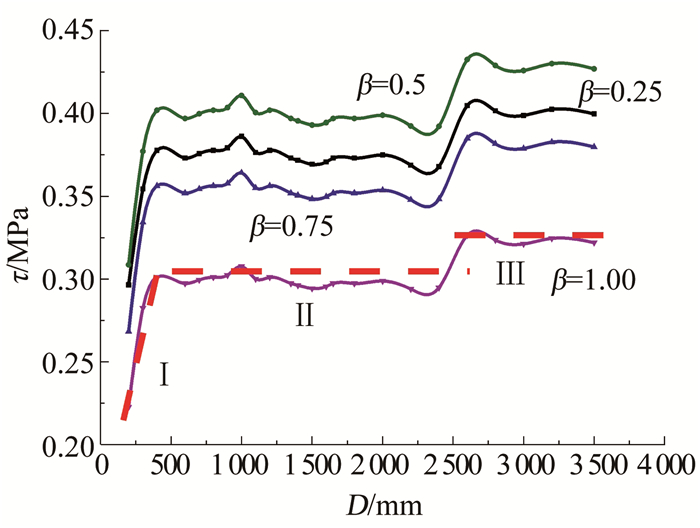
3.2的研究表明,界面剪切应力是内衬壁厚设计的控制因素,而界面径向应力条件往往都能满足.因此,下文仅研究不同参数对界面剪切应力的影响.图 7为不同直径管道在修复后的界面剪切应力分布情况,图中给出了4种β(内衬厚度与既有管道壁厚比值)的界面剪切应力-管径曲线.
|
图 7 几种β值对应的界面剪切应力-直径关系(η=1.19) Fig. 7 Relation between interface shear stress and pipe diameter with different β(η=1.19) |
随着β的增加,界面剪切应力并非单调递增变化,在β=0.5附近达到峰值,不同β值对应的界面剪切应力-管径曲线的走势大致相同,且可分为3个区段,即小于500 mm、500~2 600 mm及大于2 600 mm.因此,在分析叠合曲梁界面剪切应力的过程中,小于500 mm管道-内衬界面的剪切应力可按照管径-界面剪切应力的线性关系进行简化,而500 ~2 600 mm区间及大于2 600 mm区间的管道-内衬界面应力则可按照不同的“区间极限剪切应力”进行近似计算,如图中β=1.00时Ⅰ、Ⅱ、Ⅲ剪切应力极值线.
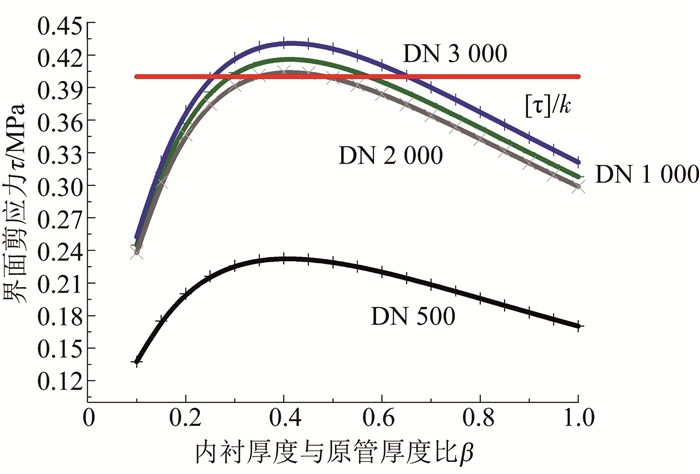
3.4 内衬厚度对界面剪切应力的影响图 8为同一管径不同β值既有管道与内衬之间界面的剪切应力分布,给出了DN500、DN1 000、DN2 000及DN3 000的情形.管径相同时,界面剪切应力随β变化呈类抛物线分布,并且均在β=0.4处达到峰值,说明修复材料的厚度并非越厚越好.
|
图 8 几种不同管径对应的τ-β变化关系 Fig. 8 Relation between interface shear stress and β with different diameters |
图中红色的线段为抗力/安全系数界限,管径小于500 mm的管道,内衬修复厚度为0.1~1倍的管道厚度时,整体的界面剪切应力均低于0.24 MPa,都在抗力/安全系数界限之下,说明小管径的修复结构形成叠合面后,叠合界面基本不会因为剪切作用失效; 另外,管径大于1 000 mm的界面剪切应力相差小于0.06 MPa,并且在β=0.1~0.2内DN 1 000~ DN3 000的管材界面剪切应力较为接近,这是因为Ⅱ、Ⅲ阶段的应力间距较小(取决于管材的破坏荷载),图中所列出的管径大于DN1 000的管道均已出现了应力分布于抗力/安全系数界限之上的情况,在这种情形下管道界面会发生剪切破坏,导致结构的受力模式改变.
3.5 界面剪切应力的简化公式通过分析发现,既有管道直径D、内衬厚度与既有管道壁厚比值β及材料的弹性模量比η是影响界面剪切应力的主要因素.尽管本文通过严格的理论推导,给出了叠合曲梁的界面剪切应力计算公式(3),但是公式的形式过于复杂,不便于使用.通过对相关数值的拟合,本节给出了界面应力的简化公式.界面剪切应力的拟合公式如下:
| $ \tau = \frac{{DV}}{{b(D - 2y)}} \cdot {\kappa _\tau } \cdot {D^{ - 0.911}}. $ | (9) |
式中:κτ=aη2+bη+c,a=-8.23β0.035+8.02,b= 8.65 e-0.69β-8.95e-7.85β,c=-3.41e-2.17β+3.96e-14.95β.
研究表明,经过拟合后的界面剪切应力计算公式与式(3)的计算结果误差小于1%.表 3给出了不同β、η值对应的界面剪切应力系数κτ.
| 表 3 界面剪切应力系数 Tab. 3 Interface shear stress coefficients |
修复旧管道的内衬厚度设计方法与新建管道的壁厚设计方法不同,因为两种结构模型的承载力及力的传递方式发生了改变.界面的作用效果直接影响着“管道-内衬”体系的实际受力及变形.因此,提出了除管顶拉应力、内衬开裂裂缝宽度之外的第3种“管道-内衬”体系内衬厚度的设计方法.
4.1 管道的破坏模式混凝土管道和钢筋混凝土管道的破坏模式主要有3类,即产生纵向裂缝、管顶坍塌和管道腐蚀减薄.
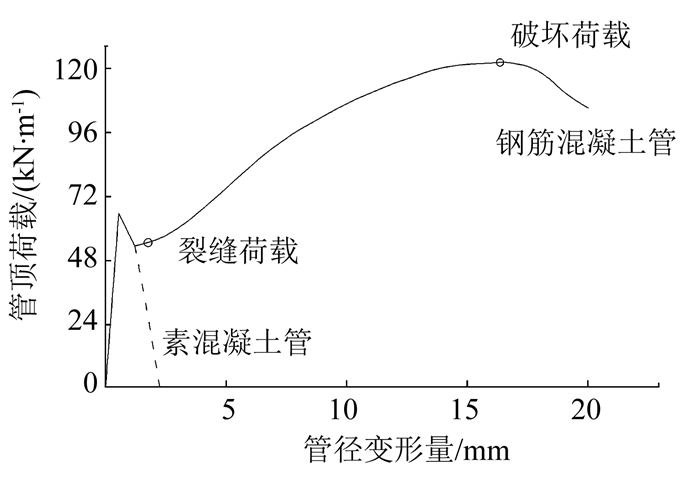
混凝土(钢筋混凝土)管道在三边承载试验下的荷载-位移曲线如图 9所示.对于素混凝土管道,产生裂缝之后再经过很小的变形就破坏,刚度随之降为零; 而钢筋混凝土管道由于钢筋的加强作用,在混凝土开裂之后既有管道仍有剩余承载力; 对于管道上部出现坍塌的情况,无论是混凝土管道还是钢筋混凝土管道,承载力都降为零; 由于既有管道的腐蚀并未产生显著的变形,可根据相关试验重新确定管道及钢筋的等效弹性模量和等效壁厚等参数.
|
图 9 三边承载试验中管顶荷载与管径变形量关系 Fig. 9 Relation between pipe top load and pipe diameter deformation in TEBT |
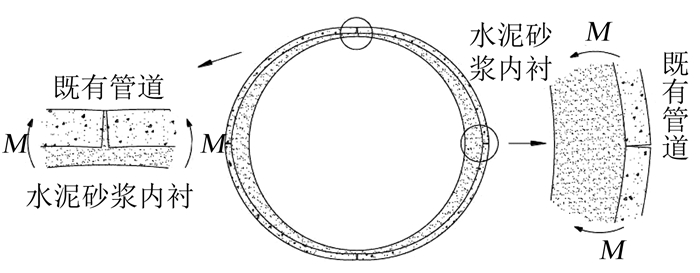
通过合理的壁厚设计,水泥砂浆修复后的管道-内衬结构,在正弯矩区(管道内侧受拉外侧受压)既有管道承受压应力,水泥砂浆修复层承受拉应力; 而负弯矩区与之相反,如图 10所示.
|
图 10 内衬与既有管道形成叠合结构受力模式 Fig. 10 Patterns of composite structure between lining and host pipeline |
但在素混凝土管道中,由于产生裂缝后既有管道无法再承担拉应力,负弯矩区的外力应由修复层全部承担; 而钢筋混凝土管表面出现裂缝时,钢筋仍能承担拉应力,在分析中只需将既有管道的壁厚做相应折减即可.同样地,管顶坍塌的模型也应该考虑正弯矩区域的剩余抗弯承载力和抗压承载力,忽略负弯矩区的剩余抗弯承载力和抗压承载力.因此,在内衬壁厚设计时,需要同时考虑管顶、管底和起拱线处等危险点.
根据前述理论的分析推导,对相关参数进行简化后可得界面剪切应力及径向应力判断条件式
| $ \left\{ {\begin{array}{*{20}{l}} {\tau = \frac{V}{{b(D - 2y)}} \cdot {\kappa _\tau } \cdot {D^{0.089}} < [\tau ],}\\ {{\sigma _r} = \frac{1}{{b(r - y)}}({\kappa _{{\sigma _1}}}N \pm {\kappa _{{\sigma _2}}}M) < [{\sigma _{\rm{r}}}].} \end{array}} \right. $ | (10) |
其中κσ1、κσ2为径向张拉拟合系数.
以及基于材料抗拉强度的叠合结构设计校核式
| $ {\sigma _{\rm{z}}} = \frac{N}{{\bar A}} \pm \frac{{My}}{{\bar I}} < [{\sigma _{\rm{z}}}]. $ | (11) |
其中A为等效截面面积,I为等效惯性矩.
图 11给出了叠合曲梁模型的内衬修复层设计原理,内衬壁厚设计时应首先考虑材料界面的剪切应力和径向拉伸应力,即式(10).当条件满足时,按照叠合结构进行壁厚设计,并根据式(11)进行材料抗拉强度校核; 当条件不满足时,应按照复合结构理论,依据抗拉强度(11)进行壁厚设计.
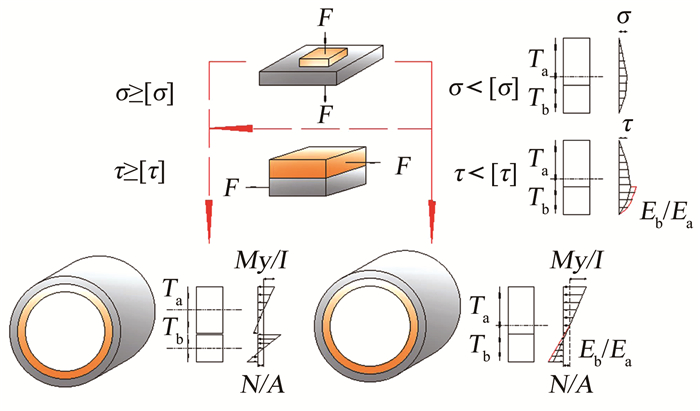
|
图 11 “管道-内衬”体系内衬壁厚设计示意 Fig. 11 Design of lining wall thickness in"pipe-lining" system |
1) 内衬层与既有管道协调变形的条件是界面的径向张拉应力与黏结张拉强度、界面剪切应力与抗剪强度的大小关系.当抗力大于荷载时,两者协调变形,形成叠合结构,否则形成复合结构.
2) 通常界面的抗剪条件为不同受力模型的主要判断标准.界面的剪切应力可简化为与旧管管径D、内衬厚度与既有管道壁厚比值β及材料的弹性模量比η等参数相关的函数.
3) 当修复材料与既有管道材料的弹性模量比值较大时(如用玻纤树脂及碳纤维塑料内衬修复既有管道),必须大幅度增加两种材料界面的抗剪强度,以保证“管道-内衬”体系协调变形.
4) 界面叠合作用会随着外荷载的增加而逐步失效,为了兼顾工程安全性及经济性,应以管道正常使用极限状态,根据界面剪切应力公式设计修复壁厚.最理想的状态是界面脱离均发生在荷载达到Pc之后.
5) 内衬壁厚设计时应进行剩余强度评价,并选取管顶、管底和起拱线等危险点进行设计.应同时考虑协调变形条件及材料的性能,若协调变形条件无法满足,则只能按照复合结构模型进行壁厚设计.
| [1] |
钟紫蓝, 王书锐, 甄立斌, 等. 经垫衬法修复后铸铁管道接口力学性能试验[J]. 哈尔滨工业大学学报, 2019, 51(6): 141. ZHONG Zilan, WANG Shurui, ZHEN Libin, et al. Experimental study on mechanical properties of ductile iron pipeline rehabilitated by corrosion protection lining[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 141. DOI:10.11918/j.issn.0367-6234.201812142 |
| [2] |
赵维, 李东旭, 李清海. 聚合物改性砂浆综述[J]. 材料导报, 2016, 24(11): 136. ZHAO Wei, LI Dongxu, LI Qinghai. Review of polymer modified mortar[J]. Materials Review, 2016, 24(11): 136. |
| [3] |
Water Research Centre. Sewerage rehabilitation manual[M]. London: WRC, 1983.
|
| [4] |
ZHAO J Q, DAIGLE L. Structural performance of sliplined watermain[J]. Canadian Journal of Civil Engineering, 2001, 28(6): 969. DOI:10.1139/l01-068 |
| [5] |
SHI Zihai, NAKANO M, TAKAHASHI Y. Structural analysis and renovation design of ageing sewers[M]. Warsaw, Poland: De Gruyter Open, 2016.
|
| [6] |
刘德军, 黄宏伟, 岳清瑞, 等. 隧道衬砌张拉裂缝开裂机制及快速修复方法初探[J]. 土木工程学报, 2015, 48(增刊1): 236. LIU Dejun, HUANG Hongwei, YUE Qingrui, et al. Study on cracking mechanism and rapid repair method for tensile cracks of tunnel lining[J]. China Civil Engineering Journal, 2015, 48(S1): 236. |
| [7] |
KANG J S, DAVIDSON J S. Structural effects of concrete lining for concrete-lined corrugated steel pipes[J]. Structure and Infrastructure Engineering, 2013, 9(2): 130. DOI:10.1080/15732479.2010.532809 |
| [8] |
DYM C L, WILLIAMS H E. Stress and displacement estimates for arches[J]. Journal of Structural Engineering, 2011, 137(1): 49. DOI:10.1061/(asce)st.1943-541x.0000267 |
| [9] |
刘鸿文. 高等材料力学[M]. 北京: 高等教育出版社, 1985. LIU Hongwen. Advanced material mechanics[M]. Beijing: Higher Education Press, 1985. |
| [10] |
UGURAL A C, FENSTER S K. Advanced strength and applied elasticity[M]. 2nd ed. New York: Elsevier Science Publishing Company Inc, 1987.
|
| [11] |
YOUNG W, BUDYNAS R. Roark's formulas for stress and strain[M]. 8th ed. New York: McGraw-Hill, 2011.
|
| [12] |
赵志方, 赵国藩, 刘健, 等. 新老混凝土黏结抗拉性能的试验研究[J]. 建筑结构学报, 2001, 22(2): 51. ZHAO Zhifang, ZHAO Guofan, LIU Jian, et al. Experimental study on adhesive tensile performance of young on old concrete[J]. Journal of Building Structures, 2001, 22(2): 51. DOI:10.3321/j.issn:1000-6869.2001.02.009 |
| [13] |
北京市市政工程设计研究总院.给水排水工程埋地预制混凝土圆形管道结构设计规程: CECS143—2002[S].北京: 中国计划出版社, 2003
|
 2020, Vol. 52
2020, Vol. 52


