2. 纽卡斯尔大学 工程与建筑环境学院,澳大利亚 纽卡斯尔;
3. 中国石油大学(华东) 储运与建筑工程学院,山东 青岛 266580
2. Faculty of Engineering and Built Environment, University of Newcastle, Callaghan, Australia;
3. College of Pipeline and Civil Engineering, China University of Petroleum, Qingdao 266580, Shandong, China
渗透注浆是在满足地层可注性条件下,将浆液注入地层空隙,从而达到降低土体渗透性、提高土体强度的目的[1].目前,渗透注浆技术已在各类岩土工程中得到了广泛应用[2-6].与化学浆液相比,水泥浆液价格低廉,环境友好,其应用最为广泛.满足地层可注性标准是渗透注浆工程设计首要前提,因此,对于水泥浆液渗透注浆可注性的研究具有重要意义.
水泥浆液可注性影响因素众多、机理复杂,导致其准确评估困难.诸多学者基于可注性室内试验,各自提出相应的可注性评价模型.Burwell等[7]基于大量可注性试验数据提出相应的可注性模型,该模型定义如下:当D15/d85>25、D10/d95>11时,为可注; 当D15/d85<11时,为不可注; 当11<D15/d85<25时,可注性未定义.其中,D15和D10分别为土体级配曲线上15%、10%对应的直径; d85和d95分别为水泥粒度曲线上85%、95%对应的直径.此外,Incecik等[8]认为D10/d90>10即可判定为可注.Krizek等[9-10]总结提出了与Burwell类似模型.Akbulut等[11]考虑浆液水灰比及砂层相对密实度等参数,提出了低压(p < 200 kPa)注浆下的可注性标准.
以上研究皆是基于室内可注性试验结果提出的可注性分类研究方法,然而不同学者提出的可注性分类标准不尽相同.其原因主要为,在渗透注浆过程中,水泥颗粒由于受砂土骨架的阻挡,将发生明显的滤过效应,表现为随注浆进行,砂层孔隙率持续衰减,最终造成浆液扩散存在极限扩散距离[12-15].浆液极限扩散距离大小取决于浆液性质、被注介质性质和注浆压力等参数,在可注性试验中,若被注试样尺寸小于或等于浆液极限扩散距离,则浆液将在整个试样中充分渗透扩散,即表现为可注,反之为不可注.可注性分类标准各不相同,不利于其在实际工程中的推广应用.因此,建立具有普适性的可注性量化评价模型具有重要意义.
为量化评价砂层可注性,开展了可注性室内试验,以水泥浆液水灰比RWC、相对密实度Dr、细颗粒(直径<0.075 mm)含量θ、砂层特征粒径D10和D15为控制变量,测量记录浆液渗透扩散距离,以扩散距离作为可注性量化评价指标,分析得到了各因素对可注性的影响规律.
近年来,以神经网络(ANN)为代表的人工智能方法被广泛应用到可注性分类预测研究领域,推动了可注性理论进展[16-21].然而,神经网络方法具有过度拟合、泛化性能不高等缺点,最小二乘支持向量机(LSSVM)作为新一代机器学习算法,能较好解决小样本、非线性和高维问题求解,逐渐被应用于岩土工程问题分析中[22-25].此外,传统人工智能模型参数搜索常采用网格搜索和交叉验证方法,搜索效率及精度相对较低[26-27].而粒子群算法作为一种新型仿生进化算法,采用全局优化方法,可有效提高收敛速度及精度.
砂层可注性影响因素众多,分析可注性各影响因素的敏感性分布对实际工程中注浆参数优化调整具有指导意义.现有研究多为可注性分类预测,缺乏可注性量化评价研究,而可注性量化评价是因素敏感性分析的基础,相关研究鲜有报道.敏感性分析方法可以分为局部敏感性分析以及全局敏感性分析.其中,局部敏感性分析只检验单因素变动对结果的影响程度,计算方便,但是分析往往需要一定假设,不能全面反应实际情况[28].而全局敏感性分析考虑了因素相互作用对结果的影响,更符合实际情况,在土木工程等多个领域应用广泛[29-31].其中,傅里叶幅度敏感性测试方法(FAST)即是典型全局敏感性分析方法.
本文将粒子群算法(PSO)和最小二乘支持向量机(LSSVM)相结合,通过粒子群算法搜索最佳的支持向量机参数,建立了浆液扩散距离预测的粒子群最小二乘支持向量机方法(PSO-LSSVM).以可注性室内试验测试结果作为模型训练和测试样本,建立了可注性PSO-LSSVM预测模型.基于PSO-LSSVM浆液扩散距离预测模型,采用FAST方法开展全局敏感性分析,得到了可注性影响因素敏感性分布.
1 可注性室内试验以P.O. 42.5R普通硅酸盐水泥为试验材料,以水泥浆液水灰比RWC、相对密实度Dr、细颗粒(直径<0.075 mm)含量θ、砂层特征粒径D10和D15为控制变量,开展129组砂样渗透注浆试验,试验测量记录浆液渗透扩散距离,以扩散距离定量表征可注性.
1.1 试验材料 1.1.1 普通硅酸盐水泥试验用水泥为42.5R普通硅酸盐水泥,水泥品质符合GB175—99《硅酸盐水泥、普通硅酸盐水泥》.水泥烧失量为0.56%.水泥颗粒粒径分布为0.4~80 μm,颗粒粒径分布范围相对较广,水泥颗粒特征粒径d85=23.872 μm,d90=28.93 μm,d95=36.127 μm.
1.1.2 被注介质以石英砂作为试验被注介质.所用石英砂中,二氧化硅(SiO2)质量分数大于96%,烧失量不超过0.40%,含泥量(包括可溶性盐类)不超过0.20%.
试验采用11种粒径配比砂样开展渗透性试验,每种砂样特征粒径如表 1所示.
| 表 1 砂样特征粒径 Tab. 1 Characteristic sand particle size of specimens |
试验装置由氮气瓶、承压储浆桶、试验架3部分构成,承压储浆桶与氮气瓶相连,氮气瓶输出的空气压力转换为浆液压力,储浆桶顶盖上设置压力表监测注浆压力,压力表量程为0~3 MPa.试验架由上部顶盖、中部钢制承压管、下部底盘3部分构成.钢制承压管内部盛放待注浆砂样,砂样上方设置滤网,防止松散的砂颗粒移动,砂样下方设置透水石.砂样尺寸为标准试件尺寸,高度为10 cm,直径为5 cm.试验装置如图 1所示.试验装置具体研发过程见文献[32].
为系统研究砂层的可注性,在试验过程中充分考虑各个因素对砂层可注性的影响,除砂层粒径外,设定砂层相对密度Dr、细颗粒含量θ及浆液水灰比RWC为自变量.砂层相对密度Dr变化范围为0~100%;水灰比调节范围为0.8~1.6;细颗粒含量变化范围为0~16%.
渗透注浆主要有恒压力和恒流速两种施工工艺,可注性试验采用恒压注浆方式.注浆压力越大浆液扩散距离越大,然而过大注浆压力易于引起地层劈裂,破坏原状土体结构,在实际工程中常采用低压渗透注浆[1, 16].砂层可注性试验中,为确保水泥浆液在砂样中充分扩散,试验中注浆压力控制为1.0 MPa.具体试验影响因素设置及试验结果见文献[32].
2 基于PSO-LSSVM的可注性预测模型将粒子群算法(PSO)和最小二乘支持向量机(LSSVM)相结合,通过粒子群算法搜索最佳的支持向量机(SVM)的参数,提出了浆液扩散距离预测的粒子群最小二乘支持向量机方法(PSO-LSSVM).以可注性室内试验测试结果作为训练、测试样本,最终建立了基于PSO-LSSVM的浆液扩散预测模型.在此基础上,根据浆液扩散状态定义可注性分类临界指标,进而建立了相应的可注性分类模型.以测试集试验数据为样本,将可注性分类模型预测结果与现有可注性评价方法进行了对比分析.
2.1 LSSVM回归原理最小二乘支持向量机(LSSVM)是在SVM基础上用等式约束代替不等式约束,避免了二次回归问题,计算精度和效率更高[33].假设训练样本数据为{xi, yi},(i=1, 2, …, l),xi∈Rn为n维系统输入向量,yi∈R为输出值.高维非线性映射φ:Rn→H,H为高维特征空间.在特征空间H中,拟合样本集为
| $ {y_i} = \mathit{\boldsymbol{w}}\varphi ({\mathit{\boldsymbol{x}}_i}) + b. $ | (1) |
式中:w为权向量; b为偏置量.xi、yi分别为系统输入向量和输出值.Suykens等[34]基于正则化理论,采用最小二乘成本函数和等式约束建立了LSSVM优化问题的最小化函数,其表达式为
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{w}},b,\xi } \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\frac{1}{2}\sum\limits_{i = 1}^l {\xi _i^2} . $ | (2) |
约束条件
| $ {y_i} - \mathit{\boldsymbol{w}}\varphi ({\mathit{\boldsymbol{x}}_i}) = b + {\xi _i}. $ | (3) |
式中:C为惩罚因子,即拟合误差容忍度,C值越高,误差容忍度越小,越容易过拟合,C值越小,则容易欠拟合,合理取值可使所求的函数具有较好的泛化能力; ξi为松弛因子.
最小化函数的拉格朗日求解方程为
| $ \begin{array}{*{20}{l}} {L(\mathit{\boldsymbol{w}},b,\xi ,a) = \frac{1}{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2} + }\\ {C\sum\limits_{i = 1}^l {{\xi ^2}} - \sum\limits_{i = 1}^l {{a_i}} [\mathit{\boldsymbol{w\varphi }}({\mathit{\boldsymbol{x}}_i}) + b + {\xi _i} - {y_i}].} \end{array} $ | (4) |
式中ai(i=1, 2, …, l)为拉格朗日乘子.最优的参数a和b可以通过KKT条件获得.
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial L}}{{\partial b}} = 0 \Rightarrow \sum\limits_{i = 1}^l {{a_i}} = 0,}\\ {\frac{{\partial L}}{{\partial \xi }} = 0 \Rightarrow {a_i} = C{\xi _i},}\\ {\frac{{\partial L}}{{\partial \mathit{\boldsymbol{w}}}} = 0 \Rightarrow \mathit{\boldsymbol{w}} = \sum\limits_{i = 1}^l {{a_i}} \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{x}}_i}),}\\ {\frac{{\partial L}}{{\partial a}} = 0 \Rightarrow \mathit{\boldsymbol{w\varphi }}({\mathit{\boldsymbol{x}}_i}) + b + {\xi _i} - {y_i} = 0.} \end{array}} \right. $ | (5) |
消去式(5)中的w和ξ,优化问题转化为求解如下方程
| $ \left[ {\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}}\\ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}&{\mathit{\boldsymbol{K}} + {C^{ - 1}}\mathit{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{b}}\\ \mathit{\boldsymbol{a}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} 0\\ \mathit{\boldsymbol{y}} \end{array}} \right]. $ | (6) |
式中:I为l阶单位矩阵; Θ=[1, …, l]T; a=[a1, a2, …, al]T; y=[y1, y2, …, yl]T. K为核函数矩阵,其元素Kij=φ(xi)Tφ(xj); i, j=1, 2, …, l, 其回归函数为
| $ {y_i} = \sum\limits_{i = 1}^l {{a_i}} K(x,{x_i}) + b. $ | (7) |
LSSVM模型预测精度取决于核函数的参数取值.为提高预测精度,采用粒子群算法对其参数进行优化.
2.2 粒子群算法粒子群优化算法(PSO)中,每个潜在解都被当成一个点或“粒子”,所有潜在解组成“粒子群”[35-36].任意一次迭代,粒子群基于单个粒子个体极值Pbest和群全局极值gbest来不断更新.群体中第i个粒子在n维空间的位置表示为xi=(xi1, xi2, …, xin),其速度vi=(vi1, vi2, …, vin),第i个粒子的个体极值Pbest=(Pi1, Pi2, …, Pin),整个粒子群的全局极值gbest=(g1, g2, …, gn).在极值点处,通过方程(8)和(9)来更新自己的速度和位置:
| $ \begin{array}{*{20}{l}} {{v_i}(k + 1) = q{v_i}(k) + {c_1} {\rm{rand}}{ _1}({P_{{\rm{ best }}}} - {x_i}(k)) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2} {\rm{rand}}{ _2}({g_{{\rm{ best }}}} - {x_i}(k)),} \end{array} $ | (8) |
| $ {x_i}(k + 1) = {x_i}(k) + {v_i}(k + 1). $ | (9) |
式中:c1、c2为学习因子,c1、c2∈(0,2);rand1和rand2为(0, 1)之间的随机数; q为动量系数,随迭代计算更新.
2.3 PSO-LSSVM可注性预测模型建立采用LSSVM方法建立砂层特征参数及注浆参数与浆液扩散距离之间的非线性映射关系.假设有n组训练样本数据(xi, yi)(i=1, 2, …, n),在本模型中,任一组砂层可注性试验对应一个样本数据,其中xi为五维实数输入向量,分别包括水泥浆液水灰比RWC、砂层相对密实度Dr、细颗粒含量θ、砂层特征粒径D10和D15,yi表示该组试验测得的浆液扩散距离,以浆液扩散距离作为可注性量化评价指标.建模的过程即是寻找输入向量xi与输出值yi之间的非线性映射关系,关系模型示意图如图 2所示.
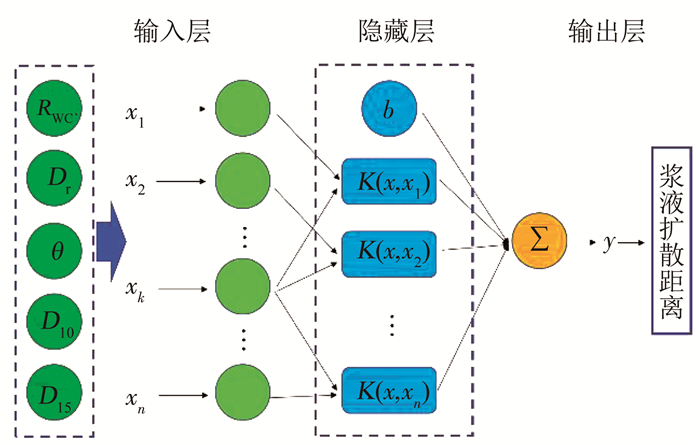
|
图 2 基于LSSVM建立的可注性预测关系模型示意 Fig. 2 Relational model of groutability prediction based on LSSVM method |
根据最小二乘支持向量机理论,相应的映射模型如式(7)所示.式(7)中,a和b可以通过解式(6)的线性方程组求出; yi为LSSVM模型的浆液扩散距离预测值.通过可注性试验获得的样本数据,对非线性映射模型进行训练.LSSVM模型核函数为RBF核,方程为
| $ K({x_i},{x_k}) = {\rm{exp}}( - \gamma {\left\| {{x_i} - {x_k}} \right\|^2}),\gamma > 0. $ | (10) |
式中γ为核函数参数,其值越小越容易欠拟合,值越大越容易过拟合.模型预测精度取决于C、γ的取值.根据文献[37]的结论,训练集样本数据占总样本数量的80%左右时,预测模型可得到最佳效果.本文在样本空间内均匀选取105组试验样本数据作为模型训练集,试验样本数据占样本总量81.4%.采用粒子群优化算法,对参数C、γ的取值进行优化.根据训练集试验样本数据,求得参数最优解为C=2.02、γ=1 854.41,以C、γ最优取值建立可注性影响参数与浆液扩散距离的关系模型.
图 3为训练集中浆液扩散距离PSO-LSSVM预测值和试验值对比.采用拟合优度R2为指标,定量评价基于PSO-LSSVM方法建立的可注性预测模型表现性能,即
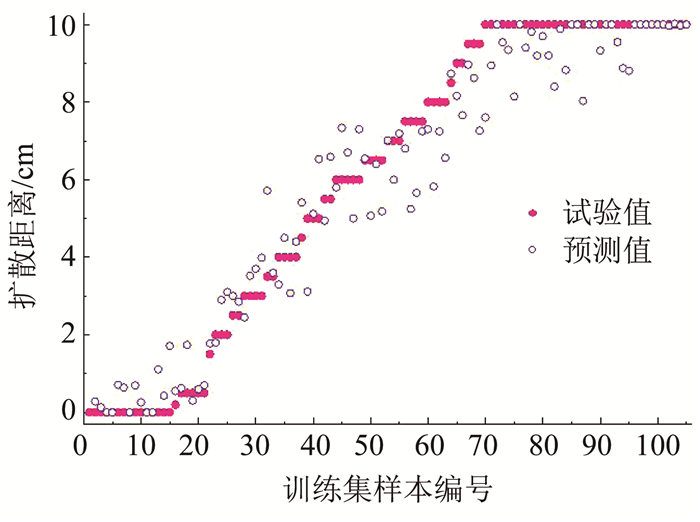
|
图 3 训练集中扩散距离预测值与试验值对比 Fig. 3 Comparison between prediction and test values of diffusion distance in training set |
| $ \begin{array}{*{20}{c}} {{R^2} = {{[\sum\limits_{i = 1}^n {({y_i} - \bar y)} ({H_i} - \bar H)]}^2} \times }\\ {{{[\sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} {{({H_i} - \bar H)}^2}]}^{ - 1}}.} \end{array} $ | (11) |
式中:yi为扩散距离预测值,Hi为扩散距离试验测量值,y和H分别为yi和Hi的平均值.
R2值越接近1,说明关联度越好.图 4为训练集扩散距离预测值与试验测定值之间拟合优度R2的表现.如图 3, 4所示,扩散距离预测值与模型值之间较为接近,拟合优度R2为0.962,模型拟合度较高.
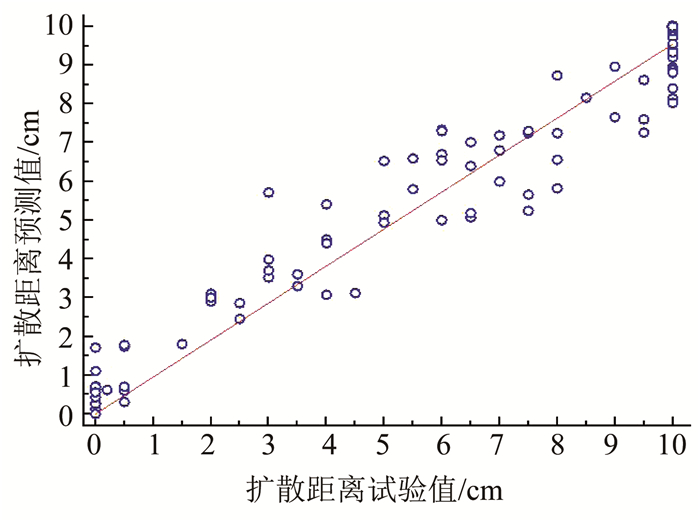
|
图 4 训练集中扩散距离预测拟合优度R2 Fig. 4 Goodness of fit R2 of diffusion distance predicted in training set |
将浆液扩散距离PSO-LSSVM预测值与测试集样本数据对比,评价扩散距离预测准确性.图 5为测试集浆液扩散距离预测值与试验值对比.图 6为浆液扩散距离预测值与试验值的拟合优度R2表现.

|
图 5 测试集中扩散距离预测值与试验值对比 Fig. 5 Comparison between prediction and test values of diffusion distance in test set |
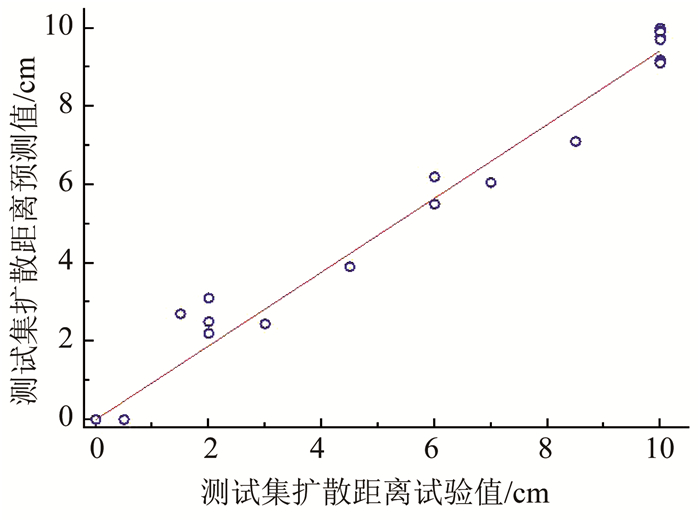
|
图 6 测试集中扩散距离预测值拟合优度R2 Fig. 6 Goodness of fit R2 of diffusion distance predicted in test set |
如图 5, 6所示,浆液扩散距离预测值与试验值较为接近,R2=0.982,说明所建立的PSO-LSSVM浆液扩散距离预测模型具有较好的泛化能力及良好的预测精度.本文为浆液扩散距离预测提供了有效方法,下一阶段将广泛开展不同注浆施工参数(包括注浆速率、注浆压力等)条件下的可注性试验,扩充试验训练样本,建立基于PSO-LSSVM方法的多种常用浆液的渗透扩散预测模型,并对其工程应用效果进行评价.
2.5 与现有方法对比考虑柱形砂样中浆液扩散锋面起伏以及试验测量误差,认为浆液在砂样扩散距离L≤1 cm时,为不可注; 1<L≤9 cm,为注入不充分; 9<L≤10 cm为完全可注.基于以上可注性分类标准,对测试集样本进行可注性分类划分,将本文所建模型与现有可注性评价方法的分类结果作对比分析.
Burwell模型和Incecik模型仅以被注砂层和水泥颗粒两者特征粒径比值作为可注性评判指标,在实际工程中应用较为广泛,可作为本文可注性预测对比方法.为保证所选取样本具有较好代表性,测试集样本数据均从样本空间中均匀选取,共计24组,约占总样本数18%.PSO-LSSVM的测试集样本可注性预测结果与经典Burwell模型和Incecik模型判定结果对比如表 2所示.可以看出,PSO-LSSVM模型对24组测试集可注性结果进行了完全准确预测.Burwell模型对测试集中不可注样本和完全可注样本进行准确预测.然而由于模型自身限制,无法对不完全可注样本进行判识,或模型未定义,或判定为可注性样本,总体而言,该模型对样本可注性做出了过高的估计.
| 表 2 可注性结果预测及对比 Tab. 2 Prediction and comparison of groutability results |
与Burwell模型类似,Incecik模型对完全可注和不可注样本进行了准确估计,然而模型无法对注入不充分样本进行有效识别.此外,Burwell模型和Incecik模型预测结果不完全一致,不利于工程应用.总体而言,本文模型优于Burwell模型和Incecik模型,可注性预测精度更高,可为实际工程应用提供指导.
3 可注性影响因素全局敏感性分析为评价影响因素对可注性敏感度,基于所建立的PSO-LSSVM浆液扩散距离预测模型,研究了各控制变量对可注性的敏感度,采用全局敏感性分析方法FAST,获得了可注性影响因素敏感性分布.
3.1 FAST方法简介FAST方法是以方差分析为基础的灵敏性分析方法.通过对每个系统待分析参数分配一个特征频率值,求解傅里叶变换变量离散值的系统方程,计算与各参数频率相关的傅里叶系数,确定系统灵敏度[38-39].FAST方法可以在高维非线性系统参数发生较大变化情况下,进行有效分析计算.可注性影响因素全局灵敏性指数反映的是某个注浆参数变化对浆液渗透扩散距离的影响程度.全局灵敏度指数为
| $ {S_{{X_i}}} = \frac{{{V_i}}}{{V(y)}}. $ | (12) |
式中:Vi=V(E(y|Xi)),V(y)为总方差,SXi为参数Xi对模型输出总方差的贡献率.
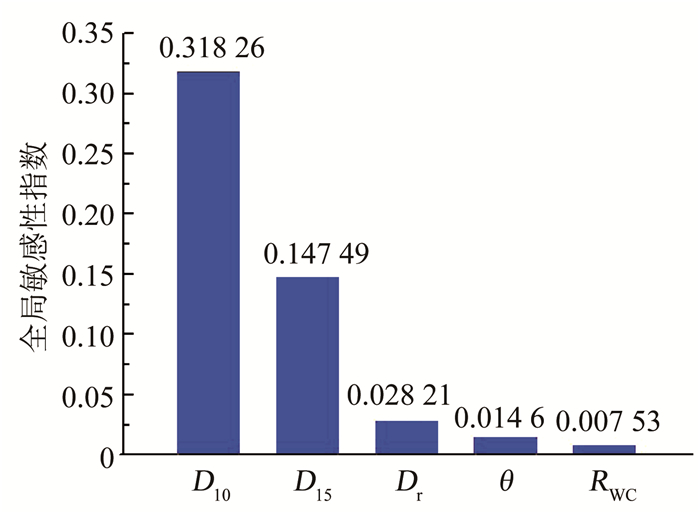
3.2 敏感性分析结果选取水泥浆液水灰比RWC、相对密实度Dr、细颗粒含量θ、砂层特征粒径D10和D15共5个参数,分析其对浆液扩散距离敏感性分布.假定各参数服从均匀分布,采用拉丁超立方抽样方法对参数抽样,抽样范围见表 3所示.采用所建立的PSO-LSSVM预测模型计算样本浆液扩散距离,在此基础上,采用FAST方法计算参数敏感性指标.敏感性计算结果如图 7所示.
| 表 3 影响因素及其抽样范围 Tab. 3 Influencing factors and sampling scope |
|
图 7 影响因素敏感性指数分布 Fig. 7 Sensitivity index distribution of influencing factors |
由图 7可知,砂层可注性敏感性排序为D10>D15>Dr>θ>RWC,其中D10和D15敏感度远大于其他3个参数,影响最为显著.以Burwell模型[7]为代表的诸多传统可注性评判方法认为,当水泥浆液材料一定,砂层可注性取决于D10和D15,即认为D10和D15为除浆液材料之外的对可注性影响最为显著因素,这与本文敏感性分析结果较为一致.相比而言,砂层相对密实度Dr、细颗粒含量θ以及浆液水灰比RWC对可注性影响相对较小,因此,在实际可注性预测中,需尽量减少D10和D15参数量测的不确定性,从而为可注性的精确预测提供保证.
4 结论1) 基于PSO-LSSVM方法建立的预测模型具有较高预测精度.浆液扩散距离预测值和试验测量值相近,拟合优度R2为0.982,可以准确预测样本完全可注、注入不充分以及完全不可注情况,而传统分类方法无法对注入不充分情况进行有效识别.
2) 可注性影响因素敏感性排序为:砂层粒径D10>砂层粒径D15>相对密实度Dr>细颗粒含量θ>浆液水灰比RWC,其中D10和D15敏感性显著高于Dr、θ和RWC.
3) 本文的研究也为渗透注浆扩散距离预测提供了新的思路,但还需广泛开展不同注浆参数(包括浆液类型、注浆速率、注浆压力等)条件下的渗透注浆试验,扩充训练样本,基于PSO-LSSVM方法建立适用范围更广的渗透注浆扩散预测模型,并对预测模型在工程中的应用效果进行评价.
| [1] |
邝键政, 昝月稳, 王杰, 等. 岩土工程注浆理论与工程实例[M]. 北京: 科学出版社, 2001. KUANG Jianzheng, ZAN Yuewen, WANG Jie, et al. Theory and project example of grout in geotechnical engineering[M]. Beijing: Science Press, 2001. |
| [2] |
WELSH J P. In situ testing for ground modification techniques[C]//Proceedings of GSP Geotechnical Special Publication No. 6. Reston, VA: ASCE, 1986: 322
|
| [3] |
WELSH J P, BURKE G K. Jet grouting: Uses for soil improvement[C]//Proceedings of Geotechnical Engineering Congress—1991. Reston, VA: ASCE, 1991: 334
|
| [4] |
GOUVENOT D. State of the art in European grouting[J]. Proceedings of the Institution of Civil Engineers—Ground Improvement, 1998, 2(2): 51. DOI:10.1680/gi.1998.020201 |
| [5] |
DUPLA J C, CANOU J, GOUVENOT D. An advanced experimental set-up for studying a monodirectional grout injection process[J]. Proceedings of the Institution of Civil Engineers—Ground Improvement, 2004, 8(3): 91. DOI:10.1680/grim.8.3.91.41117 |
| [6] |
KIM J S, LEE I M, JANG J H, et al. Groutability of cement-based grout with consideration of viscosity and filtration phenomenon[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(16): 1771. DOI:10.1002/nag.785 |
| [7] |
BURWELL E B. Cement and clay grouting of foundations: Practice of the corps of engineers[J]. Journal of the Soil Mechanics and Foundations Division, 1958, 84(1): 1. |
| [8] |
INCECIK M, CERAN I. Cement grouting model tests[J]. Bulteni-Istanbul Teknik Universitesi, 1995, 48: 305. |
| [9] |
KRIZEK R J, LIAO H J, BORDEN R H. Mechanical properties of microfine cement/sodium silicate grouted sand[J]. Geotechnical Special Publication, 1992, 1(30): 688. |
| [10] |
HUANG C L, FAN J C, YANG W J. A study of applying microfine cement grout to sandy silt soil[J]. Sino-Geotech, 2007, 111(1): 71. |
| [11] |
AKBULUT S, SAGLAMER A. Estimating the groutability of granular soils: A new approach[J]. Tunnelling and Underground Space Technology, 2002, 17(4): 371. DOI:10.1016/S0886-7798(02)00040-8 |
| [12] |
YOON J, EL MOHTAR C S. A filtration model for evaluating maximum penetration distance of bentonite grout through granular soils[J]. Computers and Geotechnics, 2015, 65: 291. DOI:10.1016/j.compgeo.2015.01.004 |
| [13] |
李术才, 冯啸, 刘人太, 等. 考虑渗滤效应的砂土介质注浆扩散规律研究[J]. 岩土力学, 2017, 38(4): 925. LI Shucai, FENG Xiao, LIU Rentai, et al. Diffusion of grouting cement in sandy soil considering filtration effect[J]. Rock and Soil Mechanics, 2017, 38(4): 925. DOI:10.16285/j.rsm.2017.04.001 |
| [14] |
李术才, 郑卓, 刘人太, 等. 基于渗滤效应的多孔介质渗透注浆扩散规律分析[J]. 岩石力学与工程学报, 2015, 34(12): 2401. LI Shucai, ZHENG Zhuo, LIU Rentai, et al. Analysis of diffusion of grout in porous media considering infiltration effects[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(12): 2401. DOI:10.13722/j.cnki.jrme.2014.1624 |
| [15] |
SAADA Z, CANOU J, DORMIEUX L, et al. Evaluation of elementary filtration properties of a cement grout injected in a sand[J]. Canadian Geotechnical Journal, 2006, 43(12): 1273. DOI:10.1139/T06-082 |
| [16] |
TEKIN E, AKBAS S O. Artificial neural networks approach for estimating the groutability of granular soils with cement-based grouts[J]. Bulletin of Engineering Geology and the Environment, 2011, 70(1): 153. DOI:10.1007/s10064-010-0295-x |
| [17] |
LIAO Kuowei, FAN Jenchen, HUANG Chienlin. An artificial neural network for groutability prediction of permeation grouting with microfine cement grouts[J]. Computers and Geotechnics, 2011, 38(8): 978. DOI:10.1016/j.compgeo.2011.07.008 |
| [18] |
CHENG Minyuan, HOANG N D. A novel groutability estimation model for ground improvement projects in sandy silt soil based on Bayesian framework[J]. Tunnelling and Underground Space Technology, 2014, 43: 453. DOI:10.1016/j.tust.2014.07.001 |
| [19] |
TEKIN E, AKBAS S O. Predicting groutability of granular soils using adaptive neuro-fuzzy inference system[J]. Neural Computing and Applications, 2017, 1. DOI:10.1007/s00521-017-3140-3 |
| [20] |
HOANG N D, BUI D T, LIAO K W. Groutability estimation of grouting processes with cement grouts using differential flower pollination optimized support vector machine[J]. Applied Soft Computing, 2016, 45: 173. DOI:10.1016/j.asoc.2016.04.031 |
| [21] |
TRAN H H, HOANG N D. An artificial intelligence approach for groutability estimation based on autotuning support vector machine[J]. Journal of Construction Engineering, 2014. |
| [22] |
邬凯, 盛谦, 梅松华, 等. PSO-LSSVM模型在位移反分析中的应用[J]. 岩土力学, 2009, 30(4): 1109. WU Kai, SHENG Qian, MEI Songhua, et al. A model of PSO-LSSVM and its application to displacement back analysis[J]. Rock and Soil Mechanics, 2009, 30(4): 1109. |
| [23] |
黄发明, 殷坤龙, 张桂荣, 等. 多变量PSO-SVM模型预测滑坡地下水位[J]. 浙江大学学报(工学版), 2015, 49(6): 1193. HUANG Faming, YIN Kunlong, ZHANG Guirong, et al. Prediction of groundwater level in landslide using multivariable PSO-SVM model[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(6): 1193. DOI:10.3785/j.issn.1008-973X.2015.06.027 |
| [24] |
郑志成, 徐卫亚, 徐飞, 等. 基于混合核函数PSO-LSSVM的边坡变形预测[J]. 岩土力学, 2012, 33(5): 1421. ZHENG Zhicheng, XU Weiya, XU Fei, et al. Forecasting of slope displacement based on PSO-LSSVM with mixed kernel[J]. Rock Soil Mechanics, 2012, 33(5): 1421. |
| [25] |
XUE Xinhua, XIAO Ming. Deformation evaluation on surrounding rocks of underground caverns based on PSO-LSSVM[J]. Tunnelling and Underground Space Technology, 2017, 69: 171. DOI:10.1016/j.tust.2017.06.019 |
| [26] |
BARZEGAR R, SATTARPOUR M, NIKUDEL M R, et al. Comparative evaluation of artificial intelligence models for prediction of uniaxial compressive strength of travertine rocks, case study: Azarshahr area, NW Iran[J]. Modeling Earth Systems and Environment, 2016, 2(2): 1. DOI:10.1007/s40808-016-0132-8 |
| [27] |
万智, 董辉, 刘宝琛. 基于正交设计下SVM滑坡变形时序回归预测的超参数选择[J]. 岩土力学, 2010, 32(2): 503. WAN Zhi, DONG Hui, LIU Baochen. On choice of hyper-parameters of support vector machines for time series regression and prediction with orthogonal design[J]. Rock and Soil Mechanics, 2010, 32(2): 503. |
| [28] |
王振, 钟登华, 朱晓斌. 基于EFAST法的地下洞室静动力稳定参数全局敏感性分析[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(6): 615. WANG Zhen, ZHONG Denghua, ZHU Xiaobin. Parameter global sensitivity analysis of static and dynamic stability of underground cavern based on EFAST method[J]. Journal of Tianjin University (Science and Technology), 2016, 49(6): 615. DOI:10.11784/tdxbz201501087 |
| [29] |
张云, 薛禹群. 一维非线性地面沉降模型参数敏感性分析[J]. 水文地质工程地质, 2009, 32(3): 1. ZHANG Yun, XUE Yuqun. Sensitivity of parameters in one-dimensional nonlinear model for land subsidence[J]. Hydrogeology and Engineering Geology, 2009, 32(3): 1. |
| [30] |
金晓飞, 范峰, 沈世钊. 巨型射电望远镜(FAST)反射面支承结构参数敏感性分析[J]. 土木工程学报, 2010, 43(2): 12. JIN Xiaofei, FAN Feng, SHEN Shizhao. Parameter sensitivity analysis of the cable-net structure supporting the reflector of a large radio telescope-FAST[J]. China Civil Engineering Journal, 2010, 43(2): 12. |
| [31] |
罗跃, 叶淑君, 吴吉春, 等. 地面沉降模型的参数全局敏感性[J]. 浙江大学学报(工学版), 2018, 52(10): 2007. LUO Yue, YE Shujun, WU Jichun, et al. Global sensitivity analysis of parameters in land subsidence model[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(10): 2007. DOI:10.3785/j.issn.1008-973X.2018.10.021 |
| [32] |
张连震.地铁穿越砂层注浆扩散与加固机理及工程应用[D].济南: 山东大学, 2017 ZHANG Lianzhen. Study on penetration and reinforcement mechanism of grouting in sand layer disclosed by subway tunnel and its application[D]. Jinan: Shandong University, 2017 |
| [33] |
VAPNIK V N. An overview of statistical learning theory[J]. Neural Networks, IEEE Transactions, 1999, 10(5): 988. DOI:10.1109/72.788640 |
| [34] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293. DOI:10.1023/A:1018628609742 |
| [35] |
高尚, 杨静宇. 群智能算法及其应用[M]. 北京: 中国水利水电出版社, 2006. GAO Shang, YANG Jingyu. Swarm intelligence algorithms and their applications[M]. Beijing: China Water and Power Press, 2006. |
| [36] |
陈昌富, 肖重阳, 唐仁华. 基于PSO搜索潜在滑裂面非极限状态土压力计算[J]. 湖南大学学报(自然科学版), 2013, 40(2): 9. CHEN Changfu, XIAO Chongyang, TANG Renhua. Computation of earth pressure under non-limit state based on PSO search of potential slip surface[J]. Journal of Hunan University (Natural Sciences), 2013, 40(2): 9. |
| [37] |
SHAHIN M A, MAIER H R, JAKSA M B. Data division for developing neural networks applied to geotechnical engineering[J]. Journal of Computing in Civil Engineering, 2004, 18(2): 105. DOI:10.1061/(ASCE)0887-3801(2004)18:2(105) |
| [38] |
TARANTOLA S, GATELLI D, MARA T A. Random balance designs for the estimation of first order global sensitivity indices[J]. Reliability Engineering & System Safety, 2006, 91(6): 717. DOI:10.1016/j.ress.2005.06.003 |
| [39] |
XU Chonggang, GERTNER G Z. A general first-order global sensitivity analysis method[J]. Reliability Engineering and System Safety, 2008, 93(7): 1060. DOI:10.1016/j.ress.2007.04.001 |
 2020, Vol. 52
2020, Vol. 52




