欠驱动USV是一种新兴的水面无人舰艇,可实现海洋环境观测、资源勘查、水面运载等海洋作业;但是由于大多USV为复杂的欠驱动系统,各自由度之间存在较大的非线性耦合,给USV的运动控制带来了较大困难;另外,USV易受到恶劣海洋环境的影响,难以获得动力学参数,从而造成了欠驱动USV难以实现轨迹跟踪的难题.针对欠驱动USV跟踪问题,沈智鹏等[1]通过设计神经网络观测器来获得船舶速度,仿真结果验证了该观测器的有效性,但是并未考虑未知缓慢时变海流干扰问题;杜佳璐等[2]通过采用自适应律来估计外部干扰,提高了船舶定位精度;张天平等[3]采用神经网络逼近系统中不确定函数,经过仿真验证了该控制算法的有效性.廖煜雷等[4]采用滑模控制补偿外界干扰,经仿真验证,该控制系统具有较好的鲁棒性,但是该控制方法并未考虑难以获得准确水动力系数问题;王金强等[5]通过设计自适应律补偿难以测定的水动力系数,经仿真验证了该控制系统的有效性,但是该方法只是针对位置跟踪问题;Teek等[6]采用高增益观测器获得难以测定的船舶速度,经过仿真验证了该控制器的有效性;Shojaei[7]将神经网络自适应方法运用到船舶编队方面,经过仿真验证了该方法的鲁棒性;Wang等[8]运用RBF神经网络自适应方法逼近不确定函数,通过仿真验证了该控制器的稳定性与鲁棒性,该方法仍然未考虑未知海流干扰影响;Pan等[9]通过设计神经网络动态模型的方法获取虚拟变量的导数,运用级联控制方法验证了该控制系统的稳定性;Wang等[10]采用自适应动态面方法解决了水面船的协同跟踪问题;Liu等[11-12]采用基于预估器的神经网络逼近不确定函数,取得了较好的效果,但是并未考虑海流干扰问题.
基于上述分析,对欠驱动USV受未知时变海流影响的研究较少,本文针对未知缓慢时变海流影响,提出了一种自适应海流观测器,并且采用神经网络逼近不确定函数,避免了因水动力学系数、速度等难以测定带来的困扰,通过采用动态面方法获取虚拟控制变量的导数,减少了直接求导的计算量,通过运用李雅普诺夫函数证明了该控制系统的稳定性,仿真验证了该控制器的有效性与鲁棒性.
1 问题描述 1.1 神经网络简述RBF神经网络能在一个紧凑集和任意精度下逼近任何非线性函数.本文运用RBF神经网络逼近未知函数,RBF神经网络算法为:
| $ {{h_j} = \exp \left( {\frac{{{{\left\| {\mathit{\boldsymbol{x}} - {c_j}} \right\|}^2}}}{{2b_j^2}}} \right),} $ |
| $ {f = {W^{*{\rm{T}}}}\mathit{\boldsymbol{h}}(\mathit{\boldsymbol{x}}) + {\varepsilon _0}.} $ |
式中:x为神经网络输入;i为神经网络的输入个数;j为神经网络隐含层第j个节点;h=[hj]T为高斯函数的输出;W*为神经网络的理想权值;μ为神经网络的逼近误差;且ε0≤εN.
RBF神经网络的输出为
| $ \hat f = {W^{\rm{T}}}\mathit{\boldsymbol{h}}(\mathit{\boldsymbol{x}}). $ |
式中:
对于欠驱动USV,设定固定坐标系为{OE, XE, YE},随体坐标系为{OB, XB, YB};对于USV而言,本文只研究水平面内运动控制问题,USV位姿及速度可表示为{x, y, ψ}和{u, v, r},USV轨迹跟踪如图 1所示,期望运动轨迹为ηc(t),运动轨迹误差为{xe, ye}.
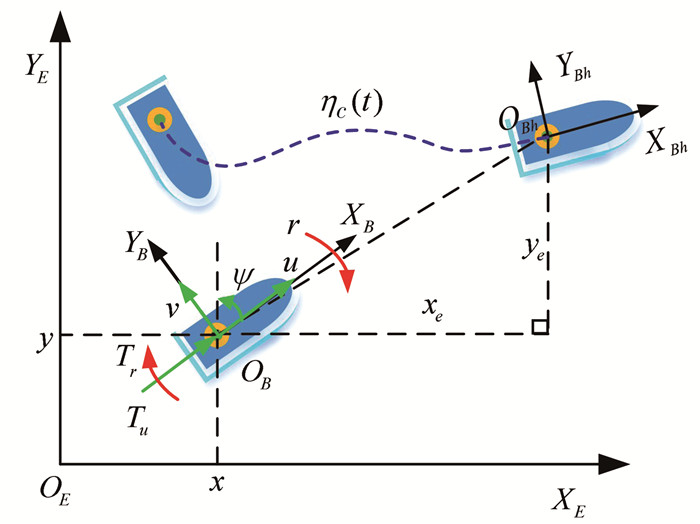
|
图 1 USV水平面轨迹跟踪 Fig. 1 USV trajectory tracking on horizontal plane |
对于欠驱动USV, 选取简化的USV运动数学方程和动力学方程为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{J}}(\psi )\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{v}}_c},}\\ {\mathit{\boldsymbol{M\dot v}} + \mathit{\boldsymbol{C}}(v)\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{Dv}} = \mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{d}}.} \end{array} $ | (1) |
式中:η=[x y ψ]T∈R3为欠驱动USV惯性坐标系下的横坐标x、纵坐标y和偏航角ψ组成的向量;v=[u v r]T∈R3为欠驱动USV体坐标系下的横向速度u、纵向速度v和偏航角速度r组成的向量;vc=[vcx vcy 0]T∈R3为欠驱动USV惯性坐标下的横向海流速度vcx和纵向海流速度vcy组成的向量;τ=[τu 0 τr]T∈R3为欠驱动USV体坐标系下推力τu和偏转力矩τr组成的向量;d=[d1 d2 d3]T∈ R3为欠驱动USV体坐标系下受到的横向干扰力d1、纵向干扰力d2和偏航干扰力矩d3组成的向量;J(ψ)∈R3×3为坐标系转换矩阵,且满足ηc=[xc yc ψc]T和‖J(Ψ)‖=1;M∈ R3×3为欠驱动USV惯性质量和水动力附加惯性矩阵;C(v)∈ R3×3为科氏向心矩阵;D∈ R3×3为非线性水动力阻尼矩阵.
J(ψ)、M和D分别为:
| $ \mathit{\boldsymbol{J}}(\psi ) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0\\ {\sin \psi }&{\cos \psi }&0\\ 0&0&1 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}&0&0\\ 0&{m - {Y_{\dot v}}}&0\\ 0&0&{m - {N_{\dot r}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&0&0\\ 0&{{m_{22}}}&0\\ 0&0&{{m_{33}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{X_u} + {X_{u|u}}|u|}&0&0\\ 0&{{Y_v} + {Y_{v|v|}}|v|}&0\\ 0&0&{{N_r} + {N_{r|r}}|r|} \end{array}} \right]. $ |
式中:m11, m22, m33分别为欠驱动USV的惯性矩阵在船体坐标系上的3个分量;Xu、Yv、Nr分别为欠驱动USV阻尼矩阵在体坐标系上的3个分量;Xu|u、Yv|v、Nr|r分别为欠驱动USV的非线性阻尼项.
2 控制器设计 2.1 建立轨迹跟踪误差方程定义欠驱动USV在惯性坐标系下的期望位置和偏航角为ηc=[xc yc ψc]T,则欠驱动USV在惯性坐标下的轨迹跟踪误差为:
| $ {x_e} = {x_c} - x,{y_e} = {y_c} - y,{\psi _e} = {\psi _c} - \psi . $ | (2) |
根据式(2),可得体坐标下轨迹跟踪误差为
| $ \left\{ {\begin{array}{*{20}{l}} {{e_x} = {x_e}\cos \psi + {y_e}\sin \psi ,}\\ {{e_y} = - {x_e}\sin \psi + {y_e}\cos \psi ,}\\ {{e_\psi } = {\psi _e},} \end{array}} \right. $ | (3) |
对式(3)求导,可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_x} = - u + {v_m}\cos {\psi _e} + r{e_y} - {v_{cx}}\cos \psi - {v_{cy}}\sin \psi ,}\\ {{{\dot e}_y} = - v + {v_m}\sin {\psi _e} - r{e_x} + {v_{cx}}\sin \psi - {v_{cy}}\cos \psi ,}\\ {{{\dot e}_\psi } = {{\dot \psi }_e},} \end{array}} \right. $ |
式中,期望合速度为
定义一个李雅普诺夫函数为
| $ {V_1} = \frac{1}{2}(e_x^2 + e_y^2), $ | (4) |
对式(4)求导,可得:
| $ \begin{array}{l} {{\dot V}_1} = {e_x}( - u + {v_m}\cos {\psi _e} + r{e_y} - {v_{cx}}\cos \psi - {v_{cy}}\sin \psi ) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_y}( - v + {v_m}\sin {\psi _e} + r{e_x} + {v_{cx}}\sin \psi - {v_{cy}}\cos \psi ). \end{array} $ | (5) |
定义一个新的变量: κ=vmsin ψe.
为保证
| $ \left\{ {\begin{array}{*{20}{l}} {{u_c} = {\alpha _1}{e_x} + {v_m}\cos {\psi _e} - {{\hat v}_{cx}}\cos \psi - {{\hat v}_{cy}}\sin \psi ,}\\ {{\kappa _c} = - {\alpha _2}{e_y} + v - {{\hat v}_{cx}}\sin \psi + {{\hat v}_{cy}}\cos \psi ,} \end{array}} \right. $ | (6) |
式中,α1>0,α2>0,且均为正实数.
将式(6)代入式(5),可得:
| $ {\dot V_1} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 + \xi , $ | (7) |
式中,ξ=vcxe(eysin ψ-excos ψ)-vcye(exsin ψ+eycos ψ).
由于对虚拟控制变量直接求导较为复杂,为减小直接求导的复杂性,将uc、κc和后文的rc通过一阶滤波器,即
| $ \left\{ {\begin{array}{*{20}{l}} {{\gamma _u}{\kern 1pt} {\kern 1pt} {{\dot u}_{cf}}(t) + {u_{cf}}(t) = {u_c}(t),}\\ {{\gamma _\kappa }{\kern 1pt} {\kern 1pt} {{\dot \kappa }_{cf}}(t) + {\kappa _{cf}}(t) = {\kappa _c}(t),}\\ {{\gamma _r}{\kern 1pt} {\kern 1pt} {{\dot r}_{cf}}(t) + {r_{cf}}(t) = {r_c}(t),} \end{array}} \right. $ |
其中初始值为:
| $ {u_{cf}}(0) = {u_c}(0),{\kappa _{cf}}(0) = {\kappa _c}(0),{r_{cf}}(0) = {r_c}(0). $ |
式中:ucf、vcf、rcf为虚拟控制变量通过一阶滤波器后的滤波值;γu>0, γκ>0, γr>0且均为正实数.
2.3 稳定eu和zu定义欠驱动USV系统的速度误差变量:
| $ {e_u} = u - {u_{cf}},{z_u} = {u_{cf}} - {u_c}. $ | (8) |
将式(8)代入方程(7),可得:
| $ {\dot V_1} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {e_u}{e_x} + {e_\kappa }{e_y} + \xi . $ |
定义一个新的李雅普诺夫函数为
| $ {V_2} = {V_1} + \frac{1}{2}(e_u^2 + z_u^2), $ | (9) |
对式(9)求导,可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_2} = {{\dot V}_1} + {e_u}{{\dot e}_u} + {z_u}{{\dot z}_u} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {e_u}{e_x} + {e_\kappa }{e_y} + {e_u}{{\dot e}_u} + {z_u}{{\dot z}_u} + \xi = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 + {e_u}({{\dot e}_u} - {e_x}) + {e_\kappa }{e_y} + {z_u}{{\dot z}_u} + \xi .} \end{array} $ |
定义欠驱动USV系统的速度误差变量:
| $ {e_\kappa } = \kappa - {\kappa _{cf}},{z_\kappa } = {\kappa _{cf}} - {\kappa _c}. $ | (10) |
定义一个新的李雅普诺夫函数为
| $ {V_3} = {V_2} + \frac{1}{2}(e_\psi ^2 + e_\kappa ^2 + z_\kappa ^2), $ | (11) |
对式(11)求导,可得:
| $ \begin{array}{l} {{\dot V}_3} = {{\dot V}_2} + {e_\psi }{{\dot e}_\psi } + {e_\kappa }{{\dot e}_\kappa } + {z_\kappa }{{\dot z}_\kappa } = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} { - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 + {e_u}({{\dot e}_u} - {e_x}) + {z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + }\\ {{e_\psi }{{\dot e}_\psi } + {e_\kappa }{{\dot e}_\kappa } + {e_\kappa }{e_y} + \xi = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{e_u}({{\dot e}_u} - {e_x}) + {z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + \xi + }\\ {{e_\psi }\left[ {{e_y} + {v_m}\sin {\psi _e} + ({v_m}\cos {\psi _e} + \frac{{{e_\psi }}}{{{e_\kappa }}})({{\dot \psi }_d} - r) - {{\dot \kappa }_{cf}}} \right],} \end{array} \end{array} $ | (12) |
式中r为虚拟控制变量.
可设定r的期望值为
| $ {r_c} = - {\alpha _3}{e_\kappa } + {\dot \psi _c} + \frac{{{e_y} + {{\dot v}_m}\sin {\psi _e} - {{\dot \kappa }_{cf}}}}{{{v_m}\cos {\psi _e} + {e_\psi }/{e_\kappa }}}, $ | (13) |
式中,α3>0,且为正实数.
将式(13)代入式(12),可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_3} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 + {e_u}({{\dot e}_u} - {e_x}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + \xi .} \end{array} $ | (14) |
定义速度误差变量为:
| $ {e_r} = r - {r_{cf}},{z_r} = {r_{cf}} - {r_c}, $ | (15) |
将式(15)代入式(14),可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_3} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 + {e_u}({{\dot e}_u} - {e_x}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_m}{e_\kappa }{e_r}\cos {\psi _e} + {z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + \xi .} \end{array} $ |
定义一个新的李雅普诺夫函数为
| $ {V_4} = {V_3} + \frac{1}{2}(e_r^2 + z_r^2), $ | (16) |
对式(16)求导,可得:
| $ \begin{array}{l} {{\dot V}_4} = {{\dot V}_3} + {e_r}{{\dot e}_r} + {z_r}{{\dot z}_r} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_u}({{\dot e}_u} - {e_x}) + {e_r}({{\dot e}_r} - {v_m}{e_\kappa }{e_r}\cos {\psi _e}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + {z_r}{{\dot z}_r} + \xi . \end{array} $ | (17) |
由于欠驱动USV速度难以准确测定以及水动力学系数难以确定,此处定义不确定函数:
| $ \left\{ {\begin{array}{*{20}{l}} {{\vartheta _1} = {m_{22}}vr - {X_u}u - {X_{u|u|}}u|u|,}\\ {{\vartheta _3} = ({m_{11}} - {m_{22}})uv - {N_r}r - {N_{r|r}}r|r|.} \end{array}} \right. $ |
针对不确定函数,采用神经网络进行逼近,定义神经网络预测误差为:
| $ {\dot \delta _1} = {\vartheta _1} - {\hat \vartheta _1},{\dot \delta _3} = {\vartheta _3} - {\hat \vartheta _3}. $ | (18) |
选取控制输入为
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _u} = - {m_{11}}({\beta _1}{e_u} + {e_x} + {{\dot u}_{cf}}) + {{\mathit{\boldsymbol{\hat W}}}_1}h({\mathit{\boldsymbol{x}}_u}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\delta _1}{\sigma _1} + {\eta _1} {\rm{sgn}} ({e_u}),}\\ {{\tau _r} = - {m_{33}}({\beta _3}{e_r} + {e_\kappa }{v_m}\cos {\psi _e} + {{\dot r}_{cf}}) + {{\mathit{\boldsymbol{\hat W}}}_3}h({\mathit{\boldsymbol{x}}_r}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\delta _3}{\sigma _3} + {\eta _3} {\rm{sgn}} ({e_r}).} \end{array}} \right. $ | (19) |
式中:
选取自适应律为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat W}}}_1} = {\chi _1}[({e_u} + {\lambda _1}{\delta _1})h({\mathit{\boldsymbol{x}}_u}) - {\rho _1}{{\mathit{\boldsymbol{\hat W}}}_1}],}\\ {{{\mathit{\boldsymbol{\hat W}}}_3} = {\chi _3}[({e_r} + {\lambda _3}{\delta _3})h({\mathit{\boldsymbol{x}}_r}) - {\rho _3}{{\mathit{\boldsymbol{\hat W}}}_3}],} \end{array}} \right. $ | (20) |
式中,χ1>0、χ3>0均为正实数.
将式(1)代入式(19),可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{m_{11}}{{\dot e}_u} = - {m_{11}}({\beta _1}{e_u} + {e_x} + {{\dot u}_{cf}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat W}}}_1}h({\mathit{\boldsymbol{x}}_u}) - {\vartheta _1} + {d_1} - {\eta _1} {\rm{sgn}} ({e_u}),}\\ {{m_{33}}{{\dot e}_r} = - {m_{33}}({\beta _3}{e_r} + {e_\kappa }{v_m}\cos {\psi _e} + {{\dot r}_{cf}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat W}}}_3}h({\mathit{\boldsymbol{x}}_r}) - {\vartheta _3} + {d_3} - {\eta _3} {\rm{sgn}} ({e_r}).} \end{array}} \right. $ | (21) |
将式(21)代入式(17), 可得:
| $ \begin{array}{l} {{\dot V}_4} = - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 - {\beta _1}e_u^2 - {\beta _3}e_r^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde W}}}_1}h\left( {{\mathit{\boldsymbol{x}}_u}} \right){e_u} - {m_{11}}\left( {{\mathit{\boldsymbol{\eta }}_1}\left| {{e_u}} \right| - {d_1}{e_u}} \right) + }\\ {{{\mathit{\boldsymbol{\tilde W}}}_3}h\left( {{\mathit{\boldsymbol{x}}_r}} \right){e_r} - {m_{33}}\left( {{\mathit{\boldsymbol{\eta }}_3}\left| {{e_u}} \right| - {d_3}{e_r}} \right) + }\\ {{z_u}{{\dot z}_u} + {z_\kappa }{{\dot z}_\kappa } + {z_r}{{\dot z}_r} + \xi ,} \end{array} \end{array} $ | (22) |
式中,
假设1 对所有神经网络理想权值矩阵W*和逼近误差ε有界,即存在正常数WM和有界函数εM,使得‖W*‖≤WM和‖ε‖≤εM.
2.7 海流观测器设计针对海洋环境中未知时变海流,本文设计了一种指数收敛自适应观测器,目标为海流估计值指数趋近于未知时变海流,即
| $ {\mathit{\boldsymbol{\hat v}}_c} = \mathit{\boldsymbol{\dot \eta }} - \mathit{\boldsymbol{J}}(\psi )\mathit{\boldsymbol{v}}. $ | (23) |
对于设计的海流观测器,可以选择:
| $ {\mathit{\boldsymbol{\dot {\hat v}}}_c} = - \mathit{\boldsymbol{\hat K}}{\mathit{\boldsymbol{v}}_c} + \mathit{\boldsymbol{K\dot \eta }} - \mathit{\boldsymbol{KJ}}(\psi )\mathit{\boldsymbol{v}}. $ | (24) |
式中:
将式(24)代入式(23),可得:
| $ \mathit{\boldsymbol{\dot v}}_c^e = {\mathit{\boldsymbol{\dot v}}_c} - \mathit{\boldsymbol{\dot {\hat v}}} = \mathit{\boldsymbol{\hat K}}{\mathit{\boldsymbol{v}}_c} - \mathit{\boldsymbol{K\dot \eta }} + \mathit{\boldsymbol{KJ}}(\psi )\mathit{\boldsymbol{v}} = - \mathit{\boldsymbol{Kv}}_c^e, $ | (25) |
式中,vce=[vcxe vcye 0]T∈ R 3为海流观测器观测误差组成的向量.
根据式(25)可知,设计的未知海流观测器是指数稳定的;但是,在欠驱动USV实际航行过程中,惯性坐标系下的速度
| $ \begin{array}{l} \mathit{\boldsymbol{\dot v}}_c^e = {{\mathit{\boldsymbol{\dot v}}}_c} - {{\mathit{\boldsymbol{\dot {\hat v}}}}_c} = - \mathit{\boldsymbol{\dot \zeta }} - \mathit{\boldsymbol{K\dot \eta }} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{K\zeta }} - \mathit{\boldsymbol{K}}( - \mathit{\boldsymbol{K\eta }} - \mathit{\boldsymbol{J}}(\psi )\mathit{\boldsymbol{v}}) - \mathit{\boldsymbol{K\dot \eta }} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{K}}({{\mathit{\boldsymbol{\hat v}}}_c} - {\mathit{\boldsymbol{v}}_c}) = - \mathit{\boldsymbol{Kv}}_c^e. \end{array} $ |
综上所述,设计的海流观测器是指数收敛的.
3 稳定性分析为稳定欠驱动USV轨迹跟踪控制器与海流观测器所组成的闭环系统,将整个控制系统分解为两个子系统.
定义第1个子系统∑1为
| $ \left\| {{\mathit{\boldsymbol{x}}_1}} \right\| = \left[ {\begin{array}{*{20}{l}} {{e_x}}&{{e_y}}&{{e_\psi }}&{{e_u}}&{{e_\kappa }}&{{e_r}}&{{{\tilde W}_1}}&{{{\tilde W}_3}}&{{\delta _1}}&{{\delta _3}} \end{array}} \right]. $ |
根据文献[13]可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot z}_u} = {{\dot u}_{cf}} - {{\dot u}_c} = - {z_u}/{\gamma _u} + {\rm{d}}{u_c}/{\rm{d}}t,}\\ {|{\rm{d}}{u_c}/{\rm{d}}t| \le {\zeta _u},} \end{array}} \right. $ | (26) |
式中,ζu>0,且为正实数.
将式(10)代入式(26),可得:
| $ {z_u}{\dot z_u} \le - \frac{{z_u^2}}{{{\gamma _u}}} + {\zeta _u}|{\zeta _u}| \le - \frac{{z_u^2}}{{{\gamma _u}}} + z_u^2 + \frac{1}{4}\zeta _u^2. $ | (27) |
将不等式(27)代入式(22),可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_4} \le - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 - {\beta _1}e_u^2 - {\beta _3}e_r^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde W}}}_1}h({x_u}){e_u} - {m_{11}}({\eta _1}|{e_u}| - {d_1}{e_u}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde W}}}_3}h({x_r}){e_r} - {m_{33}}({\eta _3}|{e_r}| - {d_3}{e_r}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {1 - \frac{1}{{{\gamma _u}}}} \right)z_u^2 - \left( {1 - \frac{1}{{{\gamma _\kappa }}}} \right)z_\kappa ^2 - \left( {1 - \frac{1}{{{\gamma _r}}}} \right)z_r^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{4}(\zeta _u^2 + \zeta _\kappa ^2 + \zeta _r^2).} \end{array} $ |
式中,ζκ>0,ζr>0,且均为正实数.
根据式(18),可得:
| $ {\dot \delta _i} = {\vartheta _i} - {\hat \vartheta _i} = \mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}h(\mathit{\boldsymbol{x}}) + {\varepsilon _i} - {\sigma _i}{\delta _i},(i = 1,3) $ | (28) |
式中,ε1>0,ε3>0,均为待定的正实数.
根据式(28),可得:
| $ {\delta _i}{\dot \delta _i} = {\delta _i}\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}h(\mathit{\boldsymbol{x}}) + {\delta _i}{\varepsilon _i} - {\sigma _i}\delta _i^2,(i = 1,3). $ |
定义一个新的李雅普诺夫函数:
| $ \begin{array}{*{20}{l}} {{V_5} = {V_4} + \frac{1}{{2{\chi _1}}}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_1} + \frac{1}{{2{\chi _3}}}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_3} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\lambda _1}\delta _1^2 + \frac{1}{2}{\lambda _3}\delta _3^2,} \end{array} $ | (29) |
对式(29)求导,可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_5} = {{\dot V}_4} - \frac{1}{{{\chi _1}}}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat W}}}}_1} - \frac{1}{{{\chi _3}}}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat W}}}}_3} + {\lambda _1}{\delta _1}{{\dot \delta }_1} + {\lambda _3}{\delta _3}{{\dot \delta }_3} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\dot V}_4} - \mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}h({\mathit{\boldsymbol{x}}_u})({e_u} + {\lambda _1}{\delta _1}) + {\rho _1}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}{{\mathit{\boldsymbol{\hat W}}}_1} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}h({\mathit{\boldsymbol{x}}_r})({e_r} + {\lambda _3}{\delta _3}) + {\rho _3}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}{{\mathit{\boldsymbol{\hat W}}}_3} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _1}{\delta _1}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}h({\mathit{\boldsymbol{x}}_u}) + {\lambda _1}{\delta _1}{\varepsilon _1} - {\lambda _1}{\sigma _1}\delta _1^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _3}{\delta _3}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}h({\mathit{\boldsymbol{x}}_r}) + {\lambda _3}{\delta _3}{\varepsilon _3} - {\lambda _3}{\sigma _3}\delta _3^2.} \end{array} $ | (30) |
将式(20)代入式(30),可得:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{{\dot V}_5} \le - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 - {\beta _1}e_u^2 - {\beta _3}e_r^2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {m_{11}}({\eta _1}|{e_u}| - {d_1}{e_u}) - {m_{33}}({\eta _3}|{e_r}| - {d_3}{e_r}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _1}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_1} + {\rho _1}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}\mathit{\boldsymbol{W}}_1^* + {\lambda _1}{\delta _1}{\varepsilon _1} - {\lambda _1}{\sigma _1}\delta _1^2 - } \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _3}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_3} + {\rho _3}\mathit{\boldsymbol{\tilde W}}_3^{\rm{T}}\mathit{\boldsymbol{W}}_3^* + {\lambda _3}{\delta _3}{\varepsilon _3} - {\lambda _3}{\sigma _3}\delta _3^2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {1 - \frac{1}{{{\gamma _u}}}} \right)z_u^2 - \left( {1 - \frac{1}{{{\gamma _\kappa }}}} \right)z_\kappa ^2 - \left( {1 - \frac{1}{{{\gamma _r}}}} \right)z_r^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{4}(\zeta _u^2 + \zeta _\kappa ^2 + \zeta _r^2).} \end{array} \end{array} $ | (31) |
根据文献[14], 可得以下方程:
| $ \left\{ \begin{array}{l} {\delta _i}{\varepsilon _i} - {\sigma _i}\delta _i^2 = - {\sigma _i}{({\delta _i} - \frac{{{\varepsilon _i}}}{{2{\sigma _i}}})^2} + \frac{1}{{4{\sigma _i}}}\varepsilon _i^2,(i = 1,3)\\ \mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}\mathit{\boldsymbol{W}}_i^* - \mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_i} = - {\left\| {{{\mathit{\boldsymbol{\tilde W}}}_i} - \frac{{\mathit{\boldsymbol{W}}_i^*}}{2}} \right\|^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{4}{\left\| {\mathit{\boldsymbol{W}}_i^*} \right\|^2},(i = 1,3) \end{array} \right. $ | (32) |
将式(32)代入式(31),可得:
| $ \begin{array}{l} {{\dot V}_5} \le - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 - {\alpha _4}e_u^2 - {\alpha _5}e_r^2 - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{m_{11}}({\eta _1}|{e_u}| - {d_1}{e_u}) - {m_{33}}({\eta _3}|{e_r}| - {d_3}{e_r}) - }\\ {{\rho _1}{{\left[ {\left\| {{{\mathit{\boldsymbol{\tilde W}}}_1} - \frac{{\mathit{\boldsymbol{W}}_1^*}}{2}} \right\| - \frac{1}{4}{{\left\| {\mathit{\boldsymbol{W}}_1^*} \right\|}^2}} \right]}^2} - }\\ {{\lambda _1}{{\left[ {{\sigma _1}{{\left( {{\delta _1} - \frac{{{\varepsilon _1}}}{{2{\sigma _1}}}} \right)}^2} - \frac{1}{{4{\sigma _1}}}\varepsilon _1^2} \right]}^2} - } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rho _3}{{\left[ {{{\left\| {{{\mathit{\boldsymbol{\tilde W}}}_3} - \frac{{\mathit{\boldsymbol{W}}_3^*}}{2}} \right\|}^2} - \frac{1}{4}{{\left\| {\mathit{\boldsymbol{W}}_3^*} \right\|}^2}} \right]}^2} - }\\ {{\lambda _3}{{\left[ {{\sigma _3}{{\left( {{\delta _3} - \frac{{{\varepsilon _3}}}{{2{\sigma _3}}}} \right)}^2} - \frac{1}{{4{\sigma _3}}}\varepsilon _3^2} \right]}^2} - }\\ {\left( {1 - \frac{1}{{{\gamma _u}}}} \right)z_u^2 - \left( {1 - \frac{1}{{{\gamma _\kappa }}}} \right)z_\kappa ^2 - \left( {1 - \frac{1}{{{\gamma _r}}}} \right)z_r^2 + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{1}{4}(\zeta _u^2 + \zeta _\kappa ^2 + \zeta _r^2) \le - {\alpha _1}e_x^2 - {\alpha _2}e_y^2 - {\alpha _3}e_\kappa ^2 - }\\ {{\alpha _4}e_u^2 - {\alpha _5}e_r^2 - {m_{11}}({\eta _1}|{e_u}| - {d_1}{e_u}) - }\\ {{m_{33}}({\eta _3}|{e_r}| - {d_3}{e_r}) - } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {_{\min }{\sigma _{\min }}\left[ {{{\left( {{\delta _1} - \frac{{{\varepsilon _1}}}{{2{\sigma _1}}}} \right)}^2} + {{\left( {{\delta _3} - \frac{{{\varepsilon _3}}}{{2{\sigma _3}}}} \right)}^2}} \right] - }\\ {\lambda {\rho _{\min }}\left[ {{{\left\| {{{\mathit{\boldsymbol{\tilde W}}}_1} - \frac{{\mathit{\boldsymbol{W}}_1^*}}{2}} \right\|}^2} + {{\left\| {{{\mathit{\boldsymbol{\tilde W}}}_3} - \frac{{\mathit{\boldsymbol{W}}_3^*}}{2}} \right\|}^2}} \right] + \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}.} \end{array} \end{array} $ | (33) |
式中:
根据式(33)可知,通过选取不同的控制器参数,可保证
定义第2个子系统∑2为
| $ \left\| {{\mathit{\boldsymbol{x}}_2}} \right\| = \left[ {\begin{array}{*{20}{l}} {v_{cx}^e}&{v_{cy}^e} \end{array}} \right]. $ |
定义一个新的李雅普诺夫函数为
| $ {V_6} = \frac{1}{2}({(v_{cx}^e)^2} + {(v_{cy}^e)^2}), $ | (34) |
对式(34)求导,可得:
| $ {\dot V_6} = v_{cx}^e\dot v_{cx}^e + v_{cy}^e\dot v_{cy}^e = - {k_1}{(v_{cx}^e)^2} - {k_2}{(v_{cy}^e)^2}, $ |
则子系统∑2为指数稳定的.
定义一个新的李雅普诺夫函数为
| $ V = {V_5} + {V_6}, $ |
则
| $ \dot V \le - 2\mu V + \varPhi , $ | (35) |
式中,μ、Φ分别为:
| $ \begin{array}{*{20}{l}} {\mu = \min \{ {\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4},{\alpha _5},{\rho _1},{\lambda _1},{\rho _3},{\lambda _3},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 - \frac{1}{{{\gamma _u}}}),(1 - \frac{1}{{{\gamma _\kappa }}}),(1 - \frac{1}{{{\gamma _r}}}),{k_1},{k_2}\} ,} \end{array} $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \frac{1}{4}(\zeta _u^2 + \zeta _\kappa ^2 + \zeta _r^2) + \frac{{{\lambda _{\max }}}}{{2{\sigma _{\min }}}}\varepsilon _M^2 + \frac{{{\rho _{\max }}}}{2}W_M^2. $ |
对式(35)求解可得:
| $ V \le \frac{\varPhi }{{2\mu }} + \left[ {V(0) - \frac{\varPhi }{{2\mu }}} \right]{{\rm{e}}^{ - 2\mu t}}. $ |
显然,当t→∞时,有V→Φ/2μ,则闭环系统的所有信号是半全局一致最终有界的,即所设计的控制器是稳定的.
4 仿真分析本文选取文献[15]欠驱动USV系统模型和外界干扰,验证文中设计的控制算法, 取欠驱动USV初始条件为:
| $ \mathit{\boldsymbol{\eta }}(0) = {\left[ {\begin{array}{*{20}{l}} 0&{17}&0 \end{array}} \right]^{\rm{T}}},v(0) = {\left[ {\begin{array}{*{20}{l}} {0.4}&0&0 \end{array}} \right]^{\rm{T}}}. $ |
欠驱动USV应用过程中,τu、τr是有限的,在控制器设计中,设定控制输入为有限值,即
| $ 0 \le |{\tau _u}| \le 90{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}},0 \le |{\tau _r}| \le 20{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}}. $ |
控制器参数为:α1=0.5, α2=0.4, α3=0.3, α4=0.2, α5=1.0, γu=0.1, γκ=0.1, γr=0.1, η1=0.2, η3=0.2, χ1=0.1, χ3=0.1, λ1=0.15,λ3=0.10, ρ1=0.3, ρ3=0.2, 神经网络的初始权值取0.1, cj=[-1.0 -0.5 0 0.5 1.0]和bj =5.0.
缓慢变化海流选取为
| $ \left\{ {\begin{array}{*{20}{l}} {{v_{cx}} = ( - 0.1 - 0.1\sin (0.01t)),}\\ {{v_{cy}} = ( - 0.1 - 0.1\cos (0.01t)).} \end{array}} \right. $ |
为验证该控制器控制性能,选取预期圆轨迹为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_c}(t) = 15\sin (0.05t),}\\ {{y_c}(t) = 15\cos (0.05t).} \end{array}} \right. $ |
为便于仿真结果分析,仿真时间为200 s,可清晰地看出运动轨迹,仿真结果如图 2~图 7所示.
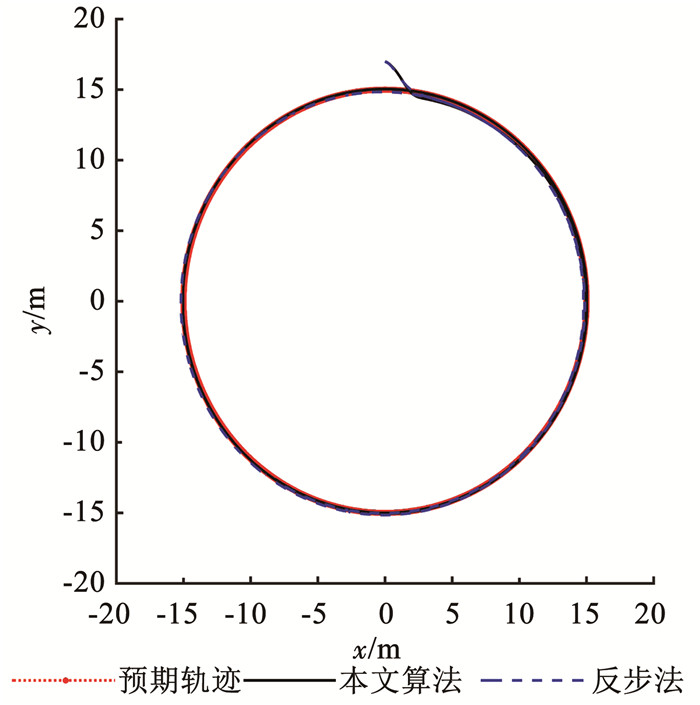
|
图 2 预期轨迹与实际运动轨迹 Fig. 2 Desired trajectory and actual trajectory |
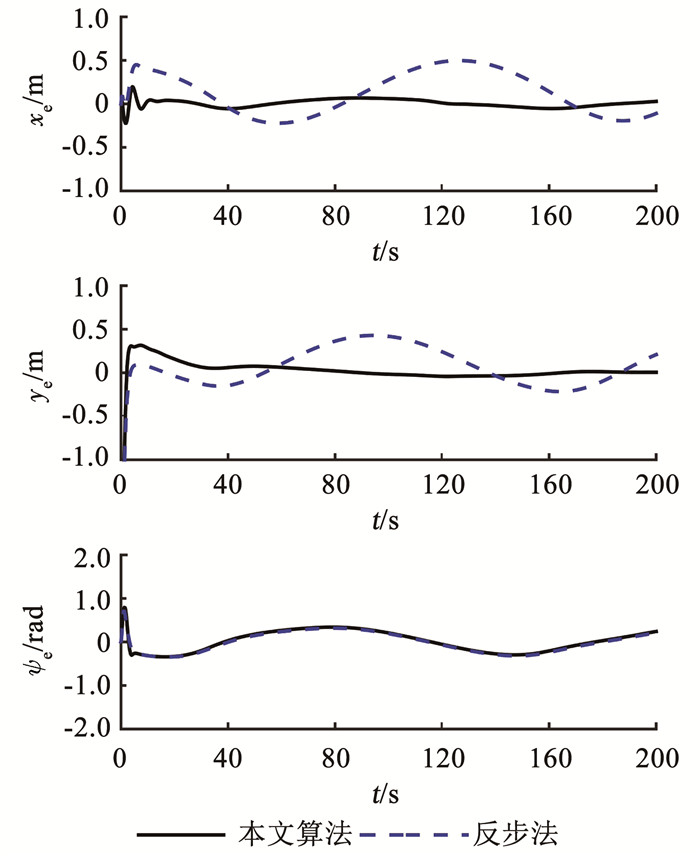
|
图 3 位置跟踪误差与偏航误差 Fig. 3 Position tracking errors and yaw errors |
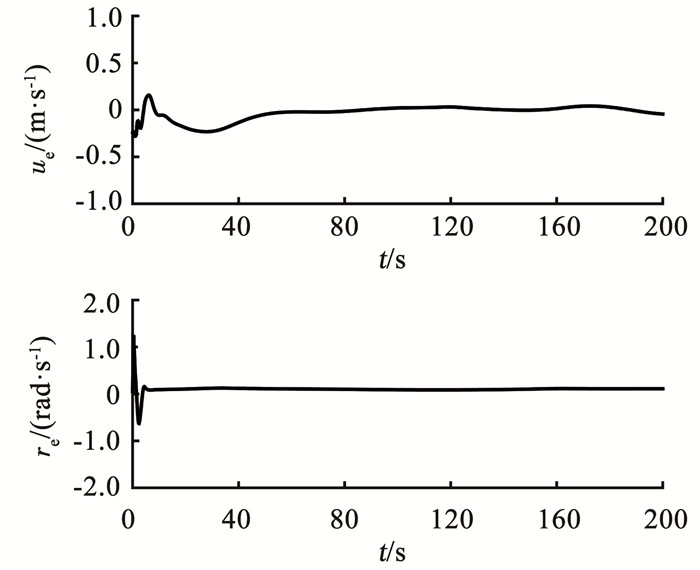
|
图 4 速度跟踪误差 Fig. 4 Velocity tracking errors |
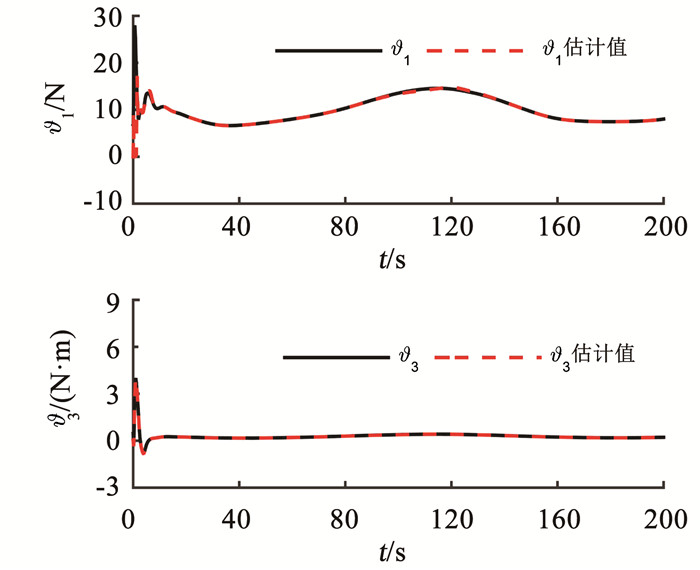
|
图 5 函数逼近误差 Fig. 5 Function approximation errors |
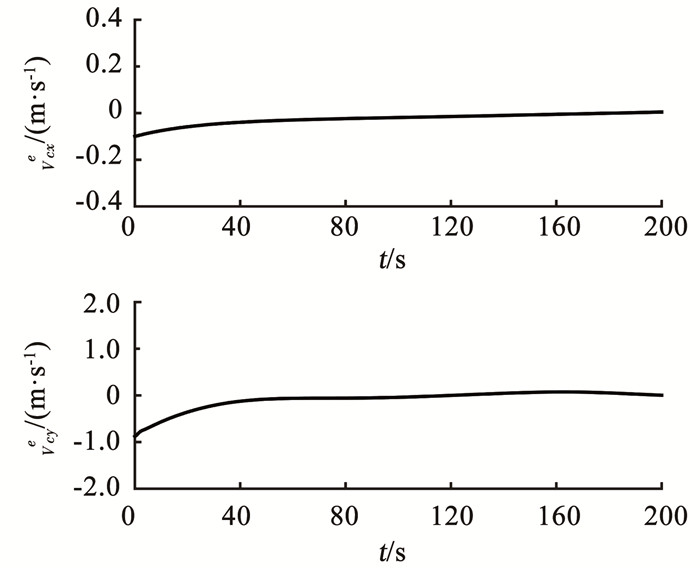
|
图 6 海流速度观测误差 Fig. 6 Current velocity observation errors |
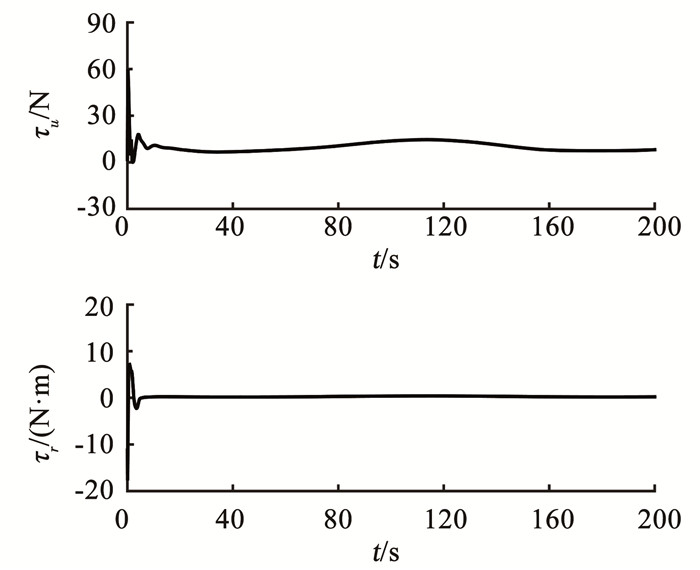
|
图 7 控制力与控制力矩 Fig. 7 Control force and control moment |
根据图 2可知,在欠驱动USV航行初始阶段受海流影响较大,但在较短时间内有效地实现了轨迹跟踪;根据图 3、4可得出,位置跟踪误差、速度跟踪误差均收敛到零附近的一个区域内;根据图 5可知,设计的神经网络自适应模型可有效逼近欠驱动USV系统未知函数;根据图 6可知,设计的自适应海流观测器可有效观测未知缓慢时变海流.根据图 7可知,控制力及控制力矩较为稳定,且在设定范围内.
5 结论1) 设计了一种自适应海流观测器,有效地估计了未知缓慢时变海流.
2) 运用李雅普诺夫稳定性理论验证了欠驱动USV闭环控制系统的稳定性.
3) 仿真结果表明,欠驱动USV轨迹跟踪误差、速度跟踪误差均收敛到零附近的一个区域内,验证了该控制系统的有效性.
| [1] |
沈智鹏, 张晓玲, 张宁, 等. 基于神经网络观测器的船舶轨迹跟踪递归滑模动态面输出反馈控制[J]. 控制理论与应用, 2018, 35(8): 1092. SHEN Zhipeng, ZHANG Xiaoling, ZHANG Ning, et al. Recursive sliding mode dynamic surface output feedback control for ship trajectory tracking based on neural network observer[J]. Control Theory & Applications, 2018, 35(8): 1092. DOI:10.7641/CTA.2018.70456 |
| [2] |
杜佳璐, 杨杨, 胡鑫, 等. 基于动态面控制的船舶动力定位控制律设计[J]. 交通运输工程, 2014, 14(5): 362. DU Jialu, YANG Yang, HU Xin, et al. Control law design of dynamic positioning for ship based on dynamic surface control[J]. Journal of Traffic and Transportation Engineering, 2014, 14(5): 362. DOI:10.3969/j.issn.1671-1637.2014.05.005 |
| [3] |
张天平, 施枭铖, 沈启坤, 等. 具有未建模动态的自适应神经网络动态面控制[J]. 控制理论与应用, 2013, 30(4): 475. ZHANG Tianping, SHI Xiaocheng, SHEN Qikun, et al. Adaptive neural-network dynamic surface-control with unmodeled dynamics[J]. Control Theory & Applications, 2013, 30(4): 475. DOI:10.7641/CTA.2013.21022 |
| [4] |
廖煜雷, 万磊, 庄佳园. 欠驱动船路径跟踪的反演自适应动态滑模控制方法[J]. 中南大学学报(自然科学版), 2012, 43(7): 2655. LIAO Yulei, WAN Lei, ZHUANG Jiayuan. Backstepping adaptive dynamical sliding mode control method for path following of underactuated surface vessel[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2655. |
| [5] |
王金强, 王聪, 魏英杰, 等. 未知海流干扰下自主水下航行器位置跟踪控制策略研究[J]. 兵工学报, 2019, 40(3): 583. WANG Jinqiang, WANG Cong, WEI Yingjie, et al. Position tracking control of autonomous underwater vehicles in the disturbance of unknown ocean currents[J]. Acta Armamentarii, 2019, 40(3): 583. DOI:10.3969/j.issn.1000-1093.2019.03.018 |
| [6] |
TEEK P, GE S S. Control of fully actuated ocean surface vessels using a class of feedforward approximators[J]. IEEE Transactions on Control Systems Technology, 2006, 14(4): 750. DOI:10.1109/tcst.2006.872507 |
| [7] |
SHOJAEI K. Observer-based neural adaptive formation control of autonomous surface vessels with limited torque[J]. Robotics and Autonomous Systems, 2016, 78(C): 83. DOI:10.1016/j.robot.2016.01.005 |
| [8] |
WANG Jinqiang, WANG Cong, WEI Yingjie, et al. Three-dimensional path following of an underactuated AUV based on neuro-adaptive command filtered backstepping control[J]. IEEE Access, 2018, 6: 74355. DOI:10.1109/ACCESS.2018.2883081 |
| [9] |
PAN Changzhong, LAI Xuzhi, YANG S X, et al. A bioinspired neural dynamics-based approach to tracking control of autonomous surface vehicles subject to unknown ocean currents[J]. Neural Computing and Applications, 2015, 26(8): 1929. DOI:10.1007/s00521-015-1839-6 |
| [10] |
WANG Hao, WANG Dan, PENG Zhouhua. Neural network based adaptive dynamic surface control for cooperative path following of marine surface vehicles via state and output feedback[J]. Neurocomputing, 2014, 133: 170. DOI:10.1016/j.neucom.2013.11.019 |
| [11] |
LIU Lu, WANG Dan, PENG Zhouhua. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances[J]. Neurcomputing, 2016, 173: 799. DOI:10.1016/j.neucom.2015.08.033 |
| [12] |
LIU Lu, WANG Dan, PENG Zhouhua. Direct and composite iterative neural control for cooperative dynamic positioning of marine surface vessels[J]. Nonlinear Dynamics, 2015, 81: 1315. DOI:10.1007/s11071-015-2071-8 |
| [13] |
SHOJAEI K, DOLATSHAHI M. Line-of-sight target tracking control of underactuated autonomous underwater vehicles[J]. Ocean Engineering, 2017, 133: 244. DOI:10.1016/j.oceaneng.2017.02.007 |
| [14] |
XU Bin, SHI Zhongke, YANG Chenguang, et al. Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form[J]. IEEE Transactions on Cybernetics, 2014, 44(12): 2626. DOI:10.1109/TCYB.2014.2311824 |
| [15] |
DO K D, PAN J. Robust path-following of underactuated ships: Theory and experiments on a model ship[J]. Ocean Engineering, 2006, 33(10): 1354. DOI:10.1016/j.oceaneng.2005.07.011 |
 2020, Vol. 52
2020, Vol. 52


