2. 哈尔滨工业大学 航天学院, 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
某空间飞行器为实现对地观测等任务,在飞行过程中可能需要进行多次大角度姿态调整,以满足观测角度的要求.根据实际情况,该空间飞行器采用6个安装在尾部的小型姿控发动机作为姿控系统的执行机构,姿态机动过程中需要消耗燃料.燃料的消耗量与姿态控制律密切相关.由于空间飞行器总质量的限制,其携带的燃料有限,为保障机动全程的燃料消耗,需要优化设计姿态控制律,以期兼顾控制精度和能量消耗.
关于空间飞行器姿态机动优化控制方法,一些文献已经给出了相关的研究成果,减少能量消耗的思路集中在姿态控制律的设计上.文献[1]采用自抗扰技术设计姿态机动控制器,仿真结果显示该控制器能够减少能量消耗.但是该方法参数整定繁琐,且对观测器性能有较高要求.文献[2]也采用自抗扰控制器设计了姿态控制律,并给出了控制参数优化的方法.文献[3]通过对bang-bang控制的优化减少了姿态机动的振动问题,从而实现对能量时间的优化.上述3种方法仅能实现能量消耗的降低,并非最优能量控制.
通过应用最优控制方法设计姿态控制律,从而降低航天器姿态控制系统的能量消耗,是一种常见的设计思路.例如,文献[4]设计了一种反最优控制器,从而避免了直接求取Hamilton-Jacobi方程.仿真结果显示能够实现能量的优化.文献[5]把姿态控制问题转化为一个具有平方和约束的参数优化问题,利用平方和优化技术,实现了能量的最优控制.文献[6]讨论了采用变速控制力矩陀螺的一种姿态/能量一体化控制方法.文献[7]不仅设计了能量姿态一体化控制律,并进一步考虑了执行器饱和及四元数漂移等问题,对其漂移进行了整定,实现了姿态能量的一体化控制.实际上,上述这些文献均采用了庞特里亚金最小值法设计姿态最优控制律.
最优控制理论中的非线性规划方法也在最优姿态控制律的设计中的得到应用.文献[8-10]均把姿态机动问题转化为非线性规划问题.文献[8-9]使用非线性规划的方法描述了姿态机动问题,并提出了解的构造方法,避免了求解高阶微分方程,但仍存在计算复杂的问题;文献[10]进一步对初始可行解进行了改进优化,仿真结果显示该方法能够有效减少寻优计算的时间.文献[11]通过伪谱法计算全局路径节点,减少了全局规划的计算量,结合预测控制实现能量节省.
另外,针对非对称航天器姿态机动问题,文献[12]则基于Krotov-Bellman充分条件求取了最小燃料消耗解.
上述的文献在求解姿态最优控制律的过程中,均假设姿态控制系统执行机构能够输出连续变化的控制力矩,从而实现最优控制律所需要的连续型控制变量.但在许多特定应用背景下,例如本文所研究的某空间小型飞行器上,只能安装小型姿控发动机组,每个姿控发动机的输出均为开关型的控制力,即使采用脉冲调宽方式,也无法准确输出最优控制律所要求的连续型控制力矩.因此,需要结合特定的问题优化设计特定的姿态控制律,达到优化燃料消耗量的目的.
为避免奇异并有利于非线性系统的稳定性分析,宜采用四元数描述空间飞行器的大角度姿态运动.因此,在姿态控制律优化设计中,本文采用鲁棒性相对较好的基于四元数的非线性PD姿态控制律,并在这种控制律中引入3个姿态控制通道的开关门限,从而即有利于用脉冲调宽方式近似实现该控制律,又能有效地降低燃料消耗.另外,本文还采用一种新的改进的粒子群寻优(PSO)算法对非线性PD控制律的开关门限进行寻优设计.
对于许多执行大角度姿态机动的空间飞行器而言,经常采用的机动模式是从一种姿态指向到另外一种姿态指向的Rest-To-Rest机动.Rest-To-Rest姿态机动指令的规划也直接影响姿控系统的燃料消耗量.阶跃型指令只强调了快速性,而忽略了姿态机动指令对燃料消耗的影响.本文针对Rest-To-Rest姿态机动模式,研究用四元数描述的姿态指令规划问题,通过指令设计进一步减少燃料消耗,同时兼顾一定的响应速度.
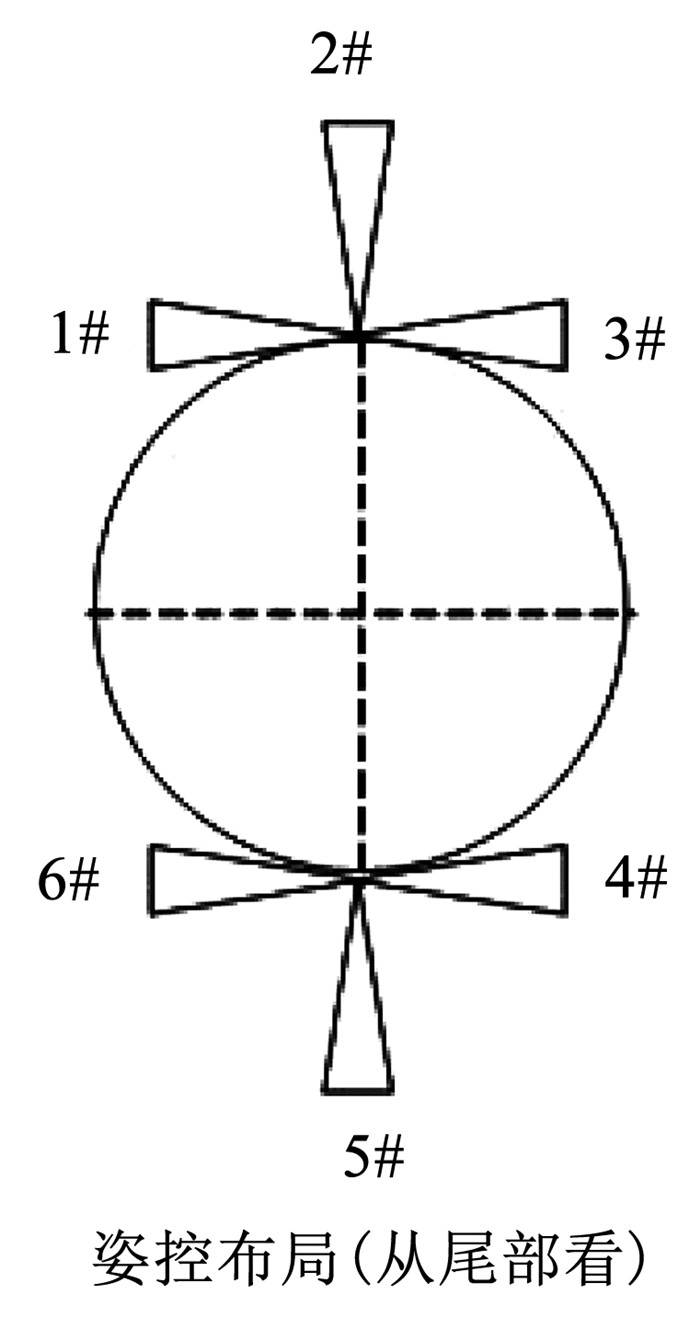
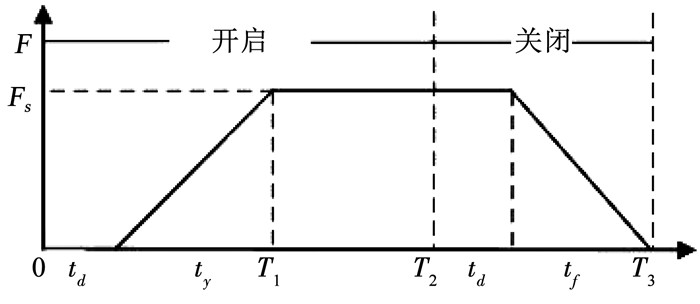
1 空间飞行器的姿态运动数学描述假设某空间飞行器需要在飞行过程中进行大角度姿态机动,为实现姿态控制,在飞行器的尾部安装了6台姿控发动机,发动机采用倒T型布局,如图 1所示,每个姿控发动机可以工作与开启或关闭状态,其推力工作曲线如图 2所示.
|
图 1 空间飞行器姿控发动机布局 Fig. 1 Configuration of the attitude control thruster in the spacecraft |
|
图 2 姿控发动机推力上升和下降动态特性 Fig. 2 Rising and falling properties of the attitude control thruster |
定义四元数q=[q0, qv]T,qv=[q1, q2, q3]T,则四元数描述的姿态运动方程为[13]
| $ \mathit{\boldsymbol{\dot q}} = \frac{1}{2}\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} q}}. $ |
式中,
考虑到存在干扰,姿态动力学方程写作:
| $ \mathit{\boldsymbol{J \boldsymbol{\dot \varOmega} }} = - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^ \times }\mathit{\boldsymbol{J \boldsymbol{\varOmega} }} + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}. $ |
式中:J =diag[Jx Jy Jz]为转动惯量矩阵;u∈R3为控制力矩;d∈R3为干扰力矩.
2 基于误差四元数的姿态跟踪非线性PD控制器设计 2.1 误差四元数的姿态跟踪控制系统数学模型设qd=[qd0 qd1 qd2 qd3]T=[qd0 qdvT]T为单位期望四元数,满足‖qd‖=1,Ωd∈R3为期望角速率.
| $ \mathit{\boldsymbol{e}} = {\left[ {\begin{array}{*{20}{l}} {{e_0}}&{{e_1}}&{{e_2}}&{{e_3}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{l}} {{e_0}}&{\mathit{\boldsymbol{e}}_v^{\rm{T}}} \end{array}} \right]^{\rm{T}}}, $ |
其中
| $ {e_0} = {q_0}{q_{d0}} + \mathit{\boldsymbol{q}}_{dv}^{\rm{T}}{\mathit{\boldsymbol{q}}_v},{\mathit{\boldsymbol{e}}_v} = {\mathit{\boldsymbol{q}}_{d0}}{\mathit{\boldsymbol{q}}_v} - \mathit{\boldsymbol{q}}_{dv}^ \times {\mathit{\boldsymbol{q}}_v} - {\mathit{\boldsymbol{q}}_0}{\mathit{\boldsymbol{q}}_{dv}}, $ |
不难证明‖e‖=1.定义由体坐标系到期望的体坐标系的转换矩阵为C1→d,则坐标转换矩阵可以表示为
| $ {\mathit{\boldsymbol{C}}_{1 \to d}} = {[(1 - 2\mathit{\boldsymbol{e}}_v^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}){\mathit{\boldsymbol{I}}_3} + 2{\mathit{\boldsymbol{e}}_v}{\kern 1pt} \mathit{\boldsymbol{e}}_v^{\rm{T}} - 2{e_0}{\kern 1pt} \mathit{\boldsymbol{e}}_v^ \times ]^{\rm{T}}}. $ |
定义角速度跟踪误差为
| $ \mathit{\boldsymbol{\omega }} = {\left[ {\begin{array}{*{20}{l}} {{\omega _1}}&{{\omega _2}}&{{\omega _3}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d}, $ |
式中,C=C1→dT.那么,误差四元数运动学方程为
| $ {\mathit{\boldsymbol{\dot e}}_0} = - \frac{1}{2}\mathit{\boldsymbol{e}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }},{\mathit{\boldsymbol{\dot e}}_v} = \frac{1}{2}({e_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{e}}_v^ \times )\mathit{\boldsymbol{\omega }}, $ | (1) |
而跟踪误差动力学方程为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{J\dot \omega }} = - {{(\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d})}^ \times }\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{J}}({\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d} - \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_d}) + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}},} \end{array} $ | (2) |
式中,ω=Ω-CΩd为角速度跟踪误差.
2.2 非线性PD控制律设计本文先给出应用Back-Stepping方法设计的非线性PD控制律[16].
ω可以视作运动学方程式(1)的虚拟输入,选取:
| $ \mathit{\boldsymbol{\omega }} = - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{e}}_v},{\mathit{\boldsymbol{k}}_1} > 0, $ |
预选Lyapunov函数为
| $ {V_1} = e_0^2 + \mathit{\boldsymbol{e}}_v^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}, $ |
沿着状态轨迹(1)求导得到:
| $ {\dot V_1} = - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} \mathit{\boldsymbol{e}}_v^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}, $ |
易得ev→0.
由于ω不是真实输入,把ω与理想值-k1ev之差记为
| $ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{\omega }} - ( - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}). $ | (3) |
Lyapunov函数V1的真实导数表达式为
| $ {\dot V_1} = - \mathit{\boldsymbol{e}}_v^{\rm{T}}{\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{e}}_v^{\rm{T}}\mathit{\boldsymbol{\sigma }}, $ |
由式(3)和式(1)、(2)可以改写为
| $ \begin{array}{l} \mathit{\boldsymbol{J\dot \sigma }} = - {(\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d})^ \times }\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{J}}({{(\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v})}^ \times }\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_d} - \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_d}) + }\\ {\frac{{{\mathit{\boldsymbol{k}}_1}}}{2}\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{e}}_v^ \times \mathit{\boldsymbol{\sigma }} + {e_0}(\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{k}}_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v})) + \mathit{\boldsymbol{u}}.} \end{array} \end{array} $ | (4) |
本文重新选取Lyapunov函数为
| $ V = {V_1} + \frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{J\sigma }}, $ |
沿着式(4)求导可得:
| $ \begin{array}{l} \dot V = - {k_1}{\kern 1pt} \mathit{\boldsymbol{e}}_v^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\{ - {(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}})^ \times }\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}) + \mathit{\boldsymbol{J}}({{(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v})}^ \times }\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}} - \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_\mathit{\boldsymbol{d}}}) + }\\ {\frac{{{k_1}}}{2}\mathit{\boldsymbol{J}}({\mathit{\boldsymbol{e}}_v}^ \times (\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}) + {e_0}(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v})) + \mathit{\boldsymbol{u}}\} = }\\ { - {k_1}{\kern 1pt} \mathit{\boldsymbol{e}}_v^{\rm{T}}{\mathit{\boldsymbol{e}}_v} + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}{\mathit{\boldsymbol{e}}_v} + {k_1}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}{\kern 1pt} \mathit{\boldsymbol{e}}_v^ \times \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}) + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {2{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{J}}{{(\mathit{\boldsymbol{\sigma }} - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v})}^ \times }\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}} - {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}} \times \mathit{\boldsymbol{JC}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}} - }\\ {{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{JC}}{{\mathit{\boldsymbol{\dot Q}}}_\mathit{\boldsymbol{d}}} + \frac{{{k_1}{e_0}}}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{JC}}(\sigma - {k_1}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}) + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{u}}.} \end{array} \end{array} $ | (5) |
本文为式(4)所示的非线性系统设计如下PD控制器:
| $ \mathit{\boldsymbol{u}} = - {k_2}\mathit{\boldsymbol{\sigma }} - {k_3}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}, $ |
式中, k2, k3为大于零的常数.式(5)可改写为
| $ \begin{array}{l} \dot V \le - {k_1}{\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|^2} - {k_2}{\left\| \mathit{\boldsymbol{\sigma }} \right\|^2} + \left\| {1 - {k_3}} \right\|\left\| \mathit{\boldsymbol{\sigma }} \right\|\left\| {{\mathit{\boldsymbol{e}}_v}} \right\| + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{k_1}{\gamma _J}\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|\left\| \mathit{\boldsymbol{\sigma }} \right\|(\left\| \mathit{\boldsymbol{\sigma }} \right\| + {k_1}\left\| {{\mathit{\boldsymbol{e}}_v}} \right\| + \left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|) + }\\ {2{\gamma _J}\left\| \mathit{\boldsymbol{\sigma }} \right\|\left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|(\left\| \mathit{\boldsymbol{\sigma }} \right\| + {k_1}\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|) + }\\ {{\gamma _J}\left\| \mathit{\boldsymbol{\sigma }} \right\|{{\left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|}^2} + {\gamma _J}\left\| \mathit{\boldsymbol{\sigma }} \right\|\left\| {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_\mathit{\boldsymbol{d}}}} \right\| \le } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\left( { - {k_2} + \frac{3}{2}{k_1}{\gamma _J} - 2{\gamma _J}{\gamma _{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}}}} \right){{\left\| \mathit{\boldsymbol{\sigma }} \right\|}^2} + }\\ {\left( {3{k_1}{\gamma _J}{\gamma _{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}}} + \frac{3}{2}k_1^2{\gamma _J} + \left\| {1 - {k_3}} \right\|} \right)\left\| \mathit{\boldsymbol{\sigma }} \right\|\left\| {{\mathit{\boldsymbol{e}}_v}} \right\| - }\\ {{k_1}{{\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|}^2} + {\gamma _J}({{\left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|}^2} + \left\| {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_\mathit{\boldsymbol{d}}}} \right\|)\left\| \sigma \right\| = }\\ { - {\mathit{\boldsymbol{\chi }}^{\rm{T}}}\mathit{\boldsymbol{Q\chi }} + {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{\chi }},} \end{array} \end{array} $ |
其中:
| $ {\gamma _J} = \left\| \mathit{\boldsymbol{J}} \right\|,{\gamma _{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}}} = \mathop {{\rm{sup}}}\limits_{t \ge 0} \left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|, $ |
| $ \mathit{\boldsymbol{\chi }} = \left[ {\begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{e}}_v}} \right\|}\\ {\left\| \mathit{\boldsymbol{\sigma }} \right\|} \end{array}} \right],\mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\gamma _J}\left( {\left\| {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_\mathit{\boldsymbol{d}}}} \right\| + {{\left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|}^2}} \right)} \end{array}} \right], $ |
| $ {{Q_{11}} = {k_1},{Q_{12}} = - \frac{3}{4}k_1^2{\gamma _J} - \frac{3}{2}{k_1}{\gamma _J}{\gamma _{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}}} + \left\| {1 - {k_3}} \right\|,} $ |
| $ {{Q_{22}} = {k_2} - \frac{3}{2}{k_1}{\gamma _J} - 2{\gamma _J}{\gamma _{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}}}.} $ |
本文假定k3=1/3,保证矩阵Q正定的约束条件可由下式给出:
| $ {k_1}{k_2} - \frac{4}{9} > k_1^2\left( {\frac{9}{{16}}{\gamma _J}k_1^2 + \frac{9}{4}\gamma _J^2{\gamma _{C{\varOmega _d}}}{k_1} + \frac{9}{4}\gamma _J^2\gamma _{C{\varOmega _d}}^2 + \frac{1}{2}{\gamma _J}} \right), $ |
如果合理选择k1, k2满足上述不等式,则有
| $ \dot V \le - \lambda {\left\| \mathit{\boldsymbol{\chi }} \right\|^2} + \rho (t)\left\| \mathit{\boldsymbol{\chi }} \right\|, $ |
式中,λ为矩阵Q的最小特征值,即
| $ \rho (t) = {\gamma _J}(\left\| {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_\mathit{\boldsymbol{d}}}} \right\| + {\left\| {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_\mathit{\boldsymbol{d}}}} \right\|^2}). $ |
借鉴文献[16]中的进一步分析结果,当t→∞时,σ和ev趋于有界,进而ω趋于有界.
为了简单起见,对控制器的形式做一些改写,令
| $ \mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{l}} {M{z_x}}&{M{z_y}}&{M{z_z}} \end{array}} \right]^{\rm{T}}} = - {K_1}{\kern 1pt} \mathit{\boldsymbol{\omega }} - {K_2}{\kern 1pt} {\mathit{\boldsymbol{e}}_v}. $ | (6) |
式中:Mzx、Mzy和Mzz分别为滚转、偏航和俯仰力矩;K1=k2,K2=k2k1+k3.
按照PD控制律(6),得到控制指令力矩指令Mzx,Mzy,Mzz后,需要根据控制力矩指令对图 1所示的6个发动机的工作方式进行分配.
2.2.1 滚转和偏航通道由于滚转和偏航方向具有耦合作用,本文对滚转和偏航同时进行控制.本文采取以下的发动机分配方式:
当Mzx≥0,让1号和4号发动机进行配合工作,来计算一个指令周期内1号和4号发动机所需要的等效力
| $ {{M_{{z_x}}} = {F_{z1}}{l_x} + {F_{z4}}{l_x},} $ | (7) |
| $ {{M_{{z_y}}} = {F_{z1}}{l_y} - {F_{z4}}{l_y},} $ | (8) |
式中,lx、ly分别为滚转和偏航力臂.联立式(7)、(8),解出:
| $ {{{\bar F}_{z1}} = \frac{{{M_{{z_x}}}{l_y} + {M_{{z_y}}}{l_x}}}{{2{l_x}{l_y}}},} $ |
| $ {{{\bar F}_{z4}} = \frac{{{M_{{z_x}}}{l_y} - {M_{{z_y}}}{l_x}}}{{2{l_x}{l_y}}}.} $ |
当Mzx < 0,让3号和6号发动机进行配合工作来计算一个指令周期内3号和6号发动机所需要的等效力
| $ {{M_{{z_x}}} = - {F_{z3}}{l_x} - {F_{z6}}{l_x},} $ | (9) |
| $ {{M_{{z_y}}} = - {F_{z1}}{l_y} + {F_{z6}}{l_y},} $ | (10) |
联立式(9)、(10),解出:
| $ {{{\bar F}_{z1}} = - \frac{{{M_{{z_x}}}{l_y} + {M_{{z_y}}}{l_x}}}{{2{l_x}{l_y}}},} $ |
| $ {{{\bar F}_{z4}} = - \frac{{{M_{{z_x}}}{l_y} - {M_{{z_y}}}{l_x}}}{{2{l_x}{l_y}}}.} $ |
当Mzx=0时,1,3,4,6号发动机均不输出控制力.
2.2.2 俯仰通道俯仰通道没有耦合,很容易得出2号和5号发动机所需产生的等效力:
| $ {{{\bar F}_{z2}} = M{z_z}/{l_z}(M{z_z} \ge 0),} $ |
| $ {{{\bar F}_{z5}} = - M{z_z}/{l_z}(M{z_z} < 0).} $ |
由于姿控发动机只能工作于完全开启状态或完全关闭状态,不能输出所需要的连续控制力,所以只能采用脉宽调制(PWM)方法,在一个给定的控制周期Tc内,通过调整发动机开启和关闭时间的占空比,利用冲量等效原理近似实现PD控制律[17-18].
根据动量等效原则,发动机产生的等效力Fe为
| $ {F_e} = \frac{1}{{{T_c}}}\int_0^{{T_c}} F (t){\rm{d}}t, $ |
在一个控制周期Tc内,上式中
| $ F(t) = \left\{ {\begin{array}{*{20}{l}} {{F_{zs}},0 < t < {T_{{\rm{on}}}};}\\ {0,{T_{{\rm{on}}}} < t < {T_c}.} \end{array}} \right. $ |
通过调整开启时间Ton可近似输出不同的等效控制力Fe.
为了节省燃料,并降低姿控发动机的开启频率,本文在非线性PD控制规律中引入开关门限δx、δy、δz,它们均为大于零的常值.这样,实际实现的PD控制律表达如下:
| $ M{z_x} = \left\{ {\begin{array}{*{20}{l}} { - {K_1}{\omega _1} - {K_2}{e_1},{\rm{ }}}&{{\rm{if }}{\kern 1pt} {\kern 1pt} {\kern 1pt}| - {K_1}{\omega _1} - {K_2}{e_1}| > {\delta _x};}\\ {0,}&{{\rm{if }}{\kern 1pt} {\kern 1pt} {\kern 1pt}| - {K_1}{\omega _1} - {K_2}{e_1}| \le {\delta _x},} \end{array}} \right. $ |
| $ M{z_y} = \left\{ {\begin{array}{*{20}{l}} { - {K_1}{\omega _2} - {K_2}{e_2},{\rm{ }}}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} | - {K_1}{\omega _2} - {K_2}{e_2}| > {\delta _y};}\\ {0,}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} | - {K_1}{\omega _2} - {K_2}{e_2}| \le {\delta _y},} \end{array}} \right. $ |
| $ M{z_z} = \left\{ {\begin{array}{*{20}{l}} { - {K_1}{\omega _3} - {K_2}{e_3},{\rm{ }}}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} | - {K_1}{\omega _3} - {K_2}{e_3}| > {\delta _z};}\\ {0,}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} | - {K_1}{\omega _3} - {K_2}{e_3}| \le {\delta _z}.} \end{array}} \right. $ |
首先选择适当的PD控制律参数,在跟踪指令信号时,满足跟踪速率快,基本无超调,而且在连续控制量下稳态误差也很小.
进一步设计中,本文在PD姿态控制律引入了开关门限δx、δy、δz,目的是在满足姿控精度和姿控效率的情况下,尽量减小燃料的消耗量.为实现控制能量的优化,并保证一定的控制误差,选取下式作为优化指标:
| $ J = \int_0^\infty {\left( {{w_1}\left\| {\mathit{\boldsymbol{u}}(t)} \right\| + {w_2}\left\| {\mathit{\boldsymbol{e}}(t)} \right\|} \right)} {\rm{d}}t. $ |
式中:u(t)为控制输入;e(t)为控制系统误差;w1、w2为权值.
本文引用文献[19]的算法,利用粒子群算法(PSO)和遗传算法(GA)结合,来实现PD姿态控制律开关门限参数的寻优.PSO和GA都是群体智能优化算法.每一种寻优算法都有其缺陷.由于缺乏选择机制,传统粒子群算法会在较差个体上浪费过多资源,从而降低效率.在传统遗传算法中,如果某个个体未被选中,那么该个体的信息就会丢失.因此,PSO-GA的基本思想是将PSO的群体搜索能力和GA的局部搜索能力相结合.同时,利用粒子群速度更新算法中的“记忆”功能,来保留搜索过程中的较好解.粒子群的位置更新由个体最优位置和群体最优位置构成.在粒子群迭代中形成新一代粒子后,选取新群体中一定数量的粒子,分别应用遗传算法对其进行求解.选取的数量如下:
| $ {\rm{G}}{{\rm{A}}_{{\rm{Num}}}} = {\rm{G}}{{\rm{A}}_{{\rm{ NumMax }}}} - \left( {\frac{{{\rm{PS}}{{\rm{O}}_i}}}{{{\rm{PS}}{{\rm{O}}_{{\rm{ MaxIter }}}}}}} \right)({\rm{G}}{{\rm{A}}_{{\rm{ NumMax }}}} - {\rm{G}}{{\rm{A}}_{{\rm{ NumMin }}}}). $ |
每一个选中的粒子加上在粒子群中随机选择一定数量的粒子作为进化算法的初始种群,该算法从种群中通过选择、交叉和变异算子,选择最优个体后,通过遗传原理将当前种群中的点替换为当前最优点.遗传算法的种群大小GAPS和最大迭代次数GAMaxIter随着PSO迭代次数的增加而逐渐减小,其关系定义如下:
| $ {\rm{G}}{{\rm{A}}_{{\rm{PS}}}} = {\rm{G}}{{\rm{A}}_{{\rm{MinPS}}}} + \left( {\frac{{{\rm{PS}}{{\rm{O}}_i}}}{{{\rm{PS}}{{\rm{O}}_{{\rm{MaxIter}}}}}}} \right)({\rm{G}}{{\rm{A}}_{{\rm{MaxPS}}}} - {\rm{G}}{{\rm{A}}_{{\rm{ MinPS }}}}), $ |
| $ {\rm{G}}{{\rm{A}}_{{\rm{ MaxIter }}}} = {\rm{G}}{{\rm{A}}_{{\rm{ MinIter }}}} + \left( {\frac{{{\rm{PS}}{{\rm{O}}_i}}}{{{\rm{PS}}{{\rm{O}}_{{\rm{MaxIter}}}}}}} \right)({\rm{G}}{{\rm{A}}_{{\rm{ MaxIter }}}} - {\rm{G}}{{\rm{A}}_{{\rm{ Minter }}}}). $ |
通过上述迭代过程,种群趋于全局最优状态.
3 大角度姿态机动角速度和四元数指令规划方法以Rest-To-Rest大角度姿态机动问题为例,研究大角度姿态机动指令规划方法.
大角度姿态机动的指令规划思路是:令姿态初始的欧拉角按照某种运动规律在期望的时间内变化到终端欧拉角,然后求出这种运动规律下对应的姿态角速度指令和四元数指令.以欧拉角作为考核指标,设按照312转序旋转3次得到的期望Euler角分别为ϑd、γd和ψd.设初始欧拉角为ϑd0、γd0和ψd0,经过时间td到达期望的终端姿态角ϑdf、γdf和ψdf.
这里,本文给出一种令欧拉角匀速变化的角速度和四元数指令设计方法.令3个欧拉角匀速变化的姿态指令,即:
| $ {{{\dot \vartheta }_{\rm{d}}} = \frac{{{\vartheta _{{\rm{df}}}} - {\vartheta _{{\rm{d0}}}}}}{{{t_{\rm{d}}}}},} $ |
| $ {{{\dot \gamma }_{\rm{d}}} = \frac{{{\gamma _{{\rm{df}}}} - {\gamma _{{\rm{d0}}}}}}{{{t_{\rm{d}}}}},} $ |
| $ {{{\dot \psi }_{\rm{d}}} = \frac{{{\psi _{{\rm{df}}}} - {\psi _{{\rm{d0}}}}}}{{{t_{\rm{d}}}}}.} $ |
这样, 不仅可以独立控制3个欧拉角的变化规律,使得四元数描述的姿态控制系统3个欧拉角的运动相互之间不产生耦合影响,而且姿态角和姿态角速率指令的变化也始终是平滑的,易于保证姿态控制系统的动态特性,并有助于减小能量消耗.
根据
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} { - {{\dot \vartheta }_{\rm{d}}}\sin {\psi _{\rm{d}}}\cos {\gamma _{\rm{d}}} + {{\dot \gamma }_{\rm{d}}}\cos {\psi _{\rm{d}}}}\\ {{{\dot \vartheta }_{\rm{d}}}\sin {\gamma _{\rm{d}}} + {{\dot \psi }_{\rm{d}}}}\\ {{{\dot \vartheta }_{\rm{d}}}\cos {\psi _{\rm{d}}}\cos {\gamma _{\rm{d}}} + {{\dot \gamma }_{\rm{d}}}\sin {\psi _{\rm{d}}}} \end{array}} \right], $ |
并可推导出四元数指令,即
| $ \left\{ {\begin{array}{*{20}{l}} {{q_{{\rm{d0}}}} = \cos \frac{{{\psi _{\rm{d}}}}}{2}\cos \frac{{{\gamma _{\rm{d}}}}}{2}\cos \frac{{{\vartheta _{\rm{d}}}}}{2} - \sin \frac{{{\psi _{\rm{d}}}}}{2}\sin \frac{{{\gamma _{\rm{d}}}}}{2}\sin \frac{{{\vartheta _{\rm{d}}}}}{2},}\\ {{q_{{\rm{d1}}}} = \cos \frac{{{\psi _{\rm{d}}}}}{2}\sin \frac{{{\gamma _{\rm{d}}}}}{2}\cos \frac{{{\vartheta _{\rm{d}}}}}{2} - \sin \frac{{{\psi _{\rm{d}}}}}{2}\cos \frac{{{\gamma _{\rm{d}}}}}{2}\sin \frac{{{\vartheta _{\rm{d}}}}}{2},}\\ {{q_{{\rm{d2}}}} = \sin \frac{{{\psi _{\rm{d}}}}}{2}\cos \frac{{{\gamma _{\rm{d}}}}}{2}\cos \frac{{{\vartheta _{\rm{d}}}}}{2} + \cos \frac{{{\psi _{\rm{d}}}}}{2}\sin \frac{{{\gamma _{\rm{d}}}}}{2}\sin \frac{{{\vartheta _{\rm{d}}}}}{2},}\\ {{q_{{\rm{d3}}}} = \sin \frac{{{\psi _{\rm{d}}}}}{2}\sin \frac{{{\gamma _{\rm{d}}}}}{2}\cos \frac{{{\vartheta _{\rm{d}}}}}{2} + \cos \frac{{{\psi _{\rm{d}}}}}{2}\cos \frac{{{\gamma _{\rm{d}}}}}{2}\sin \frac{{{\vartheta _{\rm{d}}}}}{2}.} \end{array}} \right. $ |
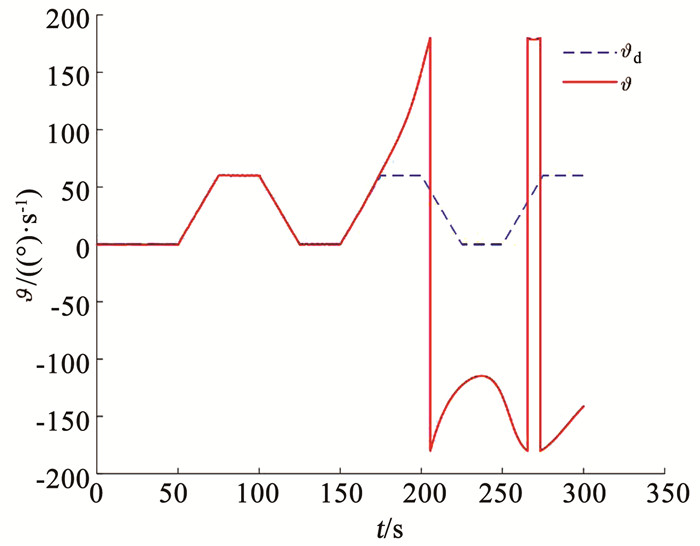
假设飞行器携带的燃料总质量为2.0 kg,姿控发动机的稳态推力设计为Fzs=18 N.以一种Rest-To-Rest的大角度姿态机动过程为研究对象,设计指令时,取动态上升时间td=30 s,在300 s内完成5次大角度姿态机动.采用欧拉角匀速变化的角速度和四元数指令,令俯仰角ϑ和偏航角ψ同时在0°~60°之间作5次大角度姿态机动,而滚转角γ保持为0°.具体设计出来的俯仰角指令ϑd如图 4中的虚线所示.
|
图 3 俯仰角变化情况(无开关门限) Fig. 3 Pitch angle (no threshold) |
|
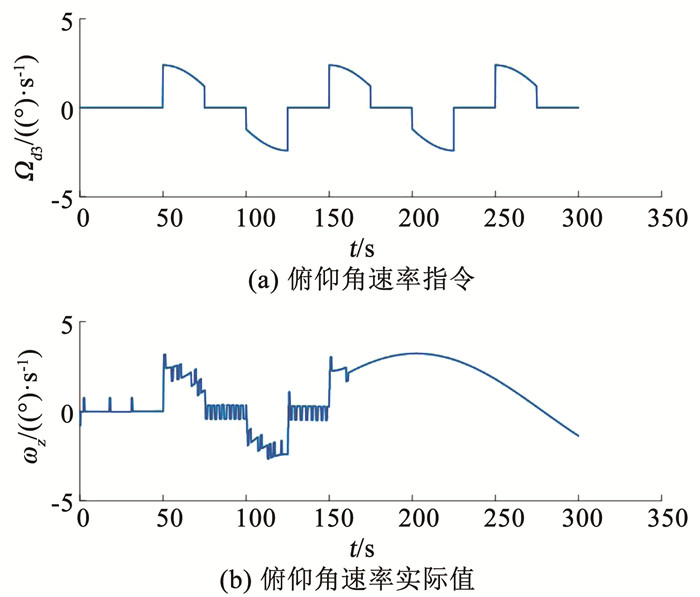
图 4 俯仰角速率指令和实际值变化情况(无开关门限) Fig. 4 Pitching angular rate and its command (no threshold) |
采用基于误差四元数的姿态跟踪PD控制律和姿控发动机开关逻辑.PD控制律为u=-K1ω-K2ev,取K1=6,K2=32.在这组参数满足跟踪速率快,基本无超调的要求,而且在连续控制量下稳态误差远小于1°.
姿控指令更新的周期取2 ms,PWM控制周期Tc=0.3 s.
4.1 无开关门限时的Rest-To-Rest姿态机动令δx=0,δy=0,δz=0,这种情况相当于没有在PD控制律中加入开关门限.
无开关门限情况下,图 3所示的俯仰角变化过程表明,在大约前155 s,姿控系统跟踪指令的过程良好,但155 s时燃料耗尽,姿控系统发散,无法继续跟踪姿态指令.图 4显示的俯仰角速度指令跟踪过程也呈现同样情况. 图 5显示的姿态角的跟踪误差在前155 s均小于0.5°,但155 s后发散.偏航角和滚转角的控制也表现出同样的特性.
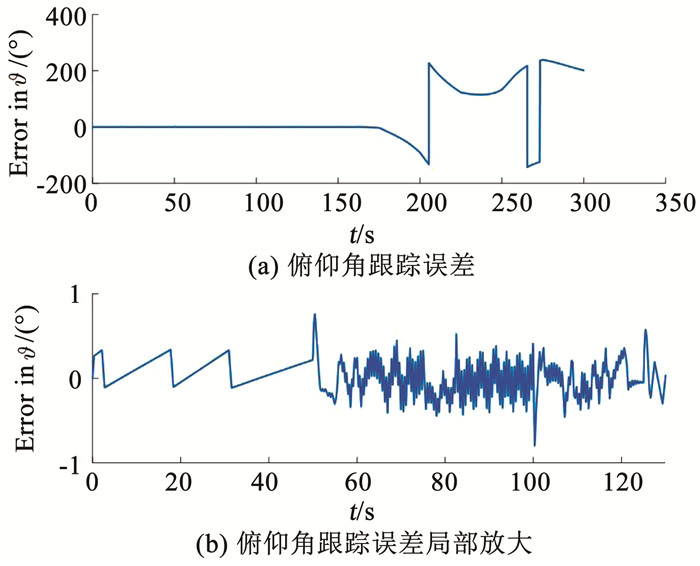
|
图 5 俯仰角跟踪误差(无开关门限) Fig. 5 Tracking error of pitch angle (no threshold) |
为实现飞行器大角度姿态机动的能量优化管理,在PD姿态控制律设计中,引入了开关门限δx,δy和δz,目的是在满足一定姿态控制精度的情况下,尽可能减小燃料的消耗量.在上述给定的Rest-To-Rest姿态机动指令下,采用的粒子群寻优算法对开关门限δx,δy和δz进行寻优.为了保证姿态控制有一定的稳态精度,δx,δy和δz每一个参数的寻优范围都限定在[0 10/57.3]范围内.设种群大小为100,循环迭代500次.求得的最优解δx=4.09/57.3,δy=3.35/57.3,δz=3.35/57.3.
采用这组最优开关门限,在进行大角度姿态机动的过程中,俯仰角可以很好地跟踪设计的机动指令,动态过程几乎无超调,如图 6、7所示.图 8(a)给出的是整个300 s仿真过程中俯仰角指令的跟踪误差,无论动态跟踪误差还是稳态跟踪误差均较小,图 8(b)给出的是前120 s的俯仰角指令跟踪误差,更清楚地显示了俯仰角指令动态跟踪误差和稳态跟踪误差均较小.
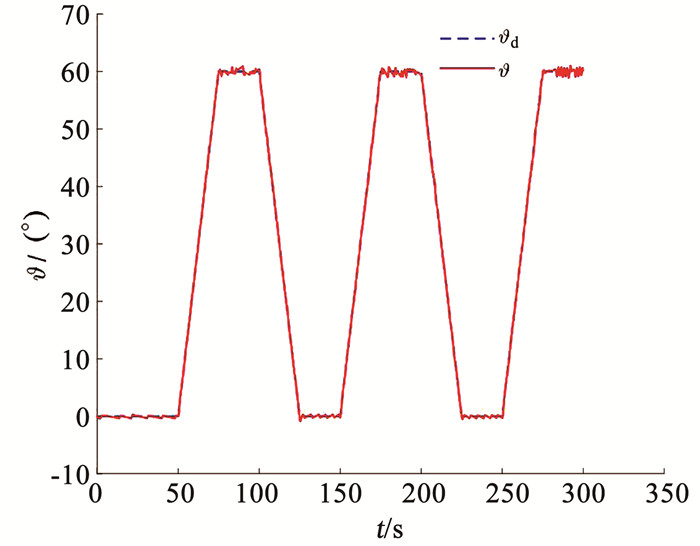
|
图 6 俯仰角变化情况(有开关门限) Fig. 6 Pitch angle (with threshold) |
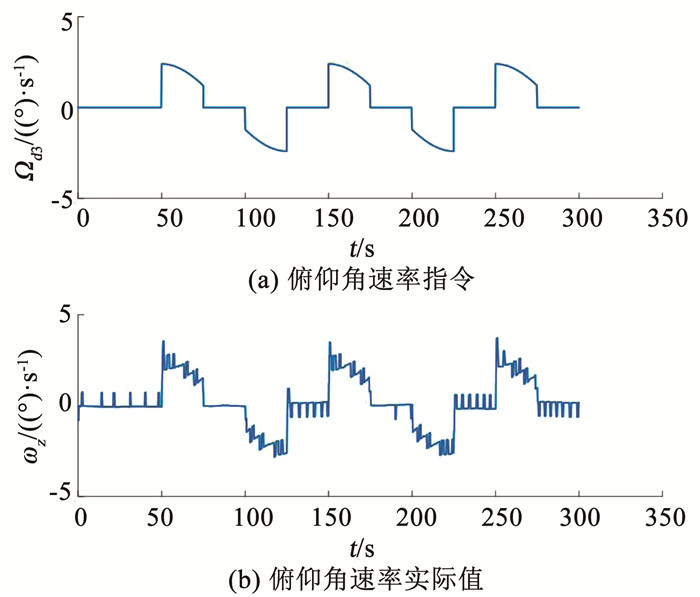
|
图 7 俯仰角速率指令及实际值(有开关门限) Fig. 7 Pitching angular rate and its command (with threshold) |
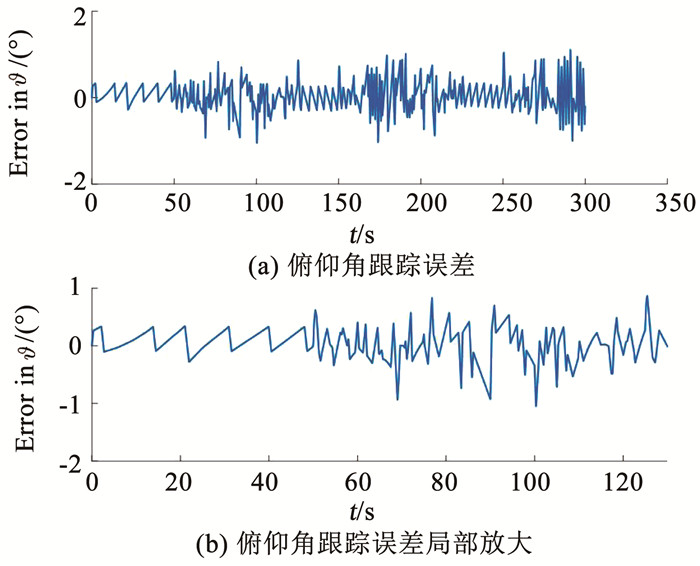
|
图 8 俯仰角跟踪误差(有开关门限) Fig. 8 Tracking error of pitch angle (with threshold) |
偏航角和滚转角的控制也表现出同样的特性.仿真得到的最优解保证了姿态控制3个欧拉角的姿态控制误差小于1°,最小燃料消耗为0.89 kg.
在同样的控制器参数下, 如果简单地采用阶跃型四元数指令, 那么在85 s时燃料消耗殆尽, 也无法完成5次姿态机动的任务.
5 结论1) 提出了一种含开关门限的大角度姿态机动PD控制律,并利用粒子群算法和遗传算法相结合的方法,寻找到开关门限的最优解.
2) 数值仿真结果表明,采用这种含开关门限的大角度姿态机动PD控制律,可以显著减小姿控系统的燃料消耗,且动态跟踪误差和稳态跟踪误差均较小.
3) 设计了令欧拉角匀速变化的角速度和四元数指令,有助于保证系统良好的瞬态特性, 并节省燃料.
| [1] |
周黎妮, 唐国金, 李海阳. 航天器姿态机动的自抗扰控制器设计[J]. 系统工程与电子技术, 2007, 29(12): 2122. ZHOU Lini, TANG Guojin, LI Haiyang. Active disturbance rejection controller design for spacecraft attitude maneuver[J]. Systems Engineering and Electronics, 2007, 29(12): 2122. DOI:10.3321/j.issn:1001-506x.2007.12.029 |
| [2] |
杨瑞光, 孙明玮, 陈增强. 飞行器自抗扰姿态控制优化与仿真研究[J]. 系统仿真学报, 2010, 22(11): 2689. YANG Ruiguang, SUN Mingwei, CHEN Zengqiang. ADRC-based attitude control optimization and simulation[J]. Journal of System Simulation, 2010, 22(11): 2689. DOI:10.16182/j.cnki.joss.2010.11.066 |
| [3] |
耿云海, 杨涤, 崔祜涛. 挠性飞行器时间燃料优化姿态机动控制的振动抑制[J]. 控制理论与应用, 2001, 18(2): 253. GENG Yunhai, YANG Di, CUI Hutao. Vibration suppression of time-fuel optimal attitude maneuver control for flexible spacecraft[J]. Control Theory and Applications, 2001, 18(2): 253. DOI:10.3969/j.issn.1000-8152.2001.02.021 |
| [4] |
毕显婷, 史小平. 带有输入时延的刚性航天器反最优姿态控制[J]. 电机与控制学报, 2017, 21(3): 83. BI Xianting, SHI Xiaoping. Inverse optimal stabilization of rigid spacecraft in presence of input delay[J]. Electric Machines and Control, 2017, 21(3): 83. DOI:10.15938/j.emc.2017.03.012 |
| [5] |
马清亮, 杨海燕, 岳瑞华, 等. 空间飞行器大角度姿态机动优化控制[J]. 空间控制技术与应用, 2013, 39(3): 8. MA Qingliang, YANG Haiyan, YUE Ruihua, et al. Optimization control of spacecraft large angle attitude maneuvers[J]. Aerospace Control and Application, 2013, 39(3): 8. DOI:10.3969/j.issn.1674-1579.2013.03.002 |
| [6] |
贾英宏, 徐世杰. 采用变速控制力矩陀螺的一种姿态/能量一体化控制研究[J]. 宇航学报, 2003, 24(1): 32. JIA Yinghong, XU Shijie. Study on integrated attitude/power control using variable speed control moment gyros[J]. Journal of Astronautics, 2003, 24(1): 32. DOI:10.3321/j.issn:1000-1328.2003.01.006 |
| [7] |
汤亮, 徐世杰. 灵敏小卫星能量/姿态一体化控制研究[J]. 北京航空航天大学学报, 2005, 31(6): 668. TANG Liang, XU Shijie. Integrated power and attitude control system based on VSCMGs for agile small agile satellite[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(6): 668. DOI:10.3969/j.issn.1001-5965.2005.06.016 |
| [8] |
YANG C C, WU C J. Optimal large-angle attitude control of rigid spacecraft by momentum transfer[J]. IET Control Theory & Applications, 2007, 1(3): 657. DOI:10.1049/iet-cta:20060132 |
| [9] |
YANG C C, LAI L C, WU C J. Minimal energy maneuvering control of a rigid spacecraft with momentum transfer[J]. Journal of the Franklin Institute, 2007, 344(7): 991. DOI:10.1016/j.jfranklin.2007.05.001 |
| [10] |
张士峰, 钱山, 李鹏奎. 刚体航天器的最小能量姿态机动最优控制研究[J]. 宇航学报, 2009, 30(4): 1504. ZHANG Shifeng, QIAN Shan, LI Pengkui. Study on the minimal energy maneuvering control of a rigid spacecraft with momentum transfer[J]. Journal of Astronautics, 2009, 30(4): 1504. DOI:10.3873/j.issn.1000-1328.2009.04.032 |
| [11] |
程小军, 崔祜涛, 徐瑞, 等. 几何约束下的航天器姿态机动控制[J]. 控制与决策, 2012, 27(5): 724. CHENG Xiaojun, CUI Hutao, XU Rui, et al. Attitude maneuver control of spacecraft under geometric constraints[J]. Control and Decision, 2012, 27(5): 724. DOI:10.13195/j.cd.2012.05.87.chengxj.005 |
| [12] |
IOSLOVICH I. Arbitrary fuel-optimal attitude maneuvering of a non-symmetric space vehicle in a vehicle-fixed coordinate frame[J]. Automatica, 2003, 39(3): 557. DOI:10.1016/s0005-1098(02)00247-9 |
| [13] |
SIDI M J. Spacecraft dynamics and control[M]. Cambridge: Cambridge University Press, 1997.
|
| [14] |
YUAN J S. Closed-loop manipulator control using quaternion feedback[J]. IEEE Journal of Robotics and Automation, 1988, 4(4): 434. DOI:10.1109/56.809 |
| [15] |
CHEN Zhiyong, HUANG Jie. Attitude tracking and disturbance rejection of rigid spacecraft by adaptive control[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 600. DOI:10.1109/tac.2008.2008350 |
| [16] |
FUKAO T, YAMAGUCHI M, ADACHI N. Backstepping design for attitude control of a spacecraft[J]. Transactions of the Japan Society of Mechanical Engineers Series C, 2001, 67(653): 131. DOI:10.1299/kikaic.67.131 |
| [17] |
耿云海, 张明国, 曹喜滨. 挠性飞行器姿态机动脉冲调宽控制系统设计[J]. 飞行力学, 2005, 23(4): 40. GENG Yunhai, ZHANG Mingguo, CAO Xibin. Pulse width modulated attitude maneuver control system design for a flexible vehicle[J]. Flight Dynamics, 2005, 23(4): 40. DOI:10.3969/j.issn.1002-0853.2005.04.011 |
| [18] |
王谦, 李新洪, 贺广松, 等. 脉冲调制在小型姿控推力器中的应用仿真[J]. 空间控制技术与应用, 2017, 43(6): 40. WANG Qian, LI Xinhong, HE Guangsong, et al. Application simulation of pulse modulation in small attitude control thruster[J]. Aerospace Control and Application, 2017, 43(6): 40. DOI:10.3969/j.issn.1674-1579.2017.06.007 |
| [19] |
GARG H. A hybrid PSO-GA algorithm for constrained optimization problems[J]. Applied Mathematics and Computation, 2016, 274: 292. DOI:10.1016/j.amc.2015.11.001 |
| [20] |
黄圳圭. 航天器姿态动力学[M]. 长沙: 国防科技大学出版社, 1997. HUANG Zhengui. Attitude dynamics of spacecraft[M]. Changsha: Press of National University of Science and Technology, 1997. |
 2020, Vol. 52
2020, Vol. 52


