2. 高温合金新材料北京市重点实验室(钢铁研究总院),北京 100081;
3. 北京钢研高纳科技股份有限公司, 北京 100081
2. Beijing Key Laboratory of Advanced High Temperature Materials (Central Iron and Steel Research Institute), Beijing 100081, China;
3. Beijing CISRI-GAONA Materials and Technology Co., Ltd., Beijing 100081, China
GH4169合金作为一种时效沉淀强化型镍基变形高温合金,在高温下具有良好的力学性能,广泛用于航空发动机涡轮盘等热端部件中.该合金在热加工过程中包括固溶处理、时效处理等一系列工艺,最终获得具有时效沉淀相的组织结构形态,称为时效态.固溶态是指合金完成固溶处理之后, 尚未进行时效处理的状态,是该合金热处理过程的一种中间状态,该状态下合金组织结构中不含有沉淀相,其力学性能与时效态的合金有较大差异.目前对于该合金的力学性能研究主要集中在时效态,而对于固溶态的性能研究相对较少.为保证材料的服役性能,在GH4169合金固溶处理后常使用水淬或油淬的方法进行快速冷却,该过程会导致淬火残余应力的产生,淬火残余应力会对后续时效处理效过产生影响[1].掌握固溶态GH4169合金的高温力学性能,对研究GH4169合金淬火残余应力的演化,从而优化热加工工艺具有重要意义.
研究者们对固溶态GH4169合金高温下析出行为及力学行为进行了相关研究.Han[2]对析出相随温度、时间的演化关系进行了研究,结果表明析出相体积分数随时间的演化符合Johnson-Mehl-Arvami (JMA)方程,析出相粗化满足LSW理论. Du等[3]在对该合金的研究中,也形成了成熟的热处理工艺,即980 ℃固溶处理,以及720 ℃加620 ℃时效处理,并对热处理后该合金显微组织及力学性能进行了研究.Rezende等[4]对固溶态GH4169合金进行了速率为3.2×10-4 s-1的高温单轴拉伸实验,结果显示,屈服强度在600 ℃以下时随温度的升高而降低,600 ℃以上则随温度升高而显著提高,这是动态应变时效及强化相析出的作用所导致.Fisk等[5]对GH4169合金热处理过程中的高温力学行为进行了数值模拟,考虑了析出相演化的因素,并指出GH4169合金存在动态应变时效现象,但未将动态应变时效的因素加入到模型中.
动态应变时效现象是合金中溶质原子移动对可动位错造成拖拽所导致的强化现象,也被称为Portevin-LeChatelier(PLC)效应.主要表现为具有负的应变率敏感性(negative strain rate sensitivity, NSRS)以及出现锯齿流变现象.动态应变时效现象在铝合金[6]、钛合金[7]、镍基合金[8]等材料中广泛存在.McCormick[9]在20世纪80年代发展出DSA模型,提出了溶质原子钉扎位错所需的时效时间以及位错移动所需的热激活等待时间等理论,该模型可以对负的应变率依赖性以及锯齿流变进行预测.Ren等[10]运用McCormick模型对C-Mn钢的DSA现象进行了实验及有限元模拟工作,分析了合金在室温至350 ℃下不同应变率的负应变率依赖性、锯齿流变等现象.但是,尚未有研究者运用该模型对GH4169合金的的DSA现象展开过研究.
本文对固溶态GH4169合金的高温拉伸行为进行了实验及数值模拟研究,实验中观测到负的应变率敏感性以及锯齿流变现象,然后通过数值模拟对该现象进行了分析.该工作可以对高温合金力学行为研究提供参考,同时对热加工工艺的改进起到借鉴作用.
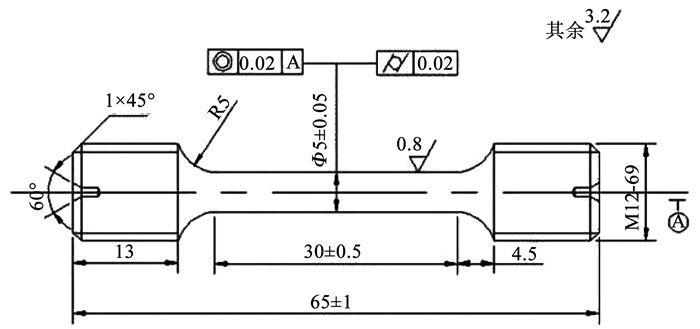
1 实验表征 1.1 实验方法实验材料为固溶态GH4169合金,化学成分见表 1,拉伸试样尺寸如图 1所示.高温单轴拉伸实验在MTS-C45型万能试验机上进行,拉伸实验温度为620 ℃,采用MTS-653型高温炉对试样进行加热及保温,采用热电偶进行试样的温度检测.拉伸进程开始前,待试样加热至620 ℃后,进行5 min保温,以保证试样温度达到均匀.采用陶瓷引伸计记录应变信息(如图 2所示),拉伸实验分别以10-2、10-3、10-4 s-1的拉伸速率拉伸至断裂.
| 表 1 GH4169合金化学成分 Tab. 1 Chemical composition of GH4169 superalloy |
|
图 1 拉伸试样尺寸 Fig. 1 Schematic diagram of tensile specimen |

|
图 2 高温拉伸实验台 Fig. 2 Photo of high temperature tensile test bed |
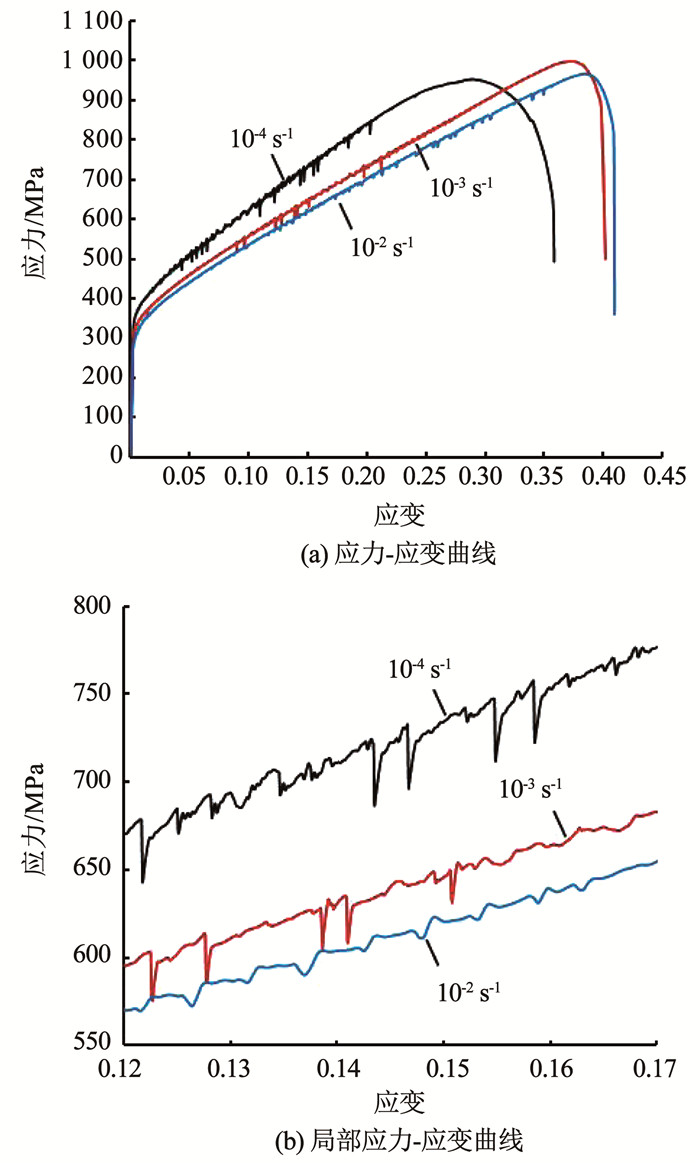
将高温拉伸实验中获得的载荷-位移曲线进行数据处理,获得真实应力-应变曲线如图 3所示.屈服强度见表 2,10-2 s-1速率下屈服强度为305.10 MPa,10-3 s-1速率下屈服强度为328.51 MPa,10-4 s-1速率下屈服强度为357.44 MPa,屈服强度随拉伸速率的降低而升高,表现出负的应变率敏感性.
|
图 3 固溶态GH4169在620 ℃下不同拉伸速率的拉伸实验曲线 Fig. 3 Tensile test results obtained at 620 ℃ with different strain rates |
| 表 2 固溶态GH4169合金620 ℃不同速率下屈服强度 Tab. 2 Yield strength of solid solution treated GH4169 at 620 ℃ with different strain rates |
同时,应力-应变曲线在达到屈服点后,应力值开始出现振动,呈现出锯齿状波形.其中,10-2 s-1速率振幅最小,振动频率较低;10-3 s-1速率振幅次之,振动频率与10-2 s-1速率下的结果相近;10-4 s-1速率振幅最大,振动频率也最高.
1.3 结果分析合金的强度受多方面因素影响,除本文研究的动态时效应变的影响外,还可能受到合金自身微观组织结构的影响.为进一步研究动态时效应变效应,需要排除其他强化因素对于合金材料强度的影响.
固溶态GH4169合金在经过长时间时效处理后,在晶粒内部会产生细小的沉淀强化相,强化相会阻碍可动位错的运动,这是导致材料强度变化的关键因素.在对GH4169合金析出行为研究的文献中可以发现[1],强化相以γ″为主,其形貌为扁饼状,强化相体积分数随时间的变化符合JMA方程,即析出过程初期速度较慢,随后逐渐升高,最后析出速度逐渐降低直至饱和,呈现倒“S”型曲线.研究者们也通过实验[11]及模拟[12]的方法,获得了该合金析出相等温转变动力学图(TTT图),文献中采用JMatPro软件进行相变动力学模拟,与实验结果一致性较好.结果显示在620 ℃高温条件下,固溶态GH4169合金析出体积分数0.5%的γ″相所需的时间约为3 h.
本文中,高温拉伸实验在620 ℃进行,3个速率的拉伸实验从试样加热至指定温度到拉伸至断裂,持续时间分别为6、11、50 min,根据上述分析,该温度下γ″相的析出速度很慢,并处于析出过程的体积分数增长速度较低的早期阶段,因此可以近似认为实验过程中未产生沉淀强化相.所以本文中的高温拉伸实验结果,排除了沉淀强化相对材料强度的影响,材料强度随应变速率的变化表现出的负敏感性主要由DSA效应导致.
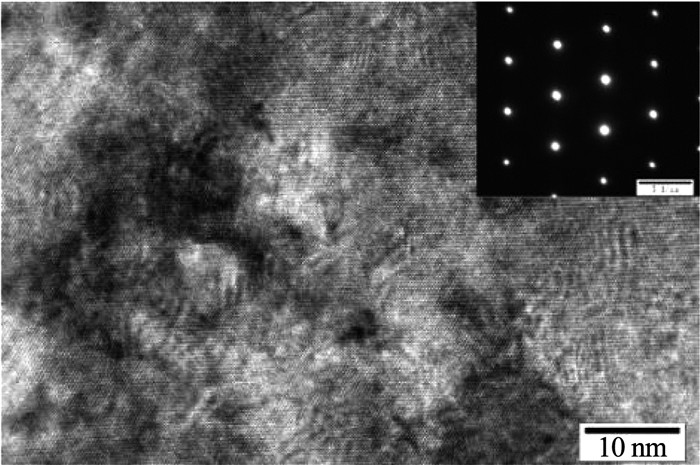
为了进一步验证假设的合理性,本文对高温拉伸实验后的试样进行扫描电子显微镜(SEM)及透射电子显微镜(TEM)表征,如图 4、5所示. SEM表征采用研磨并电解抛光,然后进行电解腐蚀的方法制备试样,该方法是表征GH4169合金中沉淀强化相γ″相的常用方法[13]. 图 4展示了10-4 s-1速率的高温拉伸实验后的试样的微观组织形貌,可以观察到针状的δ相,这是固溶处理后残余的δ相,该相粗化速度较慢,对高温拉伸结果不产生影响.而对合金强度影响较大的扁饼状γ″相并未被发现.TEM表征试样取自10-4 s-1速率的高温拉伸实验后试样的标距段,表征结果如图 5所示.高分辨TEM二维晶格像显示,材料基体内并未出现γ′及γ″相,选区衍射结果也证明了材料中仅有基体相,这与SEM表征结果相一致.

|
图 4 10-4 s-1高温变形后试样微观组织结构 Fig. 4 Microstructure of specimen at strain rate of 10-4 s-1 |
|
图 5 10-4 s-1高温拉变形后试样高分辨TEM及选区衍射结果 Fig. 5 HR-TEM image and SAED pattern of specimen at strain rate of 10-4 s-1 |
由图 3(b)局部锯齿状屈服曲线可以看出,随着应变速率的降低,应力-应变曲线中锯齿状波动的应力降幅呈现增大的趋势.根据研究者们已得出的结论[9, 13],动态时效应变的微观机理是溶质原子气团与可动位错的相互作用,即固溶原子在扩散的过程中会移动到位错核内,使得可动位错被钉扎,材料强度出现短暂升高,随后可动位错挣脱固溶原子的钉扎继续移动,材料强度下降,该过程使得材料的宏观拉伸曲线出现锯齿状波动.该理论可以解释图 3(b)中锯齿波振幅随应变速率降低而升高的现象.这是由于固溶原子扩散速度有限,当应变速率较快时,可动位错的移动速度较快,固溶原子扩散过程钉扎到的可动位错较少,因此应力的涨幅及降幅也较小.而当应变速率较慢时,固溶原子的移动可以钉扎到较多位错,此时锯齿波动的振幅相较于高应变速率条件下的振幅更高.
2 数值模拟 2.1 一维本构模型总应变速率
| $ \dot \varepsilon = {\dot \varepsilon ^e} + {\dot \varepsilon ^p}, $ |
其中,弹性应变速率可以表示为应力变化率
| $ {\dot \varepsilon ^e} = \frac{{\dot \sigma }}{E}. $ |
塑性应变率由基于运动位错的热激活机制的流动法则表示[14]:
| $ {\dot \varepsilon ^p} = \dot \varepsilon _0^p\exp \left( { - \frac{{{F_0}}}{{kT}}{{\left\langle {1 - {{\left\langle {\frac{{\sigma - S}}{{{\tau _0}}}} \right\rangle }^p}} \right\rangle }^q}} \right). $ |
式中:F0、k、T分别为Helmholtz自由能常数、Boltzmann常数以及绝对温度;p、q、
位错滑移阻力由两部分组成:
| $ S = {S_{{\rm{disl }}}} + {S_{{\rm{DSA}}}}. $ | (1) |
式中:Sdisl为受位错密度影响的滑移阻力,SDSA为由DSA效应引发的滑移阻力.
受位错密度影响的滑移阻力变化率可表示为
| $ {\dot S_{{\rm{disl }}}} = {\dot \varepsilon ^p}\frac{{{S_{{\rm{sat }}}} - {S_{{\rm{disl }}}}}}{{{S_{{\rm{sat }}}} - {S_0}}}{h_{\rm{s}}}. $ |
式中:hs为硬化系数;S0、Ssat分别为初始及饱和滑移阻力.
由DSA效应引发的滑移阻力可表示为
| $ {S_{{\rm{DSA}}}} = k\left( {1 - \exp \left( { - {{\left( {\frac{{{t_a}}}{{{t_0}}}} \right)}^n}} \right)} \right). $ |
式中:t0为与原子扩散速度有关的常数;ta为溶质原子钉扎位错所需的等效时效时间;n为常数;k为锯齿状屈服中与最大振幅相关的参数[15].
等效时效时间的变化率可表示为:
| $ {\dot t_{\rm{a}}} = 1 - \frac{{{t_{\rm{a}}}}}{{{t_{\rm{w}}}}}, {t_{\rm{w}}} = \frac{w}{{{{\dot \varepsilon }^p}}}, {t_{\rm{a}}}(t = 0) = {t_{{\rm{a}}0}}. $ |
式中:tw为位错移动所需的热激活等待时间;w为材料参数;ta0初始时刻等效时效时间的值[10].
2.2 参数标定及模拟结果固溶态GH4169合金的弹性模量由拉伸实验获得,为160 GPa.流动法则中的参数,可由文献[16-17]获得,F0取286 KJ·mol-1,p、q、
将应变率分别设置为10-2、10-3、10-4 s-1,基于一维本构模型中的本构模型模拟拉伸实验曲线.需要拟合的参数包括:临界分切应力τ0,材料硬化参数hs、S0、Ssat,以及DSA效应参数t0、k.
| $ \sum\limits_{i = 1}^n {{{\left\{ {\sigma _i^{{\rm{simulation}}} - \sigma _i^{{\rm{experiment }}}} \right\}}^2}} \to \min . $ | (2) |
通过最小二乘法进行参数拟合,拟合区间为总应变0~10%.拟合方法如式(2)所示,拟合结果见表 3.
| 表 3 固溶态GH4169合金本构模型的参数标定 Tab. 3 Parameters of constitutive model of solid solution treated GH4169 |
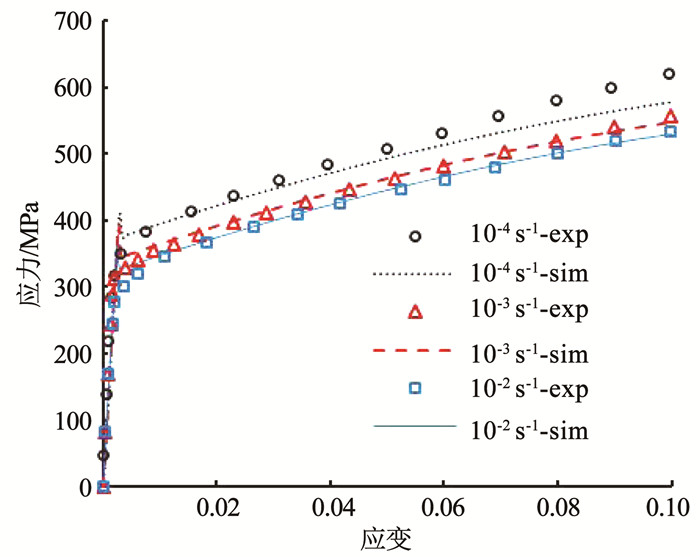
图 6给出了模拟结果与实验结果的对比,这里的实验结果是对图 3的实验数据进行Ramberg-Osgood拟合后所得的数据[18].可以看出,本文模型对固溶态GH4169合金的高温拉伸模拟结果与实验曲线较为吻合,能定量地模拟实验中所观察到的负应变率敏感性现象.在模拟曲线中可以看出,应力-应变曲线在达到屈服点后出现波动,即材料强度屈服后迅速下降.这是由于内变量ta的值在出现塑性变形后迅速升高,随后迅速下降所导致,在物理上与DSA效应中单个位错被运动的固溶原子阻碍,然后脱离的过程相对应,这是锯齿状屈服现象的成因.但由于本文模型为一维模型,而实验中所观察到的硬化阶段的连续锯齿状波动现象与材料非局部的屈服失稳有关,因此其尚不能定量模拟硬化过程中锯齿状应力应变曲线.
|
图 6 模拟结果与实验曲线对比 Fig. 6 Comparison of model results with experimental data |
金属材料在高温条件下通常会展现出强度的正应变率依赖性:即强度随着应变率的提高而增大.为了深入分析固溶态GH4169合金的负应变率依赖性,本文根据所标定的一维本构模型定量地考察了材料强度与应变率之间的关系,计算了应变率在10-8~102 s-1区间内总应变为10%时的应力随应变率的变化曲线,如图 7中“With DSA”曲线所示.可以看到,应变率在一定区间时,材料强度具有明显的负应变率依赖性.为了参考对比,本文进一步将式(1)中的SDSA取为恒定值0,获得不考虑DSA效应的基于热激活能的材料本构模型,采用与考虑DSA效应时相同的材料参数进行拉伸模拟.得到应变10%时不考虑DSA效应的应力值.计算该应力值在应变速率10-8~102s-1区间内的变化趋势,得到图 7中“Without DSA”曲线.结果显示,该应力值随应变速率的提高呈现单调递增的趋势,这说明无DSA效应时材料强度具有正常的应变率依赖性.这些结果说明在高温620 ℃条件下固溶态GH4169合金内存在着较强烈的正负应变率依赖性之间的竞争,并且由DSA效应导致的负应变率依赖性占优.
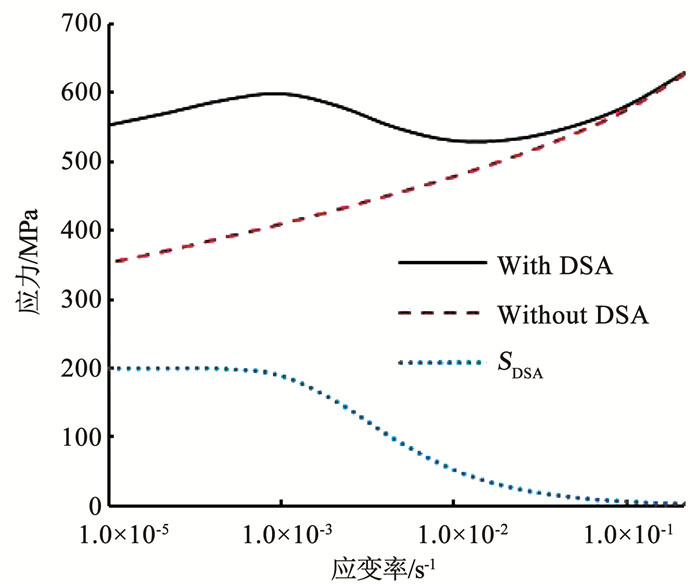
|
图 7 应变10%时的应力与应变速率的关系预测 Fig. 7 Prediction of relation between stress and strain rate at total strain of 10% |
图 7中还给出了DSA效应引发的滑移阻力SDSA与应变率之间的关系,如图 7中“SDSA”曲线所示.结果显示,DSA效应对滑移阻力的贡献值随应变速率的升高,呈现逐渐下降的趋势,下降曲线为先平缓,再快速,最后再平缓,最后趋于0.可以看出DSA效应在一定应变率区间内比较强烈,因此在该应变率区间内材料展现出负应变率依赖性.
4 结论1) 对固溶态GH4169合金进行了620 ℃下的单轴拉伸实验,应变速率为10-2、10-3、10-4 s-1.结果表明,材料强度呈现出由DSA效应所导致的负的应变率效应及锯齿状屈服现象.
2) 基于热激活能的塑性流动法则并考虑DSA效应,建立了材料的一维本构模型.基于实验数据进行了参数拟合,模拟结果与实验结果相吻合.
3) 本文通过分析DSA效应对材料强度的贡献指出实验观察到的负应变率依赖性是DSA效应及正的率效应两种机制之间的竞争所导致.
| [1] |
QIN Hailong, BI Zhongnan, YU Hongyao, et al. Assessment of the stress-oriented precipitation hardening designed by interior residual stress during ageing in IN718 superalloy[J]. Materials Science and Engineering: A, 2018, 728: 183. DOI:10.1016/j.msea.2018.05.016 |
| [2] |
HAN Yafang. The coarstning bthaviour of γ″ and γ' particles in inconel 718[D]. Winnipeg: University of Manitoba, 1982
|
| [3] |
DU Jinhui, LV Xudong, DENG Qun. Effect of solution treatment on the microstructure and mechanical properties of IN718 alloy[J]. Rare Metal Materials and Engineering, 2017, 46(9): 2359. DOI:10.1016/s1875-5372(17)30197-2 |
| [4] |
REZENDE M C, ARAUJO L S, GABRIEL S B, et al. Oxidation assisted intergranular cracking under loading at dynamic strain aging temperatures in Inconel 718 superalloy[J]. Journal of Alloys and Compounds, 2015, 643(S1): S256. DOI:10.1016/j.jallcom.2014.12.279 |
| [5] |
FISK M, ANDERSSON J, DU RIETZ R, et al. Precipitate evolution in the early stages of ageing in Inconel 718 investigated using small-angle x-ray scattering[J]. Materials Science and Engineering: A, 2014, 612: 202. DOI:10.1016/j.msea.2014.06.036 |
| [6] |
BENALLAL A, BERSTAD T, BØRVIK T, et al. An experimental and numerical investigation of the behaviour of AA5083 aluminium alloy in presence of the Portevin-Le Chatelier effect[J]. International Journal of Plasticity, 2008, 24(10): 1916. DOI:10.1016/j.ijplas.2008.03.008 |
| [7] |
MARCHENKO A, MAZIÈRE M, FOREST S, et al. Crystal plasticity simulation of strain aging phenomena in α-titanium at room temperature[J]. International Journal of Plasticity, 2016, 85: 1. DOI:10.1016/j.ijplas.2016.05.007 |
| [8] |
GOPINATH K, GOGIA A K, KAMAT S V, et al. Dynamic strain ageing in Ni-base superalloy 720Li[J]. Acta Materialia, 2009, 57(4): 1243. DOI:10.1016/j.actamat.2008.11.005 |
| [9] |
MCCORMICK P G. Theory of flow localisation due to dynamic strain ageing[J]. Acta Metallurgica, 1988, 36(12): 3061. DOI:10.1016/0001-6160(88)90043-0 |
| [10] |
REN Sicong, MAZIÈRE M, FOREST S, et al. A constitutive model accounting for strain ageing effects on work-hardening. Application to a C-Mn steel[J]. Comptes Rendus Mécanique, 2017, 345(12): 908. DOI:10.1016/j.crme.2017.09.005 |
| [11] |
ORADEI-BASILE A, RADAVICH J F. A current T-T-T diagram for wrought alloy 718[J]. Superalloys, 1991, 718(625): 325. DOI:10.7449/1991/SUPERALLOYS_1991_325_335 |
| [12] |
QIN Hailong, BI Zhongnan, LI Dongfeng, et al. Study of precipitation-assisted stress relaxation and creep behavior during the ageing of a nickel-iron superalloy[J]. Materials Science and Engineering: A, 2019, 742: 493. DOI:10.1016/j.msea.2018.11.028 |
| [13] |
BAI Zhitong, FAN Yue. Abnormal strain rate sensitivity driven by a unit dislocation-obstacle interaction in bcc Fe[J]. Physical review letters, 2018, 120(12): 125504. DOI:10.1103/PhysRevLett.120.125504 |
| [14] |
BUSSO E P, MCCLINTOCK F A. A dislocation mechanics-based crystallographic model of a B2-type intermetallic alloy[J]. International Journal of Plasticity, 1996, 12(1): 1. DOI:10.1016/s0749-6419(95)00041-0 |
| [15] |
CHABOCHE J L, GAUBERT A, KANOUTÉ P, et al. Viscoplastic constitutive equations of combustion chamber materials including cyclic hardening and dynamic strain aging[J]. International Journal of Plasticity, 2013, 46: 1. DOI:10.1016/j.ijplas.2012.09.011 |
| [16] |
BUSSO E P, MEISSONNIER F T, O'DOWD N P. Gradient-dependent deformation of two-phase single crystals[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(11): 2333. DOI:10.1016/s0022-5096(00)00006-5 |
| [17] |
LI Dongfeng, GOLDEN B J, O'DOWD N P. Multiscale modelling of mechanical response in a martensitic steel: A micromechanical and length-scale-dependent framework for precipitate hardening[J]. Acta Materialia, 2014, 80: 445. DOI:10.1016/j.actamat.2014.08.012 |
| [18] |
RAMBERG W, OSGOOD W R. Description of stress-strain curves by three parameters: NACA-TN-902[R]. Washington: National Advisory Committee for Aeronautics, 1943
|
 2020, Vol. 52
2020, Vol. 52


