高超声速飞行器突防、侦察能力强，反应时间短，飞行速度快，在军事和民用领域有着众多需求^[1-2].但是由于其具有严重非线性、强耦合性、不确定性等特性，这给飞控系统的设计增加了难度，特别是在爬升段，飞行器要穿越对流层、平流层、中间层以及部分电离层，飞行速度从超声速加速到高超声速，不确定性因素^[3]更多.

超螺旋滑模控制算法^[4]因其具有强鲁棒性且只需要知道滑模量的信息，无需知道其一阶导数的信息等特性，已广泛应用于干扰估计^[5]、极值搜索控制^[6]、容错控制^[7]等相关领域.文献[8]提出了一种快速超螺旋算法，通过在普通超螺旋算法中加入线性项，提高了算法的收敛速度，并基于此算法设计干扰观测器对干扰连续估计和补偿.文献[9]同样通过加入线性项来提升收敛速度，并在假设干扰上界未知的前提下，设计了一种新的自适应律，提出一种新型的快速自适应超螺旋算法.文献[10-12]通过设计一种自适应参数既可增大又可减小的自适应律，以解决参数过大估计问题.上述这些算法由于积分项中含有不连续的符号函数项，只可得到连续的控制输入曲线，控制输入不平滑，与传统一阶滑模相比，这些控制算法的确减小了抖振，但是并不能极大减小甚至消除抖振.2007年文献[13]提出一种平滑的二阶滑模控制算法，其主要思想就是在超螺旋算法的积分项中使用连续的函数，以此得到平滑的控制输入，但是这种控制方法需要非线性观测器来估计干扰，而且算法的收敛速度上还有提升的空间.

本文针对上述所存在的问题，提出一类新型的快速平滑自适应超螺旋滑模控制算法.采用滑模微分器逼近反馈线性化过程中不准确的量；控制律设计时，在普通超螺旋算法中增加线性项，并在积分项中使用连续的函数，以加快收敛速度且达到平滑控制的效果；最后，为避免参数过大估计，设计了一种自适应参数可增可减的自适应律.

1 问题描述 1.1 动力学模型

高超声速飞行器爬升段纵向动力学模型可以描述为：

$ \begin{array}{l} \begin{array}{*{20}{l}} {\dot V = \frac{{T\cos \alpha - D}}{M} - \frac{{{\mu _0}\sin \gamma }}{{{r^2}}} + {d_{v1}},}\\ {\dot \gamma = \frac{{L + T\sin \alpha }}{{MV}} - \frac{{({\mu _0} - {V^2}r)\cos \gamma }}{{V{r^2}}} + {d_\gamma },} \end{array}\\ \begin{array}{*{20}{l}} {\dot h = V\sin \gamma ,}\\ {\dot \alpha = q - \dot \gamma ,}\\ {\dot q = {M_y}/{I_{yy}} + {d_q},}\\ {\dot M = - \frac{T}{{{I_{{\rm{sp}}}}{g_0}}}.} \end{array} \end{array} $

(1)

式中：M为飞行器质量；V为飞行速度；γ为航迹倾斜角；h为飞行高度；α为飞行迎角；q为俯仰角速率；I_yy为纵向转动惯量；r=R+h为飞行器地心距，其中R为地球半径；μ₀=3.986×10¹⁴ m³/s²为地球重力常数；g₀为地表重力加速度；I_sp为燃料比冲；L、D分别为飞行器升力、阻力；T为发动机推力；M_y为俯仰力矩；d_v1、d_γ、d_q分别为模型不确定性、外部干扰等复合干扰.

1.2 发动机推力模型

高超声速飞行器的推力模型可简化为一个二阶模型：

$ \ddot \beta = - 2\zeta {\omega _{\rm{n}}}\dot \beta - \omega _{\rm{n}}^2\beta + \omega _{\rm{n}}^2{\beta _c}. $

式中：β_c为发动机节流阀的调定值；阻尼比ζ为0.7；固有频率ω_n为5.

推力系数以及燃料比冲公式为：

$ {C_T} = \left\{ {\begin{array}{*{20}{l}} {0.025{\kern 1pt} {\kern 1pt} {\kern 1pt} 76\beta ,}&{{\rm{ if }}(\beta < 1);}\\ {0.022{\kern 1pt} {\kern 1pt} {\kern 1pt} 4 + 0.003{\kern 1pt} {\kern 1pt} {\kern 1pt} 36\beta ,}&{{\rm{ if }}(\beta \ge 1),} \end{array}} \right. $

$ {I_{{\rm{sp}}}} = \left\{ {\begin{array}{*{20}{l}} {4{\kern 1pt} {\kern 1pt} {\kern 1pt} 700 - \frac{h}{{100}},}&{Ma < 4;}\\ {5{\kern 1pt} {\kern 1pt} {\kern 1pt} 680 - 245Ma - \frac{h}{{100}},}&{Ma \ge 4.} \end{array}} \right. $

式中：C_T为推力系数，Ma为马赫数.

1.3 空气动力与动力矩

高超声速飞行器的气动力与气动力矩可表示为：

$ {T = \frac{1}{2}\rho {V^2}{S_{\rm{w}}}{C_T},L = \frac{1}{2}\rho {V^2}{S_{\rm{w}}}{C_L},} $

$ {D = \frac{1}{2}\rho {V^2}{S_{\rm{w}}}{C_D},{M_y} = \frac{1}{2}\rho {V^2}{S_{\rm{w}}}{c_{\rm{A}}}{C_{{M_y}}}.} $

式中：S_w为机翼浸润面积；c_A为平均气动弦长；ρ为空气密度；C_T、C_L、C_D、C_My分别为推力、升力、阻力以及俯仰力矩系数，其均与α、Ma相关，具体值详见文献[14].

1.4 控制问题

1) 由于高超声速飞行器本身缺乏飞行试验数据等^[15]问题，加上爬升的过程中，飞行速度、高度急剧增加，燃料大量消耗导致重心较宽范围变化等因素，将会造成模型、参数等不确定性.本文主要研究高超声速飞行器在爬升的过程中参数S_w，c_A，I_y，ρ，C_D, C_M, C_L存在摄动，且存在除参数不确定外的复合干扰时的轨迹控制问题.

2) 抖振普遍存在于滑模控制中，如何削弱抖振，将其抑制到极小范围内甚至消除，一直是控制领域的热点问题.二阶超螺旋滑模将符号函数放到积分里，有效地抑制了抖振，但是并没有消除抖振.假设某系统有如下控制算法:

$ u = - {k_1}|e{|^{\frac{1}{2}}} {\rm{sgn}} (e) - \int_0^t {{k_2}} {\rm{sgn}} (e(\tau )){\rm{d}}\tau . $

(2)

式中：u为控制输入; e为跟踪误差; k₁、k₂为控制参数.由式(2)可知，虽然符号函数通过积分，使得控制输入连续，但是不平滑，当e在0附近变化时，控制输入曲线会呈锯齿状.本文控制算法旨在既能将控制输入平滑化，又能提升收敛速度.

2 精确反馈线性化 2.1 输入/输出反馈线性化

定义向量x=[V, γ, α, β, h, M]^T，将V、h分别对时间求三次和四次微分，微分表达式中将出现控制输入量，将其作为整体提取出来，可得：

$ \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {\dot V = \frac{{T\cos \alpha - D}}{M} - \frac{{{\mu _0}\sin \gamma }}{{{r^2}}} + {d_{v1}},}\\ {\ddot V = L_\mathit{\boldsymbol{f}}^2V(\mathit{\boldsymbol{x}}) + {d_{v2}},}\\ {\dddot V = L_\mathit{\boldsymbol{f}}^3V(\mathit{\boldsymbol{x}}) + {L_\mathit{\boldsymbol{g}}}L_\mathit{\boldsymbol{f}}^2V(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{u}} + {d_{v3}},} \end{array}} \right.\\ \left\{ {\begin{array}{*{20}{l}} {\dot h = V\sin \gamma ,}\\ {\ddot h = L_\mathit{\boldsymbol{f}}^2h(\mathit{\boldsymbol{x}}) + {d_{h1}},}\\ {\dddot h = L_\mathit{\boldsymbol{f}}^3h(\mathit{\boldsymbol{x}}) + {d_{h2}},}\\ {{h^{(4)}} = L_\mathit{\boldsymbol{f}}^4h(\mathit{\boldsymbol{x}}) + {L_\mathit{\boldsymbol{g}}}L_\mathit{\boldsymbol{f}}^3h(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{u}} + {d_{h3}},} \end{array}} \right.\\ \left[ {\begin{array}{*{20}{c}} {\dddot V}\\ {{h^{(4)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{f_v}}\\ {{f_h}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{d_{v3}}}\\ {{d_{h3}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{b_{11}}}&{{b_{12}}}\\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\beta _{\rm{c}}}}\\ {{\delta _{\rm{e}}}} \end{array}} \right]. \end{array} $

(3)

式中：L_g ·、L_fⁱ·(i=1, 2, 3)为李导数^[14]；d_v1、d_v2、d_h1、d_h2为非匹配不确定性；d_v2、d_h3为匹配不确定性；u= [β_c  δ_e] ^T为控制输入；f_v、f_h、b_ij(i, j=1, 2)表达式见文献[14].

2.2 滑模微分器

由于非匹配不确定性d_v1、d_v2、d_h1、d_h2的存在，导致反馈线性化的结果不准确，鉴于滑模微分器有良好的逼近效果^[16]，所以本文采用滑模微分器来逼近$\dot V、\ddot V、\ddot h、\mathop h\limits^{...} $，以得到更加精确的值，提高反馈线性化结果的准确性，减小模型(1)与模型(3)的偏差.

滑模微分器设计为

$ \left\{ {\begin{array}{*{20}{l}} {{{\dot z}_0} = {v_0},}\\ {{v_0} = - \lambda _2^i|{z_0} - f(t){|^{2/3}} {\rm{sgn}} ({z_0} - f(t)) + {z_1},}\\ {{{\dot z}_1} = {v_1},}\\ {{v_1} = - \lambda _1^i|{z_1} - {v_0}{|^{1/2}} {\rm{sgn}} ({z_1} - {v_0}) + {z_2},}\\ {{{\dot z}_2} = - \lambda _0^i {\rm{sgn}} ({z_2} - {v_1}),} \end{array}} \right. $

式中λ₀ⁱ、λ₁ⁱ、λ₂ⁱ>0(i=V, h)为滑模微分器的设计参数.

引理1 ^{[4, 16]}  设f(t)=f₀(t)是定义在[0, ∞]上的函数，且有|f⁽ⁿ⁺¹⁾|≤S_n，∀t，其中S_n为已知正常数.则在经历有限时间的瞬态过程后，有z₀=f₀(t)，z_j=v_j－1=f₀^j(t)，j=1, …, n.

引理1中的n为滑模微分器阶数，本文n=2.其中：1)速度微分器.当f(t)=V，i=V时，z₁、z₂分别跟踪$\dot V、\ddot V$; 2)高度微分器.当f(t)=Vsin γ，i=h时，z₁、z₂分别跟踪$\ddot h、\mathop h\limits^{...} $.

根据引理1，选择合适的参数，可以保证滑模微分器的状态量在有限时间内精确跟踪速度和高度的各阶导数.

3 快速平滑自适应二阶滑模算法 3.1 积分滑模面

定义速度和高度的跟踪误差：

$ {e_V} = V - {V_{\rm{d}}},{e_h} = h - {h_{\rm{d}}}, $

(4)

式中V_d、h_d为指令信号.

为了保证稳态跟踪精度，选择积分滑模面.根据式(3)，系统的相对阶次分别为3和4，所以设计滑模面如下：

$ \mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{l}} {{s_V}}\\ {{s_h}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{{({\rm{d}}/{\rm{d}}t + {\lambda _V})}^3}\int_0^t {{e_V}} (\tau ){\rm{d}}\tau }\\ {{{({\rm{d}}/{\rm{d}}t + {\lambda _h})}^4}\int_0^t {{e_h}} (\tau ){\rm{d}}\tau } \end{array}} \right], $

(5)

式中λ_V、λ_h为待设计参数.

假设1 ^[17]  系统(3)的匹配不确定性表示为d=[d_v3  d_h3]^T，且满$\left\| {\mathit{\boldsymbol{\dot d}}} \right\| \le {g_1}{\zeta _1}\left( \mathit{\boldsymbol{s}} \right)$.其中，g₁为未知正常数，${\zeta _1}(\mathit{\boldsymbol{s}}) = {\left\| \mathit{\boldsymbol{s}} \right\|^{\frac{{m - 1}}{m}}}$是滑模变量的函数.

3.2 控制器结构

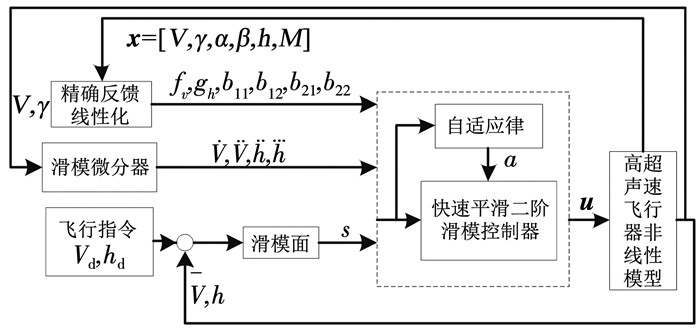
快速平滑自适应二阶滑模控制系统结构框图如图 1所示.

在图 1中，快速平滑二阶滑模控制律可设计为：

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\beta _c}}\\ {{\delta _e}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{l}} {{b_{11}}}&{{b_{12}}}\\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]^{ - 1}}\left( {\left[ {\begin{array}{*{20}{c}} {{{\ddot V}_\rm{d}}}\\ {h_\rm{d}^{(4)}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{f_v}}\\ {{f_h}} \end{array}} \right] + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} { - 3{\lambda _V}{{\ddot e}_V}}&{ - 3\lambda _V^2{{\dot e}_V} - \lambda _V^3{e_V}}\\ { - 4{\lambda _h}{{\dddot e}_h} - 6\lambda _h^2{{\ddot e}_h}}&{ - 4\lambda _h^3{{\dot e}_h} - \lambda _h^4{e_h}} \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} { - {a_{V1}}{b_{V1}}|{s_V}{|^{\frac{{m - 1}}{m}}} {\rm{sgn}} ({s_V}) - {a_{V1}}{b_{V2}}{s_V}}\\ { - {a_{h1}}{b_{h1}}|{s_h}{|^{\frac{{m - 1}}{m}}} {\rm{sgn}} ({s_h}) - {a_{h1}}{b_{h2}}{s_h}} \end{array}} \right.\\ \left. {\left. {\begin{array}{*{20}{l}} { - \int_0^t {({a_{V2}}{b_{V1}}|{s_V}(} \tau ){|^{\frac{{m - 2}}{m}}} {\rm{sgn}} ({s_V}(\tau )) + {a_{V2}}{b_{V2}}{s_V}(\tau )){\rm{d}}\tau }\\ { - \int_0^t {({a_{h2}}{b_{h1}}|{s_h}(} \tau ){|^{\frac{{m - 2}}{m}}} {\rm{sgn}} ({s_h}(\tau )) + {a_{h2}}{b_{h2}}{s_h}(\tau )){\rm{d}}\tau } \end{array}} \right]} \right). \end{array} $

(6)

式中：b_i=[b_Vi  b_hi]^T>0(i=1, 2)，m≥2为控制器参数; a_i=[a_Vi  a_hi]^T>0(i=1, 2)为自适应增益，其自适应律为：

$ \begin{array}{l} {{\mathit{\boldsymbol{\dot a}}}_1} = \left\{ {\begin{array}{*{20}{l}} {{\omega _1}\sqrt {\frac{{{\gamma _1}}}{2}} {\rm{sgn}} (|\mathit{\boldsymbol{s}}| - \mathit{\boldsymbol{\mu }}),}&{{\rm{ if }}|\mathit{\boldsymbol{s}}| \ne {\bf{0}};}\\ {{\bf{0}},}&{{\rm{ if }}|\mathit{\boldsymbol{s}}| = {\bf{0}},} \end{array}} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{a}}_2} = {\left[ {\begin{array}{*{20}{l}} {a_{V1}^2{b_{V1}}}&{a_{h1}^2{b_{h1}}} \end{array}} \right]^{\rm{T}}}. \end{array} $

(7)

式中：自适应律设计参数ω₁, γ₁>0，μ=[μ₁  μ₂]，μ₁、μ₂为较小的正常数.

根据式(3)、式(4)~(6)可计算得出闭环滑模面趋近动态.鉴于滑模面s_V和s_h的趋近动态形式相同，下文省去下标为s，其中a_Vi、b_Vi、a_hi、b_hi(i=1, 2)，d_v3，d_h3同理，可得：

$ \begin{array}{*{20}{l}} {\dot s = {a_1}( - {b_1}|s{|^{\frac{{m - 1}}{m}}} {\rm{sgn}} (s) - {b_2}s) + \sigma ,}\\ {\dot \sigma = {a_2}( - {b_1}|s{|^{\frac{{m - 2}}{m}}} {\rm{sgn}} (s) - {b_2}s) + \dot d.} \end{array} $

(8)

情况1   当m=2时，对比式(2)，该算法加入了线性项a₁b₂s、a₂b₂s，可保证s快速收敛到μ邻域内，但是该算法并不平滑.

情况2   当m>2时，不仅可保证快速收敛，且控制输入式(6)的积分项中均是连续的函数项，故此时的控制输入是平滑的.

3.3 收敛性证明

定理1   对于包含被控系统(1)、控制律(6)、自适应律(7)的闭环系统，若假设1满足，则s在有限时间内收敛于μ邻域内.

证明  令${\eta _1} = {a_1}{b_1}, {\eta _2} = {a_1}{b_2}, {\eta _3} = {a_2}{b_1}, {\eta _4} = {a_2}{b_2}, \zeta = {\left[ {\begin{array}{*{20}{l}} {|s{|^{\frac{{m - 1}}{m}}}{\mathop{\rm sgn}} (s)}&s&\sigma \end{array}} \right]^{\rm{T}}}$.定义一个对称正定矩阵:

$ \mathit{\boldsymbol{Q}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {4{\eta _3} + \eta _1^2}&{{\eta _1}{\eta _2}}&{ - {\eta _1}}\\ {{\eta _1}{\eta _2}}&{2{\eta _4} + \eta _2^2}&{ - {\eta _2}}\\ { - {\eta _1}}&{ - {\eta _2}}&2 \end{array}} \right]. $

定义类二次型Lyapunov函数为

$ V = \underbrace {{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{Q\zeta }}}_{{V_1}} + \underbrace {\sum\limits_{i = 1}^2 {\frac{1}{{2{\gamma _i}}}} {{({a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i})}^2}}_{{V_2}}, $

(9)

式中ȃ₁、ȃ₂分别为a₁、a₂的上界.

对V求一阶导:

$ \begin{array}{*{20}{l}} {\dot V = - |s{|^{ - \frac{1}{m}}}{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{A\zeta }} - {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{B\zeta }} + \mathit{\boldsymbol{C\zeta \dot d}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^2 {\frac{1}{{{\gamma _i}}}} ({a_i} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} ){{\dot a}_i},} \end{array} $

(10)

式中：

$ \mathit{\boldsymbol{A}} = \frac{{m - 1}}{m}{\eta _1}\left[ {\begin{array}{*{20}{c}} {\eta _1^2 + \frac{{(3m - 4){\eta _3}}}{{m - 1}}}&0&{\frac{{(2 - m){\eta _3}}}{{(m - 1){\eta _1}}} - {\eta _1}}\\ 0&{\frac{{(3m - 1)\eta _2^2 + m{\eta _4}}}{{m - 1}}}&{ - \frac{{(2m - 1){\eta _2}}}{{m - 1}}}\\ {\frac{{(2 - m){\eta _3}}}{{(m - 1){\eta _1}}} - {\eta _1}}&{ - \frac{{(2m - 1){\eta _2}}}{{m - 1}}}&1 \end{array}} \right], $

$ \mathit{\boldsymbol{B}} = {\eta _2}\left[ {\begin{array}{*{20}{c}} {\frac{{(3m - 2)\eta _1^2 + (3m - 4){\eta _3}}}{m}}&0&0\\ 0&{\eta _2^2 + {\eta _4}}&{ - {\eta _2}}\\ 0&{ - {\eta _2}}&1 \end{array}} \right], $

$ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} { - {\eta _1} - {\eta _2}}&2 \end{array}} \right]. $

根据杨氏不等式$xy \le \frac{{{x^2} + {y^2}}}{2}$，式(10)的第3项可为

$ \mathit{\boldsymbol{C\dot \zeta d}} \le {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{D\zeta }}, $

式中$\mathit{\boldsymbol{D}} = {\mathop{\rm diag}\nolimits} \left( {\frac{{{\eta _2}{g_1} + 2{g_1} + {\eta _1}{g_1}}}{2}, \frac{{{\eta _2}{g_1}}}{2}, {g_1}} \right)$.

则式(10)可为

$ \begin{array}{*{20}{l}} {\dot V \le - |s{|^{ - \frac{1}{m}}}{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{A\zeta }} - {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}(\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{D}})\mathit{\boldsymbol{\zeta }} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^2 {\frac{1}{{{\gamma _i}}}} ({a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}){{\dot a}_i}.} \end{array} $

(11)

令A和B-D均为正定矩阵，可解算得：

$ \begin{array}{l} {a_1} > \max \left[ {\frac{{2{g_1}}}{{{b_2}}},\sqrt {\frac{{16E + 2{{(2{b_1} + {b_2})}^2}}}{{16{E^2}}}} } \right],\\ E = \frac{{(6m - 6)b_1^2}}{m},\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_1} > \frac{{16{m^3} - 45{m^2} + 39m - 9}}{{3{m^2} - 4m}}{b_2},{a_2} = a_1^2{b_1}. \end{array} $

(12)

根据：

$ {{\lambda _{\min }}(\mathit{\boldsymbol{Q}}){{\left\| \mathit{\boldsymbol{\zeta }} \right\|}^2} \le {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{Q\zeta }} \le {\lambda _{\max }}(\mathit{\boldsymbol{Q}}){{\left\| \mathit{\boldsymbol{\zeta }} \right\|}^2},} $

(13)

$ {{{\left\| \mathit{\boldsymbol{\zeta }} \right\|}^2} = |s{|^{\frac{{2m - 2}}{m}}} + {s^2} + {\sigma ^2},} $

(14)

可得$|s| \le \left\| {\bf{\zeta }} \right\|\frac{m}{{m - 1}} \le {\left( {\frac{{V_1^{1/2}}}{{\lambda _{\min }^{1/2}({\bf{Q}})}}} \right)^{\frac{m}{{m - 1}}}}$.则式(11)可简化为

$ \begin{array}{*{20}{c}} {\dot V \le - {\kappa _1}V_1^{\frac{{2m - 3}}{{2m - 2}}} - {\kappa _2}{V_1} - \sum\limits_{i = 1}^2 {\frac{{{\omega _i}}}{{\sqrt {2{\gamma _i}} }}} |{a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}| + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^2 {\frac{1}{{{\gamma _i}}}} ({a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}){{\dot a}_i} + \sum\limits_{i = 1}^2 {\frac{{{\omega _i}}}{{\sqrt {2{\gamma _i}} }}} |{a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}|.} \end{array} $

(15)

式中：

$ {\kappa _1} = \frac{{{\lambda _{\min }}(\mathit{\boldsymbol{A}})\lambda _{\min }^{1/(2m - 2)}(\mathit{\boldsymbol{Q}})}}{{{\lambda _{\max }}(\mathit{\boldsymbol{Q}})}},{\kappa _2} = \frac{{{\lambda _{\min }}(\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{D}})}}{{{\lambda _{\max }}(\mathit{\boldsymbol{Q}})}}. $

根据式(7)可知，本文设计的自适应律，参数不会无限增大，总存在上界ȃ₁，ȃ₂使得a₁-ȃ₁ < 0，a₂-ȃ₂ < 0.则式(15)转化为

$ \begin{array}{*{20}{l}} {\dot V \le - {\kappa _1}V_1^{\frac{{2m - 3}}{{2m - 2}}} - {\kappa _2}{V_1} - {\kappa _3}V_2^{\frac{1}{2}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^2 {(\frac{{{{\dot a}_i}}}{{{\gamma _i}}} - \frac{{{\omega _i}}}{{\sqrt {2{\gamma _i}} }})} |{a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}| \le }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \kappa {V^\varepsilon } - \sum\limits_{i = 1}^2 {(\frac{{{{\dot a}_i}}}{{{\gamma _i}}} - \frac{{{\omega _i}}}{{\sqrt {2{\gamma _i}} }})} |{a_i} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_i}|.} \end{array} $

(16)

式中${\rm{ }}{\kappa _3} = \min \left[ {\frac{{{\omega _1}}}{{\sqrt {2{\gamma _1}} }}, \frac{{{\omega _2}}}{{\sqrt {2{\gamma _2}} }}} \right], \kappa = \min \left[ {{\kappa _1}, {\kappa _2}, {\kappa _3}} \right].因\frac{1}{2} < \frac{{2m - 3}}{{2m - 2}} < 1, 故{\rm{ }}\frac{1}{2} \le \varepsilon \le 1$.

针对滑模面趋近动态(8)，如不加入线性项a₁b₂s、a₂b₂s，并采用相似的证明过程，可得${\dot V_c} \le - {\kappa _1}V_1^{\frac{{2m - 3}}{{2m - 2}}} - {\kappa _3}V_2^{\frac{1}{2}} - \sum\limits_{i = 1}^2 {\left( {\frac{{{{\dot a}_i}}}{{{\gamma _i}}} - \frac{{{\omega _i}}}{{\sqrt {2{\gamma _i}} }}} \right)} \left| {{a_i} - {{\hat a}_i}} \right|$，对比式(16)，有$\dot V \le {\dot V_c}$，故本文方法的收敛速度更快.

情况1   当|s|>μ时，${\dot a_1} = {\omega _1}\sqrt {\frac{{{\gamma _1}}}{2}} , {\rm{令}}{b_1} = \frac{{{\omega _2}}}{{{\omega _1}}}\sqrt {\frac{{{\gamma _2}}}{{{\gamma _1}}}} $，则式(16)变为

$ \dot V \le - \kappa {V^\varepsilon } - (2{a_1} - 1)\frac{{{\omega _2}}}{{\sqrt {2{\gamma _2}} }}|{a_2} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} _2}|. $

由于ȧ₁, ω₂, γ₂>0，故a₁递增，只要选取初值a₁(0)≥0.5，则必有$\dot V \le - \kappa {V^\varepsilon }$，那么|s|可在有限时间${t_F} = \frac{1}{{\kappa (1 - \varepsilon )}}\left[ {V{{(0)}^{1 - \varepsilon }} - V{{\left( {{t_F}} \right)}^{1 - \varepsilon }}} \right]$内收敛至μ邻域内，其中V(0)为系统初始值，V(t_F)为|s|进入μ邻域时的值.

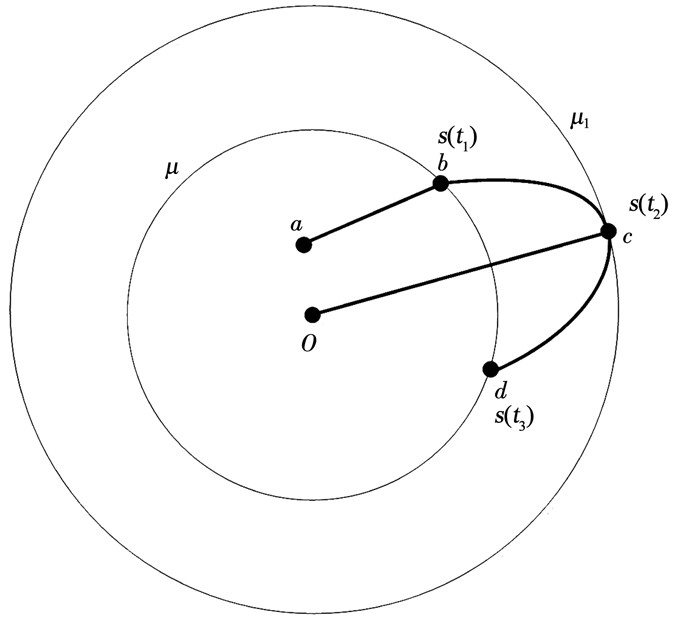
情况2   如图 2所示，当|s| < μ时，系统状态位于a点，此时${\dot a_1} = - {\omega _1}\sqrt {\frac{{{\gamma _1}}}{2}} $，a₁开始减小，当其不满足式(12)时，|s|开始增大，直至t₁时刻到达b点(s =μ)，下一时刻将满足情况1，a₁再逐渐增大，直至满足式(12)，与此同时|s|到达c点(t₂时刻)，之后再次收敛至μ邻域内(t₃时刻).

因此，在自适应过程中，|s|可能在有限的时间(t₃－t₁)内离开μ邻域，并保证其始终停留于一个更大的邻域μ₁，即|s|≤μ₁，下面估计μ₁邻域的界.

根据式(9)和式(11)，有

$ {\dot V_1} \le - |s{|^{ - \frac{1}{m}}}{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{A\zeta }} - {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}(\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{D}})\mathit{\boldsymbol{\zeta }}. $

再根据不等式(13)，可将上述不等式化为

$ \frac{{\rm{d}}}{{{\rm{d}}t}}({\lambda _1}{\left\| \mathit{\boldsymbol{\zeta }} \right\|^2}) \le {\dot V_1} \le {\lambda _2}{\left\| \mathit{\boldsymbol{\zeta }} \right\|^{2 - \frac{1}{{m - 1}}}} + {\lambda _3}{\left\| \mathit{\boldsymbol{\zeta }} \right\|^2}. $

(17)

式中: $\begin{array}{*{20}{l}} {{\rm{ }}{\lambda _1} = {\lambda _{\min }}(\mathit{\boldsymbol{Q}}), {\lambda _2} = \mathop {\sup }\limits_{{a_1}\left( {{t_1}} \right) \le {a_1}(t) \le {a_1}\left( {{t_2}} \right)} \left\{ {{\lambda _{\max }}\left[ { - \mathit{\boldsymbol{A}}\left( {{a_1}(t)} \right)} \right]} \right\}, }\\ {{\lambda _3} = \mathop {\sup }\limits_{{a_1}\left( {{t_1}} \right) \le {a_1}(t) \le {a_1}\left( {{t_2}} \right)} \left\{ {{\lambda _{\max }}\left[ {\mathit{\boldsymbol{D}}\left( {{a_1}(t)} \right) - \mathit{\boldsymbol{B}}\left( {{a_1}(t)} \right)} \right]} \right\}, }\\ {{a_1}\left( {{t_2}} \right) = \max \left[ {\frac{{2{g_1}}}{{{b_2}}}, \sqrt {\left. {\frac{{16E + 2{{\left( {2{b_1} + {b_2}} \right)}^2}}}{{16{E^2}}}} \right]} } \right..} \end{array}$

在|s(t₁)|=μ的初始条件下，求解微分不等式(17)，可得到:

$ \begin{array}{*{20}{l}} {\left\| {\mathit{\boldsymbol{\zeta }}(t)} \right\| \le }\\ {{{(({\lambda _2} - 2{\lambda _1}{{\rm{e}}^{(\frac{{{\lambda _3}}}{{2{\lambda _1}(m - 1)}}t - \log (\frac{{{\lambda _3}\left\| {\xi ({t_1})} \right\|\frac{1}{{m - 1}} + {\lambda _2}}}{{2{\lambda _1}}}))}})/{\lambda _3})}^{m - 1}}.} \end{array} $

上式可得到t₂时刻‖ζ‖的最大值，为了估计此时|s|的最大值，令等式(14)中σ=0，可获得|s(t₂)|的最大估计值μ₁= s(‖ζ(t₂)‖).

定理1得证.

注  控制参数的选择如下：滑模微分器设计参数λ₀ⁱ、λ₁ⁱ、λ₂ⁱ(i=V, h)均为正常数，为确保精确跟踪，不能过小，同时还应避免其值过大导致微分器放大噪声；滑模面设计参数λ_V、λ_h均为正常数，为确保较快的滑模运动速度，不能过小，同时还应避免其值过大导致超调；控制器参数m≥2、b_V1、b_h1、b_V2、b_h2均为正常数，应通过式(12)的不等式约束来合理选择.自适应律设计参数ω₁、γ₁、μ₁、μ₂均为正常数，为确保s_V、s_h收敛于较小邻域，μ₁、μ₂值不能过大，同时还应避免其值过小导致自适应参数过大估计.

4 数值仿真

爬升过程的初始条件以及指令信号分别设为：V₀=590 m/s，h₀=3 528 m，V_d=590+10t，hd=3 528+75t.仿真时长为t=300 s.滑模微分器的参数设置为：λ₂^V=20，λ₁^V=10，λ₀^V=80，λ₂^h=10，λ₁^h=20，λ₀^h=40.控制器参数设置：m=4，b_V1=b_h1=9.51，b_V2=b_h2=0.01，a_V1(0)=1，a_h1(0)=1.仿真条件：对参数S_w，c_A，I_y，ρ，C_D, C_M, C_L加入40%的参数摄动，此外加入除参数不确定性的复合干扰：d_v1=10 m/s²，d_γ=0.03 rad/s，d_q=0.1 rad/s².

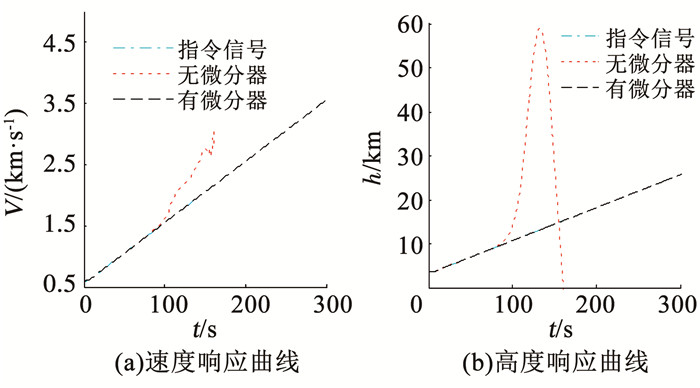
4.1 仿真1

为验证滑模微分器对反馈线性化过程中非匹配不确定性的抑制作用，进行仿真1.仿真结果如图 3所示.

为体现非匹配不确定性的影响效果，本文加入较大的不确定性及干扰，从仿真结果图 3可以看出，使用滑模微分器估计速度和高度各阶导数的控制器，高度和速度输出信号均能准确地跟踪上指令信号，而未使用滑模微分器的控制器在接近100 s时已经发散，可知在存在较大不确定性及干扰的情况下，忽略反馈线性化过程中的非匹配不确定性，是不合理的，设计出的控制器可能无法达到预期控制效果.

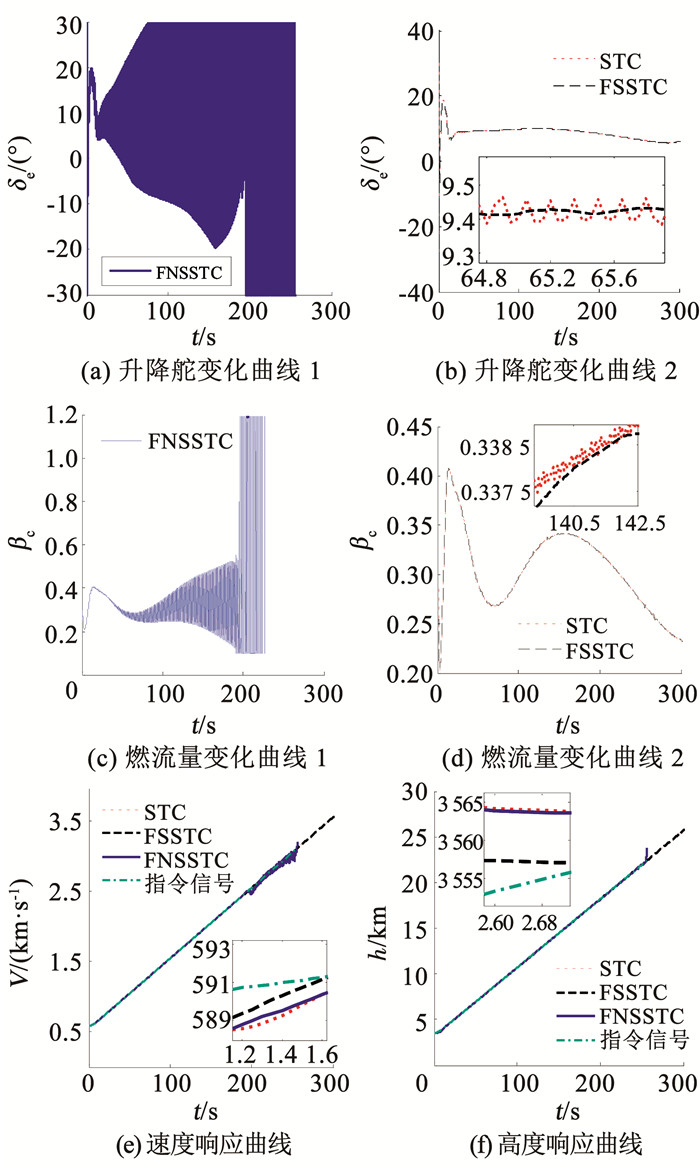
4.2 仿真2

为验证本文控制算法既快速又平滑的特性，进行仿真2，选择3种控制器：1)选取m=4的快速且平滑的超螺旋滑模控制(FSSTC)器；2)选取m=2的快速但不平滑的超螺旋滑模控制(FNSSTC)器；3)传统超螺旋滑模控制(STC)器.仿真结果如图 4所示.

从图 4(e)~图 4(f)可以看出，3种算法中，FSSTC算法的收敛速度最快，FNSSTC算法比传统STC算法的收敛速度略快一些，虽然其在收敛速度上有些许提升，但由于本文加入的不确定性及干扰较大，该算法的控制效果差，为尽量满足控制输入的真实情况，对其进行了限幅，导致无法提供理想的控制效能，逐渐振荡至发散.根据图 4(a)~图 4(d)可以看出, 传统的二阶滑模的抖振依旧没有消除，控制输入不平滑，呈现锯齿状，而本文提出的算法，控制输入平滑，基本消除了抖振.这是因为传统STC算法中，积分项下存在不连续的符号函数项sgn(s)，通过积分变成连续的三角波函数，当s在0附近变化时，控制输入高频跳变，幅值乘上系数a₂b₁，会放大抖振，而在本文方法中，积分项下原本不连续的sgn(s)变为连续的${\left| s \right|^{\frac{{m - 2}}{m}}}{\mathop{\rm sgn}} \left( s \right)$，当s在0附近变化时，该项较传统STC算法的符号函数幅值小很多，而且该项本身连续，通过一次积分后，得到类三角函数型平滑的控制输入，不会有锯齿状情况.

注  本文的控制算法中引入了线性项，原理上收敛速度较传统二阶滑模控制算法要快，但是设计自适应律可能减小其收敛速度，又由于本文设计的自适应律，其参数既可增大又可减小，不会造成参数过大估计，即可选取较大的初始值，保持更快收敛速度.

5 结论

1) 本文针对高超声速飞行器爬升段的控制问题, 提出了一种快速平滑的自适应二阶滑模控制算法.

2) 鉴于反馈线性化过程中存在的非匹配不确定性，采用了滑模微分器来逼近反馈线性化模型中速度和高度的各阶导数，同时为改善传统超螺旋控制算法的收敛速度以及控制输入平滑性，在其算法中加入了线性项，并将积分项中的符号函数项进行了连续化.

3) 仿真结果表明，加入滑模微分器后，成功消除了非匹配不确定性的影响，且该方法有较好的跟踪性能，与传统STC算法和FNSSTC算法相比，有更快的收敛速度，且控制输入平滑，基本消除了抖振.

4) 实际应用中，控制输入多为机械运动，意味着控制输入越平滑，则具有更好的工程实用价值.