捷联式惯性导航系统(strapdown inertial navigation system, SINS)根据陀螺仪输出的角速率和加速度计输出的比力可以计算出载体的姿态、速度和位置,被广泛应用于各种军用和民用行业.SINS系统在进行导航前需要进行初始对准,初始对准的精度直接影响SINS系统的导航精度.因此,精确的初始对准对SINS系统尤为重要.
对于高精度SINS系统,系统可以在静基座环境下通过感应地球自转和重力加速度确定出初始姿态,系统的位置和速度可以通过GPS系统得到.但是在一些紧急情况下,SINS系统需要在运动过程中进行初始对准,传统的静基座对准算法就不再适用.对于低精度的SINS系统,例如MEMS-IMU,系统本身的噪声大于地球自转角速率,同样无法进行静基座对准,需要在外部传感器辅助的情况下通过载体的运动进行初始对准.
近年来,研究人员对动基座初始对准进行了研究,提出了许多动基座对准算法.文献[1]对空中对准算法进行了研究,算法利用加速度计的输出计算初始水平姿态,利用GPS航迹向作为初始航向角,进行粗对准,然后利用自适应扩展卡尔曼滤波进行精对准,文章中只考虑了大方位失准角下的误差模型,但是利用加速度计得到的水平姿态可能会存在较大误差.文献[2]中算法则不用考虑初始姿态信息,使用OBA算法实现空中对准.通过引入初始导航惯性坐标系和初始载体惯性坐标系,将姿态矩阵拆分成3部分,分别为导航系与初始导航惯性系之间的方向余弦矩阵、载体系与初始载体惯性系之间的方向余弦矩阵和初始导航系与初始载体系之间的姿态矩阵.其中,前两个矩阵是时变矩阵,可以通过GPS数据和惯导数据对其进行计算,第3个矩阵为常值矩阵,利用基于优化的四元数法可以实现对常值矩阵的计算.该算法虽然能够实现快速对准,但算法没有考虑惯性器件误差带来的影响.文献[3]对文献[2]中的方法进行了进一步的研究和详细的推导,分别对速度积分和位置积分的效果进行了比较,但是文献[3]指出,该算法只适用于高精度的惯导系统.文献[3]中的算法只是单纯的对姿态进行估计,没有对惯性器件的误差进行补偿,文献[4]针对这一问题进行研究,使用迭代牛顿拉格朗日算法进行解算,对GPS杆臂误差和惯性器件的误差进行估计,然而算法依然只适用于高精度的惯导系统.文献[5-6]在假设水平姿态失准角为小角度的情况下,将方位失准角的三角函数作为状态变量,这样系统模型便转化成线性,减小计算量,但是在对准速度上并没有明显的提高.文献[7]对所有姿态角均为大失准角的情况进行了非线性误差方程的推导,并根据量测方程为线性的特性,将UKF算法进行简化,并证明了算法简化的可行性,减小了UKF算法的计算量.文献[8]用四元数定义姿态误差,对四元数形式的非线性误差方程进行推导,用UKF算法对系统进行滤波,可以实现大失准角的动基座对准,即使是90°的大方位失准角算法也可以收敛,但是算法中没有考虑UKF采样对四元数带来的影响.文献[9]将OBA算法与卡尔曼滤波结合,利用里程计作为辅助传感器对陀螺仪误差引起的失准角进行估计,并将估计结果反馈给OBA算法,从而提高对准精度,算法中虽然考虑了惯性器件误差的影响,但是没有对其进行估计,需要根据经验手动的对陀螺仪误差进行设置.文献[10]针对OBA算法会累积惯性器件误差的问题提出滑动窗积分计算的方法,防止误差的累积,但是该方法需要对窗口内的数据进行存储和积分运算,计算量会随着窗口的增大而增大.文献[11]中,根据飞机起飞前的运动特点建立了飞机的运动约束模型,从而达到在不增加其他传感器的情况下增加量测信息的效果,进一步提高动基座对准的速度和精度,但是这种方法只适用于飞机在跑道上的动基座对准,有一定的局限性.文献[12]使用IIR滤波器去除加速度计中的高频噪声,对提高对准精度有一定的帮助,但是没能从根本上解决惯性器件误差带来的问题.
本文在OBA算法的基础上,推导了陀螺仪误差与载体系和计算载体系的失准角之间的关系,并根据此关系建立非线性误差方程,然后利用UKF算法对失准角和陀螺仪常值漂移进行估计,将估计结果反馈给OBA算法,从而提高对准的精度,使算法可应用于低精度的惯导系统.考虑到量测噪声的不确定性,引入自适应滤波算法对量测噪声进行估计,提高系统的稳定性.
1 OBA动基座对准算法 1.1 姿态矩阵分解为便于表示,首先定义算法中所用坐标系.用i表示惯性坐标系,b表示载体坐标系,
在初始对准过程中,载体的速度和位置可以根据GPS的输出得到,因此,对准算法主要解决的问题是对姿态矩阵Cbn的估计.根据方向余弦矩阵的链乘规则,Cbn可以表示为
| $ \mathit{\boldsymbol{C}}_b^n(t) = \mathit{\boldsymbol{C}}_{n(0)}^{n(t)}\mathit{\boldsymbol{C}}_{b(0)}^{n(0)}\mathit{\boldsymbol{C}}_{b(t)}^{b(0)} = \mathit{\boldsymbol{C}}_{n(0)}^{n(t)}\mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}. $ | (1) |
式中:n(t)、b(t)分别为在t时刻的导航坐标系和载体坐标系;Cn(t)n(0)、Cb(t)b(0)分别为导航系和载体系由开始对准时刻到当前时刻的变化,为时变矩阵;Cbn(0)为开始对准时刻的姿态矩阵,不随时间变化,为常值矩阵.矩阵Cn(t)n(0)、Cb(t)b(0)的微分方程分别为:
| $ {\mathit{\boldsymbol{\dot C}}_{n(t)}^{n(0)} = \mathit{\boldsymbol{C}}_{n(t)}^{n(0)}\mathit{\boldsymbol{\omega }}_{in}^n \times ,} $ | (2) |
| $ {\mathit{\boldsymbol{\dot C}}_{b(t)}^{b(0)} = \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}\mathit{\boldsymbol{\omega }}_{ib}^b \times .} $ | (3) |
式中:
在不考虑误差的情况下,比力方程可表示为
| $ {\mathit{\boldsymbol{\dot v}}^n} = \mathit{\boldsymbol{C}}_b^n{\mathit{\boldsymbol{f}}^b} - (2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n) \times {\mathit{\boldsymbol{v}}^n} + {\mathit{\boldsymbol{g}}^n}. $ | (4) |
式中:vn为载体的速度在导航系下的投影;fb为加速度计的理论输出;ωien为地球自转角速度在导航系下的投影;ωenn为n系相对e系的角速度在n系的投影,将式(1)代入式(4)可得:
| $ {\mathit{\boldsymbol{\dot v}}^n} = \mathit{\boldsymbol{C}}_{n(0)}^{n(t)}\mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}{\mathit{\boldsymbol{f}}^b} - (2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n) \times {\mathit{\boldsymbol{v}}^n} + {\mathit{\boldsymbol{g}}^n}. $ | (5) |
式(5)等式两边同乘Cn(t)n(0)并移项整理可得:
| $ \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}{\mathit{\boldsymbol{f}}^b} = \mathit{\boldsymbol{C}}_{n(t)}^{n(0)}\left( {{{\mathit{\boldsymbol{\dot v}}}^n} + \left( {2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n} \right) \times {\mathit{\boldsymbol{v}}^n} - {\mathit{\boldsymbol{g}}^n}} \right). $ | (6) |
对式(6)两边同时积分并整理可得:
| $ {\mathit{\boldsymbol{C}}_b^n(0){\mathit{\boldsymbol{\alpha }}_v}(t) = {\mathit{\boldsymbol{\beta }}_v}(t),} $ | (7) |
其中:
| $ {{\mathit{\boldsymbol{\alpha }}_v}(t) = \int_0^t {\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}} {\mathit{\boldsymbol{f}}^b}{\rm{d}}t,} $ | (8) |
| $ \begin{array}{l} {\mathit{\boldsymbol{\beta }}_v}(t) = \mathit{\boldsymbol{C}}_{n(t)}^{n(0)}{\mathit{\boldsymbol{v}}^n} - {v^n}(0) + \int_0^t {\mathit{\boldsymbol{C}}_{n(t)}^{n(0)}} \mathit{\boldsymbol{\omega }}_{ie}^n \times {\mathit{\boldsymbol{v}}^n}{\rm{d}}t - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^t {\mathit{\boldsymbol{C}}_{n(t)}^{n(0)}} {\mathit{\boldsymbol{g}}^n}{\rm{d}}t. \end{array} $ | (9) |
在式(8)、(9)中,αv(t)可以通过Cb(t)b(0)和加速度计输出的比力fb积分计算得到,βv(t)可以通过对GPS输出的速度、当地重力加速度和由式(2)计算得到的Cn(t)n(0)积分计算得到,其中vn(0)为初始时刻GPS的速度.在矢量αv(t)和βv(t)已知的情况下,便可以根据文献[3]中最小二乘理论计算得到姿态矩阵Cbn(0).
OBA算法在计算方式上完全解析,不需要像传统的卡尔曼滤波一样将部分变量用上一时刻的代替,但是OBA算法没有考虑惯性器件误差带来的影响,因此OBA算法更适合用在高精度SINS系统中,当用在低精度SINS系统中时,该算法的可靠性就无法得到保障.本文接下来将对SINS/GPS组合系统的误差进行分析,对SINS系统的误差方程做一个新的推导,使其能够与OBA算法结合,然后建立一种新的非线性系统模型,利用自适应无迹卡尔曼滤波算法对失准角和陀螺仪误差进行估计,从而在保证算法对准速度的同时提高对准的精度.因为算法中考虑了陀螺仪的误差影响,所以算法可以用在低精度的SINS系统中.
2 系统的误差分析及建模 2.1 系统误差分析在计算矩阵Cn(t)n(0)时使用的是GPS信息,由于GPS不存在累积误差,且在计算Cn(t)n(0)时由GPS带来的误差很小,所以可以忽略.矩阵Cn(t)n(0)的更新公式为
| $ \mathit{\boldsymbol{C}}_{n\left( {{t_k}} \right)}^{n(0)} = \mathit{\boldsymbol{C}}_{n\left( {{t_{k - 1}}} \right)}^{n(0)}\mathit{\boldsymbol{C}}_{n\left( {{t_k}} \right)}^{n\left( {{t_{k - 1}}} \right)}. $ |
式中:tk=kT,k为采样次数,T为采样时间.矩阵Cn(tk-1)n(tk)为tk时刻导航系与tk-1时刻导航系之间的姿态矩阵,其计算公式为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_{n({t_k})}^{n({t_{k - 1}})} = \mathit{\boldsymbol{I}} + \frac{{\sin (\left\| {{\mathit{\boldsymbol{\varphi }}_n}} \right\|)}}{{\left\| {{\mathit{\boldsymbol{\varphi }}_n}} \right\|}}({\mathit{\boldsymbol{\varphi }}_n} \times ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1 - \cos (\left\| {{\mathit{\boldsymbol{\varphi }}_n}} \right\|)}}{{{{\left\| {{\mathit{\boldsymbol{\varphi }}_n}} \right\|}^2}}}{{({\mathit{\boldsymbol{\varphi }}_n} \times )}^2},} \end{array} $ | (10) |
| $ {\mathit{\boldsymbol{\varphi }}_n} = T\mathit{\boldsymbol{\omega }}_{in}^n. $ | (11) |
式中:式(10)中的φn可由式(11)计算得到,矢量φn为导航系由tk-1时刻到tk时刻的等效旋转矢量;‖φn‖为矢量φn的模.
在计算矩阵Cb(t)b(0)时使用的是陀螺仪输出,在不考虑陀螺仪误差时,tk时刻的Cb(t)b(0)更新公式为
| $ \mathit{\boldsymbol{C}}_{b({t_k})}^{b(0)} = \mathit{\boldsymbol{C}}_{b({t_{k - 1}})}^{b(0)}\mathit{\boldsymbol{C}}_{b({t_k})}^{b({t_{k - 1}})}, $ | (12) |
其中,矩阵Cb(tk)b(tk-1)的计算公式为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_{b({t_k})}^{b({t_{k - 1}})} = \mathit{\boldsymbol{I}} + \frac{{\sin (\left\| {{\mathit{\boldsymbol{\varphi }}_b}} \right\|)}}{{\left\| {{\mathit{\boldsymbol{\varphi }}_b}} \right\|}}({\mathit{\boldsymbol{\varphi }}_b} \times ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1 - \cos (\left\| {{\mathit{\boldsymbol{\varphi }}_b}} \right\|)}}{{{{\left\| {{\mathit{\boldsymbol{\varphi }}_b}} \right\|}^2}}}{{({\mathit{\boldsymbol{\varphi }}_b} \times )}^2},} \end{array} $ | (13) |
| $ {\mathit{\boldsymbol{\varphi }}_b} = \Delta {\mathit{\boldsymbol{\theta }}_1} + \Delta {\mathit{\boldsymbol{\theta }}_2} + \frac{2}{3}\Delta {\mathit{\boldsymbol{\theta }}_1} \times \Delta {\mathit{\boldsymbol{\theta }}_2}. $ | (14) |
式中:式(13)中的φb可由式(14)计算得到,矢量φb为载体系由tk-1时刻到tk时刻的等效旋转矢量,其计算方式采用双子样计算;Δθ1、Δθ2为相邻两时刻的陀螺仪角增量.
由于陀螺仪误差的存在,陀螺仪输出的角增量Δθ中包含误差,所以由式(12)~(14)计算出的Cb(tk)b(0)也带有误差,将带有误差的Cb(tk)b(0)记为
| $ \mathit{\boldsymbol{C}}_{\hat b(t)}^{b(0)} = \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}\mathit{\boldsymbol{C}}_{\hat b(t)}^{b(t)}. $ | (15) |
式中,矩阵
| $ \mathit{\boldsymbol{C}}_{\hat b(t)}^{b(t)} = \mathit{\boldsymbol{I}} + \frac{{\sin (\left\| \mathit{\boldsymbol{\varphi }} \right\|)}}{{\left\| \mathit{\boldsymbol{\varphi }} \right\|}}(\mathit{\boldsymbol{\varphi }} \times ) + \frac{{1 - \cos (\left\| \mathit{\boldsymbol{\varphi }} \right\|)}}{{{{\left\| \mathit{\boldsymbol{\varphi }} \right\|}^2}}}{(\mathit{\boldsymbol{\varphi }} \times )^2}. $ |
在第1部分的OBA算法中,没有考虑由陀螺仪误差引起的姿态误差
| $ \mathit{\boldsymbol{C}}_{\hat b(t)}^{b(t)} \approx \mathit{\boldsymbol{I}} + (\mathit{\boldsymbol{\varphi }} \times ). $ | (16) |
将式(16)带入式(15)可得:
| $ \mathit{\boldsymbol{C}}_{\hat b(t)}^{b(0)} = \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}(\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times ), $ | (17) |
对式(17)两端求导可得:
| $ \mathit{\boldsymbol{\dot C}}_{\hat b(t)}^{b(0)} = \mathit{\boldsymbol{\dot C}}_{b(t)}^{b(0)}(\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times ) + \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}\mathit{\boldsymbol{\dot \varphi }} \times , $ | (18) |
其中
| $ \mathit{\boldsymbol{\dot C}}_{\hat b(t)}^{b(0)} = \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}\mathit{\boldsymbol{\tilde \omega }}_{ib}^b \times , $ | (19) |
式中
| $ \mathit{\boldsymbol{\tilde \omega }}_{ib}^b = \mathit{\boldsymbol{\omega }}_{ib}^b + \delta \mathit{\boldsymbol{\omega }}_{ib}^b. $ | (20) |
将式(3)、(15)、(16)、(17)、(19)、(20)带入式(18)可得:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}(\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times )(\mathit{\boldsymbol{\omega }}_{ib}^b + \delta \mathit{\boldsymbol{\omega }}_{ib}^b) \times = }\\ {\mathit{\boldsymbol{C}}_{b(t)}^{b(0)}(\mathit{\boldsymbol{\omega }}_{ib}^b \times )(\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times ) + \mathit{\boldsymbol{C}}_{b(t)}^{b(0)}\mathit{\boldsymbol{\dot \varphi }} \times ,} \end{array} $ | (21) |
式(21)两边同乘Cb(0)b(t)可得:
| $ (\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times )(\mathit{\boldsymbol{\omega }}_{ib}^b + \delta \mathit{\boldsymbol{\omega }}_{ib}^b) \times = (\mathit{\boldsymbol{\omega }}_{ib}^b \times )(\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\varphi }} \times ) + \mathit{\boldsymbol{\dot \varphi }} \times , $ | (22) |
整理式(22)可得:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \varphi }} \times = (\mathit{\boldsymbol{\varphi }} \times )(\mathit{\boldsymbol{\omega }}_{ib}^b \times ) - (\mathit{\boldsymbol{\omega }}_{ib}^b \times )(\mathit{\boldsymbol{\varphi }} \times ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \mathit{\boldsymbol{\omega }}_{ib}^b \times + (\mathit{\boldsymbol{\varphi }} \times )(\delta \mathit{\boldsymbol{\omega }}_{ib}^b \times ),} \end{array} $ | (23) |
式中(φ×)(δωibb×)为二阶小量,可以忽略.且存在反对称矩阵的计算公式:
| $ ({\mathit{\boldsymbol{A}}_1} \times )({\mathit{\boldsymbol{A}}_2} \times ) - ({\mathit{\boldsymbol{A}}_2} \times )({\mathit{\boldsymbol{A}}_1} \times ) = ({\mathit{\boldsymbol{A}}_1} \times {\mathit{\boldsymbol{A}}_2}) \times . $ | (24) |
则式(23)可根据式(24)简化为
| $ \mathit{\boldsymbol{\dot \varphi }} \times = (\mathit{\boldsymbol{\varphi }} \times \mathit{\boldsymbol{\omega }}_{ib}^b) \times + \delta \mathit{\boldsymbol{\omega }}_{ib}^b \times , $ | (25) |
式(25)进一步化简有
| $ \mathit{\boldsymbol{\dot \varphi }} = - \mathit{\boldsymbol{\omega }}_{ib}^b \times \mathit{\boldsymbol{\varphi }} + \delta \mathit{\boldsymbol{\omega }}_{ib}^b. $ | (26) |
由于陀螺仪的实际输出值为
| $ \mathit{\boldsymbol{\dot \varphi }} = - (\mathit{\boldsymbol{\tilde \omega }}_{ib}^b - \delta \mathit{\boldsymbol{\omega }}_{ib}^b) \times \mathit{\boldsymbol{\varphi }} + \delta \mathit{\boldsymbol{\omega }}_{ib}^b. $ | (27) |
式(27)为载体系与计算载体系之间的误差方程,该误差方程反映了陀螺仪误差对SINS系统姿态估计精度的影响,通过式(27)可以对SINS系统进行建模,从而估计出SINS系统的失准角和陀螺仪误差,提高算法的对准精度和适用范围.
2.2 SINS/GPS系统建模 2.2.1 系统状态方程考虑陀螺仪误差δωibb中包含常值漂移εb和随机漂移wg,其关系如下:
| $ \delta \mathit{\boldsymbol{\omega }}_{ib}^b = {\mathit{\boldsymbol{\varepsilon }}^b} + {\mathit{\boldsymbol{w}}_{\rm{g}}}. $ |
根据式(27),选取等效旋转矢量φ和陀螺仪常值漂移εb作为状态变量X,即
| $ \mathit{\boldsymbol{X}} = {[{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\quad {({\mathit{\boldsymbol{\varepsilon }}^b})^{\rm{T}}}]^{\rm{T}}}, $ | (28) |
式中,
| $ {\mathit{\boldsymbol{\dot X}}_k} = f({\mathit{\boldsymbol{X}}_{k - 1}}) + {\mathit{\boldsymbol{W}}_k}, $ | (29) |
式中Wk是均值为零、协方差为Qk的系统白噪声.
2.2.2 系统量测方程在tk时刻,式(8)可表示为
| $ {\mathit{\boldsymbol{\alpha }}_v}({t_k}) = \int_0^{{t_k}} {\mathit{\boldsymbol{C}}_{b(\tau )}^{b(0)}} {\mathit{\boldsymbol{f}}^b}{\rm{d}}\tau , $ | (30) |
式(30)继续变换可得:
| $ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_v}({t_k}) = \int_0^{{t_k}} {\mathit{\boldsymbol{C}}_{b({t_k})}^{b(0)}} \mathit{\boldsymbol{C}}_{b(\tau )}^{b({t_k})}{f^b}{\rm{d}}\tau = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{C}}_{b({t_k})}^{b(0)}\int_0^{{t_k}} {\mathit{\boldsymbol{C}}_{b(\tau )}^{b({t_k})}} {\mathit{\boldsymbol{f}}^b}{\rm{d}}\tau . \end{array} $ | (31) |
记
| $ {\mathit{\boldsymbol{\tilde \alpha }}_v}({t_k}) = {(\mathit{\boldsymbol{C}}_{b({t_k})}^{b(0)})^{\rm{T}}}\int_0^{{t_k}} {\mathit{\boldsymbol{C}}_{b(\tau )}^{b(0)}} {\mathit{\boldsymbol{f}}^b}{\rm{d}}\tau . $ | (32) |
根据式(31)、(32),式(7)可表示为
| $ \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{b({t_k})}^{b(0)}{\mathit{\boldsymbol{\tilde \alpha }}_v}({t_k}) = {\mathit{\boldsymbol{\beta }}_v}({t_k}). $ | (33) |
考虑到在计算矩阵Cb(tk)b(0)时,实际得到的是矩阵
| $ \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}\mathit{\boldsymbol{C}}_{b({t_k})}^{\hat b({t_k})}{\mathit{\boldsymbol{\tilde \alpha }}_v}({t_k}) = {\mathit{\boldsymbol{\beta }}_v}({t_k}). $ | (34) |
将
| $ \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{\varphi }} \times ){\mathit{\boldsymbol{\tilde \alpha }}_v}({t_k}) = {\mathit{\boldsymbol{\beta }}_v}({t_k}), $ | (35) |
对式(35)化简并整理得
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\beta }}_v}({t_k}) - \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}{{\mathit{\boldsymbol{\tilde \alpha }}}_v}({t_k}) = }\\ {\mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}({{\mathit{\boldsymbol{\tilde \alpha }}}_v}({t_k}) \times )\mathit{\boldsymbol{\varphi }}.} \end{array} $ | (36) |
将系统的量测方程表示为:
| $ {{\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k},} $ | (37) |
| $ {{\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{\beta }}_v}({t_k}) - \mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}{{\mathit{\boldsymbol{\tilde \alpha }}}_v}({t_k}),} $ | (38) |
| $ {{\mathit{\boldsymbol{H}}_k} = [\mathit{\boldsymbol{C}}_b^n(0)\mathit{\boldsymbol{C}}_{\hat b({t_k})}^{b(0)}({{\mathit{\boldsymbol{\tilde \alpha }}}_v}({t_k}) \times )\quad {{\bf{0}}_{3 \times 3}}].} $ | (39) |
式(36)、(37)相对应,其对应关系如式(38)、(39)所示.量测方程中的Vk是均值为零的量测白噪声,其协方差记为Rk.
3 自适应无迹卡尔曼滤波算法由于系统的状态方程是非线性的,所以普通卡尔曼滤波不适合本文中的系统.无迹卡尔曼滤波在UT变换的基础上,根据KF滤波算法的原理,使用一系列的采样点进行采样计算来逼近系统的非线性分布,从而减小系统线性化带来的误差,提高滤波的精度[13].所以本文中选择UKF算法对状态变量进行滤波估计.
滤波过程中使用式(28)作为滤波的状态变量,使用式(29)和式(38)作为UKF滤波时的状态方程和量测方程.根据式(29)和式(37)可以看出,系统的状态方程为非线性,量测方程为线性,所以在使用UKF算法时可以对量测更新部分做进一步简化,使用线性卡尔曼滤波的方式进行量测更新,从而减少采样次数和计算量.简化后的量测更新如下:
| $ {{{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}} = {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}},} $ |
| $ {{\mathit{\boldsymbol{P}}_{ZZ}} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k},} $ |
| $ {{\mathit{\boldsymbol{P}}_{XZ}} = {\mathit{\boldsymbol{P}}_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}.} $ |
式中:
在进行UKF算法滤波时,量测噪声方差矩阵R设置的不准确会导致系统滤波的不稳定.在本文中,量测方程是由速度、比力等的积分构成的,很难通过手动调试将量测噪声方差矩阵设置准确.针对这一问题,本文引入Sage-Husa自适应滤波算法对量测噪声方差矩阵R进行实时估计,从而提高系统的滤波精度和稳定性.对量测噪声方差矩阵R的估计公式如下:
| $ {{{\mathit{\boldsymbol{\hat R}}}_k} = (1 - {\beta _k}){{\mathit{\boldsymbol{\hat R}}}_{k - 1}} + {\beta _k}({{\mathit{\boldsymbol{\tilde Z}}}_{k/k - 1}}\mathit{\boldsymbol{\tilde Z}}_{k/k - 1}^{\rm{T}} - {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}),} $ |
| $ {{{\mathit{\boldsymbol{\tilde Z}}}_{k/k - 1}} = {\mathit{\boldsymbol{Z}}_k} - {{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}},} $ |
| $ {{\beta _k} = \frac{{{\beta _{k - 1}}}}{{{\beta _{k - 1}} + b}}.} $ |
式中:
在生成仿真轨迹时主要是对SINS系统中陀螺仪和加速度计的参数、GPS系统的参数、SINS系统的初始条件和SINS系统的运动状态进行设置.
1) 仿真参数设置为:陀螺仪的常值漂移和随机噪声分别为1.0°/h和0.1°/h,加速度计的常值零偏和随机噪声分别为100 ug和50 ug,陀螺仪和加速度计的输出频率均为100 Hz;GPS系统的速度误差为0.05 m/s,位置误差为5 m,GPS系统的输出频率为10 Hz.
2) SINS系统的初始状态设置为:SINS系统的初始位置为北纬45°和东经126°,初始姿态为航向角45°、俯仰角0°和横滚角0°,初始速度为东向速度5 m/s、北向速度5 m/s和天向速度0 m/s.
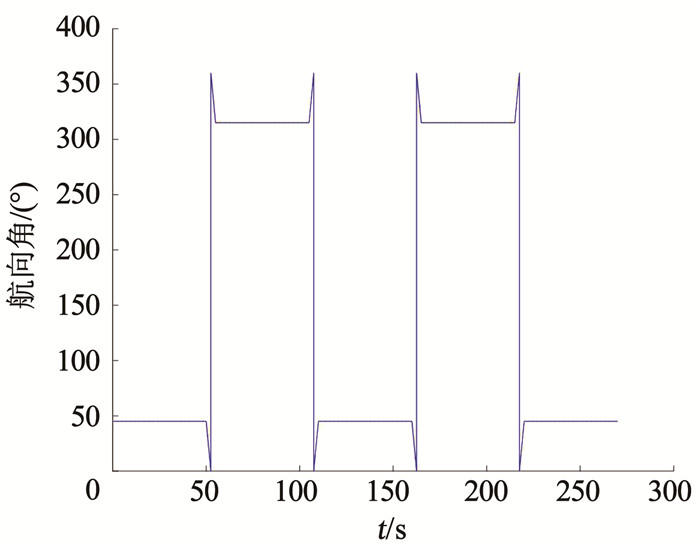
3) SINS系统的状态变化为:载体匀速运动50 s→左转弯90°,用时5 s→匀速运动50 s→右转弯90°,用时5 s→匀速运动50 s→左转弯90°,用时5 s→匀速运动50 s→右转弯90°,用时5 s→匀速运动50 s,总的运动时长为270 s.图 1为载体运动轨迹变化,图 2为载体的航向角变化.

|
图 1 仿真运动轨迹 Fig. 1 Simulation of motion trajectory |
|
图 2 航向角变化 Fig. 2 Variation of heading angle |
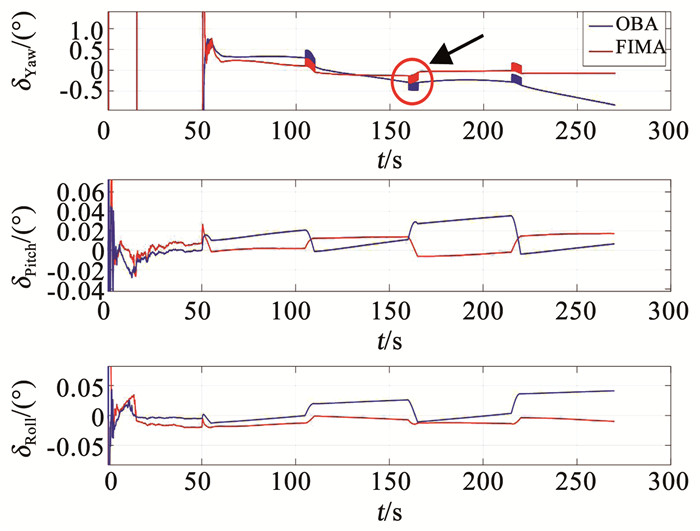
使用设计好的运动轨迹对所提出的快速动态对准算法(FIMA)以及现有的算法进行仿真对比.图 3为仿真过程中OBA算法与所提出的FIMA算法的姿态误差对比图,由图 2中效果可以看出,使用所提出的FIMA算法航向角误差δYaw在80 s可以收敛到0.2°,并且航向角误差能够始终保持在0.2°以内,而OBA算法虽然也可以快速收敛,但是其航向角误差会随着对准时间的延长而变大.图中两算法的俯仰角误差δPitch和横滚角误差δRoll均能快速收敛,且收敛的精度相差不大,但是FIMA算法的水平姿态误差更稳定.图中黑色箭头所指部分红色和蓝色凸起是由于参考姿态与算法解算姿态频率不一致引起的.
|
图 3 与OBA算法的姿态误差对比图 Fig. 3 Comparison of attitude error between FIMA algorithm and OBA algorithm |
图 4为FIMA算法与文献[1]中的EKF算法的姿态误差对比图,因为FIMA算法针对的是任意初始姿态,所以为了对比算法的效果,在仿真时EKF算法的姿态初始误差设置为航向角误差50°、俯仰角误差15°和横滚角误差15°的大失准角误差.由图中效果可以看出,与非线性EKF动态对准算法相比,当姿态初始值存在大失准角时,FIMA算法的航向角对准速度更快,水平姿态的对准效果更稳定.

|
图 4 与EKF算法的姿态误差对比图 Fig. 4 Comparison of attitude error between FIMA algorithm and EKF algorithm |
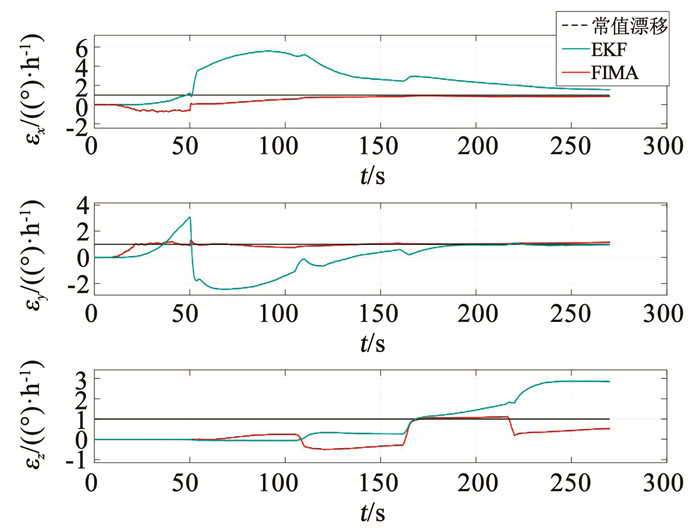
图 5是FIMA算法与EKF算法关于陀螺仪零偏估计的对比图,EKF算法的仿真条件与姿态误差对比的仿真条件相同.图 5中,黑色虚线是仿真轨迹中加入的陀螺仪常值漂移,大小为1 °/h,图中的零偏估计效果显示,FIMA算法对x轴和y轴的陀螺仪零偏估计精度高于EKF算法,而两种算法对z轴陀螺仪零偏的估计都不太准确,这一现象与仿真轨迹运动方式的设计过于单一有关.图 5的仿真效果说明,FIMA算法可以实现对陀螺仪零偏的估计.
|
图 5 与EKF算法的陀螺仪零偏估计对比 Fig. 5 Comparison of gyro bias estimation between FIMA algorithm and EKF algorithm |
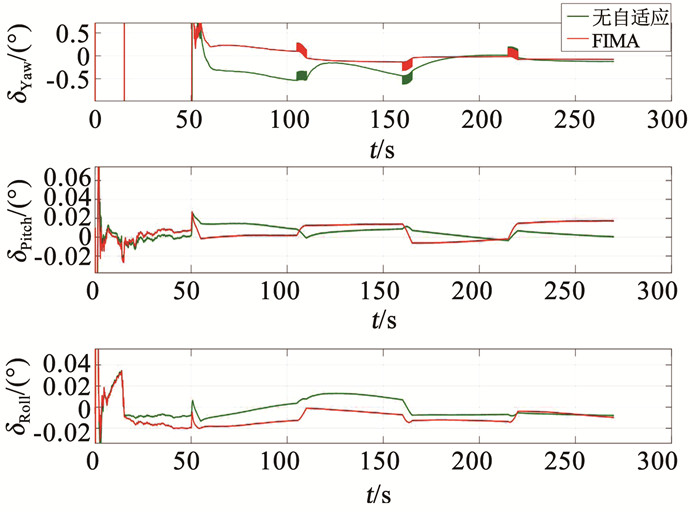
在本文的算法中,由于量测方程均有积分项构成,所以量测噪声难以确定,因此本文中FIMA算法引入自适应滤波,对量测噪声进行实时估计.图 6为FIMA算法在加入自适应算法之前与正常的FIMA算法的仿真对比.对比结果表明,加入自适应的FIMA算法姿态精度更高,估计结果也更稳定.
|
图 6 与非自适应FIMA算法的姿态误差对比 Fig. 6 Comparison of attitude error between FIMA algorithm and adaptive FIMA algorithm |
本文中算法的计算机仿真说明了算法的有效性,为了进一步验证算法的可行性,本文使用实际的实验数据进行算法验证.图 7为本次跑车实验所用设备.图中,序号1是UPS电源,为整套实验设备供电;序号2是稳压直流电源,为SINS系统供电;序号3是MEMS-IMU,其型号为ADIS16488;序号4为自制的高精度光纤惯导系统,可提供高精度的姿态参考;序号5为GPS天线,GPS接收机使用的是Trimble公司的BD982.实验中采集MEMS-IMU的陀螺仪和加速度计的数据进行算法验证,其中陀螺仪的偏置稳定度为5.1 °/h,加速度计的偏置稳定度为70 ug.

|
图 7 跑车实验设备 Fig. 7 Experimental equipment of driving test |
本次跑车实验在哈尔滨工程大学校内进行,汽车的运动轨迹如图 8中红线所示.汽车在180 s之前静止不动,180 s之后开始运动,运动过程中的姿态变化如图 9所示.

|
图 8 汽车运动轨迹 Fig. 8 Motion trajectory of the car |

|
图 9 SINS系统姿态变化 Fig. 9 Variation of SINS attitude |
为了验证算法对陀螺仪误差引起的姿态误差的补偿效果,本文先对文献[3]中的OBA算法和本文中的FIMA算法进行跑车实验比较,两种算法均是在MATLAB软件中实现的.在FIMA算法中,状态变量和相应的误差方差矩阵初始值分别设置为X0= 0 6×1和P0=diag([(0.1)l1×3(10°/h)l1×3])2,其中1 1×3为元素全为1的一行三列矢量矩阵,算法中的系统噪声和量测噪声根据所用传感器分别设置为Qk=Ts× diag([(5.1°/h)l1×3 (0)l1×3])2×2和R0=diag([(10×π/180)l1×3])2,Ts为IMU的采样频率,因为算法中用的是双子样进行的解算,所以离散化得到的Qk需要乘2,量测噪声Rk只需要对初始值R0进行设置,之后则根据自适应算法进行实时估计.
图 10是本次跑车实验中FIMA算法与OBA算法解算的姿态误差的对比,汽车是在180 s之后开始运动,两种算法均是在193 s即汽车运动13 s后开始运行.由图中姿态误差可以看出,对于低精度的SINS系统,OBA算法虽然能够快速的确定出姿态角,但是姿态角并没有随着时间的延长而趋于稳定,且航向角误差会越来越大;本文中的FIMA则克服了OBA算法的这一缺点,能够保证算法在低精度的SINS系统中依然能够稳定的收敛.

|
图 10 与OBA算法实测姿态误差对比 Fig. 10 Comparison of actual attitude error between FIMA algorithm and OBA algorithm |
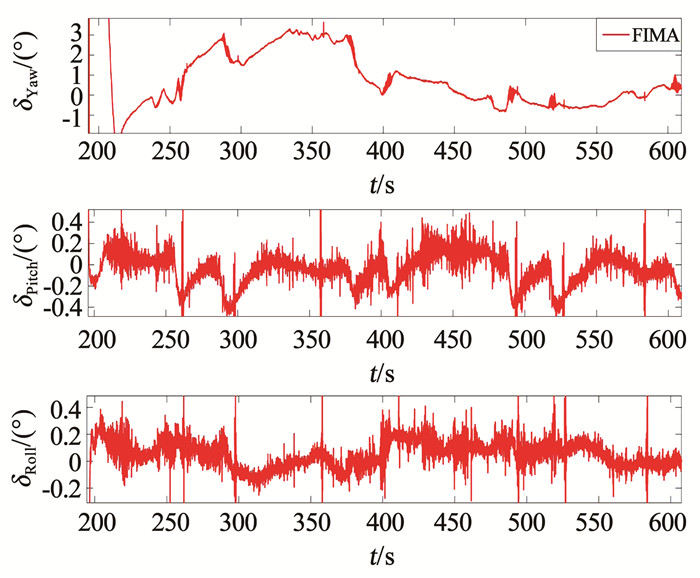
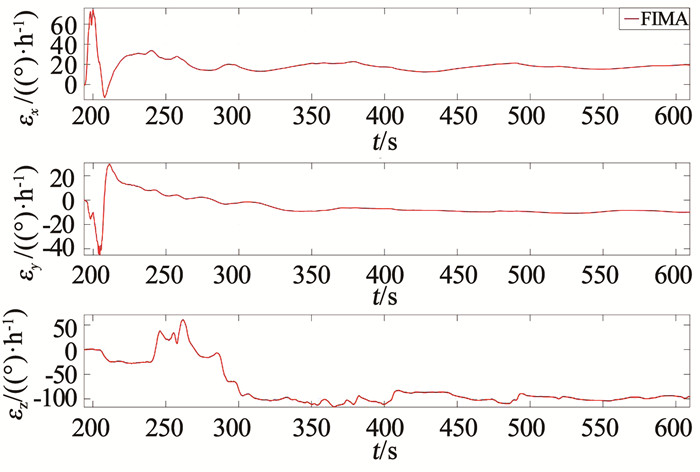
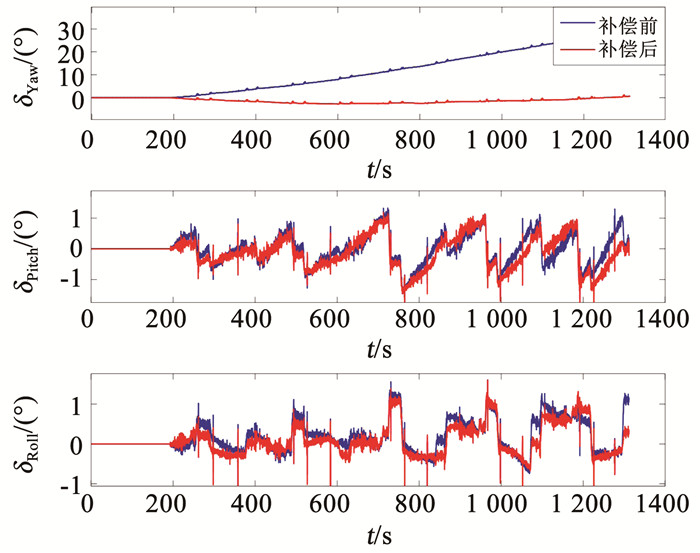
图 11为FIMA算法姿态误差放大图,由图中航向角误差可以知道,在没有任何初始姿态信息的条件下,算法用15 s的时间便可将航向角误差收敛到3°以内,俯仰角误差和横滚角误差收敛到0.4°以内.在FIMA对准算法运行190 s以后,航向角误差可收敛到1°以内.图 12为FIMA算法对陀螺仪零偏的估计结果,估计结果表明,FIMA算法能够实现对陀螺仪零偏的估计.为证明零偏估计的有效性,将FIMA算法估计的陀螺仪零偏写入纯惯导算法中进行补偿,补偿后的效果如图 13中所示.经过陀螺仪误差补偿后的纯惯导算法的航向角误差明显好于补偿前的效果,陀螺仪误差的补偿对水平姿态误差影响不大,由此可以看出,FIMA算法对陀螺仪零偏的估计是有效的.
|
图 11 FIMA算法姿态误差 Fig. 11 Attitude error of FIMA algorithm |
|
图 12 FIMA算法陀螺仪零偏估计 Fig. 12 Gyro bias estimation of FIMA algorithm |
|
图 13 纯惯导算法姿态误差对比 Fig. 13 Comparison of attitude error of inertial navigation algorithm before and after compensation |
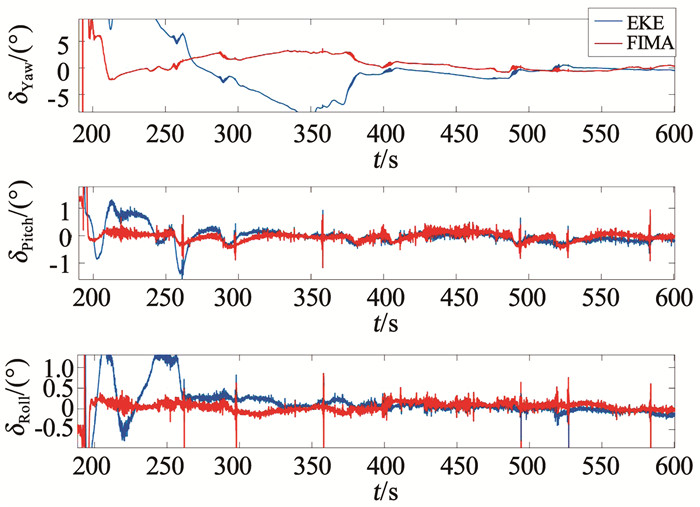
为了体现本文中算法在任意失准角条件下快速对准的优越性,本文对FIMA算法与文献[1]中EKF对准算法用跑车实测数据进行比较.在EKF对准算法运行前,设置航向角误差70°、俯仰角误差和横滚角误差20°的大失准角误差.两种算法的姿态误差对比如图 14所示,由于大失准角的原因,EKF算法的航向误差收敛速度明显比FIMA算法慢,EKF算法的水平姿态误差在对准的前期也不如FIMA算法的稳定.
|
图 14 与EKF算法实测姿态误差对比 Fig. 14 Comparison of actual attitude error between FIMA algorithm and EKF algorithm |
在文献[14-15]中,研究人员同样对OBA算法做出了改进,在文章中,使用姿态四元数作为系统的状态变量,即在进行滤波时直接对系统的载体系姿态变化进行估计.而在滤波的初始值的设置中,文章中将初始姿态矩阵Cbn(0)设置为单位矩阵,但实际的Cbn(0)是未知的姿态矩阵,这样在进行滤波时,会存在大的初始姿态误差.本文中的算法是对系统的误差进行的建模,选取的状态变量是失准角φ,在对准的初始时刻,b系和
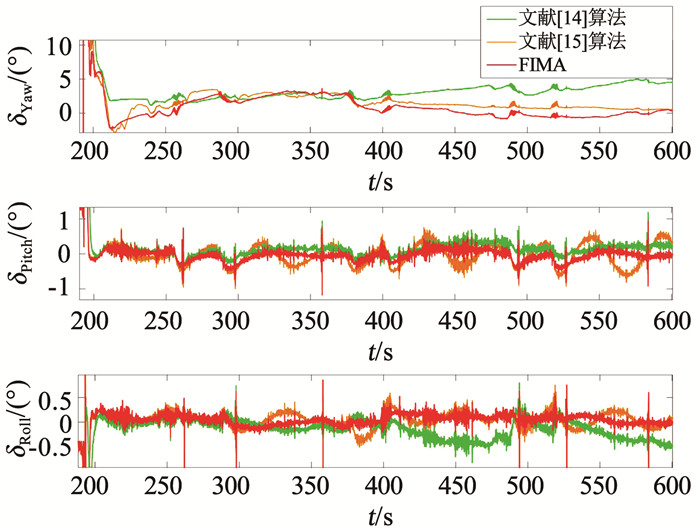
|
图 15 与其他动基座对准算法的实测姿态误差对比 Fig. 15 Comparison of actual attitude error between FIMA algorithm and other algorithms |

|
图 16 陀螺仪零偏估计对比 Fig. 16 Comparison of gyro bias estimation between FIMA algorithm and other algorithms |
1) 本文在推导了载体系与计算载体系之间失准角更新方程的基础上对SINS系统重新建立非线性系统方程,使用自适应UKF滤波算法对失准角和陀螺仪误差进行估计,同时使用OBA算法中的最小二乘原理对初始姿态矩阵进行估计,从而实现快速动基座初始对准.
2) 计算机仿真和跑车实验表明:对于低精度SINS系统,FIMA算法可在15 s左右将航向角误差收敛至3°以内,俯仰角和横滚角误差收敛至0.4°以内;当算法运行至3 min后,航向角误差可收敛至1°.
3) FIMA对准算法可以在无任何初始姿态信息的条件下实现快速动基座对准,并且能够有效的估计出陀螺仪误差,可适用于低精度的SINS系统,对准精度优于现有的GPS辅助的SINS系统OBA对准算法,对准速度比非线性EKF动态对准算法更快.
| [1] |
FANG Jiancheng, YANG Sheng. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1378. DOI:10.1109/tim.2010.2084710 |
| [2] |
KANG Taizhong, FANG Jiancheng, WANG Wei. Quaternion-optimization-based in-flight alignment approach for airborne POS[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(11): 2916. DOI:10.1109/TIM.2012.2202989 |
| [3] |
WU Yuanxin, PAN Xianfei. Velocity/position integration formula Part I: Application to in-flight coarse alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1006. DOI:10.1109/TAES.2013.6494395 |
| [4] |
WU Yuanxin, WANG Jinling, HU Dewen. A new technique for INS/GNSS attitude and parameter estimation using online optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2642. DOI:10.1109/tsp.2014.2312317 |
| [5] |
韩松来. GPS和捷联惯导组合导航新方法及系统误差补偿方案研究[D].长沙: 国防科学技术大学, 2010 HAN Songlai. Novel GPS/SINSintegration architecture and systematic error compensation methods[D]. Changsha: National University of Defense Technology, 2010 |
| [6] |
王志伟, 秦俊奇, 杨功流, 等. 大方位失准角条件下的GPS/INS动基座初始对准[J]. 压电与声光, 2018, 40(3): 428. WANG Zhiwei, QIN Junqi, YANG Gongliu, et al. Initialalignment of GPS/INS moving base with large misalignment angle[J]. Piezoelectrics & Acoustooptics, 2018, 40(3): 428. DOI:10.11977/j.issn.1004-2474.2018.03.028 |
| [7] |
严恭敏, 严卫生, 徐德民. 简化UKF滤波在SINS大失准角初始对准中的应用[J]. 中国惯性技术学报, 2008, 16(3): 253. YAN Gongmin, YAN Weisheng, XU Demin. Application of simplified UKF in SINS initial alignment for large misalignment angles[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 253. |
| [8] |
夏家和, 秦永元, 赵长山. 适用于低精度惯导的非线性对准方法研究[J]. 仪器仪表学报, 2009, 30(8): 1618. XIA Jiahe, QIN Yongyuan, ZHAO Changshan. Study on nonlinear alignment method for low precision INS[J]. Chinese Journal of Scientific Instrument, 2009, 30(8): 1618. DOI:10.19650/j.cnki.cjsi.2009.08.009 |
| [9] |
HUANG Yulong, ZHANG Yonggang, WANG Xiaodong. Kalman-filtering-based in-motion coarse alignment for odometer-aided SINS[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(12): 3364. DOI:10.1109/TIM.2017.2737840 |
| [10] |
CHANG Lubin, HU Baiqing, LI Yang. Backtracking integration for fast attitude determination-based initial alignment[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 795. DOI:10.1109/TIM.2014.2359516 |
| [11] |
赵宾, 高春雷, 陈维娜. 基于运动学约束模型辅助的地面动基座对准研究[J]. 航天控制, 2018, 36(4): 23. ZHAO Bin, GAO Chunlei, CHEN Weina. Research ofalignment on ground moving base based on kinematic constraint model[J]. Aerospace Control, 2018, 36(4): 23. DOI:10.16804/j.cnki.issn1006-3242.2018.04.005 |
| [12] |
赵政, 刘冰. 一种提高捷联惯导系统动基座初始对准精度的方法[J]. 导航与控制, 2018, 17(5): 69. ZHAO Zheng, LIU Bing. Akind of method on moving base initial alignment for SINS[J]. Navigation and Control, 2018, 17(5): 69. DOI:10.3969/j.issn.1674-5558.2018.05.011 |
| [13] |
黄小平, 王岩. 卡尔曼滤波原理及应用[M]. 北京: 电子工业出版社, 2015. HUANG Xiaoping, WANG Yan. Theprinciple and application of Kalman filter[M]. Beijing: Publishing House of Electronics Industry, 2015. |
| [14] |
CHANG Lubin, LI Jingshu, CHEN Shengyong. Initial alignment by attitude estimation for strapdown inertial navigation systems[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 784. DOI:10.1109/tim.2014.2355652 |
| [15] |
HUANG Yulong, ZHANG Yonggang, CHANG Lubin. A new fast in-motion coarse alignment method for GPS-aided low-cost SINS[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(3): 1303. DOI:10.1109/TMECH.2018.2835486 |
 2020, Vol. 52
2020, Vol. 52


