星敏感器是目前公认的精度最高的姿态敏感器之一[1].在航空、航天领域,无论是近地卫星或者深空探测,还是弹道导弹或者小卫星上,星敏感器都得到了广泛的应用.星敏感器通常捷联安装于上述的载体上,若载体受到外界环境的冲击或者进行大姿态角机动时,星敏感器拍摄的星图会出现运动模糊现象,导致星图信噪比降低,可能严重影响星点提取成功率和精度,进而降低星图识别成功率[2-3].
目前对运动模糊星图处理的主流思路是先复原星图再进行后续的星点提取、识别等过程.根据上述思路,运动模糊星图处理的核心在于星图复原,故而有不少学者开展了星图复原的研究.目前星图复原方法主要是非盲图像复原方法,非盲图像复原方法应用最为广泛的是逆滤波方法[4-5]、维纳滤波方法[6-7]和Lucy-Richardson(L-R)方法[8-9].逆滤波方法是应用最早的图像复原方法,但该方法缺点很明显,即对图像噪声非常敏感;维纳滤波方法可以实现最小均方复原效果,但该方法需已知图像噪声特性的峰值信噪比较高时才能获得较好的复原效果;L-R方法是一种统计学方法,如果图像的先验概率模型和条件概率模型与实际不符时,图像复原效果会受到极大影响.另外,非盲图像复原方法受图像先验信息的准确性影响很大,故而对图像的模糊核函数估计也是研究的重点,Radon变换方法[10-11]、基于星像运动轨迹的估计方法[12-14]是当前模糊核函数估计的常用方法.传统的Radon变换方法的估计精度受星图噪声影响很大,Jiang等[15]提出了改进的Radon变换方法,该方法基于模糊星图噪声特性并且结合了Z函数和双线性插值方法,取得了较好的估计效果;吴小娟等[12]基于绕星敏感器光轴或者非光轴转动时的星像运动轨迹模型进而得到相应条件下星图模糊核函数的解析表达式;廖育富等[14]根据星像运动轨迹模型提出了一种操作简单利于工程化实现的模糊核函数估计方法,但估计精度不高且容易受到噪声影响.上述都是基于星图自身信息估计模糊核函数,但星图本身的先验信息有限,所以近几年有学者提出基于惯性导航系统(inertial navigation system,INS)辅助对模糊核函数进行估计[16-18],取得了较好的估计效果.
综上所述,对于运动模糊星图的研究聚焦于模糊核函数的估计和复原方法,期望获得质量较好的复原星图以保证星点提取精度和星图识别成功率,但星图复原过程会占据星敏感器一定的计算资源,影响星敏感器的数据更新率.因此,本文提出了一种基于INS和星敏感器的先验信息直接提取运动模糊星图上星点的方法.该方法首先利用INS和星敏感器的姿态先验信息确定局部区域生长的“种子”点,从而得到运动模糊星图上的星像区域;然后基于先验信息建立了星点提取误差修正模型,补偿利用质心法直接提取运动模糊星图星点的坐标误差.该方法可以跳过星图复原操作直接对运动模糊星图进行星点提取,这对于保证高动态环境下星敏感器的数据更新率具有重要意义.
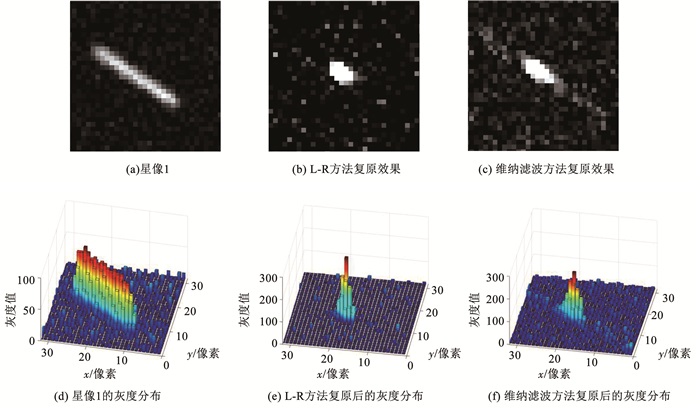
1 方法分析高动态条件下星敏感器成像受到影响,星图会出现模糊现象,图 1是模拟的一幅运动模糊星图,模拟星图的灰阶为8位,灰度范围为0~255,添加的高斯白噪声均值为0,均方差为6(灰度值),载体的角运动速度设置为ωx=-2°/s,ωy=-3°/s,ωz=2°/s.分别利用L-R方法[8-9]和维纳滤波方法[6-7]进行复原处理后,得到局部放大的复原星图以及相应的灰度分布如图 2所示.

|
图 1 运动模糊星图 Fig. 1 Motion blurred star image |
|
图 2 不同方法的星图复原结果局部放大和灰度分布图 Fig. 2 Local amplification and grayscale distribution of star image restored by different methods |
从上述星图复原的结果来看,利用维纳滤波方法和L-R方法复原星图后,并不能将星点恢复到静态条件下的高斯弥散斑,但星点“拖尾”轨迹相对缩短,利用质心法对复原星图上星点提取的误差小于直接对原始星图上星点提取的误差.如果能够估计出直接利用质心法提取模糊星图上星点的误差,然后对星点坐标进行补偿修正,这就能跳过星图复原这个过程,从而大大节省了时间,保证星敏感器数据更新率,同时仍能获得较好的星点提取精度.基于上述思想,本文提出了基于INS辅助的直接对运动模糊星图星点提取的方法.
星敏感器常与INS组合使用,虽然INS存在姿态输出误差随时间累积的缺点,但其短时间的姿态输出精度很高,文献[16-18]中将INS的姿态输出引入到模糊核函数估计中取得了较好的效果,本文进一步利用INS提供的姿态先验信息,提出一种直接对运动模糊星图进行星点提取的方法,具体思路如下:
1) 基于INS的短时姿态输出和星敏感器在上一帧星图的姿态先验信息,预测出恒星在当前帧星图的粗略星点坐标,将其作为种子点进行局部区域生长,从而获得星像区域;
2) 利用质心法[3]直接在星像区域计算星点质心坐标;
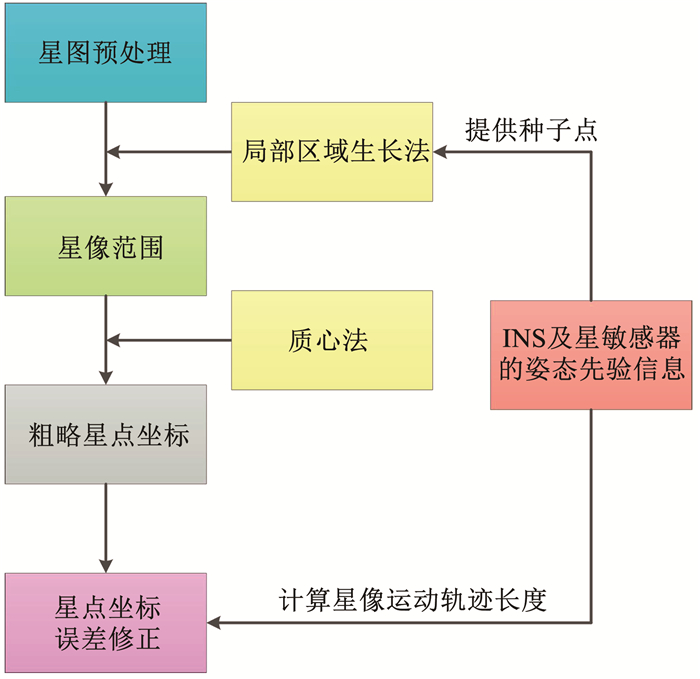
3) 根据INS得到在曝光时间内星敏感器的转动角速度,计算星图上星像的运动轨迹长度,根据星像运动轨迹与直接质心法的星点提取误差之间的关系,修正星点坐标.本文方法的实施步骤如图 3所示.
|
图 3 本文方法示意 Fig. 3 Schematic diagram of the proposed method |
局部区域生长法[19]的三要素是种子点、生长准则和终止条件,而种子点是其中最为关键的一环.利用局部区域生长可以快速而准确获取运动模糊星图上各个星像的范围,但必须首先解决如何获取满足条件的种子点的问题.单帧星图的先验信息有限,本文基于INS从t0→t0+Δt时刻的姿态输出并结合t0时刻星敏感器输出的姿态信息,得到t0+Δt时刻的粗略姿态,解得t0+Δt时刻星敏感器光轴指向,进而预测出t0+Δt时刻恒星在成像平面上的粗略坐标,将其作为种子点,利用局部区域生长法获得运动模糊星图上星像范围.为质心法提取星点坐标奠定基础,具体思路如下:
假设星敏感器根据当前这一帧星图获得t0时刻的姿态四元数为q,利用INS的姿态输出得到从t0→t0+Δt的姿态机动四元数为q′,那么根据四元数的乘法顺序和规则,t0+Δt时刻星敏感器的姿态四元数可以由下式得到:
| $ \mathit{\boldsymbol{q''}} = \mathit{\boldsymbol{q'q}}. $ | (1) |
式中:
文献[20]中关于姿态四元数与星敏感器光轴指向(A, D)和星敏感器的滚动角θ之间的关系式:
| $ \left\{ {\begin{array}{*{20}{l}} {A = \arctan \left( {\frac{{2\left( {q_2^{\prime \prime }q_3^{\prime \prime } - q_0^{\prime \prime }q_1^{\prime \prime }} \right)}}{{2\left( {q_1^{\prime \prime }q_3^{\prime \prime } - q_0^{\prime \prime }q_2^{\prime \prime }} \right)}}} \right), }\\ {D = \arcsin \left( {q_0^{\prime \prime }q_0^{\prime \prime } - q_1^{\prime \prime }q_1^{\prime \prime } - q_2^{\prime \prime }q_2^{\prime \prime } + q_3^{\prime \prime }q_3^{\prime \prime }} \right), } \end{array}} \right. $ | (2) |
| $ \theta = \arctan \left( {\frac{{ - 2\left( {q_1^{\prime \prime }q_2^{\prime \prime } - q_0^{\prime \prime }q_3^{\prime \prime }} \right)}}{{q_0^{\prime \prime }q_0^{\prime \prime } - q_1^{\prime \prime }q_1^{\prime \prime } + q_2^{\prime \prime }q_2^{\prime \prime } - q_3^{\prime \prime }q_3^{\prime \prime }}}} \right). $ | (3) |
式中:A∈[0, 2π),D∈[-π/2, π/2],θ∈[0, 2π).
得到星敏感器光轴指向(A, D)之后,预测星敏感器在t0+Δt时刻星图上星像坐标就是建立恒星在星图上质心坐标与在天球坐标系中的坐标(α, δ)之间的数学模型,利用t0时刻的星敏感器的先验信息可以得到(α, δ).根据星敏感器成像原理以及星敏感器坐标系与天球坐标系之间的坐标变换关系,在星敏感器光轴指向(A, D)、恒星在天球坐标系中的坐标(α, δ)和星敏感器视场确定的情况下,理论上出现在星图上的恒星位置也随之确定.得到此时恒星的星像坐标为
| $ \left\{ {\begin{array}{*{20}{l}} {x = f\frac{{\cos \delta \sin (\alpha - A)}}{{\sin \delta \sin D + \cos \delta \cos D\cos (\alpha - A)}}, }\\ {y = f\frac{{\sin \delta \cos D - \cos \delta \sin D\cos (\alpha - A)}}{{\sin \delta \sin D + \cos \delta \cos D\cos (\alpha - A)}}.} \end{array}} \right. $ | (4) |
如果考虑到在实际中星敏感器的滚动角θ一般不为0,那么则有
| $ \left\{ {\begin{array}{*{20}{l}} {{x^\prime } = x\cos \theta - y\sin \theta , }\\ {{y^\prime } = x\sin \theta + y\cos \theta .} \end{array}} \right. $ | (5) |
根据式(1)~(5),可以预测得到t0+Δt时刻星图上星像坐标,将这些星像坐标记为{Si},其中Si=(xi, yi),i=1, …, N,N为星图上星像个数.以{Si}作为局部区域生长的种子点,从而获得模糊星图上各个星像的实际范围关于区域生长法的原理可具体详见文献[19],在此不再赘述.
1.2 星点提取误差修正模型质心法具有操作简单、鲁棒性好的优点,是目前常用的星点提取方法.星像的能量分布对质心法的精度有很大影响,根据文献[3],星像能量分布服从二维高斯分布时,质心法精度较高.在高动态环境下,星像不再是静态时的高斯弥散斑,而是形成了一条“拖尾”.在曝光时间内Te内,星像区域的灰度也不再服从二维高斯分布,因此直接用质心法提取星点的误差会大大增加.为了对该误差进行修正,根据文献[21]的研究,首先应对高动态条件下的运动模糊星图的灰度分布进行分析建模,在此基础上分析推导直接用质心法提取星点的误差.
将星敏感器的曝光时间Te等分为N个微小的区间[ti, ti+1],i=0, 1, …, N-1,Δt=ti+1-ti=Te/N,t0=0,tN=Te,由于[ti, ti+1]非常小,因而可近似认为在[ti, ti+1]内,恒星在成像平面上所形成星像的灰度仍服从二维高斯分布,设在[ti, ti+1]的二维高斯分布的中心点坐标为(xi, yi),在[ti, ti+1]内,恒星在成像平面上所形成星像的灰度分布如下:
| $ {G_i}(x, y) = \frac{{{G_i}}}{{2{\rm{ \mathit{ π} }}{\sigma ^2}}}\exp \left[ {\frac{{{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}}{{2{\sigma ^2}}}} \right]. $ |
式中:Gi=G0/N,G0是与曝光时间Te内星像总能量相关的常值;Gi(x, y)为[ti, ti+1]内成像平面上的坐标(x, y)处的灰度值; σ为高斯弥散斑半径,代表了弥散程度,根据二维高斯分布的特点以及3σ准则,星像99%以上的能量集中于距离星点的3σ范围以内.
假设各个高斯分布的弥散斑半径相等,将各个微小曝光时间内形成的星像灰度分布函数进行叠加,得到在曝光时间Te内恒星在成像平面上星像的灰度分布函数如下:
| $ G(x, y) = \sum\limits_{i = 0}^{N - 1} {{G_i}} (x, y). $ |
取质心法的计算窗口为一矩形区域,这一区域的左上角像元坐标设为(1, 1),右下角的像元坐标为(m, n).合理选择质心法的计算窗口大小,使其能够包含所有的(xi-3σ,xi+3σ) & (yi-3σ,yi+3σ)区域,便可保证用质心法计算(xi, yi)的精度,在质心法的计算窗口区域上,由于曝光时间Te内形成星像的总灰度和G0total以及[ti, ti+1]内形成的星像灰度和Gitotal分别如下:
| $ \begin{array}{*{20}{c}} {G_0^{{\rm{total }}} \approx \sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n G } (x, y), }\\ {G_i^{{\rm{total }}} = \frac{{G_0^{{\rm{total }}}}}{N} \approx \sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {{G_i}} } (x, y).} \end{array} $ |
利用质心法可以得到[ti, ti+1]内对应的中心点(xi, yi)的计算公式如下:
| $ {x_i} \approx \frac{{\sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {\frac{{{G_0}x}}{{2{\rm{ \mathit{ π} }}{\sigma ^2}N}}} } \exp \left[ {\frac{{{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}}{{2{\sigma ^2}}}} \right]}}{{G_i^{{\rm{total }}}}}, $ | (6) |
| $ {y_i} \approx \frac{{\sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {\frac{{{G_0}y}}{{2{\rm{ \mathit{ π} }}{\sigma ^2}N}}} } \exp \left[ {\frac{{{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}}{{2{\sigma ^2}}}} \right]}}{{G_i^{{\rm{total }}}}}. $ | (7) |
利用质心法计算模糊星图上星点坐标(x′0, y′0)如下:
| $ x_0^\prime \approx \frac{{\sum\limits_{i = 0}^{N - 1} {\sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {\frac{{{G_0}x}}{{2{\rm{ \mathit{ π} }}{\sigma ^2}N}}} } } \exp \left[ {\frac{{{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}}{{2{\sigma ^2}}}} \right]}}{{G_0^{{\rm{total }}}}}, $ | (8) |
| $ y_0^\prime \approx \frac{{\sum\limits_{i = 0}^{N - 1} {\sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {\frac{{{G_0}y}}{{2{\rm{ \mathit{ π} }}{\sigma ^2}N}}} } } \exp \left[ {\frac{{{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}}{{2{\sigma ^2}}}} \right]}}{{G_0^{{\rm{total }}}}}. $ | (9) |
将式(6)、(7)分别代入式(8)、(9),则有
| $ \left\{ {\begin{array}{*{20}{l}} {x_0^\prime = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {{x_i}} , }\\ {y_0^\prime = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {{y_i}} .} \end{array}} \right. $ |
下面分析模糊星图上的(x′0, y′0)与静态星图上的(x0, y0)之间的误差与星像运动轨迹长度之间的关系.
根据文献[14, 21-22]研究可知绕光轴的角速度对星图的影响很小,因而星图上星像运动轨迹近似为匀速直线运动上的一段,假设星像在成像平面的OX及OY轴上的运动速度分别为vx≈-fωy/dCCD,vy≈fωx/dCCD[12],ωx、ωy为星敏感器转动角速度大小,逆时针转动为正.则在曝光时间Te内,星像运动轨迹在在成像平面的OX及OY轴上的分量为Lx=vxTe,Ly=vyTe,且有
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{i + 1}} - {x_i} = {v_x}\Delta t, }\\ {{y_{i + 1}} - {y_i} = {v_y}\Delta t.} \end{array}} \right. $ |
式中i=0, 1, …, N-1,Δt=ti+1-ti.
同理,可得:
| $ \left\{ {\begin{array}{*{20}{l}} {x_0^\prime = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\left( {{x_0} + i{v_x}\Delta t} \right)} = {x_0} + \frac{{N - 1}}{2}{v_x}\Delta t, }\\ {y_0^\prime = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\left( {{y_0} + i{v_y}\Delta t} \right)} = {y_0} + \frac{{N - 1}}{2}{v_y}\Delta t.} \end{array}} \right. $ |
将(x′0, y′0)与(x0, y0)作差,得到星像运动引起的星点坐标误差为
| $ \left\{ {\begin{array}{*{20}{l}} {L_x^\prime = \frac{{N - 1}}{2}{v_x}\Delta t = \frac{1}{2}{L_x}, }\\ {L_y^\prime = \frac{{N - 1}}{2}{v_y}\Delta t = \frac{1}{2}{L_y}.} \end{array}} \right. $ | (10) |
可见,星图运动模糊引起的星点坐标误差等于星像运动轨迹长度的一半.利用INS可得到星敏感器转动的角速度,进而估算出星像运动轨迹长度,根据式(10)可对星点坐标进行误差补偿,从而获得较为准确的星点坐标.
2 方法评价对于运动模糊星图处理问题,本文提出一种基于INS辅助直接对运动模糊星图进行星点提取的方法.INS的辅助作用主要体现在以下两个方面:1)根据INS的姿态输出可以得到相邻两帧星图之间星敏感器的姿态角变化量,结合星敏感器在上一帧星图的姿态输出,可以预测出当前这帧星图上星点的粗略坐标;2)基于INS的角速度输出可估算曝光时间内的星像运动轨迹长度.
本文方法需要利用恒星在上一帧星图的质心坐标和INS系统的角速度输出等先验信息来预测恒星在当前帧星图中的坐标,作为局部区域生长所需的“种子”点.在实际环境中,先验信息也不可避免的存在误差,那么预测的星点坐标也会产生误差,但若“种子”点仍在实际星像区域范围内,那么局部区域生长就能准确的获得实际星像范围.由此可见,局部区域生长法对“种子”点的精度要求不高,这在一定程度上增强了本文方法对先验信息误差的容错能力;局部区域生长只需关心存在星像的局部星图,星图其他区域不需做进一步处理,这相当于对星图做了一次去噪处理;本文方法避免了扫描整幅星图,而且不需对运动模糊星图进行复原操作,相比于先复原星图再提取星点的方法,本文方法能够大大节省星点提取时间,故本文方法还具有快速性好、抗噪能力强的优点.
值得注意的是本文方法要求已知恒星的先验信息,也就是需要已知恒星在上一帧星图的星点坐标,对应的星敏感器工作模式是星跟踪模式.如果星敏感器处于星捕获模式下,也就是有新的恒星进入视场,而新进入视场内的恒星难以获得其在上一帧星图中的先验信息,那么这种情况下本文方法可能将不再适用.
3 仿真实验及分析 3.1 仿真条件设置采用变形星敏感器视场设置为9°×9°,焦距为65.76 mm,像元大小为20 um,面阵大小为512×512,曝光时间为100 ms;从SKY2000主星表筛选出星等于小于6的恒星,并剔除其中的双星与变星,剩余4 908颗组成本文的星表;星敏感器角速度设置为(-2°/s -3°/s 2°/s),角速度方向记顺时针转动为正;模拟星图的灰阶为8位,灰度范围为0~255,添加的高斯白噪声的均值为0,均方差为6(灰度值);仿真实验工具是MATLAB(R2015a版),仿真实验的电脑配置为2.5 GHz Core(TM)i7-6500U,8.0 GB RAM.
利用Monte-Carlo方法随机产生100组星敏感器在t0时刻的姿态四元数{qi}和100组t1时刻的光轴指向{(αi, δi)}i=1, …, 100,从t0→t1时刻的星敏感器姿态变化四元数{q′i}可利用INS系统的输出而得到,根据式(2)~(5)可得出t1时刻星敏感器成像平面上星像的粗略坐标,将此作为本文方法中局部区域生长法的种子点.
3.2 仿真实验分析 3.2.1 仿真实验1为了考察“种子”点的误差对于本文方法结果的影响大小,也即考察本文方法对先验信息误差的容错能力,设计了本仿真实验.
为了便于对一幅星图上的星点提取精度进行描述,以星图上提取到的星点坐标与相应的理想星点坐标距离的平均值作为衡量星点提取精度高低的指标,定义如下:
| $ {\rm{err}} = \frac{1}{{{N_0}}}\sum\limits_{i = 1}^{{N_0}} {\sqrt {{{\left( {{{\hat x}_i} - {x_i}} \right)}^2} + {{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }. $ |
式中:N0为星图上提取到的星点个数; (xi, yi)为第i个理想的星点坐标;
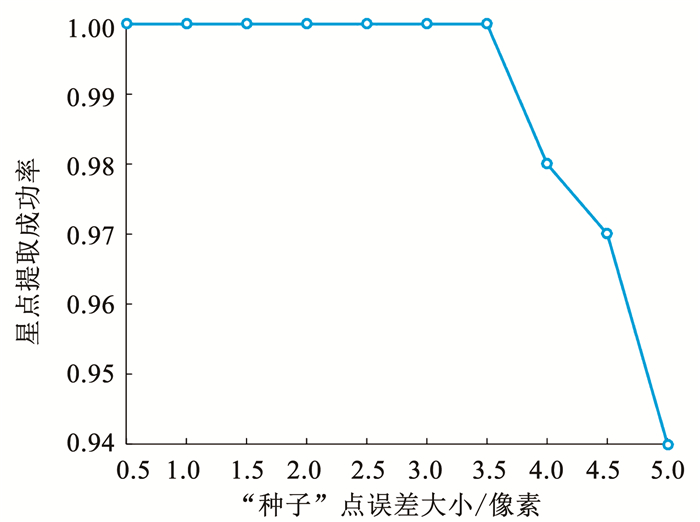
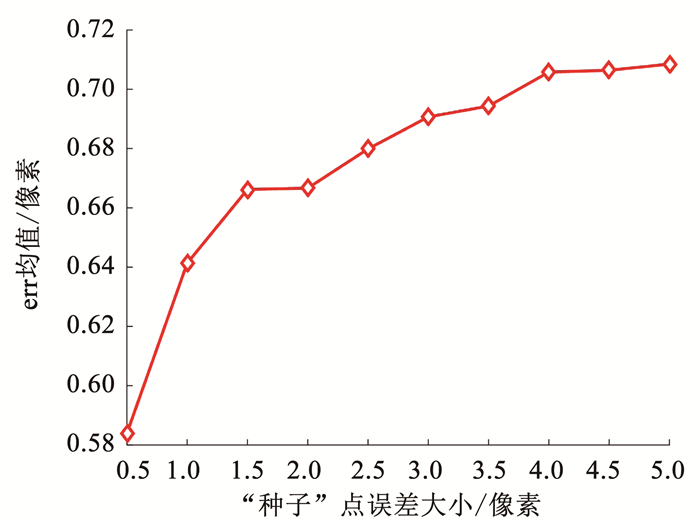
可以假设“种子”点的误差是服从均值为0的高斯白噪声,共设置10组不同大小的“种子”点的误差,分别为0.5, 1.0, …, 5.0像素.根据t1时刻的光轴指向{(αi, δi)}得到100幅模拟的运动模糊星图,其他仿真条件见仿真条件设置.得到在不同的“种子”点误差条件下,利用本文方法的星点提取误差仿真结果如图 4、5所示.图 4中的星点提取成功率定义为ratio=Nsuc/Ntotal,其中Ntotal为用于仿真实验的星图总数,Nsuc为星图上的星点被全部成功提取的星图数量.
|
图 4 不同“种子”点误差条件下的星点提取成功率 Fig. 4 Star spot extraction success rate under different noise conditions of seed points |
|
图 5 不同“种子”点误差条件下err的均值 Fig. 5 Mean value of errunder different noise conditions of seed points |
从本仿真实验条件下,“种子”点误差不超过3.5像素时,本文方法的星点提取成功率为100%,“种子”点误差大于3.5像素时,星点提取成功率略有下降;仿真结果如图 5所示,星点提取误差err的均值随着“种子”点误差的增大而略有增加,但增幅较小,上述仿真实验结果说明本文方法对“种子”点误差(即先验信息误差带来的影响)具有较好的容错能力.
3.2.2 仿真实验2根据t1时刻的光轴指向{(αi, δi)}得到100幅模拟的运动模糊星图,其他仿真条件见仿真条件设置.利用本文方法直接对模糊星图上星像质心进行提取和补偿;作为比较,利用L-R方法和维纳滤波方法对模糊星图进行复原,然后对复原星图利用块扫描法[23]+质心法进行星点提取,分别简记为Method-1和Method-2,L-R方法的迭代次数设置为10.得到仿真结果如图 6、7所示.
|
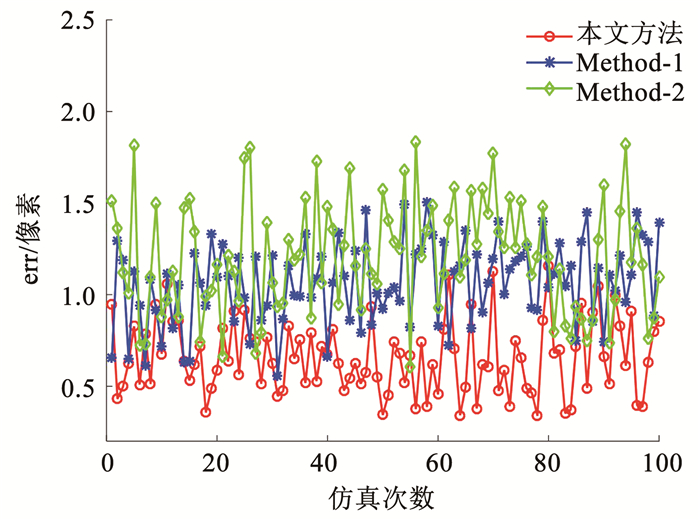
图 6 3种方法err值的对比 Fig. 6 Comparison of err values of three methods |
|
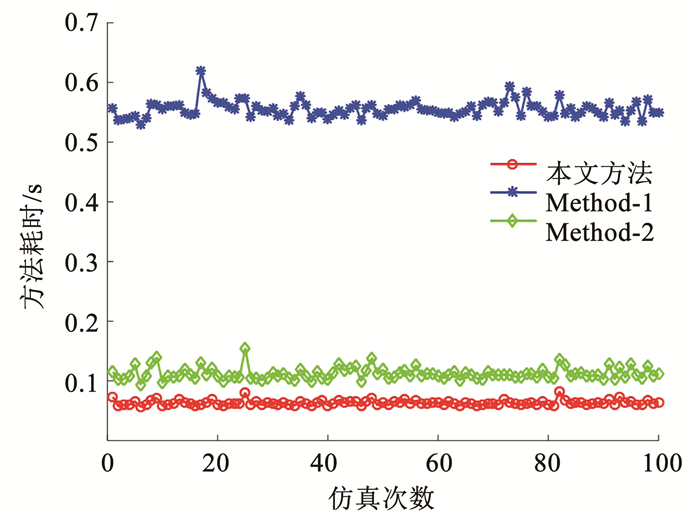
图 7 3种方法耗时的对比 Fig. 7 Comparison of time spent by three methods |
利用本文方法对100幅运动模糊星图进行星点提取以及利用L-R方法以及维纳滤波方法先对运动模糊星图复原再进行星点提取,100幅星图的星点提取精度如图 6所示,本文方法、Method-1以及Method-2这3种方法err的平均值分别为0.658、1.063、1.205像素,可以看出本文方法的星点提取误差小于Method-1和Method-2;3种方法的耗时情况如图 7的所示,本文方法、Method-1和Method-2的平均耗时分别为0.063 2、0.555 3、0.112 0 s,可知本文方法的耗时小于Method-1和Method-2.从上述仿真实验结果可知,相比于L-R方法和维纳滤波方法,本文方法在快速性方面具有一定的优势,星点提取误差虽然比其他两种方法有所降低,但误差仍然较大.
3.2.3 仿真实验3为了更全面的分析星图噪声大小对星点提取的影响,研究本文方法的抗噪性能,设计如下仿真实验.在模拟星图上加入不同强度的高斯白噪声,共设置10组不同强度的高斯白噪声,高斯白噪声均值为0,均方差分别为1, 2, …, 10(灰度值,星图灰度值范围为0~255),其他仿真条件与仿真实验2相同.得到仿真结果如图 8~10所示.
|
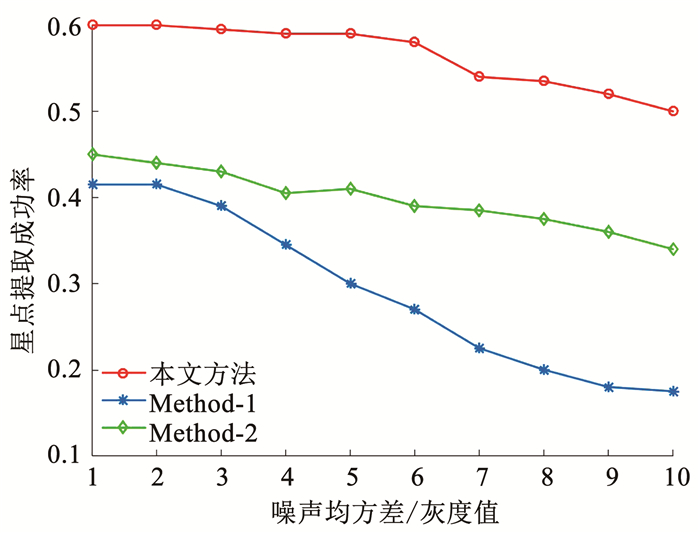
图 8 不同噪声条件下3种方法的星点提取成功率对比 Fig. 8 Comparison of star spot extraction success rates of three methods under different noise conditions |
|
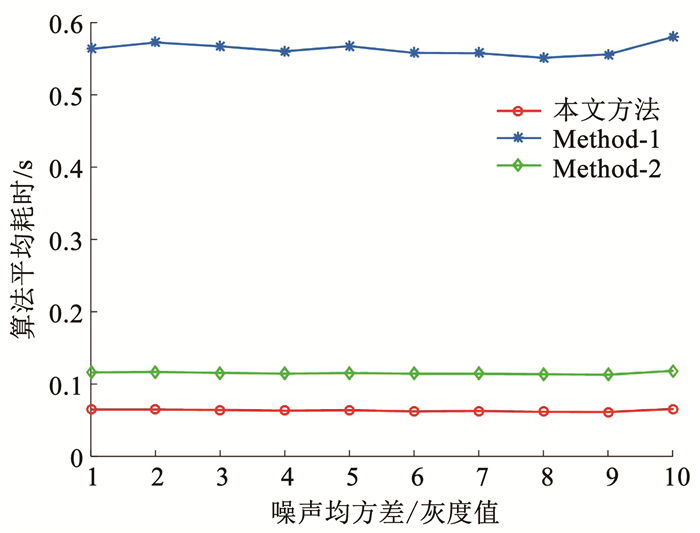
图 9 不同噪声条件下3种方法耗时的对比 Fig. 9 Comparison of time spent by three methods under different noise conditions |
|
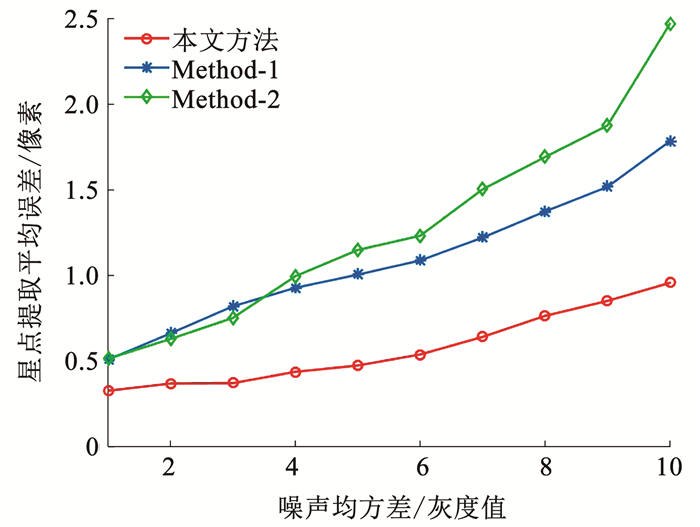
图 10 不同噪声条件下3种方法的星点提取误差对比 Fig. 10 Comparison of star spot extraction errors of three methods under different noise conditions |
根据仿真结果图 8可知,随着星图噪声增大,3种方法都受到了影响,Method-1的星点提取成功率下降幅度最大,Method-2次之,本文方法的星点提取成功率下降幅度最小,在仿真实验中,星点提取成功率最低为0.8,可见本文方法具有较好的抗噪性能.从仿真结果图 9可知,3种方法的平均耗时随着噪声的变化,波动较小,相比于Method-1和Method-2,本文方法的速度更快.为了考察在不同噪声条件下,当星图上的星点被成功提取时3种方法的星点提取精度.在上述仿真实验条件下,得到在不同噪声条件下3种方法的星点提取误差的仿真结果如图 10所示,图 10中的星点提取平均误差为每组噪声条件下err的均值.
从图 10的仿真结果可知,随着噪声的增大,3种方法的星点提取误差均有逐渐增大的趋势,但本文方法的星点误差远比其他两种方法要小,以噪声均方差等于10为例,本文方法的星点提取平均误差为0.957像素,Method-1的星点提取平均误差为1.784像素,Method-2的星点提取平均误差为2.470像素.
根据仿真实验2的结果,无论从星点提取成功率还是从星点提取平均误差来讨论,本文方法在不同噪声水平下的表现都优于Method-1和Method-2,这说明本文方法具有较好的抗噪性能.
4 结论1) 利用INS的输出和星敏感器自身已经获得的姿态先验信息预测恒星在当前帧星图上的粗略坐标,将其作为“种子”点,局部区域生长对“种子”点误差具有较好的容错能力,这在一定程度上减轻了先验信息误差对本文方法的影响.
2) 建立了利用质心法提取运动模糊星图上星点质心坐标的误差修正模型.本文方法不需要对运动模糊星图进行复原且不用对整幅星图进行扫描,这大大节省了运算时间,有利于提高星敏感器数据更新率.
3) 仿真实验表明,本文方法的快速性和抗噪能力均优于常用的L-R方法和维纳滤波方法,星点提取精度也得到了一定的提高.
| [1] |
李葆华, 王常虹, 张迎春. 适用于星敏感器的局部星像提取方法[J]. 光学精密工程, 2007, 15(9): 1427. LI Baohua, WANG Changhong, ZHANG Yingchun. Obtaining method for star locations in local region of star image for star sensor[J]. Optics and Precision Engineering, 2007, 15(9): 1427. DOI:10.3321/j.issn:1004-924x.2007.09.020 |
| [2] |
LIEBE C C, GROMOV K, MELLER D M. Toward a stellar gyroscope for spacecraft attitude determination[J]. Journal of Guidance, Control and Dynamics, 2004, 27(1): 91. DOI:10.2514/1.9289 |
| [3] |
贾辉.高精度星敏感器星点提取与星图识别研究[D].长沙: 国防科技大学, 2010 JIA Hui. Star centroid estimation and star identification of high accuracy star tracker[D]. Changsha: National University of Defense Technology, 2010 |
| [4] |
FAN Yu, WU Xuefeng. Study on motion blur Image restoration algorithms[J]. Advanced Materials Research, 2013, 753-755: 2976. DOI:10.4028/www.scientific.net/amr.753-755.2976 |
| [5] |
YU Xin, ZOU Cairong, YANG Luxi. Improved recursive inverse filtering method for blind image restoration[C]//Proceedings of the 6th International Conference on Signal Processing. Beijing: IEEE, 2003. DOI: 10.1109/ICOSP.2002.1180977
|
| [6] |
孙辉, 张葆, 刘晶红, 等. 离焦模糊图像的维纳滤波恢复[J]. 光学技术, 2009, 35(2): 295. SUN Hui, ZHANG Bao, LIU Jinghong, et al. Analysis on out of focus error and restoration of blurred image with Wiener filter[J]. Optical Technique, 2009, 35(2): 295. DOI:10.3321/j.issn:1002-1582.2009.02.037 |
| [7] |
BASELICE F, FERRAIOLI G, AMBROSANIO M, et al. Enhanced Wiener filter for ultrasound image restoration[J]. Computer Methods and Programs in Biomedicine, 2018, 153: 71. DOI:10.1016/j.cmpb.2017.10.006 |
| [8] |
LI Jing, LIU Zhaohui, ZHOU Liang. Restoration of motion blurred image with Lucy-Richardson algorithm[C]//Proceedings of the Image Processing & Analysis. Beijing: SPIE, 2015: 967519. DOI: 10.1117/12.2199337
|
| [9] |
闫河, 闫卫军, 李唯唯. 基于Lucy-Richardson算法的图像复原[J]. 计算机工程, 2010, 36(15): 204. YAN He, YAN Weijun, LI Weiwei. Image restoration based on Lucy-Richardson algorithm[J]. Computer Engineering, 2010, 36(15): 204. DOI:10.3969/j.issn.1000-3428.2010.15.072 |
| [10] |
郑天宇, 尹达一. 基于增强拉东变换及稀疏先验的模糊星斑复原[J]. 光学精密工程, 2018, 26(6): 1470. ZHENG Tianyu, YIN Dayi. Blurred star restoration based on improved Radon transform and sparse prior[J]. Optical and Precision Engineering, 2018, 26(6): 1470. DOI:10.3788/OPE.20182606.1470 |
| [11] |
CHO T S, PARIS S, HORN B K P, et al. Blur kernel estimation using the radon transform[C]//Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2011. DOI: 10.1109/CVPR.2011.5995479
|
| [12] |
吴小娟, 王新龙. 星图运动模糊及其复原方法[J]. 北京航空航天大学学报, 2011, 37(11): 1338. WU Xiaojuan, WANG Xinlong. Motion blur of star image and restoration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(11): 1338. DOI:10.13700/j.bh.1001-5965.2011.11.001 |
| [13] |
赵鹏, 曹军, 韦兴竹. 匀速直线运动模糊图像的模糊参数鲁棒识别[J]. 光学与精密工程, 2013, 21(9): 2430. ZHAO Peng, CAO Jun, WEI Xingzhu. Identification of robust blur parameter for uniform linear motion blurred images[J]. Optics and Precision Engineering, 2013, 21(9): 2430. DOI:10.3788/OPE.20132109.2430 |
| [14] |
廖育富, 钟建勇, 陈栋. 基于星点质心运动轨迹模糊星图退化参数估计[J]. 红外与激光工程, 2014, 43(9): 3162. LIAO Yufu, ZHONG Jianyong, CHEN Dong. Estimation of degradation parameters of smearing star image based on motion trajectory of star's centroid[J]. Infrared and Laser Engineering, 2014, 43(9): 3162. DOI:10.3969/j.issn.1007-2276.2014.09.067 |
| [15] |
JIANG Jie, HUANG Junnan, ZHANG Guangjun. An accelerated motion blurred star restoration based on single image[J]. IEEE Sensors Journal, 2017, 17(5): 1306. DOI:10.1109/JSEN.2016.2645861 |
| [16] |
MA Liheng, BERNELLI-ZAZZERA F, JIANG Guangwen, et al. Region-confined restoration method for motion-blurred star image of the star sensor under dynamic conditions[J]. Applied Optics, 2016, 55(17): 4621. DOI:10.1364/AO.55.004621 |
| [17] |
WANG Shiqiang, ZHANG Shijie, NING Mingfeng, et al. Motion blurred star image restoration based on MEMS gyroscope aid and blur kernel correction[J]. Sensors, 2018, 18(8): 2662. DOI:10.3390/s18082662 |
| [18] |
SUN Ting, XING Fei, YOU Zheng, et al. Deep coupling of star tracker and MEMS-gyro data under highly dynamic and long exposure conditions[J]. Measurement Science and Technology, 2014, 25(8): 085003. DOI:10.1088/0957-0233/25/8/085003 |
| [19] |
王海涌, 武文卿, 薛晓峰, 等. 分块峰值点局部区域生长的星像提取[J]. 光学精密工程, 2012, 20(11): 2507. WANG Haiyong, WU Wenqing, XUE Xiaofeng, et al. Star image extracting based on local region growing around peaks in blocks[J]. Optical and Precision Engineering, 2012, 20(11): 2507. DOI:10.3788/OPE.20122011.2507 |
| [20] |
李葆华, 陈希军, 郑循江, 等. 星敏感器高动态下自主星跟踪算法[J]. 红外与激光工程, 2012, 41(1): 190. LI Baohua, CHEN Xijun, ZHENG Xunjiang, et al. Autonomous star tracking algorithm with high dynamic spacecraft[J]. Infrared and Laser Engineering, 2012, 41(1): 190. DOI:10.3969/j.issn.1007-2276.2012.01.037 |
| [21] |
何贻洋, 王宏力, 冯磊, 等. 大角速度条件下星像运动轨迹建模及误差评估[J]. 北京航空航天大学学报, 2019, 45(8): 1653. HE Yiyang, WANG Hongli, FENG Lei, et al. Star spot motion trajectory model and error evaluation under large angular velocity[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(8): 1653. DOI:10.13700/j.bh.1001-5965.2018.0762 |
| [22] |
WANG Haiyong, ZHOU Wenrui, CHENG Xuan, et al. Image smearing modeling and verification for strap-down star sensor[J]. Chinese Journal of Aeronautics, 2012, 25(1): 115. DOI:10.1016/s1000-9361(11)60369-5 |
| [23] |
崔祥祥.基于大视场星敏感器的星图识别方法研究[D].西安: 第二炮兵工程学院, 2010 CUI Xiangxiang. Research on techniques of star pattern recognition for wide field-of-view star tracker[D]. Xi'an: The Second Artillery Engineering College, 2010 |
 2020, Vol. 52
2020, Vol. 52


