随着科学技术的日新月异与海战思想的发展进步, 舰炮武器需要具备持续的火力支援能力与精确的远程打击能力[1].舰炮制导炮弹效费比高, 可以对近岸目标进行有效毁伤, 较好地适应了信息化、远程化、精确化的现代海战需求[2].
末端导引控制是舰炮制导炮弹实现精确打击的技术核心, 直接决定其制导性能.随着攻防装备体系的升级, 弹目相对运动速度加快, 导引与控制系统的频率接近, 不再满足时标分离条件[3], 控制舱空间有限, 需要共享传感器, 以节省研发经费, 同时提高装备可靠性; 实战中客观存在的约束条件也制约着系统性能, 如攻击角约束、执行器控制饱和、视线角速率测量受限等[4].显然, 传统的时标分离设计方式与仅满足脱靶量约束的导引控制方法难以适应, 学者们开始致力于研究满足多约束的IGC设计方法.
Williams等[5]在1983年首次提出了IGC概念, 它以气动角为纽带, 建立起导引系统与控制系统的直接联系, 将两个子系统联合成为串级型的高阶非线性系统, 根据相对运动、弹体运动、弹体姿态等信息, 运用控制算法直接解算出执行器的操纵指令.此后, 学者们结合现代控制理论取得了较为丰硕的成果, 主要有最优控制[6]、鲁棒控制[7-8]、动态面控制[9-11]、自适应控制[7-9]、滑模控制[11-13](sliding mode control, SMC)、模糊控制[14]等.基于最优控制, Vaddi等[6]设计了一种适用于非线性系统的IGC方法, 降低了求解Hamilton-Jacobi-Bellman方程的难度, 并运用卡尔曼滤波估计目标机动, 缺陷是未考虑客观约束条件, 且算法繁琐.为了提升制导炮弹的制导性能, 杨靖等[7]基于滑模观测器提出了一种鲁棒IGC设计方法, 构造自适应鲁棒项有效地镇定了观测误差, 使弹体能够在打击机动目标时适应气动参数摄动, 缺陷是需要精确的视线角速率信息, 但是弹体的旋转特性会限制捷联式导引装置的测量.反步控制在求解高阶导数时易诱发微分膨胀, Seyedipour等[9]结合一阶低通滤波器构建了动态面, 既能够保证制导系统稳定, 又提升了系统性能, 同时还使控制器的设计过程得到了简化.进而, Shao等[10]设计了ESO对参数摄动等系统内外的未知干扰进行了准确而又迅速的观测, 并将观测信息运用到动态面控制器的设计当中, 有效地补偿了干扰对系统造成的负面影响, 缺陷是在分析系统稳定性时未考虑观测误差项.ESO由韩京清[15]首次提出, 其优势在于结构简易, 即使缺乏被控对象的精确数学模型, 也能够对系统状态以及未知干扰进行有效地观测, 为IGC设计方法提供必要信息.在实际飞行过程中, 舵面有时候会运行到机械极限位置, 带来了控制饱和受限问题, 这就很容易导致需用过载大于可用过载, 不能够按照所需弹道飞行.Nussbaum增益函数常常被用来设计含有执行器饱和的非线性系统控制器[8], 可以结合鲁棒、动态面以及自适应控制等, 对由舵机偏转受限诱发的控制饱和非线性问题进行妥善地处理.
SMC的优势在于能够克服线性与非线性系统的不确定性, 对作用于系统的不确定性干扰和建模误差具有良好的鲁棒性.Shtessel等[11]基于滑模控制提出了一种高阶非线性的IGC设计方法, 较好地克服了机动目标与模型气动系数摄动造成的负面影响, 使系统具备良好的鲁棒性.为了使导弹满足攻击角约束, Wu等[12]将弹体速度与水平面的夹角作为攻击角, 在基于非线性滑模控制提出了一种IGC设计方法, 提升了制导系统的综合性能.值得注意的是, 通过对现有研究文献的分析, 将命中时刻的弹体与目标速度之间的夹角视为攻击角更具有普适性[13].众所周知, 如何有效地削弱SMC切换抖振是亟待解决难点问题, 现常采用连续饱和函数替代符号函数, 由于与干扰项有关的切换增益难以确定, 削弱效果不尽如人意, 为此, Ran等[14]设计了自适应模糊系统逼近不确定干扰, 提高了IGC精度与鲁棒性, 但参数较多、结构复杂, 难以付诸实践.
综上所述, IGC是具有时变性、非线性、多不确定性的高阶次严反馈串级系统, 约束条件更是给系统的有限时间内收敛性与稳定性带来了不小的挑战, 因此, 现有文献多针对单约束, 但多约束恰是作战中存在且亟待解决的需求.本文充分考虑了客观存在的多项约束和作用于弹体的各类未知干扰, 提出了设计方法ARSMDS, 运用Lyapunov稳定性理论严谨地证明了终端视线角跟踪误差与视线角速率能够在有限时间内收敛, 以及系统的一致最终有界性.
1 系统建模 1.1 运动与力学模型舰炮制导炮弹转速较低, 马氏力与马氏力矩带来的通道耦合因素较小, 铅直面内弹目相对运动关系如图 1所示, Px0y0、Px1y1、Px2y2、Px6y6、Tx7y7、Tx8y8分别为弹体基准、弹体、弹道、视线、目标基准、目标弹道坐标系, P、T、r、θQ、θ、α、δz分别为弹体、目标、弹目距离、视线角、俯仰角、准攻角、俯仰舵偏角, vP、aP、θP与vT、aT、θT分别为P、T的速度、法向加速度、弹道倾角.

|
图 1 弹目相对运动关系 Fig. 1 Relative motion relationship of projectile and target |
假设1[8] 视T为质点, r、θQ、θP、θT易测, P、T仅在速度法向有加速度, 且始终满足vP>vT.
弹目相对运动关系为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot r = {v_{\rm{T}}}\cos ({\theta _{\rm{Q}}} - {\theta _{\rm{T}}}) - {v_{\rm{P}}}\cos ({\theta _{\rm{Q}}} - {\theta _{\rm{P}}}),}\\ {\dot r{\theta _{\rm{Q}}} = - {v_{\rm{T}}}\sin ({\theta _{\rm{Q}}} - {\theta _{\rm{T}}}) + {v_{\rm{P}}}\sin ({\theta _{\rm{Q}}} - {\theta _{\rm{P}}}).} \end{array}} \right. $ | (1) |
令θQT=θQ-θT, θQP=θQ-θP, 对式(1)求导可得:
| $ r{\ddot \theta _{\rm{Q}}} = - 2\dot r{\dot \theta _{\rm{Q}}} + {a_{\rm{T}}}\cos {\theta _{{\rm{QT}}}} - {a_{\rm{P}}}\cos {\theta _{{\rm{QP}}}}. $ |
考虑舵机一阶动态特性, 舰炮制导炮弹在铅直面内的动力学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \alpha = {\omega _z} - (Y - mg\cos {\theta _{\rm{P}}})/m{v_{\rm{P}}},}\\ {{{\dot \omega }_z} = {M_z}/{J_z},}\\ {{{\dot \delta }_z} = (\delta _z^c - {\delta _z})/{\tau _z}.} \end{array}} \right. $ |
式中:ωz、m、Y、Mz、Jz分别为弹体俯仰角速率、质量、升力、俯仰力矩、转动惯量; δzc、τz分别为俯仰舵控制指令、时间常数; Y、Mz分别为
| $ \left\{ {\begin{array}{*{20}{l}} {Y = Qsc_y^\prime \alpha + Qsc_y^{{\delta _z}}{\delta _z},}\\ {{M_z} = {Qs}lm_z^\prime \alpha - Qsldm_{zz}^\prime {\omega _z}/{v_{\rm{P}}} + Qslm_z^{{\delta _z}}{\delta _z}.} \end{array}} \right. $ |
式中:Q、s、l、d、c′y、cyδz、m′z、m′zz、mzδz分别为动压、参考面积、参考长度、弹径、组合体升力系数导数、俯仰舵升力系数导数、静力矩系数导数、赤道阻尼力矩系数导数、操纵力矩系数导数.
假设2[12] 升力主要由α产生, 将δz产生的升力视为有界不确定干扰.
1.2 近岸机动目标模型近岸机动目标由一阶惯性环节描述:
| $ {\tau _{\rm{T}}}{\dot a_{\rm{T}}} = a_{\rm{T}}^c - {a_{\rm{T}}}. $ |
式中:τT为时间常数, aTc为法向加速度指令, 显然aT、
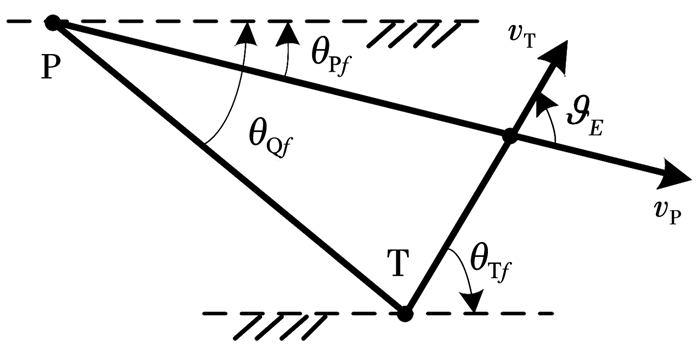
将攻击角ϑE定义为命中时刻弹目速度夹角, 如图 2所示, 攻击角约束即要求弹药以ϑE命中目标.
|
图 2 攻击角 Fig. 2 Impact angle |
通过零化弹目相对法向速度可得:
| $ {\theta _{{\rm{Q}}f}} = {\theta _{{\rm{T}}f}} - \arctan (\frac{{\sin {\vartheta _E}}}{{{v_{\rm{T}}}/{v_{\rm{P}}} - \cos {\vartheta _E}}}). $ |
由于近岸地势比较平坦, 而且能够使用无人侦察手段获取, 因此可以将θTf视为已知量.即, 对于任一给定的ϑE, 都存在着唯一的θQf与之相对应[1].
1.4 系统状态空间综上所述, 考虑模型假设、建模误差、气动参数摄动等系统内外不确定干扰与俯仰舵偏角饱和, 定义系统的状态变量为[x1, x2, x3, x4, x5]T=[θQ-θQf,
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2},}\\ {{{\dot x}_2} = {f_2}({x_2}) + {a_2}{x_3} + {d_2},}\\ {{{\dot x}_3} = {f_3}({x_3}) + {x_4} + {d_3},}\\ {{{\dot x}_4} = {f_4}({x_3},{x_4}) + {a_4} {\rm{sat}}{ _{\delta _z^{{\rm{max}}}}}({x_5}) + {d_{40}},}\\ {{{\dot x}_5} = {f_5}({x_5}) + bu + {d_5}.} \end{array}} \right. $ | (2) |
其中, 各函数与参量为
| $ \left\{ {\begin{array}{*{20}{l}} {{f_2}({x_2}) = ( - 2\dot r{x_2} + g\cos {\theta _{\rm{P}}}\cos {\theta _{{\rm{QP}}}})/r,}\\ {{f_3}({x_3}) = ( - Qsc_y^\prime {x_3}/m + g\cos {\theta _{\rm{P}}})/{v_{\rm{P}}},}\\ {{f_4}({x_3},{x_4}) = (Qslm _z^\prime {x_3} - Qsldm_{zz}^\prime {x_4}/{v_{\rm{P}}})/{J_z},}\\ {{f_5}({x_5}) = - {x_5}/{\tau _z},{a_2} = - Qsc_y^\prime \cos {\theta _{{\rm{QP}}}}/(mr),}\\ {{a_4} = Qslm _z^{{\delta _z}}/{J_z},b = 1/{\tau _z}.} \end{array}} \right. $ | (3) |
di(i=2, 3, 4, 5)是考虑目标机动、模型假设、建模误差、气动参数摄动的综合干扰项, 具体形式为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{d_2} = [{a_{\rm{T}}}\cos {\theta _{{\rm{QT}}}} - Qs\cos {\theta _{{\rm{QP}}}}\Delta c_y^\prime \alpha /m - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Qs\cos {\theta _{{\rm{QP}}}}(1 + \Delta )c_y^{{\delta _z}}{\delta _z}/m]/r - {{\dot a}_{\rm{T}}}/{v_{\rm{T}}} + {d_{2\Delta }},} \end{array}\\ \begin{array}{*{20}{l}} {{d_3} = [ - Qs\Delta c_y^\prime \alpha - Qs(1 + \Delta )c_y^{{\delta _z}}{\delta _z}]/m{v_{\rm{P}}} + {d_{3\Delta }},}\\ {{d_{40}} = (Qsl\Delta m_z^\prime \alpha - Qsld\Delta m_{zz}^\prime {\omega _z}/{v_{\rm{P}}})/{J_z} + {d_{4\Delta }},}\\ {{d_5} = {d_{5\Delta }}.} \end{array} \end{array} \right. $ |
式中:Δ为气动参数摄动百分比, diΔ为建模误差项.式(2)中, satδzmax为连续的饱和函数:
| $ {\rm{sa}}{{\rm{t}}_{\delta _z^{\max }}}({x_5}) = \left\{ {\begin{array}{*{20}{l}} {{x_5},|{x_5}| \le \delta _z^{\max };}\\ {\delta _z^{\max } {\rm{sign}} ({x_5}),|{x_5}| > \delta _z^{\max }.} \end{array}} \right. $ |
为便于IGC的设计, 现引入一种连续可微的双曲正切函数g(x5)来描述俯仰舵偏角饱和.
| $ \left\{ {\begin{array}{*{20}{l}} {g({x_5}) = \delta _z^{{\rm{max}}}({{\rm{e}}^{{x_5}/\delta _z^{{\rm{max}}}}} - {{\rm{e}}^{ - {x_5}/\delta _z^{\max }}})/({{\rm{e}}^{{x_5}/\delta _z^{\max }}} + {{\rm{e}}^{ - {x_5}/\delta _z^{\max }}}),}\\ {{g^\prime }({x_5}) = \xi ({x_5}) = 4/{{({{\rm{e}}^{{x_5}/\delta _z^{\max } + }}{{\rm{e}}^{ - {x_5}/\delta _z^{\max }}})}^2}.} \end{array}} \right. $ |
此时系统状态空间为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2},}\\ {{{\dot x}_2} = {f_2}({x_2}) + {a_2}{x_3} + {d_2},}\\ {{{\dot x}_3} = {f_3}({x_3}) + {x_4} + {d_3},}\\ {{{\dot x}_4} = {f_4}({x_3},{x_4}) + {a_4}g({x_5}) + {d_4},}\\ {{{\dot x}_5} = {f_5}({x_5}) + bu + {d_5}.} \end{array}} \right. $ | (4) |
式中, d4=d40+a4dsg, dsg=satδzmax(x5)-g(x5).
假设3[14] di(i=2, 3, 4, 5)及其1阶导数有界, 并满足不等式|di|≤ζi、
本文针对系统(4), 在状态变量x2测量受限、x5饱和受限、di未知有界的条件下, 通过设计方法ARSMDS得到控制量u, 令x1与x2在有限时间内收敛至零点的任意小邻域内, 系统一致最终有界.
2 ARSMDS设计 2.1 ESO设计为快速获取di与
为观测d2, 定义观测量[zx1, zx2, zd2], 建立ESO为
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{21}} = {z_{{x_1}}} - {x_1},{e_{22}} = {z_{{x_2}}} - {x_2},{e_{23}} = {z_{{d_2}}} - {d_2},}\\ {{{\dot z}_{{x_1}}} = {z_{{x_2}}} - {\beta _{21}}{e_{21}},}\\ {{{\dot z}_{{x_2}}} = {f_2}({x_2}) + {a_2}{x_3} + {z_{{d_2}}} - {\beta _{22}} {\rm{fal}} ({e_{21}},{\sigma _{21}},{\eta _{21}}),}\\ {{{\dot z}_{{d_2}}} = - {\beta _{23}} {\rm{fal}} ({e_{21}},{\sigma _{22}},{\eta _{22}}).} \end{array}} \right. $ | (5) |
式中, 0 < β2i(i=1, 2, 3), 0 < σ2i < 1(i=1, 2), 0 < η2i < 1(i=1, 2), 非线性函数fal为
| $ {\rm{fal}}(e,\sigma ,\eta ) = \left\{ {\begin{array}{*{20}{l}} {|e{|^\sigma } {\rm{sign}} (e),|e| > \eta ,}\\ {e/{\eta ^{1 - \sigma }},|e| \le \eta .} \end{array}} \right. $ |
通过文献[16]可推导出ESO(5)的稳态误差为
| $ \left\{ {\begin{array}{*{20}{l}} {|{e_{21}}| \le \eta _{22}^{1 - {\sigma _{22}}}{{\dot d}_{{\rm{2max}}}}/{\beta _{23}},}\\ {|{e_{22}}| \le {\beta _{21}}\eta _{22}^{1 - {\sigma _{22}}}{{\dot d}_{{\rm{2max}}}}/{\beta _{23}},}\\ {|{e_{23}}| \le [{\beta _{22}}\eta _{22}^{1 - {\sigma _{22}}}/({\beta _{23}}\eta _{21}^{1 - {\sigma _{21}}}) + {\beta _{21}}\eta _{22}^{1 - {\sigma _{22}}}/{\beta _{23}}]{{\dot d}_{{\rm{2max}}}}.} \end{array}} \right. $ | (6) |
由式(6)可知, 无论干扰项是否连续, 选择合适参数, 令β23远大于β21、β22, 就可以对其进行精确地观测, 即zx1→x1、zx2→x2、zd2→d2.同理, 为观测di(i=3, 4, 5), 定义观测量[zxi, zdi], 分别建立ESO为
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{31}} = {z_{{x_3}}} - {x_3},{e_{32}} = {z_{{d_3}}} - {d_3},}\\ {{{\dot z}_{{x_3}}} = {f_3}({x_3}) + {x_4} + {z_{{d_3}}} - {\beta _{31}}{e_{31}},}\\ {{{\dot z}_{{d_3}}} = - {\beta _{32}} {\rm{fal}} ({e_{31}},{\sigma _3},{\eta _3}),} \end{array}} \right. $ | (7) |
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{41}} = {z_{{x_4}}} - {x_4},{e_{42}} = {z_{{d_4}}} - {d_4},}\\ {{{\dot z}_{{x_4}}} = {f_4}({x_3},{x_4}) + {a_4}g({x_5}) + {z_{{d_4}}} - {\beta _{41}}{e_{41}},}\\ {{{\dot z}_{{d_4}}} = - {\beta _{42}} {\rm{fal}} ({e_{41}},{\sigma _4},{\eta _4}),} \end{array}} \right. $ | (8) |
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{51}} = {z_{{x_5}}} - {x_5},{e_{52}} = {z_{{d_5}}} - {d_5},}\\ {{{\dot z}_{{x_5}}} = {f_5}({x_5}) + bu + {z_{{d_5}}} - {\beta _{51}}{e_{51}},}\\ {{{\dot z}_{{d_5}}} = - {\beta _{52}} {\rm{fal}} ({e_{51}},{\sigma _5},{\eta _5}).} \end{array}} \right. $ | (9) |
式中, 各参数取值范围同式(5).
2.2 非奇异终端滑模设计为保证系统(4)中的x1、x2在有限时间内快速收敛至零点的任意小邻域内.
| $ \dot x = f(x,t),f(0,t) = 0,x \in {{\bf{R}}^n}. $ |
V(x)是定义在原点邻域上的连续可微正定函数, 如果存在正实数c、α < 1, 使得不等式
现选用一种非奇异终端滑模:
| $ {s_2} = {x_1} + \beta |{x_2}{|^\gamma } {\rm{sign}} ({x_2}),0 < \beta ,1 < \gamma < 2, $ | (10) |
求导可得:
| $ {\dot s_2} = {x_2} + \beta \gamma |{x_2}{|^{\gamma - 1}}[{f_2}({x_2}) + {a_2}{x_3} + {d_2}]. $ | (11) |
为了使滑模在趋近的过程中具备优良的性能, 运用弹目接近速率与弹目相对距离来设计滑模的自适应指数趋近律, 即
| $ {\dot s_2} = - {k_2} {\rm{sign}} ({s_2}) - |\dot r|{c_2}{s_2}/r. $ | (12) |
式中, |e21|≤k2, 0 < c2, 联立式(11)、(12), 并去掉奇异因子|x2|1-γ/βγ可得:
| $ \begin{array}{*{20}{l}} {{{\bar x}_3} = - [|{x_2}{|^{2 - \gamma }} {\rm{sign}} ({x_2})/\beta \gamma + {f_2}({x_2}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_{{d_2}}} + {k_2} {\rm{sign}} ({s_2}) + |\dot r|{c_2}{s_2}/r]/{a_2}.} \end{array} $ | (13) |
定理1 针对由系统(4)中第1、2个等式所组成的子系统, 通过ESO(5)与控制指令(13)的调控, x1与x2在有限时间收敛内收敛至零点附近任意小的邻域内.
证明 选取Lyapunov函数V2=s22/2, 求导可得:
| $ \begin{array}{*{20}{l}} {{{\dot V}_2} = {s_2}{{\dot s}_2} = {s_2}\{ {x_2} + \beta \gamma |{x_2}{|^{\gamma - 1}}[{f_2}({x_2}) + {a_2}{{\bar x}_3} + {d_2}]\} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta \gamma |{x_2}{|^{\gamma - 1}}{s_2}[{d_2} - {z_{{d_2}}} - {k_2} {\rm{sign}} ({s_2}) - |\dot r|{c_2}{s_2}/r] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \beta \gamma |{x_2}{|^{\gamma - 1}}({c_2}|\dot r|s_2^2/r - {e_{21}}{s_2} - {k_2}|{s_2}|) \le }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \beta \gamma |{x_2}{|^{\gamma - 1}}{c_2}|\dot r|s_2^2/r.} \end{array} $ |
根据Lyapunov稳定性定理, 当x2≠0时, s2在有限时间内收敛至零, 当x2=0时也成立[18], 在此后有
| $ {\dot x_1} = - {\beta ^{ - \frac{1}{\gamma }}}|{x_1}{|^{\frac{1}{\gamma }}} {\rm{sign}} ({x_1}). $ |
选取Lyapunov函数Vx1=x12/2, 求导可得:
| $ {\dot V_{{x_1}}} = - {\beta ^{ - \frac{1}{\gamma }}}|{x_1}{|^{\frac{1}{\gamma } + 1}} = - {2^{\frac{{1 + \gamma }}{{2\gamma }}}}{\beta ^{ - \frac{1}{\gamma }}}V_{{x_1}}^{\frac{{1 + \gamma }}{{2\gamma }}}. $ |
根据引理1, x1、x2在有限时间内收敛至零点附近任意小的邻域内.
为了削弱控制量的高频震颤, 在现有文献中, 通常引入连续饱和函数sat(s)=s/(|s|+δ)来替换滑模切换项, 0 < δ, 则有
| $ \begin{array}{*{20}{c}} {{{\bar x}_3} = - [|{x_2}{|^{2 - \gamma }} {\rm{sign}} ({x_2})/\beta \gamma + {f_2}({x_2}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_{{d_2}}} + {k_2} {\rm{sat}} ({s_2}) + |\dot r|{c_2}{s_2}/r]/{a_2}.} \end{array} $ | (14) |
针对镇定系统(4), 简化虚拟控制量的求解过程, 并结合自适应鲁棒项削弱抖振.
步骤1 定义s2为动态面2
令x3作为虚拟控制量, 使s2→0, 为避免对x3直接微分, 通过一阶滤波器得到x3d:
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _3}{{\dot x}_{3d}} + {x_{3d}} = {{\bar x}_3},}\\ {{x_{3d}}(0) = {{\bar x}_3}(0).} \end{array}\quad 0 < {\tau _3}} \right. $ |
步骤2 定义动态面3为
| $ {s_3} = {x_3} - {x_{3d}}, $ |
求导可得:
| $ {\dot s_3} = {\dot x_3} - {\dot x_{3d}} = {f_3}({x_3}) + {x_4} + {d_3} - {\dot x_{3d}}. $ |
设计虚拟控制量x4, 使s3→0, 即
| $ {\bar x_4} = \underbrace { - {f_3}({x_3}) - {z_{d3}} + {{\dot x}_3}d}_1\underbrace { - {{\hat \zeta }_3}{s_3}}_2\underbrace { - {c_3}{s_3}}_3. $ | (15) |
式中包括3部分:线性反馈项、负定增益项与自适应鲁棒项,
| $ {\dot {\hat \zeta _i}} = {\kappa _i}(s_i^2 - {\mu _i}{\hat \zeta _i}),0 < {\kappa _i},0 < {\mu _i}. $ | (16) |
选取观测误差:
| $ {\tilde \zeta _i} = {\zeta _i} - {\hat \zeta _i}. $ |
为避免对x4直接微分, 通过一阶滤波器得到x4d为
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _4}{{\dot x}_{4d}} + {x_{4d}} = {{\bar x}_4},}\\ {{x_{4d}}(0) = {{\bar x}_4}(0).} \end{array}\quad 0 < {\tau _4}} \right. $ |
步骤3 定义动态面4为
| $ {s_4} = {x_4} - {x_{4d}}, $ |
求导可得:
| $ {\dot s_4} = {\dot x_4} - {\dot x_{4d}} = {f_4}({x_3},{x_4}) + {a_4}g({x_5}) + {d_4} - {\dot x_{4d}}. $ |
同理设计虚拟控制量g, 使s4→0,即
| $ \bar g = - [{f_4}({x_3},{x_4}) - {\dot x_{4d}} + {z_{d4}} + {\hat \zeta _4}{s_4} + {c_4}{s_4}]/{a_4}. $ | (17) |
为避免对g直接微分, 通过一阶滤波器得到gd:
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _5}{{\dot g}_d} + {g_d} = \bar g,}\\ {{g_d}(0) = \bar g(0).} \end{array}\quad 0 < {\tau _5}} \right. $ |
步骤4 定义动态面5为
| $ {s_5} = g - {g_d}, $ |
求导可得:
| $ {\dot s_5} = \dot g - {\dot g_d} = \xi [{f_5}({x_5}) + bu + {d_5}] - {\dot g_d}. $ |
定义1[19] 若连续函数N(χ)满足以下性质:
| $ \mathop {{\rm{lim}}}\limits_{t \to \pm \infty } {\rm{sup}}\frac{1}{t}\int_0^t N (\chi ){\rm{d}}\chi = \infty , $ |
| $ \mathop {\lim }\limits_{t \to \pm \infty } {\rm{inf}}\frac{1}{t}\int_0^t N (\chi ){\rm{d}}\chi = - \infty , $ |
则N(χ)为Nussbaum函数.
为有效地处理出现的控制输入饱和受限问题, 设计控制量为:
| $ {u = [N(\chi )\bar u - {z_{d5}}]/b,} $ | (18) |
| $ {\bar u = - \xi {f_5}({x_5}) + {{\dot g}_d} - {{\hat \zeta }_5}{s_5} - {c_5}{s_5}.0 < {c_5}} $ | (19) |
选取Nussbaum函数, 设计其自适应律为:
| $ {N(\chi ) = {{\rm{e}}^{{\chi ^2}}}\cos (\chi ),} $ |
| $ {\dot \chi = {\gamma _\chi }\overline u {s_5}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < {\gamma _\chi }} $ |
引理2[20] 对任意给定的1阶线性非齐次微分方程dy/dt+P(x)y=Q(x), 它的通解形式为
| $ y = C{{\rm{e}}^{ - \int P (x){\rm{d}}x}} + {{\rm{e}}^{ - \int P (x){\rm{d}}x}}\int Q (x){{\rm{e}}^{\int P (x){\rm{d}}x}}{\rm{d}}x, $ |
其中, C为任意常数.
引理3[21] V(t)与χ(t)是定义域为[0, tf)的光滑函数, 0≤V(t), N(·)是光滑Nussbaum函数, ∀t∈[0, tf), 若有不等式下式成立, 则V(t)与χ(t)是有界的.
| $ \begin{array}{*{20}{l}} {V(t) \le V(0){{\rm{e}}^{ - Ct}} + \frac{M}{C}(1 - {{\rm{e}}^{ - Ct}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{{\rm{e}}^{ - Ct}}}}{{{\gamma _\chi }}}\int_0^t {\dot \chi } [\xi N(\chi ) - 1]{{\rm{e}}^{C\tau }}{\rm{d}}\tau .}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < C,0 < M} \end{array} $ |
虚拟控制量的误差项为
| $ {y_i} = {x_{id}} - {\bar x_i},{y_g} = {g_d} - \bar g,(i = 3,4) $ |
求导可得:
| $ {\dot x_{id}} = - {y_i}/{\tau _i},{\dot g_d} = - {y_g}/{\tau _5}.\quad (i = 3,4) $ |
进一步推导可得:
| $ {\dot y_i} = - {y_i}/{\tau _i} - {\dot {\bar x}_i},{\dot y_g} = - {y_g}/{\tau _5} - \dot {\bar g} \cdot (i = 3,4) $ |
由文献[22]可知, 存在正实数Mi、Mg使得
经推导可得:
| $ {x_i} = {s_i} + {y_i} + {\bar x_i},g = {s_5} + {y_g} + \bar g.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 3,4) $ |
选取全系统Lyapunov函数V, 即
| $ V = \frac{1}{2}\sum\limits_{i = 2}^5 {s_i^2} + \frac{1}{2}\sum\limits_{i = 3}^4 {y_i^2} + \frac{1}{2}y_g^2 + \frac{1}{2}\sum\limits_{i = 3}^5 {\frac{{\tilde \zeta _i^2}}{{{\mu _i}}}} . $ | (20) |
定义动态面向量s =[s2, s3, s4, s5]T, 其范数为
| $ \left\| \mathit{\boldsymbol{s}} \right\| = \frac{1}{T}\int_0^T {{\mathit{\boldsymbol{s}}^{\rm{T}}}} \mathit{\boldsymbol{s}}{\rm{d}}t. $ |
定理2 对于系统(4), 采用式(5)、(7)~(9)的ESO, 鲁棒自适应律为式(16), 控制量如式(14)、(15)、(17)、(18), (19)通过选择适宜的参数, 系统一致最终有界, 动态面向量的范数‖ s ‖满足下式:
| $ \begin{array}{l} \left\| \mathit{\boldsymbol{s}} \right\| \le \frac{1}{\varepsilon }\{ \frac{{2V(0)}}{T} + \sum\limits_{i = 3}^5 {(\frac{{{\zeta _i}}}{2} + {\kappa _i}\zeta _i^2)} + \frac{3}{2}{\rho ^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{{{\gamma _\chi }T}}\int_0^T {\dot \chi } [\xi N(\chi ) - 1]{\rm{d}}t\} ,0 < \varepsilon . \end{array} $ | (21) |
证明 对式(20)进行微分, 可得:
| $ \begin{array}{l} \dot V = \sum\limits_{i = 2}^5 {{s_i}} {{\dot s}_i} + \sum\limits_{i = 3}^4 {{y_i}} {{\dot y}_i} + {y_g}{{\dot y}_g} + \sum\limits_{i = 3}^5 {{{\tilde {\zeta }}_i}} {{\dot {\tilde \zeta }}_i} = {s_2}\{ {x_2} + \beta \gamma |{x_2}{|^{\gamma - 1}}[{f_2}({x_2}) + {a_2}({s_3} + {y_3} + {{\bar x}_3}) + {d_2}]\} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_3}[{f_3}({x_3}) + ({s_4} + {y_4} + {{\bar x}_4}) + {d_3} - {{\dot x}_{3d}}] + {s_4}[{f_4}({x_3},{x_4}) + {a_4}({s_5} + {y_g} + \bar g) + {d_4} - {{\dot x}_{4d}}] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_5}\{ \xi [{f_5}({x_5}) + bu + {d_5}] - {{\dot g}_d}\} + \sum\limits_{i = 3}^4 {{y_i}} ( - {{\dot {\bar x}}_i} - \frac{{{y_i}}}{{{\tau _i}}}) + {y_g}( - \dot {\bar g} - \frac{{{y_g}}}{{{\tau _5}}}) + \sum\limits_{i = 3}^5 - {{\tilde \zeta }_i}(s_i^2 - \kappa {{\hat \zeta }_i}) \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}{s_2}({s_3} + {y_3}) + \beta \gamma |{x_2}{|^{\gamma - 1}}{s_2}[{d_2} - {z_{d2}} - {k_2} {\rm{sign}} ({s_2}) - \frac{{|\dot r|}}{r}{c_2}{s_2}] + {s_3}({s_4} + {y_4}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_3}[{d_3} - {z_{d3}} - {{\hat \zeta }_3}{s_3} - {c_3}{s_3}] + {a_4}{s_4}({s_5} + {y_g}) + {s_4}[{d_4} - {z_{d4}} - {{\hat \zeta }_4}{s_4} - {c_4}{s_4}] + {s_5}\{ [\xi N(\chi ) - 1]\bar u + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi ({d_5} - {z_{d5}}) - {{\hat \zeta }_5}{s_5} - {c_5}{s_5}\} + \sum\limits_{i = 3}^4 {{y_i}} ( - \frac{{{y_i}}}{{{\tau _i}}} + {M_i}) + {y_g}( - \frac{{{y_g}}}{{{\tau _5}}} + {M_g}) + \sum\limits_{i = 3}^5 {( - {{\tilde \zeta }_i}s_i^2 - \frac{{{\kappa _i}}}{2}\tilde \zeta _i^2 + \frac{{{\kappa _i}}}{2}\zeta _i^2)} \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}(s_2^2 + \frac{{s_3^2}}{2} + \frac{{y_3^2}}{2}) - \beta \gamma |{x_2}{|^{\gamma - 1}}\frac{{|\dot r|}}{r}{c_2}s_2^2 + (s_3^2 + \frac{{s_4^2}}{2} + \frac{{y_4^2}}{2}) - {c_3}s_3^2 + {a_4}(s_4^2 + \frac{{s_5^2}}{2} + \frac{{y_g^2}}{2}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_4}s_4^2 - {c_5}s_5^2 + {s_5}[\xi N(\chi ) - 1]\bar u + \sum\limits_{i = 3}^4 {(\frac{{M_i^2}}{{{\rho ^2}}} - \frac{1}{{{\tau _i}}})y_i^2 + (\frac{{M_g^2}}{{{\rho ^2}}} - \frac{1}{{{\tau _5}}})} y_g^2 + \frac{3}{4}{\rho ^2} - \frac{1}{2}\sum\limits_{i = 3}^5 {{\kappa _i}} \tilde \zeta _i^2 + \sum\limits_{i = 3}^5 {(\frac{{{\zeta _i}}}{4} + \frac{{{\kappa _i}}}{2}\zeta _i^2)} \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \underbrace {\beta \gamma |{x_2}{|^{\gamma - 1}}(\frac{{|\dot r|}}{r}{c_2} - {a_2})}_{m1}s_2^2 - \underbrace {({c_3} - 1 - \frac{{\beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}}}{2})}_{m2}s_3^2 - \underbrace {({c_4} - {a_4} - \frac{1}{2})}_{m3}s_4^2 - \underbrace {({c_5} - \frac{{{a_4}}}{2})}_{m4}s_5^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\dot \chi }}{{{\gamma _\chi }}}[\xi N(\chi ) - 1] - \underbrace {(\frac{1}{{{\tau _3}}} - \frac{{M_3^2}}{{{\rho ^2}}} - \frac{{\beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}}}{2})}_{m5}y_3^2 - \underbrace {(\frac{1}{{{\tau _4}}} - \frac{{M_4^2}}{{{\rho ^2}}} - \frac{1}{2})}_{m6}y_4^2 - \underbrace {(\frac{1}{{{\tau _5}}} - \frac{{M_g^2}}{{{\rho ^2}}} - \frac{{{a_4}}}{2})y_g^2}_{m7} - \underbrace {\sum\limits_{i = 3}^5 {\frac{{{\kappa _i}{\mu _i}}}{2}} }_{m8}\frac{{\tilde \zeta _i^2}}{{{\mu _i}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{3}{4}{\rho ^2} + \sum\limits_{i = 3}^5 {(\frac{{{\zeta _i}}}{4} + \frac{{{\kappa _i}}}{2}\zeta _i^2)} . \end{array} $ | (22) |
为保证系统稳定, 选取合适的参数满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{c_2} \ge (\ell + {a_2})r/|\dot r|,}\\ {{c_3} \ge \ell + \beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}/2 + 1,}\\ {{c_4} \ge \ell + {a_4} + 1/2,}\\ {{c_5} \ge \ell + {a_4}/2,}\\ {1/{\tau _3} \ge \ell + M_3^2/{\rho ^2} + \beta \gamma |{x_2}{|^{\gamma - 1}}{a_2}/2,}\\ {1/{\tau _4} \ge \ell + M_4^2/{\rho ^2} + 1/2,}\\ {1/{\tau _5} \ge \ell + M_g^2/{\rho ^2} + {a_4}/2,}\\ {{\kappa _i}{\mu _i} \ge 2\ell .} \end{array}} \right. $ |
令正常数ε=min{mi(i=1, 2, …, 8)}, 取正常数为
| $ \dot V \le - 2\varepsilon V + \zeta + \frac{{\dot \chi }}{{{\gamma _\chi }}}[\xi N(\chi ) - 1]. $ | (23) |
由引理2可得式(23)的解满足如下不等式:
| $ \begin{array}{*{20}{l}} {V(t) \le V(0){{\rm{e}}^{ - 2\varepsilon t}} + \frac{\zeta }{{2\varepsilon }}(1 - {{\rm{e}}^{ - 2\varepsilon t}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{{\rm{e}}^{ - 2\varepsilon t}}}}{{{\gamma _\chi }}}\int_0^t {\dot \chi } [\xi N(\chi ) - 1]{{\rm{e}}^{2\varepsilon \tau }}{\rm{d}}\tau .} \end{array} $ | (24) |
由上式可知,影响系统收敛速度与精度的参数主要有ε、ζ、γχ,经分析可知ε、γχ与收敛精度成正相关,ζ与收敛精度成负相关,进一步地,可以通过调整影响ε、ζ、γχ的mi、ρ、κix等参数来间接调控收敛速度与精度,但这些参数的取值必须满足式(21).根据引理3与Barbalat引理, 系统一致最终有界.进而, 式(21)经过进一步地推导, 可得:
| $ \begin{array}{*{20}{c}} {\left\| \mathit{\boldsymbol{s}} \right\| \le \frac{1}{T}\int_0^t V {\rm{d}}t \le \frac{1}{\varepsilon }\{ \zeta - \frac{1}{T}\int_0^t {\dot V} {\rm{d}}t + }\\ {\frac{1}{T}\int_0^t {\frac{{\dot \chi }}{{{\gamma _\chi }}}} [\xi N(\chi ) - 1]{\rm{d}}t\} \le }\\ {\frac{1}{\varepsilon }\{ \zeta + \frac{{V(T) + V(0)}}{T} + }\\ {\frac{1}{T}\int_0^t {\frac{{\dot \chi }}{{{\gamma _\chi }}}} [\xi N(\chi ) - 1]{\rm{d}}t\} .} \end{array} $ |
由式(24)可得:
| $ \begin{array}{*{20}{l}} {V(T) - V(0) \le V(T) - V(0){{\rm{e}}^{ - 2\varepsilon T}} \le }\\ {\frac{\zeta }{{2\varepsilon }}(1 - {{\rm{e}}^{ - 2\varepsilon T}}) + \int_0^t {\frac{{\dot \chi }}{{{\gamma _\chi }}}} [\xi N(\chi ) - 1]{{\rm{e}}^{ - 2\varepsilon (T - t)}}{\rm{d}}t \le }\\ {\zeta + \frac{1}{{{\gamma _\chi }}}\int_0^t {\dot \chi } [\xi N(\chi ) - 1]{\rm{d}}t.} \end{array} $ | (25) |
进一步地, 由式(24)、(25), 推导可得:
| $ \left\| \mathit{\boldsymbol{s}} \right\| \le \frac{1}{\varepsilon }\{ \frac{{2V(0)}}{T} + 2\zeta + \frac{2}{{{\gamma _\chi }T}}\int_0^t {\dot \chi } [\xi N(\chi ) - 1]{\rm{d}}t\} , $ |
证毕.
4 仿真实验为验证ARSMDS的有效性与鲁棒性, 考虑了气动参数摄动, 通过数字仿真模拟复现了打击正弦与方波机动目标的工况, 并引入文献[19]中的自适应动态面控制(ADSC)作为对比, 受篇幅所限仅展示部分结果.
弹体气动参数、弹目运动参数、制导参数见表 1~3.了体现ARSMDS无需视线角速率, 式(3)、(4)、(5)、(10)、(14)中都使用zx2, 设定导引盲区为30 m, 盲区内舵机指令不变, 依靠惯性飞行.
| 表 1 弹体气动参数 Tab. 1 Aerodynamic parameters of projectile |
| 表 2 弹目运动参数 Tab. 2 Motion parameters of projectile and target |
| 表 3 导引控制参数 Tab. 3 Parameters of guidance and control |
此时, 设定aTc=3sin(t)(m/s2), 仿真实验结果见表 4与如图 3所示.
| 表 4 工况1仿真实验结果 Tab. 4 Simulation results of operating condition 1 |
|
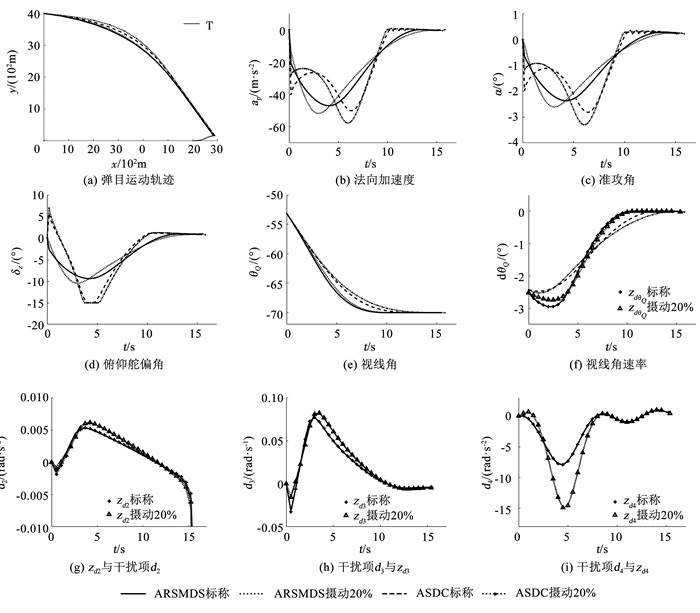
图 3 工况1仿真实验曲线 Fig. 3 Simulation curves of operating condition 1 |
图 3(a)为弹目运动轨迹, ARSMDS、ASDC都可以成功地攻击正弦机动目标, ARSMDS弹道更为平直, 通过分析表 4可知, ARSMDS使脱靶量等重要指标得到了优化, 降低了气动参数摄动对制导系统的影响.法向加速度在图 3(b)中展示, 仅采用自适应鲁棒项的ASDC不能有效地处理未知干扰, 而ARSMDS将ESO与鲁棒控制相结合, 降低了加速度的峰值与变化范围, 变化趋势更为平滑.从图 3(c)中可以看出, 准攻角的变化趋势与法向加速度保持一致, 验证了假设2的正确性, ASDC受气动参数摄动影响较大, 出现了突变与发散的现象, 而ARSMDS通过ESO与鲁棒项的调控, 使准攻角的变化始终保持在较小的范围内, 有益于弹体稳定飞行.由图 3(d)可知, 通过引入自适应Nussbaum函数, ARSMDS有效地处理了饱和非线性问题, 较好地保护了舵机, 尽量避免因舵机控制饱和而达不到战技指标.视线角、视线角速率的变化情况如图 3(e)、(f)所示, 在ARSMDS的调控下, 视线角与视线角速率自7 s后能够稳定地保持收敛状态, x1与x2有限时间收敛, ARSMDS收敛速度优于ASDC.分析图 3(f)~图 3(i)可知, ESO能够对视线角速率与干扰进行快速准确地观测, 为设计方法提供重要信息, 使弹体具备足够的可用过载, 以补偿不确定性干扰对制导飞行的负面影响.
4.2 工况2:方波机动目标设定aTc=3sign[sin(t/4)](m/s2), 结果见表 5与如图 4所示.
| 表 5 工况2仿真实验结果 Tab. 5 Simulation results of operating condition 2 |
|
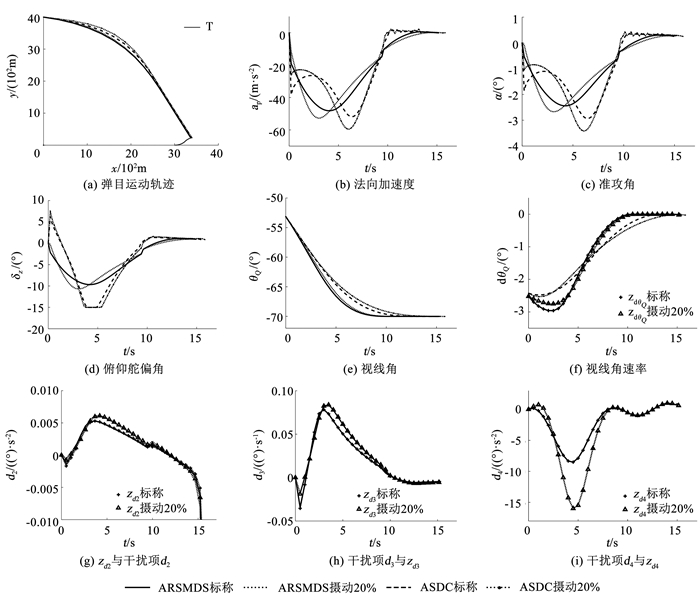
图 4 工况2仿真实验曲线 Fig. 4 Simulation curves of operating condition 2 |
图 4(a)为弹目运动轨迹, 两种设计方法都可以令弹体命中作正弦机动的目标, 通过分析表 5可知, ARSMDS在ESO与自适应鲁棒项的调控下, 降低了气动参数摄动的不利影响, 提升了制导系统性能.法向加速度的仿真曲线在图 4(b)中描述, ASDC受气动参数摄动等不确定性干扰的影响较大, 致使其加速度峰值较大、收敛速率缓慢, 并且存在抖振发散的现象, 而ARSMDS使弹体能够较好地适应气动参数在一定范围内的摄动, 制导系统具备良好的鲁棒性.图 4(c)展示了准攻角的变化曲线, 由于设计并采用了ESO、自适应鲁棒项等有效措施, ARSMDS准攻角的变化范围较小、变化趋势平缓, 这有利于弹体在末制导段的稳定飞行.观察图 4(d), 在不确定性干扰的影响下, ASDC舵偏峰值与变化范围都比较大, 而ARSMDS通过引入自适应Nussbaum增益函数, 妥善地处理了由舵偏受限诱发的控制饱和非线性.视线角与视线角速率的变化情况在图 4(e)~图 4(f)中描绘, ARSMDS可以令终端视线角跟踪误差在7 s后保持稳定的收敛状态, 充分体现出“定理1”的正确性.图 4(f)~图 4(i)表明ESO具有良好的观测性能与鲁棒性, 即使在气动参数摄动范围较大的工况下也能够快速准确地观测出视线角速率与综合干扰项, 为ARSMDS提供了准确的必要反馈信息, 使弹体具备足够的可用过载, 进一步提升了制导系统性能与战技指标.
5 结论1) ESO准确迅速地观测出视线角速率与各类未知干扰, 降低了制导炮弹的硬件设计要求.
2) 结合自适应鲁棒设计了动态面滑模,避免了微分膨胀并有效地解决了切换增益难以确定所导致的控制量抖振.
3) 严谨地证明了终端视线角跟踪误差、视线角速率的有限时间收敛性, 以及系统的一致最终有界性.
| [1] |
姜尚, 田福庆, 孙世岩, 等. 滚转舰炮制导炮弹的空间多约束导引与控制一体化设计[J]. 航空学报, 2019, 40(10): 323101. JIANG Shang, TIAN Fuqing, SUN Shiyan, et al. Design of integrated guidance and control in space with multiple constraints of rolling naval gun guided projectile[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(10): 323101. DOI:10.7527/S1000-6893.2019.23101 |
| [2] |
孙世岩, 朱惠民, 宋歆, 等. 舰炮制导炮弹发展研究[J]. 火力与指挥控制, 2016, 41(12): 5. SUN Shiyan, ZHU Huimin, SONG Xin, et al. Study of developing naval gun guided ammunition[J]. Fire Control & Command Control, 2016, 41(12): 5. DOI:10.3969/j.issn.1002-0640.2016.12.001 |
| [3] |
ZHURBAL A, IDAN M. Effect of estimation on the performance of an integrated missile guidance and control system[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2690. DOI:10.1109/TAES.2011.6034659 |
| [4] |
LI Qingchun, ZHANG Wensheng, HAN Gang, et al. Fuzzy sliding mode control guidance law with terminal impact angle and acceleration constraints[J]. Journal of Systems Engineering and Electronics, 2016, 27(3): 664. DOI:10.1109/JSEE.2016.00070 |
| [5] |
WILLIAMS D, RICHMAN J, FRIEDLAND B. Design of an integrated strapdown guidance and control system for a tactical missile[C]//Proceedings of AIAA Guidance & Control Conference. Gatlinburg, TN: AIAA, 1983: 57. DOI: 10.2514/6.1983-2169
|
| [6] |
VADDI S S, MENON P K, OHLMEYER E J. Numerical state-dependent Riccati equation approach for missile integrated guidance control[J]. Journal of Guidance Control and Dynamics, 2009, 32(2): 699. DOI:10.2514/1.34291 |
| [7] |
杨靖, 王旭刚, 王中原, 等. 基于滑模观测器的鲁棒变结构一体化导引控制律[J]. 兵工学报, 2017, 38(2): 246. YANG Jing, WANG Xugang, WANG Zhongyuan, et al. Sliding-mode-observer-based robust variable structure control for integrated autopilot-guidance[J]. Acta Armamentarii, 2017, 38(2): 246. DOI:10.3969/j.issn.1000-1093.2017.02.006 |
| [8] |
WEN Changyun, ZHOU Jing, LIU Zhitao, et al. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance[J]. IEEE Transactions on Automatic Control, 2011, 56(7): 1672. DOI:10.1109/tac.2011.2122730 |
| [9] |
SEYEDIPOUR S H, JEGARKANDI M F, SHAMAGHDARI S. Nonlinear integrated guidance and control based on adaptive backstepping scheme[J]. Aircraft Engineering and Aerospace Technology, 2017, 89(3): 415. DOI:10.1108/AEAT-12-2014-0209 |
| [10] |
SHAO Xingling, WANG Honglun. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO[J]. ISA Transactions, 2015, 57(4): 10. DOI:10.1016/j.isatra.2015.02.013 |
| [11] |
SHTESSEL Y B, TOURNES C H. Integrated higher-order sliding mode guidance and autopilot for dual-control missiles[J]. Journal of Guidance Control and Dynamics, 2009, 32(1): 79. DOI:10.2514/1.36961 |
| [12] |
WU Peng, YANG Ming. Integrated guidance and control design for missile with terminal impact angle constraint based on sliding mode control[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 623. DOI:10.3969/j.issn.1004-4132.2010.04.015 |
| [13] |
KUMAR S R, RAO S, GHOSE D. Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance Control and Dynamics, 2014, 37(4): 1114. DOI:10.2514/1.62737 |
| [14] |
RAN Maopeng, WANG Qing, HOU Delong. Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J]. Chinese Journal of Aeronautics, 2014, 27(3): 634. DOI:10.1016/j.cja.2014.04.007 |
| [15] |
韩京清. 自抗扰控制技术-估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008. HAN Jingqing. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008. |
| [16] |
ZHU Zheng, XU Dong, LIU Jingmeng, et al. Missile guidance law based on extended state observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5882. DOI:10.1109/tie.2012.2232254 |
| [17] |
GUO Chao, LIANG Xiaogeng. Integrated guidance and control based on block backstepping sliding mode and dynamic control allocation[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(9): 1559. DOI:10.1177/0954410014555558 |
| [18] |
FENG Yong, YU Xinghuo, MAN Zhihong. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159. DOI:10.1016/s0005-1098(02)00147-4 |
| [19] |
NUSSBAUM R D. Some remarks on a conjecture in parameter adaptive control[J]. Systems & Control Letters, 1983, 3(5): 243. DOI:10.1016/0167-6911(83)90021-X |
| [20] |
HOU Mingzhe, DUAN Guangren. Adaptive dynamic surface control for integrated missile guidance and autopilot[J]. International Journal of Automation and Computing, 2011, 8(1): 122. DOI:10.1007/s11633-010-0563-z |
| [21] |
LI Yongming, TONG Shaocheng, LI Tieshan. Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation[J]. Neural Computing and Applications, 2013, 23(5): 1207. DOI:10.1007/s00521-012-0993-3 |
| [22] |
YAMASAKI T, BALARISHNAN S N, TAKANO H, et al. Second order sliding mode-based intercept guidance with uncertainty and disturbance compensation[J]. AIAA Guidance, Navigation and Control, 2013, 39(5): 1. DOI:10.2514/6.2013-5115 |
 2020, Vol. 52
2020, Vol. 52


