充气膜结构由于自身轻质、可折叠、耗费低等特点，受到了航空航天领域研究者的关注.目前，研究者们已经设计出了很多充气式膜结构，比如飞艇、太阳帆、可展天线、月球定居的多球面结构体、登陆缓冲器等^[1-5].充气膜结构需要依赖内外的压差来辅助实现预期的结构形状，同时，为了有足够的承载能力，往往需要增加索结构进行辅助.对于充气式索膜结构，由于膜和索结构自身的柔性特点，在结构设计的过程中找形分析十分重要.“找形”就是在给定的预应力和边界条件下，寻找最小曲面或者平衡曲面的形状.

目前，在索膜结构的找形分析中主要使用以下3种主流的方法：动力松弛法、力密度法、非线性有限元法^[6].3种方法的基本思路都是对结构进行离散，建立几何方程和本构关系，然后建立平衡方程并进行求解.它们的区别在于对结构离散的单元形式不同.力密度法采用离散的膜线替代连续的膜面域，在计算过程中会产生膜面应力不均匀的误差现象；动力松弛法需要人工控制刚度系数和总动能限值，参数的确定带有很大的经验性，需要做大量的尝试性工作.非线性有限元格式是建立在固体力学大变形问题的基础上，相比前两种方法，它能正确地跟踪反映结构的工作机理，而且相对计算精度较高.随着计算机技术的发展和计算能力的大幅度提高，有限元法已成为较普遍的膜结构的找形方法，因此本文采用非线性有限元方法进行大型索膜结构的找形分析.

充气式索膜结构主要分为两类：气承式和气囊式结构.对于像飞艇这样封闭式的索膜结构，属于气囊式，索的作用一方面是增加膜结构的承载能力，另一方面是约束充气膜结构的形状变化，以便实现预期的外形^[7].索和膜的协同分析问题是索膜结构分析中非常关键的一点，很多学者考虑索和膜之间的滑动问题，考虑滑动索的摩擦过程^[8-11].对于气承式的张拉结构，边索的下部支撑结构对膜结构的作用明显，采用分开分析的方法比较恰当.而对于气囊式索膜结构的找形分析，绳索附着在膜体上，辅助作用为主，因此采用协同找形的方法较为合适，将索单元和膜单元设置为共节点，忽略相互之间的滑动，只关注最后的形状和应力分布.膜结构的优化形状也越来越趋于自由曲面，曲面形成的技术也更加成熟^[12].

针对充气式索膜结构受压差作用的特点，本文提出了压差预置法的概念，并且和节点平衡法相结合，提出了多目标优化的找形分析方案，对于解决工程实际中各种复杂结构的找形问题，有重要的参考价值.

1 理论分析 1.1 非线性有限元找形方法 1.1.1 非线性有限元理论

非线性有限元找形方法将膜结构有限元离散化成由节点和三角形单元构成的空间曲面结构，索结构离散为节点和杆单元构成的空间曲线结构，然后针对索膜结构的大位移小应变状态，建立以节点位移为基本未知量的非线性有限元方程进行求解.

根据虚位移原理，采用修正拉格朗日描述即U.L.方法建立非线性有限元的节点平衡方程为

$ \left( {\left[ {{\mathit{\boldsymbol{k}}_0}} \right] + \left[ {{\mathit{\boldsymbol{k}}_\sigma }} \right] + \left[ {{\mathit{\boldsymbol{k}}_L}} \right]} \right){\rm{d}}{\{ \mathit{\boldsymbol{\delta }}\} ^e} = {\rm{d}}{\{ \mathit{\boldsymbol{F}}\} ^e}. $

(1)

式中：$\left[ {{\mathit{\boldsymbol{k}}_0}} \right] = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt v} {{{\left[ {{\mathit{\boldsymbol{B}}_0}} \right]}^{\rm{T}}}} [\mathit{\boldsymbol{D}}]\left[ {{\mathit{\boldsymbol{B}}_0}} \right]{\rm{d}}\mathit{\boldsymbol{v}}$为一般线性分析的刚度矩阵，与节点位移无关；$\left[ {{\mathit{\boldsymbol{k}}_L}} \right] = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt v} {\left( {{{\left[ {{\mathit{\boldsymbol{B}}_0}} \right]}^{\rm{T}}}.[\mathit{\boldsymbol{D}}]\left[ {{\mathit{\boldsymbol{B}}_L}} \right] + {{\left[ {{\mathit{\boldsymbol{B}}_L}} \right]}^{\rm{T}}}[\mathit{\boldsymbol{D}}]\left[ {{\mathit{\boldsymbol{B}}_0}} \right] + {{\left[ {{\mathit{\boldsymbol{B}}_L}} \right]}^{\rm{T}}}[\mathit{\boldsymbol{D}}]\left[ {{\mathit{\boldsymbol{B}}_L}} \right]} \right)} {\rm{d}}\mathit{\boldsymbol{v}}$为单元的初位移矩阵或大位移矩阵，表示单元位置的变动对单元刚度矩阵的影响；$\left[ {{\mathit{\boldsymbol{k}}_\sigma }} \right] = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt v} {{\rm{d}}{{\left[ {{\mathit{\boldsymbol{B}}_L}} \right]}^{\rm{T}}}.{{\{ \mathit{\boldsymbol{\sigma }}\} }^e}{\rm{d}}\mathit{\boldsymbol{v}}} $为单元的初应力矩阵或几何刚度矩阵，它表示单元中存在的应力对单元刚度矩阵的影响；d{δ}^e为单元节点位移{δ}^e的微分；d{F}^e为载荷向量{F}^e的微分.

1.1.2 小弹性模量找形法

索膜结构的初始平衡状态分析(即找形分析)本质上属于力平衡问题，理论上与结构采用的材料属性无关，目的是让结构能够在初始位形可以自由变形，最终达到预应力分布状态的平衡形状.

不考虑材料属性的自由变形，即不考虑材料的弹性模量和泊松比，在有限元的总刚度矩阵中，线性刚度矩阵和初位移矩阵等于零，只考虑几何刚度矩阵，则非线性有限元找形的基本方程变为

$ \left[ {{\mathit{\boldsymbol{k}}_\sigma }} \right]{\rm{d}}{\{ \mathit{\boldsymbol{\delta }}\} ^e} = {\rm{d}}{\{ \mathit{\boldsymbol{F}}\} ^e}, $

(2)

但是，只考虑几何刚度矩阵，会导致具有复杂形态的结构发生畸变，导致结果很难收敛.

因此在工程实际中，通常采用小弹性模量法，选取比实际弹性模量相对较小的值，近似地将膜和索结构处理为柔性而且能自由变形的材料.假设膜材正交异性材料，应力矩阵[D]与弹性模量成正比，选取虚拟弹性模量E′=λE₀，则平衡方程为

$ \left( {\lambda \left( {\left[ {{\mathit{\boldsymbol{k}}_0}} \right] + \left[ {{\mathit{\boldsymbol{k}}_L}} \right]} \right) + \left[ {{\mathit{\boldsymbol{k}}_\sigma }} \right]} \right){\rm{d}}{\{ \mathit{\boldsymbol{\delta }}\} ^e} = {\rm{d}}{\{ \mathit{\boldsymbol{F}}\} ^e}, $

(3)

式中折减系数λ根据经验一般取1/100~1/10 000，它影响找形的计算速度和精度.若取值过大，材料属性对找形后的预应力影响较大；若取值过小，结果难以收敛.因此，根据实际情况可选取合适的值.

1.2 压差预置法 1.2.1 压差预置法的概念

传统的张拉膜结构，采用小弹性模量法，然后通过位移设置来求解预期的张拉结构.充气式索膜结构的特点是结构刚度的形成需要一定的压差，否则结构本身不能承载.要正确计算出结构的初始形态，必须考虑压差的作用.

因此，针对充气式索膜结构，本文提出了压差预置法的找形概念.所谓的压差预置法，就是在初始形态的结构上，采用小弹性模量法，以施加压力载荷的方法，使膜结构产生近似自由变形的变化直至达到设计目标，例如高度、体积、面积、应力分布等设计要求，从而得出最终的形态.

压差预置法基于小弹性模量法进行找形分析，在虚拟弹性模量设置时，折减系数λ的选取应该与压差的大小相匹配，压差相对较大，会导致过度的大变形，产生不收敛的状态，压差相对较小，不能满足设计要求.

1.2.2 节点平衡法

为介绍节点平衡法，先对自平衡状态进行说明.根据文献[13]，自平衡是针对张力集成结构提出的，该结构由杆结构和柔性索结构组成，与常规结构的不同之处在于，它是在内部预应力作用下才能具有成形能力和承受外载荷的刚度，而且不需要外部支撑就可以达到自身的平衡，“自平衡”由此而来.在自平衡状态里面，每个节点都应该是平衡的，即节点处的合力为零.在找形的过程中，一般是要得到一些参数应该满足的条件，比如长度参数l，根据节点平衡可得到：

$ {F_{{\rm{合 }}}}(k1, \cdots ,kn,l) = 0, $

(4)

式中k1, …, kn为其他参数，因此可以得到一些关于l的方程，这些方程就是本文所关心的未知量所要满足的条件.本文在有限元分析中进行节点平衡迭代的时候，是通过更新节点坐标的方法，即把每次求解的得到的节点新坐标作为平衡方程下一次求解的初始位置，从而一步步实现迭代求解.

1.2.3 压差预置法与节点平衡法相结合

压差预置法能够初步的满足设计要求，其结果可以作为初定的几何曲面.找形分析的最终目的是为了找出尽可能均匀的平衡预应力形态，因此，可以在压差预置法之后，再选用节点平衡法，在初始的几何位形上更新节点坐标，然后重新设定索膜结构真实的材料常数和预应力分布进行自平衡迭代求解，直至迭代求解的结果满足给定的精度，此时得到的几何位形即为找形分析后的初始平衡形状.

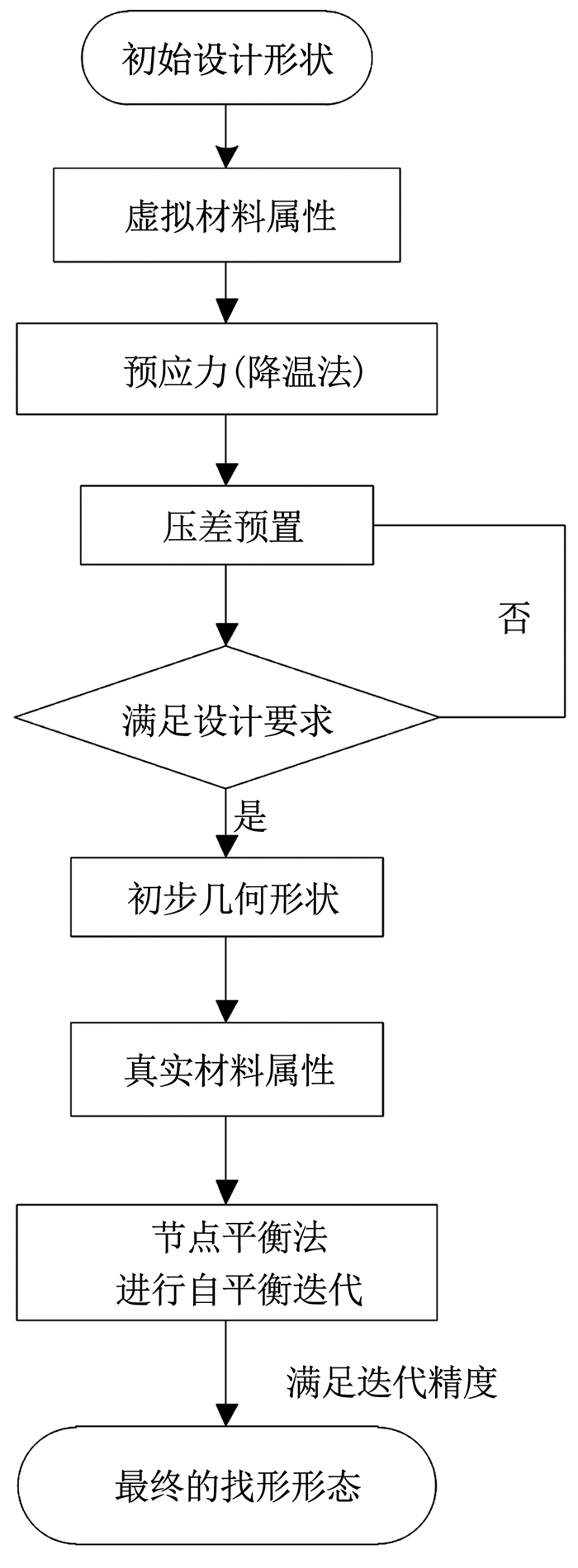
该找形方案的具体流程如图 1所示.在找形分析中，存在着2个重要的控制因素：预应力和压差，这是充气膜和张拉膜不同之处.对于预应力的选择，根据经验值，一般会选择最大应力的1%~5%，除此之外，还要考虑到具体的工况，进行合理的选择.压差预置法中，压差的施加一般采用逐步施加的方法，压差最大值依赖于设计要求，比如高度、应力分布等，在飞艇结构中，选用了索和膜的应力比值作为设计要求.节点平衡法的作用是，对结构的应力分布进行调整，每次迭代都在几何位形上更新节点坐标，然后进行位移和应力的重新求解，迭代停止的条件是可以应力均匀或者应力均衡^[14].

2 验证算例——球形充气膜的找形分析

为验证本文提出的方案，与文献[13]中的方法进行了对比，选择和参考文献中算例的相同参数进行计算.算例选择半径为$6\sqrt{2}$m的圆形，周边为固定边界，在预应力和压差作用下，由平面形状鼓起生成一定矢顶高2.101 m的球形形状.由于采用了小弹性模量法，达到目标矢顶高的过程近似看作充气泡自由膨胀的过程.在压差预置之后，采用自平衡迭代法，对前一步所得的形状进行微调，从而得到受力更加均衡的形态.

2.1 充气膜结构的模型

和对比算例取相同的参数，初始模型为$6\sqrt{2}$ m的圆形平面，膜材结构的预应力的大小取σ₀=8×10⁵ Pa，膜材的弹性模量为E=2.5×10¹⁰ Pa，折减系数为λ=1/1 000，泊松比μ=0.35，厚度为1 mm.热膨胀系数设为α=1×10^-4，采用降温法设置预应力，根据预应力与温差的关系式σ=E·α·Δt，可求得Δt=0.32 ℃.

在ANSYS12.1中，采用SHELL41的三角形单元，由于该模型由平面鼓起生成三维的曲面，大变形幅度较大，因此网格划分时，单元的大小要稍微小一些，全局大小设置为400 mm.有限元模型如图 2所示.

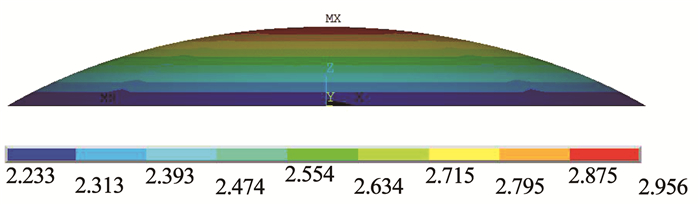
首先采用压差预置法进行找形，压力沿着Z方向，由于变形较大，需要将压强逐步加载，采用多载荷步法，从50 Pa开始，增量为50 Pa，直至加载到300 Pa，此时的矢量高为2 095 mm，在文献[15]中，此模型的解析解为2 101 mm，误差为0.29%.之后，为了使受力更均匀，使用节点平衡法.此时，更新节点坐标，然后将材料属性改为真实属性，再进行自平衡迭代，迭代4次后，达到2 100 mm，此结果也逼近了解析解，同时最大和最小应力的变化值相比第1次迭代变化很小(见表 1)，因此可以终止迭代.最终找形分析的结果如图 3所示.

2.2 压差的作用分析

充气膜结构的找形分析属于大位移小应变问题，具有很强的几何非线性，压差载荷的分步加载有利于结构形态的逐步稳定变化.压差是维持结构稳定的关键因素.

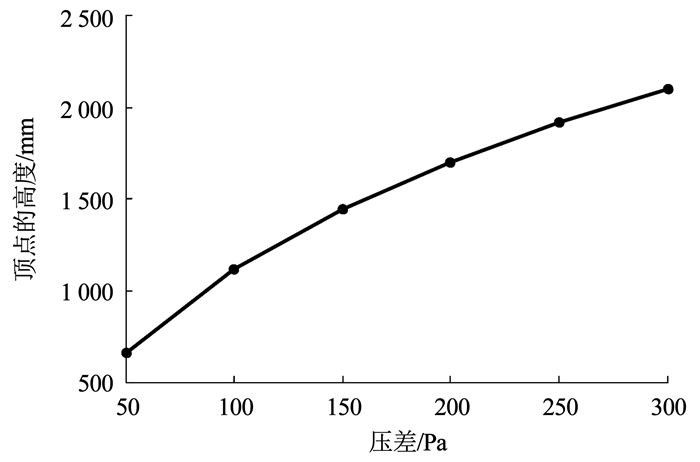
为了分析压差对结构的位移变化的影响，选取顶点的高度变化作为因变量进行分析.如图 4所示，在一定范围内，压差加载的过程中，结构的位移变化基本呈现线性增长的状态.需要注意的是，预应力的大小和压差需要控制在一定范围内，否则会产生不收敛的状态.

3 算例分析——飞艇索膜结构的找形分析

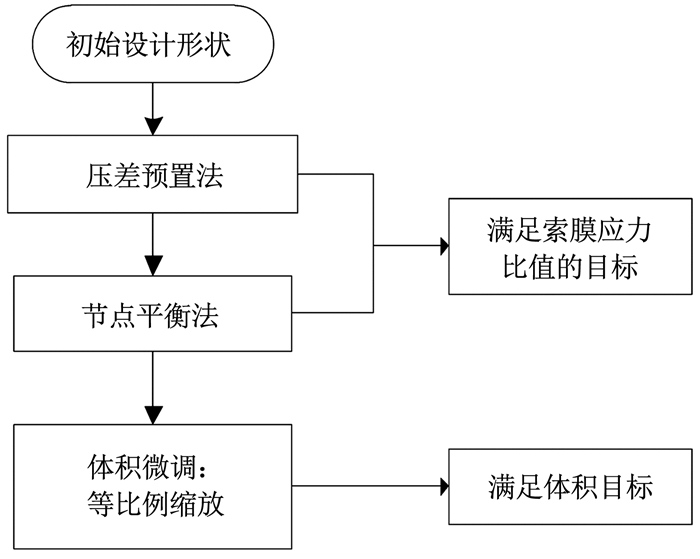
飞艇艇身属于封闭式囊体结构，在进行形状的优化时，属于多目标优化.飞艇的承载能力主要是靠浮力和重力、载荷平衡来实现的，因此囊体的体积必须满足设计要求；同时，为了充分发挥索和膜的材料性能，期望索和膜的应力之比有一个合适的值.针对飞艇的特点，本文提出了合理的找形方案，如图 5所示，先采用压差预置法与节点平衡法相结合的方法来满足索和膜结构的应力比值的设计要求，然后在此基础上，采用等比例缩放的方法，对结构进行微调以满足囊体的体积要求.

3.1 飞艇索膜结构的模型

以10 m的飞艇作为实例，模型的示意图如图 6所示，外形通过两个椭圆曲线组成，作为初步的设计模型.该艇的设计要求为满足体积为33.5 m³，并且考虑增加绳索来加强结构的承载性能，横向绳索9根，纵向绳索8.组成结构的材料属性见表 2.

特别说明，热膨胀系数不是真实的，只是为了采用降温法施加预应力需要，自行设置的.对于膜材和绳索的折减系数，均采用λ=1/1 000.

在ANSYS12.1中创建有限元模型，膜结构采用SHELL41三角单元，属性为只受拉，不受压，索结构采用LINK10单元，属性也是只受拉，不受压.索膜结构在找形分析时，采用协同找形的方式，即有共同的坐标位置，因此将索单元和膜单元进行共节点设置.全局大小设置为100 mm.约束条件为：左顶点约束住x、y、z 3个方向的位移，右顶点只约束y和z方向.

求解方式采用非线性有限元方法，考虑大变形因素，采用Newton-Raphson迭代方法求解位移，收敛准则采用力收敛准则，收敛值可在0.01~0.05之间选择.模型计算的收敛受到很多因素的影响，如结构的几何外形、网格划分的密度、预应力的设置等，需要根据算例的情况进行调整.

3.2 找形过程

飞艇结构的设计中，通常会加入索结构来增强承载能力，根据索和膜的强度值，膜材的强度800 N/cm，索的强度值为1.25 t/φ4，但是设计形状受载时，索发挥的作用不大，在支撑压差作用下，索的应力值比膜材小很多.因此，希望通过找形分析后，能让索和膜充分发挥出材料的性能.

本算例找形分析的目标为：在设计形状的基础上改善飞艇索膜结构，使索和膜在支撑压差800 Pa作用下，应力值之比在1.6倍左右，同时最终模型的总体积为33.5 m³.

预应力的选择：选择设计形状受载800 Pa时，索的最大应力值为3.512 MPa，预应力选取为该值的3%，因此，索结构的预应力为σ₁=1.053 6×10⁵ Pax；由于膜结构的弹性模量比索结构小很多，因此预应力选为索结构的预应力的9/20，σ₂=4.740 0×10⁴ Pa.预应力的施加，索和膜都选用降温法，由于虚拟弹性模量选择实际模量的1/1 000，虚拟热膨胀系数为实际值的1 000倍，根据公式σ=E·α·Δt，对应的索的降温温差为Δt₁=0.526 8 ℃，膜的降温温差为Δt₂=0.526 8 ℃，参考温度选0 ℃.

采用压差预置法进行找形分析时，压差采用多载荷步施加，压差值达到185 Pa时，索和膜的最大应力值之比为1.85.此时选取的应力比值要比设计目标大一些，因为在设计模型基础上压差施加后模型会膨胀放大，比值随着模型的扩大会增大.

在压差预置找形之后，模型的应力分布需要做微量的调整，采用自平衡迭代法，迭代5次(根据经验，一般5次之内即可满足平衡状态).由于初始模型的体积即为33.5 m³，进行压差找形后，体积增大，因此在找形结束后，把模型进行等比例缩小，缩小至体积为33.5 m³.

3.3 找形分析前、后的对比

找形分析之后，飞艇的形状有所变化.经过分析之后，发现相比横向索，纵向索的作用相对较小，因此只关注纵向截面图.

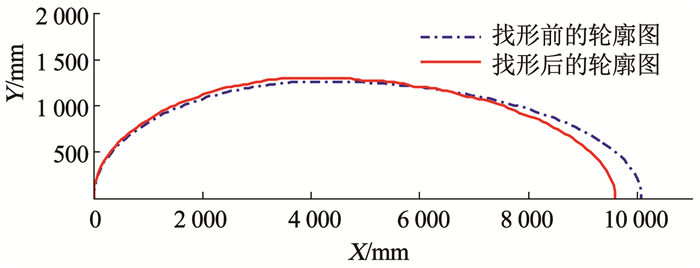
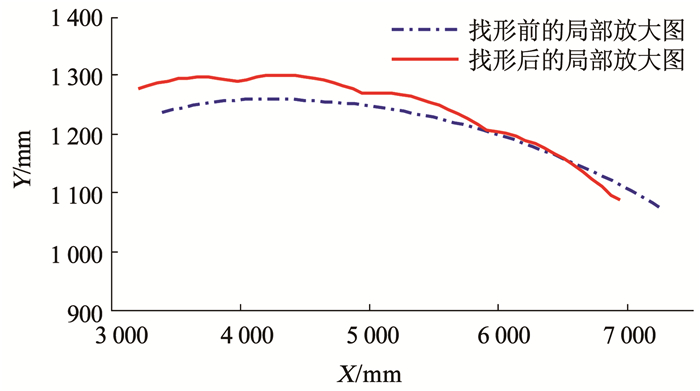
如图 7所示，总长度由10.078 m缩短为9.59 m，艇身变得更圆润一些.如图 8局部放大图所示，找形分析之后的模型存在鼓包，这样的形状会使索结构发挥本身的作用，承担更多的载荷来优化膜结构的受力.

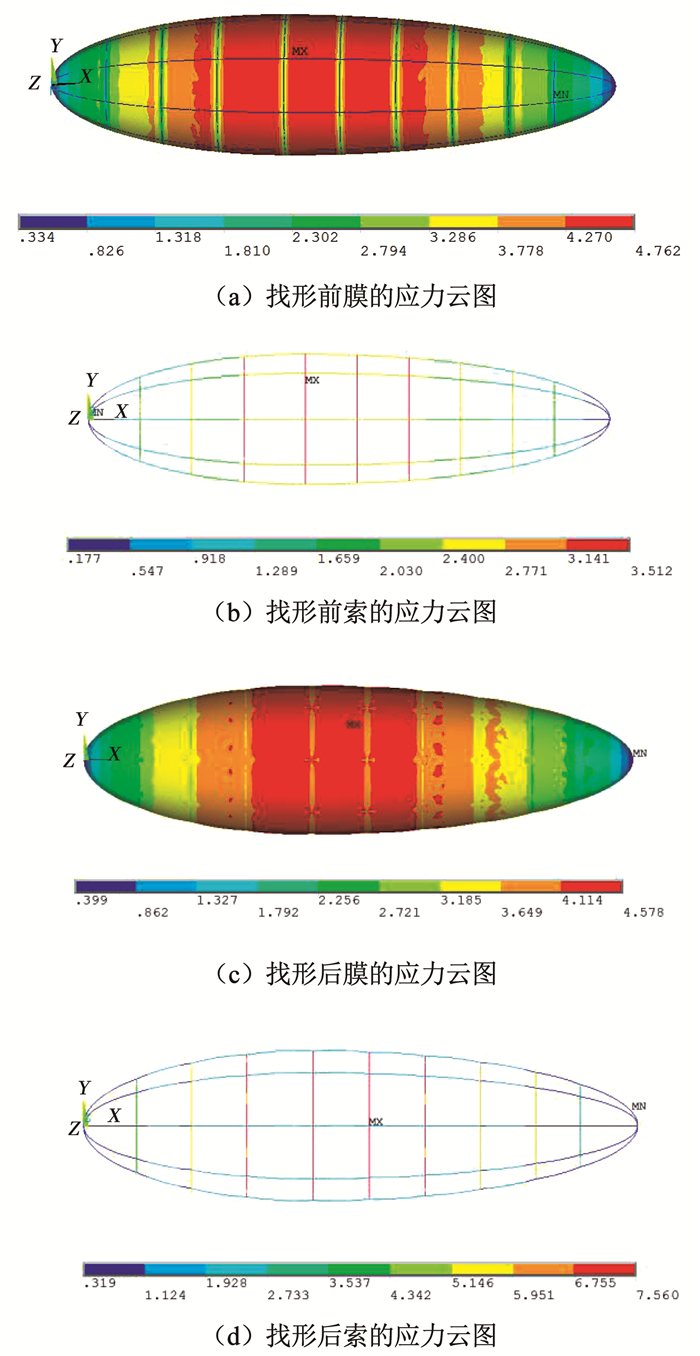
为了研究找形分析前后的模型效果，按照设计目标，分析在800 Pa压差作用下的模型的受力情况.如图 9所示，是找形分析前后的模型的应力云图.找形分析之前，索的最大应力是3.512 MPa，膜的最大应力为4.762 MPa，比值为0.74；找形分析之后的模型，索的最大应力是7.56 MPa，膜的最大应力为4.578 MPa，倍数为1.65，与设计目标1.6倍左右相符合，找形的效果很好.

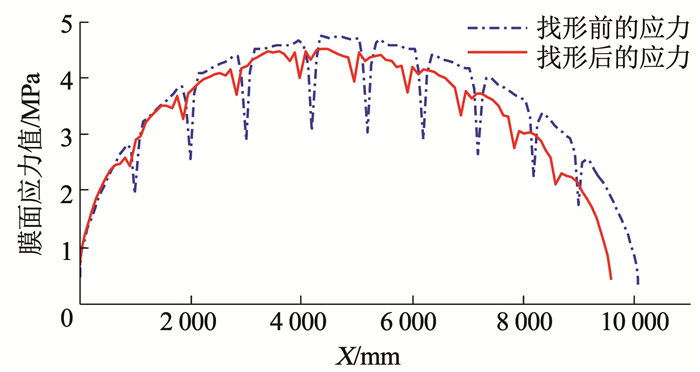
经过对比之后，发现找形之后膜的最大应力值有所减小，而且索的应力值则有明显增大，是找形前的2.15倍，索的应力值的增大改善了膜的应力分布，如图 10所示，采集了飞艇结构一条母线上的所有节点的应力值，即图 9(a)和图 9(c)中的找形前、后的膜的应力值进行对比，由图可知，膜的受力整体水平下降，而且受力更加均匀.

3.4 方案评价

通过压差预置法与节点平衡法相结合，对10 m飞艇的索膜结构进行找形分析，得到了在800 Pa压差作用下，索与膜的最大应力比值为1.65的优化模型.

最初的设计模型，索与膜的最大应力比值为0.74，但是索的强度值比膜大很多，索的材料性能没有得到充分的发挥.针对充气式索膜结构的特点，提出了多个设计目标的优化方案，索膜的应力比值为1.6左右，目标体积为33.5 m³.通过本文提出的找形方案，对设计结构进行优化之后，调整了索膜结构的应力分布状态，使膜结构的受力更加均匀，索结构充分发挥了自身的承载性能.

4 结论

1) 球形充气膜算例中，以一定的矢顶高和应力分布均衡为优化目标，采用本文的方案得到了与理论值仅仅相差0.29%的结果，验证了本文所提方案的可行性.

2) 飞艇索膜结构的找形分析中，以固定体积、固定索膜最大应力的比值和应力分布均匀为优化目标，采用本文的优化方案，最终得到了索膜最大应力的比值为1.65的优化模型，使索的最大应力值为找形前的2倍，充分发挥了索的增强承载作用.