蜂窝夹芯结构[1]被广泛应用于飞机的舵面、发动机整流罩、机翼翼尖、地板及内饰等.因此在飞机的飞行过程中可能一直处于强噪声环境中.研究表明,当飞机长时间处于这种高强噪声激励的条件下,结构会产生动力学响应,易导致结构产生声疲劳[2-3].为了使蜂窝夹芯结构可以降低噪声、吸收部分声能,在其上面板上进行开孔处理.但由于其面板上有开孔,孔边会出现应力集中导致寿命降低的问题,因此研究开孔大小对结构声疲劳寿命的影响也十分具有意义.
目前声疲劳寿命计算的方式主要分为时域和频域两种.时域的主要方法为雨流计数法[4-6],该方法需要进行循环计数、数据处理量非常大.因此目前主流的方法是频域内基于应力概率密度函数及功率谱密度法[7-8]的随机振动[9]疲劳寿命评估.
为了研究结构在声场中的响应,以及由此计算出结构的声疲劳寿命,就必须考虑声振耦合[10-12]作用.针对此问题,本文考虑到蜂窝夹芯板在强噪声载荷下的声振耦合作用,并将开孔蜂窝夹芯结构看做是多个赫姆霍兹共鸣器[13-14]的并联组合,认为不同开孔直径下具有不同的吸声能力.运用有限元与边界元耦合的方法,并基于功率谱密度法计算结构的声疲劳寿命.
1 理论基础 1.1 声振耦合基本原理在声振耦合问题中,可以运用一个耦合系数λc来判定是否需要耦合:
| $ {\lambda _c} = \frac{{{\rho _0}c}}{{{\rho _t}T\omega }}. $ |
式中:ρ0为流体的密度;c为声音在流体中的流速;ρt为结构的密度;T为结构的等效厚度;ω为角频率.
当λc>1认为是需要耦合的;当λc≪1时,可以认为是非耦合的.
耦合方程为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_s} + {\rm{j}}\omega {\mathit{\boldsymbol{C}}_s} - {\omega ^2}{\mathit{\boldsymbol{M}}_s}}&{{\mathit{\boldsymbol{L}}_c}}&0\\ {\mathit{\boldsymbol{L}}_c^{\rm{T}}}&{\frac{{{\mathit{\boldsymbol{D}}_{11}}}}{{{\rho _0}{\omega ^2}}}}&{\frac{{{\mathit{\boldsymbol{D}}_{12}}}}{{{\rho _0}{\omega ^2}}}}\\ 0&{\frac{{{\mathit{\boldsymbol{D}}_{21}}}}{{{\rho _0}{\omega ^2}}}}&{\frac{{{\mathit{\boldsymbol{D}}_{22}}}}{{{\rho _0}{\omega ^2}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{\mu _{i1}}}\\ {{\mu _{i2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_s}}\\ {{F_{a1}}}\\ {{F_{a2}}} \end{array}} \right]. $ | (1) |
式中:Ks、Cs、Ms、Dij分别为结构的刚度矩阵、阻尼矩阵、质量矩阵和系数矩阵;ui为各节点的位移;μi1为声场与结构耦合网格两侧的声压差;μi2为声场网格中未和结构耦合的网格两侧的声压差;Fs为作用在结构上的外载荷(不包括声压载荷);Fa1为作用在声场-结构耦合的网格上的声压载荷;Fa2为作用在声场非耦合的网格上声压载荷;Lc为耦合矩阵.
1.2 随机声学对于随机过程来说,输入载荷的PSD矩阵SXX和输出响应的PSD矩阵SYY可以通过传递函数矩阵H来描述:
| $ {\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{YY}}}} = {\mathit{\boldsymbol{H}}^*}{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{XX}}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}. $ | (2) |
对于输入载荷SXX,可以通过主成分分析运用SVD分解或者Schur分解为
| $ {\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{XX}}}} = {\mathit{\boldsymbol{\tilde X}}^*}{\mathit{\boldsymbol{S}}_{qq}}{\mathit{\boldsymbol{\tilde X}}^{\rm{T}}}. $ |
式中:
| $ {\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{YY}}}} = {\mathit{\boldsymbol{H}}^*}{\mathit{\boldsymbol{\tilde X}}^*}{\mathit{\boldsymbol{S}}_{qq}}{\mathit{\boldsymbol{\tilde X}}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{T}}} = {\mathit{\boldsymbol{Y}}^*}{\mathit{\boldsymbol{S}}_{qq}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}. $ | (3) |
通常来说,对于结构响应可以通过模态叠加来表示:
| $ \mathit{\boldsymbol{\tilde Y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} p}}. $ |
式中: Φ为模态应力矢量;p为模态随机参与因子.
因此式(3)可以写为:
| $ {{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{YY}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^*}{\mathit{\boldsymbol{p}}^*}{\mathit{\boldsymbol{S}}_{{\rm{qq}}}}{\mathit{\boldsymbol{p}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^*}{\mathit{\boldsymbol{S}}_{pp}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}},}\\ \;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{S}}_{pp}} = {\mathit{\boldsymbol{p}}^*}{\mathit{\boldsymbol{S}}_{qq}}{\mathit{\boldsymbol{p}}^T}.} $ |
通过数值计算得到结构各节点的互功率谱曲线,通过平稳随机过程的叠加得到结构危险点的PSD曲线,作为输入条件进行功率谱密度法的声疲劳寿命分析.
功率谱密度法计算结构的声疲劳寿命,其公式可以表示为
| $ T = \frac{C}{{E({M_T})\int_0^\infty P (s){s^b}{\rm{d}}s}}. $ |
式中:T为结构声疲劳的寿命;b、C为材料的S-N曲线的相关常数;E(MT)为单位时间内应力循环的平均发生率;P(s)为应力概率密度函数;s为应力.
S-N曲线可以用幂函数形式拟合为
| $ C = N{s^{\rm{b}}}. $ |
本文采用的S-N曲线的使用范围为102~106个循环周期.
若随机过程为窄带随机过程,则E(MT为零穿越速率E(0);对于宽带随机过程,E(MT为峰值出现速率E(p),公式如下:
| $ E(0) = \sqrt {\frac{{{m_2}}}{{{m_0}}}} ,E(p) = \sqrt {\frac{{{m_4}}}{{{m_2}}}} . $ |
式中:mn为应力功率谱密度的第n阶惯性矩,即
| $ {m_n} = \int {{f^n}} G(f){\rm{d}}f. $ |
式中:f为频率;G(f)为危险点的应力功率谱密度函数.加速度功率谱密度函数Gg(f)与应力功率谱密度函数之间的关系可以表示为
| $ G(f) = \frac{{{H^2}}}{{{\omega ^4}}}{G_{\rm{g}}}(f), $ |
式中:H与材料和结构形式以及作用点和响应点的位置有关,对于一个确定的结构,H可以近似为:
| $ H = \frac{\sigma }{A}. $ |
式中:σ为响应点的应力,A为作用点的位移.
为了判断一个平稳随机过程是属于宽带过程还是属于窄带过程,引入一个不规则因子来判断:
| $ \gamma = \frac{{{m_2}}}{{\sqrt {{m_0}{m_4}} }}. $ |
当不规则因子接近0时,可以认为平稳随机过程为宽带随机过程;当不规则因子接近1时,可以认为是窄带过程.
由随机过程理论可知,如果随机应力过程是一个窄带过程,那么应力振幅满足Rayleigh分布,即窄带的概率密度函数为
| $ {P_p}(s) = \frac{S}{{\sigma _s^2}}{{\rm{e}}^{\frac{{ - {S^2}}}{{2\sigma _s^2}}}} = \frac{S}{{{m_0}}}{{\rm{e}}^{\frac{{ - {S^2}}}{{2{m_0}}}}}. $ |
对于宽带随机过程,其相应的应力峰值概率密度函数是介于Gauss分布和Rayleigh分布之间的一种分布. Dirlik公式是通过蒙特卡罗法进行全面的计算机模拟所得到的宽带峰值概率密度公式,是具有较好精度的半经验式[8].
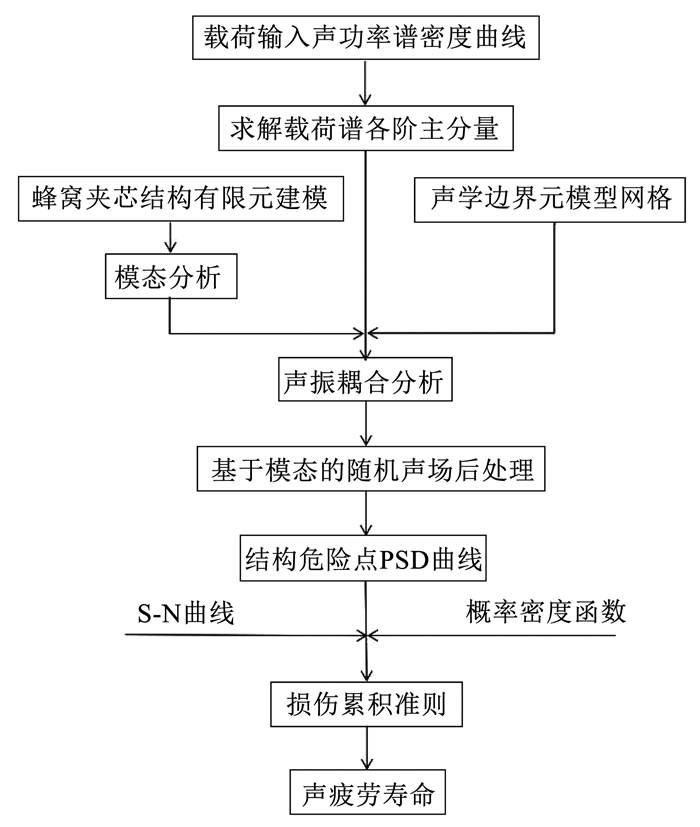
2 数值分析 2.1 技术路线本文使用的随机振动声疲劳寿命评估的技术路线如图 1所示.
|
图 1 技术流程 Fig. 1 Technical flowchart |
首先通过有限元软件进行结构的模态分析,并对结构表面的声场进行边界元网格划分,以及对输入载荷进行主成分分析[15].随后进行声振耦合的数值分析[16-17]计算并进行基于模态的随机声场后处理,得到结构危险点的PSD曲线,选取合适的概率密度函数.最后基于材料本身的S-N曲线和概率密度函数求解结构的随机振动疲劳寿命.
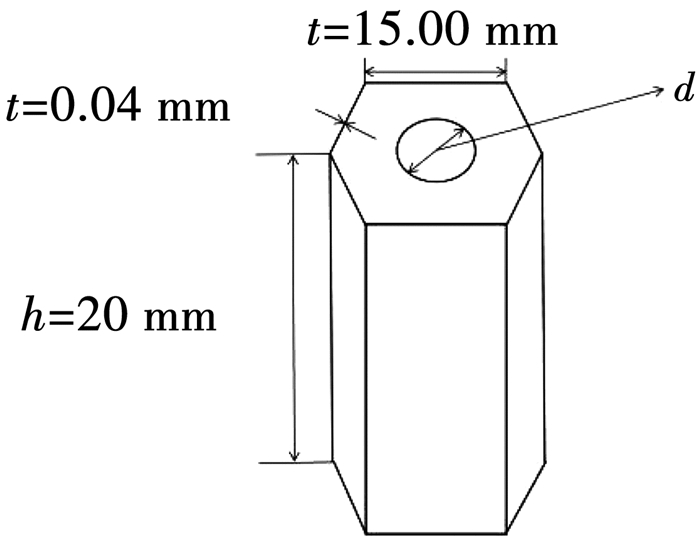
2.2 建立模型蜂窝夹芯结构整体尺寸为300.000 mm×207.846 mm×20.600 mm;上、下面板厚度均为0.3 mm,蜂窝芯子高度为20 mm;正六边形蜂窝结构边长为L=15 mm,壁厚t=0.04 mm,上面板开孔,孔径直径大小为d,d=0, 2, 4, …, 18, 20 mm.几何模型如图 2所示, 蜂窝结构细节图如图 3所示.

|
图 2 蜂窝夹芯结构几何模型 Fig. 2 Geometry model of honeycomb sandwich structure |
|
图 3 蜂窝结构细节图 Fig. 3 Detailed drawing of honeycomb structure |
当利用声学软件Virtual.lab Acoustic进行声学相关计算时,网格的尺寸大小要一致,局部网格的加密并不能提高精度,因为流体模型的计算精度是由多数单元控制的.
若已知计算的最高频率fmax,则所有的单元长度L应满足:
| $ L \le \frac{c}{{6{f_{\max }}}}. $ |
但在进行结构分析时,应在应力和位移梯度大的地方将网格细化;以及在声源附近、尖角、孔等不连续的地方以及声学网格中非常接近的面,都应将结构网格细化.
蜂窝夹芯结构分为上、下面板和中间的蜂窝夹芯,各层材料均选取LY12CZ铝合金.各层材料属性相同见表 1.空气介质材料属性见表 2.
| 表 1 LY12CZ材料属性 Tab. 1 LY12CZ material properties |
| 表 2 空气介质材料属性 Tab. 2 Air media material properties |
频带范围取:10~3 750 Hz、步长为10 Hz,载荷为分贝数是163 dB的高斯白噪声;其PSD曲线可由下式得到,并作为加载施加在整个模型的声学网格面上.而声学网格是从结构表面提取的二维边界元网格,且蜂窝夹芯结构采用壳单元建模,因此声学网格和结构的网格具有一致性.参考声压P0=2×10-5 Pa, 即
| $ {\rm{dB}} = 20 \times {\rm{lg}}\left( {\frac{P}{{{P_0}}}} \right). $ |
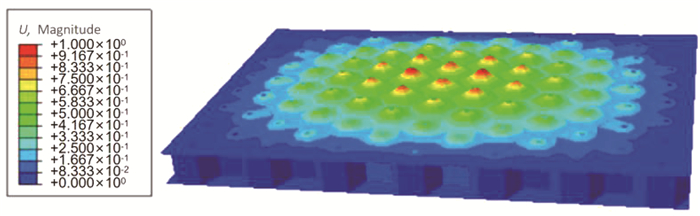
模态分析时采用的边界条件为四边固支.模态和固有频率是结构的固有属性,每一阶固有频率对应一个模态.当外界的激励载荷的频率与结构某一阶固有频率相近时,结果将产生对应的变形.由于结构仅开孔尺寸不同,因此各模型的低阶模态具有相似性,本文只给出孔径d=4 mm的前6阶模态,如图 4~图 9所示,并给出前6阶模态对应的固有频率,见表 3.
|
图 4 d=4 mm的蜂窝夹芯结构1阶模态 Fig. 4 First-order mode of honeycomb sandwich structure with d=4 mm |

|
图 5 d=4 mm的蜂窝夹芯结构2阶模态 Fig. 5 Second-order mode of honeycomb sandwich structure with d=4 mm |

|
图 6 d=4 mm的蜂窝夹芯结构3阶模态 Fig. 6 Third-order mode of honeycomb sandwich structure with d=4 mm |
|
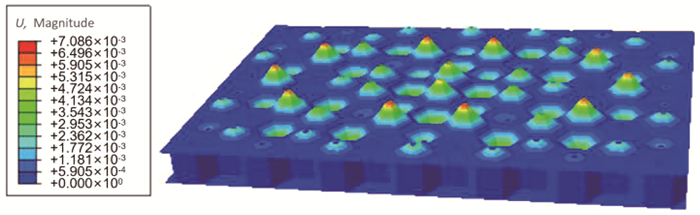
图 7 d=4 mm的蜂窝夹芯结构4阶模态 Fig. 7 Fourth-order mode of honeycomb sandwich structure with d=4 mm |

|
图 8 d=4 mm的蜂窝夹芯结构5阶模态 Fig. 8 Fifth-order mode of honeycomb sandwich structure with d=4 mm |

|
图 9 d=4 mm的蜂窝夹芯结构6阶模态 Fig. 9 Sixth-order mode of honeycomb sandwich structure with d=4 mm |
| 表 3 d=4 mm的前六阶固有频率 Tab. 3 First six natural frequencies of d=4 mm |
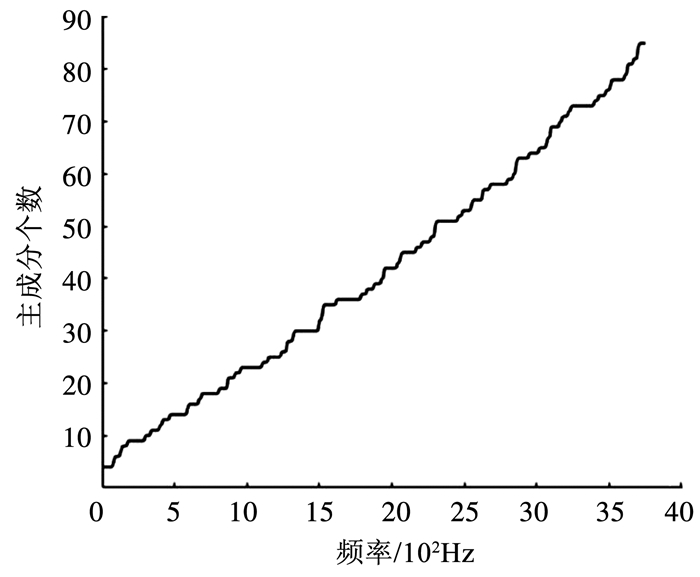
对输入载荷的PSD矩阵进行主成分分析,采用Schur分解,截断误差为0.000 1.该输入功率谱密度载荷可以提取为85阶主成分,图 10为主成分个数随频率增长图.85阶主成分全部用于后续的计算过程中.
|
图 10 主成分个数 Fig. 10 Numbers of principal components |
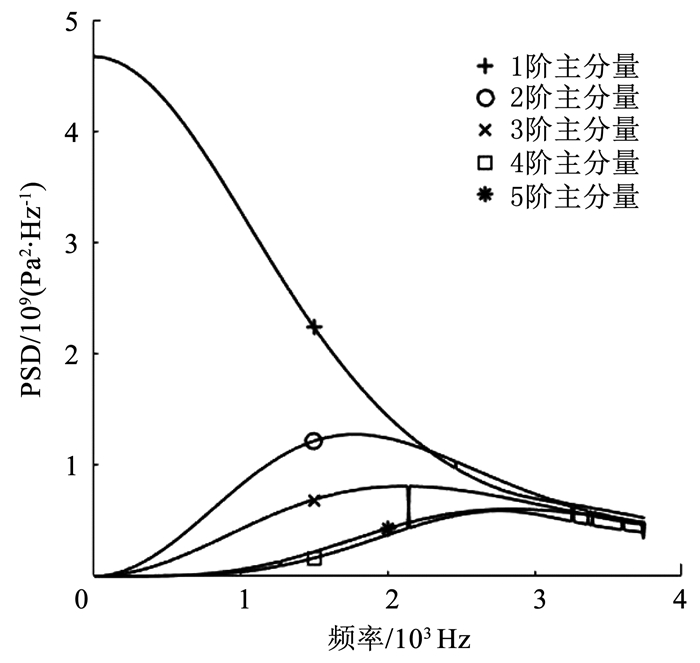
由于前几阶主成分的影响较大,只展示前5阶主成分的自功率谱曲线如图 11所示.
|
图 11 前5阶主成分的自功率谱密度曲线 Fig. 11 Auto-power spectral density curves of first five orders principal components |
由图 11可以看出,1阶主成分在低、中频时有非常显著的贡献,在高频时略低.其余阶主成分在低频较低,中频段有较大的贡献.
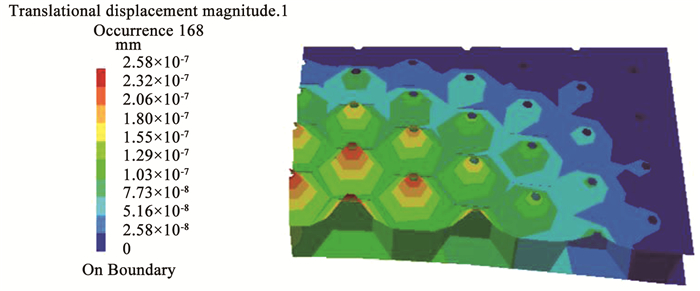
3.3 声振耦合分析通过基于模态的声振耦合分析,可以得到结构在各频率下的响应,图 12~图 14给出孔径d=4 mm的结构在1阶主成分下的前3阶固有频率处的位移云图.云图只显示结构的1/4.
|
图 12 开孔直径为4 mm 1阶主成分下的1阶固有频率的位移云图 Fig. 12 Displacement cloud map of first-order natural frequency under first-order principal component with opening diameter of 4 mm |
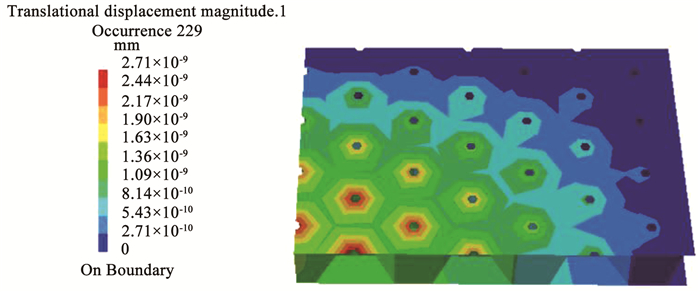
|
图 13 开孔直径为4 mm 1阶主成分下的2阶固有频率的位移云图 Fig. 13 Displacement cloud map of second-order natural frequency under first-order principal component with opening diameter of 4 mm |

|
图 14 开孔直径为4 mm 1阶主成分下的3阶固有频率的位移云图 Fig. 14 Displacement cloud map of third-order natural frequency under first-order principal component with opening diameter of 4 mm |
由于结构四边固支,因此位移较大的部位位于板的中心,又由于开孔结构,板中心的孔边位移最大,逐渐向板边递减.低阶模态对于结构的位移贡献较大,可以明显看出:1阶固有频率的位移约为2阶或3阶的100倍左右.
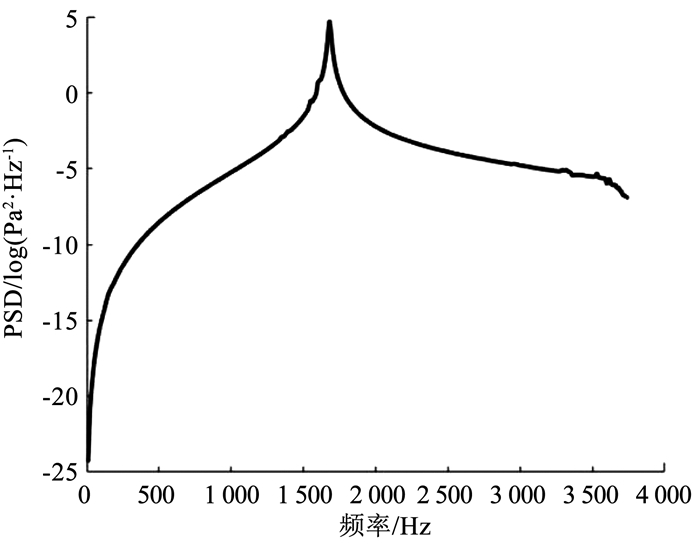
3.4 PSD曲线通过数值分析,得到结构危险点的PSD曲线,如图 15所示.
|
图 15 开孔直径为4 mm结构的输出PSD曲线 Fig. 15 Output PSD curve of structure with opening diameter of 4 mm |
图 15为对数坐标系下的输出载荷的PSD曲线,可以看出,波峰出现在1阶固有频率处,对于其余阶的固有频率,PSD曲线仅出现较小的抖动;可以看出,对结构寿命影响最为严重的是结构的1阶固有频率.
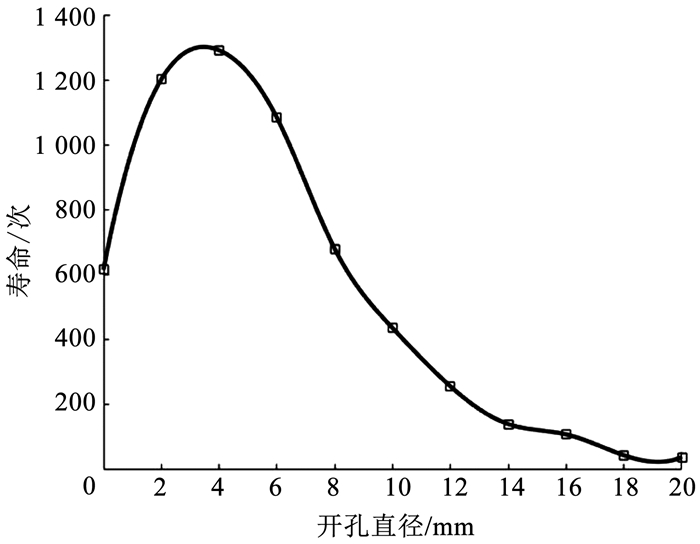
3.5 声疲劳寿命表 4、图 16给出163 dB白噪声载荷下,不同开孔直径的声疲劳寿命.
| 表 4 163 dB下不同孔径的声疲劳寿命 Tab. 4 Acoustic fatigue life of structures with different opening diameters under 163 dB |
|
图 16 163 dB下不同孔径的声疲劳寿命 Fig. 16 Acoustic fatigue life of structures with different opening diameters under 163 dB |
在163 dB的载荷下,非开孔结构的声疲劳寿命为616.13次,寿命最大的为开孔直径为4 mm的结构,寿命为1 290.72次.寿命的比值为2.09倍.整条曲线呈现先上升后下降的趋势,表明在结构开孔较小时,由于孔径的不断增大,入射进结构的声波逐渐增加,由于孔径相对较小,空气的粘滞作用较明显,因此声疲劳寿命呈现上升趋势;随着孔径逐渐增大,粘滞作用降低,孔边应力集中系数不断增大,结构声疲劳寿命呈下降趋势.
当开孔直径大于8 mm时,结构声疲劳寿命小于非开孔结构,此时开孔结构不具有优势.
3.6 不同噪声载荷下结构的疲劳寿命由上述结果可知,在163 dB的载荷条件下,结构的开孔直径小于8 mm时,开孔结构的寿命均大于非开孔结构.为了确定该结论在不同的载荷条件下均适用,下面给出145~160 dB,以每3 dB为增量的不同载荷下的结构疲劳寿命.由于当结构开孔直径大于8 mm时,163 dB载荷下的寿命已小于非开孔结构,对于结构设计来说已不可取,故后续计算只考虑开孔直径小于8 mm的结构.
对于低于157 dB的载荷,其结构的声疲劳寿命已经超过S-N曲线的计算范围,虽然计算得出的寿命已经大于S-N曲线的使用范围102~106循环周期,但是对低分贝噪声载荷的寿命计算依然很有参考意义,计算得出的寿命值大于106时,计算得出的结果仅作为参考,并不代表实际寿命.
| 表 5 不同载荷下不同孔径结构的声疲劳寿命 Tab. 5 Acoustic fatigue life of structures with different opening diameters under different loads |

|
图 17 对数坐标系下不同开孔直径声疲劳寿命 Fig. 17 Acoustic fatigue life of structures with different opening diameters in logarithmic coordinate system |
由图 17可知,对于不同载荷下的开孔结构,寿命曲线具有相似性,因此开孔直径小于8 mm时,寿命较非开孔结构更有优势.
在同一开孔直径下,噪声载荷每增加3 dB,结构寿命降低一个量级.
4 结论1) 引入声场对结构的影响,考虑声振耦合作用,当声波入射到孔隙内时,声波的振动带动空气的振动,由于空气的粘滞性作用,声波的声能转化为热能并耗散掉.相对于传统的声疲劳计算,更能发挥结构的优势.
2) 运用功率谱密度法计算结构声疲劳命,只需要获得结构的响应功率谱密度曲线,对于宽带和窄带给出相应的概率密度函数,即可计算各种形式的随机过程的声疲劳寿命.
3) 在蜂窝上面板开小孔,不但有助于降低结构的质量,同时,相较于非开孔结构,会获得更好的声疲劳寿命,边长为15 mm的蜂窝夹芯结构,开孔直径为4 mm时,具有较好的声疲劳寿命.其寿命大于非开孔结构的寿命的两倍.
| [1] |
柳敏静, 武湛君. 复合材料蜂窝夹层结构在飞机中的应用[J]. 科技导报, 2016, 34(8): 21. LIU Minjing, WU Zhanjun. Application of composite honeycomb sandwich structure in aircraft[J]. Science & Technology Review, 2016, 34(8): 21. DOI:10.3981/j.issn.1000-7857.2016.08.003 |
| [2] |
WHITE R G. Developments in the acoustic fatigue design process for composite aircraft structures[J]. Composite Structures, 1990, 16(1/2/3): 171. DOI:10.1016/0263-8223(90)90071-L |
| [3] |
VAICAITIS R. Acoustic fatigue-A Monte Carlo approach[C] //Proceedings of the 28th Structures, Structural Dynamics and Materials Conference. Monterey, CA: AIAA, 1987. DOI: 10.2514/6.1987-916
|
| [4] |
赵晓鹏, 姜丁, 张强, 等. 雨流计数法在整车载荷谱分析中的应用[J]. 科技导报, 2009, 27(3): 67. ZHAO Xiaopeng, JIANG Ding, ZHANG Qiang, et al. Application of rain-flow counting method in the analysis of load spectrum[J]. Science & Technology Review, 2009, 27(3): 67. DOI:10.1109/CLEOE-EQEC.2009.5194697 |
| [5] |
NIE Hong. A modified rainflow counting method[J]. International Journal of Fatigue, 1991, 13(6): 465. DOI:10.1016/0142-1123(91)90481-D |
| [6] |
金奕山, 李琳. 关于航空发动机结构声疲劳寿命估算方法的探讨[J]. 航空动力学报, 2003, 18(3): 373. JIN Yishan, LI Lin. Sonicfatigue life prediction of aeroengine structure[J]. Journal of Aerospace Power, 2003, 18(3): 373. DOI:10.3969/j.issn.1000-8055.2003.03.013 |
| [7] |
徐绯, 肖寿庭. 结构声疲劳寿命估算的功率谱密度法[J]. 机械强度, 1996, 18(4): 38. XU Fei, XIAO Shouting. The power spectral density method for the estimation of the sonic fatigue life[J]. Journal of Mechanical Strength, 1996, 18(4): 38. DOI:10.16579/j.issn.1001.9669.1996.04.011 |
| [8] |
王明珠.结构振动疲劳寿命分析方法研究[D].南京: 南京航空航天大学, 2009 WANG Mingzhu. Research on life analysis method for structure vibration fatigue[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009 |
| [9] |
TOVO R. Cycle distribution and fatigue damage under broad-band random loading[J]. International Journal of Fatigue, 2002, 24(11): 1137. DOI:10.1016/s0142-1123(02)00032-4 |
| [10] |
白长青, 周进雄, 闫桂荣. 声振耦合对薄壁圆柱结构动力特性的影响[J]. 机械工程学报, 2011, 47(5): 78. BAI Changqing, ZHOU Jinxiong, YAN Guirong. Effectsof sound field on thin-wall cylindrical structure dynamic characteristics[J]. Journal of Mechanical Engineering, 2011, 47(5): 78. DOI:10.3901/JME.2011.05.078 |
| [11] |
CHENG L. Fluid-structural coupling of a plate-ended cylindrical shell: Vibration and internal sound field[J]. Journal of Sound and Vibration, 1994, 174(5): 641. DOI:10.1006/jsvi.1994.1299 |
| [12] |
CRAGGS A. Coupling of finite element acoustic absorption models[J]. Journal of Sound and Vibration, 1979, 66(4): 605. |
| [13] |
GAI Xiaoling, XING Tuo, LI Xianhui, et al. Sound absorption of microperforated panel mounted with helmholtz resonators[J]. Applied Acoustics, 2016, 114: 260. DOI:10.1016/j.apacoust.2016.08.001 |
| [14] |
KOMKIN A I, MIRONOV M A, BYKOV A I. Sound absorption by a Helmholtz resonator[J]. Acoustical Physics, 2017, 63(4): 385. DOI:10.1134/S1063771017030071 |
| [15] |
TIPPING M E, BISHOP C M. Probabilistic principal component analysis[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 1999, 61(3): 611. DOI:10.1111/1467-9868.00196 |
| [16] |
康晨辰.飞机尾翼声振疲劳寿命分析[D].南京: 南京航空航天大学, 2016 KANG Chenchen. Anakysis on vibro-acoustic fatigue life of empennage[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 |
| [17] |
李增刚, 詹福良. Virtual.Lab Acoustics声学仿真计算高级应用实例[M]. 北京: 国防工业出版社, 1999.
|
 2020, Vol. 52
2020, Vol. 52


