近几年,随着世界上自然灾害频发,而灾后解决难民应急居住的临时性建筑需求日益增大.3D打印技术应用领域广泛,近年来该技术在建筑领域的使用逐渐频繁.蜂窝夹层板是建筑领域中常见的材料.目前,蜂窝夹层结构复合材料运用在临时性建筑中具有许多优点:1)具有很强的可弯曲刚性,自身强度高和优良的抗冲击性能.2)因为是粘接结构,所以表面可以做的很光滑平整,从而减振特性良好.3)又因是两重结构,所以气密性和隔热性能也非常优异[1].
传统临时性建筑在灾后施工时面临诸多问题,如何优化传统临时性建筑的生产方式,使临时性建筑结构性能更加优秀,在性能提高的同时改进组装困难、不可循环使用、节省人工与材料浪费等问题[2].李振华等[3]研究并运用了不同尺寸的纸筒,以纸筒作为材料使不同尺寸纸筒从新排列组合,制作出临时性建筑,结果表明使用纸筒作为临时性建筑建材不仅可回收利用和避免过度浪费材料,并且方便拆卸从新组装.运用3D打印材料制作的复合夹层结构,可以更好的提高遇到灾难后临时性建筑的制作效率与抗震等性能.最近几年,3D打印这一技术在建筑行业中屡见不鲜.2010年,一款名为“D-Shape”的打印机问世,这是由意大利人恩里克·蒂设计的3D打印机只要预先设定好结构图形,就能通过这款打印机一层一层喷上材料,打印出一个“完整”的建筑物体[4-6].
本文运用区别于传统人力施工的3D打印技术,使用PLA制备出在建筑中常见的蜂窝,通过密度公式设计出蜂窝夹层板芯子为六边形蜂窝结构、内凹六边形蜂窝结构、三角形蜂窝结构、手型蜂窝结构、星形蜂窝结构,从而得到力学性能更好,更加轻便的蜂窝夹层板.并且研究这5种蜂窝夹层结构中芯子的力学性能,通过进行拉伸实验、三点弯曲实验、压缩实验对5种芯子结构进行力学性能对比.根据实验得出的位移曲线图,分析这5种蜂窝芯子那种运用在临时性建筑中的力学性能更为出色.
1 实验 1.1 蜂窝芯子的设计使用3D打印机制作出5种蜂窝结构芯子,并对蜂窝结构的力学性能进行测试.设计蜂窝时,首先考虑使用这几种蜂窝结构常见的均匀分布方式,并且依靠蜂窝结构的密度公式进行设计制作.蜂窝结构的性能取决于相对密度,通过使用PLA材料制备的蜂窝结构比传统蜂窝结构使用的金属材料更加轻便,其中相对密度比是指PLA材料与蜂窝结构的体积密度之比.
星形蜂窝结构作为一种新型负泊松比蜂窝结构,在近些年间引起了国内外学者的关注与研究[7-9].Theocaris等[7]研究了均匀分布下的星形蜂窝结构复合材料其特性与该结构的影响因素;文献[9]给出了星形蜂窝结构平台应力的计算公式,并实验研究了星形蜂窝结构的变形模式、动态冲击强度.文献[9]提供的星形蜂窝相对密度公式,即
| $ \rho = \frac{{\left( {1 + 2\frac{{{L_{\rm{s}}}}}{L}} \right)\frac{t}{L}}}{{{{\left( {1 + \sqrt 2 \frac{{{L_{\rm{s}}}}}{L}\sin \frac{\beta }{2}} \right)}^2}}}. $ |
式中:Ls为星形结构胞壁的长度;L为连接两个胞壁的胞壁长度的1/2;t为星形蜂窝结构胞壁的厚度; β为星形间夹角.
六韧带手型蜂窝结构因其在压缩实验中承受载荷时产生的独特变形引起了学者们的广泛关注[10].文献[11]研究了3、4和6韧带这几种较为常见的手型结构的弹性模量,并且进一步探讨了手型蜂窝结构的变形机制.文献[10]研究了六韧带手型蜂窝结构材料的面内力学性能,并进行了理论分析与实验研究.张新春等[12]研究了六韧带手型蜂窝结构的内面冲击力学特性,并提供了六韧带手型蜂窝相对密度公式,即
| $ \rho = \frac{{{\rho ^*}}}{{{\rho _{\rm{s}}}}} = 2\beta \frac{{2{\rm{ \mathit{ π} }} + 3\alpha }}{{2{\rm{ \mathit{ π} }} + \sqrt 3 {\alpha ^2}}}. $ |
式中:ρ*为该蜂窝结构材料的密度;ρs为该基体材料的密度.α、β为量纲一的参数α=l/r,β=t/r.
正六边形蜂窝结构作为常见的蜂窝结构其在力学性能测试与理论研究上,国内外学者已经做过很多研究.富明慧等[13]研究了六边形蜂窝结构的常见形变规律,对Gibson公式进行了改进并得出了正六边形蜂窝芯子的弹性参数公式.文献[14]研究了类蜂窝与正六边形蜂窝结构等效力学参数对比与分析的方法,并提供了正六边形蜂窝相对密度公式,即
| $ \rho = \frac{{(2 + \beta )t}}{{2l(\beta + \sin \theta )\cos \theta }}{\rho _{\rm{s}}}. $ |
式中:t为蜂窝结构胞壁厚度;l为胞壁的长度;θ为六边形内夹角.内凹角蜂窝结构作为常见的负泊松比蜂窝结构,因其具有在能量吸收与抗压性能的增强,在结构抗冲击性设计上被广泛应用.Gibson等[15]就已经提出了内凹六边形蜂窝结构,并通过研究得出该结构的力学能效法.其中传统正泊松比蜂窝结构的内凹角为θ>180°,当凹角为θ<180°时该蜂窝结构为内凹六边形蜂窝结构.尹艺峰等[16]研究了内凹六边形蜂窝结构在低速载荷下的吸能特性与应力应变关系,并给出内凹六边形向对密度公式,即
| $ \rho = \frac{{{\rho _{\rm{m}}}{V_{\rm{A}}}c}}{{{V_{\rm{c}}}}} = \frac{{{\rho _{\rm{m}}}{V_{\rm{A}}}}}{V}. $ |
式中:ρm为内凹形蜂窝结构的材料密度;VA为内凹形蜂窝结构的实际体积;c为内凹形蜂窝结构的厚度;V=m×n×c为内凹形蜂窝结构的所用的体积.
三角形蜂窝结构作为一种新型蜂窝近几年已经有学者展开实验研究.文献[17]利用有限元研究了三角形蜂窝结构共面冲击与能量吸能的影响.文献[18]设计了一种旋转三角形蜂窝结构,并通过有限元模拟了其形变过程中冲击速度与旋转角对其的影响.通过比较得出了在相对密度相同的情况下,该蜂窝结构的能量吸收能力比正六边形蜂窝结构更出色.孙德强等[19]研究了冲击速度对三角形蜂窝结构共面冲击力学性能的影响,并提供了三角形蜂窝结构的相对密度公式,即
| $ \rho = \frac{{{\rho ^*}}}{{{\rho _{\rm{s}}}}} = \frac{{1 + \cos \theta }}{{\sin \theta \cos \theta }}. $ |
式中:t为蜂窝结构胞壁厚度;l为胞壁的长度;θ为斜边与底边的夹角;ρ*为三角形蜂窝的密度;ρs为该结构材料的密度.
本文在上述研究的基础上制作了手型结构、六边形结构、内凹六边形、星形、三角形蜂窝结构,利用3D打印技术制备出实验所需的试件,并对这5种蜂窝结构进行力学性能实验.通过实验所得数据进行对比,探讨了蜂窝结构运用在救灾时临时性建筑的可能性.为更好的优化传统临时性建筑的结构与材料性能做出贡献.
1.2 实验材料与对比本次实验选取聚乳酸(PLA)材料,PLA是一种合成高分子材料,因其具有良好力学性能,该材料在3D打印实验制作试件中较为常见.PLA材料在诸多领域都有广泛的应用,国内外学者对PLA材料的改性以及针对该材料在不同领域的应用进行了大量的研究与改进.本次实验使用常见的PLA材料进行试件制备,因国内外学者对PLA材料进行了大量研究,实际施工中通过对材料的改性可以得到力学性能更好的材料.目前,属于物理改进PLA材料的方法为:共混改性与复合改性,这两种改性的方法相对其他化学方法改性而言相对简单.文献[20]通过共混改性的方法对聚乳酸进行共混,并研究了打印工艺对PLA材料共混改性后制备的试件力学性能的影响.结果表明:打印材料温度220 ℃、3D打印精度在0.1 mm、填充密度为100%时,该试件材料的力学性能最佳.文献[21]通过使用3D打印制备PLA材料,对其打印速度、温度、填充密度、厚度等因素的调节.研究了3D打印工艺对PLA打印后制作出的试件的力学性能影响.结果表明:打印速度增加会导致拉伸与冲击强度的降低;打印温度的升高会使拉伸强度上升的同时导致冲击强度降低;打印密度的上升也会使PLA材料制备出的试件拉伸强度与冲击强度得到一定增强.
使用3D打印方式制作的PLA材料产品,其轻便性、可设计性强和自身材料优异的力学性能等优势,有效地解决了使用传统金属材料体量过重、制作需提前制作模具可设计性不强等不足.在本次实验中使用的PLA材料具体参数见表 1.
| 表 1 使用PLA材料具体参数 Tab. 1 Specific parameters for using PLA materials |
首先利用3DMAX软件对所需制备的5种蜂窝结构进行3D建模,根据不同实验所需试件尺寸见表 2,将制作完的3D模型以STL文件格式导入3D打印机自带的切片软件,模型的角度控制、弦长等参数均按默认设定;打印时喷头以均匀速度按数控指令运动,将材料以试件边界轮廓有序的堆积成一个平面层片,之后工作台下降一层高度按边界轮廓内一层一层堆积叠加,直至完成整个实体试件.
| 表 2 试件尺寸基本信息 Tab. 2 Basic information of specimen size |
3D打印机采用Anycubic MEGA-S单喷头3D打印机,打印机喷头温度为:220 ℃,打印机喷头直径为0.4 mm,打印速度60 mm/s.
分别根据拉伸、三点弯曲、压缩实验的试件尺寸制备出蜂窝结构为:六边形蜂窝结构、内凹六边形蜂窝结构、三角形蜂窝结构和手性形蜂窝结构,以及星形蜂窝结构.所有试件均采用均匀拓补的方式制备(蜂窝结构形状图为图 1(a)~(e)).
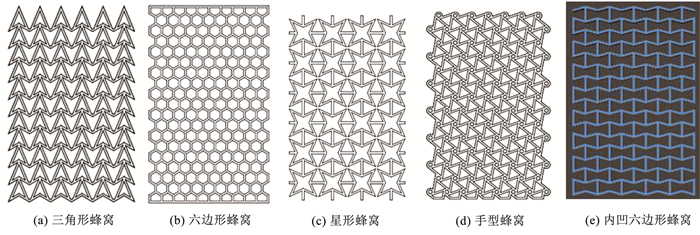
|
图 1 蜂窝结构示意 Fig. 1 Schematic diagram of honeycomb structure |
为了确保制备的实验试件在拉伸实验、三点弯曲实验、压缩实验中的准确性,减少误差,对每一种蜂窝结构在不同实验中制备出3个试件,实验后选相同试件的平均值,进行力学性能对比、并且分析载荷位移曲线图.在该实验中,使用Zwick/Z010型拉力机进行蜂窝夹层结构的力学性能测试.
2 研究 2.1 流程方案本次实验目的主要为测试手型结构、六边形结构、内凹六边形、星形、三角形蜂窝的力学性能.利用Zwick/Z010型万能拉力机对5种蜂窝进行拉伸实验、三点弯曲实验、压缩实验均满足GB/T1456-2005《夹层结构弯曲性能试验方法》规定,其中压头加载速度为:2 mm/min.实验过程如图 2所示.

|
图 2 实验过程示意 Fig. 2 Schematic diagram of experimental process |
实验以拉伸、三点弯曲、压缩为实验顺序,首先按实验顺序将试件进行排序,其次使用万能拉力机专用夹具固定实验试件,其中:拉伸实验采用拉力专用夹具,试件竖直摆放夹住上、下两端后固定试件进行实验;三点弯曲实验利用弯曲夹具,试件与工作台平行摆放,夹具固定试件两端进行实验;压缩实验利用专用压缩夹具,夹具固定试件上、下两端进行实验.试件安装后使用万能拉力机均匀速度对试件施加载荷,并由位移传感器测量位移,计算实验中试件的面内纵向拉伸、压缩和弯曲模量.载荷与位移数据利用max test软件进行采集,最后记录不同实验每组试件数据的平均值.
2.2 结果分析把测得实验数据导入Excel中,选取相同试件平均值结果导入origin对数据进行图像整理分析,5种蜂窝结构芯子的载荷位移曲线如图 3~5所示.
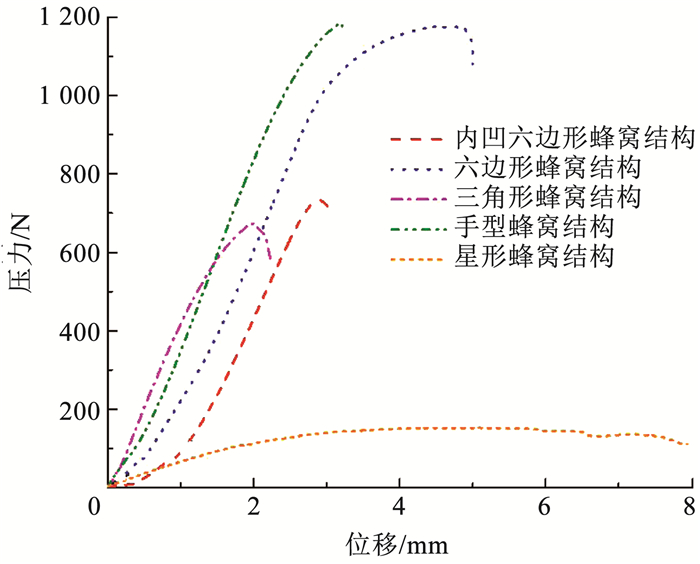
|
图 3 拉伸位移曲线 Fig. 3 Stretch displacement curve |
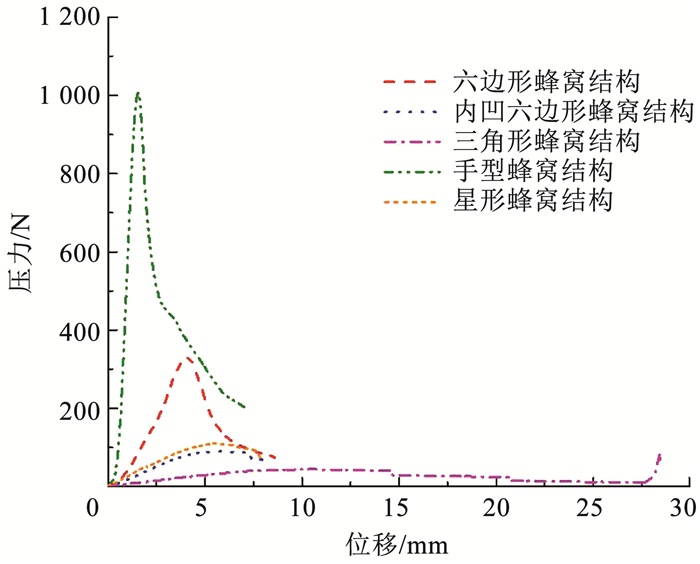
|
图 4 三点弯曲位移曲线 Fig. 4 Three-point bending displacement curve |
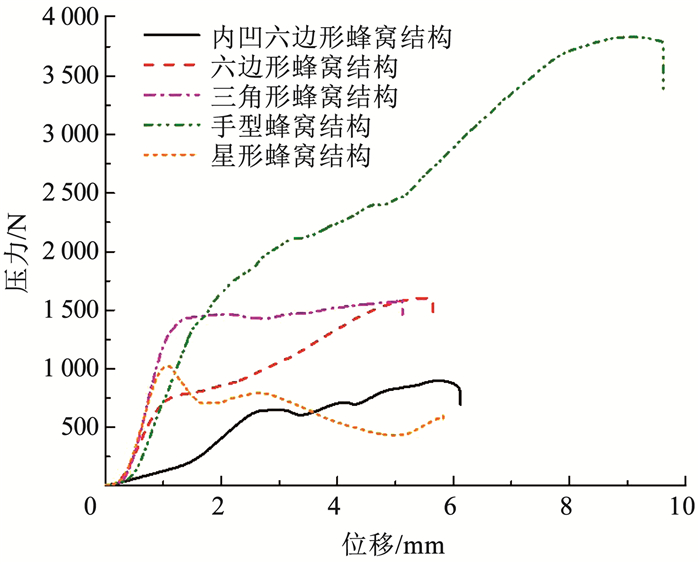
|
图 5 压缩位移曲线 Fig. 5 Compression displacement curve |
拉伸实验如图 3所示,初始阶段蜂窝芯子的拉伸曲线呈线性增加,载荷逐渐随位移逐渐上升.随着载荷逐渐上升手性蜂窝结构可承受载荷应力最大,在上升到峰值时出现剪切性断裂;六边形蜂窝所承受载荷应力在接近1 000 N时,随载荷增加位移缓慢增加,在其内部形变的过程中刚度优于手型蜂窝结构;星型、三角形与内凹六边形蜂窝结构依靠内部结构,在承受低强度载荷时可以获得更多的内面变形.
三点弯曲实验如图 4所示,曲线呈现弹性上升趋势,六边形蜂窝结构在载荷达到峰值时试件发生第1次断裂,曲线成直线下降,随后因内面形变在达到500 N是出现缓慢下降直至试件失效;手型蜂窝开始曲线呈上升状态在350 N时试件内部发生断裂,曲线呈缓慢趋势下降,在100 N时依靠内部形变继续承受载荷直至失效;内凹六边形蜂窝与星形蜂窝特性相近在承载低强度载荷时拥有更多韧性.
压缩实验如图 5所示,手型蜂窝随载荷增加缓慢增加位移,再上升至1 700 N时事件发生第1次断裂,曲线继续呈缓慢上升趋势,在经历反复内部形变与多次破坏后依旧可承载载荷值,当曲线达到峰值时发生剪切性断裂,随后试件失效;星形结构开始曲线呈上升趋势,在到达1 000 N时曲线突然下降,试件开始第1次断裂,而后曲线呈缓慢上升与缓慢下降的循环波动状态.三角形蜂窝在承受载荷到峰值时曲线呈平缓状态位移,依靠内部形变获得了更多的韧性;内凹六边形蜂窝期初曲线成缓慢上升在承载600 N是曲线平稳一段后发生破坏,随后曲线呈折叠上升趋势直至试件失效.
通过实验表明,蜂窝结构承受载荷时起初主要呈线弹性变形.在单个节点发生破坏失效后,曲线突然下降,但是结构仍可以继续承受载荷,所以曲线下降后可以继续上升.曲线中每一个突然下降的拐点,都代表了一个节点发生了破坏失效.其中六边形蜂窝芯子的弯曲刚度更好,整体力学特性较为稳定,整体实验效果韧性较为突出;负泊松比蜂窝中手型蜂窝可受载荷最多,其抗压性能相比其他4种蜂窝更强;内凹六边形蜂窝与三角形蜂窝性能相对接近,其中压缩实验中,在承受一定载荷的情况下,依靠内部结构持续增加位移;星形蜂窝综合实验结果来看效果最低.
根据以上分析手型蜂窝与六边形蜂窝的抗弯刚度与硬度、韧性更好,可以获得更多的内部变形,有较好的力学特性.可以满足使用在临时性建筑墙体中的变形与刚度需求.试件破坏图为图 6所示.

|
图 6 实验试件破坏图 Fig. 6 Diagram of damage experimental specimen |
近年来,临时性建筑所用材料多为可循环回收的生态材料如:纸筒、竹子、木头、农作物纤维以及模块化的临时性帐篷.其中文献[22]给出竹材本身拉伸强度与弯曲强度可达到150 MPa左右,抗压强度60~70 MPa.普通竹材的力学性能优于普通的木材的力学性能;文献[23]在对四川成都华林小学这一坂茂的纸建筑案例分析中给出:以纸管为建材其拉伸强度为890 kN/cm2,普通木材的拉伸强度为1 170~1 470 kN/cm2,纸管材料的力学性能与木材的力学性能接近;文献[24]给出PLA材料最大弯曲强度为114.7 MPa,压缩强度为103 MPa.PLA材料的力学性能优于普通竹板、纸筒、木材这几种常见临时性建筑材料.
通过本文实验得出的结论可知,利用PLA材料制备出的六边形蜂窝结构与手型蜂窝结构在实际应用到临时性建筑中时,其材料与结构完全可以满足实际应用需求,甚至其力学性能还优于传统材料与结构.
3 结论1) 本文利用3D打印技术,使用PLA材料设计制备了5种蜂窝结构,并通过实验分析了手型蜂窝结构、六边形蜂窝结构、内凹六边形蜂窝结构、星形蜂窝结构和三角形蜂窝结构的拉伸、三点弯曲、压缩的力学性能.
2) 手型蜂窝结构可承载力比其他4种蜂窝更为突出;六边形蜂窝的综合数值最好;其中星形蜂窝的力学性能较差.在实验中相同密度与壁厚的负泊松比蜂窝整体力学特性较传统六边形蜂窝较为不足.手型蜂窝与六边形蜂窝面内方向具有较好的可内部变形能力,外部承载力也具有良好变现.
3) 运用PLA材料制备的手型蜂窝与六边形蜂窝结构,其材料与结构特性质量比传统木材、竹子等材料更加轻便、节省人力,并且具有良好的力学特性,本文设计的蜂窝结构可以应用至灾后临时性建筑中,可以很大程度降低在遇到灾害时的二次受灾,增加人们的安全系数.同时3D打印技术的应用可以制造出结构更为复杂、稳定性强的结构.
| [1] |
赤坂隆. 蜂窝夹层结构[J]. 玻璃钢资料, 1983(5): 15. |
| [2] |
王迪, 张天宇. 新型环保材料在临时性建筑中的探索[J]. 华中建筑, 2010, 28(5): 37. WANG Di, ZHANG Tianyu. The exploration of new environment-friendly materials in a temporary building[J]. Huazhong Architecture, 2010, 28(5): 37. DOI:10.13942/j.cnki.hzjz.2010.05.011 |
| [3] |
李振华, 胡雪松. 坂茂的"纸建筑"建构研究初探[J]. 北京建筑工程学院学报, 2014, 30(2): 17. LI Zhenhua, HU Xuesong. Study on tectonic culture of the paper buildings of shigeru ban[J]. Journal of Beijing University of Civil Engineering and Architecture, 2014, 30(2): 17. DOI:10.3969/j.issn.1004-6011.2014.02.004 |
| [4] |
CECCANTI F, DINI E, DE KESTELIER X, et al. 3D printing technology for a moon outpost exploiting lunar soil[C]//Proceedings of the 61st International Astronautical Congress. Prague, CZ: IAF, 2010
|
| [5] |
COLLA V, DINI E. Large scale 3D printing: From deep sea tothe moon[J]. [S.l.]: ICTP-The Abdus Salam Center for Theoretical Physics, 2013. |
| [6] |
李有观. 用3D打印技术建造房屋[J]. 自然与科技, 2013(2): 22. |
| [7] |
THEOCARIS P S, STAVROULAKIS G E, PANAGIOTOPOULOS P D. Negative Poisson's ratios in composites with star-shaped inclusions: A numerical homogenization approach[J]. Archive of Applied Mechanics, 1997, 67(4): 274. DOI:10.1007/s004190050117 |
| [8] |
贠昊, 邓子辰, 朱志韦. 弹性波在星形节点周期结构蜂窝材料中的传播特性研究[J]. 应用数学和力学, 2015, 36(8): 814. YUN Hao, DENG Zichen, ZHU Zhiwei. Bandgap properties of periodic 4-point star-shaped honeycomb materials with negative poisson's ratios[J]. Applied Mathematics and Mechanics, 2015, 36(8): 814. DOI:10.3879/j.issn.1000-0887.2015.08.003 |
| [9] |
韩会龙, 张新春. 星形节点周期性蜂窝结构的面内动力学响应特性研究[J]. 振动与冲击, 2017, 36(23): 223. HAN Huilong, ZHANG Xinchun. In-plane dynamic impact response characteristics of periodic 4-point star- shaped honeycomb structures[J]. Journal of Vibration and Shock, 2017, 36(23): 223. DOI:10.13465/j.cnki.jvs.2017.23.033 |
| [10] |
ALDERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science and Technology, 2010, 70(7): 1042. DOI:10.1016/j.compscitech.2009.07.009 |
| [11] |
PRALL D, LAKESR S. Properties of a chiral honeycomb with a Poisson's ratio of -1[J]. International Journal of Mechanical and Science, 1996, 39(3): 305. DOI:10.1016/S0020-7403(96)00025-2 |
| [12] |
张新春, 祝晓燕, 李娜. 六韧带手性蜂窝结构的动力学响应特性研究[J]. 振动与冲击, 2016, 35(8): 1. ZHANG Xinchun, ZHU Xiaoyan, LI Na. A study of the dynamic response characteristics of hexagonal chiral honeycombs[J]. Journal of Vibration and Shock, 2016, 35(8): 1. DOI:10.13465/j.cnki.jvs.2016.08.001 |
| [13] |
富明慧, 尹久仁. 蜂窝芯层的等效弹性参数[J]. 力学学报, 1999, 31(1): 113. FU Minghui, YIN Jiuren. Equivalent elastic parameters of the honeycomb core[J]. Acta Mechanica Sinica, 1999, 31(1): 113. DOI:10.3321/j.issn:0459-1879.1999.01.014 |
| [14] |
李响, 杨祉豪, 陈波文. 类蜂窝和六边形蜂窝夹芯等效力学参数对比与仿真[J]. 三峡大学学报(自然科学版), 2019, 41(2): 88. LI Xiang, YANG Zhihao, CHEN Bowen. Comparison and simulation of equivalent mechanical parameters of quasi-honeycomb and hexagon honeycomb[J]. Journal of China Three Gorges University (Natural Sciences), 2019, 41(2): 88. DOI:10.13393/j.cnki.issn.1672-948x.2019.02.019 |
| [15] |
GIBSON L J, ASHBY M E. Cellular solids: structure and properties[M]. Cambridge: Cambridge University Press, 1997.
|
| [16] |
尹艺峰, 杜义贤, 周鹏, 等. 凹角蜂窝结构的面内低速冲击力学性能分析[J]. 三峡大学学报(自然科学版), 2017, 39(5): 90. YIN Yifeng, DU Yixian, ZHOU Peng, et al. In-plane dynamics analysis of reentrant honeycomb structure under low speed impact[J]. Journal of China Three Gorges University (Natural Sciences), 2017, 39(5): 90. DOI:10.13393/j.cnki.issn.1672-948X.2017.05.018 |
| [17] |
LIU Ying, ZHANG Xinchun. The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs[J]. International Journal of Impact Engineering, 2009, 36(1): 98. DOI:10.1016/j.ijimpeng.2008.03.001 |
| [18] |
卢子兴, 武文博. 基于旋转三角形模型的负泊松比蜂窝材料面内动态压溃行为数值模拟[J]. 兵工学报, 2018, 39(1): 153. LU Zixing, WU Wenbo. Numerical simulations for the in-plane dynamic crushing of honeycomb material with negative poisson's ratio based on rotating triangle model[J]. Acta Armamentarii, 2018, 39(1): 153. DOI:10.3969/j.issn.1000-1093.2018.01.017 |
| [19] |
孙德强, 宫凯, 李国志, 等. 三角形蜂窝的共面冲击动力学[J]. 陕西科技大学学报, 2013, 31(1): 98. SUN Deqiang, GONG Kai, LI Guozhi, et al. Dynamics of triangular honeycombs under in-plane crushing loadings[J]. Journal of Shaanxi University of Science & Technology, 2013, 31(1): 98. DOI:10.3969/j.issn.1000-5811.2013.01.024 |
| [20] |
金泽枫, 金杨福, 周密, 等. 基于FDM聚乳酸3D打印材料的工艺性能研究[J]. 塑料工业, 2016, 44(2): 67. JIN Zefeng, JIN Yangfu, ZHOU Mi, et al. Research of processing property of PLA materials for 3D printing based on FDM[J]. China Plastics Industry, 2016, 44(2): 67. DOI:10.3969/j.issn.1005-5770.2016.02.017 |
| [21] |
闫丽静, 李真真, 冯婧, 等. 聚乳酸(PLA)3D打印工艺研究[J]. 塑料工业, 2017, 45(2): 71. YAN Lijing, LI Zhenzhen, FENG Jing, et al. Research of three-dimensional printing process for PLA[J]. China Plastics Industry, 2017, 45(2): 71. DOI:10.3969/j.issn.1005-5770.2017.02.017 |
| [22] |
魏洋, 张齐生, 蒋身学, 等. 现代竹质工程材料的基本性能及其在建筑结构中的应用前景[J]. 建筑技术, 2011, 42(5): 390. WEI Yang, ZHANG Qisheng, JIANG Shenxue, et al. Basic properties and prospects of modern bamboo engineering materials applied in building structures[J]. Architecture Technology, 2011, 42(5): 390. DOI:10.3969/j.issn.1000-4726.2011.05.001 |
| [23] |
牛盛楠, 杨现国. 由坂茂的纸建筑看非传统建筑材料在建筑中的应用[J]. 福建建材, 2017(9): 57. |
| [24] |
刘晓军, DILLONL, JAMESF L, 等. 3D打印碳纤维增强PLA试件的力学性能分析[J]. 塑料, 2017, 46(3): 47. LIU Xiaojun, DILLON L, JAMES F L, et al. Analysis of mechanical properties of 3D printing PLA specimens reinforced by carbon fiber[J]. Plastics, 2017, 46(3): 47. |
 2020, Vol. 52
2020, Vol. 52


