屈服准则是判定材料在各种应力状态下是否发生塑性变形的依据,也是求解材料成形外力必须依赖的条件.合理的屈服准则对材料的选择、工艺参数的优化以及工程结构件的安全评定具有重要意义.自20世纪以来,研究者在屈服准则方面做了大量的研究,并取得了许多重要的成果.
1776年,Coulomb[1]提出一个屈服假定,即当某平面上的剪应力超过该平面上材料的内聚力和摩擦力之和时,材料就发生剪切屈服.该准则也因此被称为Coulomb准则.1864年,Tresca[2]在冲裁和挤压实验的基础上,提出了Tresca屈服准则.该准则假定,无论在何种应力状态下,当物体内某一点的最大切应力达到某一定值时,物体就发生屈服.1913年,von Mises[3]从数学的角度出发,提出以偏差应力张量的二次不变量作为判据,建立了Mises屈服准则.该准则随后由Hencky[4]进行了物理解释,即当材料内部所积累的单位体积变形达到一个临界值时,材料发生塑性变形.1950年,Hill[5]将适用于各向同性材料的Mises屈服准则推广到各向异性材料,提出了Hill屈服准则.1952年,Drucker等[6]在Mises屈服准则的基础上,考虑到静水压力对材料屈服的影响进而提出了Drucker-Prager屈服准则.为了统一表征各屈服准则,文献[7]引入了三维应力空间的概念,描述了Tresca准则和Mises准则的几何特征.1985年,俞茂宏等[8]提出了双剪应力(TSS)屈服准则,即假定当两个较大的主剪应力之和达到临界值时,材料发生塑性变形.近年来,章顺虎[9]在线性屈服准则的开发方面也取得了进展,提出了与Mises圆周长相等的线性屈服准则.2015年,杨凤等[10]基于材料屈服时应力之间的关系, 提出一种新的各向同性屈服准则.该准则包含了应力幂次在1~4之间的各种形式.2017年,高江平等[11]提出三剪应力统一强度理论,认为当作用于菱形十二面单元体上的3个主剪应力所组成的函数达到某一极值时, 材料发生破坏.
以上屈服准则的开发为各类工程结构件的塑性失效分析提供了基础.管道作为石油与天然气的输送媒介,在国民经济中发挥着至关重要的作用.然而,近年来管道安全事故频发,已造成了严重的经济损失.因此,进行管道失效分析具有重要意义.管道塑性失效分析主要用于确定受力管道的极限承载能力,称为爆破压力.国内外已有不少预测管道爆破压力的研究报道.李灿明等[12]采用MY准则求解X80管线钢爆破压力,得到逼近Mises结果的解析解.文献[13-14]应用Tresca屈服准则和Mises屈服准则分别对管道的爆破压力进行了预测, 研究发现Tresca准则的预测结果提供了管道爆破压力的下限, 而Mises准则的预测结果会比实际数值偏高.彭星煜等[15]利用双剪应力(TSS)屈服准则得到的预测值是管道爆破压力的上限.基于以上研究可见,Tresca屈服准则通常给出下限解,TSS屈服准则通常给出上限解;Mises屈服准则给出相对偏高的结果.
根据上述信息,本文提出了一种新的线性屈服准则,旨在获得更加合理的预测结果,并分析不同屈服准则以及主要参数对管道爆破压力的影响.
1 三经典屈服准则Tresca[2]屈服准则的表达式为
| $ {f^{{\rm{ Tresca }}}} = {\sigma _1} - {\sigma _3} = {\sigma _{\rm{s}}}. $ | (1) |
式中:σ1为第一主应力,σ3为第三主应力,σs为屈服强度.
Tresca屈服准则是一个线性准则,但由于只考虑了两个主应力分量,在描述金属材料的实际塑性变形方面存在不足,即通常会给出偏低的力学参数结果.
Mises[3]屈服准则的表达式为
| $ {f^{{\rm{ Mises }}}} = \frac{{\sqrt 2 }}{2}\sqrt {{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}} = {\sigma _{\rm{s}}}. $ | (2) |
根据前人的研究和验证,大多数金属材料的塑性变形满足Mises屈服准则.然而,由于其表达式的非线性,不便于复杂力学方程的联解计算.
TSS[8]屈服准则的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {f_1^{{\rm{TSS}}} = {\sigma _1} - \frac{1}{2}({\sigma _2} + {\sigma _3}) = {\sigma _{\rm{s}}},{\sigma _2} \le \frac{1}{2}({\sigma _1} + {\sigma _3});}\\ {f_2^{{\rm{TSS}}} = \frac{1}{2}({\sigma _1} + {\sigma _2}) - {\sigma _3} = {\sigma _{\rm{s}}},{\sigma _2} \ge \frac{1}{2}({\sigma _1} + {\sigma _3}).} \end{array}} \right. $ | (3) |
TSS屈服准则也是一个线性的屈服准则,但与其他准则相比,它总是提供上限解.
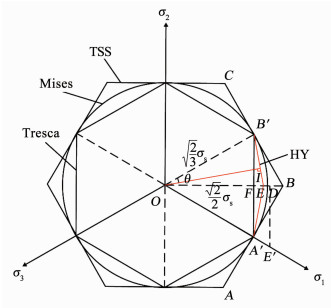
上述公式在π平面上的屈服轨迹见图 1,其中Mises屈服准则的轨迹是一个圆,Tresca屈服准则的轨迹是Mises圆的一个内接正六边形,TSS屈服准则的轨迹是Mises圆的一个外切正六边形.
|
图 1 π平面上的屈服轨迹 Fig. 1 Different loci on π-plane |
为了线性逼近Mises圆,可以在Tresca屈服准则和Mises屈服准则之间构建一个十二边形.在图 1中,Mises屈服准则的外切六边形(TSS)的边心距为OB′,内接六边形(Tresca)的边心距为OF,设线段BF上有一动点E,连接B′E,定义为本文即将开发的平均化屈服准则,OI为其边心距.
在图中,设OB′与OI之间的夹角∠B′OI为θ,则当θ=0°时,OI=OB′;当θ=30°时,OI=OF.可见,OI可在OB′与OF之间变化.
已知Mises圆的半径OB′=OD=
| $ OI = \frac{1}{{\frac{{\rm{ \mathsf{ π} }}}{6} - 0}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{6}} {\frac{{\sqrt 6 }}{3}} {\sigma _{\rm{s}}}\cos \theta {\rm{d}}\theta = \frac{{\sqrt 6 }}{{\rm{ \mathsf{ π} }}}{\sigma _{\rm{s}}}. $ | (4) |
基于上式,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\cos \theta = OI/O{B^\prime } = \frac{3}{{\rm{ \mathsf{ π} }}},}\\ {\cos \angle IOE = \cos \left( {\frac{{\rm{ \mathsf{ π} }}}{6} - \theta } \right) = 0.975{\kern 1pt} {\kern 1pt} {\kern 1pt} 4,}\\ {OE = OI/\cos \angle IOE = 0.799{\kern 1pt} {\kern 1pt} {\kern 1pt} 3{\sigma _{\rm{s}}}.} \end{array}} \right. $ | (5) |
Mises屈服轨迹上的偏差矢量模长为
| $ OD = O{B^\prime } = \frac{{\sqrt 6 }}{3}{\sigma _{\rm{s}}} \approx 0.816{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{\sigma _{\rm{s}}}. $ | (6) |
平均化屈服准则的偏差矢量模长为
| $ OE = 0.799{\kern 1pt} {\kern 1pt} {\kern 1pt} 3{\sigma _{\rm{s}}}. $ | (7) |
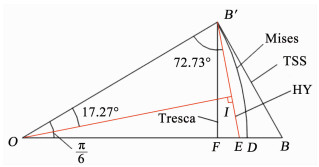
由此可见,平均化屈服准则的偏差矢量模长比Mises屈服准则的小,即E点在F、D之间.在误差三角形OBB′内各种屈服准则的相互关系如图 2所示.
|
图 2 平均化屈服准则在误差三角形内轨迹 Fig. 2 Locus of homogenization yield criterion in error triangle |
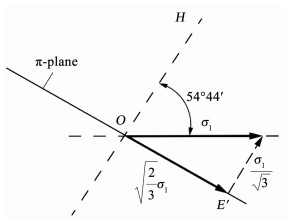
下面建立直线A′E、B′E在Haigh-Westgarrd空间中的应力方程.图 3为主应力分量在π平面上的投影,其中E点的应力状态为
|
图 3 σ1在π平面上的投影 Fig. 3 Trajectory of σ1 on π-plane |
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = \frac{{OE \times \sqrt 3 }}{{\sqrt 2 \cos {{30}^\circ }}} = 1.130{\kern 1pt} {\kern 1pt} 4{\sigma _{\rm{s}}},}\\ {{\sigma _3} = 0,}\\ {{\sigma _2} = \frac{{{\sigma _1} + {\sigma _3}}}{2} = 0.565{\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\sigma _{\rm{s}}}.} \end{array}} \right. $ | (8) |
假定直线A′E满足如下方程:
| $ {\sigma _1} - {a_1}{\sigma _2} - {a_2}{\sigma _3} - c = 0, $ | (9) |
则当材料发生屈服时有c=σs、a1+a2=1,代入应力分量式(8)可得
| $ {a_1} = 0.231,{a_2} = 0.769. $ | (10) |
将式(10)代入式(9),可得A′E的方程为
| $ {\sigma _1} - 0.231{\sigma _2} - 0.769{\sigma _3} = {\sigma _{\rm{s}}},{\sigma _2} \le \frac{1}{2}({\sigma _1} + {\sigma _3}). $ | (11) |
同理,直线B′E的方程可确定为
| $ 0.769{\sigma _1} + 0.231{\sigma _2} - {\sigma _3} = {\sigma _{\rm{s}}},{\sigma _2} \ge \frac{1}{2}({\sigma _1} + {\sigma _3}). $ | (12) |
式(11)和式(12)即为所提的屈服准则的数学表达式,它是主应力分量的线性组合.因该准则的边心距OI由积分中值定理计算而得,故导出的准则称为平均化屈服准则,简称HY准则.
由图 2可知,HY准则的轨迹在Mises圆内,各顶角计算如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\angle F{B^\prime }E = {{12.726}^\circ },}\\ {\angle O{B^\prime }E = {{60}^\circ } + {{12.726}^\circ } = {{72.726}^\circ },}\\ {\angle OE{B^\prime } = {{180}^\circ } - {{30}^\circ } - {{72.726}^\circ } = {{77.274}^\circ },}\\ {2\angle O{B^\prime }E = {{145.452}^\circ },2\angle OE{B^\prime } = {{154.548}^\circ }.} \end{array}} \right. $ | (13) |
由图 1和式(13)表明,HY准则的轨迹是在Mises圆内的等边非等角的十二边形,边长为0.418 5σs,6个顶点在Mises圆上,内接点顶角为145.452°,另外6个顶点位于Mises圆的内侧,相距0.02σs,顶角为154.548°.
HY准则的轨迹与Tresca屈服准则和Mises屈服准则轨迹之间的绝对和相对误差如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\Delta _{{\rm{AT1}}}} = OE - OF = 0.092{\kern 1pt} {\kern 1pt} 2{\sigma _s},}\\ {{\Delta _{{\rm{AT2}}}} = \frac{{(OE - OF)}}{{OF}} = 13\% ,}\\ {{\Delta _{{\rm{AM1}}}} = OE - OD = - 0.017{\kern 1pt} {\kern 1pt} 6{\sigma _s},}\\ {{\Delta _{{\rm{AM2}}}} = \frac{{(OE - OD)}}{{OD}} = - 2.1\% .} \end{array}} \right. $ | (14) |
式中:ΔAT1、ΔAT2分别为HY准则和Tresca屈服准则之间的绝对误差和相对误差,ΔAM1、ΔAM2分别为HY准则和Mises屈服准则之间的绝对误差和相对误差.
式(14)表明HY准则的轨迹位于Tresca屈服轨迹和Mises屈服轨迹之间,并且更接近Mises屈服轨迹.
2.2 实验验证在主应力状态为σ1≥σ2≥σ3时,引入Lode参数来对比不同的屈服准则,Lode参数表达式为[16]
| $ {\mu _{\rm{d}}} = \frac{{2{\sigma _2} - {\sigma _1} - {\sigma _3}}}{{{\sigma _{\rm{s}}}}}. $ | (15) |
将上式分别代入Tresca准则、Mises准则、TSS屈服准则和HY准则可得到它们含Lode参数的改写式如下:
Tresca:
| $ {\frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _{\rm{s}}}}} = 1.} $ | (16) |
Mises:
| $ {\frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _{\rm{s}}}}} = \frac{2}{{\sqrt {3 + \mu _{\rm{d}}^2} }}.} $ | (17) |
TSS:
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _{\rm{s}}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{4 + {\mu _{\rm{d}}}}}{3}, - 1 \le {\mu _{\rm{d}}} \le 0;}\\ {\frac{{4 - {\mu _{\rm{d}}}}}{3},0 \le {\mu _{\rm{d}}} \le 1.} \end{array}} \right. $ | (18) |
HY:
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _{\rm{s}}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{2{\kern 1pt} {\kern 1pt} {\kern 1pt} 000 + 231{\mu _{\rm{d}}}}}{{1769}}, - 1 \le {\mu _{\rm{d}}} \le 0;}\\ {\frac{{2{\kern 1pt} {\kern 1pt} {\kern 1pt} 000 - 231{\mu _{\rm{d}}}}}{{1769}},0 \le {\mu _{\rm{d}}} \le 1.} \end{array}} \right. $ | (19) |
基于以上改写式,并结合已有的实验数据[16-19],可以得到图 4.

|
图 4 屈服准则实验结果对比 Fig. 4 Comparison of different yield criteria and experimental data |
由图 4可知,TSS屈服准则位于最上侧,提供了计算结果的上限,Tresca屈服准则位于底部,提供下限;HY准则介于TSS准则与Tresca准则之间,靠近Mises准则结果,且与实验数据吻合较好,提供了较合理的中间结果.
3 管道失效分析为了证明新提出的HY准则的应用价值,本节将HY准则应用于内压直管道的塑性失效分析.
3.1 爆破压力模型对于受内压力的薄壁管,其主应力分量表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = {\sigma _{\rm{ \mathsf{ θ} }}} = \frac{{pd}}{{2t}},}\\ {{\sigma _2} = {\sigma _{\rm{z}}} = \frac{{pd}}{{4t}},}\\ {{\sigma _3} = {\sigma _{\rm{r}}} \approx 0.} \end{array}} \right. $ | (20) |
式中:θ、z、r分别为管道的周向、轴向和径向;d和t是管道的内直径和初始壁厚; p是管道的内部压力.
对于埋地管道,轴向应变通常很小,可看作εz=0.因此,主应变分量为
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _1} = {\varepsilon _{\rm{ \mathsf{ θ} }}} = \ln \frac{d}{{{d_0}}},}\\ {{\varepsilon _3} = {\varepsilon _{\rm{r}}} = \ln \frac{t}{{{t_0}}},}\\ {{\varepsilon _2} = {\varepsilon _{\rm{z}}} = 0.} \end{array}} \right. $ | (21) |
式中d0、t0为管道的初始直径和初始壁厚.
当塑性变形发生时,管线钢的应力-应变关系用以下幂函数表示[14]:
| $ \sigma = K{\varepsilon ^n};K = {\left( {\frac{e}{n}} \right)^n}\sigma _{\rm{u}}^\prime . $ | (22) |
式中:σ、ε分别为单向拉伸实验时的真应力和真应变,n为加工硬化系数,K为在ε=1时的强度系数,σ′u为工程抗拉强度.
通过式(20)~(22)和失效条件∂p/∂ε=0,则基于式(11)的爆破压力为
| $ p_{\rm{b}}^{{\rm{HY}}} = 4{\left( {\frac{{1{\kern 1pt} {\kern 1pt} {\kern 1pt} 000}}{{1{\kern 1pt} {\kern 1pt} {\kern 1pt} 769}}} \right)^{n + 1}}\frac{{{t_0}}}{{{d_0}}}\sigma _{\rm{u}}^\prime . $ | (23) |
该式表明,爆破压力是应变硬化指数、初始厚径比以及工程抗拉强度的函数.根据上述分析过程,还可以导出基于Tresca,Mises和TSS屈服准则的爆破压力:
| $ {p_{\rm{b}}^{{\rm{ Tresca }}} = 4{{\left( {\frac{1}{2}} \right)}^{n + 1}}\frac{{{t_0}}}{{{d_0}}}\sigma _{\rm{u}}^\prime ,} $ | (24) |
| $ {p_{\rm{b}}^{{\rm{ Mises }}} = 4{{\left( {\frac{1}{{\sqrt 3 }}} \right)}^{n + 1}}\frac{{{t_0}}}{{{d_0}}}\sigma _{\rm{u}}^\prime ,} $ | (25) |
| $ {p_{\rm{b}}^{{\rm{HY}}} = 4{{\left( {\frac{2}{3}} \right)}^{n + 1}}\frac{{{t_0}}}{{{d_0}}}\sigma _{\rm{u}}^\prime .} $ | (26) |
上述爆破压力公式的一般形式表示为
| $ {p_{\rm{b}}} = 4{\omega ^{n + 1}}\frac{{{t_0}}}{{{d_0}}}\sigma _{\rm{u}}^\prime . $ | (27) |
式中ω是一个可变系数,取决于不同的屈服准则,ω=1 000/1 769, 1/2, 1/
为验证本文结果的正确性,将本文的归一化爆破压力pn=p/(2t0σ′u/d0)=2ωn+1与文献[20-22]中的实验结果进行比较,见图 5.

|
图 5 理论爆破压力与实验数据的比较 Fig. 5 Comparison of theoretical burst pressure and experimental data |
由图 5可知,基于HY准则得到的理论管道爆破压力介于Tresca与TSS准则预测的爆破压力之间,与Mises准则结果最为接近,且比Mises准则结果更接近实验结果.
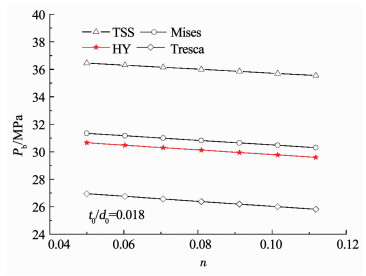
|
图 6 应变硬化指数对爆破压力的影响 Fig. 6 Effect of strain-hardening exponent on burst pressure |
|
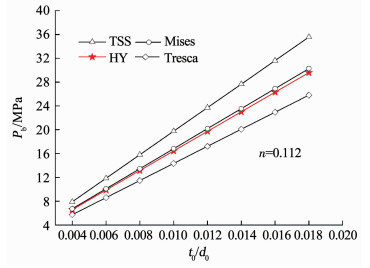
图 7 厚径比对爆破压力的影响 Fig. 7 Effect of t0/d0 on burst pressure |
由图 6、7可知,应变硬化效应和管道尺寸均对管道爆破压力产生影响,管道爆破压力随着应变硬化指数的增大而减小,随管道厚径比的增大而增大.
由于硬化指数取决于钢材生产工艺及化学成分,而厚径比又与使用条件及设计要求密切相关.因此设计管道时要综合考虑这两个关键参数,以避免管道失效.
4 结论1) 本文提出的平均化屈服准则是关于主应力分量的线性组合,它在π平面上的屈服轨迹为一个在Mises圆内的等边非等角十二边形,边长为0.418 5σs,顶角分别为154.548°与145.452°,与Mises准则之间的最大误差不超过2.1%.通过对比实验数据发现,该屈服准则的预测结果与实验数据吻合较好,给出了较为合理的中间结果.
2) 将新提出的屈服准则应用于管道失效分析,结果表明,理论爆破压力取决于不同的屈服准则,并且本文结果与实验数据吻合较好.由此可见,本文采用HY准则进行管道失效分析的方法是可行的.
3) 对各种爆破压力的变化规律分析发现,随着应变硬化指数的增加,爆破压力减小;随着厚径比的增加,爆破压力增加,表明管壁较厚或直径较小的管道可以承受更大的压力.
| [1] |
COULOMB C A. Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l'architecture[J]. Mémoires de l'Academie Royale des Sciences, 1776, 7: 343. |
| [2] |
TRESCA H. Memoir on the flow of solid bodies under strong pressure[J]. Comptes-Rendus de l'Académie des Sciences, 1864, 59: 754. |
| [3] |
VON MISES R. Mechanik der festen Körper im plastisch-deformablen Zustand[J]. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1913, 4: 582. |
| [4] |
HENCKY H. Zur theorie plastischer deformationen und der hierdurch im material hervorgerufenen nachspannungen[J]. ZAMM-Zeitschrift fur Angewandte Mathematik und Mechanik, 1924, 4(4): 323. DOI:10.1002/zamm.19240040405 |
| [5] |
HILL R. The mathematical theory of plasticity[M]. London: Oxford University Press, 1950: 18.
|
| [6] |
DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157. DOI:10.1090/qam/48291 |
| [7] |
俞茂宏. 双剪理论及其应用[M]. 北京: 科学出版社, 1998: 15. YU Maohong. Twin shear theory and its applications[M]. Beijing: Science Press, 1998: 15. |
| [8] |
俞茂宏, 何丽南, 宋凌宇. 双剪应力强度理论及其推广[J]. 中国科学:数学, 1985, 12: 5. YU Maohong, HE Linan, SONG Lingyu. Twin shear stress strength theory and its extension[J]. Scientia Sinica: Mathematica, 1985, 12: 5. |
| [9] |
章顺虎.金属塑性成形力的线性化解法研究及应用[D].沈阳: 东北大学, 2013 ZHANG Shunhu. Research on linearization analytical method of metal plastic forming forces and its applications[D]. Shenyang: Northeastern University, 2013 |
| [10] |
杨凤, 万邵华, 刘军, 等. 一种新的各向同性金属材料屈服函数[J]. 塑性工程学报, 2015, 22(6): 108. YANG Feng, WAN Shaohua, LIU Jun, et al. A new yield function on isotropic metals[J]. Journal of Plasticity Engineering, 2015, 22(6): 108. DOI:10.3969/j.issn.1007-2012.2015.06.019 |
| [11] |
高江平, 杨华, 蒋宇飞, 等. 三剪应力统一强度理论研究[J]. 力学学报, 2017, 49(6): 1322. GAO Jiangping, YANG Hua, JIANG Yufei, et al. Study of three-shear stress unified strength theory[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(6): 1322. DOI:10.6052/0459-1879-17-081 |
| [12] |
李灿明, 赵德文, 章顺虎, 等. MY准则解析X80钢油气输送管道爆破压力[J]. 东北大学学报(自然科学版), 2011, 32(7): 964. LI Canming, ZHAO Dewen, ZHANG Shunhu, et al. Analysis of burst pressure for X80 steel pipeline with MY criterion[J]. Journal of Northeastern University (Natural Science), 2011, 32(7): 964. |
| [13] |
ZHU Xiankui, LEIS B N. Strength criteria and analytical prediction of failure pressures in line pipes[J]. International Journal of Offshore and Polar Engineering, 2004, 14(2): 125. |
| [14] |
ZHU Xiankui, LEIS B N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines[J]. International Journal of Pressure Vessels and Piping, 2006, 83(9): 663. DOI:10.1016/j.ijpvp.2006.06.001 |
| [15] |
彭星煜, 张鹏, 伍颖, 等. 基于双剪屈服条件的输油管道腐蚀剩余强度可靠性研究[J]. 中国安全科学学报, 2008, 18(11): 149. PENG Xingyu, ZHANG Peng, WU Ying, et al. Study on the residual strength reliability of corroded oil pipeline based on double shear yield condition[J]. China Safety Science Journal, 2008, 18(11): 149. DOI:10.3969/j.issn.1003-3033.2008.11.025 |
| [16] |
LODE W. Versuche über den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel[J]. Zeitschrift für Physik A Hadrons and Nuclei, 1926, 36(11): 913. DOI:10.1007/BF01400222 |
| [17] |
LESSELLS J M, MACGREGOR C W. Combined stress experiments on a nickel-chrome-molybdenum steel[J]. Journal of the Franklin Institute, 1940, 230(2): 163. DOI:10.1016/S0016-0032(40)90729-3 |
| [18] |
NAGHDI P M, ESSENBURG F J, KOFF W. An experimental study of initial and subsequent yield surfaces in plasticity[R]. Ann Arbor: The University of Michigan, 1957
|
| [19] |
MAXEY W A. Measurement of yield strength in the mill expander[C]//Proceedings of the Fifth Symposium on Line Pipe Research. Houston: [s.n.], 1974: 91
|
| [20] |
HILLENBRAND H G, LIESSEM A, KNAUF G, et al. Development of large-diameter pipe in grade X100[C]//Proceedings of the Third International Conference of Pipeline Technology. Brugge: Belgium Press, 2000: 1263
|
| [21] |
PASLAY P R, CERNOCKY E P, WINK R. Burst pressure prediction on thin-walled, ductile tubulars subjected to axial load[C]//Proceedings of Applied Technology Workshop on Risk Based Design of Well Cashing and Tubing. Woodlands: Society of Petroleum Engineers, 1998: 1. DOI: 10.2118/48327-MS
|
| [22] |
AMANO K, MATSUOKA M, ISHIHARA T, et al. Significance of yield ratio limitation to plastic deformation of pipeline in high pressure proof test[C]//Proceedings of the Seventh Symposium on Line Pipe Research. Texas: Houston Press, 1986: 81
|
 2020, Vol. 52
2020, Vol. 52


