2. 金属矿山高效开采与安全教育部重点试验室(北京科技大学),北京 100083
2. State Key Laboratory of High-Efficient Mining and Safety of Metal Mines (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China
如何将地表堆积固体废弃物安全高效的回填至充填采空区,是充填采矿法的核心工程问题之一.在长期的充填实践中,人们逐渐认识到水力管道输送模式与机械搬运模式相比,具有成本低、效率高和工艺简单等诸多经济技术优势[1-2].管道输送工艺也已成为充填采矿技术的最重要的核心工艺环节[3].
管道输送工艺应用过程中,由于充填原材料物化性质的不同,所制备的充填浆体有不同的流变特性和流变参数.具备不同流变特性和流变参数的充填浆体在不同压差、管径和管路长度条件下的充填流量和沿程阻力计算结果,是充填配比优化、充填系统设计、泵送设备选型和充填管道选型的必要依据.只有准确确定充填料浆的流变参数、利用准确的流动方程才能准确计算不同工况下充填料浆的管道流量和沿程阻力,保证充填系统的安全运行.
目前关于充填料浆管道输送基础理论的研究严重滞后于技术发展[4].充填料浆一般为固液两相流,在固体质量分数低时表现为非均质流体,固体质量分数高时表现为均质流体[5-6].对于低固体质量分数的非均质充填料浆,在管道流动时绝大多数情况下为湍流,只能通过大量的试验得到经验方程,无法获取准确的数学模型[7].随着膏体充填技术的发展和推广,矿山企业逐渐意识到充填固体质量分数的提高对降低充填材料成本和保护环境的显著作用,充填浆体也由非均质流体向均质膏体转变,均质充填浆体管道输送的问题越来越多被广大矿山企业和研究单位所关注,其中以牛顿流体和非牛顿流体中的宾汉体作为本构模型的充填浆体管道流动方程应用最为广泛,上述两个本构模型所推导的流动方程分别为Poiseuille定律和Buckingham流动方程[8].由于均质充填料浆工况的复杂性[9-10],牛顿流体和宾汉体本构模型通常并不精确[11-12],而较为精确的幂率模型所得出的流动方程形式复杂、计算量大,不易进行工程应用,而盲目采用牛顿流体和宾汉体本构模型所得出的流动方程计算结果与现场实际测量结果常常存在较大误差,进而导致在充填过程中常常发生堵管事故,影响井下采矿效率[13].
针对上述问题,本文力图推导出具有普适性的非牛顿流体管道流动方程,使之适用于所有流型的非牛顿流体,从而能够有效指导充填料浆管道输送工程实践.为了便于现场工作人员应用,本文进一步推导出非牛顿流体沿程阻力和管道流量方程的近似表达式,大幅度的降低了计算量,简化了计算过程.
1 核心内容及研究路线本文核心内容是根据流变学以及流体力学理论,推导非牛顿流体管道流动方程与近似管道流量方程,建立非牛顿流体充填料浆流变参数与管道压差、管径、管路长度及充填流量的函数关系,并通过管道试验验证近似管道流量方程的准确性.具体研究路线如图 1所示.

|
图 1 本文的研究路线 Fig. 1 Research route of this paper |
充填料浆的本构模型采用可涵盖绝大多数常见非牛顿流体的幂率模型[14-21],即
| $ \tau = {\tau _{\rm{B}}} + K{\left( {\frac{{{\rm{d}}u}}{{{\rm{d}}r}}} \right)^n}. $ |
式中:τ为剪应力;τB为流变参数中的屈服应力;K为流变参数中的稠度系数;n为流变参数中的幂率指数;du/dr为速度梯度.
由幂率模型的定义可得:
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}r}} = {\left( {\frac{{\tau - {\tau _{\rm{B}}}}}{K}} \right)^{1/n}}. $ | (1) |
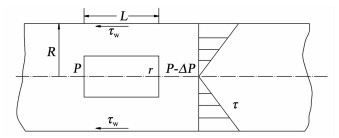
流体在一定压差作用下在管道内的剪应力分布如图 2所示.
|
图 2 流体在圆管内的剪应力分布 Fig. 2 Shear stress distribution of fluid in a circular tube |
对管壁内半径为R的流体部分,进行静力平衡分析可得:
| $ \Delta P \cdot {\rm{ \mathsf{ π} }}{R^2} - 2{\rm{ \mathsf{ π} }}RL \cdot {\tau _{\rm{w}}} = 0. $ |
式中:ΔP为管道两端压差;R为管道半径;L为管路长度;τw为管壁四周的剪切应力.
同理,对任意半径为r的流体部分,进行静力平衡分析可得:
| $ \Delta P \cdot {\rm{ \mathsf{ π} }}{r^2} - 2{\rm{ \mathsf{ π} }}rL \cdot \tau = 0. $ | (2) |
式中:ΔP为圆柱体两端压差;r为圆柱体半径;L为圆柱体长度;τ为圆柱体的剪切应力.
将式(2)代入式(1)可得:
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}r}} = {\left( {\frac{{\Delta Pr}}{{2LK}} - \frac{{{\tau _{\rm{B}}}}}{K}} \right)^{1/n}}, $ | (3) |
对式(3)两边分离变量,并进行积分可得:
| $ u = - \frac{{n(2L{\tau _{\rm{B}}} - \Delta Pr){{\left( {\frac{{{\tau _{\rm{B}}}}}{K} - \frac{{\Delta Pr}}{{2LK}}} \right)}^{1/n}}}}{{\Delta P(n + 1)}} + C, $ | (4) |
式中C为常数.根据边界条件,r=R时,u=0,可求得常数C的数值为
| $ C = \frac{{n(2L{\tau _{\rm{B}}} - \Delta PR){{\left( {\frac{{{\tau _{\rm{B}}}}}{K} - \frac{{\Delta PR}}{{2LK}}} \right)}^{1/n}}}}{{\Delta P(n + 1)}}. $ |
将常数C代入式(4)可得流体在管道内的任一流层的速度分布u为
| $ \begin{array}{l} u = \frac{{n(2L{\tau _{\rm{B}}} - \Delta PR){{\left( {\frac{{{\tau _{\rm{B}}}}}{K} - \frac{{\Delta PR}}{{2LK}}} \right)}^{1/n}}}}{{\Delta P(n + 1)}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{n(2L{\tau _{\rm{B}}} - \Delta Pr){{\left( {\frac{{{\tau _{\rm{B}}}}}{K} - \frac{{\Delta Pr}}{{2LK}}} \right)}^{1/n}}}}{{\Delta P(n + 1)}}. \end{array} $ |
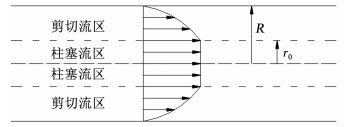
当考虑τB存在情况时,流体在管道内的速度分布如图 3所示.
|
图 3 流体在圆管内的层流流动 Fig. 3 Laminarflow of fluid in a circular tube |
当τB不为0时,管道中柱塞流区和剪切流区同时存在,柱塞流区和剪切流区的特征为:在柱塞流区r0内,各流层的速度相等且最大;在剪切流区各流层的速度不等,且越靠近管壁速度越小.
2.2 管道流量方程管道流量即管道流速与管道截面积的乘积,因此管道流量可用管道内流体速度分布方程进行积分求得,即
| $ Q = \int\limits_{{r_0}}^R u 2{\rm{ \mathsf{ π} }}r{\rm{d}}r + \int\limits_0^{{r_0}} {{u_0}} 2{\rm{ \mathsf{ π} }}r{\rm{d}}r. $ |
积分后可得流量Q的表达式为
| $ Q = \frac{{L{\rm{ \mathsf{ π} }}\tau _{\rm{B}}^2{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta P}}} \right)}^2}}}{{K\Delta P}} + \frac{{\frac{1}{{{2^{1/n}}}}n{\rm{ \mathsf{ π} }}{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta P}}} \right)}^2}\left( {R + 2Rn + \frac{{2L{\tau _{\rm{B}}}}}{{\Delta P}} + \frac{{8L{\tau _{\rm{B}}}}}{{\Delta P}}} \right){{\left( {\frac{{\Delta P\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta P}}} \right)}}{{KL}}} \right)}^{1/n}}}}{{6{n^2} + 5n + 1}}. $ | (5) |
式(5)即非牛顿流体管道流动方程.可见只要能够准确确定充填料浆的流变参数,就通过该方程能准确计算充填浆体在不同压差、管径和管路长度条件下的充填流量.反之,如果只要能够通过简单的管道试验(L管、倾斜管或环管等)准确测定充填浆体在不同压差、管径或管路长度条件下的充填流量,也就可以通过以该方程所构建的非牛顿流体管道流动方程组准确的反向求解流变参数.
当n=1时,τB不等于0时,为Buckingham流体,此时式(5)可简化为
| $ \begin{array}{*{20}{l}} {Q = \frac{{L{\rm{ \mathsf{ π} }}\tau _{\rm{B}}^2{{(R\Delta P - 2L{\tau _{\rm{B}}})}^2}}}{{K\Delta {P^3}}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\rm{ \mathsf{ π} }}{{(R\Delta P - 2L{\tau _{\rm{B}}})}^3}(3R\Delta P + 10L{\tau _{\rm{B}}})}}{{24KL\Delta {P^3}}}.} \end{array} $ | (6) |
浆体流速v的计算公式为
| $ v = \frac{Q}{{{\rm{ \mathsf{ π} }}{R^2}}}. $ | (7) |
联立式(2)、(6)、(7)可得Buckingham流动方程:
| $ \frac{{4v}}{R} = \frac{{{\tau _{\rm{w}}}}}{K} \cdot \left[ {1 - \frac{4}{3} \cdot \left( {\frac{{{\tau _{\rm{B}}}}}{{{\tau _{\rm{w}}}}}} \right) + \frac{1}{3} \cdot {{\left( {\frac{{{\tau _{\rm{B}}}}}{{{\tau _{\rm{w}}}}}} \right)}^4}} \right]. $ |
当n≠1时,τB=0时,为假塑性流体或胀塑性流体,此时式(5)可进一步简化为
| $ Q = \frac{{{R^3}n{\rm{ \mathsf{ π} }}{{\left( {\frac{{R\Delta P}}{{2KL}}} \right)}^{1/n}}}}{{3n + 1}}. $ |
当n=1时,τB=0时,为牛顿流体,此时式(5)可进一步简化为Poiseuille定律:
| $ Q = \frac{{{R^4}\Delta P{\rm{ \mathsf{ π} }}}}{{8KL}}. $ |
非牛顿流体管道流动方程仅适用于管道层流,对于非层流状态的管道流动,本方程并不适用.为了对管道流动状态进行判别,需要引入雷诺数并在此基础上推导出过渡流速方程,明确非牛顿流体管道流动方程的适用条件,从而实现料浆流态的准确判别和管道流动方程的正确应用.
雷诺数Re计算公式为
| $ Re = \frac{{Dv{\rho _m}}}{\eta }. $ | (8) |
式中:D(2R)为管道直径;η为料浆表观黏度;v为料浆平均流速;ρm为料浆比重.
根据式(8)可见,表观黏度越小,雷诺数越大.表观黏度是指在一定速度梯度下,用相应的剪切应力除以剪切速率所得的商.表观黏度η的定义为
| $ \eta = \tau /\left( {\frac{{{\rm{d}}u}}{{{\rm{d}}r}}} \right). $ | (9) |
联立式(3)、(9)可得非牛顿流体在管道内的表观黏度分布为
| $ \eta = \frac{{r\Delta P}}{{2L{{\left( {\frac{{r\Delta P - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)}^{1/n}}}}. $ | (10) |
由式(10)可知r=R时,η有最小值,由于η与Re负相关,此时Re有最大值.即管壁处的雷诺数满足层流状态时,管道内任意位置也满足层流状态.
为求解管壁处的雷诺数,取r=R,同时联立式(7)、(8)、(10)可得非牛顿流体管道流动雷诺数Re的最大值为
| $ Re = \frac{{4Q{\rho _m}L{{\left( {\frac{{R\Delta P - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)}^{1/n}}}}{{\Delta P{\rm{ \mathsf{ π} }}{R^2}}}. $ | (11) |
方程(11)即非牛顿流体过渡流速方程,当非牛顿流体在管道内流动时,根据方程(11)计算得雷诺数Re的最大值小于2 300时,充填浆体在管道内才全部呈现层流状态,此时本文推导的非牛顿流体管道流动方程才能成立.
2.4 近似管道流量方程由于本文推导的非牛顿流体管道流量方程形式复杂、计算量极大,为了便于现场工作人员应用,需要对其进行简化以减少计算量、简化计算过程.
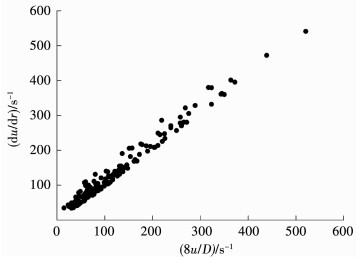
在矿山常见工况条件下(0 Pa < τB < 100 Pa、3.6 MPa < ΔP < 7.2 MPa、900 m < L < 1 100 m、0.8 < n < 1.2、0.8 < K < 1.2、0.050 m < R < 0.075 m)随机抽取100组数据,并分别计算du/dr(r=R)和8v/D(4v/R)的数值,计算完成后以8v/D为横坐标、du/dr(r=R)为纵坐标作图,如图 4所示.
|
图 4 常见工况du/dr与8v/D数值对比 Fig. 4 Comparison of values of du/dr and 8v/D in common working conditions |
由图 4可见,均质充填浆体在常见管道输送工况条件下,其实际壁面剪切速率与管道平均流速正相关、与管道直径负相关,且du/dr≈8v/D.由于管壁处du/dr≈8v/D,即
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}r}} = {\left( {\frac{{\Delta PR}}{{2LK}} - \frac{{{\tau _{\rm{B}}}}}{K}} \right)^{1/n}} \approx \frac{{8v}}{D}. $ | (12) |
将8v/D替换为4v/R,联立式(7)、(12)并化简后可得:
| $ Q = \frac{{{R^3}{\rm{ \mathsf{ π} }}}}{4}{\left( {\frac{{R\Delta P - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)^{1/n}}. $ | (13) |
式(13)即非牛顿流体近似管道流量方程.通过该方程能近似计算已知流变参数的充填浆体在不同压差、管径和管路长度条件下的充填流量.反之,也可以通过该方程所构建的近似管道流动方程组反向近似求解流变参数.
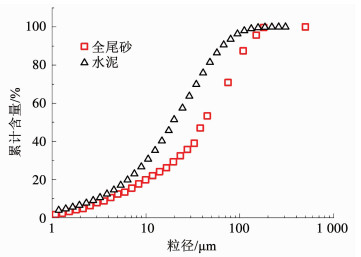
3 试验 3.1 试验材料试验中采用矿山全尾砂、325普通硅酸盐水泥混合制备非牛顿流体充填料浆.矿山全尾砂取自某铜矿山尾矿库,体积质量为2 670 kg/m3,容重为1 392 kg/m3,孔隙率为47.87%.图 5为该矿山铜尾砂及水泥的粒径分布图,全尾砂中-74 μm筛下颗粒总量占比为70.85%,-37 μm占比46.96%,水泥中的细颗粒含量占比尾砂更大,可以看出该矿山尾砂及水泥粒径较细,适于制备均质充填料浆.试验材料的化学成分分析可参考文献[22],此处不再赘述.
|
图 5 水泥和尾砂的粒径分布 Fig. 5 Size distribution of cement and tailings |
按照11%的水泥掺量与水、尾砂混合,强力搅拌制备为充填料浆,所制备的充填料浆基本物理性质见表 1.
| 表 1 充填料浆基本物理性质 Tab. 1 Basic physical properties of filling slurry |
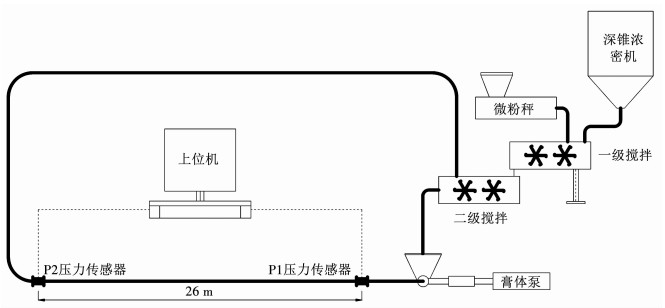
试验系统是由深锥浓密机、可储存水泥的微粉称、一级搅拌机、二级搅拌机、膏体柱塞泵、充填管道、压力传感器和上位机构成的环管实验装置,如图 6所示.
|
图 6 环管试验装置系统布置 Fig. 6 Layout of loop test equipment system |
该环管装置设置的充填管道内径为Φ150 mm.为监测管内压力,共设置压力表 2块,分别标记为P1、P2号压力表,P1与P2号压力表之间管道长度为26 m,为监测管道流量,在柱塞泵与管道接口法兰处布设OPTIFLUX 4300C型流量计.
3.3 试验原理由于本文试验采用固定式环管试验装置,其管径R、充填管路长度L不变,通过膏体泵改变不同的管道两端压差ΔP1、ΔP2和ΔP3,测出口断面流量Q1、Q2、Q3,代入下式(14),通过解方程组,即可求得料浆的屈服应力τB、稠度系数K和幂率指数n.将试验参数代入下式得到充填料浆流变参数的数值解以后,将屈服应力τB、稠度系数K和幂率指数n的数值代入式(11)判别其是否为层流,当Re < 2 300时,为层流,此时流动方程成立.
| $ \begin{array}{l} {Q_1} = \frac{{L{\rm{ \mathsf{ π} }}\tau _{\rm{B}}^2{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_1}}}} \right)}^2}}}{{K\Delta {P_1}}} + \frac{{\frac{1}{{{2^{1/n}}}}n{\rm{ \mathsf{ π} }}{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_1}}}} \right)}^2}\left( {R + 2Rn + \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_1}}} + \frac{{8L{\tau _{\rm{B}}}}}{{\Delta {P_1}}}} \right){{\left( {\frac{{\Delta {P_1}\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_1}}}} \right)}}{{KL}}} \right)}^{1/n}}}}{{6{n^2} + 5n + 1}},\\ {Q_2} = \frac{{L{\rm{ \mathsf{ π} }}\tau _{\rm{B}}^2{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_2}}}} \right)}^2}}}{{K\Delta {P_2}}} + \frac{{\frac{1}{{{2^{1/n}}}}n{\rm{ \mathsf{ π} }}{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_2}}}} \right)}^2}\left( {R + 2Rn + \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_2}}} + \frac{{8L{\tau _{\rm{B}}}}}{{\Delta {P_2}}}} \right){{\left( {\frac{{\Delta {P_2}\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_2}}}} \right)}}{{KL}}} \right)}^{1/n}}}}{{6{n^2} + 5n + 1}},\\ {Q_3} = \frac{{L{\rm{ \mathsf{ π} }}\tau _{\rm{B}}^2{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_3}}}} \right)}^2}}}{{K\Delta {P_3}}} + \frac{{\frac{1}{{{2^{1/n}}}}n{\rm{ \mathsf{ π} }}{{\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_3}}}} \right)}^2}\left( {R + 2Rn + \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_3}}} + \frac{{8L{\tau _{\rm{B}}}}}{{\Delta {P_3}}}} \right){{\left( {\frac{{\Delta {P_3}\left( {R - \frac{{2L{\tau _{\rm{B}}}}}{{\Delta {P_3}}}} \right)}}{{KL}}} \right)}^{1/n}}}}{{6{n^2} + 5n + 1}}. \end{array} $ | (14) |
以近似解方法求解流变参数近似解的原理与解析解一致,对于本文试验采用的试验装置,其管径R、充填管路长度L不变,通过膏体泵改变不同的管道两端压差ΔP1、ΔP2和ΔP3,测出口断面流量Q1、Q2、Q3,代入下式,通过解方程组,即可求得料浆的3个流变参数即屈服应力τB、稠度系数K和幂率指数n的近似解,将近似解方法所求得的流变参数数值与解析解所得流变参数数值对比,考察其差异.
| $ \begin{array}{*{20}{l}} {{Q_1} = \frac{{{R^3}{\rm{ \mathsf{ π} }}}}{4}{{\left( {\frac{{R\Delta {P_1} - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)}^{1/n}},}\\ {{Q_2} = \frac{{{R^3}{\rm{ \mathsf{ π} }}}}{4}{{\left( {\frac{{R\Delta {P_2} - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)}^{1/n}},}\\ {{Q_3} = \frac{{{R^3}{\rm{ \mathsf{ π} }}}}{4}{{\left( {\frac{{R\Delta {P_3} - 2L{\tau _{\rm{B}}}}}{{2KL}}} \right)}^{1/n}}.} \end{array} $ | (15) |
利用环管试验装置在不同ΔP条件下以某充填配比所制备的充填料浆测得的试验数据结果见表 2.
| 表 2 管道试验中测定的试验数据 Tab. 2 Test data measured in pipeline test |
将表 2试验数据与试验装置参数分别代入方程组(14)、(15),进行流变参数解析解和近似解的计算,计算结果见表 3.
| 表 3 试验料浆流变参数 Tab. 3 Rheological parameters of test slurry |
将表 2试验数据、试验装置参数和表 3中流变参数的解析解代入方程(11),可得试验中ΔP1、ΔP2和ΔP3在3组试验条件下的Re分别为287.8、143.7和29.6.由于3组实验中Re远小于2 300,所以3组管道试验中料浆均为层流状态,流动方程成立.
在3.6 MPa < ΔP < 7.2 MPa、900 m < L < 1 100 m、0.050 m < R < 0.075 m范围内随机取100组矩阵数据,分别将精确解法和近似解法得到的流变参数代入管道流量方程和近似管道流量方程求解流量,并绘制成图 7中的三维图像,可见相同坐标值的条件下(ΔP、L、R相同时),精确解法和近似解法所求得的管道流量数值大小基本一致,且有相似的变化规律,说明对于本次试验所选取的非牛顿流体充填料浆,可以以近似解方法去求得流体的流变参数和管道流量,误差较小.

|
图 7 精确解法与近似解法的三维图像对比 Fig. 7 Comparison of 3D images of exact solution and approximate solution |
1) 含屈服应力的非牛顿流体在管道内流动时,柱塞流区和剪切流区同时存在,柱塞流区和剪切流区各流层的流速、剪应力、表观黏度和管道流量等与管道参数及流变参数有明确的数学关系,通过本文非牛顿流体管道流动方程及方程组可对充填参数或流变参数等进行准确计算.
2) 均质充填浆体在常见管道输送工况条件下,其实际壁面剪切速率与管道平均流速正相关、与管道直径负相关.本文根据这一现象,通过近似计算,将非牛顿流体管道流动方程进行了简化,推导出了较为准确的非牛顿流体近似管道流量方程,该方程计算量较小、计算过程简单,对于现场工程应用有较高的实用价值.
3) 采用工业级环管管道试验系统对非牛顿流体充填料浆的流变参数进行测定.基于试验数据和方程可视化方法绘制的三维图像对比表明本文所推导的非牛顿流体管道流动方程解析解法与近似解法所得结果基本一致,可供广大矿山工作人员参考.
| [1] |
MARUFUZZAMAN M, EKSIOGLU S D, HERNANDEZ R. Truck versus pipeline transportation cost analysis of wastewater sludge[J]. Transportation Research Part A: Policy and Practice, 2015, 74: 14. DOI:10.1016/j.tra.2015.02.001 |
| [2] |
SINHA S L, DEWANGAN S K, SHARMA A. A review on particulate slurry erosive wear of industrial materials: In context with pipeline transportation of mineral-slurry[J]. Particulate Science and Technology, 2017, 35(1): 103. DOI:10.1080/02726351.2015.1131792 |
| [3] |
兰文涛, 吴爱祥. 管道层流通用方程的推导及试验验证[J]. 华中科技大学学报(自然科学版), 2019, 47(11): 61. LAN Wentao, WU Aixiang. Derivation and test verification of general equation for pipeline laminar flow[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(11): 61. DOI:10.13245/j.hust.191111 |
| [4] |
陈琴瑞, 王洪江, 吴爱祥, 等. 用L管测定膏体料浆水力坡度试验研究[J]. 武汉理工大学学报, 2011, 33(1): 108. CHEN Qinrui, WANG Hongjiang, WU Aixiang, et al. Experimental study on hydraulic gradient of paste slurry by L-pipe[J]. Journal of Wuhan University of Technology, 2011, 33(1): 108. DOI:10.3963/j.issn.1671-4431.2011.01.024 |
| [5] |
POLYANIN A D, ZAITSEV V F. Transformations, properties, and exact solutions of unsteady axisymmetric boundary layer equations for non-Newtonian fluids[J]. Theoretical Foundations of Chemical Engineering, 2017, 51(4): 437. DOI:10.1134/s004057951704025x |
| [6] |
MATVEENKO V N, KIRSANOV E A. Structural rationale of a non-Newtonian flow[J]. Moscow University Chemistry Bulletin, 2017, 72(2): 69. DOI:10.3103/s0027131417020031 |
| [7] |
陆海, 尹军, 袁一星, 等. 污泥管道输送沿程阻力影响因素分析[J]. 哈尔滨工业大学学报, 2013, 45(6): 29. LU Hai, YIN Jun, YUAN Yixing, et al. Influencing factors of on-way resistance in sludge transportation pipelines[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 29. DOI:10.11918/j.issn.0367-6234.2013.06.005 |
| [8] |
MARN J, TERNIK P. Laminar flow of a shear-thickening fluid in a 90° pipe bend[J]. Fluid Dynamics Research, 2006, 38(5): 295. DOI:10.1016/j.fluiddyn.2006.01.003 |
| [9] |
HEYWOOD N I, ALDERMAN N J. Developments in slurry pipeline technologies[J]. Chemical Engineering Progress, 2003, 12(4): 36. |
| [10] |
WILSON K C, CLIFT R, SELLGREN A. Operating points for pipelines carrying concentrated heterogeneous slurries[J]. Powder Technology, 2002, 123(1): 19. DOI:10.1016/s0032-5910(01)00423-5 |
| [11] |
GRABINSKY M W. In situ monitoring for ground truthing paste backfill design[C]//Proceedings of the 13th International Seminar on Paste and Thickened Tailings. Perth: Australian Centre for Geomechancis, 2010: 85. DOI: 10.36487/ACG_rep/1063_8_Grabinsky
|
| [12] |
杨超.金属矿山尾矿高浓度管道输送技术研究[D].淄博: 山东理工大学, 2011 YANG Chao.Technical research in high concentrations of tailings pipeline for metal mines[D]. Zibo: Shandong University of Technology, 2011 |
| [13] |
NASIR O, FALL M. Coupling binder hydration, temperature and compressive strength development of underground cemented paste backfill at early ages[J]. Tunnelling and Underground Space Technology, 2010, 25(1): 9. DOI:10.1016/j.tust.2009.07.008 |
| [14] |
兰文涛.半水磷石膏基矿用复合充填材料及其管输特性研究[D].北京: 北京科技大学, 2019 LAN Wentao. Research on hemihydrate phosphogypsum based mineral filling composites and its pipe flow performance[D]. Beijing: University of Science and Technology Beijing, 2019 |
| [15] |
王辉, 刘彦甫, 曹伟, 等. 幂律流体双股碰撞雾化特征的试验研究[J]. 哈尔滨工业大学学报, 2018, 50(7): 52. WANG Hui, LIU Yanfu, CAO Wei, et al. Atomization characteristics experiment of impinging jets with power-law fluid[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 52. DOI:10.11918/j.issn.0367-6234.201703002 |
| [16] |
BOYLU F, DINCER H, ATESOK G. Effect of coal particle size distribution, volume fraction and rank on the rheology of coal-water slurries[J]. Fuel Processing Technology, 2004, 85(4): 241. DOI:10.1016/S0378-3820(03)00198-X |
| [17] |
田兴旺, 王平, 徐士鸣. 颗粒堆积多孔介质内幂律流体的流动阻力特性[J]. 哈尔滨工业大学学报, 2017, 49(1): 126. TIAN Xingwang, WANG Ping, XU Shiming. Flow resistance characteristics of power law fluid flow through granular porous medium[J]. Journal of Harbin Institute of Technology, 2017, 49(1): 126. DOI:10.11918/j.issn.0367-6234.2017.01.018 |
| [18] |
孙洪全, 韩纪庆. 基于粒子的非牛顿流体模拟统一模型[J]. 哈尔滨工业大学学报, 2010, 42(7): 1104. SUN Hongquan, HAN Jiqing. A unified particle model for non-Newtonian fluid simulation[J]. Journal of Harbin Institute of Technology, 2010, 42(7): 1104. DOI:10.11918/j.issn.0367-6234.2010.07.021 |
| [19] |
FALL M, NASIR O. Predicting the temperature and strength development within cemented paste backfill structure[C]//Proceedings of the 13th International Seminar on Paste and Thickened Tailings. Perth: Australian Centre for Geomechancis, 2010: 125
|
| [20] |
BELEM T, FOURIE A B, FAHEY M. Time-dependent failure criterion for cemented paste backfills[C]//Proceedings of the 13th International Seminar on Paste and Thickened Tailings. Perth: Australian Centre for Geomechancis, 2010: 147
|
| [21] |
刘晓辉.膏体流变行为及其管流阻力特性研究[D].北京: 北京科技大学, 2014 LIU Xiaohui. Study on rheological behavior and pipe flow resistance of paste backfill[D]. Beijing: University of Science and Technology Beijing, 2014 |
| [22] |
LAN Wentao, WU Aixiang, YU Ping. Development of a new controlled low strength filling material from the activation of copper slag: Influencing factors and mechanism analysis[J]. Journal of Cleaner Production, 2020, 246: 119060. DOI:10.1016/j.jclepro.2019.119060 |
 2020, Vol. 52
2020, Vol. 52


