2. 哈尔滨工业大学 建筑学院,哈尔滨 150006
2. School of Architecture, Harbin Institute of Technology, Harbin 150006, China
相对于其他领域研究来说,绿色节能领域的研究以及设计需要有明确具体的指标来反映节能的效果[1].目前国内对于能耗的研究主要集中在对住宅单体节能措施的研究上,比如墙体和屋顶保温隔热等[2-4].在区域层面上,学者们从微气候环境的调节、建筑排列和群体布局的科学合理规划等方面来探讨城市居住区规划中的节能问题[5-7].但是,国内居住区节能规划的相关研究大多数仍为定性研究.近年来,为探究居住区形态与住宅能耗之间的具体关系,敏感性分析由于其定量分析的优点而被越来越多地应用于建筑形态参数与能耗关系的相关研究中,方便学者了解形态对能耗的具体影响.敏感性分析可以定量衡量包括朝向以及小区道路宽度等在内的住宅形态参数变化对住宅能耗的影响[8].目前应用在建筑领域的敏感性分析主要分为两大类,分别为全局敏感性分析和局部敏感性分析[9-10].全局敏感性分析相对于局部敏感性分析而言可以从整体视角更全面地研究输入参数与输出结果之间的关系,学者能够借此提出更可靠的建筑节能策略[11-12],因此越来越多地被作为研究建筑能耗影响因素的手段.学者们通过利用动态能耗模拟和全局敏感性分析结合的方法发现,建筑布局对建筑的制冷、供热和总能耗均有显著的影响且各个建筑形态参数的变化对建筑能耗的影响程度也各不相同[13-14].
本文以典型寒地城市哈尔滨市为例,针对不同形态居住区理想模型的住宅能耗模拟数据进行全局敏感性分析,进而从布局形态的角度对寒地城市居住区提出节能规划建议.
1 方法本文研究采用全局敏感性分析方法中的基于回归的敏感性分析方法来分析居住区的形态变化对住宅能耗的影响.
先假设居住区形态参数与住宅能耗符合线性模型,再通过修正决定系数(R2)来确定线性模型的拟合效果.一般来说,如果R2>0.7,即表示该线性模型的分析结果可靠[15].由于各个居住区形态参数的取值范围均不相同,因此,根据本次数据样本的特点,在基于回归的全局敏感性分析方法中选择了标准回归系数法(SRC).利用该方法对实际变量数据样本进行分析从而得到标准化回归系数(SRC),SRC系数为正则表示输入参数与输出结果的关系为正相关,即输出结果随着输入参数的增加而增加;负值则相反. SRC系数的绝对值代表住宅能耗受居住区形态系数变化影响的相对敏感性,绝对值越大,该居住区形态参数的变化对住宅能耗的影响就越大.SRC标准回归系数计算公式如下:
| $ {\rm{SRC}}\left( {{x_i}, y} \right) = {b_i}\frac{{{S_{{x_i}}}}}{{{S_y}}}. $ |
式中:xi为第i个输入参数;y为输出结果(能耗);Sxi为第i个输入参数的回归系数;Sxi和Sy则为输出结果和第i个输入参数的标准差;SRC标准回归系数表示各输入参数对输出结果的影响值.
2 步骤 2.1 寒地城市住宅调研及分类根据DB 23/1270―2018 《黑龙江省居住建筑节能65%设计标准》,哈尔滨市的气候区属为严寒地区(B)区,HDD18度日值为5 032.鉴于哈尔滨市既需要冬季供热采暖又需要夏季空调制冷,因此是适用于此次对寒地城市住宅能耗研究的理想城市.
研究以哈尔滨市主城区内的居住区为研究对象,采用分层抽样的方法按照年代划分从4个行政区中各抽取25个居住区,居住区的年代划分为4个区段.4个行政区一共抽取100个居住区进行住宅平面形态的研究.
研究对哈尔滨现有住宅的平面形态进行分析归类,并据此将哈尔滨市的住宅类型分为“一”字型、“L”型、“凹”字型和点式住宅4类住宅,并确定每类住宅的住宅标准层单元的长宽.住宅标准层单元根据住宅层数分为两类,分别为多层和高层住宅标准层单元.表 1为4类住宅及两类住宅标准层单元的平面形态和尺寸.
| 表 1 各区居住区按年代抽样数量 Tab. 1 Number of samples in each residential district |
利用Openstudio和EnergyPlus软件对不同形态居住区模型进行动态能耗模拟.为了在Openstudio内建立住宅模型,对4类典型住宅进行实地调研后确定每类住宅标准层单元的窗墙面积比.图 1(a)为最终建立的多层和高层住宅的标准层单元模型和住宅单体模型.为了限制模型中窗墙面积比对能耗模拟的影响,假设住宅单元东、西两面和南、北两面的开窗完全相同且对称.其中,依据调研统计结果,多层住宅单元中南、北面的窗墙面积比为0.24,东、西面为0.075;点式高层住宅单元南、北面的窗墙面积比为0.24,东、西面为0.23,均满足DB 23/1270-2018《黑龙江省居住建筑节能65%设计标准》中对严寒(B)区住宅的窗墙面积比的规定.图 1(b)为住宅单元模型基础上建立的各类住宅单体模型.

|
图 1 住宅模型模拟示意 Fig. 1 Schematic diagram of residential simulation model |
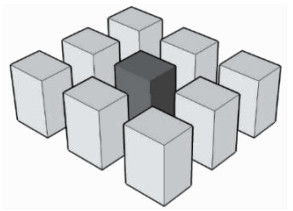
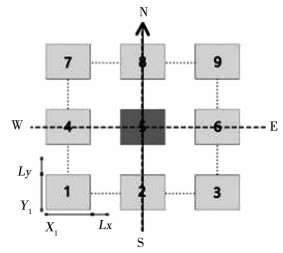
为了进行能耗模拟时方便进行变量控制,本研究建立一个3×3的行列式居住区理想模型,其中每栋住宅都完全相同,且相互之间距离相等,如图 2、3所示.在该理想模型中,5号住宅所代表的住宅能耗为周围均是相同住宅且间距相等情况下的理想住宅能耗[13-14].采用理想化模型进行能耗模拟操作简单且可重复,在面对真实城市居住区的复杂特征时可以排除其中的各种复杂因素,便于对于研究对象变量的控制以及研究,如图 4所示.
|
图 2 居住区三维模型模拟示意 Fig. 2 3D residential district simulation model |
|
图 3 居住区模型模拟平面示意 Fig. 3 Plane of residential district simulation model |
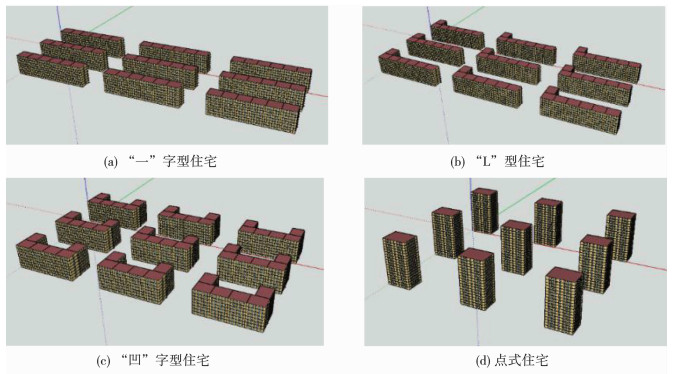
|
图 4 4类居住区理想化模型 Fig. 4 Idealized model of four types of residential districts |
本文在居住区常见的形态相关参数中挑选出4个形态参数,分别为住宅层数、住宅面宽、住宅间距和住宅朝向,并且将住宅类型分为多层和点式高层住宅两类,具体取值范围见表 2.各个居住区形态参数的取值在每一个模型中均呈均匀分布.
| 表 2 居住区形态参数取值范围 Tab. 2 Range of values of residential district morphological parameters |
结合哈尔滨市住宅实际情况,依据《严寒和寒冷地区居住建筑节能设计标准》中的建筑参数分类对住宅层数进行分类,模型模拟时多层住宅层数按5、6、7和8层分别进行能耗模拟;点式高层住宅层数按9、18和27层分别进行模拟.住宅面宽则以每个组成单元的面宽15 m为单位,各类型多层住宅的住宅面宽取值区间为30~90 m.由于点式高层住宅的住宅面宽在模拟中一直保持不变,因此对于点式高层住宅来说,住宅面宽这一变量不做考虑.在理想化的居住区模型中,住宅的前后左右间距等距,因此可以统一用一个数值代表住宅间距.多层和点式高层住宅间的住宅间距取值区间分别为6~30 m和13~65 m.在进行不同朝向的住宅能耗模拟时,在研究朝向对住宅能耗的影响模拟时,每个模型选取0°、45°和90°这3个具有代表性的角度进行模拟.各形态参数的具体模拟数值如图 5中所示.
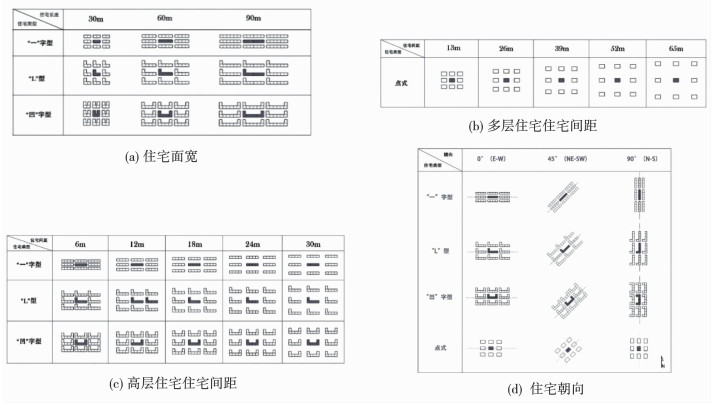
|
图 5 各形态参数模拟示意 Fig. 5 Schematic diagram of each morphological parameter |
住宅能耗模拟所用的气象文件来自EnergyPlus官网,将气象年数据导入ecotect进行形象化表示.建筑、居住、HVAC和模拟的主要设置参数均从相关的规范和数据调研中获得(见图 6).哈尔滨市采用集中供暖.研究为了排除供暖方式对模拟结果的影响,没有设定特定的供暖方式,仅假设每户住宅内为100%效率的热源.
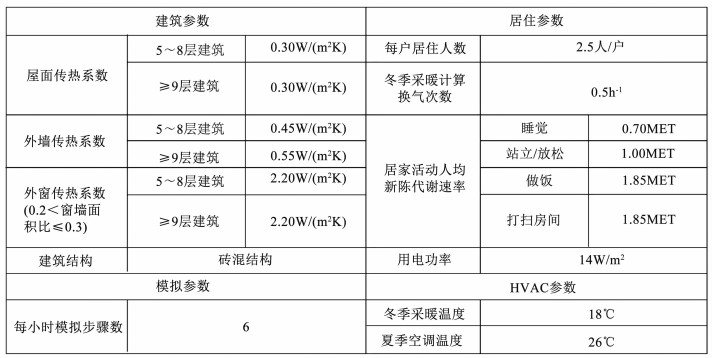
|
图 6 模型能耗模拟参数设置 Fig. 6 Settings of energy consumption simulation parameters |
住宅能耗模拟总共模拟了585个理想居住区模型,其中有540个多层住宅居住区模型,3类多层住宅各为180个;此外还模拟了45个点式高层住宅的居住区模型.图 7为各类住宅的制冷、供热和总能耗分布频率图.
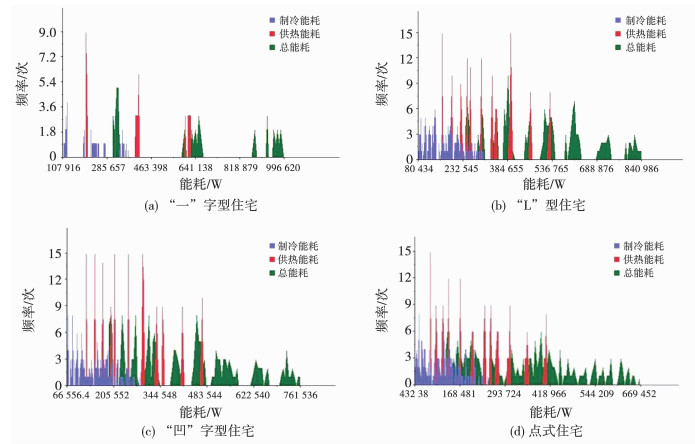
|
图 7 4类住宅能耗分布频率图 Fig. 7 Energy consumption distribution frequency of four residential types |
本次研究的标准回归系数法(SRC)分析通过SimLab2.2软件完成.具体的SRC标准回归系数结果见表 3,各项数值的置信度均为95%.
| 表 3 SRC方法下各形态变量的敏感度及R2值 Tab. 3 Sensitivity and R2 value of each morphological parameter under SRC method |
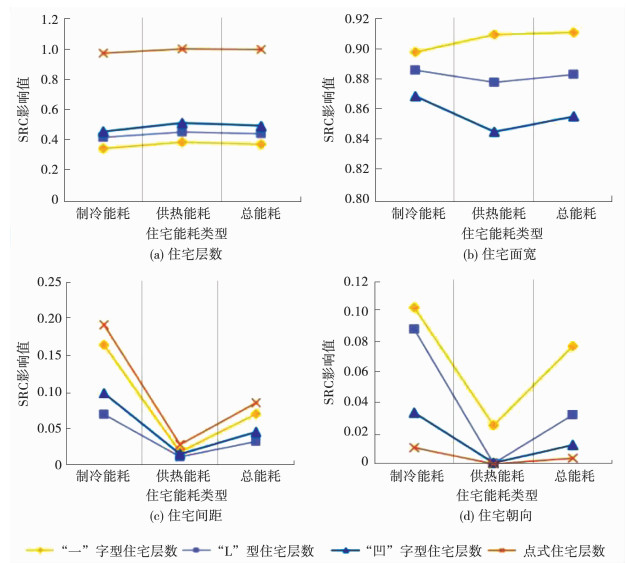
从表 3可以看出,住宅层数对点式住宅能耗的影响最大,“凹”字型和“L”型其次,对“一”字型住宅能耗的影响值最小;受住宅面宽影响最大的为“一”字型住宅,而影响最小的是“凹”字形住宅;住宅间距对能耗的影响从大到小依次为点式住宅、“一”字型、“凹”字形、“L”型住宅;最后,住宅朝向的变化对“一”字型住宅能耗的影响最大,“L”型和“凹”字型其次,点式住宅最小.
2.3.2 不同季节下居住区形态对住宅制冷和供暖能耗影响图 8显示各类住宅的制冷能耗受住宅层数变化的影响不如供热能耗敏感,即相较于夏季而言,冬季的住宅能耗受层数变化影响较大;除了“一”字型住宅,住宅面宽的变化在夏季对其他3类住宅的影响均比在冬季大;住宅间距的变化对住宅能耗的影响与住宅面宽类似,同样也是在夏季比冬季大,且在冬季对供热能耗基本没有影响;最后,研究结果表明各类住宅的制冷能耗对朝向变化的敏感度均大于供热能耗,且供热能耗对朝向变化的敏感度近乎为0,也就是说在冬季住宅的不同朝向对能耗基本没有影响.产生这一现象的原因与哈尔滨市供暖期间的太阳辐射值较低有关.因此,住宅能耗在冬季受住宅朝向变化(即受太阳辐射面积的变化)影响较小.
|
图 8 各形态参数对4类住宅能耗影响值 Fig. 8 Impact of morphological parameters on energy consumption of four residential types |
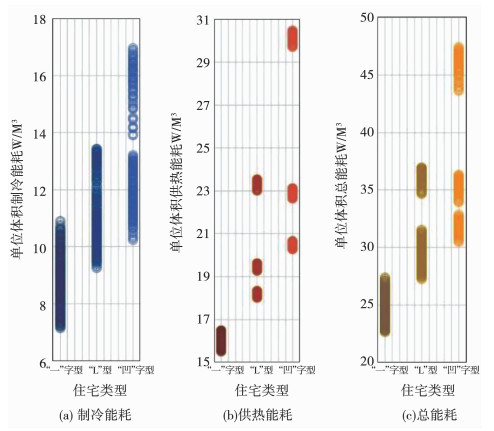
通过对比多层住宅的各类型住宅单位体积的供热、制冷和总能耗平均值可知,“一”字型住宅的总能耗平均值最低,为24.79 W/m3,“凹”字型住宅是最高的,为37.69 W/m3,如图 9所示.因此,在多层住宅类型的选择上,应该以“一”字型为主,且住宅的造型宜对称简洁.
|
图 9 多层住宅单位体积制冷、供热及总能耗分布 Fig. 9 Cooling, heating, and total energy consumption distributions of multi-story residential building |
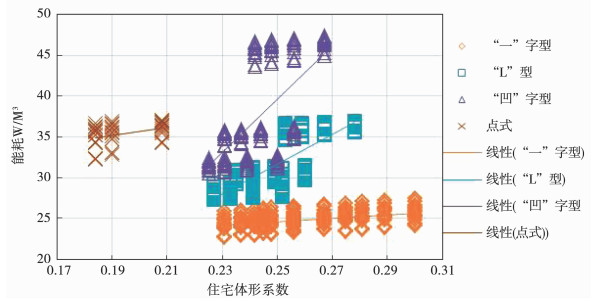
研究引入住宅的体形系数来研究住宅能耗与住宅形态之间的关系,研究结果表明各类住宅的体形系数均与住宅单位体积总能耗成正比(如图 10所示).
|
图 10 住宅体形系数与各类住宅能耗关系图 Fig. 10 Relationship between residential shape coefficient and various types of residential energy consumption |
因此,在进行寒地城市居住区规划时,应该在满足各项规范的基础上尽可能地使住宅体形系数最小化即在同“一”类型住宅层数不变时尽可能让住宅单元数最多,这样即满足了开发商的收益需求又有利于实现住宅总能耗的最小化.
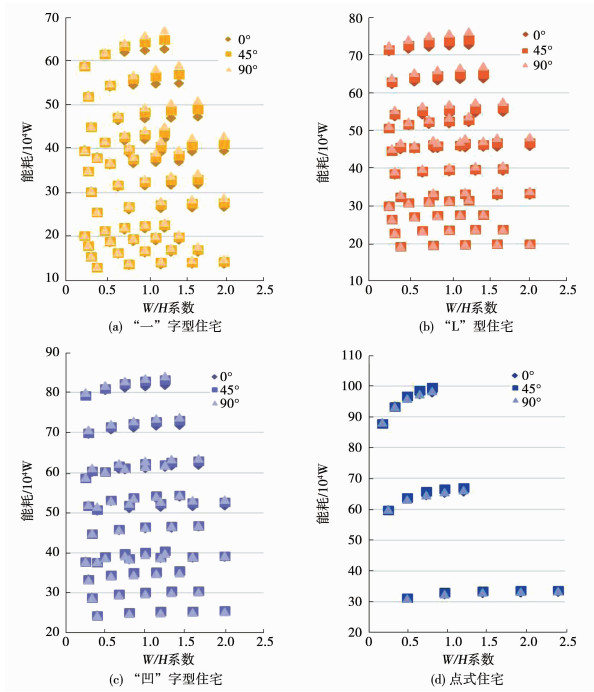
3.1.3 住宅间距住宅间距与住宅高度的比值(简称W/H系数)与住宅能耗存在一定关系(如图 11所示).在同一朝向并且体形系数保持不变时,住宅总能耗与W/H系数的关系成正比.因此,当住宅高度不变时,随着W/H系数的增加即住宅间距的增大,住宅的总能耗也随之增加.
|
图 11 4类住宅总能耗与W/H系数和朝向关系图 Fig. 11 Variation of total energy consumption with W/H coefficient and orientation of four residential types |
因此,在对寒地城市居住区的住宅日照间距进行规划时,应该取寒地城市住宅日照间距的最小值(多层住宅高度的1.8倍和点式高层高度的1.0倍),以紧凑的布局为主,避免松散的住区规划,从而可以减少居住区住宅总能耗.
3.1.4 住宅朝向在冬季,住宅朝向对住宅的供热能耗基本没有影响,但是在夏季,住宅朝向对住宅的制冷能耗会有影响.本研究主要考虑住宅形态(体形系数和W/H系数)和住宅间距对不同朝向的住宅总能耗的影响.
从图 11~图 13可以看出,当W/H系数大于0.5时,“一”字型和点式住宅的朝向应以正南正北为主,尽量避免朝向为90°的情况发生;当“L”型住宅面宽大于60 m时,朝向应以正南正北为主,减少住宅朝向为90°的布局规划;对于“凹”字型住宅来说,当其住宅面宽大于90 m时朝向应尽量为正南正北,避免朝向为90°的情况,而当长度小于90 m时,朝向应以90°为主,避免45°的朝向.“一”字型住宅、“L”型住宅、“凹”字型住宅和点式住宅在布局规划时的朝向均应该以正南正北为主,且“凹”字型住宅在布局规划时要尽量避免朝向为45°,而其他3类住宅要尽量避免朝向为90°.
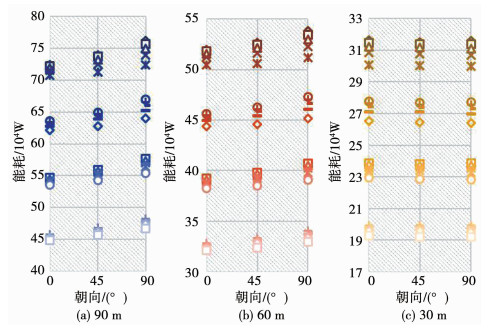
|
图 12 “L”型住宅总能耗与朝向和面宽关系 Fig. 12 Variation of total energy consumption with orientation and building length of L-shaped housing |
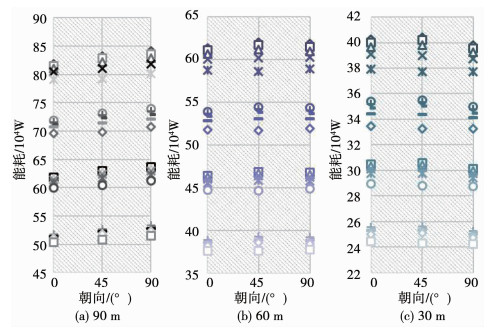
|
图 13 “凹”字型住宅总能耗与朝向和面宽关系 Fig. 13 Variation of total energy consumption with orientation and building length of U-shaped housing |
住宅类型中已经论证了“一”字型住宅为能耗最低多层住宅类型,因此多层住宅组合中仅由“一”字型住宅的不同形态组成.高层住宅类型为本次研究中仅有的点式高层.
首先,将住宅分为多层Ⅰ类、Ⅱ类、高层Ⅰ类和Ⅱ类,对应住宅用地容积率范围按照GB50180—2018《城市居住区规划设计标准》中规定.
其次,根据本文的住宅间距分析,住宅的间距取符合规范的最小值,侧间距根据GB 50016—2014《建筑设计防火规范》规定取数值10 m和13 m,多层和高层住宅的日照间距则在满足GB50180—2018《城市居住区规划设计标准》规定前提下,取《哈尔滨市城市规划管理条例》中规定日照间距系数最小值1.8和1.0.此外,在上述有关住宅朝向的研究中已经论证,“一”字型和点式高层住宅在日照间距系数为1.8和1.0的情况下均在住宅朝向为0°时能耗最小.建筑退让用地红线距离按照住宅建筑用地红线退让距离指标规范进行取值.
在规定的容积率范围内,按照住宅用地内住宅的侧间距、日照间距和用地红线退让距离这3项取值对各个住宅形态参数组合进行筛选.其中,为了更直观地表达住宅形态参数组合的取值范围,将之前研究中的“住宅面宽”参数替换为“住宅单元数”.
根据本文的住宅体形系数分析,多层住宅的最低能耗参数组合是同一住宅层数下挑选住宅单元数最多的参数组合;而点式高层的最低能耗组合为住宅层数最高的形态参数组合.表 4为在3×3的行列式小区中5~6层住宅在低容积率要求下的最低能耗参数组合模型示意图以及4项基本形态参数值.由于在高容积率下,在3×3的行列式小区中住宅层数为7层时住宅单元数没有最大值,住宅层数为8层时住宅单元数最大值为15个超出了常规值,因此在常规情况下7、8层的住宅最低能耗参数组合中住宅单元数分别大于4和3即可,没有最低能耗参数组合,但住宅单元数越多能耗越低.表 5中左、右两个示意图分别为低和高容积率要求下的点式高层住宅最低能耗参数组合.多层和高层住宅的最低能耗形态参数组合中的详细各项参数值在表 6中进行总结.
| 表 4 多层住宅低容积率下最低能耗参数组合模型示意 Tab. 4 Schematic diagram of parameter combination model of minimum energy consumption for multi-story housing under low floor area ratio |
| 表 5 点式高层住宅最低能耗参数组合模型示意 Tab. 5 Schematic diagram of parameter combination model of minimum energy consumption for slab type high-rise housing |
| 表 6 住宅能耗最低参数组合结果 Tab. 6 Parameter combination results of minimum housing energy consumption |
综上所述,本文所得出的住宅最低参数能耗组合结论,可作为寒地城市居住区平面规划布局的一种设计依据,设计者可参照表 6中多层和点式高层的最低能耗参数组合进行节能规划.
4 结论1) 本次研究设计了定性与定量相结合的方法从住宅类型、住宅体形系数、住宅间距以及住宅朝向4个方面对居住区形态与住宅能耗的关系进行了分析研究,研究结果发现对住宅能耗的影响最大的形态参数为层数和面宽,而住宅间距和朝向对住宅能耗的影响较小.
2) 通过对住宅类型、住宅体形系数、住宅间距以及住宅朝向这4个布局形态方面的研究探讨了如何进行节能规划并提出了住宅最低能耗形态参数组合.
3) 由于本文采用理想模型的研究方法,在研究结论以及建议方面尚有许多限制条件,在日后的研究中将会逐步进行优化完善.
| [1] |
龙惟定, 梁浩. 低碳生态城区能源规划的目标设定[J]. 城市发展研究, 2011, 18(12): 13. LONG Weiding, LIANG Hao. Goal setting of community energy planning in low-carbon eco-cities[J]. Urban Studies, 2011, 18(12): 13. DOI:10.3969/j.issn.1006-3862.2011.12.003 |
| [2] |
孙澄, 董琪. 东北地区农村住宅设计适宜性节能技术策略研究[J]. 建筑学报, 2016(S2): 72. SUN Cheng, DONG Qi. Study on the suitable energy saving technology strategy of rural house of northeast China[J]. Architectural Journal, 2016(S2): 72. |
| [3] |
龙惟定, 白玮, 马素贞, 等. 中国建筑节能现状分析[J]. 建筑科学, 2008, 24(10): 1. LONG Weiding, BAI Wei, MA Suzhen, et al. Status analysis of building energy efficiency in China[J]. Building Science, 2008, 24(10): 1. DOI:10.3969/j.issn.1002-8528.2008.10.001 |
| [4] |
孙海玲, 王红平. 基于岭回归的城市建筑能耗增长驱动因素研究[J]. 城市发展研究, 2013, 20(5): 21. SUN Hailing, WANG Hongping. The driving factors of the increace of the building energy consumption based on ridge regression[J]. Urban Development Studies, 2013, 20(5): 21. DOI:10.3969/j.issn.1006-3862.2013.05.029 |
| [5] |
何艳. 城市居住区规划中的节能与省地问题探析[J]. 建筑设计管理, 2013(3): 39. HE Yan. Analysis on energy saving and land saving in urban residential district planning[J]. Architectural Design Management, 2013(3): 39. DOI:10.3969/j.issn.1673-1093.2013.03.012 |
| [6] |
吴凌雁. 节能理念指导下的居住区规划研究[J]. 建材与装饰, 2016(2): 89. WU Lingyan. Residential area planning research under the guidance of energy saving concept[J]. Construction Materials & Decoration, 2016(2): 89. |
| [7] |
刘大龙, 刘加平, 杨柳. 气候变化下我国建筑能耗演化规律研究[J]. 太阳能学报, 2013, 34(3): 439. LIU Dalong, LIU Jiaping, YANG Liu. Building energy consumption principia under climate change in China[J]. Acta Energiae Solaris Sinica, 2013, 34(3): 439. DOI:10.3969/j.issn.0254-0096.2013.03.014 |
| [8] |
TIAN Wei. A review of sensitivity analysis methods in building energy analysis[J]. Renewable and Sustainable Energy Reviews, 2013, 20: 411. DOI:10.1016/j.rser.2012.12.014 |
| [9] |
SALTELLI A, RATTO M, TARANTOLA S, et al. Update 1 of: Sensitivity analysis for chemical models[J]. Chemical Reviews, 2012, 112(5): PR1. DOI:10.1021/cr200301u |
| [10] |
KRISTENSEN M H, STEFFEN P. Choosing the appropriate sensitivity analysis method for building energy model-based investigations[J]. Energy and Buildings, 2016, 130: 166. DOI:10.1016/j.enbuild.2016.08.038 |
| [11] |
MENBERG K, HEO Y, CHOUDHARY R. Sensitivity analysis methods for building energy models: Comparing computational costs and extractable information[J]. Energy and Buildings, 2016, 133: 433. DOI:10.1016/j.enbuild.2016.10.005 |
| [12] |
HEISELBERG P, BEOHUS H, HESSELHOLT A, et al. Application of sensitivity analysis in design of sustainable buildings[J]. Renewable Energy, 2009, 34(9): 2030. DOI:10.1016/j.renene.2009.02.016 |
| [13] |
TATHIANE A D L M, LUC A, LEOPOLDO E G B, et al. Sensitivity analysis of urban morphology factors regarding solar energy potential of buildings in a Brazilian tropical context[J]. Solar Energy, 2016, 137: 11. DOI:10.1016/j.solener.2016.07.053 |
| [14] |
VARTHOLOMAIOS A. A parametric sensitivity analysis of the influence of urban form on domestic energy consumption for heating and cooling in a Mediterranean city[J]. Sustainable Cities and Society, 2017, 28: 135. DOI:10.1016/j.scs.2016.09.006 |
| [15] |
SALTELLI A, RATTO M, TARANTOLA S, et al. Sensitivity analysis practices: Strategies for model-based inference[J]. Reliability Engineering and System Safety, 2006, 91(10/11): 1109. DOI:10.1016/j.ress.2005.11.014 |
 2020, Vol. 52
2020, Vol. 52