2. 水利工程仿真与安全国家重点实验室(天津大学), 天津 300350
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University), Tianjin 300350, China
海风具有速度大、剪切变小及主导方向稳定等优势,因此海上风能发电受到各国的高度重视[1].现有的海上风电机组根据与海床固定方式不同分为固定式与浮式两大类.固定式基础一般应用于浅海,适应水深在0~30 m.随着水深增加,固定式基础的造价会大幅提高,安全性也受到挑战,因此目前通常采用TLP、Spar或者半潜式等浮式基础型式,这3种基础采用系泊线与海底连接,适应水深一般在100 m[2].Cermelli等[3]设计了一种Mini-Float多立柱式半潜平台,这种平台具有良好的运动性能,但主要适用于深水边际油田.Withee[4]将Spar与TLP基础相结合,提出了一种新的浮式基础型式,验证了其良好的水动力性能.但由于系泊系统限制,当水深小于100 m时,此类浮式基础稳定性严重不足,运动难以控制,不能够正常发电.中国海域近海海底地貌平坦,水深难以达到100 m,因此难以采用目前的Spar等浮式基础支撑5 MW风力机.针对中国近海海底地貌平坦、水深较浅情况,本文提出了一种新的铰接式基础型式,如图 1所示.基础的结构包括:海底地基、铰接万向接头、压载舱、下部塔柱、浮力舱、上部塔柱.海底地基和塔柱之间的连接采用铰接万向接头,大大减小了海底部分的弯矩; 压载舱可以降低风力机的重心高度; 浮力舱起到稳定风力机作用.与固定基础相比,铰接式基础的万向接头可释放平台底部的巨大弯矩,从而可减小基础结构的结构尺寸,节约钢材; 底部设置压载舱和上部设置浮力舱,可提高塔柱稳定性,提高浅水适用性并减小波浪载荷的影响.因此这种铰接式基础风力机的工作原理和力学性能具有明显优势.

|
图 1 铰接式海上风力机示意 Fig. 1 Articulated offshore wind turbine sketch |
Wu等[5]提出了一种90 m水深的单腿铰接式海上风力机,计算结果表明其摇摆运动较小.Joy等[6]对三腿铰接式5 MW风力机进行了模型实验,实验结果表明其幅频运动响应较小,适合作为海上风力机基础.但这两种铰接式基础都没有设置压载舱与浮力舱,适应水深相对较深.同时,尚未有研究考虑湍流风对铰接式海上风力机的影响.对于其他型式的海上风力机,丁勤卫等[7]以NREL实测数据为湍流风场数据源,研究了漂浮式风力机在湍流风和波浪联合作用下的结构运动响应,计算风力机功率无法稳定在5 MW附近,且存在较大程度波动,说明湍流风对其动力响应有较大影响. Robertson等[8]使用OpenFAST软件分析了来流风的一系列因素对NREL 5 MW风力机气动载荷的影响,结果表明风的湍流性质对气动载荷的影响最大.但截至目前为止,湍流风对于铰接式基础风力机的运动影响还研究很少,湍流风对于铰接式基础风力机的影响机理还不清楚.
本文基于75 m水深的海域,改进了铰接式基础风力机的结构型式,设置了压载舱和浮力舱,考虑湍流风的作用,研究铰接塔式基础风力机的运动响应特性,分析不同参数对于铰接式基础风力机运动的影响.
1 计算模型 1.1 设计参数参考90 m水深铰接式风力机[5],添加浮力舱和压载舱从而降低水深,针对75 m水深初步设计了一种海上铰接式风力机,上部搭载NREL 5MW海上风力机[9].铰接式风力机的主要设计参数及铰接式基础的结构布置见表 1、2[10].其中,根据Ramalingam等[11]的方法,采用基于三维势流理论的水动力软件Seasam计算了铰接式基础的固有频率.
| 表 1 铰接式风力机主要设计参数 Tab. 1 Main design parameters of the articulated wind turbine |
| 表 2 铰接式基础结构布置 Tab. 2 Structure of the articulated foundation |
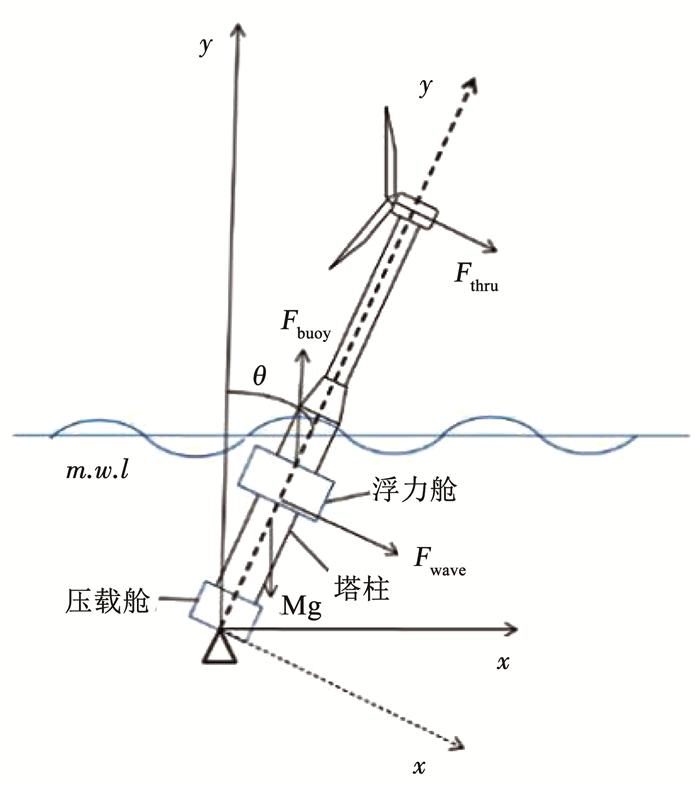
考虑本文的重点在于研究铰接式基础风力机的运动,因此建模时忽略了弹性变形的影响,假定组成铰接式基础风力机的部件为刚体.铰接式基础风力机的运动主要体现为一个方向的摇摆运动,因此可以采用摇摆角为参数的单自由度刚体模型,如图 2所示.
|
图 2 铰接式海上风力机分析模型 Fig. 2 Articulated offshore wind turbine analysis model |
风力机叶片旋转过程中,通常采用动量理论、叶素-动量理论或CFD方法计算气动载荷.叶素动量理论兼具较高的计算效率和准确性,适用于海上风力发电机的计算[12].因此,叶片正常运行下,本文采用叶素-动量理论计算气动载荷,从而得到风轮推力和转矩[13],进而发电功率P可由下式计算:
| $ P = \omega \cdot{M_{{\rm{wind}}}}. $ |
式中:Mwind为由叶素动量理论计算而得的风轮转矩; ω为NREL 5 MW风力机的额定角速度,由风速决定[9].在极限工况下,叶片处于停转状态,此时叶片所受的风压载荷按照CCS规范[14]由下式计算:
| $ {F_{{\rm{wind}}}} = 0.613\sum\limits_{i = 1}^n {({C_h}{C_{\rm{s}}}{A_i}\left( \alpha \right)V_{\rm{r}}^2)}. $ | (1) |
式中:i为受风构件的编号; n为受风构件的个数; Ch为受风构件的高度系数; Cs为受风构件的形状系数; Ai(α)为风向角为α时第i个构件在风向上的投影面积; Vr为受风构件与风的相对速度.
对于湍流风,Hannesdottir等[15]研究表明,虽然叶素动量理论忽略了弹性变形,但在复杂来流工况下结论仍然大致可行,因此本文仍使用叶素动量理论计算气动载荷,并采用NPD谱模拟湍流风.强风条件下,海平面以上高度z处,平均维持时长t≤t0=3 600 s设计风速u(z, t)按下式计算[16]:
| $ u\left( {z, t} \right) = {U_z}\left[ {1 - 0.41 \cdot {I_u}\left( z \right) \cdot \ln \left( {\frac{t}{{{t_0}}}} \right)} \right], $ | (2) |
式中,Uz为海平面以上高度z处3 600 s平均风速,按下式计算:
| $ \left\{ \begin{array}{l} {U_z} = {U_0}\left[ {1 + C \cdot \ln \left( {\frac{z}{{10}}} \right)} \right], \\ C = 5.73 \times {10^{ - 2}}{\left( {1 + 0.15 \cdot {U_0}} \right)^{0.5}}. \end{array} \right. $ | (3) |
Iu(z)为湍流强度因子,按下式计算:
| $ {I_u}\left( z \right) = 0.061 + 0.043 \cdot {U_0}{\left( {\frac{z}{{10}}} \right)^{ - 0.02}}, $ | (4) |
式中U0为海平面10 m高度处3 600 s的平均风速.
对于对风速波动较为敏感的结构物,采用下式的谱函数生成时变风速[17]:
| $ \left\{ \begin{array}{l} S\left( f \right) = \frac{{320 \cdot {{\left( {\frac{{{U_0}}}{{10}}} \right)}^2} \cdot {{\left( {\frac{z}{{10}}} \right)}^{0.45}}}}{{{{(1 + f_m^n)}^{\frac{5}{{3n}}}}}}{\rm{ }}, \\ {f_m} = 172 \cdot f \cdot {\left( {\frac{{{U_0}}}{{10}}} \right)^{ - 0.75}} \cdot {\left( {\frac{z}{{10}}} \right)^{2/3}}. \end{array} \right. $ | (5) |
式中:n=0.468,S(f)为谱密度函数; f为频率.本文基于式(1)~(4)生成湍流风速.
2.2 波流载荷对于本文研究的铰接塔式风力机,浮力舱和压载舱均为大尺度构件,可采用三维势流理论计算波浪力[18],塔柱采用莫里森(Morisson)公式计算波浪力,海流载荷按照CCS规范[14]由下式计算:
| $ {F_{{\rm{cur}}}} = \frac{1}{2}{C_{\rm{d}}}{\rho _{\rm{w}}}AV_{{\rm{cur}}}^2. $ |
式中:Cd为拖曳力系数; ρw为海水密度; A为构件在与流速垂直平面上的投影面积; Vcur为海流速度.
2.3 铰接接头摩擦阻尼在铰接塔基础摇摆运动过程中,铰接接头内部会相互摩擦,产生摩擦阻尼.该阻尼对铰接塔的运动会产生较大影响,不可忽略.
对于球形铰接点,其摩擦力矩可由下式[19]求得:
| $ {M_{{\rm{fr}}}} = \mu NR[sign\left( {\mathit{\boldsymbol{\dot \theta }}} \right)]. $ |
式中:μ为摩擦系数(0.1~0.4),本文取μ=0.1;N为法向力; R为球形铰接点半径,R=1.5 m;
考虑铰接式海上风力机绕铰接万向接头摇摆运动,摇摆自由度为θ,运动方程可以写作:
| $ \begin{array}{l} [I + {I_{\rm{a}}}\left( \omega \right)]\ddot \theta + \left( {{C_1}\left( \omega \right) + {C_2}} \right)\dot \theta + {M_{{\rm{fr}}}}\left( {\dot \theta } \right) + \\ {M_{{\rm{gb}}}}\left( \theta \right) = {F_{{\rm{wave}}}} + {F_{{\rm{wind}}}} + {F_{{\rm{cur}}}}. \end{array} $ |
式中:I为转动惯量; Ia(ω)为附加转动惯量; C1(ω)为势流阻尼; C2为粘性阻尼;
其中,Ia(ω)、C1(ω)和一阶波浪力传递函数通过水动力软件Seasam计算; 量纲一的阻尼比ζ根据工程经验取5%,继而通过公式
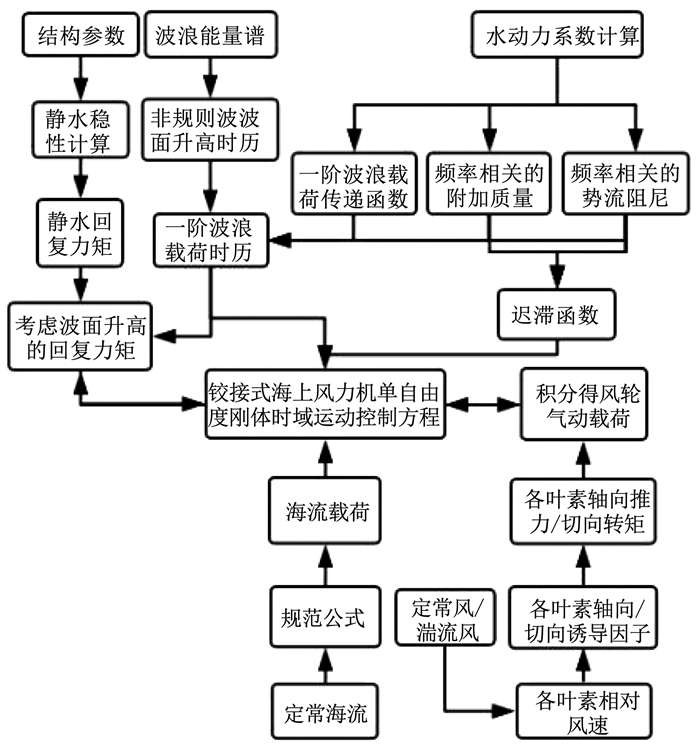
|
图 3 铰接式海上风力机时域运动响应计算流程 Fig. 3 Calculation flow for time domain dynamic response of articulated offshore wind turbine |
考虑风浪流联合且同向最危险的情况,在正常工况和极限工况时分别模拟定常风、湍流风下铰接式风力机的动力响应.通过Jonswap波浪谱生成的随机波,谱峰因子取为3.3,波浪入射角为0°.风向角为0°,风速为海平面以上90 m处风速,选取了4种海况,前2种为作业海况,后2种为极限海况,见表 3.
| 表 3 计算工况一览表 Tab. 3 List of calculation conditions |
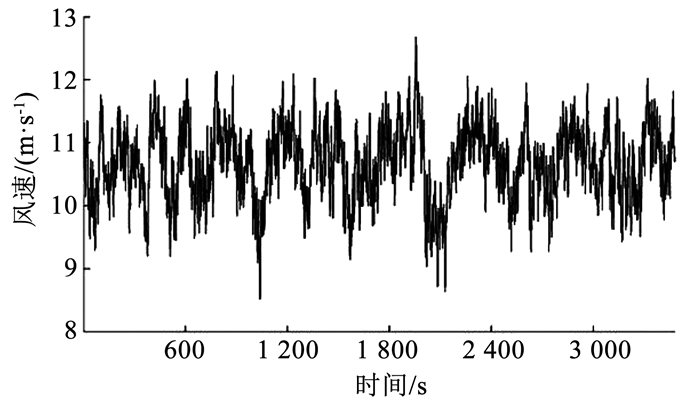
对于湍流风,以额定风速下的作业海况为例,z=90 m轮毂高度处3 600 s平均风速为11.4 m·s-1,基于风剪切模型[21]换算到海面以上10 m高度处参考风速,根据式(5)计算得到轮毂处风速幅值,结合式(2)得到轮毂处时变风速,以3 600 s的模拟结果为例,湍流风风速时间历程如图 4所示.
|
图 4 额定风速作业海况下轮毂处湍流风风速时历曲线 Fig. 4 Time history of rated turbulent wind speed on wind turbine hub under working condition |
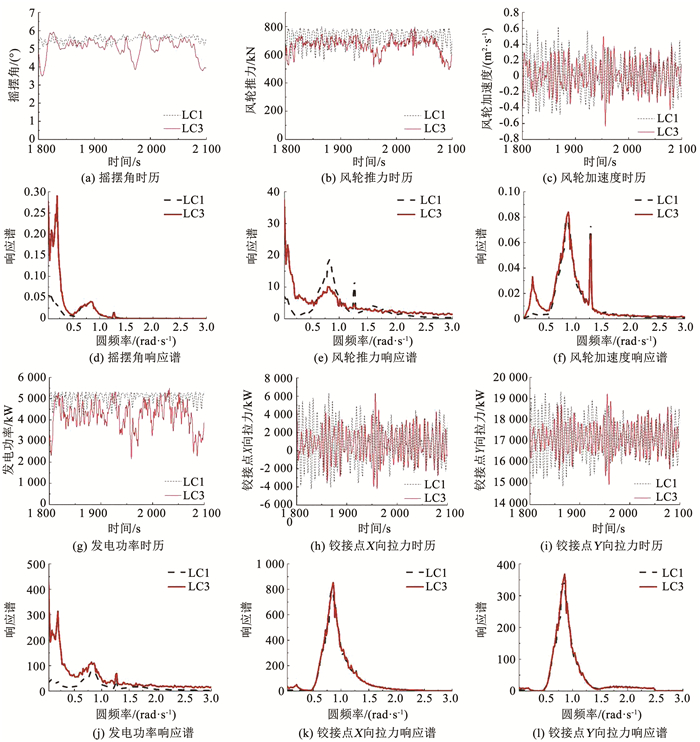
针对表 3中LC1和LC3两种海况,分析作业海况下湍流风对风力机时域运动响应的影响规律,此时风速为额定风速.在时域内对铰接式海上风力机在风浪流联合作用下的动力响应进行了数值模拟,模拟时间为3 600 s,模拟结果取600 s之后的稳定状态.统计结果见表 4,时域曲线以1 800~2 100 s之间的数据为例作图,通过傅里叶变换将时历结果转换到频域进行对比分析,如图 5所示.
| 表 4 定常风与湍流风下铰接式风力机动力响应结果对比(工作海况) Tab. 4 Comparison of dynamic responses of articulated wind turbine under different types of wind (working condition) |
|
图 5 工作海况铰接式风力机动力响应 Fig. 5 Dynamic response of articulated wind turbineunder working condition |
从LC1和LC3两种海况的统计结果表和时域曲线图中可以看到,相比于LC1定常风作用下的响应,湍流风对摆角、风轮推力、发电功率和铰接点X向拉力的响应影响最大,使得这三者的响应平均值有所减小,但摆角和发电功率响应幅值的变化显著增大.而湍流风对风轮加速度和铰接点Y向拉力影响相对较小.这是由于风载荷只作用在水面以上的结构,相比于风轮的气动推力,塔架所受风压载荷为小量,因此风的湍流特性主要影响风轮的气动推力,而气动推力主要影响系统摆角和铰接点X向拉力响应的平衡位置.同时,风轮轴向推力和切向转矩为气动载荷的不同方向分量,变化趋势一致,因此发电功率会受到湍流风的较大影响.对风轮加速度和铰接点Y向拉力响应而言,它们的平衡位置不受风轮气动推力影响,响应幅值主要由波浪载荷决定,因此受湍流风影响很小.
从LC1和LC3两种海况的响应谱对比图中可以看到,相比于LC1定常风作用下的响应,湍流风诱发了系统摆角、风轮推力和发电功率更大的、频率小于0.2 rad·s-1的低频响应,同时显著增大了摆角、风轮推力、风轮加速度和发电功率0.21 rad·s-1固有频率处的响应,使铰接点的X向和Y向拉力产生了固有频率处较小的响应.另外,风轮推力0.85 rad·s-1附近的波频响应和1.27 rad·s-1处的1P荷载频率响应明显减小,可见湍流风的作用削弱了波浪载荷和风轮转动对风轮推力的影响.由此可判断,由于湍流风的作用,再加上气动载荷与波浪载荷同时作用于结构时产生了耦合低频载荷,系统发生了更大的低频响应.并且它们在系统运动固有频率处引起了共振,导致各动力响应要素均出现了固有频率处的响应.因此,在进行铰接式海上风力机基础设计时,应通过调整系统运动固有频率或设置阻尼等方法避免湍流风作用时产生过大的共振.
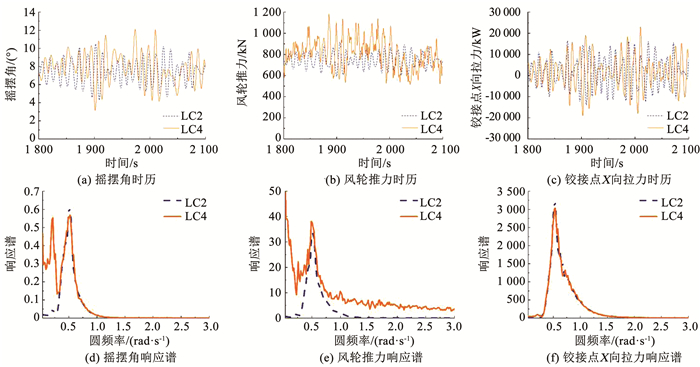
4.2 极限海况响应分析从上述分析可知,湍流风对系统摆角的响应幅值产生影响,导致其最大值增大,需要重新评估铰接式风力机系统在极限海况湍流风作用下的运动可靠性和结构安全性.因此,选取了LC2和LC4两种海况,在时域内对铰接式海上风力机在风浪流联合作用下的运动响应进行了数值模拟,统计结果见表 5,时域曲线以1 800~2 100 s之间的数据为例如图 6所示.由于湍流风对风轮加速度和铰接点Y向拉力响应影响不大,不再给出.
| 表 5 定常风与湍流风下铰接式风力机动力响应结果对比(极限海况) Tab. 5 Comparison of dynamic responses of articulated wind turbine under different types of wind (extreme sea condition) |
|
图 6 极限海况铰接式风力机动力响应 Fig. 6 Dynamic response of articulated wind turbine under extreme sea condition |
从LC2和LC4两种海况的统计结果表和时域曲线图中可以看到,相比于LC2定常风作用下的响应,湍流风作用下,系统运动的最大摆角显著增大,达到12.11°,但还是远远小于铰接塔平台所允许的最大摆角20°,满足系统在极限海况下的生存要求.但此时风轮推力、风轮加速度最大值显著增加,应注意校核此时上部风机结构包括叶片、机舱与塔架连接处的强度问题.其中风轮加速度的增加主要是由于海况的变化,受湍流风影响不大.对铰接点而言,极限海况下X向拉力最大值增加较大,设计时需要特别关注.另外,与表 4相比可以看出,无论是工作海况还是极限海况,定常风或是湍流风,铰接点Y向拉力均变化不大,说明Y向拉力受海况影响很小.
5 结论1) 工作海况下,湍流风使摆角和发电功率的响应幅值的变化显著增大,但对风轮加速度和铰接点Y向拉力影响较小,因此工作海况下需要重点关注摆角和发电功率的变化.
2) 湍流风本身具有低频特性,与波浪载荷同时作用于结构时会产生耦合低频载荷,系统会发生更大的低频响应,并且在运动固有频率处产生共振.
3) 极限海况下,湍流风显著增大了系统的风轮推力、风轮加速度及铰接点X向拉力的最大值,说明湍流风的影响不可忽略.
| [1] |
李晓宇, 王伟. 基于SWOT分析我国海上风力发电的发展现状[J]. 华北电力大学学报(社会科学版), 2018, 115(5): 42. LI Xiaoyu, WANG Wei. The status quo of China's offshore wind power generation development based on SWOT analysis method[J]. Journal of North China Electric Power University (Social Sciences), 2018, 115(5): 42. DOI:10.14092/j.cnki.cn11-3956/c.2018.05.006 |
| [2] |
高伟, 李春, 叶舟. 深海漂浮式风力机研究及最新进展[J]. 中国工程科学, 2014, 16(2): 79. GAO Wei, LI Chun, YE Zhou. The current situation and latest research of deep-sea floating wind turbine[J]. Engineering Science, 2014, 16(2): 79. |
| [3] |
CERMELLI C, RODDIER D, BUSSO C C. MINIFLOAT: A novel concept of minimal floating platform for marginal field development[C]//Proceedings of the 14th International Offshore and Polar Engineering Conference. Toulon, France: ISOPE, 2004: 538
|
| [4] |
WITHEE J E. Fully coupled dynamic analysis of a floating wind turbinesystem[D]. Cambridge: Massachusetts Institute of Technology, 2004
|
| [5] |
WU Haitao, ZHANG Liang, ZHAO Jing. Primary design and dynamic analysis of an articulated floating offshore wind turbine[J]. Advanced Materials Research, 2011, 347-353: 2191. DOI:10.4028/www.scientific.net/AMR.347-353.2191 |
| [6] |
JOY C M, JOSEPH A, MANGAL L. Experimental investigation on the dynamic response of a three legged articulated type off-shore wind tower[C]//Proceedings of the ASME 35th International Conference on Ocean, Offshore and Arctic Engineering. Busan: ASME, 2016. DOI: 10.1115/OMAE2016-54635
|
| [7] |
丁勤卫, 李春, 王东华, 等. 漂浮式风力机的结构动力学响应[J]. 水资源与水工程学报, 2015, 26(4): 169. DING Qinwei, LI Chun, WANG Donghua, et al. Response of structural dynamics of floating wind turbine[J]. Journal of Water Resources and Water Engineering, 2015, 26(4): 169. DOI:10.11705/j.issn.1672-643X.2015.04.32 |
| [8] |
ROBERTSON A, SHALER K, SETHURAMAN L, et al. Sensitivity analysis of the effect of wind characteristics and turbine properties on wind turbineloads[J]. Wind Energy Science, 2019, 4(3): 479. DOI:10.5194/wes-4-479-2019 |
| [9] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development: NREL/TP-500-38060[R]. Golden, CO: National Renewable Energy Laboratory, 2009
|
| [10] |
朱希洋.铰接式海上风力机方案设计及耦合动力响应分析[D].天津: 天津大学, 2018 ZHU Xiyang. Study on concept design and coupling dynamic responses of the articulated offshore wind turbine[D]. Tianjin: Tianjin University, 2018 |
| [11] |
RAMALINGAM V, RAMALINGAM S, SRINIVASAN R, et al. Parametric study on the hydrodynamic response of DSI polygonal shaped FPSO[J]. Brodogradnja, 2017, 68(2): 93. DOI:10.21278/brod68207 |
| [12] |
叶舟, 成欣, 周国龙, 等. 漂浮式风力机平台动态响应的优化方法探讨[J]. 振动与冲击, 2016, 35(3): 20. YE Zhou, CHENG Xin, ZHOU Guolong, et al. Optimization method for dynamic responses of floating offshore windturbines[J]. Journal of Vibration and Shock, 2016, 35(3): 20. DOI:10.13465/j.cnki.jvs.2016.03.004 |
| [13] |
HU Zhiqiang, LI Liang, WANG Jin, et al. Dynamic responses of a semi-type offshore floating wind turbine during normal state and emergency shutdown[J]. China Ocean Engineering, 2016, 30: 97. DOI:10.1007/s13344-016-0005-y |
| [14] |
中国船级社. 海上移动平台入级与建造规范[M]. 2016版. 北京: 人民交通出版社, 2016. China Classification Society. Rules for construction and classification of mobile offshore drilling units[M]. 2016 Edition. Beijing: China Communications Press, 2016. |
| [15] |
HANNESDOTTIR A, KELLY M, DIMITROV N. Extreme wind fluctuations: Joint statistics, extreme turbulence, and impact on wind turbine loads[J]. Wind Energy Science, 2019, 4(2): 325. DOI:10.5194/wes-4-325-2019 |
| [16] |
左其华, 杜齐鲁, 赵一晗, 等. 随机风谱研究及其在海岸工程应用述评[J]. 海洋工程, 2016, 34(2): 111. ZUO Qihua, DU Qilu, ZHAO Yihan, et al. Review of studies on random wind spectrum and its application in coastal engineering[J]. The Ocean Engineering, 2016, 34(2): 111. DOI:10.16483/j.issn.1005-9865.2016.02.015 |
| [17] |
蒋汝斌.半潜式钻井服务支持平台风载荷数值模拟计算[D].镇江: 江苏科技大学, 2016 JIANG Rubin. Numerical computational of wind load on semi-submersible tender support platform[D]. Zhenjiang: Jiangsu University of Science and Technology, 2016 |
| [18] |
SHOELE K, PROWELL I, ZHU Qiang, et al. Dynamic and structural modeling of a floating wind turbine[J]. International Journal of Offshore and Polar Engineering, 2011, 21(2): 155. |
| [19] |
周满红.铰接塔平台非线性动力响应分析[D].天津: 天津大学, 2005 ZHOU Manhong. Analysis of nonlinear dynamics response of an articulated tower platform[D]. Tianjin: Tianjin University, 2005 |
| [20] |
LI Yan, ZHU Qiang, LIU Liqin, et al. Transient response of a SPAR-type floating offshore wind turbine with fractured mooring lines[J]. Renewable Energy, 2018, 122: 576. DOI:10.1016/j.renene.2018.01.067 |
| [21] |
卢东海.基于ANSYS的导管架式海上风力发电机组支撑结构分析[D].北京: 华北电力大学, 2016 LU Donghai. Analysis of jacket support structure for offshore wind turbine based on ANSYS[D]. Beijing: North China Electric Power University, 2016 |
 2020, Vol. 52
2020, Vol. 52


