为降低空调水系统的输送能耗,变频控制技术得到越来越广泛的应用.用变频水泵替换调节阀,不仅可以让系统更平稳运行,还能实现空调系统在部分负荷率下的节能运行[1].变流量的控制策略按照控制参考量可分为:压差控制方法和温差控制方法.压差控制响应速度较快,故大部分变频控制下采用压差控制策略[2].为优化计算压差设定值,许多学者对冷冻水系统及设备的特性进行了研究,主要包括风机盘管[3]、冷机[4]、循环泵[5-6]、管网[7]、房间动态负荷[8]等,并提出了诸多基于变压差设定值的控制策略,主要包括末端压差控制[9]、最小阻力法[10]等.
空调系统是以向末端用户提供能量为目的的系统,空调系统循环水只是运输能量的载体.在实际空调系统中,各末端用户负荷大小是不断变化的,只针对某一个用户的压差或者水量进行调节不够合理,因此,赵天怡[11]提出了空调水系统最不利热力环路的概念,阐述了其存在的客观性,并对空调水系统进行仿真和试验研究.上述研究主要针对具有阀位反馈的连续调节型的空调水系统,而风机盘管系统末端仅包含通断阀,因此,风机盘管系统中最不利热力环路的模型及数学描述方法仍需要确定,其辨识方法也应该进一步研究.
1 最不利热力环路及其辨识方法研究定义各末端支路热能供需不平衡度为某时刻第i支路的热能供给量与其服务的空调区域热能需求量之差的相对值,即
| $ {\mathit{\Phi }_i}\left( \tau \right) = \frac{{{{\dot Q}_{{\rm{rmd}}\_i}}\left( \tau \right) - {{\dot Q}_{{\rm{fcu}}\_i}}\left( \tau \right)}}{{{{\dot Q}_{{\rm{fcu}}\_i}}\left( \tau \right)}}, i = 1, 2, \ldots , n. $ |
式中:Φi(τ)为第i个支路在某时刻的热能供需不平衡度;
具有n个末端支路的空调水系统(或其他暖通空调系统形式)在某时刻实际运行时,由于各末端空调房间受室内外负荷影响程度不同,各支路的热能供需平衡度也不同,其中必然存在一个或多个支路的热能供需平衡度处于最严重的状态,满足该状态的支路为该时刻系统中的最不利热力环路,即最不利热力环路的Φi(τ)为正最大值或负最大值,可表示为
| $ \begin{array}{l} {\mathit{\Phi }_{\max \_j}}\left( \tau \right) = \left\{ {{\mathit{\Phi }_j}\left( \tau \right)\left| {{\mathit{\Phi }_i}\left( \tau \right) > } \right|{\mathit{\Phi }_i}\left( \tau \right)| - \varphi , } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1, 2, \ldots , n} \right\}. \end{array} $ |
式中:Φmax_j(τ)为最不利热力环路的热能供需不平衡度的集合; Φj(τ)为系统中存在的各最不利热力环路的热能供需不平衡度; φ为不平衡度的设定阈值,其大小可根据实际运行情况调整,在模糊控制中为模糊等级.
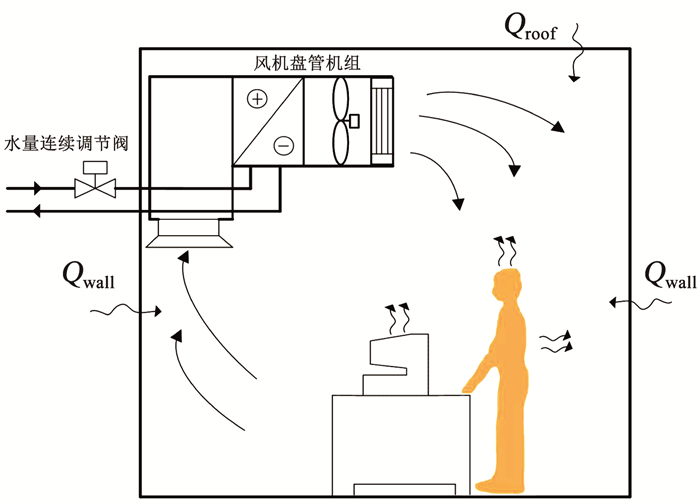
1.1 最不利热力环路的数学描述室内空气传热模型主要使用热平衡方法.目前计算室内空气获得热量时,多采用集总热容法,即将空气温度集总为单一节点进行处理,如图 1所示.
|
图 1 空调系统房间模型 Fig. 1 Room model of air conditioning system |
热力学室内空气节点的热平衡方程如下[12]:
| $ \begin{array}{l} {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{V_{\rm{a}}}\frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }} = \sum\limits_{i = 1}^n {{h_i}{f_i}({t_i} - {t_{\rm{a}}})} + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}({t_{{\rm{out}}}} - {t_{\rm{a}}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}}({t_{{\rm{adj\_m}}}} - {t_{\rm{a}}}) + {q_{{\rm{cov}}}} - {q_{{\rm{hvac}}}}} . \end{array} $ |
式中:cpa为空气比热容,J/(kg·℃); ρa为空气密度,kg/m3; Va为房间体积,m3; ta为室内空气温度,℃; hi为第i面墙体对流换热系数; fi为房间中第i面墙体换热面积,m2; Gout为房间与室外的换气量,W; tout为室外温度,℃; Gadj_m为房间与相邻房间的换气量,W; tadj_m为临室空气温度,℃; qcov为内热源产生的对流换热量,W; qhvac为空调供冷量,W.
冷负荷是指为了维持设定的室温即室温设定值,空调设备在单位时间内必须向室内空气供给的冷量.下式中引入室温设定值tas后拆分移项可得:
| $ \begin{array}{l} {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{V_{\rm{a}}}\frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }} = \left[ {\sum\limits_{i = 1}^n {{h_i}{f_i}({t_i} - {t_{{\rm{as}}}}) + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}({t_{{\rm{out}}}} - {t_{{\rm{as}}}})} + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}}({t_{{\rm{adj\_m}}}} - {t_{{\rm{as}}}})} } \right] + {q_{{\rm{cov}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{h_i}{f_i}({t_{{\rm{as}}}} - {t_{\rm{a}}}) + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}({t_{{\rm{as}}}} - {t_{\rm{a}}}) + } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}}({t_{{\rm{as}}}} - {t_{\rm{a}}}) - {q_{{\rm{hvac}}}}} , \end{array} $ | (1) |
其中,冷负荷ql为
| $ \begin{array}{l} {q_{\rm{l}}} = \sum\limits_{i = 1}^n {{h_i}{f_i}({t_i} - {t_{{\rm{as}}}}) + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}({t_{{\rm{out}}}} - {t_{{\rm{as}}}}) + } \\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}}({t_{{\rm{adj\_m}}}} - {t_{{\rm{as}}}}) + {q_{{\rm{cov}}}}} , \end{array} $ | (2) |
则式(1)可移项整理为
| $ \begin{array}{l} (\sum\limits_{i = 1}^n {{h_i}{f_i} + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}} + \sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}}} )({t_{{\rm{as}}}} - {t_{\rm{a}}}) + \\ {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{V_{\rm{a}}}\frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }} = {q_{\rm{l}}} - {q_{{\rm{hvac}}}}. \end{array} $ |
由下式则当前能量供应量与负荷的差值Δq为
| $ \begin{array}{l} \Delta q = {q_{\rm{l}}} - {q_{{\rm{hvac}}}} = (\sum\limits_{i = 1}^n {{h_i}{f_i} + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{out}}}}} + \\ \;\;\;\;\;\;\;\;\sum\limits_{k = 1}^m {{c_{{\rm{pa}}}}{\rho _{\rm{a}}}{G_{{\rm{adj\_m}}}})({t_{{\rm{as}}}} - {t_{\rm{a}}}) + {c_{{\rm{pa}}}}{\rho _{\rm{a}}}{V_{{\rm{aj}}}}\frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }}} . \end{array} $ |
若房间供冷量与负荷匹配,即能量差Δq=0,则满足:
| $ \left\{ \begin{array}{l} {t_{\rm{a}}} = {t_{{\rm{as}}}}, \\ \frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }} = 0. \end{array} \right. $ |
e为当前室温与室温设定值之间偏差,ec为偏差变化,即:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} e = {t_{\rm{a}}} - {t_{{\rm{as}}}}, \\ ec = \frac{{{\rm{d}}e}}{{{\rm{d}}\tau }} = \frac{{{\rm{d}}{t_{\rm{a}}}}}{{{\rm{d}}\tau }} \end{array}. $ |
e和ec可反映房间能量供需平衡与否,但由于负荷的来源较为复杂,与维护结构物性参数、位置等诸多不可测参数有关,因此,在不同支路中e和ec系数不同,且不易计量其比值大小,仅根据e和ec,只能定性比较该房间供冷量与负荷的大小,无法准确找到能量差最大的支路,即不宜确定最不利热力环路.
针对二阶及以下非线性微分方程的求解可采用相平面法.作为一种图解法,相平面是把x和x′(x′表示对x的一阶导数)作为直角坐标组成的平面,系统的某一状态对应于相平面上的一点,相平面上的点随时间变化描绘出来的曲线叫做相轨迹[13].本文中e、ec组成相平面,上面的每个相点(e, ec)对应室温的状态.各相点随时间变化描绘出相轨迹,表征温度状态的演变过程.当e=0且ec=0时,Δq=0,该区域空调供冷量与房间冷负荷相等.因此O(0, 0)可作为参考点,相平面中各点的坐标及与O点的相对位置可反映各支路能量差或热力不平衡程度大小,离O点越近热力不平衡程度越小; 离O点越远,热力不平衡程度越大; 最大者为最不利热力环路.
1.2 最不利热力环路辨识方法研究在模糊模式识别算法中,一个识别算法作用于对象时,就产生一组隶属函数,它们分别表示对象隶属于类别的程度,建立了隶属函数组之后,可以按照某种隶属原则对对象进行判断,指出它应归于哪个类别[14].
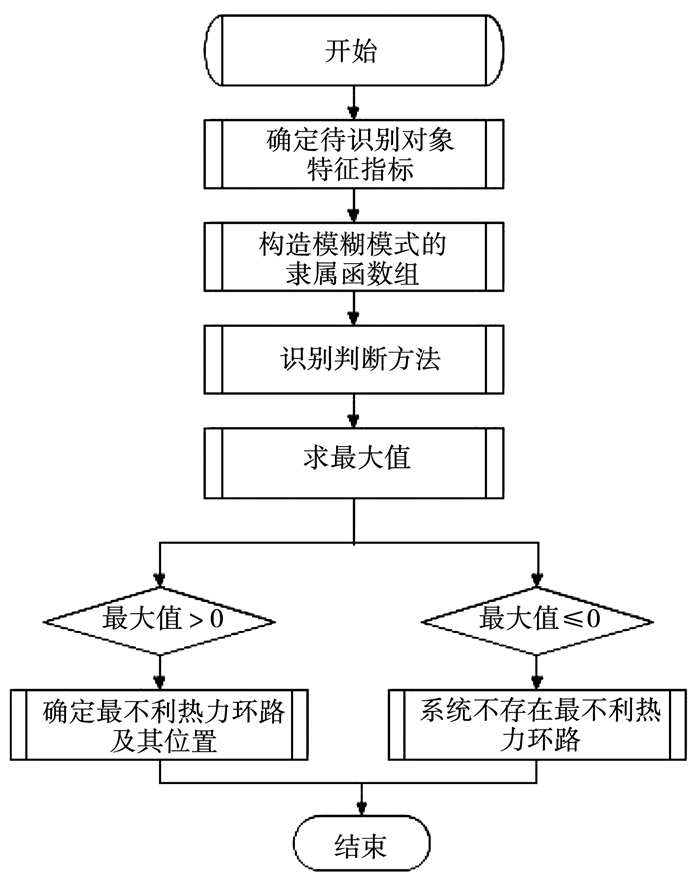
本文建立了最不利热力环路的相平面模糊模式辨识方法.如图 2所示,首先,选取合理的参数作为待识别对象的特征指标,风机盘管末端的特征指标主要包括阀门状态、风机档位、室温、室温设定值等; 其次,构造或者选取该特征指标的隶属函数组; 最后,基于所建立的隶属函数对待识别对象进行分类识别.系统中可能不存在最不利热力环路,也可能存在多条.
|
图 2 辨识方法流程 Fig. 2 Flow chart of the identification method |
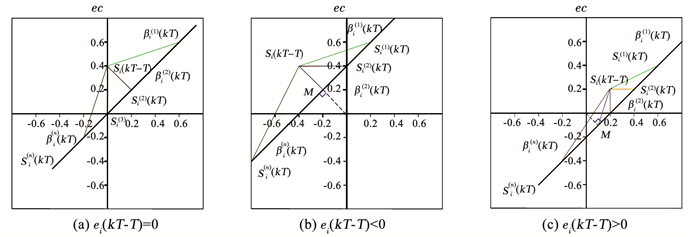
O(0, 0)为参考点,Si(ei, eci)为当前时刻室温状态,Si-1(ei-1, eci-1)为前一时刻室温状态,
|
图 3 Si-1点在不同象限的轨迹图 Fig. 3 Trajectory of point Si-1 in different quadrants |
若Si与点M重合,则热力最不利程度最小,点Si与M距离越远,热力最不利程度越大.由于ei的范围为(-∞,+∞),已知点Si时无法量化描述其与点M的位置远近关系,因此,引入实时示踪方向向量夹角的概念.
直线l的方向向量:
| $ \begin{gathered} {\beta _i} = \arccos \left( {\frac{{\overrightarrow {{\mathit{\boldsymbol{S}}_{i - 1}}{\mathit{\boldsymbol{S}}_i}} \cdot \mathit{\boldsymbol{\vec d}}}}{{|\overrightarrow {{\mathit{\boldsymbol{S}}_{i - 1}}{\mathit{\boldsymbol{S}}_i}} | \cdot |\mathit{\boldsymbol{\vec d}}|}}} \right), \hfill \\ {\gamma _i} = \arccos \left( {\frac{{\overrightarrow {{\mathit{\boldsymbol{S}}_{i - 1}}\mathit{\boldsymbol{M}}} \cdot \mathit{\boldsymbol{\vec d}}}}{{|\overrightarrow {{\mathit{\boldsymbol{S}}_{i - 1}}\mathit{\boldsymbol{M}}} | \cdot |\mathit{\boldsymbol{\vec d}}|}}} \right). \hfill \\ \end{gathered} $ |
实时示踪方向向量夹角βi可反映室温变化的方向及大小,当前时刻的温差ei判断目前室温状态.因此,取βi及ei为最不利热力环路辨识的特征指标.当βi=γi时,热力最不利程度最小.
1.2.2 隶属函数的确定由βi的定义可知,当
工况1
工况2
|
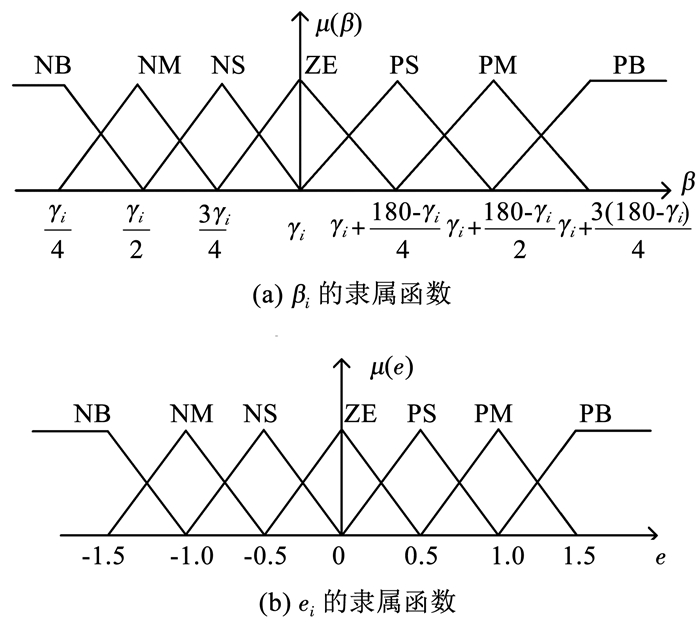
图 4 特征指标的隶属函数 Fig. 4 Subordinate function of characteristic indexes |
ei的辨识范围为(-1.5, +1.5),分为7个等级,因此,-3~3各级对应的论域为{(-∞, -1.0), (-1.5, -0.5), (-1.0, 0), (-0.5, 0.5), (0, 1.0), (0.5, 1.5), (1.0, +∞)},如图 4(b)所示.
隶属函数的特性对模糊识别的控制效果影响不大,对识别效果影响较大的是相邻模糊子集交集的最大隶属度的大小,即其内积的大小.选用三角形隶属函数足以使得模型健壮且分辨率足够高[15].
1.2.3 识别判断对于对象u,若存在k0∈{1, 2, …, n}, 使得
为综合考虑βi及ei对模糊识别结果的影响,通过βi及ei得到的辨识结果叠加得辨识过程的最终结果,制冷工况下风机盘管系统中各环路最不利热力程度模糊识别规则见表 1.
| 表 1 制冷工况模糊识别规则表 Tab. 1 Fuzzy identification rules for refrigeration conditions |
本文试验的目的是实现最不利热力环路的辨识试验及验证,过程如下:在一个较小的初始流量的前提下,确保各分支冷冻水流量相等.若支路供冷能力足够,则保证该区域室温稳定在设定值附近.在该工况下,完成最不利热力环路的辨识方法的试验研究,得到最不利热力环路的位置及程度.随后逐步增大各分支流量设定值,同时相应增大干管流量,通过各支路温差的变化及达到设定值的先后次序,便得到了最不利热力环路的位置,同时其他各环路热力最不利程度也能逐步显现出来.
为实现上述辨识及结果验证过程,需确保实现以下控制回路:
1) 末端室温控制回路.通过控制开关阀状态及风机档位,将室温控制在室温设定值范围区内;
2) 支路流量控制.通过调节支路上连续调节阀开度,使得该支路流量达到设定值并维持稳定;
3) 总流量控制回路.通过调控水泵转速,使系统总流量达到设定值并维持稳定.
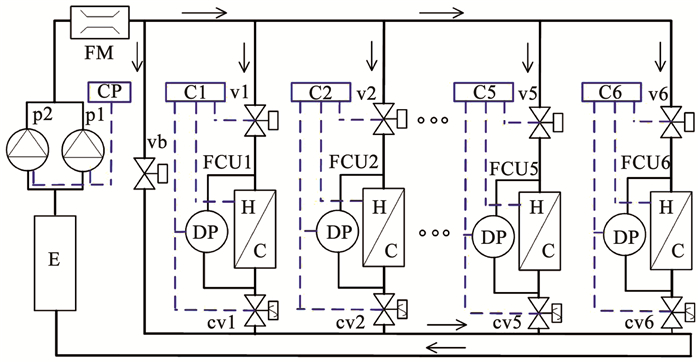
2.1 变流量空调水系统及测控系统的设计如图 5所示,建立了变水量空调及监控系统试验台.该系统中冷源为水-水热泵机组,水泵组可变频控制,各风机盘管支路安装压差传感器、电动连续调节阀、电动开关阀及温控器等测控装置.
|
图 5 变流量空调水系统及控制原理图 Fig. 5 Schematic diagram of variable flow air conditioning water system |
图中,E为冷机蒸发器; p1、p2分别为冷冻水系统循环泵; CP为机房控制器; FM为流量计; vb为旁通阀; v1~v6为支路1~6中电磁通断阀; FCU1~FCU6为支路1~6中的风机盘管; DP为压差传感器; cv1~cv6为支路1~6中电动连续调节阀; C1~ C6为末端支路1~6控制器.如图 6所示,实验室分4个区域,分别为设备间、办公室、走廊及监控室.1#FCU位于设备间,冷机、水泵等变流量空调系统用设备均放置在该区域内; 办公室分两个区域,内区面积约9 m2,由2#风机盘管承担该区域负荷,外侧(靠门侧)为办公区,面积约20 m2,由3#及4#风机盘管共同承担该区域负荷; 大厅配有VRV空调,5#风机盘管只承担走廊负荷; 6#FCU所在监控室内外围护结构墙面上无明窗,与大厅之间的间墙上有窗,面积约30 m2,人员流动就大.系统中FCU的编号按照设备与冷冻水泵的距离进行排序.表 2中列出了变流量空调水系统及控制系统中所用设备的详细信息.

|
图 6 变流量空调水系统及设备平面图 Fig. 6 Plane graph of variable flow air conditioning water system |
| 表 2 变水量空调系统试验台用主要设备信息 Tab. 2 Equipment information for variable water volume air conditioning system test bed |
基于搭建的变流量空调水系统及测控系统,根据上述控制回路的要求,在试验前需完成以下控制过程:
1) 风机盘管阻力特性研究.为减小各分支阻力,各分支中未安装流量计,而是在各风机盘管进出口设置压差传感器,因此,需确定各风机盘管阻力特性,通过压差测量值确定该分支水流量.
2) 支路流量控制回路.应用PID算法,基于分支流量/压差设定值调节阀门开度,使得分支冷冻流量值等于设定值.
3) 室温控制回路.应用传统的温差控制方法,基于房间温度测量值及设定值,调节风机档位及水阀启停状态,使得房间室温等于设定值.本实验中各区域面积较小,室温可控制在设定值±0.2 ℃范围内.
4) 系统总流量控制回路.应用PID算法,基于主干管流量测量值及设定值,调节水泵转速,使得系统总流量等于设定值.
2.2.1 风机盘管阻力特性研究风机盘管作为局部阻力部件,进出口压差与流量之间的阻力特性关系式为形如y=a * xb的幂指数[10],a、b需要通过实验数据拟合得到.以1#风机盘管为例详述其研究过程.首先,1#支路开关阀打开,其余分支阀门及旁通阀均关闭,则流量计可测得1#支路中流经风机盘管的流量,通过测量风机盘管进出口压差与流量,并应用最小二乘法进行拟合,得到参数a、b的数值.1#~6#分支风机盘管均进行上述试验研究,得到拟合参数并汇总见表 3,各支路拟合度R2均满足试验要求.
| 表 3 1#~6#风机盘管阻力系数汇总表 Tab. 3 Resistance coefficients of fan-coil units No.1-No.6 |
为实现各支路变流量调控,基于风机盘管进出口压差的测量值及设定值,应用PID算法,改变各连续调节阀开度.以1#支路为例详述控制过程,压差设定值设为15.6 kPa,PID参数采用自整定方法确定,结果如图 7所示,风盘进出口压差最大值15.57 kPa,最小值15.46 kPa,误差不超过5%.满足试验需求.

|
图 7 1#支路连续调节阀控制过程 Fig. 7 Control process of continuous regulating valve in branch No.1 |
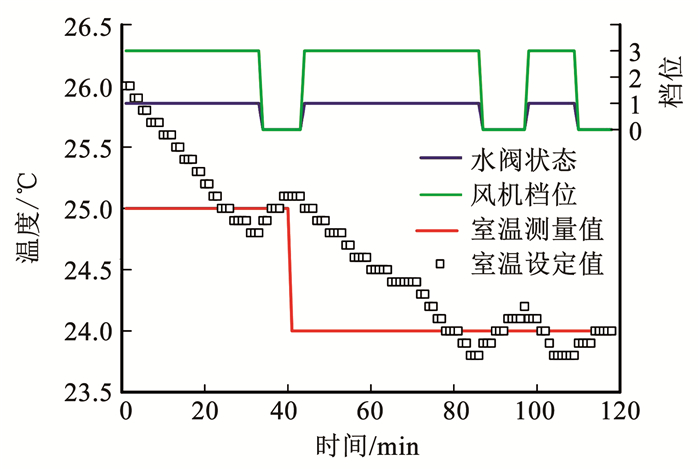
依据室温设定值及测量值的差值,考虑人体可接受温度变化的范围区,通过改变风机档位及水阀的开关状态,实现室温的稳定控制.以1#房间为例详述室温调节过程及效果,如图 8所示,当房间温度高于设定值时,水阀开,风机高档运行,当室温低于设定值时,水阀关,风机停.控制结果表明,该方法可实现室温稳定的效果,由于房间较小,该试验台中房间温度可控制在±0.2 ℃范围内.其他房间控制过程相同.
|
图 8 1#房间室温调节过程及调节效果 Fig. 8 Room temperature regulation process in room No.1 and its effect |
基于干管流量的测量值及设定值,应用PID调控算法,通过改变水泵的转速,从而实现变流量空调系统中干管流量的控制.为减小各支路阀门调节对总流量的影响,在试验过程中旁通阀全开.对上述控制过程进行试验,PID参数采用自整定方法确定,结果如图 9所示,流量设定值分别为:2.0, 2.5, 3.0 m3/h,流量最大偏差值0.12 m3/h,误差不超过5%,满足试验需求.
|
图 9 系统干管流量调控结果 Fig. 9 Flow rate of system total flow in control process |
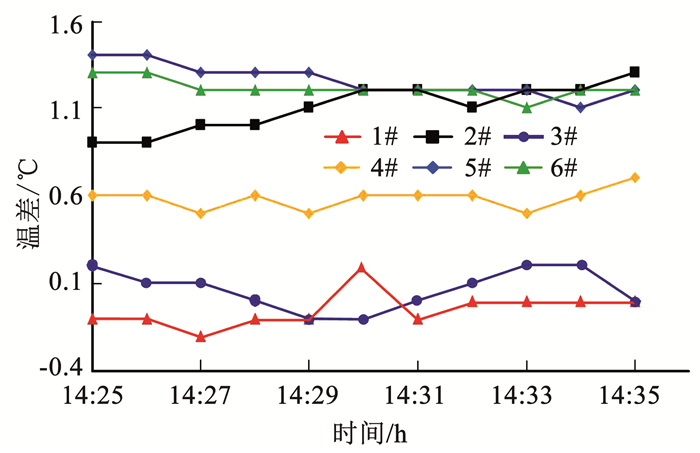
8月1号14:25—14:35时间段内对最不利热力环路的辨识过程进行了试验,随后对辨识结果进行验证.首先,通过干管流量控制回路,系统冷冻水流量稳定在2.4 m3/h左右,此时,通过支路流量控制回路,确保各分支冷冻水流量相等,各支路末端应用室温控制算法.如图 10所示,在试验期间,除1#、3#支路房间温度达到设定值以外,其他支路房间温度都不能满足.其中,2#支路温差从0.9 ℃上升至1.3 ℃,且有继续上升趋势,4#房间温差0.6 ℃左右,且保持稳定,5#、6#房间状态相似,温差大于1.0 ℃,有轻微下降趋势.1#~6#支路房间室温测量值与设定值温差趋势如图 10所示.
|
图 10 各支路室温测量值与设定值温差趋势图 Fig. 10 Trend of temperature difference between measured and set values of each branch |
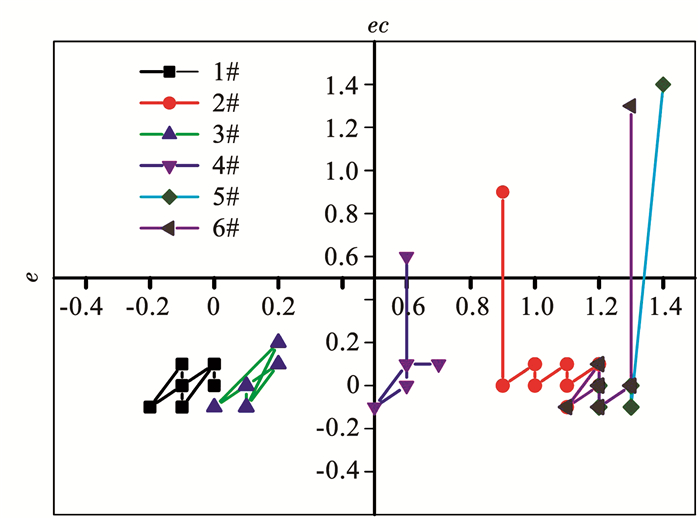
上述结果中各支路房间室温及室温设定值的差值及其变化值构成的相平面图如图 11所示.1#~6#分支的房间状态中,在x轴方向上2#分支离目标点(0, 0)最远,且趋势依旧呈现远离趋势.
|
图 11 1#~6#支路房间室温与设定值的偏差及偏差变化相平面图 Fig. 11 Phase plane of deviation and variation between room temperature and set value of branches No.1-No.6 |
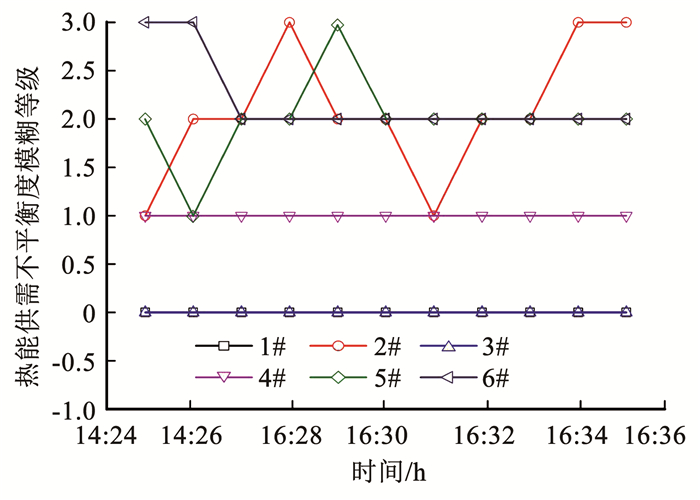
基于上述相平面图及辨识方法,得到各支路最不利热程度的辨识结果.如图 12所示,支路1#、3#辨识结果均为0,4#辨识结果为1,虽出现能量供需不平衡现象,但程度轻微,5#、6#及2#支路最不利程度较为严重.
|
图 12 最不利热力环路辨识结果 Fig. 12 Identification results of the most unfavorable thermal loop |
为综合考虑整个辨识周期内各支路能量供需不平衡程度,对辨识周期内得到的辨识结果求平均值,该运行阶段内各分支的最不利程度分别为{0,2.6,0,1.0,2.0,2.1},最不利程度值越大,表明该分支供冷量与需求量之差越大,不平衡率也越大.因此该运行阶段内系统中2#支路所在环路为最不利热力环路,最不利程度最高的依次为2#、6#、5#支路,应作为压差设定值优化计算的参考支路.
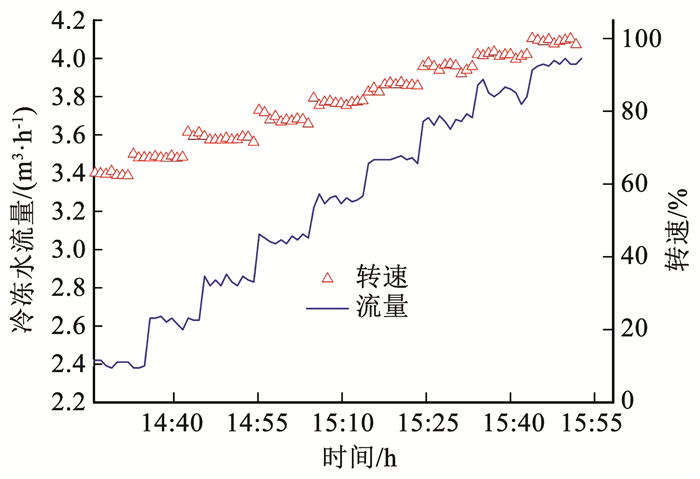
3.2 结果验证最不利程度越严重的环路室温达到设定值所需的冷冻水流量越大,因此,为验证上述得到的辨识结果,逐步增加各分支流量,热力最不利程度越高,室温越晚达到设定值.控制周期为10 min,流量由2.4 m3/h增至4.0 m3/h,水泵转速及系统总流量变化如图 13所示.
|
图 13 水泵转速及干管流量趋势图 Fig. 13 Trend of pump speed and total flow |
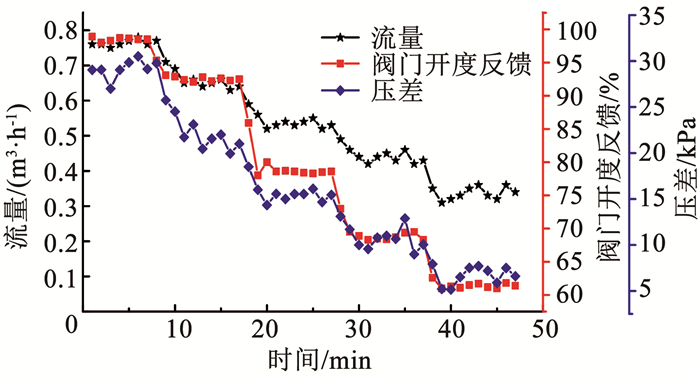
各末端连续调节阀通过PID调节开度,试验阶段各支路阀位反馈趋势如图 14所示,使得各支路水流量相同,各分支中风机盘管进出口压差如图 14所示.当该支路电磁开关阀处于关闭状态,调节阀开度维持不变.

|
图 14 各支路阀门调节趋势图 Fig. 14 Trend of valve regulation for each branch |
在试验阶段(14:25—15:55),室外气温平稳,最低31.00 ℃,最高31.90 ℃,平均温度31.48 ℃,该时间段内最大温差0.90 ℃.此时室内外温差6 ℃左右,因此室外温度的变化对围护结构引起的负荷变化不大.该时间段内,各区域人员、使用设备等内热源无变化.因此,可认为该时间段内房间负荷无变化.
随着各支路流量的不断增加,各区域室温下降并逐渐接近设定值,如图 15所示,4#分支最先达到设定值,随后5#、6#支路也能实现,分支当分支流量达到0.67 m3/h时,2#支路中室温与设定值之差至0.2 ℃左右.按照温差变化速度,各分支温差小于0.2 ℃的顺序为4#、5#、6#及2#,其中,5#、6#室温几乎同时达到设定值,与辨识结果基本一致,基于相平面轨迹特征的最不利热力环路辨识方法准确可靠.

|
图 15 室温测量值与设定值之差趋势图 Fig. 15 Trend of difference between measured and set room temperature |
1) 室温测量值及设定值的偏差e及偏差变化ec可定性反映当前房间能量供需平衡与否,由于负荷形成的复杂因素较多,实时负荷计算较为困难,但不能准确反映能量供需不平衡程度.
2) 在e-ec组成的相平面中,实时示踪向量
3) 以βi及ei为特征指标的相平面辨识方法准确可靠,可反映各支路能量供需不平衡程度.最不利热力环路是在变流量空调水系统运行过程中应避免的不利工况,是系统节能运行调控的重要参考依据.
| [1] |
江亿. 管网可调性和稳定性的定量分析[J]. 暖通空调, 1997, 27(3): 1. JIANG Yi. Adjustability and stability of hydraulic networks[J]. HV & AC, 1997, 27(3): 1. |
| [2] |
晋欣桥, 李晓锋, 惠广海, 等. 中央空调水系统控制的优化分析[J]. 系统仿真学报, 2003, 15(8): 1113. JIN Xinqiao, LI Xiaofeng, HUI Guanghai, et al. Analysis of optimal control for chilling systems of central air-conditioning systems[J]. Journal of System Simulation, 2003, 15(8): 1113. DOI:10.3969/j.issn.1004-731X.2003.08.016 |
| [3] |
朱伟峰, 江亿. 风机盘管水系统电磁阀总开启率的变化范围及其影响[J]. 暖通空调, 2002, 32(6): 4. ZHU Weifeng, JIANG Yi. Possibility analysis of the fan-coil unit water system[J]. HV & AC, 2002, 32(6): 4. DOI:10.3969/j.issn.1002-8501.2002.06.002 |
| [4] |
蔡镇兵, 廖云丹, 樊成亮, 等. 中央空调系统制冷机组群控研究综述[J]. 建筑热能通风空调, 2018, 37(9): 43. CAI Zhenbing, LIAO Yundan, FAN Chengliang, et al. A review of chiller sequencing control of centralized chiller plant[J]. Building Energy & Environment, 2018, 37(9): 43. DOI:10.3969/j.issn.1003-0344.2018.09.011 |
| [5] |
赵天怡, 张吉礼, 马良栋. 供热空调系统并联变频水泵转速比配置优化分析[J]. 大连理工大学学报, 2011, 51(5): 701. ZHAO Tianyi, ZHANG Jili, MA Liangdong. Analyses of optimal allocation scheme for speed ratio of parallel variable speed pump in heating and air-conditioning system[J]. Journal of Dalian University of Technology, 2011, 51(5): 701. DOI:10.7511/dllgxb201105013 |
| [6] |
陈峰, 刘金祥, 李沁, 等. 变流量冷冻水系统温差控制法的适用性[J]. 土木建筑与环境工程, 2015, 37(3): 94. CHEN Feng, LIU Jinxiang, LI Qin, et al. Applicability of temperature difference control mode for variable chilled water flow systems[J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(3): 94. DOI:10.11835/j.issn.1674-4764.2015.03.013 |
| [7] |
门玉葵.基于次优方法的冷冻水系统优化设计及诊断[D].广州: 华南理工大学, 2018 MEN Yukui. The optimal design and diagnosis of chilled water system on suboptimal method[D]. Guangzhou: South China University of Technology, 2018 |
| [8] |
巫江虹, 姜峰. 基于动态负荷的空调生命周期气候性能[J]. 浙江大学学报(工学版), 2017, 51(10): 2061. WU Jianghong, JIANG Feng. Life cycle climate performance of air conditioner based on dynamic loads[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(10): 2061. DOI:10.3785/j.issn.1008-973X.2017.10.022 |
| [9] |
陈定艺, 刘金祥, 徐稳龙, 等. 基于末端压差控制的变流量空调水系统水力特性[J]. 暖通空调, 2013, 43(3): 30. CHEN Dingyi, LIU Jinxiang, XU Wenlong, et al. Hydraulic characteristics of variable chilled water flow systems based on the terminal device pressure difference control[J]. HV & AC, 2013, 43(3): 30. |
| [10] |
闫唯嘉.变风量空调冷冻水最小阻力控制与节能效果研究[D].西安: 西安建筑科技大学, 2011 YAN Weijia. Research on the minimal resistance control and energy-saving effect ofVAV air-conditioning chilled water[D]. Xi'an: Xi'an University of Architectural and Technology, 2011 |
| [11] |
赵天怡.空调冷冻水系统变压差设定值优化控制方法[D].哈尔滨: 哈尔滨工业大学, 2009 ZHAO Tianyi. Optimal control method with variable differential pressure setpoint in air conditioning chilled water system[D]. Harbin: Harbin University of Technology, 2009 |
| [12] |
张晓亮, 谢晓娜, 燕达, 等. 建筑环境设计模拟分析软件DeST:第3讲建筑热环境动态模拟结果的验证[J]. 暖通空调, 2004, 34(9): 37. ZHANG Xiaoliang, XIE Xiaona, YAN Da, et al. Building environment design simulation software DeST (3): Validation of dynamic simulation resultsof building thermal progres[J]. HV & AC, 2004, 34(9): 37. DOI:10.3969/j.issn.1002-8501.2004.09.011 |
| [13] |
路兆梅, 柏广昌, 冷增祥. 模糊控制系统的相平面分析[J]. 电气自动化, 1996(6): 11. LU Zhaomei, BAI Guangchang, LENG Zengxiang. Phase plane analysis of fuzzy control system[J]. Electrical Automation, 1996(6): 11. |
| [14] |
陈振华, 余永权, 张瑞. 模糊模式识别的几种c基本模型研究[J]. 计算机技术与发展, 2010, 20(9): 32. CHEN Zhenhua, YU Yongquan, ZHANG Rui. Research on several models of fuzzy pattern recognition problems[J]. Computer Technology and Development, 2010, 20(9): 32. DOI:10.3969/j.issn.1673-629X.2010.09.008 |
| [15] |
张吉礼, 欧进萍, 于达仁. 基于相平面轨迹特征的规则自调整模糊控制方法[J]. 控制理论与应用, 2003, 20(4): 607. ZHANG Jili, OU Jinping, YU Daren. Method of rule self-tuning fuzzy control based on trajectory performance of phase plane[J]. Control theory and Application, 2003, 20(4): 607. DOI:10.3969/j.issn.1000-8152.2003.04.028 |
| [16] |
王静, 董肖丽. 模糊评价中最大隶属度原则的改进[J]. 河北水利, 2011(2): 27. DOI:10.3969/j.issn.1004-7700.2011.02.018 |
 2020, Vol. 52
2020, Vol. 52


