海底管线是海洋油气开采系统中重要的组成部分.在管线投入使用时，需要对管线进行升温，受热后管线发生膨胀; 在管线关闭停用时，管线与海水发生热交换，冷却收缩.由于各种诱因，管线的膨胀和收缩过程中的对称点不重合，导致部分管线在膨胀和收缩过程中的变形方向一致，从而引起整条管线朝向某一固定方向移动，称之为管线轴向步进现象.正常情况下，管线在工作年限内，会经历多次启动和关闭的循环(如Tahiti油田的某管线，设计使用年限25年，年均启闭次数为4.3次^[1]).每一次启动和关闭的循环都会产生一定的管线轴向步进值，因此，在管线的使用寿命内，多次启闭累积的轴向步进值将十分可观.在海洋油气开发的早期实践中，就已经发现了这种管线在循环加载后产生定向位移的现象，但近海油气管线承受的温差及海底地质条件较好，管线轴向步进并未成为威胁管线系统安全的主要因素，仅有部分学者对管线轴向步进机理的一些假设，如认为管线受热后与外层混凝土发生相对位移是管线轴向步进的主要因素(Driskill，1981^[2])，或认为海底土体对管线的约束力是引起管线轴向步进的主要因素(Konuk，1998^[3]; Tornes等，2000^[4]).但这些研究都具有一定的片面性，未能全面地解释管线轴向步进现象.随着海洋石油开采技术的不断发展，工程界开始往蕴含更多油气资源的深海海域进军，油田的离岸距离和管线的输送长度也在不断刷新记录.长距离输送需要更高的温度和压强，造成管线轴向步进值大幅度提升，管线轴向步进的安全性校核已经成为管线设计中的重要校核项目.

2003年，Carr等首次提出了管线轴向步进的概念^[5]，并在2006年开展了关于管线轴向步进机理最早的系统性分析^[6].研究指出管线连接端受到的拉力、海底表面的坡度和管线升温过程中离热源较远管线升温的滞后性是引起管线轴向步进的3个主要因素，并根据土体阻力与管线热膨胀力的相对大小，定义了管线轴向步进分析中的“长管”和“短管”.研究采用理论分析和数值模拟相结合的方法，给出管线轴向步进量的简化计算公式.在此基础上，研究人员又对管线工作状态下一些可能引起管线轴向步进的状态量进行了分析，如2007年，Olunloyo等推导了热流在管线中流动时，流速、温度等参量的瞬时变化对管线轴向步进的影响，指出热流状态量的瞬态变化对walking的影响很小^[7]; 2009年，Cumming等采用数值模拟方法，分析了当升温达到稳定后的管线，其沿长度方向存在的温度梯度对管线轴向步进的影响^[8]; 2010年，Chen等研究了双层管夹层与内层管线间的摩擦系数对双层管线轴向步进量的影响^[9]; 2010年，Bruton等分析了管线内存在的气液两相流对管线轴向步进的影响^[10]; 此外，文献[11-16]对管线的轴向步进进行了分析.

管线轴向步进研究中，土体对管线的约束力决定管线有效轴力及轴向应变的分布，进而直接影响管线的轴向步进值.因此，管线轴向步进的计算过程中，准确地描述轴向土体阻力模型是保证计算结果可靠性的首要条件.管土轴向相互作用新近的室内研究试验结果显示^[17]，深海土体强度在经历管线剪切破坏后，管线周围土体产生固结，海床土体强度和对管线的轴向约束力系数随时间增大.Randolph^[18]和Yan等^[19]分别采用理论分析和数值模拟方法研究了土体这种硬化现象，并提出了相应的计算公式.

本文通过理论研究，考虑了土体硬化导致管线降温过程中土体阻力系数上升的情况，对管线沿程轴力分布进行了分析，并在此基础上提出了考虑土体阻力增长情况下，计算管线轴向步进的解析解.

1 管线轴向步进现象的机理 1.1 管线轴向步进现象

在输送石油资源时需要对海底管线施加一定的温度和压强，温压联合作用下管线会发生轴向的膨胀.理想状态下的自由管线在升温膨胀和冷却收缩过程中，膨胀和收缩变形总是关于管线中点对称产生的，因此，经历一次完整的荷载循环后每段管段的膨胀和收缩相互抵消，整个管线不会出现整体性位移.管线膨胀和收缩的变形过程中，变形的对称点称为虚拟锚固点，该点处轴向位移为0.

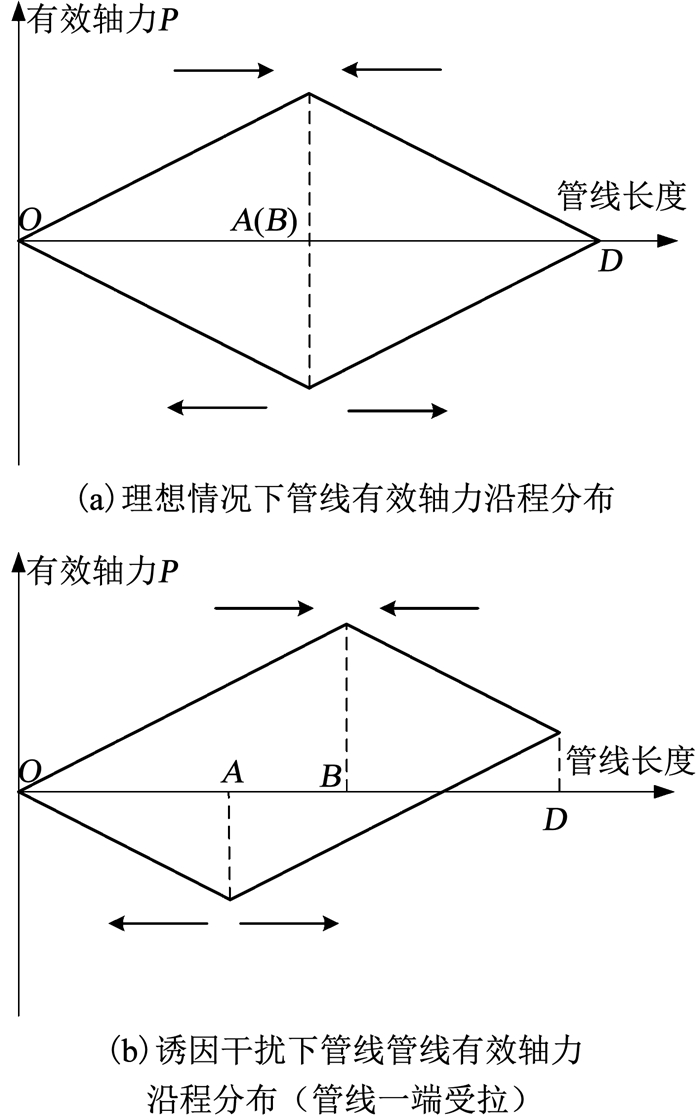
当管线受某些外界因素干扰，如管线一端受拉、管线铺设于倾斜的海床上或管线升温过程中温度衰减这3种情况时，管线膨胀和收缩过程的虚拟锚固点不再重合，导致管线中的部分管段在升温和降温过程中轴向变形方向相同，管线因此产生了轴向步进现象.理想情况和受诱因干扰情况下管线沿程的轴力分布如图 1所示，图中横坐标为管线长度，纵坐标为管线的有效轴力，纵坐标以拉力为正，压力为负.升温过程中管线膨胀，有效应力为负值; 降温过程中管线收缩，有效应力为正值.图中箭头方向代表管线的变形方向.可以看出，理想情况下升温和降温过程中虚拟锚固点A和B重合，一个荷载循环周期管线无整体性位移.而受诱因作用下的管线，虚拟锚固点A和B的位置不同，A、B两点间的管段在升温过程中产生朝向B点的膨胀，而在降温过程中产生朝向B点的收缩.整个荷载循环周期中，A、B两点间的管段一直朝向B点移动，导致管线出现了轴向步进现象.

1.2 土体阻力增长

在管线轴向步进分析中，管线受到的土体阻力决定有效轴力的分布，进而影响轴向步进量的大小.管线有效轴力曲线的斜率等于单位长度管线受到的土体阻力值f.

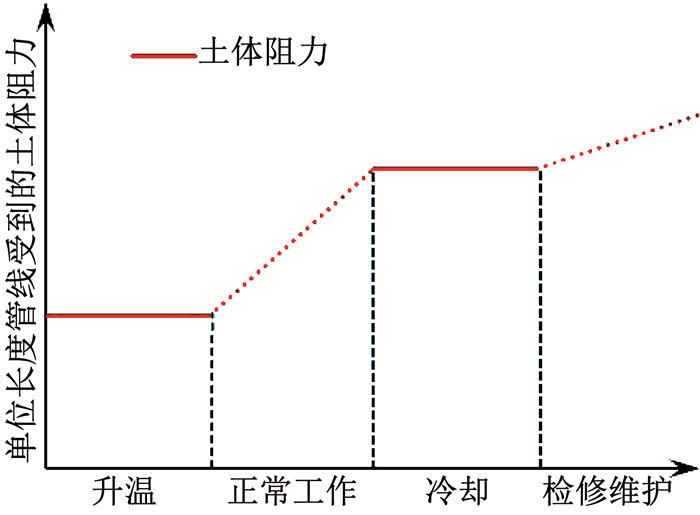
一个完整的管线荷载循环周期分为升温、工作、降温和检修4个阶段.升温和降温阶段中管线承受的温度差发生变化，产生轴向变形剪切周围土体而产生超孔隙水压力.在工作和检修阶段，管线与土体保持相对静止，超孔隙水压力逐渐消散，土体强度增大而导致管线受到的阻力上升.因此，管线在同一个循环过程中，升温和降温阶段剪切土体时受到的土体阻力是不同的.图 2为考虑单次循环周期内土体阻力的增长曲线.可以看出，在升温过程时，管线膨胀剪切土体，此时单位长度管线受到的土体阻力为f₁.当管线升温结束进入工作状态时，管线与土体间不再发生相互位移，土体中不再产生超孔压，且工作状态持续时间很长，因此，在升温过程中产生的孔压能够充分消散，土体阻力上升.当管线进入降温过程时，管线冷却收缩，单位长度管线受到的土体阻力为f₂.管线在同一个循环过程中，升温和降温阶段剪切土体时受到的土体阻力有所不同.

2 考虑土体阻力变化时轴向步进理论解

对3种不同诱因下管线轴向步进进行分析，推导相应条件下考虑土体阻力变化时轴向步进解析解.

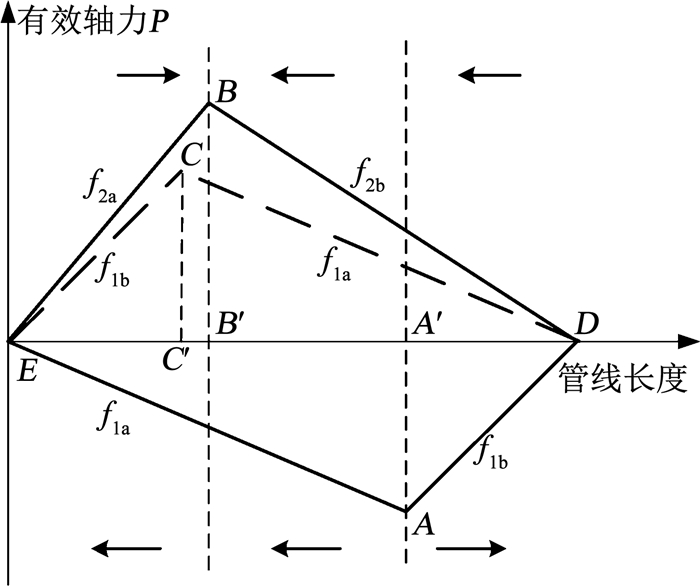
2.1 由管端受拉激发的轴向步进

图 3为一个荷载循环周期内长度为L的自由管线(管线两端自由变形)轴力分布图，图中横坐标为管线长度，以朝向管线受SCR牵引处为正; 纵坐标为管线沿程的轴力分布，以管线受拉为正，管线受压为负.图中箭头表示管线的变形方向.

管线有效轴力发展全过程：1)当管线在升温前，管线一段(D点)受到牵引力F的作用，D点初始轴力为F_t.由于受到土体的约束作用，仅靠近D点的局部管段中存在拉力，OD段斜率为f₁，整个管线的轴力分布为折线COD′; 2)在升温过程中，管线温度不断升高，管线内产生温度应力.由于温度应力会引起管线膨胀，管线轴力分布曲线向纵坐标的负轴方向偏移，管线轴力分布为折线CAD′，A点即为管线膨胀的虚拟锚固点，管线以A点为对称中心，向两侧膨胀.CA段和AD′段斜率都为f₁; 3)在工作状态下，管线与海床相对静止不会继续发生膨胀变形，沿程轴力仍为折线CAD′.但在整个工作过程中，土体阻力上升; 4)当管线降温时，温度降低引起管线收缩，管线向纵坐标正轴方向偏移.管线轴力分布为折线CBD′，B点为收缩过程的虚拟锚固点，管线以B点为对称中心自两端向B点处收缩.CB段和BD′段斜率都为f₂; 5)在检修过程中管线与海床相对静止不会继续发生膨胀变形，沿程轴力仍为折线CBD′.

为便于分析，在降温过程中引入折线CED′，表示不考虑土阻力上升后，降温过程中管线沿程轴力分布.由图 3可知：1)CA′段管线虽在升温和降温过程中变形方向相反，但由于降温过程中的土体阻力上升，CA′段管线收缩变形量小于膨胀量，CA′段管线产生负向的整体位移Δw₁; 2)A′B′段在升温和降温过程中变形方向相同，都为正向，A′B′段管线产生正向的整体位移Δw₂; 3)B′E′段管线虽在升温和降温过程中变形方向相反，但由于降温过程中土体阻力上升，B′E′段管线收缩变形量小于膨胀量，B′E′段管线产生正向的整体位移Δw₃; 4)E′D′段管线虽在升温和降温过程中变形方向相反，但由于降温过程中土体阻力上升，收缩变形量小于膨胀量，E′D′段管线产生正向的整体位移Δw₄.上述4部分整体位移(Δw₁~Δw₄)之和即为最终管线轴向步进值Δw_te.

对于CA′段，变形量等于变形段长度与平均应变的乘积，因此

$ \begin{array}{l} \Delta {w_1} = - \left| {C{A^\prime }} \right| \cdot \Delta \bar \varepsilon = - \left| {C{A^\prime }} \right| \cdot \frac{{{P_2} - {P_1}}}{{EA}} = \\ \;\;\;\;\;\;\;\;\; - \left| {C{A^\prime }} \right| \cdot \frac{{\frac{1}{2}\left| {C{A^\prime }} \right| \cdot {f_2} - \frac{1}{2}\left| {C{A^\prime }} \right| \cdot {f_2}}}{{EA}} = \\ \;\;\;\;\;\;\;\;\; - \left| {C{A^\prime }} \right| \cdot \frac{{\left| {C{A^\prime }} \right| \cdot \left( {{f_2} - {f_1}} \right)}}{{2EA}}. \end{array} $

(1)

同理，对于A′B′段，

$ \begin{array}{l} \Delta {w_2} = \left| {{A^\prime }{B^\prime }} \right| \cdot \Delta \bar \varepsilon = \left| {{A^\prime }{B^\prime }} \right| \cdot \frac{{\Delta s - \Delta p}}{{EA}} = \left| {{A^\prime }{B^\prime }} \right| \cdot \\ \frac{{{P_{{\rm{te}}}} + \frac{1}{2} \cdot \left[ {{F_{\rm{t}}} - \left| {C{B^\prime }} \right| \cdot {f_2} - \left( {L - \left| {C{B^\prime }} \right|} \right) \cdot {f_1} - \left| {C{A^\prime }} \right| \cdot \left( {{f_2} + {f_1}} \right)} \right]}}{{EA}}. \end{array} $

(2)

式中：P_te为温度应力，$P_{\mathrm{te}}=E A \alpha \cdot \Delta T $; E为管线钢材的弹性模量; A为钢材的截面积; α为钢材热膨胀系数; ΔT为管线承受的总温度差; F_t为管端受到的拉力值.

对于B′E′段

$ \begin{array}{l} \Delta {w_3} = \left| {{B^\prime }{E^\prime }} \right| \cdot \Delta \bar \varepsilon = \left| {{B^\prime }{E^\prime }} \right| \cdot \\ \frac{{\left| {{D^\prime }{B^\prime }} \right| \cdot \left( {{f_2} - {f_1}} \right) + \left| {{D^\prime }{E^\prime }} \right| \cdot \left( {{f_2} - {f_1}} \right)}}{{2EA}}. \end{array} $

(3)

对于E′D′段

$ \Delta {w_4} = \left| {{D^\prime }{E^\prime }} \right| \cdot \Delta \bar \varepsilon = \left| {{D^\prime }{E^\prime }} \right| \cdot \frac{{\left| {{D^\prime }{E^\prime }} \right| \cdot \left( {{f_2} - {f_1}} \right)}}{{2EA}}. $

(4)

根据图 3中的几何关系，可以得出

$ \left| {{A^\prime }C} \right| \cdot {f_1} = \left( {L - \left| {{A^\prime }C} \right|} \right) \cdot {f_1} - {F_{\rm{t}}}. $

(5)

因此

$ \left| {{A^\prime }C} \right| = \frac{{L \cdot {f_1} - {F_{\rm{t}}}}}{{2{f_1}}} = \frac{L}{2} - \frac{{{F_{\rm{t}}}}}{{2{f_1}}}, $

(6)

$ \left| {{B^\prime }{D^\prime }} \right| = \frac{{L \cdot {f_2} - {F_{\rm{t}}}}}{{2{f_2}}} = \frac{L}{2} - \frac{{{F_{\rm{t}}}}}{{2{f_2}}}. $

(7)

考虑土体阻力变化后，由管端受拉激发的轴向步进值为

$ \begin{array}{l} \Delta {w_{{\rm{te}}}} = \frac{1}{2} \cdot \alpha \cdot \Delta T \cdot {F_t} \cdot \left( {\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}} \right) + \frac{{F_t^2}}{{2EA}} \cdot \\ \left( {\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}} \right) - \frac{{{F_{\rm{t}}} \cdot L}}{{EA}} + \frac{{{F_{\rm{t}}} \cdot \left( {{f_2} - {f_1}} \right)}}{{4EA}} \cdot \left( {\frac{1}{{{f_1}}} - \frac{1}{{{f_2}}}} \right) \cdot \\ \left[ {L - \frac{{{F_{\rm{t}}}}}{2}\left( {\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}} \right)} \right]. \end{array} $

(8)

管线朝向受拉一端产生整体移动.

2.2 由海床坡度激发的轴向步进

图 4为铺设于坡度为φ的海床上的管线在各个过程中的轴力分布图，横坐标为管线长度，管线长度为L，D点为海床坡顶，E点为海床坡底，以管线朝向坡底E处的位移为正; 纵坐标为管线沿程的轴力分布，以管线受拉为正，管线受压为负.由于管线在斜坡上运动时受到重力平行于斜坡分量的影响，管线有效轴力分布曲线的斜率为土体阻力与重力切线分量的矢量和，因此，管线在斜坡上产生正向位移(朝向坡顶D点运动)和负向位移(朝向坡底E运动)时，轴力斜率不同.图中箭头表示管线的变形方向.

管线有效轴力发展全过程：1)当管线安装完毕时，由于没有施加任何荷载，管线与海床保持相对静止且没有任何方向的运动趋势，管线沿程轴力为0，轴力分布为线段DE; 2)在升温过程中，管线温度不断升高，管线内产生温度应力，引起管线膨胀，因此，管线轴力分布曲线向纵坐标负轴的方向偏移.管线轴力分布为折线EAD，A点即为管线膨胀的虚拟锚固点，管线以A点为对称中心，向两侧膨胀.由于A点两侧运动方向不同，EA段和AD段斜率分别为f_1a和f_1b.EA段朝向坡底运动，与重力切线分量方向相同，因此，有效轴力的斜率f_1a小于水平海床上单位管线受到的土体阻力f₁，${f_{1{\rm{a}}}} = {f_1} - {w^\prime }\sin \varphi $.AD段朝向坡顶运动，需克服重力切线分量，有效轴力的斜率f_1b大于水平海床上的最大土体阻力，$ {f_{1{\rm{b}}}} = {f_1} + {w^\prime }\sin \varphi $.3)在工作状态下，升温过程剪切土体产生的超孔压逐渐消散，管线周围土体强度上升，但由于工作过程中，管线与海床相对静止不会继续发生膨胀变形，沿程轴力仍为折线EAD.4)当管线降温时，温度降低引起管线收缩，管线向纵坐标正轴方向偏移.管线轴力分布为折线EBD，B点为收缩过程的虚拟锚固点，管线以B点为对称中心自两端向B点处收缩.EB段和BD段斜率分别为f_2a和f_2b.同升温过程类似，B点两侧运动方向不同，EB段朝向坡顶运动，$ {f_{{\rm{2a}}}} = {f_2} + {w^\prime }\sin \varphi $.BD段朝向坡底运动，$ {f_{{\rm{2a}}}} = {f_2} - {w^\prime }\sin \varphi $; 5)在检修过程中，管线与海床相对静止不会继续发生膨胀变形，沿程轴力仍为折线EBD.

同样，为便于进行分析计算，在降温过程中引入折线ECD，表示不考虑正常工作过程中土体超孔压消散引起土阻力系数上升后，降温过程中管线沿程轴力分布.由图 4可知：1)EB′段管线虽在升温和降温过程中变形方向相反，但由于降温过程中的土体阻力上升，收缩变形量小于膨胀量，EB′段管线产生负向的整体位移Δw₁; 2)B′A′段在升温和降温过程中变形方向相同，都为负向，A′B′段管线产生负向的整体位移Δw₂; 3)A′D段管线虽在升温和降温过程中变形方向相反，但由于降温过程中的土体阻力上升，收缩变形量小于膨胀量，A′D段管线产生正向的整体位移Δw₃.上述3部分整体位移(Δw₁~Δw₃)之和即为考虑土体阻力变化后最终管线的轴向步进值Δw_s.

由上述分析可知：

$ {f_{1{\rm{a}}}} = {f_1} - w'\sin \varphi ,{f_{1{\rm{a}}}} = {f_1} + w'\sin \varphi , $

$ {f_{2{\rm{a}}}} = {f_1} + {w^\prime }\sin \varphi ,{f_{2{\rm{a}}}} = {f_1} - {w^\prime }\sin \varphi . $

f₁和f₂分别代表平坦海床上单位长度管线在升温和降温过程中受到的土体阻力.

对于EB′段

$ \Delta {w_1} = - \left| {E{B^\prime }} \right| \cdot \Delta \bar \varepsilon = - \left| {E{B^\prime }} \right| \cdot \frac{{\left| {E{B^\prime }} \right| \cdot \left( {{f_{2{\rm{a}}}} - {f_{1{\rm{b}}}}} \right)}}{{2EA}}. $

(9)

对于B′A′段

$ \begin{array}{l} \Delta {w_2} = - \left| {{B^\prime }{A^\prime }} \right| \cdot \Delta \bar \varepsilon = - \left| {{B^\prime }{A^\prime }} \right| \cdot \\ \frac{{EA\alpha \Delta T - \frac{1}{2} \cdot \left( {\left| {E{B^\prime }} \right| \cdot \left( {{f_{2{\rm{a}}}} + {f_{1{\rm{a}}}}} \right) + \left| {D{A^\prime }} \right| \cdot \left( {{f_{2{\rm{b}}}} + {f_{1{\rm{b}}}}} \right)} \right)}}{{EA}}. \end{array} $

(10)

对于DA′段

$ \Delta {w_3} = \left| {D{A^\prime }} \right| \cdot \Delta \bar \varepsilon = \left| {D{A^\prime }} \right| \cdot \frac{{\left| {D{A^\prime }} \right| \cdot \left( {{f_{2{\rm{b}}}} - {f_{{\rm{1a}}}}} \right)}}{{2EA}}. $

(11)

由图 4中几何关系可知：$ \left|D A^{\prime}\right|=\frac{f_{1 \mathrm{a}} \cdot L}{f_{\mathrm{la}}+f_{1 \mathrm{b}}}$, $ \left|E B^{\prime}\right|=\frac{f_{2 \mathrm{b}} \cdot L}{f_{2 \mathrm{a}}+f_{2 \mathrm{b}}}$.

因此，考虑土体阻力变化后由海床坡度引起的管线轴向步进值Δw_s为

$ \begin{array}{l} \Delta {w_{\rm{s}}} = \frac{{{f_1} + {f_2}}}{{2{f_1}{f_2}}}\tan \varphi \cdot \alpha \cdot \Delta T \cdot L + \\ \frac{{{L^2}}}{{2EA}} \cdot \left( {\frac{{{w^\prime } \cdot \tan \varphi }}{{{f_1}}} + \frac{{{w^\prime } \cdot \tan \varphi }}{{{f_2}}} - 2} \right) \cdot {w^\prime } \cdot \sin \varphi . \end{array} $

(12)

管线朝向坡脚产生整体移动.

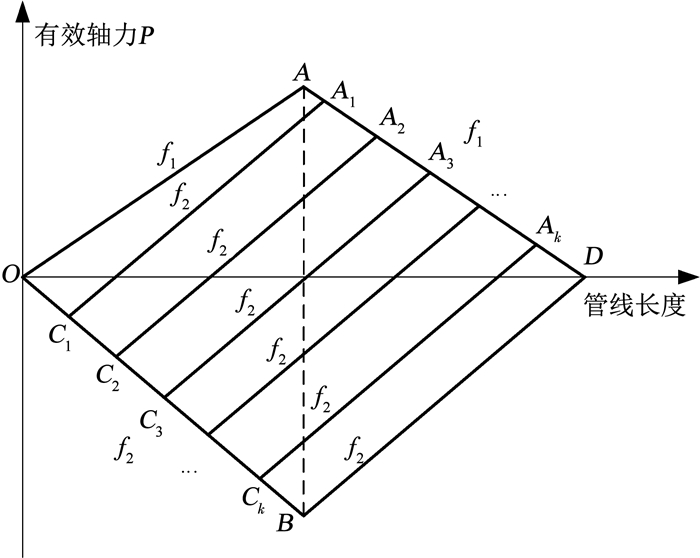
2.3 由温度梯度激发的轴向步进

图 5为升温过程中存在温度梯度管线(管线两端自由变形)的轴力分布图，横坐标为管线长度，管线长L，C点为靠近热源的一端(热端)，D点为远离热源的一端(冷端)，以管线发生朝向冷端D点的位移为正; 纵坐标为管线沿程的轴力，以管线受拉为正，管线受压为负.

受温度梯度激发产生的轴向步进现象中，前一次荷载循环降温过程产生的残留于管线中的拉力大小，会对步进值产生较大影响，因此，常以前一次荷载循环的降温和检修过程和本次荷载循环的升温和正常工作过程作为一个分析周期.由于前一次荷载循环的降温过程中土阻力小于本次荷载周期中的升温过程，且前述分析中f₂常大于f₁的假定，在本次分析中将前一次荷载循环降温过程中管线受到的土阻力记为f₁，将本次荷载周期升温过程中管线受到的土阻力记为f₂.

1) 前一次荷载循环降温过程中，管线与周围海水热交换而自然降温，整条管线以中点A为对称点收缩，管线轴力分布为折线OAD，降温过程中单位长度管线受到的土体阻力为f₁，管线剪切海床土体产生超孔隙水压力; 2)在检修维护过程中，降温过程产生的超孔压逐渐消散，管线周围土体强度上升.由于管线与海床相对静止，沿程轴力仍为折线OAD.3)在升温过程中，离热源近的管段先受热升温，随着被加热管段范围的增大，发生膨胀的管线长度也不断增加.将管线热端从开始升温到整条管线全部被加热的这一连续过程分解成n(n=1，2，3，…，k，…)个升温步.则第1，2，3，…，k个升温步时管线轴力曲线为折线$O{C_1}{A_1}D, O{C_2}{A_2}D, O{C_3}{A_3}D, \cdots , O C_{k} A_{k} D $.虚拟锚固点分别为$ C_{1}, C_{2}, C_{3}, \cdots, C_{k}$.虚拟锚固点随被加热管段长度的增加而逐渐向冷端移动，直至整个管线开始受热膨胀，此时虚拟锚固点移动至整条管线的中点B处.在此之后，管线温度继续上升，管线关于中点对称性地膨胀变形.升温过程中管线受到的土体阻力保持f₂，即线段$O{C_1}, O{C_2}, O{C_3}, \cdots , O{C_k} $和线段$ C_{1} A_{1}, C_{2} A_{2}, C_{3} A_{3}, \cdots, C_{k} A_{k}$的斜率为f₂.4)在正常工作状态下，管线与海床相对静止不会继续发生膨胀变形，沿程轴力仍为折线OBD.

由上述分析可以看出，由于管线是逐段升温的，且升温过程中受前一次循环后残余拉力的影响，虚拟锚固点需要一定时间才能位于管线中点，在此之前管线发生的朝向冷端的位移导致了管线产生轴向步进，即管线从升温膨胀开始，到膨胀过程的虚拟锚固点C_k移动至B点这段时间内发生的变形导致了管线轴向步进.

假定管线热端从开始升温到整条管线全部被加热的这一连续过程分解成n(n=1，2，3，…，k，…)个升温步，每个升温步中管线虚拟锚固点朝向管线中点B前进x_A的距离，则$ n=\frac{L}{2 \cdot x_{A}}$.

记第k个升温步中被加热的管段长度为x_θk，第k个升温步中产生的步进值为Δw_k则

$ \Delta {w_k} = {x_A} \cdot \frac{{\Delta s - \Delta p}}{{EA}} = x_A^2 \cdot \frac{{\left( {2k - 1} \right) \cdot \left( {{f_1} + {f_2}} \right)}}{{2EA}}. $

(13)

由于当x_θk大于L/2时，位于BD段内的管线产生的膨胀变形在降温过程中是可恢复的，因此，需要根据x_θk与L/2的相对大小对式(13)进行修正，修正后结果为

$ \begin{array}{l} \Delta {w_k} = \left\{ {\begin{array}{*{20}{l}} {{x_A} \cdot \frac{{\Delta s - \Delta p}}{{EA}},{x_{\theta k}} < \frac{L}{2},}\\ \begin{array}{l} {x_A} \cdot \frac{{\Delta s - \Delta p}}{{EA}} - \frac{{{f_\theta } \cdot {{\left( {{x_{\theta k}} - \frac{L}{2}} \right)}^2}}}{{2EA}},{x_{\theta (k - 1)}} < \frac{L}{2} < {x_{\theta k}},\\ {x_A} \cdot \frac{{\Delta s - \Delta p}}{{EA}} - \frac{{{f_\theta } \cdot \left[ {L \cdot \left( {{x_{\theta (k - 1)}} - {x_{\theta k}}} \right) + \left( {x_{\theta k}^2 - x_{\theta (k - 1)}^2} \right)} \right]}}{{2EA}},{x_{\theta k}} > \frac{L}{2}, \end{array} \end{array}} \right.\\ = \left\{ \begin{array}{l} x_A^2 \cdot \frac{{(2k - 1) \cdot \left( {{f_1} + {f_2}} \right)}}{{2EA}},{x_{\theta k}} < \frac{L}{2},\\ x_A^2 \cdot \frac{{(2k - 1) \cdot \left( {{f_1} + {f_2}} \right)}}{{2EA}} - \frac{{{f_\theta } \cdot {{\left( {{x_{\theta k}} - \frac{L}{2}} \right)}^2}}}{{2EA}},{x_{\theta (k - 1)}} < \frac{L}{2} < {x_{\theta k}},\\ x_A^2 \cdot \frac{{(2k - 1) \cdot \left( {{f_1} + {f_2}} \right)}}{{2EA}} - \frac{{{f_\theta } \cdot \left[ {L \cdot \left( {{x_{\theta (k - 1)}} - {x_{\theta k}}} \right) + \left( {x_{\theta k}^2 - x_{\theta (k - 1)}^2} \right)} \right]}}{{2EA}},{x_{\theta k}} > \frac{L}{2}, \end{array} \right.\\ 1 \le k \le \frac{L}{{2{x_A}}}. \end{array} $

(14)

式中：f_θ为单位长度管线的温度应力，$f_{\theta}=E A \alpha q ; q $为升温过程中管线的温度梯度; x_A为选定的每个升温步中虚拟锚固点增长的距离，当x_A趋近于0时，即为实际发生的连续升温过程.x_θk为第k个升温步中被加热的管段长度，可根据虚拟锚固点两侧变形量相等求得表达式.

$ {x_{\theta k}} = \left\{ {\begin{array}{*{20}{l}} {{x_A} + \sqrt {x_A^2 + \frac{{{x_A} \cdot \left( {{f_{{\rm{C}},i - 1}} + {f_{{\rm{H}},i}}} \right) \cdot \left( {L - {x_A}} \right)}}{{{f_\theta }}}} ,k = 1,}\\ {k \cdot {x_A} + \sqrt {{{\left( {k \cdot {x_A} - {x_{\theta (k - 1)}}} \right)}^2} + \frac{{2 \cdot {f_{{\rm{H}},i}} \cdot {x_A} \cdot \left( {L - {x_A}} \right)}}{{{f_\theta }}}} ,k \ge 2.} \end{array}} \right. $

(15)

考虑土体阻力变化后由海床坡度引起的管线轴向步进值Δw_th为n个升温步中产生的Δw_k的累加，即

$ \Delta {w_{{\rm{th}}}} = \sum\limits_1^{\frac{L}{{{x_A}}}} \Delta {w_k}. $

(16)

3 工程算例

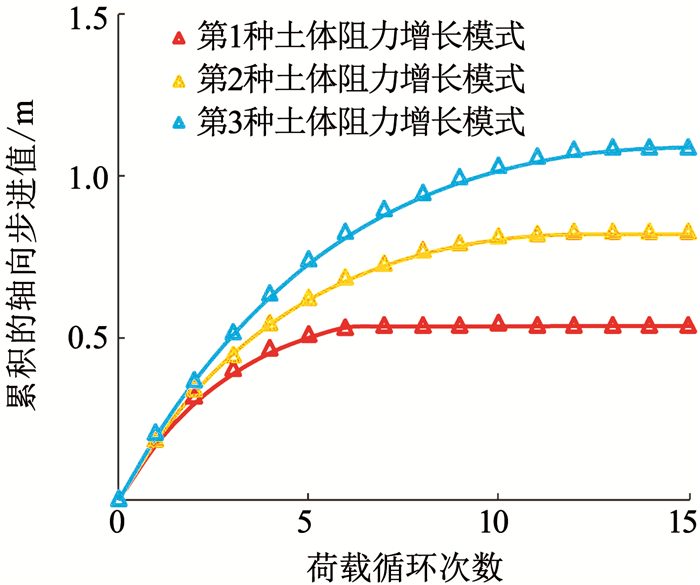
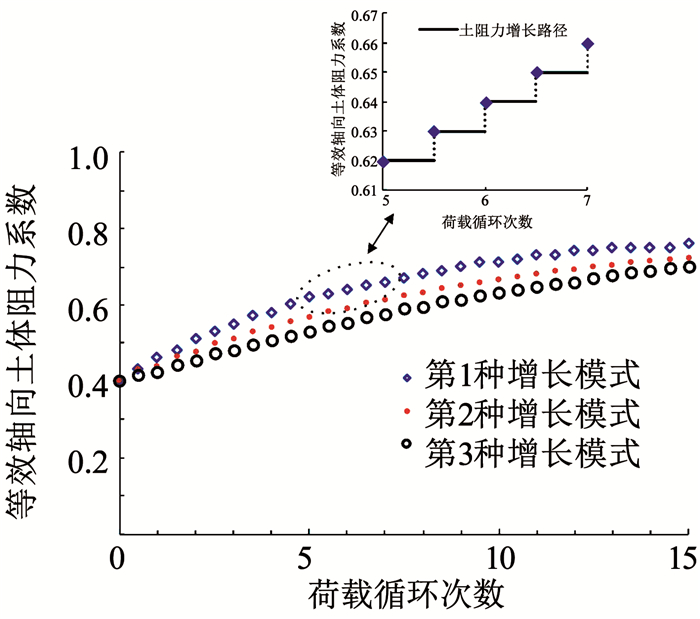
该工程中管线铺设于倾斜的海床表面，并由此产生了轴向步进现象^[20].共有3种土体阻力增长模型，每个增长模型中，管线在降温过程受到的土体阻力大于升温过程受到的土体阻力，且土体阻力大小随循环次数的上升而不断增大.算例中管线计算参数如表 1所示.3种土体阻力增长模型在15次循环中的取值如图 6所示.

采用上述推导的公式对算例数据进行计算分析，并将结果和文献[20]中所得数据进行对比，结果如图 7所示.图中点状数据为文献[20]给出的结果，线状数据为本文推导解析解的计算结果.可以看出，3种土体增长模式下，所推演的理论解结果与文献[20]给出的结果之间误差几乎为0，所推导的理论解能够精确地计算管线的轴向步进值.

4 结语

本文对管线的轴向步进现象进行了分析，基于管线有效轴力沿程分布曲线，推导出能够考虑单次荷载循环周期内土体阻力增长后轴向步进的理论解，并通过对比工程实例数据，揭示了所推导结果的适应性和可靠性，为预测单次荷载循环周期内土体阻力增长情况下管线所产生的轴向步进值，提供了简便可靠的解析解算法.