2. 村镇建设防灾减灾四川省高等学校工程研究中心,四川 都江堰 611830;
3. 冻土工程国家重点实验室中国科学院西北生态环境资源研究院,兰州 730000
2. Sichuan Higher Education Engineering Research Center for Disaster Prevention and Mitigation of Village Construction, Dujiangyan 611830, Sichuan, China;
3. State Key Laboratory of Frozen Soil EngineeringNorthwest Institute of Eco-Environment and Resources, CAS, Lanzhou 730000, China
多年冻土区路基沉降变形是冻土工程研究中的核心,也是铁路正常运营之安全隐患,更是制约寒区工程建设和资源开发的关键因素.冻土因其冰的存在,即使在很小的荷载下也会出现强度和变形随时间而变化的蠕变现象[1-2].青藏铁路通车近十年的现场实测资料表明,部分多年冻土路段路基不断补碴、抬道使道床厚度甚至达到1.7 m以上[3],路基稳定性、行车安全问题日渐凸显,冻土蠕变机理与沉降控制措施研究迫切需要深入开展.
冻土的蠕变特性受土的类型、密度、含水率、温度、应力水平等多种因素影响[4-5],在变形过程中还同时存在强化和弱化作用[6].蠕变曲线分为衰减蠕变和非衰减蠕变两种类型,建立冻土蠕变模型常用3种途径[7]:1)基于试验结果通过数学公式推导、拟合建立的经验模型.2)应力-应变-时间模型.Bray[8]基于松弛试验得到了冻土的蠕变参数,并研究了温度和应力对冻土和多晶冰蠕变特性的影响; Arenson等[9]通过冻土蠕变试验,得到温度接近于0 ℃富冰冻土的蠕变模型; 周志伟等[10]进行不同温度和围压条件下的三轴压缩和蠕变试验,基于超塑性理论和过应力原理建立了冻结黄土的率相关本构模型; 朱元林等[11]通过冻土动三轴蠕变试验,回归分析得出了冻土动蠕变模型.3)利用基本的虎克弹性体、牛顿黏性体、圣-维南塑性体等力学模型元件,构建的流变模型.经典的流变模型有Kelvin模型、Burgers模型、Bingham模型以及Nishihara模型等,其模型由一系列力学模型元件组成,概念直观被广泛应用于描述岩土材料的蠕变特性.但这些模型采用的都是线性元件,无法很好地描述蠕变的全过程,尤其是无法描述加速蠕变[12].故此,学者们提出采用非线性流变元件代替常规的线性流变元件,或者引入损伤断裂力学等新的理论建立冻土蠕变模型.康永刚等[13]用幂律流体元件替代牛顿黏壶,提出一种经验函数描述加速蠕变阶段; 孙凯等[14]将黏弹性元件中黏滞系数修正为关于时间的函数来描述非线性蠕变过程,并将一维蠕变模型推广到三维中; 赵晓东等[15]通过GFC(不经历K0固结,不均匀温度冻结)的方法,对不同温度梯度和蠕变应力下的冻结饱和黏土进行了一系列单轴蠕变试验,并建立了考虑热梯度的修正Kelvin模型; 赵延林等[16]在Burgers模型基础上,串联一个能描述蠕变过程中强度参数非线性衰减特性的M-C塑性元件,并利用FLAC3D实现了新建蠕变损伤模型的二次开发.李栋伟等[17]引入服从D-P屈服准则的黏塑损伤变量,结合西原模型推导出冻土黏弹塑性损伤耦合本构方程.各学者针对建立的蠕变模型参数的影响因素也进行了深入探讨,获得大量有益认识.
冻土的蠕变是典型的非线性流变,应力和时间都能引起非线性,且对非线性的影响是耦合的.要想合理描述冻土非线性蠕变特征,修正的非定常黏滞系数应是流变时间和应力水平的函数[18],然而大部分改进的非线性黏弹性元件很少有考虑应力水平对黏滞系数的影响.鉴于此,以Nishihara模型为基础,将黏弹性元件中的黏滞系数修正为应力水平和流变时间的函数,并在黏塑性元件中引入损伤变量D,进而建立简单而适用的冻结砂土的蠕变本构关系.不同温度和干密度条件下的冻结砂土三轴蠕变试验结果对比表明,该模型能较好地描述不同温度、应力水平条件下冻结砂土的衰减、稳态和加速蠕变特性.本模型可为冻结砂土蠕变预测提供一种新的选择.
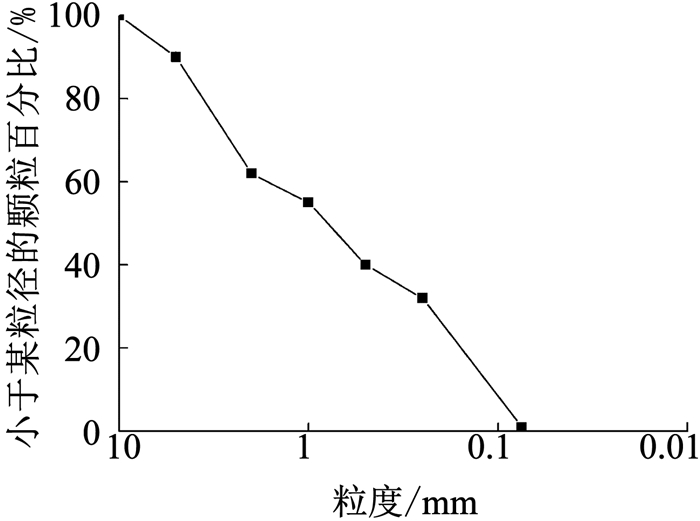
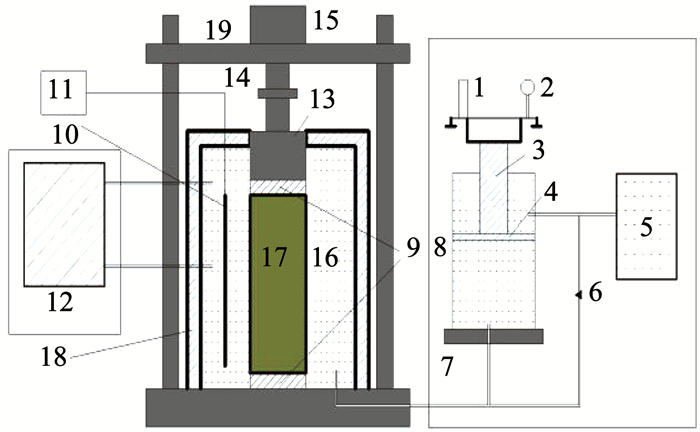
1 冻土三轴蠕变试验 1.1 试验条件试验用土为青藏铁路沿线砂土,初始含水率15.6%,颗粒级配曲线见图 1.采用标准方法批量制备试件[19],制成61.8 mm×125 mm的圆柱形试件.试验在MTS Landmark370.10材料试验机上进行(见图 2).仪器控温精度为±0.1 ℃,最大轴向加载100 kN.在0.1 MPa围压下开展5个温度(-0.5, -0.9, -1.2, -1.5和-2.0 ℃)、两种干密度(1.75和1.92 g/cm3)的三轴蠕变试验.当土体发生非衰减蠕变时,轴向应变达24%试验终止; 当土体发生衰减蠕变时,轴向应变速率≤0.000 5/h试验终止.
|
1—活塞; 2—表盘; 3—活塞; 4—的位移传感器; 5—围压伺服作动器; 6—阀门; 7—高压油管; 8—高压泵; 9—压板; 10—温度传感器; 11—温度显示器; 12—冷浴系统; 13—轴向荷载活塞; 14—轴向力传感器; 15—轴向伺服作动器; 16—航空液压油; 17—冻土试样; 18—冷冻液; 19—高强横梁 图 1 土体颗粒级配曲线 Fig. 1 Particles gradation curve |
|
图 2 三轴试验系统示意 Fig. 2 Schematic diagram of the tri-axial testing system |
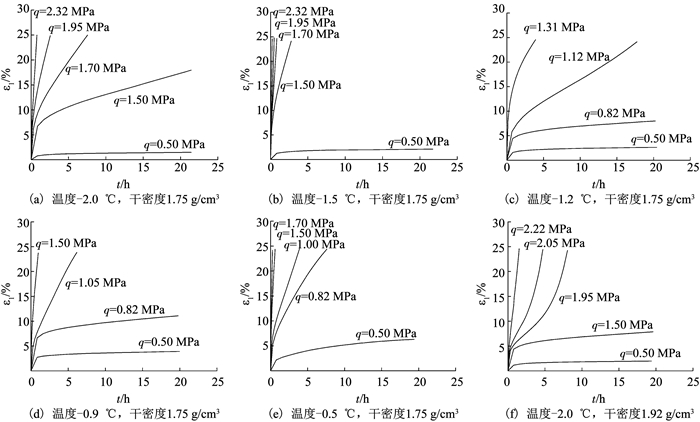
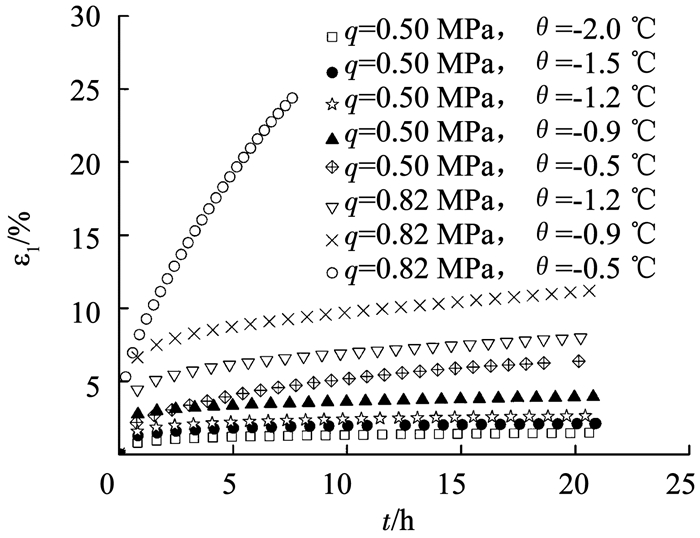
冻土在不同温度、干密度和剪切应力条件下的蠕变曲线见图 3,ε1为轴向应变,q为广义剪应力,t为蠕变时间.可以看出,当剪应力水平较低时,硬化作用占优势,表现为衰减蠕变; 随着剪应力增大,弱化作用占优势,表现为非衰减蠕变.当冻土干密度为1.75 g/cm3时,非衰减蠕变过程主要表现为非稳定和稳定蠕变两个阶段,加速阶段并不明显; 而当冻土干密度为1.92 g/cm3时,加速蠕变阶段明显.不同温度和相同应力条件下冻土的三轴蠕变曲线见图 4,θ为试验温度.可以看出,温度越高,未冻水含量增多,冻土内部矿物颗粒和冰胶结作用削弱,蠕变量较大.
|
图 3 冻结砂土三轴蠕变试验曲线 Fig. 3 Creep curves for frozen sand under tri-axial conditions |
|
图 4 不同温度相同应力下的蠕变曲线(干密度1.75 g/cm3) Fig. 4 Creep curves under the same shear stress and different temperatures (dry density is 1.75 g/cm3) |
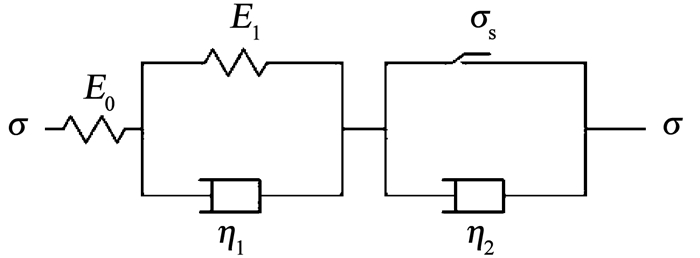
Nishihara模型由一个广义Kelvin体和一个黏塑性体串联而成(见图 5),可用来描述岩土材料的蠕变特性[14, 18],式(1)为蠕变方程:
| $ \varepsilon = \left\{ {\begin{array}{*{20}{l}} {\frac{\sigma }{{{E_0}}} + \frac{\sigma }{{{E_1}}}\left( {1 - {{\rm{e}}^{ - \frac{{{E_1}}}{{{\eta _1}}}t}}} \right),\sigma < {\sigma _{\rm{s}}};}\\ {\frac{\sigma }{{{E_0}}} + \frac{\sigma }{{{E_1}}}\left( {1 - {{\rm{e}}^{ - \frac{{{E_1}}}{{{\eta _1}}}t}}} \right) + \frac{{\sigma - {\sigma _{\rm{s}}}}}{{{\eta _2}}}t,\sigma \ge {\sigma _{\rm{s}}}.} \end{array}} \right. $ | (1) |
|
图 5 Nishihara模型 Fig. 5 Nishihara model |
式中:E0为虎克弹性体的弹性模量,E1和η1分别为Kelvin体中的弹性模量和黏滞系数,η2为黏塑性体中的黏滞系数,σ为蠕变应力,σs为屈服应力.
由式(1)可知,该模型能够反映材料的弹性、黏弹和黏塑等蠕变特性,适用范围较广[18].但由于其组成元件均为线性的,无法描述加速蠕变过程.故采用非线性元件替换线性元件,对Nishihara模型进行改进,见图 6.

|
图 6 改进的Nishihara模型 Fig. 6 Improved Nishihara model |
黏弹性部分由一个弹簧和一个非线性黏性元件并联组成.冻土蠕变具有明显的非线性特征,其非线性程度与荷载大小及荷载持续时间有关.为反映冻土蠕变的非线性特性,参考文献[14, 20-21]将黏滞系数修正为应力水平和流变时间的函数,即
| $ {\eta _1}\left( {t,\sigma } \right) = {\eta _{10}}\left( {\frac{{2{\sigma _0} - \sigma }}{\sigma }} \right)\frac{{{{\left( {t/{t_0}} \right)}^{1/3}}}}{{\left[ {{{\left( {t/{t_0}} \right)}^{1/3}} + 1} \right]}}. $ | (2) |
式中:σ0为相同温度和围压条件下的常规三轴抗压强度,σ为蠕变应力大小,η10为黏弹性体的初始黏滞系数,t0为流变时间参考值(h), 本试验t0=1.
式(2)对时间求导得
| $ {{\dot \eta }_1}\left( {t,\sigma } \right) = {\eta _{10}}\left( {\frac{{2{\sigma _0} - \sigma }}{\sigma }} \right)\frac{{\frac{1}{3}{{\left( {t/{t_0}} \right)}^{ - 2/3}}}}{{{{\left[ {{{\left( {t/{t_0}} \right)}^{1/3}} + 1} \right]}^2}}} \ge 0. $ | (3) |
由式(2),(3)可知,当t=0时,η1(t, σ)=0;当t→∞,σ不变时,
| $ \sigma = {E_1}\varepsilon \left( t \right) + {\eta _1}\left( {t,\sigma } \right)\frac{{{\rm{d}}\varepsilon \left( t \right)}}{{{\rm{d}}t}}. $ | (4) |
在常应力条件下对式(4)分离变量求定积分(t=0,ε(t)=0),得到非定常Kelvin体的蠕变方程为
| $ \varepsilon \left( t \right) = \frac{{{\sigma _0}}}{{{E_1}}}\left[ {1 - \exp \left( { - \alpha t - \frac{3}{2}\alpha {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right]. $ | (5) |
其中
| $ \alpha = \frac{{{E_1}}}{{{\eta _{10}}}}\left( {\frac{\sigma }{{2{\sigma _0} - \sigma }}} \right). $ | (6) |
修正后的具有非线性元件的Kelvin体可用于描述冻结砂土的衰减蠕变特性.
2.2 黏塑性部分大量研究表明[4, 23],冻土中存在损伤效应,当剪应力大于某一个临界值时,损伤效应就会出现,当损伤效应占优势时,会发生非衰减蠕变[24].通过引入损伤变量D定量描述非衰减蠕变过程中的稳定和加速蠕变阶段,基于损伤机理定义损伤变量[4, 19]
| $ D\left( {\sigma ,t} \right) = 1 - \frac{{E\left( {\sigma ,t} \right)}}{{{E_0}}}. $ | (7) |
| $ E(\sigma ,t) = \left\{ {\begin{array}{*{20}{l}} {{E_0},\sigma - {\sigma _\infty } < 0;}\\ {{E_0}{{\rm{e}}^{ - c{t^R}}},\sigma - {\sigma _\infty } \ge 0.} \end{array}} \right. $ | (8) |
| $ D(\sigma ,t) = \left\{ {\begin{array}{*{20}{l}} {0,\sigma - {\sigma _\infty } < 0;}\\ {1 - {{\rm{e}}^{ - c{t^R}}},\sigma - {\sigma _\infty } \ge 0.} \end{array}} \right. $ | (9) |
式中:D(σ, t)为损伤变量,弹性模量E(σ, t)为随时间变化的函数,E0为初始弹性模量,c,R为反映损伤程度的材料参数,σ∞为长期强度,是指稳定蠕变阶段的轴向蠕变速率为0时对应的最大剪应力.可以基于蠕变稳定阶段的速率法来确定长期强度[19],即
| $ q = {\sigma _\infty } + k\ln \left( {1 + \frac{\nu }{{{\nu _0}}}} \right). $ | (10) |
式中:q为剪切应力,k为试验参数(MPa),v为稳定阶段蠕变速率,v0为蠕变速率参考值,本试验v0=1.0.
根据有效应力定义[25]:
| $ {\sigma ^\prime } = \frac{\sigma }{{1 - D}}. $ | (11) |
| $ {\sigma ^\prime } = \left\{ {\begin{array}{*{20}{l}} {\sigma ,\sigma - {\sigma _\infty } < 0;}\\ {\sigma {{\rm{e}}^{c{t^R}}},\sigma - {\sigma _\infty } \ge 0.} \end{array}} \right. $ | (12) |
式中:σ′为有效应力,σ为蠕变应力.
采用由非定常黏性体与塑性体并联的黏塑性元件来描述冻土加速蠕变阶段的非线性特征.当σ<σ∞,塑性体不发生变形,此时,黏性体不起作用; 当σ≥σ∞时,塑性体屈服.因此,非定常黏性元件的黏滞系数可以表示
| $ {\eta _2}(t,\sigma ) = {\eta _{20}}\left[ {1 + \frac{{2{\sigma _\infty }}}{\sigma }\left( {1 - {{\rm{e}}^{ - t/{t_0}}}} \right)} \right]. $ | (13) |
η20为黏塑性元件的初始黏滞系数.
根据串联时合应变为各部分应变之和得到蠕变函数:
| $ \begin{array}{*{20}{c}} {\varepsilon = \frac{\sigma }{{{E_0}}} + \frac{\sigma }{{{E_1}}}\left[ {1 - \exp \left( { - \alpha t - \frac{3}{2}\alpha {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right],}\\ {\sigma < {\sigma _\infty },} \end{array} $ | (14) |
| $ \begin{array}{l} \varepsilon = \frac{\sigma }{{{E_0}}} + \frac{\sigma }{{{E_1}}}\left[ {1 - \exp \left( { - \alpha t - \frac{3}{2}\alpha {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\sigma ^\prime } - {\sigma _\infty }}}{{{\eta _2}\left( {t,\sigma } \right)}}t,\sigma \ge {\sigma _\infty }. \end{array} $ | (15) |
三维应力条件下,总应变可以表示为
| $ {\varepsilon _{ij}} = \varepsilon _{ij}^{\rm{e}} + \varepsilon _{ij}^{{\rm{ve}}} + \varepsilon _{ij}^{{\rm{vp}}}. $ | (16) |
根据广义虎克定律,弹性体三维本构关系为
| $ {\sigma _{kk}} = 3K{\varepsilon _{kk}},{S_{ij}} = 2G{e_{ij}}, $ | (17) |
式中:Sij、eij分别为应力偏张量和应变偏张量,σkk、εkk分别为应力张量和应变张量第一不变量,G和K分别为剪切模量和体积模量.
结合式(17),弹性体、黏弹性体和黏塑性体的应变分别为
| $ \varepsilon _{ij}^{\rm{e}} = \frac{1}{{3K}}{\sigma _{\rm{m}}}{\delta _{ij}} + \frac{{{S_{ij}}}}{{2{G_0}}}, $ | (18) |
| $ \varepsilon _{ij}^{{\rm{ve}}} = \frac{{{S_{ij}}}}{{2{G_1}}}\left[ {1 - \exp \left( { - \beta t - \frac{3}{2}\beta {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right], $ | (19) |
| $ \varepsilon _{ij}^{{\rm{vp}}} = \frac{1}{{{\eta _2}\left( {t,q} \right)}}\left[ {\varphi \left( {\frac{F}{{{F_0}}}} \right)\frac{{\partial Q}}{{\partial \sigma _{ij}^\prime }}} \right]t. $ | (20) |
将式(18)、(19)和(20)代入式(16),三维蠕变本构模型可统一表示为
| $ \begin{array}{l} {\varepsilon _{ij}} = \frac{1}{{3K}}{\sigma _{\rm{m}}}{\delta _{ij}} + \frac{{{S_{ij}}}}{{2{G_0}}} + \\ \frac{{{S_{ij}}}}{{2{G_1}}}\left[ {1 - \exp \left( { - \beta t - \frac{3}{2}\beta {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right],q < {\sigma _\infty }; \end{array} $ | (21) |
| $ \begin{array}{l} {\varepsilon _{ij}} = \frac{1}{{3K}}{\sigma _{\rm{m}}}{\delta _{ij}} + \frac{{{S_{ij}}}}{{2{G_0}}} + \\ \;\;\;\;\;\;\;\frac{{{S_{ij}}}}{{2{G_1}}}\left[ {1 - \exp \left( { - \beta t - \frac{3}{2}\beta {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right] + \\ \;\;\;\;\;\;\;\frac{1}{{{\eta _2}\left( {t,q} \right)}}\left[ {\varphi \left( {\frac{F}{{{F_0}}}} \right)\frac{{\partial Q}}{{\partial \sigma _{ij}^\prime }}} \right]t,q \ge {\sigma _\infty }. \end{array} $ | (22) |
式中:σmδij为球应力张量,G0为弹性元件的剪切模量,G0=q/3ε0,ε0为初始应变值,q为剪应力,G1为黏弹性元件的剪切模量,F为屈服函数,F0为屈服函数初始参考值,本试验F0=1,Q为塑性势函数,假设试验材料满足相关联流动法则,F=Q,φ(·)为幂函数形式,其指数符号为1,σ′ij为柯西有效应力张量.
本次试验假定应力偏量在冻土蠕变中起主要作用,因此,屈服函数表达式为[26-27]
| $ F = \sqrt {{J_2}} - \frac{{{\sigma _{\rm{s}}}}}{{\sqrt 3 }}. $ | (23) |
其中:J2为第二偏应力不变量.在常规三轴试验中,σ2=σ3,因此,
| $ {\sigma _{\rm{m}}} = \frac{1}{3}\left( {{\sigma _1} + 2{\sigma _3}} \right), $ | (24) |
| $ {S_{11}} = {\sigma _1} - {\sigma _{\rm{m}}} = \frac{2}{3}\left( {{\sigma _1} - {\sigma _3}} \right), $ | (25) |
| $ \sqrt {{J_2}} = \frac{1}{{\sqrt 3 }}\left( {{\sigma _1} - {\sigma _3}} \right). $ | (26) |
最终三维蠕变模型为
| $ \begin{array}{*{20}{c}} {{\varepsilon _1} = \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_0}}} + }\\ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}}\left[ {1 - \exp \left( { - \beta t - \frac{3}{2}\beta {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right],}\\ {q < {\sigma _\infty };} \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{\varepsilon _1} = \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_0}}} + }\\ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}}\left[ {1 - \exp \left( { - \beta t - \frac{3}{2}\beta {{\left( {t/{t_0}} \right)}^{2/3}}} \right)} \right] + }\\ {\frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}^\prime } - {\sigma _\infty }}}{{3{\eta _2}\left( {t,q} \right)}}t,q \ge {\sigma _\infty }.} \end{array} $ | (28) |
其中
| $ \beta = \frac{{{G_1}q}}{{{\eta _{10}}\left( {3{\sigma _0} - q} \right)}}, $ |
| $ {\eta _2}\left( {t,q} \right) = {\eta _{20}}\left[ {1 + \frac{{3{\sigma _\infty }}}{q}\left( {1 - {{\rm{e}}^{ - t/{t_0}}}} \right)} \right], $ |
| $ {\left( {{\sigma _1} - {\sigma _3}} \right)^\prime } = \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)}}{{1 - D}} = \left( {{\sigma _1} - {\sigma _3}} \right){{\rm{e}}^{c{t^R}}}. $ |
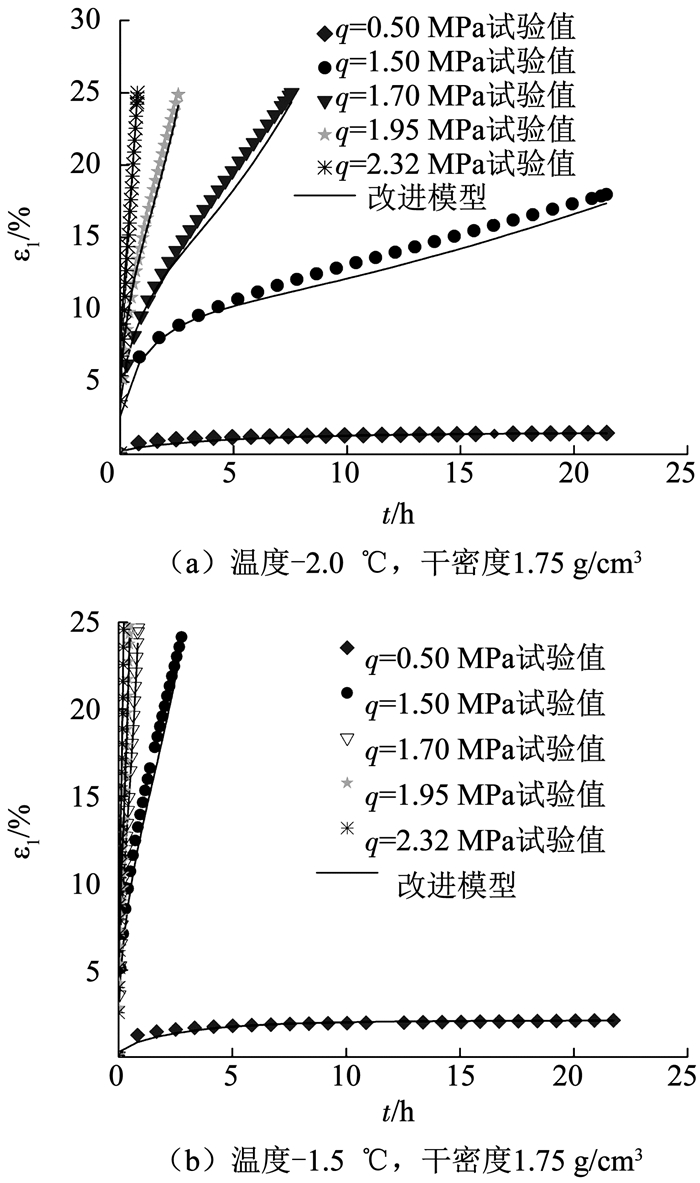
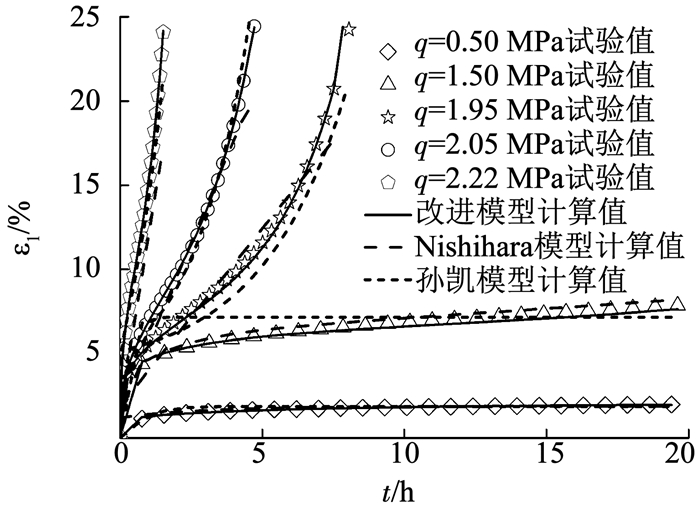
改进的模型有K、G0、G1、c、R、η10、η20共7个参数,能通过蠕变试验曲线直接测得或者回归分析获得.基于试验数据,模型参数见表 1.ρd为土样干密度,拟合曲线与试验曲线对比见图 7(仅列出部分温度条件下的参数值和拟合结果).为了验证模型的适用性,将温度为-2.0 ℃、干密度为1.92 g/cm3的冻结砂土试验结果,与Nishihara模型、孙凯等[14]建立的模型和改进模型的模拟结果绘在同一图幅内,结果见图 8.可以看出,3种模型均能够较好地描述低应力条件下冻结砂土的衰减蠕变特性,但Nishihara模型不能很好地反映非衰减蠕变过程; 孙凯等[14]建立的模型,考虑了时间对模型元件的影响,能够描述加速蠕变过程,与孙凯等[14]建立的模型相比,改进模型考虑了时间和应力对模型元件的耦合影响,不仅能描述衰减和稳态蠕变过程,还能反映加速蠕变特征,拟合精度也要高于Nishihara模型和孙凯等[14]建立的模型.由图 7, 8可知,改进模型拟合精度较高,数据吻合良好,表明该模型能较好地描述不同温度和剪应力条件下冻结砂土的蠕变过程.
| 表 1 改进蠕变模型参数 Tab. 1 Parameters ofthe improved creep model |
|
图 7 试验曲线和改进模型拟合曲线对比 Fig. 7 Comparison of testing curves and fitting curves of the improved creep model |
|
图 8 3种模型计算值 Fig. 8 Results predicted by three different models |
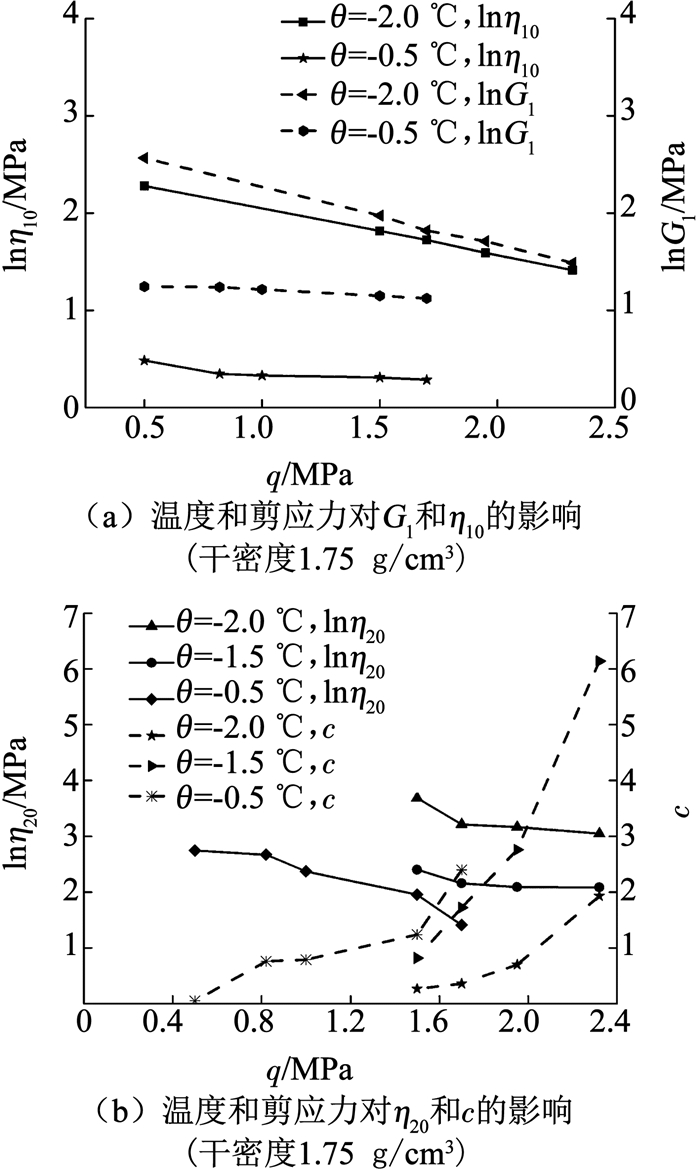
温度和剪应力对模型参数的影响见图 9,可以看出,改进模型中黏弹性元件的黏滞系数η10、剪切模量G1和黏塑性元件的黏滞系数η20均随着温度降低而增大,随应力水平增大而减小,损伤变量参数c随温度降低而减小,随应力水平增大而增大.
|
图 9 参数随温度和剪应力q变化 Fig. 9 Relationship between the parameters and temperatures under different q |
为厘清温度、剪应力与模型参数的关系以及为不同温度、剪应力下模型参数的确定提供参考,回归分析得到模型参数与剪应力q、温度θ的函数关系:
| $ \begin{array}{*{20}{c}} {\ln {G_1} = {A_1} + {A_2}q,}\\ {\ln {\eta _{10}} = {B_1} + {B_2}q.} \end{array} $ | (29) |
其中
| $ {A_1} = 0.84 - 1.035\theta ,R = 0.9878, $ |
| $ {A_2} = - 0.715 - 0.306{\theta ^{ - 1}},R = 0.9378, $ |
| $ {B_1} = - 0.242 - 1.369\theta ,R = 0.9786, $ |
| $ {B_2} = {\left( {79.775 + 67.83\theta } \right)^{ - 1}},R = 0.8040. $ |
| $ c = {C_1} + {C_2}q + {C_3}{q^3}, $ |
| $ R = {D_1} + {D_2}q + {D_3}{q^3}. $ | (30) |
其中
| $ {C_1} = - 1.805 - 2.944\theta ,R = 0.9486, $ |
| $ {C_2} = 2.345 + 3.207\theta ,R = 0.9052, $ |
| $ {C_3} = 3.039 + 9.563\theta + 9.338{\theta ^2} + 2.598{\theta ^3},R = 0.9945, $ |
| $ {D_1} = \frac{{ - 0.077\theta }}{{1 + 0.694\theta }},R = 0.9626, $ |
| $ {D_2} = \frac{{0.193 + 0.211\theta }}{{1 + 0.698\theta }},R = 0.9384, $ |
| $ {D_3} = {\left( {14.828 + 16.755{\theta ^3}} \right)^{ - 1}},R = 0.8964. $ |
| $ \ln {\eta _{20}} = {N_1} + {N_2}q, $ |
| $ \ln K = {W_1} + {W_2}q. $ | (E31) |
其中
| $ {N_1} = \frac{{2.663 - 2.792{\theta ^2}}}{{1 - 0.81{\theta ^2}}},R = 0.9224, $ |
| $ {N_2} = 0.023{\left( {1.195 + \theta } \right)^{ - 1}},R = 0.9761, $ |
| $ {W_1} = 4.247 + 0.613{\theta ^{ - 1}},R = 0.9623, $ |
| $ {W_2} = \frac{{ - 1.186 - 0.935\theta }}{{1 + 0.802\theta }},R = 0.9049. $ |
1) 试验表明温度对冻结砂土的蠕变特性影响显著,尤其当温度高于-1.5 ℃时,即使在很小的荷载作用下也能产生明显的蠕变变形.
2) 以Nishihara模型为基础,将黏弹性元件中定常的黏滞系数修正为时间和剪切应力的函数,在黏塑性元件中引入损伤变量D,来描述非衰减蠕变的稳定和加速蠕变阶段,建立了冻结砂土弹黏塑性蠕变模型.该模型能较好地描述不同温度、应力水平下冻结砂土的衰减、稳态和加速蠕变特性.拟合结果与试验数据吻合较好.
3) 改进模型中黏弹性元件的黏滞系数、剪切模量和黏塑性元件的黏滞系数均随着应力水平增大而减小,随温度降低而增大.损伤变量随着应力水平增大而增大,随温度降低而减小.本研究可为冻土蠕变理论研究积累资料.
| [1] |
马巍, 王大雁. 冻土力学[M]. 北京: 科学出版社, 2014. MA Wei, WANG Dayan. Permafrost mechanics[M]. Beijing: Science Press, 2014. |
| [2] |
朱占元, 李静, 邹祖银, 等. 动力荷载作用下冻土变形特性研究[J]. 低温建筑技术, 2008, 30(2): 112. ZHU Zhanyuan, LI Jing, ZOU Zuyin, et al. Study on deformation characters of frozen soil under long-term dynamic loading[J]. Low Temperature Architecture Technology, 2008, 30(2): 112. DOI:10.3969/j.issn.1001-6864.2008.02.048 |
| [3] |
李林. 高原多年冻土路基沉降整治[J]. 铁道建筑技术, 2013(1): 90. LI Lin. Plateau permafrost subgrade settlement remediation[J]. Railway Construction Technology, 2013(1): 90. DOI:10.3969/j.issn.1009-4539.2013.01.025 |
| [4] |
YANG Yugui, LAI Yuanming, CHANG Xiaoxiao. Experimental and theoretical studies on the creep behavior of warm ice-rich frozen sand[J]. Cold Regions Science and Technology, 2010, 63: 61. DOI:10.1016/j.coldregions.2010.04.011 |
| [5] |
ANDERSLAND O B, LADANYI B. Frozen ground engineering[M]. New York: Chapman & Hall, 2003.
|
| [6] |
吴紫汪, 马巍, 蒲毅彬, 等. 冻土蠕变变形特征的细观分析[J]. 岩土工程学报, 1997, 19(3): 4. WU Ziwang, MA Wei, PU Yibin, et al. Submicroscopic analysis on deformation characteristics in creep process of frozen soil[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(3): 4. |
| [7] |
LⅡNGAARD M, AUGUSTESEN A, LADE P V. Characterization of models for time-dependent behavior of soils[J]. International Journal of Geomechanics, 2004, 4(3): 157. DOI:10.1061/(ASCE)1532-3641(2004)4:3(157) |
| [8] |
BRAY M T. Secondary creep approximations of ice-rich soils and ice using transient relaxation tests[J]. Cold Regions Science and Technology, 2013, 88(2): 17. DOI:10.1016/j.coldregions.2012.12.011 |
| [9] |
ARENSON L U, SPRINGMAN S M. Mathematical descriptions for the behavior of ice-rich frozen soils at temperatures close to 0℃[J]. Canadian Geotechnical Journal, 2005, 42(2): 431. DOI:10.1139/t04-109 |
| [10] |
ZHOU Zhiwei, MA Wei, ZHANG Shujuan, et al. Multiaxial creep of frozen loess[J]. Mechanics of Materials, 2016, 95: 172. DOI:10.1016/j.mechmat.2015.11.020 |
| [11] |
朱元林, 何平, 张家懿, 等. 冻土在振动荷载作用下的三轴蠕变模型[J]. 自然科学进展:国家重点实验室通讯, 1998, 8(1): 60. ZHU Yuanlin, HE Ping, ZHANG Jiayi, et al. Triaxial creep model of frozen soil under vibratory load[J]. Progress in Natural Science, 1998, 8(1): 60. DOI:10.1088/0256-307X/15/12/010 |
| [12] |
杨圣奇, 徐鹏. 一种新的岩石非线性流变损伤模型研究[J]. 岩土工程学报, 2014, 36(10): 1847. |
| [13] |
康永刚, 张秀娥. 一种改进的岩石蠕变本构模型[J]. 岩土力学, 2014, 35(4): 1049. KANG Yonggang, ZHANG Xiue. An improved constitutive model for rock creep[J]. Rock and Soil Mechanics, 2014, 35(4): 1049. |
| [14] |
孙凯, 陈正林, 陈剑, 等. 一种基于修正西原模型的冻土蠕变本构关系[J]. 岩土力学, 2015, 36(增刊1): 142. SUN Kai, CHEN Zhenglin, CHEN Jian, et al. A modified creep constitutive equation for frozen soil based on Nishihara model[J]. Rock and Soil Mechanics, 2015, 36(S1): 142. |
| [15] |
ZHAO Xiaodong, ZHOU Guoqing, CHEN Guozhou. Triaxial compression strength for artificial frozen clay with thermal gradient[J]. Journal of Central South University of Technology, 2013, 20(1): 218. DOI:10.1007/s11771-013-1479-x |
| [16] |
赵延林, 唐劲舟, 付成成, 等. 岩石黏弹塑性应变分离的流变试验与蠕变损伤模型[J]. 岩石力学与工程学报, 2016, 35(7): 1297. ZHAO Yanlin, TANG Jinzhou, FU Chengcheng, et al. Rheological test of separation between viscoelastic-plastic strains and creep damage model[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1297. |
| [17] |
LI Dongwei, FAN Juhong, WANG Renhe. Research on visco-elastic-plastic creep model of artificially frozen soil under high confining pressures[J]. Cold Regions Science and Technology, 2011, 64: 219. DOI:10.1016/j.coldregions.2010.08.006 |
| [18] |
孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999. SUN Jun. Geotechnical material rheological and its engineering application[M]. Beijing: China Architecture and Building Press, 1999. |
| [19] |
HOU Feng, LAI Yuanming, LIU Enlong, et al. A creep constitutive model for frozen soils with different contents of coarse grains[J]. Cold Regions Science and Technology, 2018, 145: 119. DOI:10.1016/j.coldregions.2017.10.013 |
| [20] |
孙钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报, 2007, 26(6): 1081. SUN Jun. Rock rheological mechanics and its advance in engineering applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081. DOI:10.3321/j.issn:1000-6915.2007.06.001 |
| [21] |
赵延林, 曹平, 文有道, 等. 岩石弹黏塑性流变试验和非线性流变模型研究[J]. 岩石力学与工程学报, 2008, 27(3): 477. ZHAO Yanlin, CAO Ping, WEN Youdao, et al. Elastovisco-plastic rheological experiment and nonlinear rheological model of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 477. DOI:10.3321/j.issn:1000-6915.2008.03.006 |
| [22] |
阎岩, 王思敬, 王恩志. 基于西原模型的变参数蠕变方程[J]. 岩土力学, 2010, 31(10): 3025. YAN Yan, WANG Sijing, WANG Enzhi. Creep equation of variable parameters based on Nishihara model[J]. Rock and Soil Mechanics, 2010, 31(10): 3025. DOI:10.3969/j.issn.1000-7598.2010.10.001 |
| [23] |
LI Xiang, CAO Wengui, SU Yonghua. A statistical damage constitutive model for softening behavior of rocks[J]. Engineering Geology, 2012, 143/144: 1. DOI:10.1016/j.enggeo.2012.05.005 |
| [24] |
C.C维亚洛夫.冻土流变学[M].刘建坤, 刘尧军, 徐艳, 译.北京: 中国铁道出版社, 2005 ВЯЛОВ С С. Rheology of frozen soil[M]. LIU Jiankun, LIU Yaojun, XU Yan, translate. Beijing: China Railway Publishing House, 2005 |
| [25] |
KACHANOV L M. Introduction to continuum damage mechanics[M]. Dordrecht, Netherlands: Martinus Nijhoff Publishers, 1986
|
| [26] |
齐亚静, 姜清辉, 王志俭, 等. 改进西原模型的三维蠕变本构方程及其参数辨识[J]. 岩石力学与工程学报, 2012, 31(2): 347. QI Yajing, JIANG Qinghui, WANG Zhijian, et al. 3D creep constitutive equation of modified Nishihara model and its parameters identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 347. DOI:10.3969/j.issn.1000-6915.2012.02.014 |
| [27] |
余启华. 岩石的流变破坏过程及有限元分析[J]. 水利学报, 1985, 6(1): 55. YU Qihua. Rheological failure process of rock and finite element analysis[J]. Journal of Hydraulic Engineering, 1985, 6(1): 55. DOI:10.3321/j.issn:0559-9350.1985.01.007 |
 2020, Vol. 52
2020, Vol. 52


