2. 武汉大学 土木建筑工程学院, 武汉 430072
2. School of Civil Engineering, Wuhan University, Wuhan 430072, China
土石混合体边坡成因多样,分布广泛.随着中国社会经济的不断发展,越来越多的水利水电工程、高速公路和高速铁路工程都不可避免地要涉及到土石混合体边坡.土石混合体边坡极易引发滑坡等地质灾害,三峡库区、攀西地区等地发生的滑坡中土石混合体滑坡占相当大的比例.此类滑坡影响因素众多、规模较大、突发性强,严重影响了国民经济建设和人民正常生活,造成了大量的人民生命和财产损失[1-2].因此,有必要对土石混合体边坡的变形破坏和稳定性开展专门的研究.
近十几年来,研究者通过不同手段对土石混合体边坡的稳定性进行了研究,主要包括物理模型试验[3-6]和数值模拟等.其中,数值模拟主要有基于连续介质理论的有限元法、有限差分法和基于非连续模型的离散元法.目前,有限元法和有限差分法在土石混合体边坡稳定性分析中已获得了一定的应用,根据其数值模型的不同可以分为两种:一种方法是将土石混合体边坡当作等效均质体来进行分析; 另一种方法是考虑土石混合体的细观结构特征,建立土石混合体边坡的非均质细观结构模型,分别给土体基质和块石赋对应的强度变形参数,进而进行稳定性分析.
油新华等[1]对土石混合体边坡分别采用均质模型和非均质细观结构模型进行了对比分析,结果表明,两者的临界坡度、最大位移等都有显著差异,并指出对于具有一定含石量的土石混合体边坡应当考虑其非均质结构的影响.徐文杰等[7]对西南地区某一土石混合体边坡采用数字图像处理技术建立其二维细观结构模型,并运用有限元强度折减法开展了稳定性分析.李亮等[8-10]建立了土石混合体边坡的二维随机细观结构模型,研究了块石含量、块石空间分布、土-石接触面参数等对土石混合体边坡稳定性的影响.
基于连续介质理论的有限元法和有限差分法仍存在一些不足,如常作为失稳判别标准的计算结果发散也有可能是计算网格的质量不好或网格发生大变形,并不一定都是由贯穿性破坏引起.另一方面,即使形成贯穿性破坏也并不能说明最终会产生滑坡灾害,即有限元法很难进一步描述失稳破坏后边坡的离散性破坏和运动破坏等问题[11].而基于非连续模型的离散元法则能有效地克服这些困难.近十几年来,颗粒离散单元法因其特有的优势而被越来越多的学者应用于边坡稳定性分析中,特别是在边坡破坏机理研究方面取得了较大的成功[12-15].
综上,考虑土石混合体非均质、非连续的细观结构特征并采用颗粒离散元法进行分析应是研究土石混合体边坡稳定性和破坏机理更为有效的手段.截至目前,该方面研究成果仍鲜有报道.为此,在已提出的不规则块石和土石混合体三维离散元建模方法的基础上,进一步运用土工离心模型试验基本原理构建土石混合体边坡细观机构的三维离散元模型; 引入颗粒流强度折减法并提出基于能量演化的方法来判别边坡的失稳破坏; 分析不同块石含量、块石形状、空间结构、空间形态等因素对土石混合体边坡稳定性和破坏模式的影响,并揭示这些因素影响的细观机理.
1 土石混合体边坡的三维离散元模型土石混合体内部的块石含量、形状、空间分布等细观结构特征对其力学特性都有不同程度的影响.因此,要对土石混合体边坡的稳定性进行分析,首要条件是要建立合理的土石混合体边坡细观结构模型.
自然界中的土石混合体边坡往往规模较大、地质条件复杂、内部结构变异性大,受目前技术条件的限制很难针对某一具体的土石混合体边坡建立其真实的三维细观结构模型.这里暂且采用简单的理想边坡形态,建立块石均匀随机分布的土石混合体边坡三维离散元模型,以便进行机理性研究.
目前,边坡离散元模型常用的建模方法是先在一定的区域生成疏松的颗粒集合体并让其在重力作用下下落到模型区域并平衡,以此便可获得初始场地,然后根据边坡形状削去多余的颗粒形成边坡并再进行一次平衡.在建模过程中,一个关键问题就是如何达到计算效率与计算精度间的平衡.由于实际边坡尺度较大,若要直接采用实际的边坡尺寸和颗粒大小,模型的颗粒数量将达到几百万甚至更多,目前的计算机容量和速度远远不能满足要求.为了解决这个问题,目前常用的方法有3种:①边坡尺寸不变,将颗粒的尺寸进行放大[13, 15]; ②边坡尺寸不变,坡体内部采用大粒径颗粒而潜在破坏面附近采用小粒径颗粒,即所谓的变粒径法[12]; ③基于土工离心模型试验的基本原理,将边坡进行缩尺处理,同时施加考虑相似比的重力加速度[14].采用这些方法建立的边坡模型虽与原型边坡有一定差异,但只要颗粒数量不是很少,就已能满足机理性研究的需要.
本文采用上述第③种边坡离散元建模方法,即基于离心模型试验的基本原理将边坡模型进行缩尺处理.需要特别说明的是土石混合体细观结构具有相对性,不同尺寸的土石混合体边坡中土-石阈值也不同,这样经缩尺的土石混合体边坡模型中块石和土颗粒的粒径也应相应减小[16].为了将文献[17]中已建立的不规则块石三维离散元模型与通过大型三轴试验离散元模拟所标定的块石和土颗粒的细观力学参数(表 1)直接应用于土石混合体边坡数值模型中,相应边坡模型的高度即土石混合体边坡问题的特征工程尺度可与大型三轴试验的试样直径取相同值,即取为0.3 m.重力加速度取50g,因而对应的原型边坡高度为15 m,这在土石混合体边坡中具有一定的代表性.
| 表 1 土石混合体边坡模型的细观力学参数 Tab. 1 Meso-mechanical parameters of SRM slope |
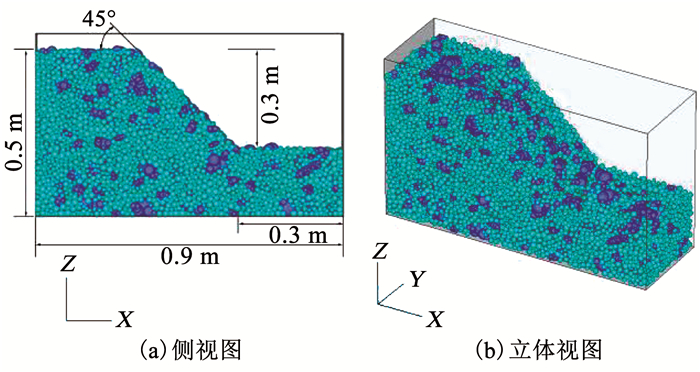
采用文献[17]中提出的土石混合体大型三轴试样离散元建模方法即可生成土石混合体边坡的三维离散元细观结构模型,只要将模型形状稍作改变.图 1示出了含石量为40%(质量分数,下同)的土石混合体边坡细观结构三维离散元模型,其中浅蓝色颗粒仍表示块石颗粒,土颗粒为青色.模型底部和侧面边界均采用平面墙模拟,为了减小模型边界的影响,边界墙均无摩擦且模型各方向上都进行了一定的延拓,厚度即Y方向长为0.3 m,模型截面具体尺寸如图所示.图中坐标轴反映了模型的方位,后文相关的模型侧视图和立体视图方位与此一致.
|
图 1 土石混合体边坡的三维离散元模型(含石量为40%) Fig. 1 3-D DEM model of SRM slope with 40% rock blocks by mass |
周健等[13]将强度折减法引入砂性土坡和黏性土坡的稳定性PFC2D分析中,形成了颗粒流强度折减法.具体方法是:对颗粒细观摩擦系数和颗粒间黏结强度进行逐步折减,直到刚使边坡破坏时的折减系数就是边坡的安全系数.采用颗粒流强度折减法确定边坡安全系数的关键问题是边坡失稳破坏的判断标准.周健等[13]提出采用累积位移或不平衡力来作为边坡失稳破坏的判断标准,但并未给出具体的临界累积位移值,且经笔者测试发现采用不平衡力作为判断标准也不完全可靠.
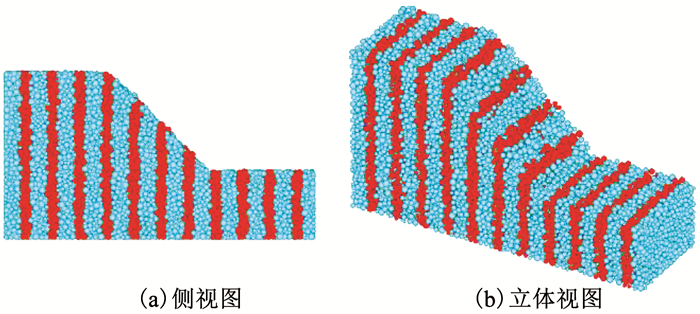
本文土石混合体边坡的稳定性分析也采用颗粒流强度折减法进行,鉴于已有的边坡失稳判断标准仍不够明确,这里提出一种基于能量演化的判断方法.本节就以含石量为0的土石混合体即均质土体边坡模型为例来说明具体的判断方法.为了便于观察边坡的变形情况,在边坡模型中每隔一定距离设置一定宽度的深色竖向条带,生成的初始均质土体边坡模型如图 2所示,模型尺寸与图 1所示模型相同.细观力学参数取表 1中土颗粒参数.

|
图 2 均质土体边坡初始数值模型 Fig. 2 Initial numerical model of homogeneous soil slope |
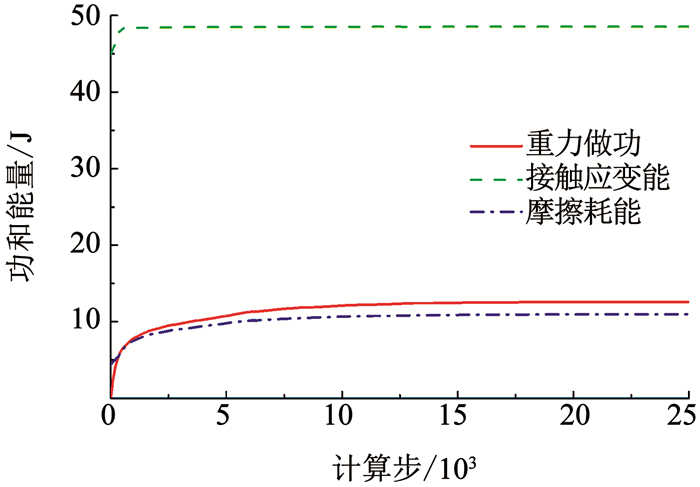
图 3给出了模型中土颗粒细观摩擦系数折减1.1倍后计算过程中重力做功、颗粒接触应变能和摩擦耗能的演化情况.图 4示出了计算停止时(强度折减后计算了28 500步)的均质土体边坡模型.

|
图 3 细观摩擦系数折减1.1倍后边坡模型能量演化 Fig. 3 Energy evolution of the soil slope model after reduction of the friction coefficient by 1.1 times |
|
图 4 细观摩擦系数折减1.1倍后边坡模型 Fig. 4 Soil slope model after reduction of the friction coefficient by 1.1 times |
由图 3可知,当将土颗粒细观摩擦系数折减1.1倍后,在重力作用下颗粒之间由于摩擦阻力降低将产生一定的错动,模型发生一定程度的压密,所以,重力做功、摩擦耗能和颗粒接触应变能均有少量的增长.但增长过程很快逐渐停止,随后便不再发生变化,且最终的重力做功和摩擦耗能都很小,均低于颗粒接触应变能,说明模型已经重新回到静止状态.
由图 4可以看出,稳定后的边坡模型中深色条带在竖向和水平向均未发生明显变形,只有坡面上极少数颗粒发生了少许滑动,这表明边坡并未发生整体的失稳滑动.
作为对比,图 5给出了模型中土颗粒细观摩擦系数折减2.0倍后计算过程中重力做功、颗粒接触应变能和摩擦耗能的演化情况.图 6示出了计算停止时(强度折减后计算了49 900步)的均质土体边坡模型.

|
图 5 细观摩擦系数折减2.0倍后边坡模型能量演化 Fig. 5 Energy evolution of the soil slope model after reduction of the friction coefficient by 2.0 times |

|
图 6 细观摩擦系数折减2.0倍后边坡模型 Fig. 6 Soil slope model after reduction of the friction coefficient by 2.0 times |
由图 5可知,当将土颗粒细观摩擦系数折减2.0倍后,初始压密过程中重力做功、颗粒接触应变能和摩擦耗能都有一定的增长,这之后接触应变能便不再增长,而重力做功和摩擦耗能超过颗粒接触应变能且仍保持一定速率继续增长.
由图 6可以看出,此时边坡模型中的深色条带在竖向和水平向上均发生了明显的错动,形成了从坡肩到坡脚的浅层滑动面,且滑体上的深色颗粒与其他颗粒混杂在了一起,呈现出典型的无黏性土坡上部材料离散下滑的塑性流动破坏特征[18].
图 7示出了均质土体边坡模型在土颗粒细观摩擦系数折减1.1和2.0后计算停止时的位移场侧视图.可以看出,细观摩擦系数折减1.1倍后颗粒并未发生明显滑动,边坡未形成滑动面; 而细观摩擦系数折减2.0倍后浅部颗粒沿坡面向下发生了明显的滑动,边坡中也形成了近直线型的滑动面.

|
图 7 颗粒细观摩擦系数折减后边坡模型的位移场 Fig. 7 Particle displacement distribution of the soil slope model after reduction of the friction coefficient |
通过以上对比分析,提出一种基于能量演化的边坡离散元模型失稳滑动的判断方法:若边坡模型在强度折减后的初始压密过程后很快就达到静止状态,且最终的重力做功和摩擦耗能都很小,均低于颗粒接触应变能,则该强度折减系数下边坡是稳定的; 反之,若重力做功和摩擦耗能超过颗粒接触应变能且保持一定速率持续增长,则该强度折减系数下边坡失稳.
上述能量演化判断方法中提到以颗粒接触应变能为对比的基准,但颗粒细观摩擦系数折减后对接触应变能也有一定影响.对上述模型折减1.1倍后,颗粒接触应变能从45.1 J增加到46.3 J,增长2.66%;折减2.0倍后增加到51.0 J,增长13.1%.故接触应变能只有少许增长,且该过程很短暂,其后无论模型是否失稳滑动都保持稳定.然而,重力做功和摩擦耗能在稳定和失稳时量值上的差异是非常显著的,另外一个重要的方面是要观察重力做功和摩擦耗能的变化趋势,稳定时其表现为压密后随即保持不变,而失稳滑动时其在初始压密后仍保持较长时间的持续增长.因此,可以认为由于细观摩擦系数折减引起接触应变能的变化并不影响上述判断方法的实施.
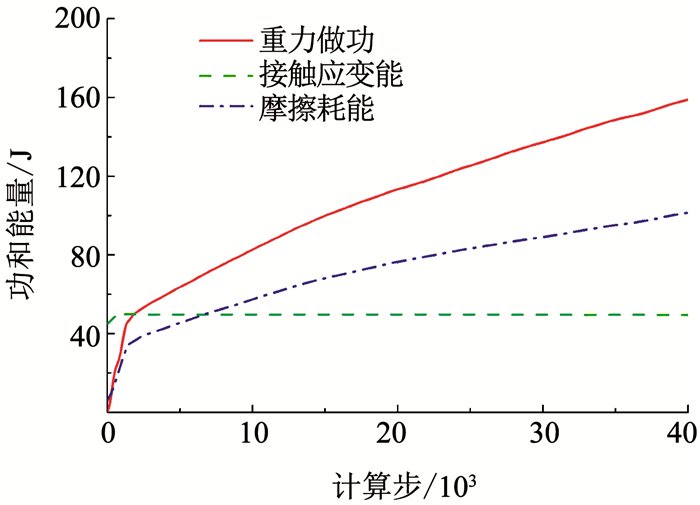
按照上述方法确定的该均质土体边坡的安全系数为1.2,细观摩擦系数折减1.2和1.3倍时对应的能量演化曲线分别如图 8,9所示.用简化Bishop法计算的安全系数为1.157,也表现为从坡肩到坡脚的浅层滑动,如图 10所示.这也进一步证明了提出的边坡稳定性颗粒流分析方法是可行的.
|
图 8 细观摩擦系数折减1.2倍后边坡模型能量演化 Fig. 8 Energy evolution of the soil slope model after reduction of the friction coefficient by 1.2 times |
|
图 9 细观摩擦系数折减1.3倍后边坡模型能量演化 Fig. 9 Energy evolution of the soil slope model after reduction of the friction coefficient by 1.3 times |

|
图 10 用简化Bishop法计算的土坡安全系数 Fig. 10 Safety factor calculated by simplified Bishop method |
有了上述边坡三维离散元建模方法和稳定性分析方法,就可以进一步研究块石含量等因素对土石混合体边坡稳定性的影响.考虑块石含量分别为0,40%和70%的土石混合体边坡,块石形状为碎石,块石位置和方向随机,模型尺寸同图 1,细观力学参数同表 1.图 11为各含石量的土石混合体边坡数值模型初始稳定状态下中间断面上的接触力分布图.

|
图 11 土石混合体边坡数值模型初始稳定状态下中间断面上的接触力分布 Fig. 11 Contact force distribution on the intermediate sections of SRM slope numerical models in the initial steady state |
观察图 11可知:
1) 各含石量土石混合体边坡初始稳定状态下的接触力分布呈现一些共同的特征,如接触力从坡面到坡体内部逐渐增大; 坡面附近的主力链方向近似平行于坡面; 坡体内部左侧部分的主力链主要沿竖直方向; 而靠近右侧边界部分的主力链主要沿水平方向分布.这些特征在均质土体边坡中表现得较为显著.
2) 相比均质土体边坡,土石混合体边坡的接触力分布很不均匀,在土-石界面及块石与块石的接触处有明显的应力集中现象.
3) 含石量为40%的土石混合体边坡为骨架-悬浮结构,重力由块石和土体共同承担.
4) 含石量为70%的土石混合体边坡为骨架-空隙结构,重力主要由块石相接触形成的骨架承担.
已有研究成果表明剪切带(滑动带)内的颗粒旋转量明显大于模型中其他区域,通过颗粒旋转图可以直观地表现出模型中变形局部化和剪切带的特征[19-20].为此,将各含石量的土石混合体边坡失稳滑动后中间断面上的颗粒旋转图绘于图 10,这里给出的是颗粒旋转量的Y分量.
观察图 12可知:

|
图 12 土石混合体边坡失稳滑动后中间断面上的颗粒旋转图(Y分量) Fig. 12 Particle rotations on the intermediate sections of SRM slope numerical models after sliding (Y component) |
1) 各含石量土石混合体边坡失稳后都表现为上部浅层颗粒的顺坡向下滑动.
2) 均质土体边坡的滑动面比较规则,近似为直线型,滑动部分在中下部较顶部的要深,模型其他部分受浅部颗粒滑塌的影响很小.
3) 含石量为40%和70%的土石混合体边坡中呈现出多滑动面现象,且滑面较为曲折具有明显的绕石特征,坡脚部位的部分大块石使得剪出口的位置发生了明显的改变,坡面上部滑体较深而下部较浅.这与龚健等[6]室内物理模型试验及徐文杰等[7-9]有限元和有限差分模拟得出的结果是一致的.
4) 土石混合体边坡失稳滑动后的坡体内部左侧和右侧坡底部位的部分颗粒也有明显旋转,这说明浅部块石骨架结构的滑塌对坡体其他部位产生了一定的影响,这在含石量为70%的土石混合体边坡中表现得尤为显著.
对于不同含石量土石混合体边坡的稳定性,可应用颗粒流强度折减法进行分析,具体实施时本文采取的方法是将土颗粒与块石颗粒细观摩擦系数同时折减,且它们的折减系数相同.分析的结果是含石量为0,40%和70%的土石混合体边坡的安全系数分别为1.2,1.5和1.6.因此,随含石量增加,土石混合体边坡的稳定性逐渐提高,这与张森等[9]有限元模拟所得基本规律是一致的.
含石量为40%的土石混合体边坡由于较多大块石的存在使得其安全系数较均质土体边坡的提高幅度达25%.因此,一定含量大块石的存在将显著影响土石混合体边坡的应力分布和失稳破坏模式,进而影响土石混合体边坡的稳定性.
4 土石混合体边坡的块石形状效应为研究块石形状对土石混合体边坡稳定性的影响,在节3中含石量为40%、块石形状为碎石的土石混合体边坡模型的基础上,进一步考虑块石形状为卵石和球体2种情况.碎石和卵石是自然界中两种常见形状的块石颗粒,增加块石为球体的情形是因为颗粒离散元计算中的基本单元为球体.图 13即为3种不同块石形状的土石混合体边坡模型,为直观起见,这里给出的是中间断面图.图 13中还示意了各模型中块石和土颗粒的形状,其中土颗粒均由相切的两个小球模拟,碎石由随机不规则颗粒模拟,卵石用椭球体颗粒模拟.

|
图 13 不同块石形状的土石混合体边坡模型 Fig. 13 SRM slope models with different rock block shapes |
应用颗粒流强度折减法对不同块石形状的土石混合体边坡模型的稳定性进行计算,求得块石为碎石、卵石和球体时边坡的安全系数分别为1.5,1.4和1.2.为探究块石形状对边坡稳定性影响的细观机理,通过PFC3D内嵌的Fish语言编程实现了数值模型中颗粒(块石和土体颗粒均设置为Clump)平均旋转量的计算和监测,平均旋转量指的是各颗粒旋转量绝对值的平均值,由3个分量组成,分别对应了颗粒相对于其质心绕3个坐标轴的旋转量.颗粒平均旋转量的大小反映了模型中颗粒之间抗转动的能力,因此,可在一定程度上反映颗粒之间相互嵌入咬合的强弱.
图 14为块石为碎石的土石混合体边坡模型在细观摩擦系数折减2.0倍后颗粒平均旋转量的变化.可以看出,平均旋转量的3个分量都随计算步增加而逐渐增长; Z分量最小即水平面内的转动要难一些; 竖直面内的2个分量也有明显区别,表现为Y分量明显比X分量大,原因是边坡失稳时颗粒主要是沿坡面向下运动(垂直于Y轴).块石为卵石和球体的土石混合体模型中3个分量的平均旋转量变化规律与图 14基本相同,这里不再给出.

|
图 14 土石混合体边坡中颗粒平均旋转量的变化(块石为碎石) Fig. 14 Particle mean rotations of SRM slope model after sliding versus step number (gravel rock blocks) |
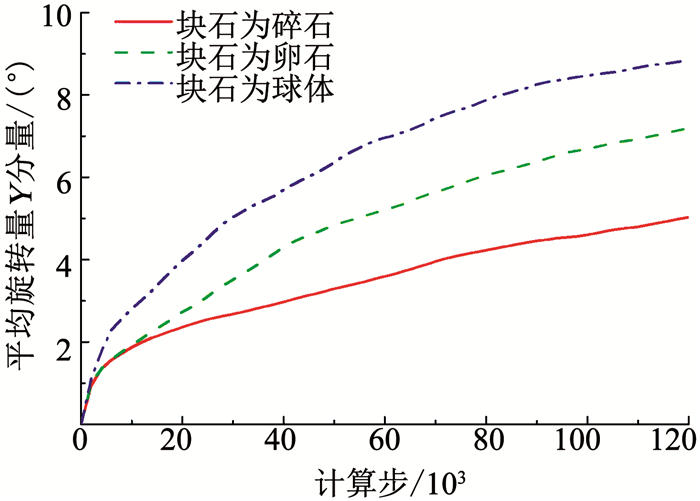
图 15为不同块石形状土石混合体边坡模型当细观摩擦系数折减2.0倍后颗粒平均旋转量Y分量的变化,X、Z分量变化规律与Y分量基本相同.可以看出,随着块石形状由球体、卵石到碎石,边坡中颗粒的平均旋转量依次减小,且随着计算步的增加三者之间的差异越来越大.
|
图 15 不同块石形状条件下土石混合体边坡中颗粒平均旋转量的变化(Y分量) Fig. 15 Particle mean rotations of SRM slope models with different rock block shapes versus step number after sliding (Y component) |
含石量为40%的土石混合体中既有土颗粒与块石颗粒间的接触,又有块石颗粒与块石颗粒间的接触.当块石为球体时,球体间为点接触,接触力法向分量通过球心,因而无法形成抗转动力矩,易发生相互滑动和旋转,故其平均旋转量较大,对应的边坡稳定性最差.而当块石为碎石时,其表面凹凸不平,在重力作用下能有效地相互嵌入咬合,故其平均旋转量较小,对应的边坡稳定性最好.
此外,值得注意的是,块石形状为球体时,含石量为40%的边坡模型与相应均质土体边坡的安全系数相同.这主要是因为含石量增加会使边坡安全系数增大,但此时块石形状较土颗粒更规则,这又使得边坡安全系数降低,在本文中综合作用的效果是安全系数保持不变.
5 土石混合体边坡的空间结构效应土石混合体边坡按空间结构可以分成一元结构和二元结构.一元结构边坡指的是整个坡体都是由土石混合体组成,边坡的特性取决于土石混合体自身的特性; 二元结构边坡是由下部基岩和上覆土石混合堆积体所构成,它的特性除了与土石混合体自身的性质有关外,还与下部基岩面的产状和基-覆界面的强度有关[1].前文分析的对象都是一元结构土石混合体边坡,本节针对二元结构土石混合体边坡中不同覆盖层厚度下边坡的破坏模式进行简要的分析.
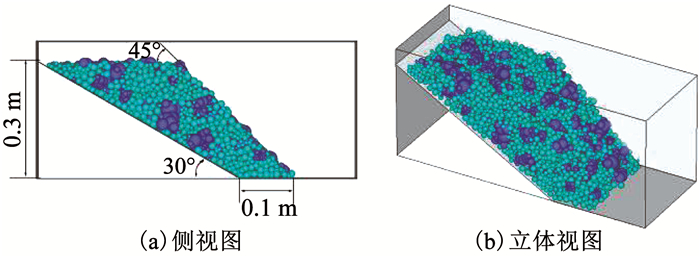
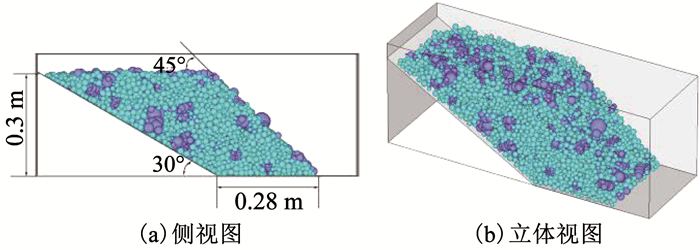
以含石量为40%的土石混合体边坡为例,分别考虑上覆土石混合体较薄和较厚两种情况,模型其他条件保持相同:基-覆界面为平面,其倾角为30°,坡面倾角为45°,坡高为0.3 m,厚度即Y方向长仍为0.3 m,重力加速度为50g.由于基岩一般强度很高,暂不考虑其变形破坏,直接采用平面墙来模拟基-覆界面,其刚度和摩擦系数与块石颗粒取相同值.两种覆盖层厚度的土石混合体二元结构边坡数值模型如图 16,17所示.
|
图 16 较薄上覆土石混合体的二元结构边坡模型 Fig. 16 Dual structural slope model with a thin SRM |
|
图 17 较厚上覆土石混合体的二元结构边坡模型 Fig. 17 Dual structural slope model with a thick SRM |
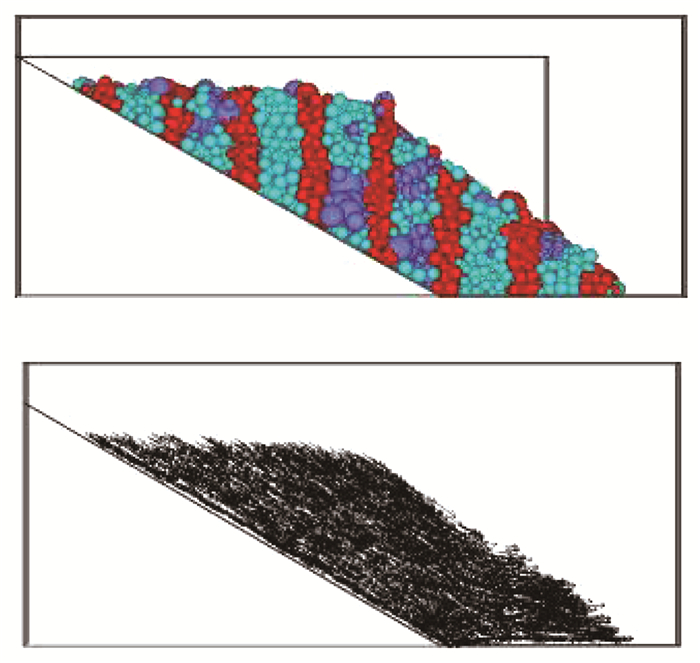
图 18,19为两种覆盖层厚度的土石混合体二元结构边坡模型在颗粒细观摩擦系数折减后失稳滑动的深色条带变形情况及颗粒位移场,为了更直观地反映上覆土石混合堆积体的滑移情况,分别在初始状态时的坡顶和坡脚处加了一个水平面和一个竖直面作为参考,图中显示的均为侧视图.
|
图 18 较薄上覆土石混合体边坡模型的破坏模式 Fig. 18 Failure mode of dual structural slope model with a thin SRM |
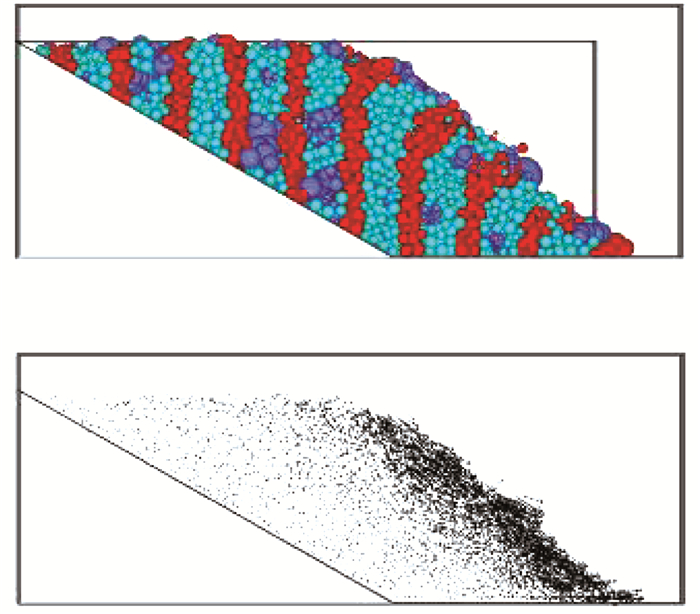
|
图 19 较厚上覆土石混合体边坡模型的破坏模式 Fig. 19 Failure mode of dual structural slope model with a thick SRM |
由图 18,19可知,当上覆土石混合堆积体的厚度较薄时,堆积体将沿着基-覆界面整体滑移,而坡体内部则没有明显的变形破坏发生; 而当上覆土石混合堆积体的厚度较厚时,深色条带发生了明显的扭曲,边坡的破坏模式与土石混合体一元结构边坡类似,即为堆积体内部的弧形滑动破坏.这与油新华等[1]根据大量工程实践总结出的基本规律是吻合的.
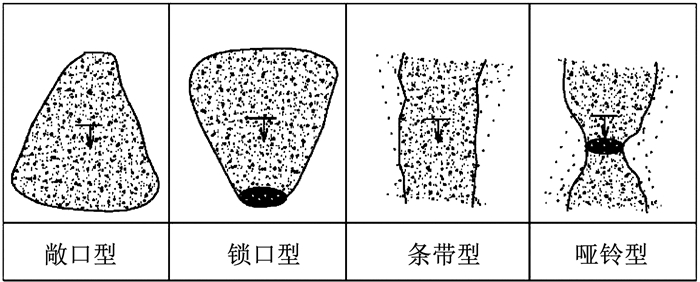
6 土石混合体边坡的空间形态效应陈红旗等[21]根据自然界中土石混合堆积体的几何形状,将其空间形态分为敞口型、锁口型、条带型和哑铃型等,并对各空间形态堆积体边坡的稳定性进行了初步定性描述,如图 20所示.根据前文提出的土石混合体边坡三维离散元建模方法和稳定性分析方法,对较常见的条带型、敞口型和锁口型堆积体边坡的稳定性和破坏机制开展进一步数值分析.
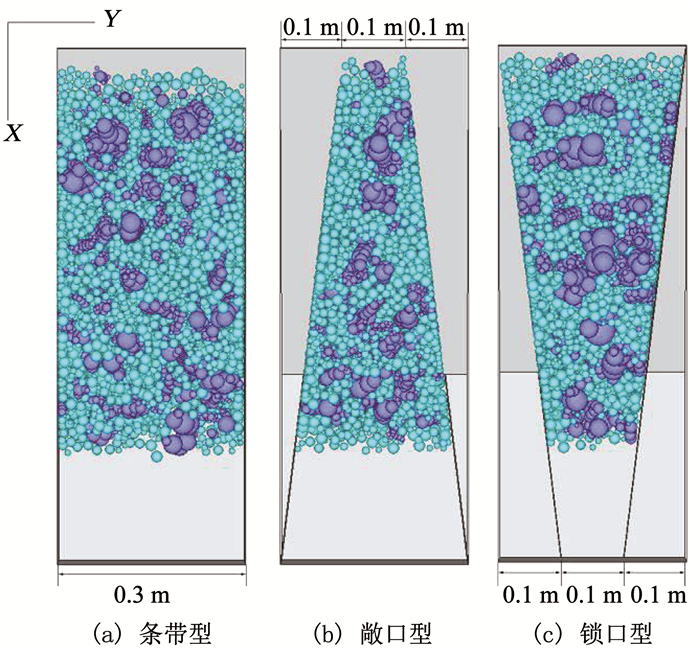
以图 16所示模型作为条带型土石混合体边坡的实例,并在此基础上将垂直于Y方向的两个侧边界的方位进行调整以生成敞口型和锁口型土石混合体边坡数值模型,其他条件保持不变.建立的3种空间形态的土石混合体边坡数值模型的俯视图如图 21所示.
|
图 21 不同空间形态的土石混合堆积体边坡数值模型俯视图 Fig. 21 Top view of SRM slope models with different spatial configurations |
通过颗粒流强度折减法计算得条带型、敞口型、锁口型土石混合体边坡安全系数分别为1.1,1.2和1.9.因此,随空间形态由条带型、敞口型到锁口型,土石混合堆积体边坡的稳定性逐渐提高,这与陈红旗等[21]的现场统计分析结论是一致的.此外,3种形态下边坡的破坏模式有所不同,条带型和敞口型均为整体沿基岩面滑动,而锁口型的破坏模式是前缘浅层发生滑动.
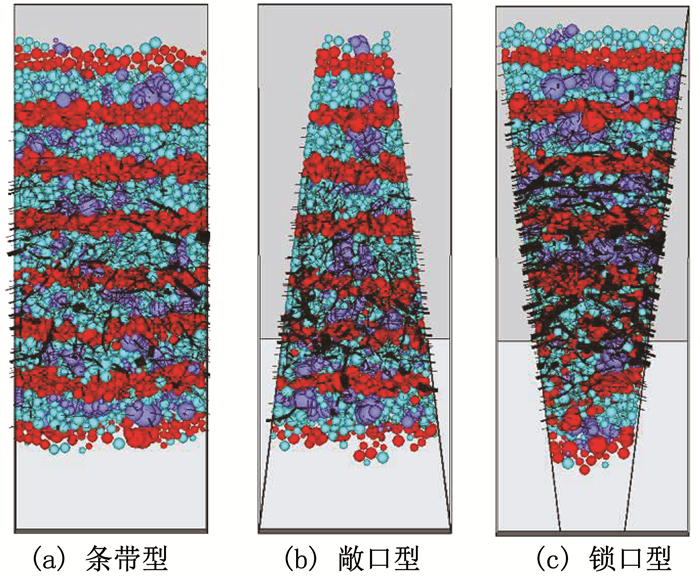
为了探究上述不同空间形态对土石混合体边坡稳定性影响的细观机制,将失稳后土石混合体边坡数值模型中的颗粒间接触力分布绘于图 22,这里给出的仍是俯视图.
|
图 22 不同空间形态的土石混合堆积体边坡数值模型接触力分布 Fig. 22 Contact force distribution of SRM slope models with different spatial configurations (top view) |
观察图 22可知:
1) 在重力作用下滑体前部受到挤压,所以,其接触力要明显大于后缘部分.
2) 接触力的主力链均大致沿Y方向分布,反映了两侧边界对颗粒向下滑动的阻碍作用.
3) 随着边坡空间形态由条带型、敞口型到锁口型,Y方向的接触主力链连接越来越好,接触力也越来越强,且向后缘延伸越多.
根据上述边坡滑动后的接触力分布特征,并考虑各空间形态堆积体边坡的一般形成过程,可以解释不同空间形态堆积体边坡的稳定性差异.条带型边坡在其形成过程中,堆积物运移路径前方没有显著的抗滑体,因此,形成的堆积体边坡往往处于亚稳定状态,容易失稳.敞口型边坡在其形成过程中,堆积物向前扩散,前缘横向分离度较高,堆积后形成的边坡一般情况下较为稳定.锁口型边坡在其形成过程中,堆积物向收缩部位汇聚,前缘不断压密,形成了较为显著的向后缘凸出的接触主力链,即形成了明显的支撑拱效应,这使得其稳定性大大提高.
针对锁口型土石混合体边坡,进一步考虑不同含石量对其稳定性和破坏特征的影响.在前述含石量为40%的锁口型土石混合体边坡的基础上,增加含石量为0和70%的情形,其他条件保持相同,滑动后的边坡形态侧视图如图 23所示.可以看出,含石量越大,滑动停止后滑体的滑出距离越小,方量也越小.其原因就是随着含石量增加,较多的大块石形成稳定骨架,坡体前缘锁口部位的支撑拱效应更显著.

|
图 23 锁口型土石混合堆积体边坡滑动后的形态 Fig. 23 Configuration of SRM slope with a locked outlet after sliding |
1) 提出了一种基于能量演化的边坡离散元模型失稳滑动判断方法:若边坡模型在强度折减后的初始压密过程后很快就达到静止状态,且最终的重力做功和摩擦耗能都很小,均低于颗粒接触应变能,则该强度折减系数下边坡是稳定的; 反之,若重力做功和摩擦耗能超过颗粒接触应变能且保持一定速率持续增长,则该强度折减系数下边坡失稳.
2) 随着含石量增加,土石混合体边坡的安全系数逐渐提高.
3) 含石量为40%和70%的土石混合体边坡中呈现出多滑动面现象,且滑面较为曲折,具有明显的绕石特征,坡脚部位的部分大块石使得剪出口的位置发生了明显的改变.
4) 随块石形状由球体、卵石到碎石,土石混合体边坡的安全系数逐渐提高.
5) 上覆堆积体相对较厚且坡度不是很大的二元结构边坡或一元结构边坡的破坏模式主要是弧形滑动破坏; 上覆堆积体厚度不大且基岩面相对平整的二元结构边坡的破坏模式主要是沿基-覆界面的整体平移滑动破坏.
6) 随着土石混合体边坡空间形态由条带型、敞口型到锁口型,其安全系数逐渐提高.锁口型边坡具有显著的支撑拱效应,且含石量越大这种效应越明显.
| [1] |
油新华.土石混合体的随机结构模型及其应用研究[D].北京: 北方交通大学, 2001 YOU Xinhua. Stochastic structural model of the earth-rock aggregate and its application[D]. Beijing: Northern Jiaotong University, 2001 http://d.wanfangdata.com.cn/Thesis/Y479787 |
| [2] |
徐文杰, 胡瑞林. 土石混合体概念、分类及意义[J]. 水文地质工程地质, 2009, 36(4): 50. XU Wenjie, HU Ruilin. Conception, classification and significations of soil-rock mixture[J]. Hydrogeology and Engineering Geology, 2009, 36(4): 50. DOI:10.3969/j.issn.1000-3665.2009.04.012 |
| [3] |
董云, 黄湖锋, 柴贺军, 等. 土石混填路基变形破坏机制的底摩擦试验模拟[J]. 中南公路工程, 2006, 31(4): 4. DONG Yun, HUANG Hufeng, CHAI Hejun, et al. Floor-friction simulation on the deformation and failure mechanism of the rock-soil filled roadbed[J]. Central South Highway Engineering, 2006, 31(4): 4. DOI:10.3969/j.issn.1674-0610.2006.04.002 |
| [4] |
周中, 傅鹤林, 刘宝琛, 等. 土石混合体边坡人工降雨模拟试验研究[J]. 岩土力学, 2007, 28(7): 1391. ZHOU Zhong, FU Helin, LIU Baochen, et al. Artificial rainfall tests on a well-instrumented soil-rock-mixture slope[J]. Rock and Soil Mechanics, 2007, 28(7): 1391. DOI:10.3969/j.issn.1000-7598.2007.07.020 |
| [5] |
孙永帅, 胡瑞林. 土石混合体变形破坏的不同形态基覆面效应试验研究[J]. 岩石力学与工程学报, 2016, 35(增刊): 2907. SUN Yongshuai, HU Ruilin. Experimental study of different shape bedrock surfaces about deformation and failure of soil and rock mixture[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S): 2907. DOI:10.13722/j.cnki.jrme.2015.0184 |
| [6] |
龚健, 刘君. 基于PIV分析的含石量对土石混合体边坡破坏过程及模式的影响[J]. 岩土力学, 2017, 38(3): 696. GONG Jian, LIU Jun. Influences of rock proportion on failure process and failure mode of soil-rock-mixture slope with PIV analysis[J]. Rock and Soil Mechanics, 2017, 38(3): 696. DOI:10.16285/j.rsm.2017.03.011 |
| [7] |
徐文杰, 王玉杰, 陈祖煜, 等. 基于数字图像技术的土石混合体边坡稳定性分析[J]. 岩土力学, 2008, 28(增刊): 341. XU Wenjie, WANG Yujie, CHEN Zuyu, et al. Stability analysis of soil-rock mixed slope based on digital image technology[J]. Rock and Soil Mechanics, 2008, 28(S): 341. DOI:10.3969/j.issn.1000-7598.2008.z1.069 |
| [8] |
李亮, 李彦军, 赵炼恒, 等. 土石混合边坡块石随机生成方法与稳定性分析[J]. 湖南大学学报(自然科学版), 2017, 44(7): 170. LI Liang, LI Yanjun, ZHAO Lianheng, et al. Method for generating random soil-rock mixed slope and stability analysis[J]. Journal of Hunan University (Natural Sciences), 2017, 44(7): 170. DOI:10.16339/j.cnki.hdxbzkb.2017.07.022 |
| [9] |
张森, 曾亚武, 夏磊. 块石含量对土石混合体边坡稳定性影响的数值研究[J]. 长江科学院院报, 2016, 33(5): 83. ZHANG Sen, ZENG Yawu, XIA Lei. Numerical study on the influence of rock block proportion on SRM slope's stability[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(5): 83. DOI:10.11988/ckyyb.20150314 |
| [10] |
邵帅, 季顺迎. 块石空间分布对土石混合体边坡稳定性的影响[J]. 工程力学, 2014, 31(2): 177. SHAO Shuai, JI Shunying. Effect of rock spatial distributions on stability of rock-soil-mixture slope[J]. Engineering Mechanics, 2014, 31(2): 177. DOI:10.6052/j.issn.1000-4750.2012.04.0248 |
| [11] |
李世海, 刘天苹, 刘晓宇. 论滑坡稳定性分析方法[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3309. LI Shihai, LIU Tianping, LIU Xiaoyu. Analysis method for landslide stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3309. DOI:10.3321/j.issn:1000-6915.2009.z2.004 |
| [12] |
WANG C, TANNANT D D, LILLY P A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(3): 415. DOI:10.1016/s1365-1609(03)00004-2 |
| [13] |
周健, 王家全, 曾远, 等. 颗粒流强度折减法和重力增加法的边坡安全系数研究[J]. 岩土力学, 2009, 30(6): 1549. ZHOU Jian, WANG Jiaquan, ZENG Yuan, et al. Slope safety factor by methods of particle flow code strength reduction and gravity increase[J]. Rock and Soil Mechanics, 2009, 30(6): 1549. DOI:10.3969/j.issn.1000-7598.2009.06.003 |
| [14] |
JIANG M J, MURAKAMI A. Distinct element method analyses of idealized bonded-granulate cut slope[J]. Granular Matter, 2012, 14(3): 393. DOI:10.1007/s10035-012-0347-y |
| [15] |
SHI C, LI D J, CHEN K H, et al. Failure mechanism and stability analysis of the Zhenggang landslide in Yunnan Province of China using 3D particle flow code simulation[J]. Journal of Mountain Science, 2016, 13(5): 891. DOI:10.1007/S11629-014-3399-0 |
| [16] |
XU W J, YUE Z Q, HU R L. Study on the mesostructure and mesomechanical characteristics of the soil-rock mixture using digital image processing based finite element method[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(5): 749. DOI:10.1016/j.ijrmms.2007.09.003 |
| [17] |
金磊, 曾亚武. 土石混合体宏细观力学特性和变形破坏机制的三维离散元精细模拟[J]. 岩石力学与工程学报, 2018, 37(6): 1540. JIN Lei, ZENG Yawu. Refined simulation for macro-and meso-mechanical properties and failure mechanism of soil-rock mixture by 3D DEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1540. DOI:10.13722/j.cnki.jrme.2017.1378 |
| [18] |
CHEN H J, LIU S H. Slope failure characteristics and stabilization methods[J]. Canadian Geotechnical Journal, 2007, 44(4): 377. DOI:10.1139/t06-131 |
| [19] |
LU M, MCDOWELL G R. The importance of modelling ballast particle shape in the discrete element method[J]. Granular Matter, 2007, 9: 69. DOI:10.1007/s10035-006-0021-3 |
| [20] |
BONO D, MCDOWELL G R, WANATOWSKI D. Discrete element modelling of a flexible membrane for triaxial testing of granular material at high pressures[J]. Géotechnique Letters, 2012, 2(4): 199. DOI:10.1680/geolett.12.00040 |
| [21] |
陈红旗, 黄润秋, 林峰. 大型堆积体边坡的空间工程效应研究[J]. 岩土工程学报, 2005, 27(3): 323. CHEN Hongqi, HUANG Runqiu, LIN Feng. Study on the spatial engineering effect of large accumulation slope[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(3): 323. DOI:10.3321/j.issn:1000-4548.2005.03.016 |
 2020, Vol. 52
2020, Vol. 52