2. 四川大学 水利水电学院,成都 610065;
3. 西北矿冶研究院,甘肃 白银 730900
2. College of Water Resources and Hydropower, Sichuan University, Chengdu 610065, China;
3. Northwest Institute of Mining and Metallurgy, Baiyin 730900, Gansu, China
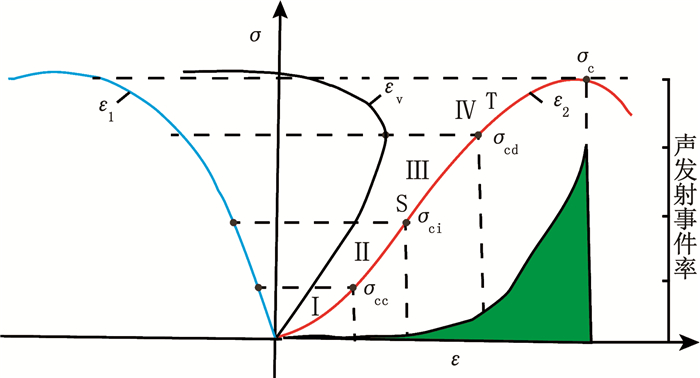
岩石是一种包含如孔穴、微裂纹、节理等各种缺陷的材料.在外界荷载作用下,必然引起这些缺陷扩展、汇合,并产生新的微裂纹.岩石变形破坏与微裂纹的活动状态密切相关,是细观裂纹不断扩展的宏观结果.Bieniawski[1-2]按照不同应力水平下岩石内部微裂纹活动状态的差异,将岩石的峰前应力-应变曲线划分为4个阶段,如图 1所示.阶段Ⅰ:原生裂纹压缩闭合阶段; 阶段Ⅱ:线弹性阶段; 阶段Ⅲ:裂纹稳定扩展阶段; 阶段Ⅳ:裂纹非稳定扩展阶段.各阶段结束点对应的应力值分别为闭合应力σcc、起裂应力σci、损伤应力σcd和峰值应力σc.其中岩石的起裂应力σci(图 1中S点)和损伤应力σcd(图 1中T点)作为表征岩石内部裂纹扩展的两个重要特征应力引起广泛关注.
|
图 1 根据微裂纹发展划分不同阶段的应力-应变曲线 Fig. 1 Stress-strain curves of different stages based on the development of micro-cracks |
Martin等[3-4]研究了Lac du Bonnet花岗岩,发现其σci、σcd分别为单轴压缩峰值强度的0.4~0.5倍和0.8倍;Everitt[5]发现岩石内部结构对其σci、σcd有较大影响;汪斌等[6]获得锦屏大理岩的σci、σcd与σc比值范围分别为0.38~0.52和0.82~0.86;彭俊等[7]研究了在围压和水压作用下砂岩σci、σcd的变化,发现随水压增大,岩石的σci有逐渐增大的趋势,而σcd和峰值应力σc逐渐减小,随围压增大,其σci、σcd和σc均逐渐增大.起裂应力σci和损伤应力σcd的确定方法有多种,包括应力-应变曲线判定法、体积应变法、AE声发射法、移动点回归法等,但其精确性受到岩石类型、试验方法等因素的影响[8-10].综合各类确定方法发现,目前确定特征应力值多为试验方法,数值模拟方法鲜有报道.
工程岩体受到荷载的变化速率对岩石的力学性能有较大影响,岩石荷载变化速率效应分析一直被广泛研究.普遍认为,加载速率越高,岩石内部微裂隙来不及扩展、贯通,使其抗压强度增加[11-15].也有学者发现在某些加载速率范围内,岩石强度出现下降[16-17].总结以上研究成果发现,针对岩石特征应力的加载速率效应研究较少.另外,由于加载速率效应研究试样个体数多,试验重复性大,数值模拟方法将突破这一成本局限而成为一种便捷途径.
为研究不同加载速率下脆性岩石的特征应力变化规律,设计了3种加载速率下大理岩的单轴压缩试验.采用体积应变法、声发射法和黏结颗粒离散元(bonded particle model, BPM)数值方法(下文简称BPM模拟法),确定其特征应力,通过对比分析验证数值法的可靠性.并采用数值法模拟6种不同加载速率下的单轴压缩试验,综合分析了大理岩特征应力的加载速率效应.
1 特征应力的确定 1.1 特征应力确定方法岩石的起裂应力σci是裂纹稳定扩展的起始点,此时岩石内部的微缺陷(孔洞、微裂纹等)开始萌生、扩展.损伤应力σcd是裂纹非稳定增长对应的强度阈值.前一阶段萌生、扩展的裂纹大量汇合、贯通,发生非稳定性扩展.为探究采用BPM模拟法确定σci、σcd的合理性并保证取值准确,本文采用体积应变法、声发射法、BPM数值模拟法确定特征应力值.
1.1.1 体积应变法对于常规单轴压缩实验,体积应变εv可通过测试近似计算,即
| $ {\varepsilon _{\rm{v}}} \approx 2{\varepsilon _1} + {\varepsilon _2}. $ | (1) |
式中:ε1为横向应变,ε2为轴向应变.
当外力超过岩石的起裂应力时,内部裂纹开始萌生、扩展,横向应变和体积应变曲线开始偏离线性,该点对应的应力为起裂应力σci.当外力超过损伤应力时,内部裂纹汇合贯通,体积应变曲线出现拐点,该点对应的应力为损伤应力σcd(图 1).
1.1.2 声发射法声发射(AE)是材料内部能量迅速释放而产生的弹性波.可以通过监测到的声发射信号来判断微裂纹的发展情况.Eberhardt等[8]研究指出,声发射信号第1次明显增加时的应力即为起裂应力σci,第2次突然跃起时的应力即为损伤应力σcd(图 1).声发射特征参数中,考虑振铃计数比较敏感,容易受到外界干扰,所以,多选用AE事件率和AE累计事件数,必要时结合幅值、能量曲线来研究特征应力.
1.1.3 数值法颗粒流法是由Cundall P A和Strack O D L[18]在离散元理论基础上提出的,在岩石损伤和细观裂纹发展等方面应用广泛.岩石宏观破裂如断裂破坏都是由于细观结构的贯通,微观裂纹的分析是研究破裂问题的根本.Diederichs等[19]运用离散元模拟花岗岩并分析其损伤破坏过程.Sharafisafa等[20]采用离散元研究了脆性岩石的裂纹萌生、延伸和贯通机制.
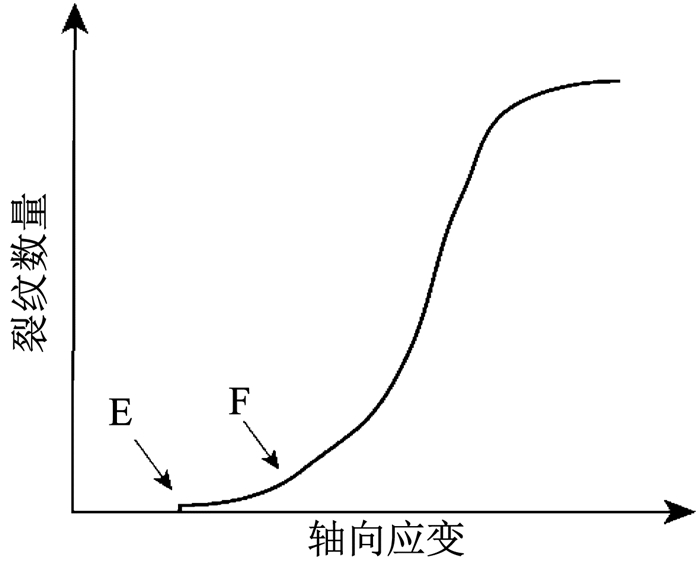
BPM模拟法可以监控岩石压缩破坏过程中微裂纹数量增长过程和分布特征,其典型的微裂纹数增长情况如图 2所示,基于微裂纹数的BPM模拟法可以确定岩石的特征应力.在加载初期未出现微裂纹,此时岩石试件处于压密和弹性阶段.随着应变增大,在E点后破裂开始出现并增加,此时的突变点E对应的应力即为岩石的起裂应力σci,微裂纹数量经过一段较平稳线性增加后,进入非线性增长阶段,其突变点F对应应力即为岩石的损伤应力σcd.
|
图 2 压缩过程典型裂纹数量变化 Fig. 2 Variation diagram of crack numbers during compression |
试验用大理岩取样于四川省雅安市宝兴县,别名“蜀白玉”.采用X射线单晶衍射仪测定其矿物成分为方解石,达到99%以上.按照水利水电工程岩石试验规范,加工成直径50 mm,高度100 mm的标准圆柱体试样,试样两端平行度和垂直度满足规范要求.试验加载速率控制为5×10-6,8×10-6,5×10-5 m/s,每一加载速率下进行试验的岩样4个,共计12个.
为保证采用体积应变法和声发射法获得大理岩的特征应力,设计如图 3所示的试验方案:采用MTS815型岩石力学加载系统和PCI-2声发射信号采集系统记录试验过程中力学数据和声发射数据,每个岩样共布置8个Micro30高精度探头,采用环向和轴向引伸计测定环向和轴向位移.各岩样的物理力学参数如表 1所示.

|
图 3 声发射探头和位移传感器布置 Fig. 3 Layout of AE and displacement sensors |
| 表 1 岩样物理力学参数 Tab. 1 Basic physical and mechanical parameters of samples |
采用PFC2D软件模拟大理岩单轴压缩过程以确定其特征应力.PFC2D采用细观力学参数表征颗粒及黏结的力学性质.在数值模型计算分析前,需进行大量的模型验证工作,即通过不断调整细观参数,将计算得到的试样宏观力学参数与室内试验结果对比.当计算结果与试验结果基本接近或一致时,便可选择该组细观力学参数构建实际计算模型.
当采用表 2所示细观参数时,生成与试验试样尺寸一致的数值模型,如图 4所示.模型共计颗粒13 054个,颗粒间黏结采用平行黏结.
| 表 2 模型细观力学参数 Tab. 2 Micro mechanical parameters of numerical model |

|
图 4 PFC2D数值试件及局部放大图 Fig. 4 PFC2D numerical specimen and local magnification image |
加载速率为5×10-5 m/s时,数值模拟与室内试验试样(3-D2)的破裂面比较如图 5所示.限于篇幅,其余试样对比不一一给出.可以看出,试验岩样和模拟岩样主次破坏面均为剪切破坏面,试样右下端部出现剪切破坏.

|
图 5 模拟和试验岩样破裂特征对比 Fig. 5 Comparison of failure characteristics between the simulated and test rock samples |
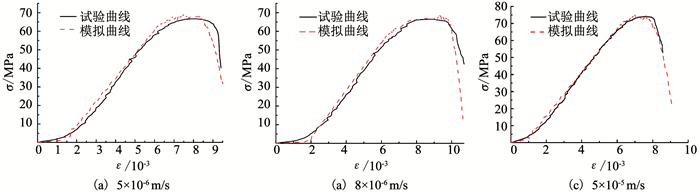
图 6为不同加载速率下试样试验与数值模拟应力-应变曲线对比.考虑岩样个体差异性,选取每一加载速率下,与该组单轴抗压强度均值最为接近且典型的岩样作为数值模拟比较对象,选取岩样分别为1-D2、2-D4、3-D2.由图 6对比可以看出,不同加载速率下模拟结果和试验所获得的应力-应变曲线基本吻合,表现在峰值强度、弹性模量、峰值应变等基本接近或一致.
|
图 6 不同加载速率下模拟和试验岩样应力-应变曲线对比 Fig. 6 Comparison of stress-strain curves between simulated and tested rock samples at different loading rates |
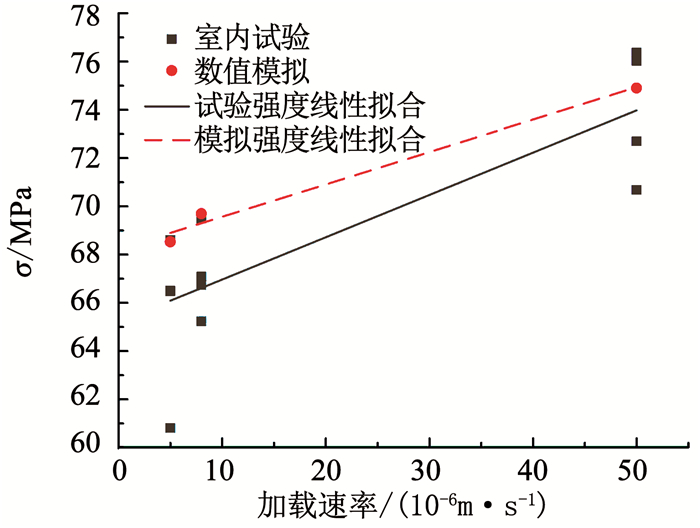
不同加载速率下岩样的试验峰值强度和数值模拟峰值强度对比如图 7所示.可以看出,试验用岩样在5×10-6~5×10-5 m/s加载范围内表现出加载速率效应,其强度随加载速率增大而增大.另外,试验和模拟峰值强度随加载速率变化趋势基本一致,拟合曲线较为接近.
|
图 7 颗粒细观摩擦系数折减后边坡模型的位移场 Fig. 7 Comparison of peak strength between test and numerical simulation of samples at different loading rates |
通过对比应力应变曲线、破裂形态和峰值强度,发现PFC2D数值模拟结果与室内试验结果较为接近,认为建立的数值模型较为可靠.
2 特征应力结果分析 2.1 试验结果室内试验可以获得各岩样的力学数据和声发射监测数据,限于篇幅,这里仅以加载速率5×10-5m/s的岩样3-D2为例,说明特征应力确定的过程.
图 8为岩样3-D2的压缩变形曲线.在岩样变形曲线中,横向应变曲线偏离线性段的应力对应起裂应力σci(如图 8中的A点),体积应变曲线的拐点对应应力即为损伤应力σcd.为准确确定拐点并保证拟合效果,通过对一定范围内的数据进行拟合,得到拟合曲线的解析式,并利用Matlab软件编程求得拐点的解析解,如图 8中B点所示.同样,可以获得所有岩样的特征应力值.

|
图 8 岩样3-D2压缩试验过程变形曲线 Fig. 8 Deformation curves of rock sample 3-D2 during compression test |
图 9为岩样3-D2的应力、AE事件率、AE累计数和时间的关系曲线.结合图中的AE事件率和AE累计数曲线可以发现,在加载初期,两者均维持在较低的水平,到达C点后开始增加,增加幅度较稳定,一直到D点急剧增加.点C、D点对应的应力即为起裂应力和损伤应力.需要说明的是,试件在钻取和加制样过程中受到不同程度的扰动,导致其起裂应力不能通过声发射进行较精准的识别,这里结合两个特征参数进行综合分析,必要时考虑分析其他更多特征参数,以减少识别误差.
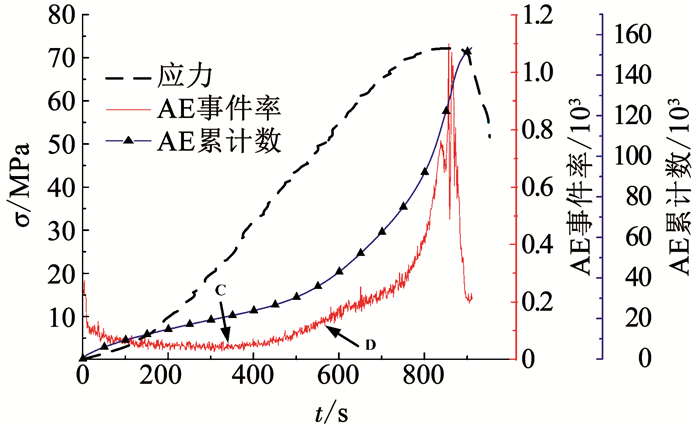
|
图 9 岩样3-D2应力、AE事件率-时间关系曲线 Fig. 9 Relation curves of stress and AE event rates of sample 3-D2 with time |
以加载速率为5×10-5 m/s时数值试件为例.试件在单轴压缩过程中微裂纹的数量增长情况如图 10所示.可以看出,随着应变增加,微裂纹开始出现并稳定增加,曲线的突变点对应的应力为起裂应力(图 10中E点),此时裂纹数为2条,应力值为23.96 MPa,微裂纹数经过一段较平稳增加后,进入线性增长阶段,此时的突变点对应的应力为损伤应力(图 10中F点),值为45.68 MPa.同样,采用此方法可以获得不同加载速率下试件的特征应力值.
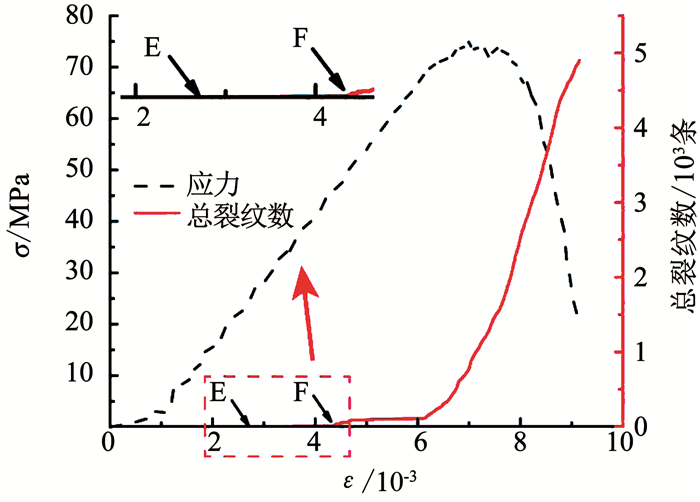
|
图 10 PFC2D数值模拟微裂纹数量变化和局部放大图 Fig. 10 Variation of micro-crack numbers simulated by PFC2D and local magnification image |
由以上试验法(体积应变法、声发射法)和数值模拟法确定的大理岩特征应力归一化结果如表 3和图 11所示.其中σc′为PFC2D数值模拟获得的峰值应力.结合表 3、图 11可以看出,采用试验体积应变法、声发射法和BPM模拟法确定的不同加载速率下大理岩归一化起裂应力范围在0.30~0.41,归一化损伤应力范围在0.58~0.80.同一加载速率下各岩样特征应力归一化结果离散性较小,说明试验用岩样较均致,个体差异性较小.
| 表 3 不同加载速率下大理岩归一化特征应力 Tab. 3 Normalized characteristic strength of marble at different loading rates |
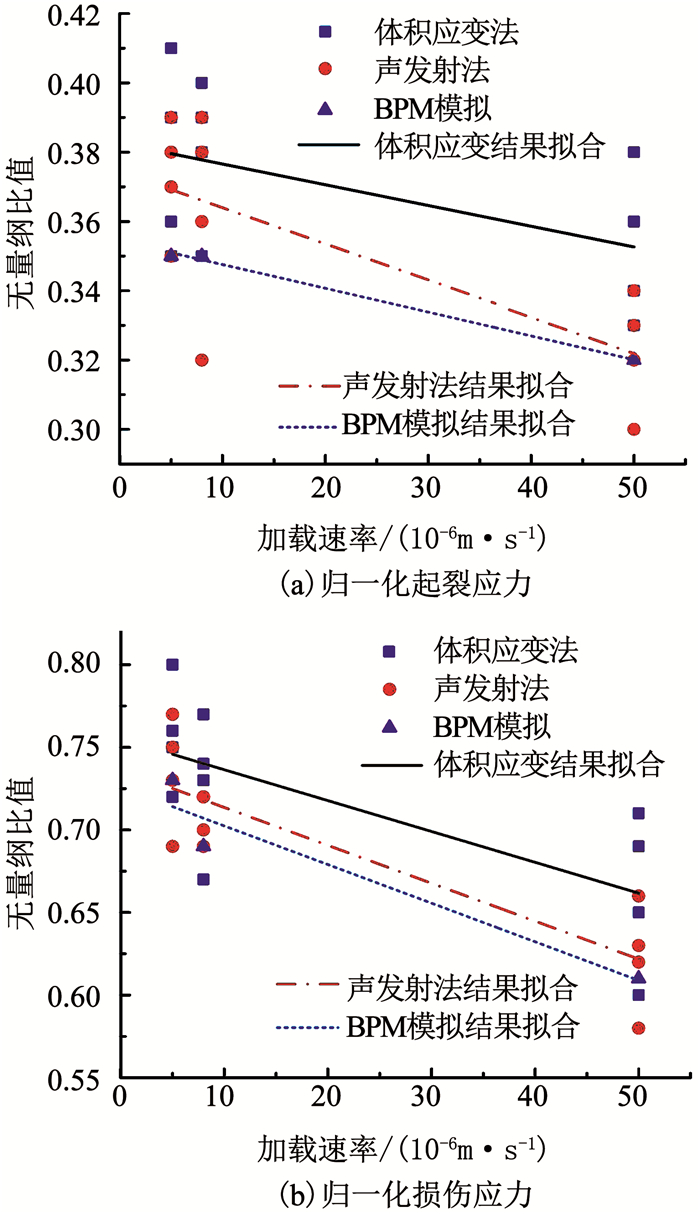
|
图 11 采用不同方法确定的岩样归一化特征应力 Fig. 11 Normalized characteristic stresses of rock samples determined by different methods |
当加载速率为5×10-6 m/s,采用体积应变法、声发射法确定的归一化起裂应力均值与BPM模拟法确定的结果差值分别为0.03,0.02,归一化损伤应力差值分别为0.03,0.01;当加载速率为8×10-6 m/s,归一化起裂应力差值分别为0.03,0.01,归一化损伤应力差值分别为0.04,0.02;当加载速率为5×10-5 m/s,归一化起裂应力差值分别为0.03,0,归一化损伤应力差值分别为0.05,0.01.发现不同加载速率下,BPM模拟法确定的特征应力值与体积应变法、声发射法确定结果很接近,尤其与声发射法结果相差无几,且均小于后两种方法确定值.普遍认为,由于材料宏观响应滞后于细观变化,BPM模拟法、声发射法确定的特征应力一般小于宏观体积应变法.以上说明基于微裂纹数量变化确定大理岩特征应力是一种较可靠有效的方法,其确定的特征应力较宏观体积应变法偏小,但结果较为吻合.
加载速率由8×10-6 m/s增加至5×10-5 m/s时,3种方法确定的归一化特征应力值均呈现减小规律.反映岩石在高加载速率条件下更容易形成内部损伤,微裂纹将在相对较低的应力时出现稳定和非稳定性扩展.
3 加载速率效应数值分析为全面分析大理岩特征应力的加载速率效应,包括同一数量级不同加载速率和不同数量级加载速率,在试验用3种加载速率基础上,增加3种加载速率进行单轴压缩数值模拟,加载速率分别为8×10-5,5×10-4,8×10-4 m/s.数值模型与前文1.3节组建的模型一致.不同加载速率下PFC2D模拟得到试件的归一化特征应力规律曲线如图 12所示.可以看出,在加载速率为5×10-6~8×10-4 m/s内,随着加载速率增大,各试件的归一化起裂应力和损伤应力减小.这主要是因为在较快速率加载下,岩石内部几乎来不及发生应力松弛,较小的裂纹等缺陷处于激活状态,更容易满足起裂条件,进而发生扩展和贯通,导致其归一化起裂应力和损伤应力随加载速率增大而减小.

|
图 12 不同加载速率下PFC2D数值试件归一化特征应力 Fig. 12 Normalized characteristic stresses of PFC2D numerical specimens at different loading rates |
当加载速率小于5×10-5 m/s,即中低加载速率时,其归一化特征应力降幅较大.当加载速率大于5×10-5 m/s,即较高加载速率时,归一化特征应力值整体上趋于平稳,尤其是归一化损伤应力.岩石的变形破坏受多种因素影响,其中包括载荷速率.当加载速率较低时,岩石有流变趋势;在中低加载速率条件下,表现为岩石变形的时效特征;当加载速率较高时,岩石出现延迟破坏特性.模拟结果显示,在高加载速率时,损伤应力下降幅度较中低加载速率时小.说明对试验用较均致的脆性大理岩而言,由于受到延迟破坏特性影响,没有在预想的较低的应力水平发生微裂纹非稳定性扩展.值得注意的是,在加载速率为5×10-4 m/s时,归一化起裂应力出现增长,说明岩石的延迟破坏特性和前文提到的高加载速率下容易起裂的特性存在主次关系,且加载速率影响两个归一化特征应力值的规律似乎不完全相同.这也是后面可以深入研究的内容.
相比较而言,归一化损伤应力的加载速率效应整体上比归一化起裂应力明显.
4 结论1) 体积应变法、声发射法、BPM模拟法3种方法确定的特征应力值较为接近,基于微裂纹数量变化的BPM模拟法确定大理岩特征应力是一种较可靠有效的方法.
2) 试验结果显示,加载速率由8×10-6 m/s增加至5×10-5 m/s时,3种方法确定的归一化特征应力值均呈现减小规律.
3) 数值结果显示,加载速率由5×10-6 m/s增加至8×10-4 m/s时,归一化起裂应力和损伤应力减小.当处于中低加载速率时,其归一化特征应力降幅较大.当处于较高加载速率时,归一化特征应力值趋于平稳,尤其是归一化损伤应力.相比较而言,归一化损伤应力的加载速率效应整体上比归一化起裂应力明显.
| [1] |
BIENIAWSKI Z T. Mechanism of brittle fracture of rock. Part Ⅰ: Theory of the fracture process[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1967, 4(4): 395, IN11, 405-404, IN12, 406. DOI:10.1016/0148-9062(67)90030-7 |
| [2] |
BIENIAWSKI Z T. Mechanism of brittle rock fracture. Part Ⅱ: Experimental studies[J]. International Journal of Rock Mechanics & Mining Sciences, 1967, 4(4): 407. DOI:10.1016/0148-9062(67)90031-9 |
| [3] |
MARTIN C D. The strength of massive Lac du Bonnet granite around underground openings[D]. Manitoba, Canada: University of Manitoba, 1993
|
| [4] |
MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1994, 31(6): 643. DOI:10.1016/0148-9062(94)90005-1 |
| [5] |
EVERITT R A, LAJTAI E Z. The influence of rock fabric on excavation damage in the Lac du Bonnett granite[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(8): 1277. DOI:10.1016/j.ijrmms.2004.09.013 |
| [6] |
汪斌, 朱杰兵, 严鹏, 等. 大理岩损伤应力的识别及基于损伤控制的参数演化规律[J]. 岩石力学与工程学报, 2012(增刊2): 3967. WANG Bin, ZHU Jiebing, YAN Peng, et al. Damage strength determination of marble and its parameters evaluation based on damage control test[J]. Chinese Journal of Rock Mechanics and Engineering, 2012(S2): 3967. |
| [7] |
彭俊, 荣冠, 周创兵, 等. 水压影响岩石渐进破裂过程的试验研究[J]. 岩土力学, 2013, 34(4): 941. PENG Jun, RONG Guan, ZHOU Chuangbing, et al. Experimental study of effect of water pressure on progressive failure process of rocks under compression[J]. Rock and Soil Mechanics, 2013, 34(4): 941. |
| [8] |
EBERHARDT E, STEAD D, STIMPSON B, et al. Identifying crack initiation and propagation thresholds in brittle rock[J]. Canadian Geotechnical Journal, 1998, 35(2): 222. DOI:10.1139/cgj-35-2-222 |
| [9] |
EBERHARDT E, STEAD D, STIMPSON B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression[J]. International Journal of Rock Mechanics & Mining Sciences, 1999, 36(3): 361. DOI:10.1016/S0148-9062(99)00019-4 |
| [10] |
周辉, 孟凡震, 卢景景, 等. 硬岩裂纹起裂强度和损伤强度取值方法探讨[J]. 岩土力学, 2014(4): 913. ZHOU Hui, MENG Fanzhen, LU Jingjing, et al. Discussion on methods for calculating crack initiation strength and crack damage strength for hard rock[J]. Rock and Soil Mechanics, 2014(4): 913. |
| [11] |
QI C, WANG M, QIAN Q. Strain-rate effects on the strength and fragmentation size of rocks[J]. International Journal of Impact Engineering, 2009, 36(12): 1355. DOI:10.1016/j.ijimpeng.2009.04.008 |
| [12] |
HUANG B, LIU J. The effect of loading rate on the behavior of samples composed of coal and rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 61(10): 23. DOI:10.1016/j.ijrmms.2013.02.002 |
| [13] |
黄达, 黄润秋, 张永兴. 粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J]. 岩石力学与工程学报, 2012, 31(2): 245. HUANG Da, HUANG Runqiu, ZHANG Yongxing. Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 245. DOI:10.3969/j.issn.1000-6915.2012.02.003 |
| [14] |
王笑然, 王恩元, 刘晓斐, 等. 裂隙砂岩裂纹扩展声发射响应及速率效应研究[J]. 岩石力学与工程学报, 2018, 37(6): 1446. WANG Xiaoran, WANG Enyuan, LIU Xiaofei, et al. Macro-crack propagation process and corresponding AE behaviors of fractured sandstone under different loading rates[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1446. |
| [15] |
宋义敏, 邢同振, 邓琳琳, 等. 不同加载速率下岩石变形场演化试验研究[J]. 岩土力学, 2017, 38(10): 2773. SONG Yimin, XING Tongzhen, DENG Linlin, et al. Experimental study of evolution characteristics of rock deformation field at different loading rates[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 38(10): 2773. |
| [16] |
STAVROGIN A N, TARASOV B, FAIRHURST C. Experimental physics and rock mechanics: Results of laboratory studies[M]. Tokyo: A A Balkema, 2001.
|
| [17] |
张连英, 茅献彪. 高温状态下加载速率对石灰岩力学效应研究[J]. 岩土力学, 2010, 31(11): 3511. ZHANG Lianying, MAO Xianbiao. Experimental study of the mechanical effects of loading rates on limestone at high temperature[J]. Rock and Soil Mechanics, 2010, 31(11): 3511. DOI:10.3969/j.issn.1000-7598.2010.11.026 |
| [18] |
CUNDALL P A, STRACK O D. Particle flow code in 2D[M]. Minnesota: Itasca Consulting Group Inc, 1999.
|
| [19] |
DIEDERICHMS K. Stress induced damage accumulation and implications for hard rock engineering[C]//Proceedings of Narms 2002. Toronto: University of Toronto Press, 2002: 3
|
| [20] |
SHARAFISAFA M, NAZEM M. Application of the distinct element method and the extended finite element method in modelling cracks and coalescence in brittle materials[J]. Computational Materials Science, 2014, 91(2): 102. DOI:10.1016/j.commatsci.2014.04.006 |
 2020, Vol. 52
2020, Vol. 52


