2. 中国矿业大学 力学与土木工程学院,江苏 徐州 221116
2. School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China
中国中西部地区山岭众多,地势条件复杂,随着中国地下工程建设的快速发展,修建穿越富水断层破碎带的隧道工程不断涌现,隧道掌子面岩体由于高水压、高地应力引发富水断层破碎带突水突泥灾害时有发生.例如,宜万铁路马鹿箐隧道和野三关隧道、吉莲公路永莲隧道等工程建设过程中,由于揭露富水断层破碎带发生多起突水突泥事故,造成了严重的经济损失和人员伤亡[1].
近十几年来,国内外学者对隧道施工过程中穿越富水断层带发生的突水突泥问题进行了大量研究.主要集中在两个方面,一是突水灾害赋存地质环境的研究.李晓昭等[4]提出断层带在开挖扰动条件下的受力变化作用,并对人工扰动作用下断层的突水过程进行模拟分析,研究断层的渗导水破坏机制.何发亮等[5]通过对国内外深长隧道突水突泥灾害产生原因的充分调研,系统提出了深长隧道5种突水致灾构造.张庆松等[6]研制了断层破碎带隧道突水突泥模型试验系统,试验揭示隧道开挖过程中及揭露断层后的围岩渗流压力、应力应变、位移以及涌出物等特征参数的变化规律.二是对隧道周围岩体破坏力学特征的研究[7].宋瑞刚等[9]根据总势能原理,建立了穿越断层破碎带深埋隧道围岩失稳尖点突变模型,推导出失稳的力学判据条件.张明聚等[10]采用岩体极限平衡理论,给出了突水临界水压力计算公式,并将其应用于翔安隧道突水风险的计算预测.张雨帆等[11]基于隧道渗流场的流固耦合原理,引入隧道穿越富水断层带设防长度概念,对隧道穿越富水断层带的加固范围进行研究.王德明等[12]建立了断层地质构造力学模型,通过时效损伤本构模型描述围岩在动态破坏中的黏性和损伤特性,研究岩石体在突水突泥过程中的空间破坏形态.对于富水断层破碎带的突水突泥问题,因断层破碎带充填物由片状角砾石为主组成的混合物,遇水不融化,发生突水突泥时呈流塑状态,带有压力与碎屑流情况很像,因此, 也有一些学者将其看成是“碎屑流”模型[13].其中于琳茗等[14]认为隧道掘进过程中,掌子面和碎屑流地层之间的距离小于最小安全距离时,在高水压和高地应力的共同作用下,掌子面会由于经受不住其后方的水土压力而发生碎屑流,即突水突泥.张志强等[15]自主研制“碎屑流发生”的模拟试验装置,“再现”碎屑流发生过程、形成条件,揭示碎屑流发生、发展规律,并分析碎屑流发生的影响因素.
由以上分析可以看出,目前对于断层破碎带突水的研究以模型试验和数值模拟为主,少量的理论研究[14]也仅仅考虑掌子面后面的水压或者直接把断层破碎带看成半无限体来分析临界掌子面的土压力,尚未考虑断层破碎带的长、宽对突水判据的影响.为此,本文首次将筒仓理论运用到断层破碎带突水研究中,结合极限平衡理论综合分析了断层破碎带的宽度、长度对于隔水岩盘最小安全厚度的影响,推导出最小安全厚度的理论公式,为断层破碎带构造突水、突泥预测预防提供一种行之有效的计算方法,具有一定的理论研究意义与工程应用价值[2].
1 筒仓理论的基本原理散体是大型离散宏观粒子的混合体, 散体物料不同于其他的气体、固体和液体,具有自身独特的特性,在筒仓中可以储存任何的散装物料[17].针对存储这些散粒的筒仓压力计算,最早的筒仓侧压力计算公式是由Janssen提出的, 他推导的Janssen公式对此后的筒仓压力计算产生了深远的影响.直到今天,大多数国家筒仓设计规范所使用的侧压力计算公式还是以Janssen公式为基础,Janssen公式做了以下假设[18]:1)筒仓内同一水平面上各点的竖向侧压力是相等的; 2)散体任意一点的水平压力与垂直压力成正比; 3)假定筒仓为无限深,且储料不可压缩.
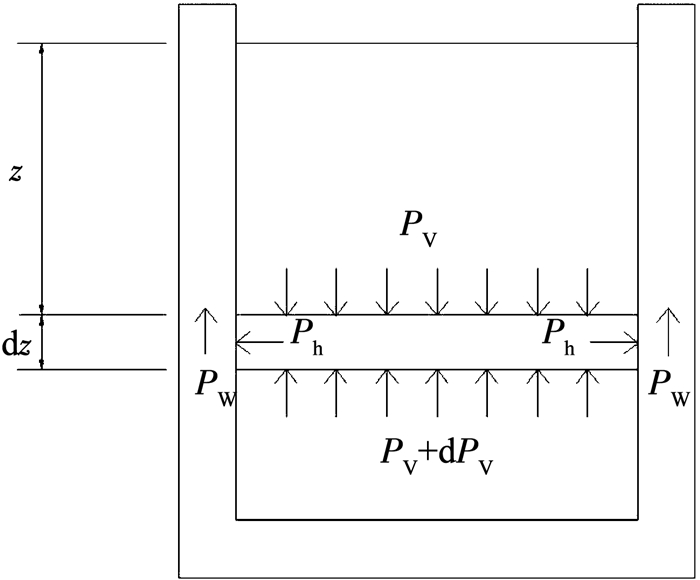
根据上述假设求出静态下不同深度的贮料压力公式.如图 1所示, 在距物料表面Z处取一厚度为dz的单元体进行受力分析[18],其截面积为F, 周长为C.物料单元体所受的垂直载荷与该层物料的自重及周边承受的摩擦力相平衡,静止平衡条件为
| $ \left( {{P_{\rm{V}}} + {\rm{d}}{P_{\rm{V}}}} \right)F - {P_{\rm{V}}}F + {P_{\rm{W}}}C{\rm{d}}z - \gamma F{\rm{d}}z = 0. $ | (1) |
|
图 1 筒仓内物料薄层受力情况 Fig. 1 Stress situation of silo material layer |
式中:PW为物料与仓壁摩擦力,kPa; PV为垂直方向上单位面积贮料压力,kPa; γ为物料重度,kN/m3; C为筒仓横截面周长,m.
设水平截面水力半径ρ=F/C,Ph/PV=K为侧压力系数,PW/Ph=μ,代入式(1)结合初始条件z=0时,PV=0得
| $ {P_{\rm{v}}} = \frac{{\gamma \rho }}{{\mu K}}\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right), $ | (2) |
| $ {P_{\rm{h}}} = \frac{{\gamma \rho }}{\mu }\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right). $ | (3) |
式中:Ph为水平方向上单位面积贮料压力,kPa; μ为物料与仓壁摩擦系数.
2 基于筒仓理论断层破碎带防突岩盘最小安全厚度 2.1 假设条件张性或张扭性断层受压应力较小,内部结构松散,裂隙发育,主要由大小不规则的断层角砾岩构成,当空隙不被后期物质充填胶结时,断层富水性强,富水部位主要集中在破碎带[6].因此,富水断层破碎带充填物既不是纯固体,也不是气体和液体,而是固、液、气混合在一起的三相物质.本文主要研究未胶结的富水断层破碎带,筒仓存储的物料散体特性基本一致.因此,将断层破碎带简化成筒仓模型是合理可行的.
根据之前研究[8],可以将断层破碎带引发的突水破坏模式简化为相似的力学模型来分析.将富水断层破碎带位于隧道开挖工作面前方的简化成岩塞模型,破坏形式是极限平衡条件下沿着防突岩墙发生直接的剪切破坏,即常说的拔塞效应,岩墙在没有发生较大变形或开裂的情况,突然发生整体破坏[5].将富水断层破碎带位于隧道开挖轮廓线一侧的简化成梁破坏模型[5].假设条件如下:
1) 将隧道掌子面与断层破碎带之间岩盘看成岩塞,岩盘为连续均匀的各向同性弹性体,符合小变形理论;
2) 断层破碎带对临界掌子面的作用力简化成水压力Q和地应力P分别作用;
3) 张性或者顺层错动富水破碎带时两盘影响带岩盘作为防突隔水层,压性断层富水破碎带隧道施工由下盘向上盘施工,突破的隔水岩盘为压性断层主干隔水层,由上盘往下盘施工时突破的隔水层为上盘影响带岩盘;
4) 断层破碎带对隔水岩盘的侧向压力P通过将断层破碎带简化成筒仓模型进行计算;
5) 本研究针对断层倾角比较大,规模较大的断层破碎带,并忽略水对岩盘的水合作用影响.
2.2 筒仓理论求解断层破碎带地应力P对于富水断层破碎带在隧道施工掌子面前方临界掌子面的压力,通常将水土分开考虑,其中水压力Q考虑成静水压力跟地下水位到隧道掌子面或者开挖轮廓线之间的高程差h成正比等于γwh,当断层破碎带与地表水相通时,为地表水位与隧道掌子面或者开挖轮廓线之间的高程差h等于γwh.
针对地应力P, 之前学者很少考虑断层破碎带规模的影响,将断层破碎带看成半无限体来计算地应力,然后再乘以一个侧向土压力系数[14].然而,实际上断层破碎带的规模并没有那么大,一般在几十厘米到几百米,尤其对于那些宽段小于100 m的,长度也不是很大的断层破碎带按照半无限体来计算侧向土压力会带来相当大的误差.本文基于筒仓理论,充分考虑断层破碎带的规模,尤其是断层破碎带宽度b的影响.
将整个断层破碎带看成一个大的深筒仓,断层破碎带四周的岩盘看成仓壁,断层破碎带的充填破碎岩块和碎石就是贮料.结合筒仓模型和断层破碎带的实际情况,建立如图 2的力学受力模型,建立断层破碎带的平衡方程:
| $ \begin{array}{*{20}{c}} {\left( {{P_{\rm{V}}} + {\rm{d}}{P_{\rm{V}}}} \right)F - {P_{\rm{V}}}F + \mu \left( {{P_{\rm{h}}} + 0.5\gamma b\cos \theta } \right)C{\rm{d}}z - }\\ {\gamma \sin \theta F{\rm{d}}z = 0.} \end{array} $ | (4) |
| $ \begin{array}{*{20}{c}} {{\rm{d}}{P_{\rm{V}}}F + \mu \left( {{P_{\rm{h}}} + 0.5\gamma b\cos \theta } \right)C{\rm{d}}z - }\\ {\gamma \sin \theta F{\rm{d}}z = 0.} \end{array} $ | (5) |

|
图 2 断层破碎带力学模型 Fig. 2 Mechanical model of fault fracture zone |
式中:F为截面面积,C为截面周长,令ρ=0.5bl/(b+l)为截面水力半径,Ph/PV=K为侧压力系数,μ为摩擦系数,b为断层破碎带宽度,l为断层破碎带长度,γ为断层破碎带充填物的容重,θ为倾角,将ρ和K代入式(5),整理得
| $ {\rm{d}}z = {\rm{d}}{P_{\rm{V}}}\frac{\rho }{{\rho \gamma \sin \theta - 0.5\gamma \mu b\cos \theta - \mu K{P_{\rm{V}}}}}. $ | (6) |
求积分并代入初始条件z=0时,PV=0, 计算可得
| $ {P_{\rm{h}}} = \frac{{\gamma \rho \left( {\sin \theta - \frac{{\mu b\cos \theta }}{{2\rho }}} \right)}}{\mu }\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right), $ | (7) |
| $ {P_{\rm{V}}} = \frac{{\gamma \rho \left( {\sin \theta - \frac{{\mu b\cos \theta }}{{2\rho }}} \right)}}{{\mu K}}\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right), $ | (8) |
| $ P = \frac{{\gamma \rho \left( {\sin \theta - \frac{{\mu b\cos \theta }}{{2\rho }}} \right)}}{\mu }\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right) + \gamma b\cos \theta . $ | (9) |
当l=b趋于无穷大时,ρ趋近无穷大,有
| $ {P_{\rm{V}}} = \gamma z(\sin \theta - 2\mu \cos \theta ), $ | (10) |
| $ {P_{\rm{h}}} = \gamma z(\sin \theta - 2\mu \cos \theta )/K. $ | (11) |
再取θ为90°,则式(10)和(11)可以简化成PV=γz,Ph=γz/K,显然这是断层破碎带半无限大且垂直时的情况,也就是半无限大弹性地基地应力的一般解,是筒仓理论解的一种特殊情况.
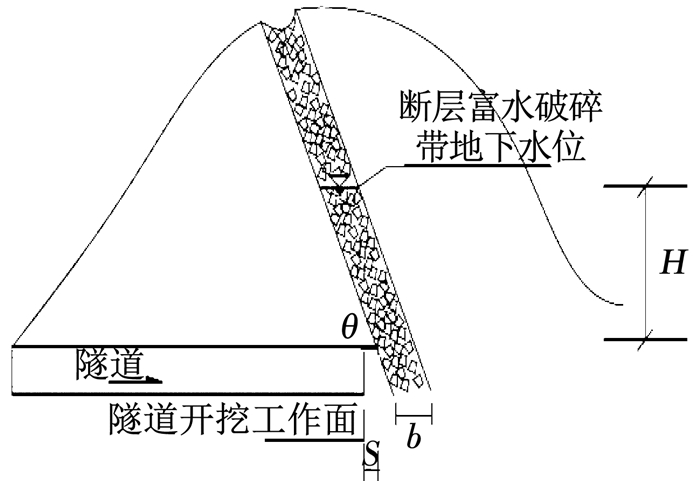
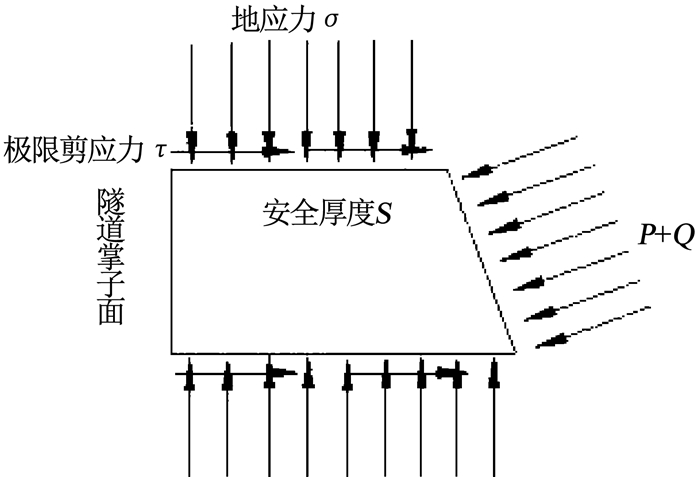
2.3 断层与隧道轴线正交突水模式及力学模型未胶结的富水断层破碎带位于隧道掌子面前方的突水模式以及防突岩体力学模型[5]如图 3,4所示.基于极限平衡原理,由图 4所示的岩塞破坏力学模型,可以得到该模型下富水断层破碎带发生突水突泥时的力学极限平衡条件是作用在临界掌子面上侧向压力的水平分量FS与岩盘阻力FH相等,即FS=FH.根据力学平衡条件便可求出隧道发生突水突泥时的最小安全厚度S.该模型下破坏首先发生在掌子面前上方,防突岩墙厚度最小的部分,然后地下水孕育发展最终防突岩墙发生整体破坏.
|
图 3 断层破碎带与隧道轴线正交的突水模式[5] Fig. 3 Water inrush pattern orthogonal to the tunnel axis in the fault fracture zone[5] |
|
图 4 岩塞力学模型 Fig. 4 Mechanical model of rock plug |
水压力和地应力作用在临界掌子面垂直压力的水平分量
| $ {F_{\rm{s}}} = (P + Q)A\sin \theta = \frac{{\rm{ \mathit{ π} }}}{4}{D^2}(P + Q). $ | (12) |
防突岩盘的岩盘阻力FH由力学模型可以推出
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\rm{H}}} = {\rm{ \mathit{ π} }}DS\tau , }\\ {\sigma = \sum {{\gamma _i}} {H_i}, }\\ {\tau = \sigma \tan {\varphi ^\prime } + {c^\prime } = \sum {{\gamma _i}} {H_i}\tan {\varphi ^\prime } + {c^\prime }.} \end{array}} \right. $ | (13) |
根据力学平衡方程和筒仓理论结果得出岩塞力学模型下最小安全厚度的表达式如下
| $ \begin{array}{l} S = \frac{{P + Q}}{{4\tau }}D = \\ \frac{{\frac{{\gamma \rho \left( {\sin \theta - \frac{{\mu b\cos \theta }}{{2\rho }}} \right)}}{\mu }\left( {1 - \exp \left( { - \frac{{\mu Kz}}{\rho }} \right)} \right) + \gamma b\cos \theta + {\gamma _{\rm{w}}}h}}{{4\left( {\sum {{\gamma _i}} {H_i}\tan {\varphi ^\prime } + {c^\prime }} \right)}}. \end{array} $ | (14) |
式中:γi为上覆第i层土的容重,kN/m3; γ为断层破碎带岩体容重,kN/m3; Hi为上覆第i层岩层的厚度,m; ∑Hi防突岩墙中心的埋深,m; P为断层岩盘所受地应力, kPa; Q为掌子面前方岩墙中心处的水压力,kPa; φ′, c′分别为防突岩墙墙体的饱和内摩擦角和饱和黏聚力,kPa; θ为断层破碎带倾角,(°); μ为摩擦系数; D为隧道的直径或等效直径,m; z为计算点处的埋深,m.
考虑开挖扰动的影响,选择爆破开挖方式,岩体受爆破开挖扰动损伤后阻水能力也大幅下降,可视为无阻水能力岩带,即称为爆破开挖扰动损伤带.本文选用爆破开挖扰动损伤带的取值为1.50 m[19],则最小安全距离为(S+1.5)m.
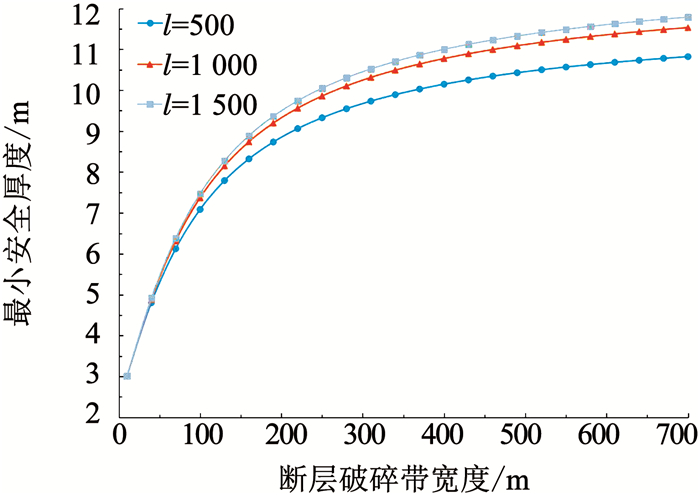
2.4 最小安全厚度影响因素分析由式(14)可以明显看出,隧道埋深、断层破碎带的宽度、断层破碎带水头高度、容重还有防突岩体的物理力学性质均对最小安全厚度有影响.埋深、水头高度、容重对最小安全厚度的影响基本上是线性的,随着埋深、水头高度、容重的增大而增大,与文献[14]的结论基本一致.本文重点基于筒仓理论分析得到了断层破碎带的宽度,以及截面水力半径ρ的影响.水力半径与断层破碎带宽度和断层延展长度有关,在不同延伸长度下,最小安全厚度随断层破碎带宽度变化如图 5所示.可以看出,在断层破碎带延伸长度分别为500,1 000,1 500 m情况下,其他各参数取值如下:γ′=20 kN/m3,φ′=25°,c′=300 kPa,γ=18 kN/m3,μ=0.1,D=20 m,Q=3 500 kPa, H=500 m, K=1.2,θ=90°.随着断层破碎带宽度的增大,最小安全厚度逐渐趋于一定值,即宽度和长度均无穷大情况.另外在延展长度较大的情况下,长度的变化对于安全厚度的影响较小.由图 5可以看出,在宽度小于500 m的情况下,最小安全厚度随断层破碎带宽度变化特别明显,差距很大,而在实际工程中断层破碎带宽度从几十厘米到几百米不等,正是处于变化特别大的范围中,因而在确定最小安全厚度时,考虑断层破碎带宽度的影响特别有必要,而筒仓理论可以很好地实现这一点.
|
图 5 不同长度下最小安全厚度随断层破碎带宽度变化 Fig. 5 Curve of minimum safe thickness varying with the width of fracture zone at different lengths |
未胶结的富水断层破碎带位于隧道开挖轮廓线外侧的突水模式以及防突厚度力学模型[5]如图 6,7所示.富水张性断层破碎带位于隧道开挖轮廓线外的防突岩墙简化成两端固定的固支梁,固支梁的长度即为断层破碎带的长度L,断层破碎带两端就是固定端两端,梁上受均布荷载P+Q的作用.梁的截面取矩形截面尺寸为B×S, S为矩形的宽度,B为长度,随断层倾角的变化取值不同,不考虑防突岩墙的自重.

|
图 7 固支梁突水模型 Fig. 7 Water inrush model of clamping beam |
根据力学知识可知,固支梁的最大弯矩和最大剪力均出现在两端固定端[20],即
| $ \left\{ {\begin{array}{*{20}{l}} {M = \frac{{(P + Q)}}{{12}}{L^2}, }\\ {Q = \frac{{(P + Q)}}{2}L.} \end{array}} \right. $ | (15) |
固支梁按抗弯强度准则计算:
| $ {\sigma _{\max }} = \frac{M}{{{I_{\rm{Z}}}}}{y_{\max }} = \frac{{6M}}{{B{S^2}}} \le [\sigma ], $ | (16) |
| $ S \ge n\sqrt {\frac{{(P + Q){L^2}}}{{2B[\sigma ]}}} . $ | (17) |
固支梁按抗剪强度准则计算:
| $ {\tau _{\max }} = \frac{{Q{S_{{\rm{Z}}\max }}}}{{{I_{\rm{Z}}}B}} = \frac{{3Q}}{{2BS}} \le [\tau ]. $ | (18) |
| $ S \ge n\frac{{3(P + Q)}}{{4B[\tau ]}}L. $ | (19) |
式中:[σ]为岩体许用抗弯强度,[τ]为岩体许用抗剪强度,L为与断层破碎带平行隧道临空面长度,S为岩墙安全厚度,其他参数同上文.因未考虑开挖扰动圈的影响,最小安全厚度需要乘以一个安全系数n, 然后最小安全厚度要取按抗弯强度和抗剪强度计算的安全厚度数值中的较大值,这里只考虑未支护情况.隧道轴线与断层破碎带平行情况下工程中几乎不会发生突水情况,因为在设计时取一个大一点的安全系数,即远离断层是完全可以做到的也不会增加大的成本.
3 工程案例 3.1 永莲隧道工程应用永莲隧道隧址区地质构造发育,隧道出口段以砂岩、页岩及灰岩为主,次生构造较为发育,隧道左侧发育一条与隧道同向的大型断裂带F5,并以F5断裂带为主干,衍生F1~F4 4条次生断层破碎带,其中F2断层破碎带对隧道影响最显著.断层破碎带岩体破碎-极破碎,采芯率为55%~65%,RQD < 10,[fa0]=400 kPa.进口左洞在K91+313-364附近与F2断层相交(设计线与地面线高差185 m).进口右洞在K91+389-425附近与F2断层相交(设计线与地面线高差198 m)[12].永莲隧道设计为双向分离式隧道,隧道开挖断面高度为9.06 m,宽度为12.6 m,单洞长约2.6 km,隧道平均埋深180 m,地下水位距离隧道拱顶约150 m,隧道进口施工至揭露F2断层时发生大规模塌方、突水突泥灾害.F2断层与隧道轴线45°相交,倾向E,倾角84°,宽度15~35 m,查明延伸长度520 m,断层破碎带物质泥化后主要呈流塑状态,看成Ⅵ围岩,容重16 kN/m3,泊松比0.45,内摩擦角20°.正常围岩段则主要以泥岩、页岩为主,遇水不崩解可作为相对隔水层,可以看成是Ⅴ围岩, 对应围岩的物理力学为:容重20 kN/m3,泊松比0.4,黏聚力150 kPa,内摩擦角25°,D=12.6 m,H=180 m, 地下水位高度h=150 m,θ=84°,断层长度L=520 m,宽度b=35 m,断层泥饱和呈流塑状态,摩擦阻力取μ=0.1,侧压力系数K取1.2,爆破开挖扰动距离取1.5 m,分别将数据代入式(9)和(13)得P=1 889 kPa, τ=1 829 kPa,Q=γwh=1 500 kPa, 再将其代入式(14)得S=5.84 m加上扰动距离1.5 m, 最终最小安全厚度为7.34 m.
显然,当防突厚度接近7.34 m时,需要采取相应的措施防止突水,而永莲隧道接近F2断层破碎带时并没有做出相关应对措施,而实际工程结果证明,当掌子面揭露F2断层后,隧道发生了多次大规模灾害.
3.2 祁连山隧道工程应用祁连山隧道位于祁连山冷龙岭断层褶皱带,通过钻探、物探及地表地质调绘,隧道共含有F6, F7等2条断层破碎带.F6断层为逆断层,其上盘、下盘分别为志留系下统板岩、二叠系砂岩.断层带以断层角砾为主,且岩体较为破碎.隧道洞身通过F6断层地段为DK336+050-140,长约90 m.F7断层为逆断层,断层产状为其上盘、下盘分别为志留系下统板岩、泥盆系砂岩.F7断层属冷龙岭深断裂,其于加里东早期或更早时形成,并在家里东晚期时受到强烈挤压,致使活动期长,规模巨大.隧道洞身通过F7断层地段为DK337+320-450,长约130 m.施工过程中预留了12 m的安全厚度,采取一些措施顺利地通过了断层破碎带没有发生突水突泥事故[16].根据地质资料,断层破碎带处隧道埋深750 m, 水头高度350 m, 洞径20 m宽,断层面摩擦系数μ取0.1,侧压力系数K取1.2,开挖扰动距离取1.5 m, 隧道岩盘处岩体容重20 kN/m3,摩擦角25°,内聚力300 kPa,断层破碎带处岩体容重18 kN/m3,断层破碎带倾角取90°计算.
用筒仓理论建立的模型和式(9), (13), (14)计算得到过F6断层破碎带宽度b=90 m的最小防突安全厚度8.52 m, 通过F7断层,断层破碎带宽度b=130 m时最小防突安全厚度9.66 m.而在洞室实际开挖过程中,取安全距离为12 m,采取相应的措施,安全通过了断层破碎带地段.在工程施工中安全距离往往需要理论值乘以大于1的安全系数n,取n=1.2则按照筒仓理论计算得到的理论值换成实际值得到10.22和11.59 m,和实际工程中的预留厚度12 m很接近,说明理论求解出的最小安全厚度具有一定的可靠性.
4 结论与展望1) 首次将筒仓理论引入到隧道断层破碎带突水的力学判据研究中,为未胶结的大倾角断层破碎带隧道突水、突泥最小安全隔水岩层厚度计算提供了一种新思路和方法.
2) 分别建立了隧道轴线与富水断层破碎带正交和水平两种情况下的力学模型,得到最小防突安全厚度的计算公式,考虑了断层破碎带宽度的影响,得到在断层破碎带宽度小于500 m,特别是200 m以内的情况下,断层破碎带宽度对于最小安全厚度的影响非常明显的结论.
3) 将研究成果应用于永莲隧道和祁连山隧道工程,对理论计算结果与实际工程结果进行比较,与实际工程结果具有较好的一致性,证明了本文得到的力学判据具有一定的合理性和有效性.
4) 本文Janssen公式推导过程中假定了垂直压力与水平压力之比K为一常数,而实际情况中K会随着埋深高度而变化,目前还没有成熟的理论结果,进一步研究可以考虑K的变化情况.
| [1] |
钱七虎. 隧道工程建设地质预报及信息化技术的主要进展及发展方向[J]. 隧道建设, 2017, 37(3): 251. QIAN Qihu. Main developments and directions of geological prediction and informatized technology of tunnel construction[J]. Tunnel Construction, 2017, 37(3): 251. DOI:10.3973/j.issn.1672-741X.2017.03.001 |
| [2] |
李术才, 林鹏, 许振浩, 等. 基于条分法原理的充填型岩溶蓄水构造突水突泥最小安全厚度[J]. 岩土力学, 2015, 36(7): 1989. LI Shucai, LIN Peng, XU Zhenhao, et al. Minimum safety thickness of water and mud inrush induced by filled-type karst water bearing structures based on theory of slice method[J]. Rock and Soil Mechanics, 2015, 36(7): 1989. DOI:10.16285/j.rsm.2015.07.021 |
| [3] |
李廷春, 吕连勋, 段会玲, 等. 深埋隧道穿越富水破碎带围岩突水机理[J]. 中南大学学报(自然科学版), 2016, 47(10): 3469. LI Tingchun, LYU Lianxun, DUAN Huiling, et al. Water burst mechanism of deep buried tunnel passing through weak water-rich zone[J]. Journal of Central South University (Science and Technology), 2016, 47(10): 3469. DOI:10.11817/j.issn.1672-7207.2016.10.025 |
| [4] |
李晓昭, 罗国煜, 陈忠胜. 地下工程突水的断裂变形活化导水机制[J]. 岩土工程学报, 2002, 24(6): 695. LI Xiaozhao, LUO Guoyu, CHEN Zhongsheng. The mechanism of deformation and water conduction of fault due to excavation in water inrush in underground engineering[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 695. DOI:10.3321/j.issn:1000-4548.2002.06.005 |
| [5] |
罗雄文, 何发亮. 深长隧道突水致灾构造及其突水模式研究[J]. 现代隧道技术, 2014, 51(1): 21. LUO Xiongwen, HE Faliang. A study of geological structures inclined to disaster and models of water burst in deep-buried long tunnels[J]. Modern Tunnelling Technology, 2014, 51(1): 21. DOI:10.13807/j.cnki.mtt.2014.01.006 |
| [6] |
张庆松, 王德明, 李术才, 等. 断层破碎带隧道突水突泥模型试验系统研制与应用[J]. 岩土工程学报, 2017, 39(3): 417. ZHANG Qingsong, WANG Deming, LI Shucai, et al. Development and application of model test system for inrush of water and mud of tunnel in fault rupture zone[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(3): 417. DOI:10.11779/CJGE2017.03.004 |
| [7] |
WANG Y C, JING H W, ZHANG Q, et al. Prediction of collapse scope of deep-buried tunnels using pressure arch theory[J]. Mathematical Problems in Engineering, 2016, 7: 1. DOI:10.1155/2016/2628174 |
| [8] |
李术才, 李晓昭, 靖洪文, 等. 深长隧道突水突泥重大灾害致灾机理及预测预警与控制理论研究进展[J]. 中国基础科学, 2017, 19(3): 27. LI Shucai, LI Xiaozhao, JING Hongwen, et al. Research development of catastrophe mechanism and forecast controlling theory of water inrush and mud gushing in deep long tunnel[J]. China Basic Science, 2017, 19(3): 27. DOI:10.3969/j.issn.1009-2412.2017.03.005 |
| [9] |
宋瑞刚, 张顶立, 文明. 穿越断层破碎带深埋隧道围岩失稳的突变理论分析[J]. 土木工程学报, 2015, 48(增刊1): 289. SONG Ruigang, ZHANG Dingli, WEN Ming. The cusp catastrophe theory analysis for instability of deep-buried tunnels surrounding rock through fault fracture zone[J]. China Civil Engineering Journal, 2015, 48(S1): 289. |
| [10] |
张明聚, 郜新军, 郭衍敬. 海底隧道突水分析及其在翔安隧道中的应用[J]. 北京工业大学学报, 2007, 33(3): 273. ZHANG Mingju, GAO Xinjun, GUO Yanjing. Analysis of water inrush in under sea tunnel and its application in Xiang'an tunnel[J]. Journal of Beijing University of Technology, 2007, 33(3): 273. DOI:10.3969/j.issn.0254-0037.2007.03.010 |
| [11] |
张雨帆, 周佳媚, 周生波, 等. 基于流固耦合原理隧道穿越富水断层带设防长度研究[J]. 铁道标准设计, 2018(8): 1004. ZHANG Yufan, ZHOU Jiamei, ZHOU Shengbo, et al. Study on tunnel through the water-rich fault fracture zone based on solid-fluid coupling[J]. Railway Standard Design, 2018(8): 1004. DOI:10.13238/j.issn.1004-2954.201708290006 |
| [12] |
王德明.泥质断层破碎带隧道突水突泥灾变机理研究及应用[D].山东: 山东大学, 2017 WANG Deming. Inrush of water and clay disaster mechanism and application research on politic fault fracture zone tunnel[D]. Shandong: Shandong University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10422-1017081867.htm |
| [13] |
任少强, 谭忠盛, 张德华. 碎屑流地层大断面铁路隧道施工技术研究[J]. 土木工程学报, 2015, 48(增刊1): 368. REN Shaoqiang, TAN Zhongsheng, ZHANG Dehua. Research on construction technique of large-section railway tunnels in debris flow strata[J]. China Civil Engineering Journal, 2015, 48(S1): 368. |
| [14] |
于琳茗, 郭永春, 张志强. 隧道掘进掌子面与前方碎屑流区域安全距离的计算[J]. 铁道建筑, 2016(4): 47. YU Linming, GUO Yongchun, ZHANG Zhiqian. Calculation about safe distance for tunnel driving between working face and debris flow area ahead[J]. Railway Engineering, 2016(4): 47. DOI:10.3969/j.issn.1003-1995.2016.04.13 |
| [15] |
张志强, 阚呈, 孙飞, 等. 碎屑流地层隧道发生灾变的模型试验研究[J]. 岩石力学与工程学报, 2014, 33(12): 2451. ZHANG Zhiqiang, KAN Cheng, SUN Fei, et al. Experimental study of catastrophic behavior for NATM tunnel in debris flow strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2451. DOI:10.13722/j.cnki.jrme.2014.12.010 |
| [16] |
陈天宇.碎屑流地层隧道区域渗流场以及发生灾变的模型试验研究[D].西安: 西南交通大学, 2013 CHEN Tianyu. Study on regional seepage field of NATM tunnel and modal tests of catastrophe occurrence in debris flow strata[D]. Xi'an: Southwest Jiaotong University, 2013 http://d.wanfangdata.com.cn/Thesis/Y2335213 |
| [17] |
郭慧珠.筒仓中物料流动特性研究[D].太原: 太原科技大学, 2014 GUO Huizhu. Study on the material properties in silos[D]. Taiyuan: Taiyuan University of Science and Technology, 2014 |
| [18] |
张光武. 基于筒仓理论的近接断层掌子面稳定分析模型[J]. 地下空间与工程学报, 2016, 12(增刊2): 663. ZHANG Guangwu. Stability analysis model of tunnel face closed to fault based on silo theory[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(S2): 663. |
| [19] |
李术才, 袁永才, 李利平, 等. 钻爆施工条件下岩溶隧道掌子面突水机制及最小安全厚度研究[J]. 岩土工程学报, 2015, 37(2): 313. LI Shucai, YUAN Yongcai, LI Liping, et al. Water inrush mechanism and minimum safe thickness of rock wall of karst tunnel face under blast excavation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 313. DOI:10.11779/CJGE201502015 |
| [20] |
张军伟, 谭阳, 陈拓, 等. 岩溶隧道侧部岩盘突水机制研究[J]. 公路交通科技, 2017, 34(5): 109. ZHANG Junwei, TAN Yang, CHEN Tuo, et al. Study on mechanism of batholite water inrush in lateral karst tunnel[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 109. DOI:10.3969/j.issn1002-0268.2017.05.015 |
 2020, Vol. 52
2020, Vol. 52

