目前,存在于中国的大量钢结构建筑物和构筑物无时无刻不处于大气环境、海洋环境或工业环境的侵蚀之下,即使采用了构造和防护措施,其锈蚀仍然无法完全避免[1-3].发生锈蚀后的钢材表面会出现大量蚀坑,这些蚀坑造成的应力集中效应不仅会降低构件的承载性能,而且会加速疲劳裂纹的萌生和扩展,大幅降低疲劳寿命[4-5].因此,锈蚀钢材的表面分析对其承载和疲劳性能的研究具有重要意义.
随着分形理论的不断发展,许多学者采用分形维数作为评价材料表面不规则程度的参数.然而,简单分形维数通常不足以反映材料表面的丰富内涵[6-7],往往需要引入多重分形,即以一个分形维数的谱来描述被简单分形维数忽略的信息.郑山锁等[8]通过对混凝土断裂面的多重分形谱进行二次拟合,研究了谱线的变化规律;蒋国平等[9]通过多重分形谱得出了冲击荷载下混凝土表面的裂纹特性;严安等[10]通过多重分形谱建立了混凝土断面与其材料组成之间的关系.然而,多数文献集中在对混凝土断面的研究上,对钢材表面形貌进行的研究较少.
本文拟根据多重分形理论对不同锈蚀龄期下的钢材表面进行分析.通过扫描处于中性盐雾环境下的锈蚀钢试件,得到表面的几何形貌和测点的三维坐标值,计算其多重分形谱并根据特征参数Δα和Δf的变化规律来研究钢材的表面形貌与锈蚀龄期之间的关系.
1 试验 1.1 材料和试件根据《钢材力学性能及工艺性能试验取样规定》(GB/T 2975—1998),将来自同一批次的厚度为8 mm的Q235B钢板按轧制方向用气割切割成280 mm×50 mm的试件,长边沿钢板轧制方向.试件切割完成后,用打磨机除掉切割边缘的毛刺,再用丙酮清洗掉表面的油脂和灰尘,最后置于室内环境下干燥.
1.2 快速锈蚀试验试件制作完成后,置于锈蚀试验箱中且与水平方向成45°,如图 1所示.根据推荐性国家标准《金属和合金的腐蚀循环暴露在盐雾、“干”和“湿”条件下的加速试验》(GB/T20854—2007/ISO 14993:2001),以质量百分数为5%的NaCl溶液为腐蚀介质对试件进行喷雾试验.当试件上的液滴聚成股流下时,停止喷雾,翻转试件并重复上一步骤以保证两面锈蚀的一致性;喷雾每2 d进行一次,在试验开始后的第0, 30, 70, 110, 150, 250, 310, 370, 440天分别取出一组试件,试件编号见表 1.

|
图 1 腐蚀试件摆放示意 Fig. 1 Placement of corrosion pieces |
| 表 1 试件及锈蚀天数 Tab. 1 Specimens and corroded days |
试件取出后,首先用打磨机除掉其表面的锈蚀产物,然后浸没于12%的稀盐酸中,10~20 min后取出并用钢丝刷刷洗,接着放入Ca(OH)2溶液中除掉残余盐酸,最后蒸馏水清洗、干燥.
1.3 表面形貌扫描采用PS50三维非接触式表面形貌扫描仪对除锈后的试件表面进行扫描,如图 2(a)所示.参照文献[11-12]中关于扫描区域及参数的设置,将扫描中心设置为与试件几何中心重合,扫描范围为40 mm×20 mm(沿长度方向40 mm,扫描步长50 μm;沿宽度方向20 mm,扫描步长50 μm),如图 2(b)所示.由于本文的研究对象为钢试件表面,需对试件表面进行编号,将试件C0的正反两个表面分别记为C0-1和C0-2,以此类推.

|
图 2 PS50三维非接触式表面形貌扫描仪及测试区域 Fig. 2 PS50 3D profiler and the test area |
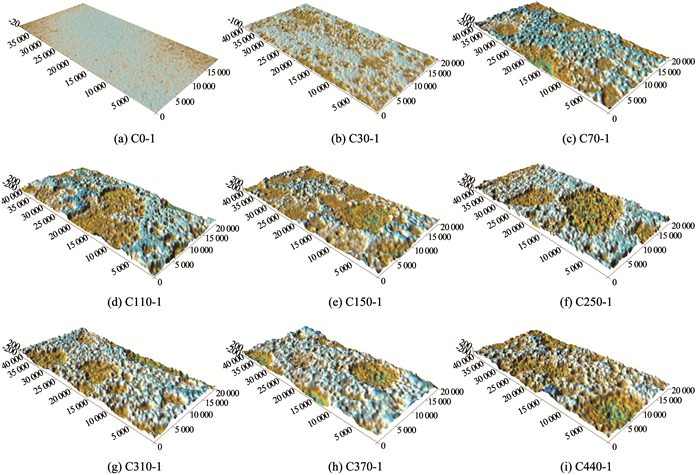
试件经过扫描后,其正、反表面的三维坐标值可以被PS50三维非接触式表面形貌扫描仪输出.由于处于同一龄期下的钢板其表面几何形貌基本相似,每个龄期下仅展示一个表面的几何形貌,如图 3所示.
|
图 3 表面形貌扫描结果 Fig. 3 Scanning results of surface topography |
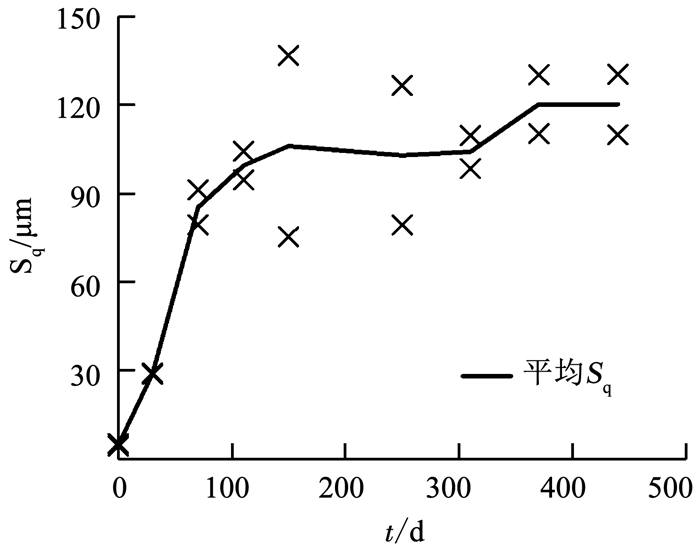
为了对试件表面进行评价,采用各扫描点高度值的均方根Sq作为参数来描述表面的粗糙程度[13],其计算方法参考推荐性国家标准GB/T 33523.2—2017《产品几何技术规范(GPS)表面结构区域法第2部分:术语、定义及表面结构参数》(ISO 25178-2:2012).试件表面的Sq随锈蚀龄期的变化规律如图 4所示.可以看出,当锈蚀龄期处于0~150 d时,试件表面的平均Sq随着锈蚀龄期的增长而增大.在前70 d,Sq呈现出较快的线性增长趋势,从4.87 mm增大到85.34 mm;在接下来的80 d内,Sq的增长速率明显放缓,仅从85.34 mm增大到106.08 mm.该阶段试件表面的形貌发生了明显的变化.从阶段初期相对平整的表面(图 3(a))变成了密布着片状蚀坑的表面(图 3(e)).
|
图 4 表面粗糙度随锈蚀龄期的变化 Fig. 4 Variation of surface roughness with corrosion age |
当锈蚀龄期处于150~310 d时,Sq不再随着锈蚀龄期的增长而发生明显变化,在160 d内仅从106.08 mm减小到104.00 mm.该阶段试件的表面相对稳定(图 3(e)~(g)),始终大量分布着片状蚀坑,且片状蚀坑内又密布着点状蚀坑.
当锈蚀龄期处于310~440 d时,Sq继续增大,但变化并不显著.在130 d内从104.00 mm增大到120.07 mm.该阶段试件的表面形貌与上一阶段类似,但粗糙程度大于上一阶段.
3 钢材表面的多重分形分析 3.1 多重分形谱的计算为了更加全面深入地研究锈蚀环境下试件表面的变化规律,根据多重分形理论对表面进行分析.首先,将测点的Z坐标全部转化为正值.记第i个测点的Z坐标为Zi,则该测点处的高度Hi定义为
| $ {H_i} = {Z_i} - {Z_{\min }}. $ | (1) |
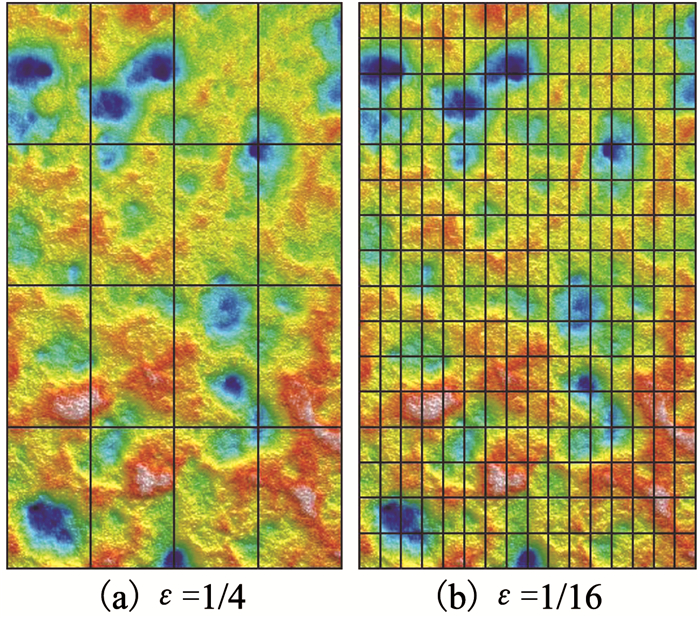
采用盒计数法统计高度分布概率.如图 5所示,将单元尺寸为ε的网格附在扫描平面上.计算每个网格内所有测点的平均高度, 第(i, j)个网格内测点的平均高度记作Hi, j,定义其高度分布概率为
| $ {P_{i, j}} = \frac{{{{\bar H}_{i, j}}}}{{\sum {{{\bar H}_{i, j}}} }}. $ | (2) |
|
图 5 盒计数法 Fig. 5 Box counting method |
高度分布概率Pi, j在不同的网格尺寸下具有不同的值,故可将Pi, j视为ε的函数,记作Pi, j(ε).把所有网格的高度分布概率组成的集合按照Pi, j(ε)的大小划分为一系列满足以下条件的子集:
| $ {P_{i, j}}(\varepsilon ) \propto {\varepsilon ^a}. $ | (3) |
同时,把每个子集内的网格数N(ε)和ε的关系定义为
| $ N(\varepsilon ) \propto {\varepsilon ^{ - f(\alpha )}}(\varepsilon \to 0). $ | (4) |
在以上两式中,α反映了各网格的奇异程度,称为奇异指数.f(α)则表示对应α值的子集分形维数,称为多重分形谱.
下面按照统计物理学的方法计算多重分形谱[14].定义q阶配分函数为
| $ {\chi _q}(\varepsilon ) \equiv \sum {{P_{i, j}}} {(\varepsilon )^q} = {\varepsilon ^{\tau (q)}}. $ | (5) |
结合式(3)和(4),式(5)可以改写为
| $ \begin{array}{*{20}{c}} {{\chi _q}(\varepsilon ) \equiv \sum {{P_{i, j}}} {{(\varepsilon )}^q} = \sum N (P){P^q} = }\\ {\sum {{\varepsilon ^{ - f(\alpha )}}} {\varepsilon ^{\alpha q}} = \sum {{\varepsilon ^{\alpha q - f(\alpha )}}} = {\varepsilon ^{\tau (q)}}.} \end{array} $ | (6) |
其中,N(P)为高度分布概率为P的网格数.由上式可得
| $ \sum {{\varepsilon ^{\alpha q - f(\alpha ) - \tau (q)}}} = 1. $ | (7) |
随着网格尺寸越来越小,即ε从正向趋近于零时,为保证式(7)左边不出现无穷大且趋近于1,αq-f(α)-τ(q)项也应该从正向趋近于零.故有
| $ f(\alpha ) = \alpha q - \tau (q). $ | (8) |
其中,τ(q)可由式(5)求得,即
| $ \tau (q) = \frac{{\ln {\chi _q}(\varepsilon )}}{{\ln \varepsilon }}(\varepsilon \to 0). $ | (9) |
α可从以下的微商得出
| $ \alpha = \frac{{{\rm{d}}\tau (q)}}{{{\rm{d}}q}}. $ | (10) |
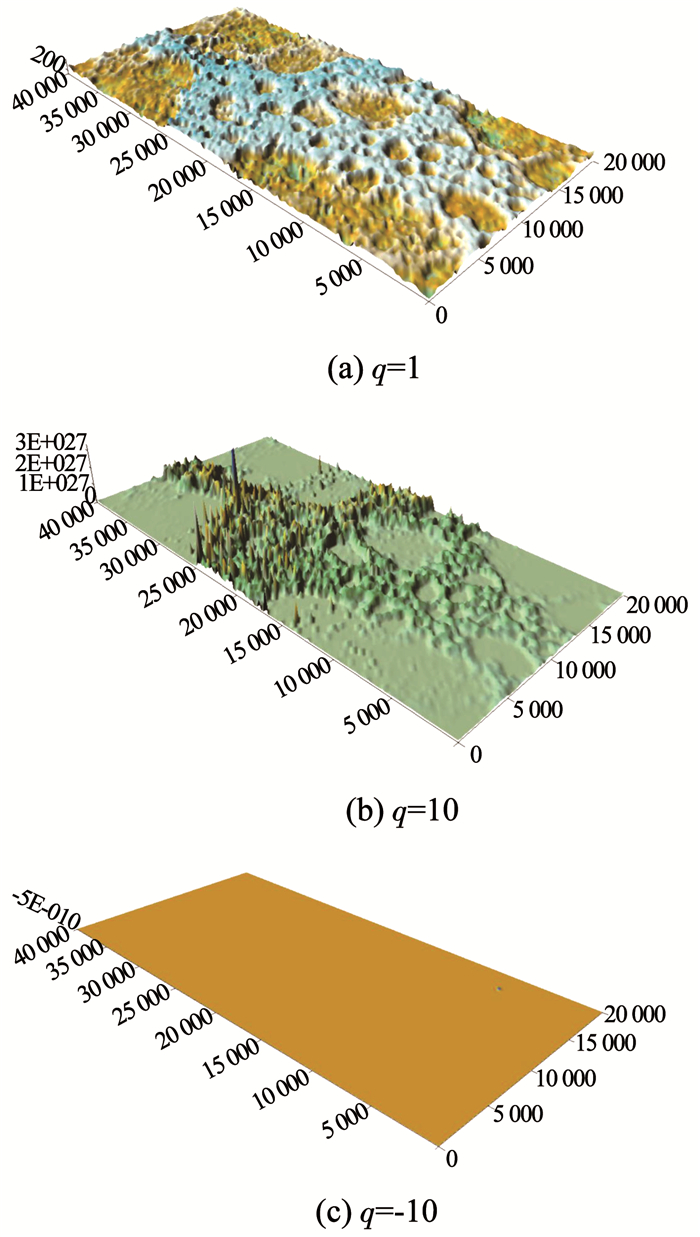
由式(5)可以得出,多重分形谱通过改变指数q来形成新表面以突出不同的高度区域,就像用不同放大倍数的显微镜观察表面.以C70-2为例,如图 6所示,若q取正值,则表面较大高度区域所占的权重增加,且q越大权重越大;若q取负值,则表面较小高度区域所占的权重增加,且q越小权重越大.理论上讲,q的范围越广,多重分形谱就越能完整地反映钢材表面的分形特征.但当q的取值范围增大到一定程度时,多重分形谱变化不大而计算量却急剧增加[14-15].在综合考虑了多重分形谱完整性和计算强度之后,选取|q|max=40作为q的取值范围.
|
图 6 C70-2表面取不同q值时的形貌 Fig. 6 Morphology of C70-2 surface with different q values |
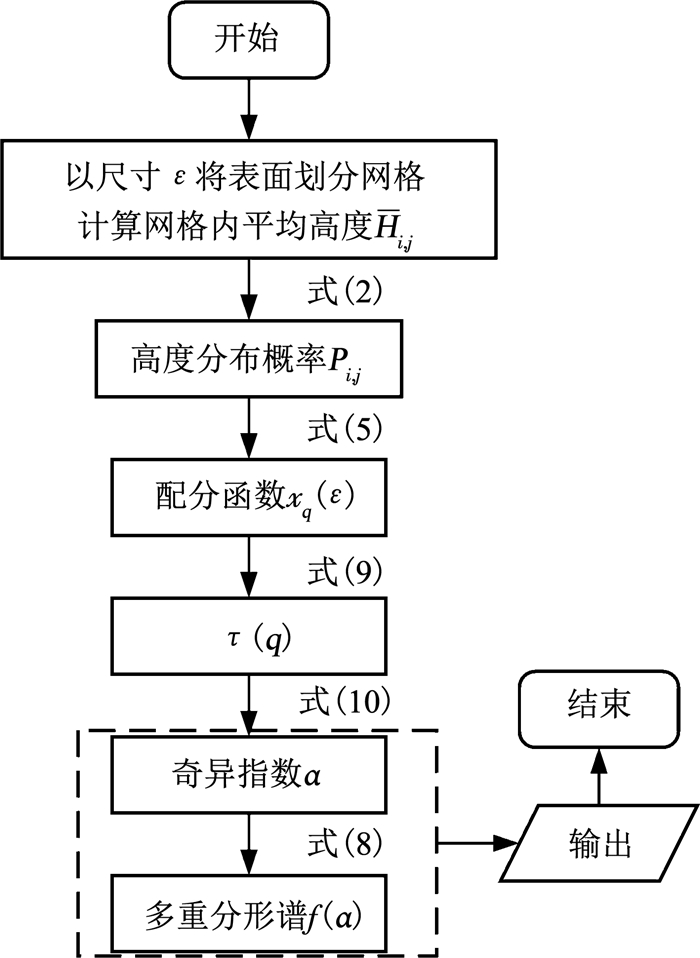
试件表面多重分形谱的计算利用MATLAB软件按照图 7所示的流程进行,计算完成后,将结果绘制于图 8中.
|
图 7 多重分形谱计算流程 Fig. 7 Flow diagram of multifractal spectrum calculation |
|
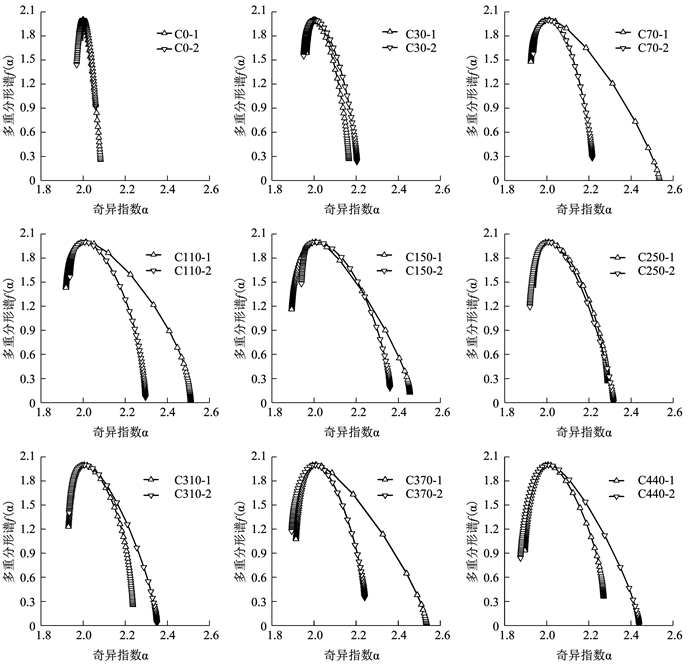
图 8 试件表面的多重分形谱 Fig. 8 Multifractal spectra of test pieces surfaces |
由于ε介于0和1之间,根据式(3)可以推得,αmin为权重q=40表面的奇异指数,f(αmin)为表面的分形维数.同理,αmax和f(αmax)则分别为权重q=-40表面的奇异指数和分形维数.定义多重分形谱的特征参数[15-16]:
| $ \Delta \alpha = {\alpha _{\max }} - {\alpha _{\min }}, $ | (11) |
| $ \Delta f = f\left( {{\alpha _{\min }}} \right) - f\left( {{\alpha _{\max }}} \right). $ | (12) |
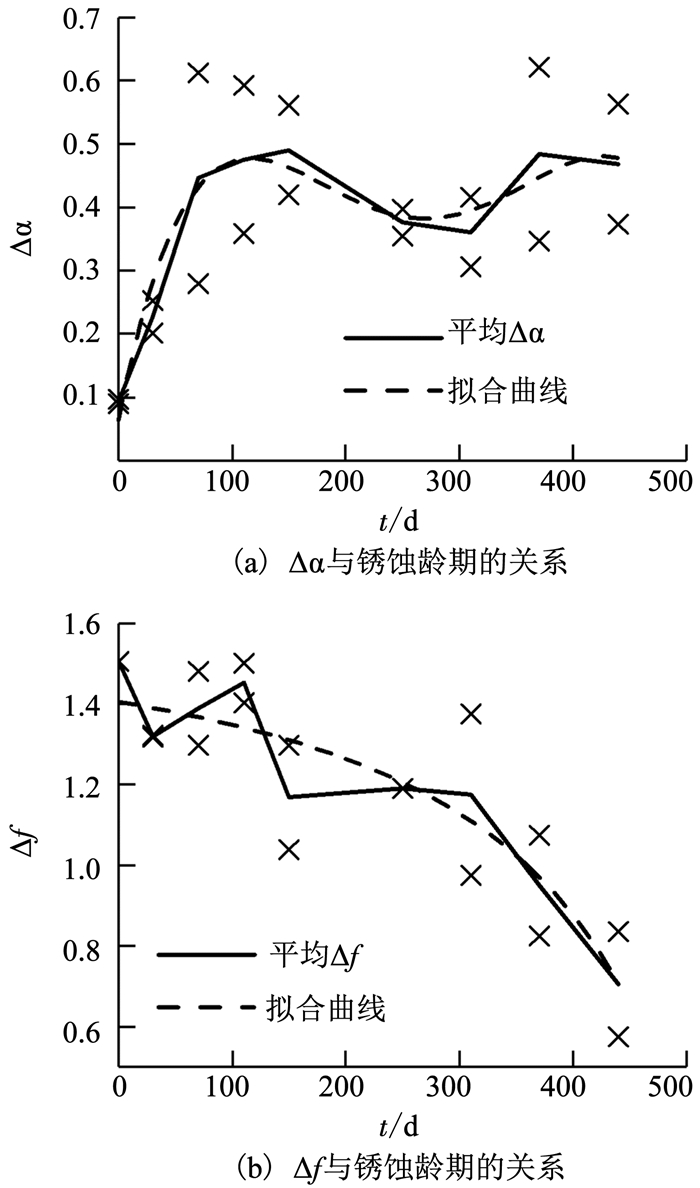
多重分形谱的谱宽Δα反映了试件在增加不同区域权重之后形成的新表面之间的差别,表征了试件表面的高度差异[14-15].图 9(a)表示了试件表面的Δα、各龄期下的平均Δα与锈蚀龄期之间的关系.可以看出,随着锈蚀龄期的增加,平均Δα呈现出“增大—减小—增大”的变化趋势.当锈蚀龄期处于0~150 d时,平均Δα随着龄期的增加而显著增大(约424.34%),且前70 d的增长速率明显大于后80 d;当锈蚀龄期处于150~310 d时,平均Δα发生了显著减小(约26.5%),且减小速率逐渐降低;而当锈蚀龄期处于310~440 d时,平均Δα先随着锈蚀龄期的增加而增大(约29.7%),而后趋于稳定.通过对平均Δα进行拟合,得到如下的四次函数关系,且拟合结果良好(COD为0.95).
| $ \begin{array}{l} \Delta \alpha = 0.06 + 0.01t - 6.62 \times {10^{ - 5}}{t^2} + \\ \;\;\;\;\;\;\;\;1.83 \times {10^{ - 7}}{t^3} - 1.69 \times {10^{ - 10}}{t^4}. \end{array} $ | (13) |
|
图 9 特征参数与锈蚀龄期之间的关系 Fig. 9 Relationship between characteristic parameters and corrosion age |
多重分形谱的谱差Δf则表征了表面不同高度区域之间的比例关系[14-15],若Δf为正,则大高度区域面积大于小高度区域,且Δf越大两区域面积相差越大;若Δf为负,则小高度区域面积大于大高度区域,且Δf越小两区域面积相差越大.图 9(b)显示了试件表面的Δf、各龄期下的平均Δf与锈蚀龄期之间的关系.可以看出,随着锈蚀龄期的增加,平均Δf表现出显著的下降趋势(约53.2%),且下降速率逐渐增大.通过对平均Δf进行拟合,得到如下的二次函数关系,且拟合效果良好(COD为0.88).
| $ \Delta f = 1.42 - 1.73 \times {10^{ - 4}}t - 3.04 \times {10^{ - 6}}{t^2}. $ | (14) |
文献[11]通过定义蚀坑的深度与直径之比Ra/Rc将蚀坑的形态分为3类:深窄型蚀坑(Ra/Rc>1)、浅宽型蚀坑(Ra/Rc≤1)以及二级蚀坑(在原蚀坑的基础上进一步演化出的蚀坑).参考以上分类,本节讨论随着锈蚀龄期的增加,试件的多重分形特征与表面形貌和蚀坑形态之间的关系.
对于未锈蚀试件,其表面相对平整,但不可避免地存在着由于制作、加工的误差或运输过程中的碰撞导致的细小凹陷.这些凹陷与平整区域之间的高度差异不大,因而Δα也较小;同时平整区域的面积要远远大于凹陷区,即二者的面积之差比较大,故Δf较大.
在锈蚀初期(0~70 d),钢材锈蚀主要导致蚀坑深度和数量的增加.该阶段试件表面的Δα较小而Δf较大,且呈点状分布着大量的深窄型蚀坑.随着锈蚀龄期的增加,蚀坑不断沿着深度方向进行扩展,造成试件表面的高度差异迅速提高,Δα也随之显著增大;同时,随着蚀坑数量的增加,试件表面小高度区域所占的比重不断增大,Δf随之减小.
在锈蚀中期(70~150 d),钢材锈蚀主要导致蚀坑的径向扩展和深度的增加.在这一阶段,由于蚀坑的径向扩展,其形态由锈蚀初期的深窄型逐渐过渡为浅宽型.相邻的蚀坑互相连通、融合,最终在试件表面形成了片状分布的小高度区域(图 3(d)),即小高度区域所占的比重继续增加,Δf进一步减小.同时,由于蚀坑沿深度方向的扩展,许多浅宽型蚀坑的底部出现了二级蚀坑,表面高度差异性进一步提升,Δα也进一步增大,但由于蚀坑的径向扩展分担了锈蚀反应的作用,Δα的增长速率远小于锈蚀初期.
在锈蚀后期(150~310 d),钢材锈蚀主要体现在大高度区域蚀坑在深度和径向的扩展上.在这一阶段,试件表面小高度区域的蚀坑变化不大,但大高度区域的蚀坑则沿着深度方向和径向快速地扩展,从而形成了更多的小高度区域(图 3(g)),致使Δf快速减小;同时,由于大高度区域高度的降低,试件表面的高差减小,Δα也随之减小.
当锈蚀龄期大于310 d时,试件表面的大高度区域已被锈蚀殆尽,面积进一步减小.在这一阶段,由于小高度区域的大量存在,钢材的锈蚀反应集中体现在二级蚀坑沿深度方向的扩展和数量的增加上(图 3(i)).该阶段与锈蚀初期较为相似,Δα显著增加,同时Δf继续减小.
综上,随着锈蚀龄期的增加,Δf始终表现出下降的趋势,表明试件表面不同高度区域之间的面积差逐渐减小,大高度和小高度区域之间的过渡越来越平缓.同时,试件表面的Δα经历了“显著增大—增速减缓—显著减小—继续增大”的变化过程.
4 结论1) 在锈蚀前期,钢材表面以点状零散分布的深窄型蚀坑为主;在锈蚀中期,钢材表面同时存在着深窄型蚀坑、浅宽型蚀坑和二级蚀坑;在锈蚀后期,钢材表面以浅宽型蚀坑为主.
2) 随着锈蚀龄期的增加,表征表面高度差异的Δα经历了“显著增大—增速减缓—显著减小—继续增大”的变化,其过程大致符合四次幂函数曲线.
3) 表征不同高度区域面积比例的Δf始终表现出大致符合二次曲线的下降趋势,表明不同高度区域之间的过渡越来越平缓.
| [1] |
贺栓海, 宋一凡, 黎宝松, 等. 海珠大桥静动力分析与荷载试验研究[J]. 西安公路交通大学学报, 1997(3): 45. HE Shuanhai, SONG Yifan, LI Baosong, et al. Study on the statical and dynamic analyses and loading experiments for the Haizhu Bridge[J]. Journal of Xi'an Highway University, 1997(3): 45. DOI:10.19721/j.cnki.1671-8879.1997.03.011 |
| [2] |
吴华新, 黄涛, 黄增红. 冶金企业钢结构锈蚀与防护处理[J]. 江西冶金, 2005, 25(2): 21. WU Huaxin, HUANG Tao, HUANG Zenghong. Protection handing and rusting of steel structure in the metallurgical enterprise[J]. Jiangxi Metallurgy, 2005, 25(2): 21. |
| [3] |
徐兴平, 黄东升, 李继志. 渤海八号平台腐蚀评估[J]. 中国海洋平台, 2001, 16(3): 39. XU Xingping, HUANG Dongsheng, LI Jizhi. The corrosion assessment of Bohai No.8 offshore platform[J]. China Offshore Platform, 2001, 16(3): 39. |
| [4] |
秦广冲.腐蚀坑对钢材应力集中系数及疲劳损伤影响研究[D].西安: 西安建筑科技大学, 2014 QIN Guangchong. The study of corrosion pits impact on steel stress concentration factor and fatigue damage[D]. Xi'an: Xi'an University of Architecture and Technology, 2014 |
| [5] |
杨晓华.腐蚀累积损伤理论研究与飞机结构日历寿命分析[D].南京: 南京航空航天大学, 2002 YANG Xiaohua. Study on corrosion cumulative damage rules and the calendar life of aircraft structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2002 http://d.wanfangdata.com.cn/Thesis/Y637329 |
| [6] |
王晓平, 吴自勤. 多重分形谱及其在材料研究中的应用[J]. 物理, 1999, 28(6): 26. WANG Xiaoping, WU Ziqin. Multifractal spectra and their applications in materials research[J]. Physics, 1999, 28(6): 26. |
| [7] |
张济忠. 分形[M]. 北京: 清华大学出版社, 1995: 363. ZHANG Jizhong. Fractal[M]. Beijing: Tsinghua University Press, 1995: 363. |
| [8] |
郑山锁, 任梦宁, 谢明, 等. 混凝土断裂面多重分形谱的二次拟合研究[J]. 工程力学, 2013, 30(5): 97. ZHENG Shansuo, REN Mengning, XIE Ming, et al. Study on quadratic fitting of multi-fractal spectrum of fracture surface in concrete[J]. Engineering Mechanics, 2013, 30(5): 97. DOI:10.6052/j.issn.1000-4750.2011.12.0822 |
| [9] |
蒋国平, 焦楚杰, 刘洁. 冲击作用下混凝土表面裂纹多重分形研究[J]. 混凝土, 2010(2): 35. JIANG Guoping, JIAO Chujie, LIU Jie. Multifractal study on the crack surface of concrete under impact loading[J]. Concrete, 2010(2): 35. DOI:10.3969/j.issn.1002-3550.2010.02.011 |
| [10] |
严安, 吴科如, 张东, 等. 混凝土材料断裂表面的多重分形特征研究[J]. 建筑材料学报, 2002, 5(1): 46. YAN An, WU Keru, ZHANG Dong, et al. Study on the multi-fractal characterization offracture surface of concrete materials[J]. Journal of Building Materials, 2002, 5(1): 46. |
| [11] |
XU Shanhua, WANG Youde. Estimating the effects of corrosion pits on the fatigue life of steel plate based on the 3D profile[J]. International Journal of Fatigue, 2015, 72: 27. DOI:10.1016/j.ijfatigue.2014.11.003 |
| [12] |
TANUMA A, MATSUOKA T, SUGAI M, et al. Non-contact 3D surface profiler based on white-light interferometry[J]. 電気学会研究会資料. mss, マイクロマシン·センサシステム研究会, 2006, 28: 21. |
| [13] |
ZUO Xue, TAN Yu, ZHOU Yuankai, et al. Multifractal analysis of three-dimensional surface topographies of GCr15 steel and H70 brass during wear process[J]. Measurement, 2018, 125: 196. DOI:10.1016/j.measurement.2018.04.082 |
| [14] |
孙霞, 吴自勤, 黄畇. 分形原理及其应用[M]. 合肥: 中国科学技术大学出版社, 2003: 53. SUN Xia, WU Ziqin, HUANG Yun. Fractal theory and its applications[M]. Hefei: China Science and Technology University Press, 2003: 53. |
| [15] |
SUN Xia, CHEN Huiping, WU Ziqin, et al. Multifractal analysis of Hang Seng index in Hong Kong stock market[J]. Physica A: Statistical Mechanics and its Applications, 2001, 291(1): 553. DOI:10.1016/S0378-4371(00)00606-3 |
| [16] |
ZHANG Guofu, LI Jingjing. Multifractal analysis of Shanghai and Hong Kong stock markets before and after the connect program[J]. Physica A: Statistical Mechanics and its Applications, 2018, 503: 611. DOI:10.1016/j.physa.2018.02.139 |
 2020, Vol. 52
2020, Vol. 52


