箱梁弯曲变形时,由于翼板中剪力滞后的影响使截面的应力分布不均匀,存在剪力滞效应.目前,剪力滞效应常用的分析方法有协调函数法、比拟杆法、变分法、有限元解法等.其中,E Reissner[1]基于最小势能原理的剪力滞效应分析方法,由于计算简便且精度较高而得到广泛应用.Kuzmanovic等[2]在此基础上分析了带对称伸臂的矩形箱梁的剪力滞.张士铎等[3]用有限差分法对变截面悬臂梁的变系数剪力滞微分方程进行分析,研究了负剪力滞规律.肖军等[4]采用级数展开的方法构造了剪力滞翘曲位移函数的解析解.雒敏等[5]提出了满足全截面轴力平衡的附加轴向位移参数用于荷载作用下双箱室简支箱梁剪力滞分布.何志刚等[6]研究了配筋对箱梁剪力滞效应的影响.
除荷载外,凡能引起箱梁轴向应力的作用都将引起剪力滞效应,如惯性力作用[7]、温度作用等.由于箱梁的竖向温度分布是非线性的[8-10],即使静定结构也会产生温度自应力.刘兴法[11]基于平截面假定建立了内力平衡的箱梁温度自应力简化分析方法,也是目前分析温度自应力的常用方法[12-14],本文将这种方法简称为平截面方法.事实上,在非线性温度梯度作用下箱梁并不符合平截面假定,而存在剪力滞效应,平截面方法无法考虑自应力中的剪力滞效应.郑日亮等[15-16]采用有限元方法研究了混凝土梁桥的温度剪力滞效应.文献[17]针对在非线性温度作用下,上、下翼板可能呈现同凹同凸的情况,提出了考虑翼板厚度范围内应力变化的双参数位移函数,建立单箱单室悬臂梁的自应力求解微分方程.但该方法在建立位移函数时,没有考虑截面的轴力平衡.
本文在文献[17]的基础上,结合雒敏等[5]的研究成果建立了满足截面轴力平衡的双参数位移函数,基于最小势能原理建立了箱梁温度自应力温度剪力滞效应的微分方程和边界条件.对简支箱梁在非线性温度作用下的自应力进行分析,讨论了简支箱梁温度自应力的变化规律,可供类似工程的计算分析参考.
1 温度剪力滞方程简支箱梁在非线性温度作用下上下翼板的轴向应力和变形示意如图 1所示.其中坐标原点位于端部截面形心点.在讨论其剪力滞效应时,做出如下假设:1)仅考虑温度沿z轴的分布,不考虑沿y轴及x轴的分布.2)忽略σy、σz对σx的影响.3)腹板仍符合平截面假定.4)简支梁的约束施加在梁端腹板中面上,x=0,z=0处加x和z方向约束,即ux=0, uz=0,x=l,z=0处仅施加z向约束,uz=0,其中l为全桥长度.
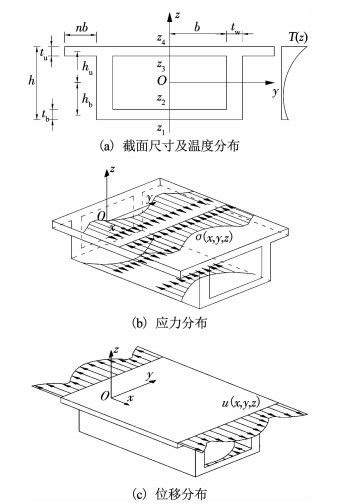
|
图 1 箱形简支梁温度自应力计算模型 Fig. 1 Calculation model of self-equilibrating thermal stresses in box girder |
在应用最小势能原理分析箱梁的变形时,梁的竖向位移w(x)、上翼板轴向位移uu(x, y, z)和下翼板轴向位移ub(x, y, z)分别为
| $ w = w(x), $ | (1) |
| $ {u_{\rm{w}}}(x,y,z) = {u_0}(x) - z\frac{{{\rm{d}}w}}{{{\rm{d}}x}} + Dv(x), $ | (2) |
| $ {u_{\rm{u}}}(x,y,z) = {u_0}(x) - z\frac{{{\rm{d}}w}}{{{\rm{d}}x}} + \left[ {z\beta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]v(x), $ | (3) |
| $ {u_{\rm{b}}}(x,y,z) = {u_0}(x) - z\frac{{{\rm{d}}w}}{{{\rm{d}}x}} + \left[ { - z\eta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]v(x). $ | (4) |
式中:u0(x)为截面形心点轴向位移,v(x)为剪切转角的最大差值,b为箱室净宽的一半,z为到截面形心的距离,nb为悬臂翼缘板宽度.D为满足全截面轴力自平衡的附加轴向位移.β和η为描述剪切转角最大差值方向与幅值的参数.当β=1,η=-1,且z分别取上下翼板中面到原点距离时,式(3)及(4)分别为荷载作用下的上下翼板位移函数.而在非线性温度梯度作用下,上下翼板出现剪力滞效应的原因不同,温度的影响和截面整体协调平衡的影响占比不同,导致v(x)的幅值和方向有较大差别.因此,引入β和η两个参数.
全截面的剪力滞翘曲位移函数为
| $ f\left( {y,z} \right) = \left\{ \begin{array}{l} z\beta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D,上中部翼板;\\ z\beta \left( {1 - \frac{{{{\left( {y - {t_{\rm{w}}} - b - nb} \right)}^2}}}{{{n^2}{b^2}}}} \right) + D,上悬臂翼板;\\ - z\eta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D,下翼板;\\ D,腹板. \end{array} \right. $ | (5) |
根据弯曲构件其截面轴力为零的平衡条件,即
| $ D = \frac{b}{3}\frac{{\eta \left( {z_2^2 - z_1^2} \right) - \beta (n + 1)\left( {z_4^2 - z_3^2} \right)}}{{b\left( {{z_4} - {z_3}} \right)(1 + n) + {t_{\rm{w}}}\left( {{z_4} - {z_1}} \right) + b\left( {{z_2} - {z_1}} \right)}}. $ | (6) |
在温度变化情况下,弹性体系的总势能Π可表示为
| $ \mathit{\Pi } = U + {U_{\rm{t}}}. $ | (7) |
式中:U表示体系温度变形过程中所存储的应变能.Ut表示温度变形势能.在温度作用下梁顺桥向应变的势能为
| $ {U_{\rm{t}}} = - \int_\Omega \varepsilon E\alpha T(z){\rm{d}}\mathit{\Omega }\mathit{.} $ | (8) |
式中:E为杨氏弹性模量,α为材料的热膨胀系数,T(z)为温度沿高度的分布函数.ε为梁的轴向应变.根据前述假定,可得梁腹板应变εw、上翼板应变εu和下翼板应变εb分别为
| $ {\varepsilon _{\rm{w}}} = u_0^\prime - z{w^{\prime \prime }} + D{v^\prime }, $ | (9) |
| $ {\varepsilon _{\rm{u}}} = u_0^\prime - z{w^{\prime \prime }} + \left[ {z\beta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]{v^\prime }, $ | (10) |
| $ {\varepsilon _{\rm{b}}} = u_0^\prime - z{w^{\prime \prime }} + \left[ { - z\eta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]{v^\prime }. $ | (11) |
对于对称截面,根据对称性,取一半进行势能计算.将式(9)~(11)代入Ut,得到不同部位的温度变形势能
| $ \begin{array}{l} {U_{{\rm{tw}}}} = - E\alpha {t_{\rm{w}}}\left( {{A_{{\rm{Tw}}}}\int_0^l {u_0^\prime } {\rm{d}}x - {S_{{\rm{Tw}}}}\int_0^l {{w^{\prime \prime }}} {\rm{d}}x + } \right.\\ \;\;\;\;\;\;\left. {D{A_{{\rm{Tw}}}}\int_0^l {{v^\prime }} {\rm{d}}x} \right). \end{array} $ | (12) |
| $ \begin{array}{l} {U_{{\rm{tu}}}} = - E\alpha b(1 + n)\left[ {{A_{{\rm{Tu}}}}\int_0^l {u_0^\prime } {\rm{d}}x - {S_{{\rm{Tu}}}}\int_0^l {{w^{\prime \prime }}} {\rm{d}}x + } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {\frac{2}{3}{S_{{\rm{Tu}}}}\beta + D{A_{{\rm{Tu}}}}} \right)\int_0^l {{v^\prime }} {\rm{d}}x} \right]. \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {{U_{{\rm{tb}}}} = - E\alpha b\left[ {{A_{{\rm{Tb}}}}\int_0^l {u_0^\prime } {\rm{d}}x - {S_{{\rm{Tb}}}}\int_0^l {{w^{\prime \prime }}} {\rm{d}}x + } \right.}\\ {\left. {\left( {D{A_{{\rm{Tb}}}} - \frac{2}{3}{S_{{\rm{Tb}}}}\eta } \right)\int_0^l {{v^\prime }} {\rm{d}}x} \right].} \end{array} $ | (14) |
式中:Utw、Utu和Utb分别为腹板、上翼板和下翼板的温度变形势能,
在温度作用下,梁发生轴向变形和弯曲变形,梁不同部位的应变能分别为
腹板:
| $ {U_{\rm{w}}} = \frac{1}{2}\int E {I_{\rm{w}}}{\left( {{w^{\prime \prime }}} \right)^2}{\rm{d}}x + \frac{1}{2}\int E {A_{\rm{w}}}{\left( {u_0^\prime + D{v^\prime }} \right)^2}{\rm{d}}x. $ | (15) |
上下翼板应变能:
| $ \begin{array}{l} {U_{\rm{u}}} = \frac{1}{2}\int_0^l {\rm{d}} x\int_0^b {\rm{d}} y\int_{{z_3}}^{{z_4}} {\left( {E\varepsilon _{\rm{u}}^2 + G\gamma _{\rm{u}}^2} \right)} {\rm{d}}z + \\ \frac{1}{2}\int_0^l {\rm{d}} x\int_{b + {t_{\rm{w}}}}^{b + {t_{\rm{w}}} + nb} {\rm{d}} y\int_{{z_3}}^{{z_4}} {\left( {E\varepsilon _{\rm{u}}^2 + G\gamma _{\rm{u}}^2} \right)} {\rm{d}}z. \end{array} $ | (16) |
| $ {U_{\rm{b}}} = \frac{1}{2}\int_0^l {\rm{d}} x\int_0^b {\rm{d}} y\int_{{z_1}}^{{z_2}} {\left( {E\varepsilon _{\rm{b}}^2 + G\gamma _{\rm{b}}^2} \right)} {\rm{d}}z. $ | (17) |
式中:
| $ {\gamma _{\rm{u}}} = \frac{{\partial u(x,y,z)}}{{\partial y}} = - \beta \frac{{2y}}{{{b^2}}}zv, $ | (18) |
| $ {\gamma _{\rm{b}}} = \frac{{\partial {u_{\rm{b}}}(x,y,z)}}{{\partial y}} = \eta \frac{{2y}}{{{b^2}}}zv. $ | (19) |
将式(9)~(11)及式(18)、(19)代入式(16)、(17)中得到上下翼板应变能,即
| $ \begin{array}{l} {U_{\rm{u}}} = \frac{1}{2}E{I_{\rm{u}}}\int_0^l {\left( {{w^{\prime 2}} + \frac{8}{{15}}{\beta ^2}{v^{\prime 2}} - \frac{4}{3}\beta {w^{\prime \prime }}{v^\prime }} \right)} {\rm{d}}x + \\ \frac{1}{2}E{S_{\rm{u}}}\int_0^l {\left[ {\frac{4}{3}D\beta {v^2} + \frac{4}{3}\beta {v^\prime }u_0^\prime - 2{w^{\prime \prime }}\left( {u_0^\prime + D{v^\prime }} \right)} \right]} {\rm{d}}x + \\ \frac{1}{2}E{A_u}\int_0^l {\left( {u_0^{\prime 2} + 2Du_0^\prime {v^\prime } + {D^2}{v^{\prime 2}}} \right)} {\rm{d}}x + \\ \frac{1}{2}\frac{{4G}}{{3{b^2}}}{I_u}{\beta ^2}\int_0^l {{v^2}} {\rm{d}}x. \end{array} $ | (20) |
| $ \begin{array}{l} {U_{\rm{b}}} = \frac{1}{2}E{I_{\rm{b}}}\int_0^l {\left( {{w^{\prime 2}} + \frac{8}{{15}}{\eta ^2}{v^{\prime 2}} + \frac{4}{3}\eta {w^{\prime \prime }}{v^\prime }} \right)} {\rm{d}}x + \\ \frac{1}{2}E{S_b}\int_0^l {\left[ { - \frac{4}{3}D\eta {v^{\prime 2}} - \frac{4}{3}\eta {v^\prime }u_0^\prime - 2{w^{\prime \prime }}\left( {u_0^\prime + D{v^\prime }} \right)} \right]} {\rm{d}}x + \\ \frac{1}{2}E{A_{\rm{b}}}\int_0^l {\left( {u_0^{\prime 2} + 2Du_0^\prime {v^\prime } + {D^2}{v^{\prime 2}}} \right)} {\rm{d}}x + \\ \frac{1}{2}\frac{{4G}}{{3{b^2}}}{I_{\rm{b}}}{\eta ^2}\int_0^l {{v^2}} {\rm{d}}x. \end{array} $ | (21) |
式中:Au=tub+nbtu,Su=Auhu,Iu=tubhu2+nbtuhu2,
则杆件总势能为
| $ \begin{array}{*{20}{c}} {\mathit{\Pi } = {U_{{\rm{tw}}}} + {U_{\rm{w}}} + {U_{{\rm{tu}}}} + {U_{\rm{u}}} + {U_{{\rm{th}}}} + {U_{\rm{b}}},}\\ {\mathit{\Pi } = - E\alpha \left[ {{T_1}\int_0^l {u_0^\prime } {\rm{d}}x - {T_2}\int_0^l {{w^{\prime \prime }}} {\rm{d}}x + \frac{2}{3}{T_3}\int_0^l {{v^\prime }} {\rm{d}}x} \right] + }\\ {\frac{1}{2}\int E {I_{\rm{w}}}{{\left( {{w^{\prime \prime }}} \right)}^2}{\rm{d}}x + \frac{1}{2}\int E {A_{\rm{w}}}u_0^{\prime 2}{\rm{d}}x + \frac{1}{2}\int E {A_{\rm{w}}}{D^2}{v^{\prime 2}}{\rm{d}}x + }\\ {\int E {A_{\rm{w}}}D{v^\prime }u_0^\prime {\rm{d}}x + \frac{1}{2}E{I_{\rm{s}}}\int_0^l {{w^{\prime \prime 2}}} {\rm{d}}x + }\\ {\frac{1}{2}E{I_{{\rm{s2}}}}\int_0^l {\frac{8}{{15}}} {v^2}{\rm{d}}x - \frac{1}{2}E{I_{{\rm{sl}}}}\int_0^l {\frac{4}{3}} {w^{\prime \prime }}{v^\prime }{\rm{d}}x + }\\ {\frac{1}{2}\frac{{4G}}{{3{b^2}}}{I_{{\rm{s2}}}}\int_0^l {{v^2}} {\rm{d}}x + \frac{1}{2}E{A_{\rm{s}}}\int_0^l {u_0^{\prime 2}} {\rm{d}}x + }\\ {\frac{1}{2}E{A_{{\rm{s}}1}}\int_0^l 2 u_0^\prime {v^\prime }{\rm{d}}x + \frac{1}{2}E{A_{{\rm{s}}2}}\int_0^l {{v^{\prime 2}}} {\rm{d}}x + }\\ {\frac{1}{2}E{S_{{\rm{sl}}}}\int_0^l {\frac{4}{3}} u_0^\prime {v^\prime }{\rm{d}}x + \frac{1}{2}E{S_{{\rm{s}}2}}\int_0^l {\frac{4}{3}} {v^{\prime 2}}{\rm{d}}x - }\\ {\frac{1}{2}E{S_{\rm{s}}}\int_0^l 2 u_0^\prime {w^{\prime \prime }}{\rm{d}}x - \frac{1}{2}E{S_{{\rm{s}}3}}\int_0^l 2 {w^{\prime \prime }}{v^\prime }{\rm{d}}x.} \end{array} $ | (22) |
式中:T1=twATw+bATu(1+n)+bATb,T2=twSTw+bSTu(1+n)+bSTb,T3=
将式(22)求变分,由其一阶变分等于零δΠ=0,可得非线性温度梯度作用下箱梁的微分方程和边界条件:
| $ - E\alpha {T_1} + EAu_0^\prime - E{S_{\rm{s}}}{w^{\prime \prime }} + \frac{2}{3}E{S_1}{v^\prime } = 0, $ | (23) |
| $ E\alpha {T_2} + EI{w^{\prime \prime }} - \frac{2}{3}E{S_2}{v^\prime } - E{S_{\rm{s}}}u_0^\prime = 0, $ | (24) |
| $ \frac{2}{3}E{S_2}{w^{\prime \prime }} - \frac{8}{{15}}E{S_3}{v^{\prime \prime }} + \frac{{4G{I_{{\rm{s2}}}}}}{{3{b^2}}}v - \frac{2}{3}E{S_1}u_0^{\prime \prime } = 0, $ | (25) |
| $ \left. {\left( { - \frac{2}{3}E\alpha {T_3} - \frac{2}{3}E{S_2}{w^{\prime \prime }} + \frac{8}{{15}}E{S_3}{v^\prime } + \frac{2}{3}E{S_1}u_0^\prime } \right)\delta v} \right|_0^l = 0. $ | (26) |
式中:S1=
若忽略式(23)中的-ESsw″+
| $ u_0^\prime = \frac{{\alpha {T_1}}}{A}, $ | (27) |
| $ {w^{\prime \prime }} = - \frac{{\alpha {T_2}}}{I}. $ | (28) |
则式(27)和(28)就是基于平截面假定所得截面的轴向变形和曲率.通常剪力滞引起杆件形心点的轴向变形很小,忽略式(23)中-ESsw″+
| $ I{w^{\prime \prime }} - \frac{2}{3}{S_2}{v^\prime } = - \alpha \left( {{T_2} - \frac{{{S_{\rm{s}}}{T_1}}}{A}} \right), $ | (29) |
| $ \frac{2}{3}{S_2}{w^{\prime \prime \prime }} - \frac{8}{{15}}{S_3}{v^{\prime \prime }} + \frac{{4G{I_{{\rm{s}}2}}}}{{3E{b^2}}}v = 0, $ | (30) |
| $ \left. {\left[ { - \frac{2}{3}{S_2}{w^{\prime \prime }} + \frac{8}{{15}}{S_3}{v^\prime } + \frac{2}{3}\alpha \left( { - {T_3} + \frac{{{S_1}{T_1}}}{A}} \right)} \right]\delta v} \right|_0^l = 0. $ | (31) |
式(29)~(31)的形式与文[17]的双参数相同,差别在于本文中的参数包括满足全截面轴力自平衡的附加轴向位移值D.为描述方便,将文献[17]的方法称为双参数法,本文方法称为修正双参数法.将式(29)进行求导,代入式(30)可得
| $ {v^{\prime \prime }} - {k^2}v = 0. $ | (32) |
其中
由此可得方程的通解为
| $ v = {c_1}\cosh kx + {c_2}\sinh kx. $ | (33) |
对于简支梁,杆件的边界条件可表示为
当x=0时,v′=ζ,则c2= ζ k;当x=l时,v′=ζ,则
式中:
由此可得
| $ v(x) = \frac{{\zeta (1 - \cosh kl)}}{{k\sinh kl}} \cdot \cosh kx + \frac{\zeta }{k}\sinh kx. $ | (34) |
对式(34)求导得
| $ {v^\prime }(x) = \frac{{\zeta (1 - \cosh kl)}}{{\sinh kl}} \cdot \sinh kx + \zeta \cosh kx. $ | (35) |
由此对式(27)和(29)积分可得
| $ {u_0} = \frac{{\alpha {T_1}}}{A}x + {D_1}, $ | (36) |
| $ {w^\prime } = - \frac{{\alpha {T_0}}}{I}x + \frac{{2{S_2}}}{{3I}}v(x) + {D_2}. $ | (37) |
式中D1和D2为积分常数,根据边界条件uw(0, ±b, 0)=u0(0)+Dv(0)=0;w′(0.5l)=0,可得
| $ {D_1} = - \frac{{D\zeta (1 - \cosh kl)}}{{k\sinh kl}}, $ | (38) |
| $ {D_2} = \frac{{\alpha {T_0}l}}{{2I}}. $ | (39) |
将式(34)、(36)、(37)代入式(3)和(4)即可求出上、下翼板的位移.则考虑剪力滞效应后翼板的自应力为
| $ {\sigma _{\rm{u}}} = E\left\{ {u_0^\prime (x) - z{w^{\prime \prime }} + \left[ {z\beta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]{v^\prime } - \alpha T(z)} \right\}, $ | (40) |
| $ {\sigma _{\rm{b}}} = E\left\{ {u_0^\prime (x) - z{w^{\prime \prime }} + \left[ { - z\eta \left( {1 - \frac{{{y^2}}}{{{b^2}}}} \right) + D} \right]{v^\prime } - \alpha T(z)} \right\}. $ | (41) |
以文献[18]无悬臂翼缘板箱梁为例,即令图 1(a)中n=0得单箱单室简支箱梁,截面几何参数和材料参数分别为b=3 m,tw=0.4 m,tu=tb=0.4 m,h=3.3 m,l=60 m,α=1×10-5/℃,E=35.5 GPa,G=15.2 GPa.假设箱梁的非线性温度梯度分布如图 2所示.
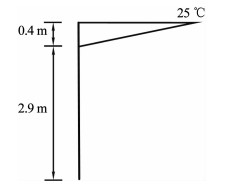
|
图 2 竖向温度分布 Fig. 2 Vertical temperature distribution |
为验证本文方法的合理性,对该箱梁分别采用有限元方法、双参数法、修正的双参数法和平截面假定方法进行计算.有限元模型如图 3所示,共有552 920个结点,441 600个面体单元.

|
图 3 有限元模型 Fig. 3 Finite element model |
图 4为x=57 m处上下翼板中面轴向应力的计算结果.基于平截面假定计算的应力在横桥向y方向顶板分布为常数,而有限元计算结果与修正双参数法计算结果均出现明显剪力滞现象.并且根据β和η的取值不同,幅度有所变化.当顶板的参数β与底板参数η的比值越大,顶板幅值越大,底板幅值越小.当β=0.64、η=0.32时,修正双参数法和有限元计算结果的变化规律吻合较好.本文其余讨论皆在β=0.64、η=0.32的基础上进行.
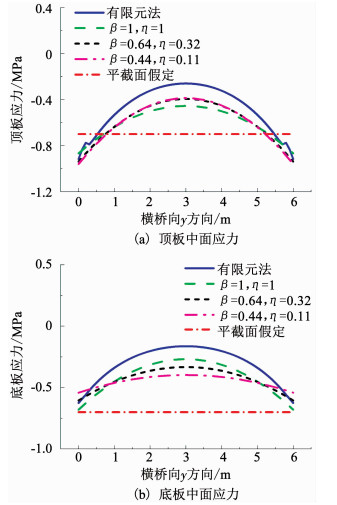
|
图 4 上下翼板中面应力(x=57 m) Fig. 4 Middle plane stresses of the top and bottom flanges(x=57 m) |
图 5为顺桥向x方向上翼板与腹板交角处的应力分布.图中包含了考虑D的修正双参数法、不考虑D的双参数法、有限元解以及平截面假定方法所得顺桥向应力.
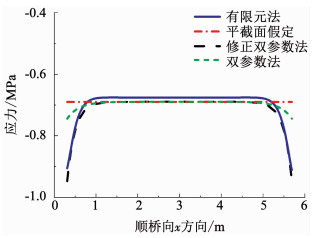
|
图 5 上翼板与腹板交角处轴向应力 Fig. 5 Axial stress at the corner of top flange and web plate |
计算结果表明:1)在非线性温度梯度作用下,有限元所得的同一高度轴向应力不是常量,而忽略剪力滞的平截面假定计算结果为常量,这表明箱梁在非线性温度作用下,将产生剪力滞效应.2)修正双参数法和双参数法在简支梁跨中附近区域的计算结果基本相同,主要差别在于支座附近.以有限元的计算结果为精确解,修正双参数法的应力结果比双参数法与有限元结果吻合更好,表明考虑D之后的位移函数与实际更为接近,从而提高了计算精度.3)由于剪力滞的影响,在简支梁的端部应力大于平截面的计算结果,影响范围为10 m左右,这表明对于简支梁而言,温度自应力所导致的剪力滞主要局限于支座附近的局部应力,影响范围约为1.5倍箱梁宽度.4)基于平截面假定的应力解沿全桥为常数-0.7 MPa,计算结果在梁中部的40 m范围内是可行的,而在端部10 m以内小于有限元解及双参数法的结果.如在57 m处,应力为-0.9 MPa.因此,按平截面假定计算简支箱梁温度自应力在工程上偏不安全.
图 6为x=57 m及x=45 m处腹板z向应力分布的计算结果.可以看出,基于平截面假定的温度自应力计算方法与本文的修正双参数法皆能较好地反应腹板自应力分布情况.其中,在简支梁端部1.5倍箱梁宽度距离内存在明显的剪力滞效应,在x=57 m处本文方法与有限元方法有偏差,但相差不大.在简支箱梁中间段剪力滞效应不明显,可认为符合平截面假定,因此,在x=45 m处腹板应力吻合较好.修正双参数法和基于平截面假定的计算方法中求得的腹板应力与有限元所求值相差较小,在计算过程中腹板采用平截面假定可满足工程计算精度要求.
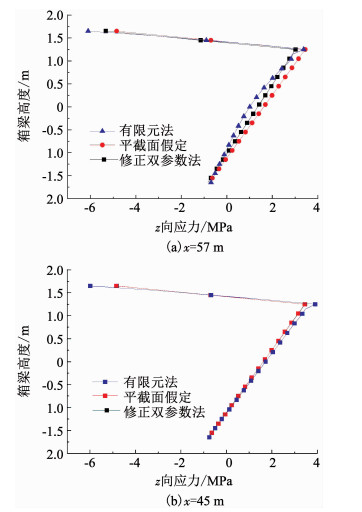
|
图 6 腹板处z向应力 Fig. 6 Axial stress of the web |
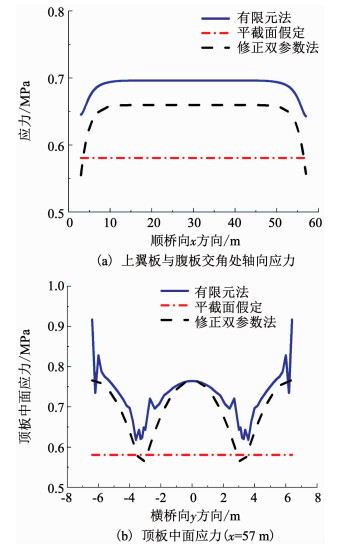
令悬臂翼板宽度为nb=3 m,截面其余的几何参数、材料参数和非线性温度分布同2.1.图 7为带悬臂翼板箱形截面的上翼板应力分布.其中图 7(a)为腹板内侧与上翼板中面交点处应力沿顺桥向x方向分布,图 7(b)为x=57 m处上翼板中面的应力沿横桥向y方向的分布图.计算结果表明,双参数法的计算结果与有限元法的结果相近,显示了良好的精度.对于平截面法所得的结果,即使在箱梁跨中附近也明显小于有限元的计算结果.这是由于平截面所得的应力为

|
图 7 带悬臂翼板截面上翼板中面应力 Fig. 7 Middle plane stresses of the top flanges with cantilever flange |
| $ \sigma _{\rm{u}}^0(z) = E\left[ {\frac{{\alpha {T_1}}}{A} + \frac{{\alpha {T_2}}}{I}z - \alpha T(z)} \right]. $ | (42) |
对于简支箱梁跨中附近,剪力滞效应很小而忽略情况下,由式(40)可得箱梁翼板的应力为
| $ {\sigma _{\rm{u}}} = E\left[ {\frac{{\alpha {T_1}}}{A} + \frac{{\alpha {T_0}}}{I}z - \alpha T(z)} \right]. $ | (43) |
对于无翼缘板截面,Ss=0,则T0=T2,因此,平截面假定的算法与双参数及有限元结果是吻合的.有翼缘板的箱形截面中上下翼板到形心的面积矩不能相互抵消,即Ss≠0,则T0=T2- SsT1 A ≠T2,由此导致平截面假定的计算结果即使在箱梁跨中附近也与有限元计算结果不同.这表明对于非对称截面,非线性温度引起的剪力将影响截面的曲率,在平截面假定中没有考虑这项影响而导致误差,在双参数法和修正双参数法中考虑了这项的影响而精度较高.
2.2.2 规范正温差分布以上两个算例中采用简化的局部三角形温度梯度分布,用以阐述非线性温度梯度作用下剪力滞效应的机理.真实桥梁暴露在大气环境中,受日辐射强度、桥梁方位、日照时间、地理位置、地形地貌等环境因素的影响而使温度分布非常复杂.许多学者对各种类型桥梁截面的温度分布进行了试验研究,提出了不同的竖向温度梯度模式[19].在实验研究的基础上,各国规范分别确定了相应的温度梯度函数.中国《公路桥涵设计通用规范》[20]和英国[21]采用的是折线型函数,新西兰规范[22]采用幂函数.本节以中国《公路桥涵设计通用规范》中正温差温度梯度为例进行温度剪力滞计算.计算中的竖向温度梯度分布如图 8所示.

|
图 8 规范温度分布 Fig. 8 Temperature distribution in specification |
在上翼板0.4 m范围内分布非线性温度,其中上部0.1 m内由25 ℃降至6.7 ℃,0.1至0.4 m内由6.7 ℃降至0 ℃.对于不同的温度梯度统一用T(z)函数进行描述,由此,对温度应力的影响反映在式(12)~(14)中改变温度变形势能的6个参数ATw、ATu、ATb、STw、STu、STb以及最后的应力表达式(40)、(41)中的T(z).其他计算过程与局部三角形温度梯度的相同.
对于带悬臂翼板的箱型截面梁,几何参数及材料参数同算例二.在图 8温度梯度作用下的应力分布如图 9所示.图 9(a)为上翼板与腹板交角中面处应力沿顺桥向x方向分布,图 9(b)为x=57 m处上翼板中面的应力沿横桥向y方向的分布图.由图 9(a)可知,在箱梁跨中附近剪力滞影响小而使应力基本为常量,但是平截面假定的应力计算结果明显小于有限元.这是由于非线性温度梯度下有翼缘板箱形截面的曲率受剪力影响,在平截面假定中没有考虑这项影响而导致误差,在修正双参数法中考虑了这项的影响而精度较高,这与局部三角形温度梯度作用下的规律相同.图 9(b)x=57 m处横桥向的应力分布可知,修正双参数法所得的应力基本反映了温度应力沿y方向的变化情况,且计算结果与有限元法吻合较好,显示了良好的适应性.
|
图 9 规范温度分布下应力 Fig. 9 Stress of temperature distribution in specification |
1) 在非线性温度梯度作用下,上下翼板形成剪力滞的原因不同导致上下翼板的纵向位移函数的幅值不同,且方向与荷载条件下的纵向位移方向有所区别.修正双参数法既反映了上下翼板变形的差异,又满足了截面轴力的平衡,从而提高了计算精度.
2) 非线性温度梯度作用下简支箱梁在端部存在剪力滞效应,影响范围约为1.5倍箱梁宽度.受剪力滞效应影响,端部的最大应力大于平截面的计算结果.因此,平截面假定算法对于端部是不安全的.
3) 对于截面上下对称的无悬臂翼板箱梁,在离开端部1.5倍箱梁宽度后的跨中区域,剪力滞影响很小,可采用平截面假定进行计算.对于截面不对称的带悬臂翼板箱梁,平截面假定无法考虑非线性温度引起的剪力对截面曲率的影响,即使在跨中区域计算误差依然较大,而双参数法修正了剪力对截面曲率的影响而显著提高了计算精度.
| [1] |
REISSNER E. On the problem of stress distribution in wide flanged box beam[J]. Journal of Aerosol Science, 1938(5): 295. DOI:10.2514/8.634 |
| [2] |
KUZMANOVIC B O, GRAHAM H J. Shear lag in box girders[J]. Journal of the Structural Division, ASCE, 1981, 107(9): 1701. DOI:10.2514/3.56113 |
| [3] |
张士铎, 丁芸. 变截面悬臂箱梁负剪力滞差分解[J]. 重庆交通学院报, 1984, 11(4): 34. ZHANG Shiduo, DING Yun. Finite difference solution in shear lag effect on cantilever box girder with linear varying depths[J]. Journal of Chongqing Jiaotong University, 1984, 11(4): 34. |
| [4] |
肖军, 李小珍, 刘德军, 等. 一种剪滞翘曲位移函数的解析构造法[J]. 哈尔滨工业大学学报, 2017, 49(3): 162. XIAO Jun, LI Xiaozhen, LIU Dejun, et al. An analytical construction method of wraping displacement function of shear lag[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 162. DOI:10.11918/j.issn.0367-6234.2017.03.026 |
| [5] |
雒敏, 蔺鹏臻, 孙理想. 单箱双室箱梁的剪力滞效应分析[J]. 力学与实践, 2013, 35(6): 70. LUO Min, LIN Pengzhen, SUN Lixiang. Analysis of shear lag effect of twin-cell box girders[J]. Mechanics in Engineering, 2013, 35(6): 70. DOI:10.6052/1000-0879-13-259 |
| [6] |
何志刚, 蔺鹏臻. 考虑截面配筋的箱梁剪力滞效应分析[J]. 铁道学报, 2018(5): 137. HE Zhigang, LIN Pengzhen. Analysisof the shear lag effect in consideration of section reinforcement[J]. Journal of the China Railway Society, 2018(5): 137. DOI:10.3969/j.issn.1001-8360.2018.05.020 |
| [7] |
潘旦光, 丁民涛, 陈钒. 简支薄壁箱梁自由振动的摄动法解析解[J]. 哈尔滨工业大学学报, 2016, 48(12): 56. PAN Danguang, DING Mintao, CHEN Fan. Analytic solution of free vibration of simply-supported thin-walled box girder by perturbation method[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 56. DOI:10.11918/j.issn.0367-6234.2016.12.007 |
| [8] |
MAMDOUH M E, AMIN G. Temperature variations in concrete bridges[J]. Journal of Structural Engineering, 1983, 109(10): 2355. DOI:10.1061/(ASCE)0733-9445(1983)109:10(2355) |
| [9] |
ENRIQUE M, ANTONIO A. Temperature and stress distributions in concrete box girder bridges[J]. Journal of Structural Engineering, 1990, 116(9): 2388. DOI:10.1061/(ASCE)0733-9445(1990)116:9(2388) |
| [10] |
SHASHI M, CHARLES W R. Temperature-dependent bridge movements[J]. Journal of Structural Engineering, 1992, 118(4): 1090. DOI:10.1061/(ASCE)0733-9445(1992)118:4(1090) |
| [11] |
刘兴法. 预应力混凝土箱梁温度应力计算方法[J]. 土木工程学报, 1986, 19(1): 44. LIU Xingfa. Computation of temperature stresses for prestressed concrete box girders[J]. China Civil Engineering Journal, 1986, 19(1): 44. DOI:10.15951/j.tmgcxb.1986.01.005 |
| [12] |
张元海, 李乔. 预应力混凝土连续箱梁桥的温度应力分析[J]. 土木工程学报, 2006(3): 98. ZHANG Yuanhai, LI Qiao. Analysis of thermal stress for prestressed concrete continuous box-girder bridges[J]. China Civil Engineering Journal, 2006(3): 98. DOI:10.3321/j.issn:1000-131X.2006.03.015 |
| [13] |
毛松鹤, 季日臣, 范琴锋, 等. 混凝土连续梁箱形输水桥日照温度应力分析[J]. 兰州交通大学学报, 2007(4): 84. MAO Songhe, JI Richen, FAN Qinfeng, et al. Analysis of lengthways thermal stress of concrete continuous box-girder water birdge by solar radiation[J]. Journal of Lanzhou Jiaotong University, 2007(4): 84. DOI:10.3969/j.issn.1001-4373.2007.04.023 |
| [14] |
彭友松, 强士中. 混凝土桥梁结构温度自应力计算方法探讨[J]. 西南交通大学学报, 2006, 41(4): 452. PENG Yousong, QIANG Shizhong. Investigation into computational method of self-equilibrating thermal stresses in concrete bridges[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 452. DOI:10.3969/j.issn.0258-2724.2006.04.010 |
| [15] |
郑日亮. 大跨混凝土箱梁桥温度荷载作用下剪力滞效应分析[J]. 湖南城市学院学报(自然科学版), 2007, 16(3): 10. ZHENG Riliang. Shear lag effect of long-span concrete box girder bridge under thermal action[J]. Journal of Hunan City University (Natural Science), 2007, 16(3): 10. DOI:10.3969/j.issn.1672-7304.2007.03.003 |
| [16] |
陈军, 李艳. 温度荷载作用下箱梁桥剪力滞效应分析[J]. 交通科技, 2010, 240(3): 23. CHEN Jun, LI Yan. Shear lag effect of concrete box girder bridge under thermal action[J]. Transportation Science & Technology, 2010, 240(3): 23. DOI:10.3963/j.issn.1671-7570.2010.03.008 |
| [17] |
潘旦光, 程业, 陈钒, 等. 非线性温度梯度下悬臂箱梁的剪力滞效应[J]. 合肥工业大学学报(自然科学版), 2018, 41(3): 384. PAN Danguang, CHENG Ye, CHEN Fan, et al. Shear lag effect on cantilever box girder under nonlinear temperature gradient[J]. Journal of Hefei University of Technology (Natural Science Edition), 2018, 41(3): 384. DOI:10.3969/j.issn.1003-5060.2018.03.016 |
| [18] |
刘兴法. 箱形桥墩(梁)的日照温度应力及位移[J]. 铁道标准设计, 1978(2): 7. LIU Xingfa. Sunshine temperature stress and displacement of box pier (box girder)[J]. Railway Standard Design, 1978(2): 7. |
| [19] |
RODRIGUEZ L E, BARR P J, HALLING M W. Temperature effects on a box-girder integral-abutment bridge[J]. Journal of Performance of Constructed Facilities, 2014, 28(3): 583. DOI:10.1061/(ASCE)CF.1943-5509.0000437 |
| [20] |
中华人民共和国交通部.公路桥涵设计通用规范: JTG60—2015[S].北京: 人民交通出版社, 2015 Ministry of Communications of the People's Republic of China. General specifications for design of highway bridges and culverts: JTG60-2015[S]. Beijing: China Communications Press, 2015 |
| [21] |
BS5400, Steel concrete and composite bridges: Part 2: 1978-specifications for loads[S]. London: British Standards Institution, 1978
|
| [22] |
Bridge Manual. Section 3: Design loading[S]. 2nd ed. Auckland: Transit New Zealand, 2003
|
 2020, Vol. 52
2020, Vol. 52


