不确定性是指事件出现或发生的结果是不能准确确定的[1],不确定性的来源在于缺乏完善的信息对问题定义和求解中涉及的数据、现象和过程进行准确表述[2].给水管网模型中的不确定性主要是由于建模人员的主观认识不足或所获得的知识和信息不够完善而导致的无法对模型参数进行准确描述或未能完全掌握系统运行的机理[3-5].模型参数的不确定性导致模型计算结果中的节点压力和管道流量也具有不确定性[6-7].相关模型参数包括节点需水量、管道摩阻系数、阀门状态和管网拓扑结构等[8].实际建模过程中,不可能逐一实测确定所有未知和不确定的参数.特别是每根管道的摩阻系数和每个节点的需水量,由于实测难度大,往往通过部分实测数据和经验数据推算得到.探究这种推算出参数取值的不确定性对模型计算结果的不确定性和可靠性的影响,是目前模型校核与应用方面的重要研究方向之一.
在模型不确定性分析的研究中,金溪(2011)[9]采用概率水力模型的线性化求解方法,分析了节点需水量的不确定性对节点压力和管道流量的影响.舒诗湖(2012)[10]采用Monte Carlo随机抽样方法,提出在管道摩阻系数和节点需水量不确定性条件下的模拟结果精度评估的方法.朱世泰和陈兵(2014)[11]也利用Monte Carlo随机抽样方法,对比分析了节点需水量、管道直径和摩阻系数的不确定性对节点压力和管道流量的影响.常丽娟等(2014)[12]同样采用Monte Carlo方法,分析了节点需水量和管道摩阻系数的不确定性对节点压力、管道流量以及管网水力可靠性的影响.Kapelan和Savic(2005)[13]采用基于拉丁超立方体抽样(LHS)的Monte Carlo方法,在给水管网优化设计时考虑了节点需水量和管道摩阻系数的不确定性.Seifollahi-Aghmiuni et al(2013)[14]在管网设计阶段,采用Monte Carlo方法研究了管道摩阻系数的不确定性对运行期间管网失效性的影响.Haghighi和Asl(2014)[15]采用模糊集理论方法,研究了管道摩阻系数和节点需水量对节点压力和管道流量的影响.Sivakumar et al(2016)[16]同样采用模糊集理论方法,研究了管道摩阻系数的不确定性对节点压力和管道流量的影响.
实际工程问题中,很多参数或事件之间是具有相关性的[17],模型参数之间也存在一定的相关性,而以上不确定性分析研究中忽略了管道摩阻系数的相关性问题.本文基于Monte Carlo随机模拟方法,提出了考虑参数相关性的给水管网模型不确定性分析方法.以管道摩阻系数(海曾-威廉系数)为研究参数,探究了模型参数的不确定性和相关性对模拟结果中节点压力和管道流量的不确定性影响.
1 管道摩阻系数的不确定性及相关性在模型中计算水流在管道中的水头损失通常采用海曾-威廉公式[18]:
| $ {{h}_{i}}=\frac{10.667\cdot {{l}_{i}}\cdot q_{i}^{1.852}}{C_{i}^{1.852}\cdot D_{i}^{4.87}}. $ | (1) |
式中:hi为管道i的水头损失(m),li为管道长度(m),qi为管道流量(m3/s),Di为管道直径(mm),Ci为管道海曾-威廉系数.
模型计算时,式(1)中{hi, qi}为待求量,{li, Di, Ci}为已知的输入参数,而Ci为随使用时间和工作环境而变化的输入参数,其数值与管材、管径、管龄、管道流速等因素有关[18],可现场测试得到[19].在实际建模时,由于条件限制,不可能实测得到所有管道Ci值,一般根据管道属性选择代表性管道实测[20],再推广应用至具有类似属性的管道,或采用文献建议的经验值[21].由于实际管道Ci值的影响因素多且复杂,以代表性管道Ci值推算出每个管道的Ci值或经验取值会有误差.因此,模型中的管道Ci值具有不确定性.
随管道使用时间延续,其摩阻系数相比初始状态已有所不同.但具有相同或相近属性的管道,其摩阻系数存在相关性.以图 1所示的管网模型为例,1)管道P2,P3的管材、管径和管龄相同,其摩阻系数往往相同或相近,相关性大.2)管道P4,P7的管材、管龄相同,虽管径不同,但摩阻系数仍可能相近,存在一定的相关性.3)对于管道P2与P13,其管材、管径和管龄均不相同,则可认为两者的摩阻系数不具相关性.为表达上述分析中各管道摩阻系数相关性大小的差异,将相关性关系分为{完全相关、部分相关、完全独立}.给水管网建模时,采用的基于属性分组确定管道摩阻系数的方法[22],实际上是基于“分组内管道摩阻系数完全相关、不同分组间管道摩阻系数完全独立或部分相关”的假定.在进行模型参数不确定分析研究时,往往将所有管道的摩阻系数认为是服从某一概率分布类型(如均匀分布和正态分布)的独立随机变量.当不同管道的摩阻系数存在局部相关性(完全相关或部分)时,与其对应的概率分析模型中的随机变量之间则不是完全独立的,而应以相关系数表示变量的相关性.

|
图 1 简单给水管网模型 Fig. 1 An example of WDN model |
现有的给水管网模型不确定性分析研究中,多采用Monte Carlo方法(包括随机抽样[11]、LHS抽样[13]等).这些方法中均假定不同管道摩阻系数对应的随机变量相互独立,没有考虑随机变量间的局部相关性.例如,在分析中会出现具有相同属性的管道P2,P3的摩阻系数取值会相差比较大的情况.由于Monte Carlo方法抽样时采用的基本假定是“各随机变量相互独立”,在进行含有相关随机变量的概率系统随机模拟时,需要将相关随机变量转化为独立随机变量.
2 考虑参数相关性的Monte Carlo模拟方法Monte Carlo方法基于统计理论,通过随机变量抽样检验或随机模拟,描述和估计函数的统计量,是一种求解不确定性问题近似解的方法,也是不确定性分析的常用方法[15].
应用Monte Carlo方法进行模型不确定性分析时,先将模型中不确定的参数定义为具有特定概率分布的随机变量,然后,进行随机变量的抽样取值(随机数),再将每次抽样得到的所有不确定参数对应的随机数作为管网模型输入参数,进行管网模型水力计算并输出该次随机抽样的模拟结果.进行多次抽样模拟并记录结果后,统计模拟结果的均值、取值频度,作为模型不确定分析结果的期望(估计)值和概率密度分布.由于Monte Carlo方法无法直接根据随机变量的相关系数产生相关随机数,需要将Monte Carlo抽样产生的独立随机数转换为相关随机数变量.
2.1 相关随机变量转换为独立正态随机变量假定模型中所有管道的摩阻系数均为不确定参数,这些不确定参数对应的随机变量向量为U ={U1, U2, …, Un} T,其中n为不确定性分析中的变量(管道摩阻系数)个数.设U的相关系数矩阵ρU=[ρUiUj]n×n,其中i,j=1~n.本节采用Nataf变换[3, 23]和正交变换[23]将相关随机变量转换为独立正态随机变量,具体步骤如下.
2.1.1 相关随机变量正态化转换采用Nataf变换,将n维相关任意分布随机变量U ={U1, U2, …, Un}T转化为相关标准正态分布随机变量X ={X1, X2, …, Xn}T,X的相关系数矩阵为ρX=[ρXiXj]n×n,U和X中的随机变量转换关系根据等概率变换原则FUi(ui)=Φ(xi)可得[23]
| $ {{x}_{i}}={{\Phi }^{-1}}\left( {{F}_{Ui}}\left( {{u}_{i}} \right) \right). $ | (2) |
式中:Φ为标准正态分布累积概率密度函数,FUi为随机变量Ui的累积概率密度函数,i=1~n.
ρU与ρX的转换关系为
| $ \begin{align} & {{\rho }_{Ui, Uj}}=\int{\begin{matrix} +\infty \\ -\infty \\ \end{matrix}}\int{\begin{matrix} +\infty \\ -\infty \\ \end{matrix}}\left( \frac{{{u}_{i}}-{{\mu }_{i}}}{{{\sigma }_{i}}} \right)\left( \frac{{{u}_{j}}-{{\mu }_{j}}}{{{\sigma }_{j}}} \right). \\ & {{\varphi }_{{{X}_{i}}{{X}_{j}}}}\left( {{x}_{i}}, {{x}_{j}}, {{\rho }_{{{X}_{i}}, {{X}_{j}}}} \right)\text{d}{{x}_{i}}\text{d}{{x}_{j}}. \\ \end{align} $ | (3) |
式中φXiXj为ρXiXj二维标准正态分布联合概率密度函数.
Ui和Uj的边缘概率分布函数及相关系数ρUiUj已知,可以求解等效的相关系数ρXiXj.本节直接根据Liu and Kiureghian [24]中拟合的转换系数简化式计算得到ρXiXj.
2.1.2 相关正态随机变量转换为独立正态随机变量采用正交变换,将n维相关正态随机变量X ={X1, X2, …, Xn} T转换为独立正态分布随机变量Y.相关正态分布随机变量X,其均值、标准差向量分别为μX和σX,相关系数矩阵ρX,协方差矩阵CX.独立正态分布随机变量Y,其均值、标准差向量分别为μY和σY,相关系数矩阵ρY,协方差矩阵CY.有如下关系[17, 23]:
| $ \mathit{\boldsymbol{Y = }}{\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot \mathit{\boldsymbol{X}}\;, $ | (4) |
| $ {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{Y}}} = {\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{X}}} \cdot \mathit{\boldsymbol{A}}. $ | (5) |
式中:CY为Y的协方差矩阵,其对角线元素为CX的特征值; AT为n个CX特征向量组成的正交矩阵,且存在AT= A-1.
根据式(5),Y的均值与方差分别为
| $ {\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{Y}}} = {\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{X}}}, $ | (6) |
| $ \mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2 = {\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{X}}} \cdot \mathit{\boldsymbol{A}}. $ | (7) |
在进行包含相关随机变量的Monte Carlo抽样模拟时,首先根据式(6)、(7)推导的独立正态分布随机变量的参数抽样产生随机数,再根据式(2)~(7)分别进行逆-正交变换和逆- Nataf变换,将Monte Carlo抽样产生的独立正态分布随机数转换为相关随机数.以管道摩阻系数为例,模型不确定性分析的具体步骤如下.
步骤1 初始参数设定.设定最大抽样模拟次数N;根据管道摩阻系数对应的随机变量U的分布参数及其相关系数矩阵ρU,采用式(2)~(7)计算ρX,A,σY.
步骤2 相关随机变量抽样.
a) 独立正态随机变量抽样.进行第k次(k=1~N)抽样模拟,随机产生n个服从Y分布的正态分布随机数集合y (k)={y1(k), y2(k), …, yn(k)}T;
b) 独立正态随机变量转换为相关标准正态随机变量.根据式(4)进行逆-正交变换,将y (k)转换为相关标准正态分布随机数集合x (k)={x1(k), x2(k), …, xn(k)}T;
c) 相关标准正态分布随机变量转换为相关任意分布随机变量.根据式(2)进行逆- Nataf变换,将x (k)转换为相关任意分布随机数集合u (k)={u1(k), u2(k), …, un(k)} T.
步骤3 参数抽样对应的管网模型结果计算.将管道摩阻系数的随机数向量u (k)输入到管网水力模型中,进行水力计算,并输出节点压力、管道流量等模拟结果.
步骤4 多次抽样模拟.若k < N,返回步骤2,循环步骤2~3;若k≥N,进入步骤5,抽样模拟结束.
步骤5 统计模拟结果.统计N次抽样模拟得到的管网水力模型计算结果(节点压力、管道流量)的均值、最大值、最小值等.
3 算例分析以文献[15]中的静态给水管网水力模型(图 2)为例,对管道摩阻系数进行不确定性分析.该管网模型覆盖面积为1.2 km2,包含1个固定水头(27 m)水源点,45个用户节点和65根管道,具体属性参数见文献[15].当管道摩阻系数为确定数值110时,管网中用户节点压力和管道流量的{最小值, 最大值, 平均值}分别为{18.11 m, 26.92 m, 22.95 m }和{2.41 L/s, 322.57 L/s, 46.27 L/s}.

|
图 2 算例给水管网模型 Fig. 2 Case study of the WDN model |
为研究管道摩阻系数的不确定性对模拟结果的影响,假设摩阻系数服从均值为110、变化区间为[99, 121]的均匀分布,Monte Carlo抽样次数为N=105次,分析结果如图 3,4和表 1所示.
|
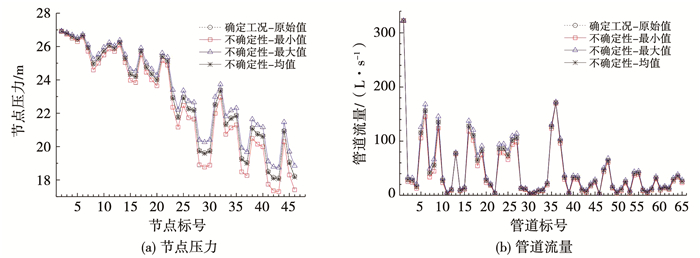
图 3 管道摩阻系数的不确定性对模拟结果的影响 Fig. 3 Influence of pipe roughness uncertainty on the simulaton results |

|
图 4 模拟结果的波动值和波动率 Fig. 4 Fluctuation and volatility of the simulaton results |
| 表 1 管道摩阻系数的不确定性对算例计算结果的影响 Tab. 1 Influence of pipe roughness uncertainty on the simulaton results of the case |
图 3,4中“确定工况-原始值”是采用确定的管道摩阻系数(110)计算得到的节点压力、管道流量,是不考虑参数不确定性的确定参数工况.由图 3可知,确定参数工况与考虑参数不确定性工况中的节点压力、管道流量平均值基本相等,这是由于确定参数工况中的管道摩阻系数等于不确定性工况中的均值.
根据图 3中模拟结果统计,对于考虑不确定性的工况,节点压力和管道流量的平均波动值、平均波动率分别为{0.84 m, 3.97%}和{7.59 L/s, 29.98%}.其中,波动值为不确定性工况中N次Monte Carlo抽样模拟结果中最大值与最小值的差值;波动率为波动值与原始值的比率.
对比图 3(a)和图 4(a)、3(b)和4(b)可知,管道摩阻系数的不确定性对距水源较远的节点压力的影响更为显著.距水源较远的典型节点集{29, 37, 46}的压力波动值、波动率均高于距水源相对较近的典型节点集{6, 17, 32},详见表 1.本文的分析结果与文献[7, 15]的分析结果一致.摩阻系数的不确定性对直径较小管道的流量波动率有更为显著的影响趋势.小直径典型管道集{11, 30, 57}的流量波动率高于大直径典型管道{5, 16, 36},其对应的直径分别为{100 mm, 100 mm, 100 mm}和{363.6 mm, 454.4 mm, 454.4 mm};而小直径管道流量波动值小于大直径管道.但并非所有管道均符合此规律.
在水源出厂总水头不变的前提下,管道摩阻系数的不确定性变化会导致管网中用户节点压力的波动.由水源向远端的节点供水,供水路径经过的管道较多,其节点压力容易受摩阻系数变化的影响,而距水源较近的节点压力主要受水源出厂总水头的影响.
对于直径较小的管道,通过单位流量的水所需的水头损失较大,管网水力平差计算时会给这些小直径管道分配较少的流量.当管网中管道的摩阻系数变化时,会导致不同的节点压力波动,进而导致管段流量的波动.这些小直径管道流量的波动绝对值并不大,但由于其原始值小,导致其流量的波动率较大.
通过上述分析,选定节点压力和管道流量的波动值、波动率作为表征管道摩阻系数不确定性对模型计算结果不确定性影响的指标.
3.2 管道摩阻系数相关性分组对不确定性分析结果的影响为研究不确定性分析中管道摩阻系数取值的相关性对模拟结果的影响,将算例管网中所有管道的摩阻系数按照管道标号顺序均分为10组、5组、3组分别进行分析,并与不分组工况的结果比较,摩阻系数的概率分布参数与不分组的工况相同.相同分组内的摩阻系数完全相关(组内相关系数ρintra=1),不同分组间完全独立(组间相关系数ρinter=0).分析结果如图 5,6和表 2所示.

|
图 5 不同分组工况对应的模拟结果的波动值和波动率 Fig. 5 Fluctuation and volatility of the simulaton results on different grouping conditions |
|
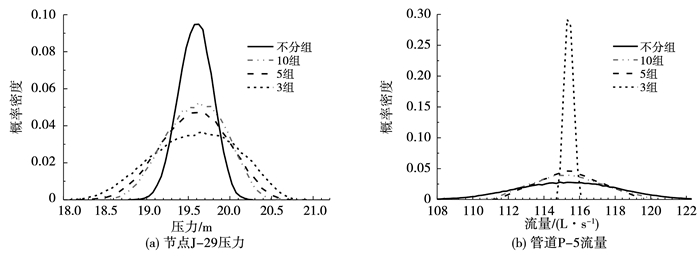
图 6 不同分组工况对应的典型模拟结果的概率密度分布 Fig. 6 Probability densities of typical simulaton results on different grouping conditions |
| 表 2 不同分组工况分析结果统计 Tab. 2 Simulation results of different grouping conditions |
由图 5(a)和6(a)可知,对于大部分节点压力,分组越少,波动值、波动率越大,节点压力概率密度函数在抽样模拟的最大值、最小值范围内分布趋于离散,模拟均值的概率密度减少,模拟值的方差增加;由图 5(b)和6(b)可知,对于大部分管道流量,分组越少,波动值、波动率越小,管道流量概率密度函数分布趋于集中,模拟均值的概率密度增大,模拟值的方差减小.统计结果详见表 2.
分组越少,管道摩阻系数相关性越显著, 即管道摩阻系数越会一致变化.对于节点压力,管道摩阻系数的一致变化会整体提高或降低管网的水头损失,表现为较大的节点压力波动;若各管道的摩阻系数随机变化,会存在部分管道摩阻系数升高,其他部分管道摩阻系数降低的工况组合,这样导致管网的整体水头损失变化不明显,表现为较小的节点压力波动.而对管道流量而言,在管网压力足够大且不考虑压力对节点需水量的影响时,若管网中所有管道摩阻系数一致提升或降低,则不会影响管道流量;而管道摩阻系数随机变化会提高管网中不同管道沿程水头损失的差异,进而引起管道流量的较大波动.其中,图 5各分组工况中波动较大的节点压力和管道流量与3.1节不分组工况中规律一致.
3.3 直接采用管道摩阻系数相关系数对不确定性分析结果的影响本节直接采用管道摩阻系数相关系数的方式,研究参数相关性对模型计算结果的影响,并与3.2节中考虑参数相关性分组工况的结果进行比较.
根据管道摩阻系数对应的相关均匀分布随机变量U的相关系数矩阵ρU=[ρUiUj]65×65,通过式(8)转换为相关标准正态分布X的相关系数矩阵ρX=[ρXiXj]65×65,矩阵中每个元素的对应关系为
| $ {\rho _{{X_i}, {X_j}}} = \left( {1.047 - 0.047\rho _{{U_i}, {U_j}}^2} \right){\rho _{{U_i}, {U_j}}}. $ | (8) |
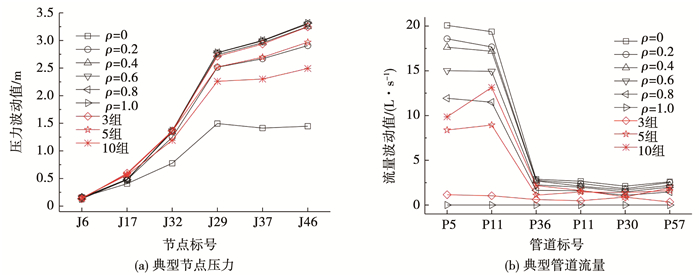
将管网模型中全部(65根)管道摩阻系数的相关系数取为在ρ=0~1.0变化的同一个数值,不同相关系数工况中典型节点压力、管道流量的结果见图 7.可以看出,3.2节中分组工况的计算结果基本分布在本节ρ=0~1.0不同工况的计算结果之间,且结果变化规律一致.分组工况体现了相关系数变化的结果,较多的分组工况体现了较小的相关系数的影响;可通过调整参数分组的数量,研究参数相关系数变化的影响.
|
图 7 不同相关系数工况对应的典型模拟结果的波动值和波动率 Fig. 7 Fluctuation and volatility of typical simulaton results on different ρ conditions and grouping conditions |
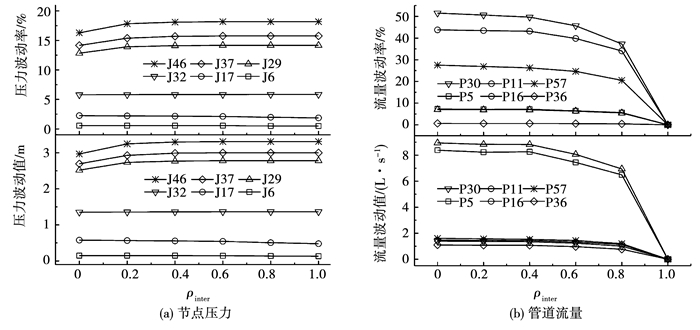
在管道摩阻系数分为5组的工况下,当组内相关系数ρintra=1、组间相关系数ρinter=0~1.0时对模拟结果的影响见图 8;当组间相关系数ρinter=0、组内相关系数ρintra=0~1.0时对模拟结果的影响见图 9,10.
|
图 8 不同组间相关系数工况对应的典型模拟结果的波动值和波动率 Fig. 8 Fluctuation and volatility of typical simulaton results on different ρinter conditions |
|
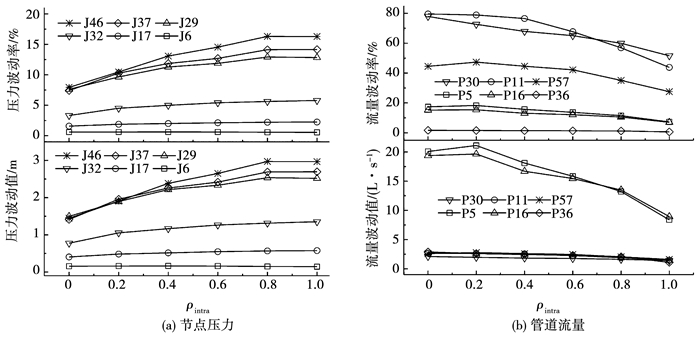
图 9 不同组内相关系数工况对应的典型模拟结果的波动值和波动率 Fig. 9 Fluctuation and volatility of typical simulaton results on different ρintra conditions |
|
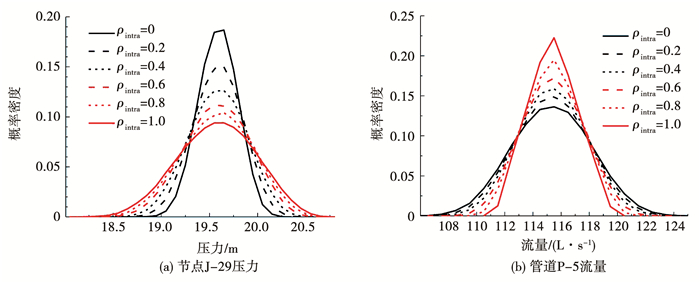
图 10 不同组内相关系数对应的典型模拟结果的概率密度分布 Fig. 10 Probability densities of typical simulaton results on different ρintra conditions |
当组内相关系数ρintra=1时,组间相关系数ρinter=0与考虑组间相关系数的其他工况(ρinter=0.2;0.4;0.6;0.8)相比,模拟结果的差异较小,节点压力和管道流量的平均波动值差异(平均波动值差异=|ρinter=0工况平均波动值-其他工况平均波动值|)的范围分别为[0.07 m, 0.09 m]、[0.05 L/s, 0.78 L/s],平均波动率差异的范围分别为[0.4%, 0.49%]、[0.24%, 3.50%].由于当ρinter=1时,管道流量值不受摩阻系数不确定性的影响,未将此工况参与波动差异比较.
当组间相关系数ρinter=0时,随着组内相关系数ρintra增加,节点压力波动值增加,其概率密度分布离散、方差增大;管道流量波动值减小,其概率密度分布集中、方差减小,与3.2节结论相同.
{ρintra=0, ρintra=1}工况的结果可以作为不同ρintra值工况对应的节点压力和管道流量波动值的上下界(包络线).{ρintra=0, ρintra=1}工况对应的节点压力波动值、波动率的平均值分别为{0.84 m, 1.44 m}、{3.97%, 6.87%};相差比率分别为71.43%,73.05%.{ρintra=0, ρintra=1}工况对应的管道流量波动值、波动率的平均值分别为{7.59 L/s, 2.99 L/s}、{29.98%, 13.35%};相差比率分别为60.61%,55.47%.
4 结论1) 管道摩阻系数的不确定性对距水源较远的节点压力的影响更显著,对直径较小的管道流量有更显著的影响趋势.
2) 在考虑管道摩阻系数相关性的影响时,直接采用相关系数的工况与采用管道摩阻系数相关性分组工况的计算结果相比,分组工况的计算结果处于不同相关系数[0, 1.0]工况的计算结果之间,且结果变化规律一致;分组工况体现了相关系数变化的结果,较多的分组工况体现了较小的相关系数的影响.
3) 管道摩阻系数相关性分组,对不确定性分析结果有显著的影响.算例中管道摩阻系数分为5组(组内完全相关、组间完全独立)的工况与不分组工况相比,节点压力、管道流量的平均波动值的相差比率为71.43%,60.61%.组间相关系数的变化对不确定性分析结果的影响不明显;而组内相关系数由0变化为1.0,即从不分组工况变化为5组(组内完全相关、组间完全独立)工况,会显著增加节点压力的不确定性而减小管道流量的不确定性.
在给水管网模型的不确定性分析中应该考虑管道摩阻系数的相关性问题,实际应用建议:根据建模过程管道摩阻系数的分组情况进行不确定性分析中的参数分组;忽略管道摩阻系数的组间相关性(组间相关系数为0),分别计算组内参数完全相关、完全独立两种工况(组内相关系数分别为0和1)的结果,对比两种工况的相应模拟结果;若差异较大,需收集实际数据确定组内管道摩阻系数的相关系数,并采用本文方法进行分析;若差异较小,则可直接采用“组内参数完全相关”的工况结果.
| [1] |
贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007. GONG Jinxin, WEI Weiwei. Engineering structure reliability design principle[M]. Beijing: China Machine Press, 2007. |
| [2] |
TUNG Y K, YEN B C. Hydrosystems engineering uncertainty analysis[M]. New York: McGraw-Hill, 2005.
|
| [3] |
熊芬芬, 杨树兴, 刘宇, 等. 工程概率不确定性分析方法[M]. 北京: 科学出版社, 2016. XIONG Fenfen, YANG Shuxing, LIU Yu, et al. Engineering probability uncertainty analysis method[M]. Beijing: Science Press, 2016. |
| [4] |
SAVIC D A, BANYARD J K. Water distribution systems[M]. London: ICE Publishing, 2011.
|
| [5] |
WALSKI T M, CHASE D V, SAVIC D A, et al. Advanced water distribution modeling and management[M]. Waterbury: Haestad Press, 2003.
|
| [6] |
KANG D S, PASHA M F K, LANSEY K. Approximate methods for uncertainty analysis of water distribution systems[J]. Urban Water Journal, 2009, 6(3): 233. DOI:10.1080/15730620802566844 |
| [7] |
SABZKOUHI A M, HAGHIGHI A. Uncertainty analysis of pipe-network hydraulics using a many-objective particle swarm optimization[J]. Journal of Hydraulic Engineering, 2016, 142(9). DOI:10.1061/(ASCE)HY.1943-7900.0001148 |
| [8] |
KAPELAN Z. Calibration of water distribution system hydraulic models[D]. School of Engineering and Computer Science, the University of Exeter, UK, 2002
|
| [9] |
金溪. 供水管网概率水力模型线性化求解方法[J]. 河海大学学报(自然科学版), 2011, 39(4): 458. JIN Xi. Probabilistic hydraulic simulation of water supply network by linearized deterministic hydraulic model[J]. Journal of Hohai University (Natural Sciences), 2011, 39(4): 458. |
| [10] |
舒诗湖. 基于不确定性分析的供水管网模型精度评估[J]. 上海水务, 2012(4): 12. SHU Shihu. Model precision assessment of water distribution system based on uncertainty analysis[J]. Shanghai Water, 2012(4): 12. |
| [11] |
朱世泰, 陈兵. 基于随机抽样的供水管网模型校核参数研究[J]. 给水排水, 2014, 40(3): 145. ZHU Shitai, CHEN Bing. Research on calibration parameters of water supply pipe network model based on random sampling[J]. Water & Wastewater Engineering, 2014, 40(3): 145. |
| [12] |
常丽娟, 王军慧, 龙天渝. 节点流量和水损系数的不确定性对供水管网水力特性的影响[J]. 水资源与水工程学报, 2014, 25(6): 86. CHANG Lijuan, WANG Junhui, LONG Tianyu. Influence of uncertainty of node flow and water loss coefficient on hydraulic characteristics of water supply pipe network[J]. Journal of Water Resources and Water Engineering, 2014, 25(6): 86. |
| [13] |
KAPELAN Z S, SAVIC D A, WALTERS G A. Multiobjective design of water distribution systems under uncertainty[J]. Water Resources Research, 2005, 41(11): 97. |
| [14] |
SEIFOLLAHI-AGHMIUNI S, HADDAD O B, OMID M H, et al. Effects of pipe roughness uncertainty on water distribution network performance during its operational period[J]. Water Resources Management, 2013, 27(5): 1581. |
| [15] |
HAGHIGHI A, ASL A Z. Uncertainty analysis of water distribution networks using the fuzzy set theory and NSGA-Ⅱ[J]. Engineering Applications of Artificial Intelligence, 2014, 32(6): 270. DOI:10.1016/j.engappai.2014.02.010 |
| [16] |
SIVAKUMAR P, PRASAD R K, CHANDRAMOULI S. Uncertainty analysis of looped water distribution networks using linked EPANET-GA method[J]. Water Resources Management, 2016, 30(1): 1. DOI:10.1007/s11269-015-1165-x |
| [17] |
侯本伟, 李小军, 刘爱文, 等. 考虑管线失效相关性的埋设管网系统地震可靠性随机模拟[J]. 防灾减灾工程学报, 2016(1): 84. HOU Benwei, LI Xiaojun, LIU Aiwen, et al. Monte Carlo simulation of buried pipeline network seismic reliability with correlated failure of pipelines[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016(1): 84. DOI:10.13409/j.cnki.jdpme.2016.01.011 |
| [18] |
舒诗湖. 供水管网系统不确定性分析的理论与发展[J]. 中国给水排水, 2011, 27(16): 30. SHU Shihu. Theory and development of uncertainty analysis of water distribution system[J]. China Water & Wastewater, 2011, 27(16): 30. |
| [19] |
袁一星, 曲世琳, 伍悦滨. 城市给水管网系统的阻力变化规律研究[J]. 中国给水排水, 2003, 19(10): 52. YUAN Yixing, QU Shilin, WU Yuebin. Study on the variability of resistance in urban water supply network[J]. China Water & Wastewater, 2003, 19(10): 52. |
| [20] |
陆海, 吕谋, 董深. 给水管网微观模型水力校正研究[J]. 青岛理工大学学报, 2008, 29(1): 84. LU Hai, LV Mou, DONG Shen. Study on hydraulic calibration of microcosmic model of municipal water distribution network[J]. Journal of Qingdao Technological University, 2008, 29(1): 84. |
| [21] |
于志强.给水管网水力模型软件与校验抽样设计研究[D].天津: 天津大学, 2010 YU Zhiqiang. Research on water distribution system hydraulic model software and sampling design for calibration[D]. Tianjin: Tianjin University, 2010 |
| [22] |
许刚.给水管网水力模型校正研究[D].杭州: 浙江大学, 2005 XU Gang. Hydraulic model calibration for water distribution system[D]. Hangzhou: Zhejiang University, 2005 |
| [23] |
张明. 结构可靠度分析—方法与程序[M]. 北京: 科学出版社, 2009. ZHANG Ming. Structural reliability analysis: Methods and procedures[M]. Beijing: Science Press, 2009. |
| [24] |
LIU P L, KIUREGHIAN A D. Multivariate distribution models with prescribed marginals and covariances[J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105. |
 2020, Vol. 52
2020, Vol. 52


