挠度是桥梁健康监测系统实时监测的关键指标之一[1],也是评定桥梁结构安全与否的关键参数[2-3].长期监测得到的挠度数据通常是由车辆及环境因素(温度、风)等综合作用下的总效应[4].为了更好地掌握桥梁的运营状况,深入分析挠度检测数据中的各项响应分量是十分必要的[5].研究表明,环境是影响主梁挠度变化的主要因素[6],结构的损伤信号往往会被其“淹没”,以致很难直接根据实测信号对结构的安全状态作出合理的评价[7].
国内外已有学者针对温度作用对桥梁挠度的影响进行过相关研究.文献[2]利用长期监测数据分析了钢箱梁斜拉桥挠度随温度的变化特征,并得到了恒载挠度评估指标的基准值.文献[8]用中心移动平均法分离挠度的温度效应.此外,也有部分学者对日周期上温度效应进行过研究.文献[9]建立有限元模型对青马大桥的温度场及挠度等响应进行模拟,发现太阳辐射对主梁竖向挠度影响明显.文献[4]基于日温差和日温差效应的线性关系,提出了分离监测信号温度效应的方法.文献[10-12]分析了长期监测数据,认为挠度与温度并非一般的线性关系.
以上研究认为温度作用对挠度的影响较大,但大多针对大气温度与挠度的关系进行分析,然而日周期中的主梁温度梯度、太阳辐射等因素对挠度的影响不可忽略.此外,基于实测数据的不同时间尺度下挠度温度效应的研究尚欠缺,因此挠度的温度效应仍需更深入的分析,从而达到为桥梁评估结果的可靠性判断提供依据的目的.本文基于有效的长期监测数据,通过多尺度分析,对挠度响应信号在温度作用的频率处进行重构,在不同时间尺度上实现挠度的温度效应分离.结合日温度作用频率处挠度响应的特点,同时考虑太阳辐射的影响,考察日温度效应与大气温度的关系,实现对日温度效应的预测.
1 挠度响应中温度效应分离方法 1.1 挠度响应的多时间尺度特征桥梁在正常运营过程中由长期监测系统采集到的主梁挠度数据是在温度、车辆、风等共同作用下的综合响应,其中影响最大的是温度和汽车作用[2],而这两种作用的作用周期和影响因素明显不同.日温度作用的周期是天,受到大气温度和太阳辐射的共同影响;年温度作用的周期是年,主要受到大气温度的影响;汽车作用的时间较短,且与地区经济发展水平、人口密度等相关.
桥梁上的不同作用具有多时间尺度的特点,其产生的响应也具有不同的周期.通常视各类效应在时间尺度上不存在耦合关系,即某一作用产生的挠度不同时受桥梁上其他作用的影响.因此,可选择加法模型[13]作为挠度响应增量ΔD和温度T的表达,即
| $ \left\{ \begin{array}{l} \Delta D = {D_T} + {D_{\rm{P}}} + {D_{\rm{R}}}, \\ \;\;\;T = {T_{\rm{d}}} + {T_y} + {T_{\rm{r}}}. \end{array} \right. $ | (1) |
式中:DT为温度效应;DP为汽车、风等其他作用效应;DR为系统的测试误差;Td为日温度作用;Ty为年温度作用;Tf为骤然降温.与温度增量信号相对应,结构的温度效应DT可以认为是由日温度效应、年温度效应和骤然降温效应组成.
由于挠度响应在时间尺度上具有多尺度特征[14-15],且温度与其他作用的作用周期差别较大,因此以温度作用周期对应的频率为基础,对挠度信号进行多尺度分析是将温度效应分离的有效手段.
1.2 多尺度分析理论多尺度分析(multi-resolution analysis, MRA)是将信号分解为一个概略部分和一系列细节部分[16].其中概略部分对应于信号的低频部分,而细节部分对应于信号的高频部分.现实中采集到信号一般是能量有限的,所有能量有限的函数集合所形成的平方可积函数空间是L2(R).对于信号S,多尺度分析即将其分解为概略部分A1及细节部分D1,针对A1部分再次分解,得到概略部分A2和细节部分D2,如此类推.
以faj(t)表示信号f(t)向尺度空间Vj投影后所得到的j尺度下的概貌信号[16],则有
| $ {f_{\rm{a}}^j(t) = \sum\limits_k {{c_{j, k}}} {\phi _k}\left( {{2^{ - j}}t} \right) = \sum\limits_k {{c_{j, k}}} {\phi _{j, k}}(t)}. $ | (2) |
| $ {{c_{j, k}} = \left\langle {f(t), {\phi _{j, k}}(t)} \right\rangle }. $ | (3) |
式中cj, k称为尺度展开系数.
若以fdj(t)表示信号f(t)向小波空间Wj投影后所得到的细节信号,则有
| $ {f_{\rm{d}}^j(t) = \sum\limits_k {{d_{j, k}}} {\psi _k}\left( {{2^{ - j}}t} \right) = \sum\limits_k {{d_{j, k}}} {\psi _{j, k}}(t)}. $ | (4) |
| $ {{d_{j, k}} = \left\langle {f(t), {\psi _{j, k}}(t)} \right\rangle }. $ | (5) |
式中dj, k称为小波展开系数.
将L2(R)按照空间组合展开,有
| $ {L^2}(\mathit{\boldsymbol{R}}) = \sum\limits_{j = - \infty }^J {{W_j}} \oplus {V_j}. $ | (6) |
其中J为任意设定的尺度.
对于f(t)∈L2(R), 可以展开为
| $ f(t) = \sum\limits_{j = - \infty }^j {\sum\limits_{k = - \infty }^\infty {{d_{j, k}}} } {\psi _{j, k}}(t) + \sum\limits_{k = - \infty }^\infty {{c_{J, k}}} {\phi _{J, k}}(t). $ | (7) |
当J→∞时,式(7)则变为
| $ f(t) = \sum\limits_{j = - \infty }^\infty {\sum\limits_{k = - x}^\infty {{d_{j, k}}} } {\psi _{j, k}}(t). $ | (8) |
对于多尺度分解问题亦可从频带划分的角度来理解.如果把原始信号X(ω)的频谱总带宽0~π定义为空间V0,经过第1级分解,V0被划分低频的V1子空间频带为0~π/2和高频的W1子空间(频带为π/2~π).经过第2级分解,V1空间被划分为低频的V2空间(频带为0~π/4)和高频的W2空间(频带为π/4~π/2),如此类推.
小波分析的数学理论基础是多尺度分析理论.由多尺度子空间上尺度基所产生的小波基是构造正交小波基的框架[16].实际上,式(8)即为离散正交小波变换.离散正交小波变换的多尺度分析实质是对频率域的划分,且按2的整数次幂变化逐次降低分辨率[17-18].小波多尺度分析的系数能够反映信号在时域和频域上的局部化特征.
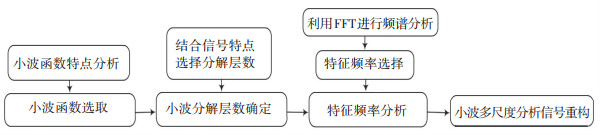
1.3 温度效应的多尺度分离方法下面将采用小波多尺度分析方法对斜拉桥主梁挠度响应中的温度效应进行分离,分离步骤包括小波函数的选取、分解层数的选择以及温度效应的重构等[19],本文对实测信号的分离步骤如图 1所示.
|
图 1 实测信号的分离步骤 Fig. 1 Separation steps of monitoring signals |
选取合适的小波函数对于信号成分的准确分离具有重要意义,小波函数选取应对小波函数的正交性、对称性、消失矩和支撑长度进行考量,表 1中归纳了常见的小波函数及其特征.
| 表 1 常见小波函数的特征 Tab. 1 Characteristics of common wavelet functions |
由表 1可知Symlet(symN)小波系列具有较好的正交性、对称性、足够的消失矩和支撑长度,能够精细除噪、快速变换、减少分析重构时的相位失真并能反映信号的奇异性.
此外,小波多尺度分析实质上是对频率域的划分,分析层数需要根据信号源及目标信号的频率范围共同确定.由于挠度响应中车辆的作用效应具有奇异性,应选择消失矩阶数稍高的小波函数.综上,本文选择分解层数为5层的Symlet(sym5)小波函数进行小波多尺度分析.
在温度效应的多尺度分离中,确定小波函数以及小波分解层数之后,再使用快速傅里叶变换对实测温度和挠度信号进行频谱分析,找出其特征频率.利用已定参数的小波多尺度分析方法对原始挠度信号进行分解,最后,利用特征频率所在层的小波系数对挠度信号进行重构,实现温度效应的分离.
2 温度效应分离示例 2.1 数据来源本文选取南京长江第三大桥为背景桥进行研究.此桥为半漂浮结构体系的双塔双索面钢塔钢箱梁斜拉桥,跨径布置为:63 m+257 m+648 m+257 m+63 m=1 288 m.钢箱梁采用正交异性板流线型扁平钢箱梁,梁高3.2 m,宽(含风嘴)37.2 m;斜拉索采用高强度平行钢丝外挤包高密度聚乙烯形式,全桥共8×21对,上下游对称分布;桥墩采用混凝土;基础采用钻孔灌注桩;索塔为钢箱形式.该桥健康监测系统于2006年投入使用,包括温湿度、风速、应力、索力、挠度、整体位移和结构动力特性监测子系统.
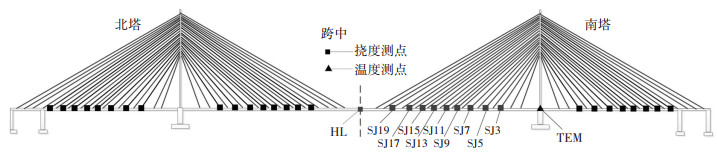
该桥主梁上的温度传感器测点位于南塔岸测0号块主梁,用于监测主梁处大气温度.温度传感器型号为Young41372,量程为-50~50 ℃,测量精度为0.3 ℃.挠度监测子系统由沿梁体布设的封闭式连通管传感器组成,用于监测各点相对于基点的相对变形量.挠度传感器型号为RoseMount 3051S,精度为0.025%.全桥共72个主梁挠度测点,位于各斜拉索与主梁锚固处,采样频率为10 Hz.上游侧挠度测点如图 2所示.作为示例,图中标注了南塔江侧的挠度测点名称分别为SJ3、SJ5、SJ7、SJ9、SJ11、SJ13、SJ15、SJ17、SJ19、HL;温度测点名称为TEM.
|
图 2 传感器的布设 Fig. 2 Sensor layout |
长期监测系统受到不可抗力因素影响时,如电力系统中断、噪声、通信故障,会导致采集数据的质量下降[20].为得到有效的数据,应对原始数据信号进行预处理.
长期监测系统的数据预处理中,对于原始数据单点缺失现象,可利用样条插值法填补缺失值,该方法利用当前数据信息,保持数据曲线的性质.对于原始数据的非连续野值,应利用统计学方法进行粗差剔除,常用方法为“3σ法则”.一般的常数测量值符合正态分布,其中σ代表标准差,μ代表均值.该法则认为测量值的取值基本集中在(μ-3σ,μ+3σ)区间.对于噪声含量较高的数据信号,应进行去噪处理.小波分析理论在时间和频率上具有很好的局部性,对信号的去噪效果良好.
因此,对于长期监测系统中的原始数据,本文依次采用三次样条差值法对缺失的数据点进行补齐、采用3σ法则进行野值剔除、采用小波滤波方法进行去噪.本文以2007年8月24日跨中挠度数据为例说明典型数据预处理过程,并将预处理结果绘于图 3.

|
图 3 原始数据预处理效果 Fig. 3 Preprocessing effect of initial data |
由图 3(a)、3(b)可知,原始数据中密集的遗漏值掩盖了真实挠度变化区域,通过样条插值法处理缺失数据,数据质量提高.值得说明的是,原始信号向挠度数据的转换遵循一定的规则,转换公式为yi=vi-vi0-vk-vk0×A,其中yi为测点i处的挠度,vi为测点i测量值,vi0为测点i零值,vk为基准点测量值,vk0为基准点零值,A为解算系数,这里A=1 500.613.将图 3(b)中的原始信号经野值剔除、数据解算后得到实际挠度数据,如图 3(c)所示.可知实际挠度数据合理,可大致看出汽车荷载和温度对挠度造成的影响.由图 3(d)可知,利用小波滤波的方法可以有效去除高频信号成分,使挠度信号更为合理.
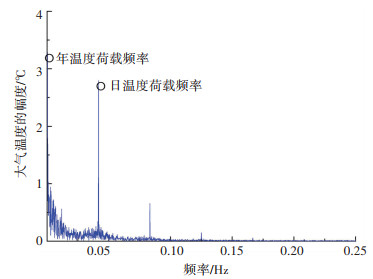
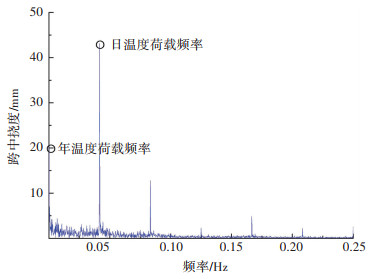
2.3 挠度响应的多尺度分离如2.2节所示,本文所用数据均按照上述步骤经过预处理.以主跨跨中测点为例,选取1 a的实测信号对大气温度和挠度信号进行分析.首先快速傅里叶变换,并以1 h的信号平均值作为该时段的特征值,得到其频谱分别如图 4、5所示.
|
图 4 大气温度实测信号频谱 Fig. 4 Spectrum of ambient temperature monitoring signals |
|
图 5 跨中挠度响应实测信号频谱 Fig. 5 Spectrum of mid-span deflection signals |
由图 4、5可知,挠度和温度信号的幅值主要分布在0.05 Hz以下的低频部分(此处视小时为秒进行频率单位刻画).在1.14×10-4 Hz(周期365×24 h=8 760 h)附近,挠度信号主要受年温度等缓慢变化的作用影响.由于该频率处温度和挠度信号均有明显的集中幅值分布且干扰较小,可认为该频率是年温度作用频率.在4.17×10-2Hz(周期24 h)附近,温度信号和挠度信号均有明显的集中幅值分布,可认为该频率是日温度作用频率.
选取2007年该桥跨中处的实测挠度数据,使用小波多尺度分析方法分别在日温度作用和年温度作用频率上重构原始挠度信号,得到日温度作用产生的挠度响应(称为日温度效应),和年温度作用产生的挠度响应(称为年温度效应),如图 6(a)、6(b)所示.选取2007年8月份连续几日内分离出的日温度效应和年温度效应进行对比,如图 6(c)所示.

|
图 6 不同时间尺度的温度效应分离结果 Fig. 6 Separation results of thermal deflection at different time scales |
由图 6(a)可知,分离的日温度效应较平稳,相邻时刻的幅值较为接近,且夏季的波动幅值明显大于冬季.由图 6(b)可知,分离出的年温度效应的变化较小,且与原始信号的总体变化趋势一致.由图 6(c)可知,日温度效应保留了日温度作用下挠度响应的细节特征,频率明显高于年温度效应.日温度效应以0 mm为零点,以24 h为周期上下波动,波动幅值受太阳辐射强度影响;年温度效应在短期内变化较小,反应挠度效应的长期变化趋势.这符合日温度作用和年温度作用的周期特性和季节特性,证实了该分离方法的有效性.此外,年温度效应的变化是[27.04 mm, 66.28 mm],日温度效应的变化是[-88.67 mm, 99.70 mm].与年温度相比,日温度效应具有幅值较大,季节性较强的特点.考虑到日温度作用中包含太阳辐射作用,因此在日温度效应的分析中要综合考虑.
3 日温度效应分析与预测 3.1 日温度效应特点日温度效应由日温度作用引起,同时受大气温度和太阳辐射的影响.太阳辐射能够在结构内部产生温度梯度,与长期缓慢变化的年温度作用相比,这种温度梯度的变化更为迅速,对结构受力的影响更大.大地表面接收的太阳辐射强度在一年中随季节不断改变,在一天中随时间不断改变[21].因此为了更准确地分析温度效应,应该对太阳辐射影响的特点进行分析.
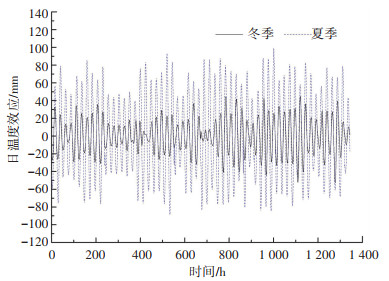
3.1.1 年周期中太阳辐射影响的特点为研究不同季节间太阳辐射对日温度效应影响的差异,选取2007年冬季和夏季各55 d的日温度效应数据进行分析,如图 7所示.日温度效应变化范围为冬季[-52.72 mm, 44.56 mm],夏季[-88.67 mm, 98.93 mm].日温度效应的变化幅值在同一季节中相对平稳,而在不同季节间差别较大.
|
图 7 冬季和夏季日温度效应对比 Fig. 7 Comparison of diurnal thermal deflection in winter and summer |
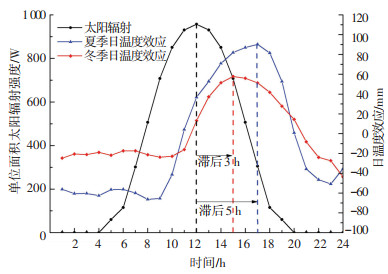
文献[22]中规定了不同纬度处、不同空气透明度等级条件下,夏季的太阳总辐射强度.背景桥处于北纬32°地区,大气透明度等级为5级,夏季水平面单位面积上的太阳辐射强度日变化曲线如图 7所示.夏季和冬季的太阳辐射日变化趋势相同,而太阳辐射强度不同[23-24].为研究日周期内太阳辐射对日温度效应的影响,选取2007年冬季、夏季中天气晴朗的两天(1月25日和8月25日)日温度效应同绘于图 8.
|
图 8 太阳辐射强度与典型日温度效应 Fig. 8 Solar radiation intensity and typical diurnal thermal deflection |
由图 8可知,日周期内太阳辐射强度的变化曲线类似余弦曲线,并于中午12:00时达到最大.日周期中挠度响应在0:00时至8:00时间没有明显的波动,8:00时开始日温度效应明显增长,主梁出现上拱.冬季主梁上拱至15:00时达到最大,夏季则上拱至17:00时达到最大,随后主梁上拱逐渐减小.挠度的日温度效应变化与太阳辐射强度的变化规律相似,但相对太阳辐射强度的变化存在一定的滞后.
取2007年冬季、夏季天气晴朗的各55 d的数据为样本,经统计可知,挠度日温度效应相对于太阳辐射强度的滞后性表现为冬季滞后3 h,夏季滞后5 h.若不考虑滞后影响,将上述典型日的日温度效应与太阳辐射强度变化曲线绘于图 9.

|
图 9 不考虑滞后日温度效应与太阳辐射的相关性 Fig. 9 Correlation between thermal deflection and solar radiation without lag |
由图 9可知,挠度的日温度效应与太阳辐射强度呈明显的正相关关系,其中冬季的相关系数均值为R2=0.795 8, 夏季的相关系数均值为R2=0.880 4.
太阳辐射对日温度效应的影响在年周期内具有季节性差异,在日周期内具有时刻间差异,因此在对日温度效应的分析中应充分考虑.
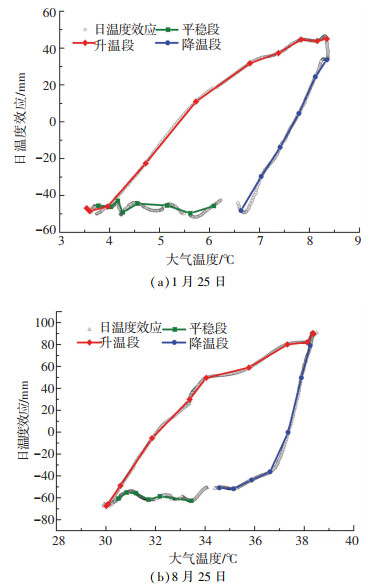
3.2 日温度效应的预测预测未来某周期内桥梁结构响应的信息,对于桥梁运营状态的预警有积极意义.为实现日温度效应的预测,应先定量研究日周期内大气温度和太阳辐射对日温度效应的影响. 图 10为典型日2007年1月25日、8月25日的大气温度和日温度效应的关系散点图(横坐标为大气温度,纵坐标为日温度效应,折线中各点对应各时刻的平均大气温度与日温度效应).
|
图 10 大气温度与日温度效应的关系 Fig. 10 Correlation between diurnal thermal deflection and ambient temperature |
根据图 10可将日温度效应分为升温段:冬季9:00—15:00,夏季9:00—17:00;降温段:冬季16:00—22:00,夏季18:00—22:00;平稳段:22:00—次日8:00.平稳段基本处于夜间,太阳辐射的影响很小,大气温度和温度效应的变化都较小;升温段和降温段分别由两条曲线构成,主梁挠度变化较大.由图 10中折线可知,在日周期内各时刻的日温度效应与大气温度表现为线性相关,日温度效应可由多折线模型描述.
为考察上述3个区段内大气温度与日温度效应之间的定量关系,分别对2007年冬季、夏季天气晴朗的55 d中各个时刻的大气温度与日温度效应进行线性拟合.其单位温度效应(即线性拟合系数)的平均绝对值及线性拟合决定系数见表 2.
| 表 2 各时刻间大气温度与日温度效应的相关性 Tab. 2 Correlation between thermal deflection and ambient temperature at different times |
由表 2可知各时刻间大气温度与日温度效应的线性相关性良好,可使用线性拟合方法对各时刻间的日温度效应进行拟合[25].
日温度效应实质上是日周期内各时刻温度效应的线性累加,满足多折线模型特征,可表示为
| $ {D_k} = {D_0} + \sum\limits_{i = 1}^k \Delta {D_i}\Delta {T_i}. $ | (9) |
其中:Dk为1 d中k时刻的日温度效应, mm; D0为1 d中0:00时的日温度效应, mm; ΔDi为i时刻的单位温度效应绝对值, mm/℃; ΔTi为i时刻大气温度的变化, ℃.
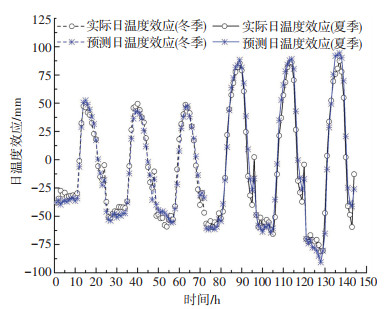
随机抽取2008年冬季和夏季中天气晴朗的几天,同样采用时间多尺度分析方法将日温度效应从总挠度响应中分离出来,再利用上述多折线模型对其日温度效应在日周期内进行预测,预测结果如图 11所示.
|
图 11 日温度效应多折线模型预测效果 Fig. 11 Prediction of diurnal thermal deflection by multi-fold line model |
由图 11可知平稳段内日温度效应的预测绝对误差在2 cm以内,升温段和降温段内日温度效应的预测绝对误差在1 cm以内,日周期内预测平均相对误差为8.86%,决定系数R2=0.973 4.预测日温度效应能反应实际日温度效应的变化趋势,且预测值与实际值能较好吻合,因此应用该方法在日周期内对日温度效应进行预测具有一定的准确性.
4 结论1) 为更好地分析温度对斜拉桥主梁挠度的影响,结合挠度响应的多时间尺度特征,对其温度效应进行多尺度分离和分析.采用小波多尺度分析方法对挠度响应信号进行不同时间尺度内的分解,能得到不同时间尺度上的温度效应,实现挠度的温度效应分离,可以对桥梁状态评估的数据选取提供参考.
2) 对背景桥挠度实测数据进行多尺度分离及分析,结果表明日温度效应的季节性明显,不考虑滞后时与太阳辐射强度呈明显相关关系.在定量研究桥梁日温度效应时,需充分考虑太阳辐射引起的季节性差异和时刻间差异.
3) 日周期内各时刻间的日温度效应与大气温度间具有良好的线性相关性,本文对其关系提出了多折线拟合模型,综合考虑大气温度和太阳辐射对日温度效应的影响,获得不同季节日周期内任意时刻的日温度效应,实现对温度效应的可靠预测.
4) 所提出的多折线预测模型可为斜拉桥主梁挠度的温度响应预测提供新思路,对基于监测数据的病害诊断和安全评估等相关研究有积极意义.
| [1] |
LI S, ZHU S, XU Y L, et al. Long-term condition assessment of suspenders under traffic loads based on structural monitoring system: application to the Tsing Ma Bridge[J]. Structural Control & Health Monitoring, 2012, 19(1): 82. |
| [2] |
刘小玲, 黄侨, 任远, 等. 大跨度钢斜拉桥主梁监测挠度的评估与预警[J]. 湖南大学学报(自然科学版), 2016, 43(9): 98. LIU Xiaoling, HUANG Qiao, REN Yuan, et al. Assessment and early warning on the monitoring girder deflection of the long-span steel cable stayed bridge[J]. Journal of Hunan University (Natural Sciences), 2016, 43(9): 98. DOI:10.3969/j.issn.1674-2974.2016.09.013 |
| [3] |
XIA Qi, ZHANG Jian, TIAN Yongding, et al. Experimental study of thermal effects on a long-span suspension bridge[J]. Journal of Bridge Engineering, 2017, 22(7): 4017034. DOI:10.1061/(ASCE)BE.1943-5592.0001083 |
| [4] |
刘纲, 邵毅敏, 黄宗明, 等. 长期监测中结构温度效应分离的一种新方法[J]. 工程力学, 2010, 27(3): 55. LIU Gang, SHAO Yimin, HUANG Zongming, et al. A new method to separate temperature effect from long-term structural health monitoring data[J]. Engineering Mechanics, 2010, 27(3): 55. |
| [5] |
任远, 刘小玲, 黄侨. 斜拉桥恒载索力长期变化趋势分析与评估[J]. 哈尔滨工业大学学报, 2015, 47(6): 103. REN Yuan, LIU Xiaoling, HUANG Qiao. The long-term trend analysis and assessment of the cable forces due to dead load in cable-stayed bridges[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 103. DOI:10.3969/j.issn.1009-1971.2015.06.019 |
| [6] |
黄侨, 任远, 许翔, 等. 大跨径缆索承重桥梁状态评估的研究现状与发展[J]. 哈尔滨工业大学学报, 2017, 46(9): 1. HUANG Qiao, REN Yuan, XU Xiang, et al. Research progress of condition evaluation for large span cable supported bridges[J]. Journal of Harbin Institute of Technology, 2017, 46(9): 1. |
| [7] |
DING Y, BIAN Y, ZHAO H, et al. Long-term monitoring and analysis of vertical deflections of a highway-railway cable-stayed bridge under operation conditions[J]. Journal of Railway Science & Engineering, 2017. |
| [8] |
陈国良, 林训根, 岳青, 等. 基于时间序列分析的桥梁长期挠度分离与预测[J]. 同济大学学报(自然科学版), 2016, 44(6): 962. CHEN Guoliang, LIN Xungen, YUE Qing, et al. Study on separation and forecast of long-term deflection based on time series analysis[J]. Journal of Tongji University (Natural Science), 2016, 44(6): 962. |
| [9] |
XIA Y, CHEN B, ZHOU X Q, et al. Field monitoring and numerical analysis of Tsing Ma Suspension Bridge temperature behavior[J]. Structural Control & Health Monitoring, 2013, 20(4): 560. |
| [10] |
梁宗保.基于监测信息统计分析的桥梁结构安全评价研究[D].重庆: 重庆大学, 2006 LIANG Zongbao. Safety evaluation of bridge structures based on statistical analysis of monitoring information[D]. Chongqing: Chongqing University, 2006 http://d.wanfangdata.com.cn/Thesis_Y1023111.aspx |
| [11] |
BROWNJOHN J M W, KOO K Y, SCULLION A, et al. Operational deformations in long-span bridges[J]. Structure & Infrastructure Engineering, 2015, 11(4): 556. |
| [12] |
CROSS E J, KOO K Y, BROWNJOHN J M W, et al. Long-term monitoring and data analysis of the Tamar Bridge[J]. Mechanical Systems & Signal Processing, 2013, 35(1/2): 16. |
| [13] |
杨红, 孙卓, 刘夏平, 等. 基于多最小二乘支持向量机的桥梁温度挠度效应的分离[J]. 振动与冲击, 2014, 33(1): 71. YANG Hong, SUN Zhuo, LIU Xiaping, et al. Separation of bridge temperature deflection effect based on M-LS-SVM[J]. Journal of Vibration and Shock, 2014, 33(1): 71. DOI:10.3969/j.issn.1000-3835.2014.01.012 |
| [14] |
LIU Xiaping, YANG Hong, SUN Zhuo, et al. Separation study of bridge deflection based on singular value decomposition[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(3): 11. |
| [15] |
刘小玲, 黄侨, 任远, 等. 斜拉桥多指标证据融合的综合评估方法[J]. 哈尔滨工业大学学报, 2017, 49(3): 74. LIU Xiaoling, HUANG Qiao, REN Yuan, et al. The long-term trend analysis and assessment of the cable forces due to dead load in cable-stayed bridges[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 74. |
| [16] |
于凤芹. 实用小波分析十讲[M]. 西安: 西安电子科技大学出版社, 2013. YU Fengqin. Ten lectures on practical wavelet analysis[M]. Xi'an: Xi'an University of Electronic Science and Technology Press, 2013. |
| [17] |
MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674. DOI:10.1109/34.192463 |
| [18] |
SPARTO P J, PARNIANPOUR M, BARRIA E A, et al. Wavelet and short-time Fourier transform analysis of electromyography for detection of back muscle fatigue[J]. IEEE Transactions on Rehabilitation Engineering, 2000, 8(3): 433. DOI:10.1109/86.867887 |
| [19] |
孙磊, 慕玉坤, 郝宪武. 基于小波变换和ARIMA模型的桥梁健康监测数据分析[J]. 中外公路, 2015, 35(1): 126. SUN Lei, MU Yukun, HAO Xianwu. Analysis of bridge health monitoring data based on Wavelet Transform and ARIMA Model[J]. Journal of China & Foreign Highway, 2015, 35(1): 126. DOI:10.3969/j.issn.1671-2579.2015.01.028 |
| [20] |
AMIRI M, JENSEN R. Missing data imputation using fuzzy-rough methods[J]. Neuro Computing, 2016, 205: 152. |
| [21] |
WESTGATE R, KOO K Y, BROWNJOHN J. Effect of solar radiation on suspension bridge performance[J]. Journal of Bridge Engineering, 2015, 20(5): 04014077. DOI:10.1061/(ASCE)BE.1943-5592.0000668 |
| [22] |
中华人民共和国住房和城乡建设部.民用建筑供暖通风与空气调节设计规范: GB 50736—2012[S].北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban Rural Development of the People's Republic of China. Design code for heating ventilation and conditioning of civil buildings: GB 50736—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [23] |
任远, 王晓春, 黄侨, 等. 中美欧公路桥梁设计规范的综合评价方法[J]. 哈尔滨工业大学学报, 2016, 48(9): 7. REN Yuan, WANG Xiaochun, HUANG Qiao, et al. The comprehensive evaluation method of highway bridge design specifications of China, U.S. and Europe[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 7. |
| [24] |
吴继臣, 徐刚. 全国主要城市冬季太阳辐射强度的研究[J]. 哈尔滨工业大学学报, 2003, 35(10): 1236. WU Jichen, XU Gang. Major Chinese cities' solar radiant intensities in winter[J]. Journal of Harbin Institute of Technology, 2003, 35(10): 1236. DOI:10.3321/j.issn:0367-6234.2003.10.024 |
| [25] |
丁幼亮, 卞宇, 赵瀚玮, 等. 公铁两用斜拉桥竖向挠度的长期监测与分析[J]. 铁道科学与工程学报, 2017(2): 73. DING Youliang, BIAN Yu, ZHAO Hanwei, et al. Long-term monitoring and analysis of vertical deflections of a highway-railway cable-stayed bridge under operation conditions[J]. Journal of Railway Science and Engineering, 2017(2): 73. |
 2020, Vol. 52
2020, Vol. 52


