颤振临界风速是衡量桥梁颤振稳定性的重要指标[1].然而,由于桥梁结构自身及外部环境的随机性,如刚度、质量、阻尼比、气动导数等的不确定,从而造成桥梁的颤振临界风速也是不确定的[2].所以桥梁颤振失效概率采用可靠度分析方法更为合理[3].
目前在桥梁颤振临界风速概率评价方面,主要还是采用矩方法[4]及替代函数法[5]进行估计.基于现有的结构可靠度理论,一些学者提出桥梁颤振稳定失效概率的计算方法:2001年,葛耀君教授运用中心点法和验算点法,基于实验与理论相结合进行桥梁颤振稳定的概率分析,并对上海杨浦大桥和江阴长江大桥进行了颤振稳定的概率性评价[6]. 2007年,周峥等提出的随机有限元方法,综合考虑了结构刚度、质量、阻尼比以及颤振导数等随机因素对颤振临界风速的影响,并对东海大桥颗珠山斜拉桥进行了颤振可靠性分析[7].
目前,对于线性系统平稳反应的分析理论基本趋于完备,并已经开始进入工程实用阶段[8].然而,对于非线性系统,人们仍然面临巨大的困难[9].近几年,李杰和陈建兵提出的广义概率密度演化方法[10],为求解非线性系统带来了巨大的方便.应用数值求解技术可获得广义概率密度演化方程的解,从而可以得到结构响应的概率密度函数(PDF)曲线,进而获得结构的可靠度.概率密度演化方法一方面包含结构中所有的概率信息,另一方面不受概率密度分布情况的影响,对于复杂形式的状态函数也适用,为结构可靠度分析提供了极大的方便.
本文采用概率密度演化方法与桥梁颤振多模态耦合分析方法相结合,以江阴长江大桥为例,选取结构质量、结构刚度、结构阻尼比、气动导数作为随机变量,对结构模态阻尼比及频率的概率密度演化过程进行分析,并给出基于概率密度演化方法得到的颤振临界风速.论文首先概述了目前结构可靠度研究的进展以及目前桥梁颤振临界风速可靠度计算的方法,第1节介绍概率密度演化方法的基本理论以及对桥梁进行颤振临界风速概率密度演化分析的主要步骤,第2节对典型桥梁的基本参数进行了介绍,第3节为概率演化计算结果及分析,第4节对研究结果进行了总结.
1 基本理论 1.1 广义概率密度演化方程一般的结构动力系统运动方程可以表述为
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = \mathit{\boldsymbol{LF}}\left( t \right). $ | (1) |
其中X =(X1, X2, …, Xn)T为结构位移向量,
结构的基本参数变异性较大[11-12].可以将这些参数表示为一系列基本随机变量的函数.记为θ1= (θ1,θ2,…, θs1),其中s1为结构随机变量的总个数,这样,方程中的质量矩阵、刚度矩阵和阻尼比矩阵都是随机向量θ1的函数.
同时,结构外部激励也具有显著的随机性,可将上述随机过程表述为θ2= (θs1+1,θs1+2,…,θs1+s2),其中s2为随机激励中基本随机变量的个数.
上述全部随机变量记为θ = (θ1, θ2) =(θ1, θ2,…,θs),其中s=s1+s2为随机变量的总个数.其中θ的联合概率密度函数pθ(θ)已知,其分布域为Ωθ,于是,方程(1)可表示为
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot X}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\theta }},t} \right). $ | (2) |
记Z = Z(Z1, Z2, …, Zm)为所要考察的物理量,令
| $ \mathit{\boldsymbol{\dot Z}}\left( t \right) = \varphi \left[ {G\left( {\mathit{\boldsymbol{\theta }},t} \right),H\left( {\mathit{\boldsymbol{\theta }},t} \right)} \right] = \mathit{\boldsymbol{h}}\left( {\mathit{\boldsymbol{\theta }},t} \right), $ | (3) |
其中φ(.)是从状态向量向所考察的物理量的转换函数,对应的概率密度函数Pzθ(z, θ, t)满足方程:
| $ \frac{{\partial {P_{z\theta }}\left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\theta }},t} \right)}}{{\partial t}} + \sum\limits_{j = 1}^m {{h_j}\left( {\mathit{\boldsymbol{\theta }},t} \right)\frac{{\partial {P_{z\theta }}\left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\theta }},t} \right)}}{{\partial {z_j}}}} = 0. $ | (4) |
一般的,方程(4)的边界条件可采用:
| $ {P_{z\theta }}\left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\theta }},t} \right)\left| {_{{z_j} \to \pm \infty }} \right. = 0,j = 1,2, \cdots ,m. $ | (5) |
而初始条件则为
| $ {P_{z\theta }}\left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\theta }},t} \right)\left| {_{t = {t_0}}} \right. = \delta \left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{z}}_0}} \right){P_\theta }\left( \mathit{\boldsymbol{\theta }} \right). $ | (6) |
z0为初始值,通过求解广义概率密度演化方程(4),可最终得到Z(t)的概率密度函数:
| $ {P_z}\left( {\mathit{\boldsymbol{z}},t} \right) = \int {{P_{z\theta }}} \left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\theta }},t} \right){\rm{d}}\mathit{\boldsymbol{\theta }}. $ | (7) |
对于一般的随机动力系统,广义概率密度演化方程的求解需要借助于有限差分法:一种是单边差分格式,另外一种是Lax-Wendroff格式.李杰和陈建兵采用具有TVD性质的有限差分格式可以获得较为理想解答[13].最近,Papadopoulos[14]和Kalogeris采用Petrov-Galerkin有限元方法也成功的应用于概率密度演化方程的求解.
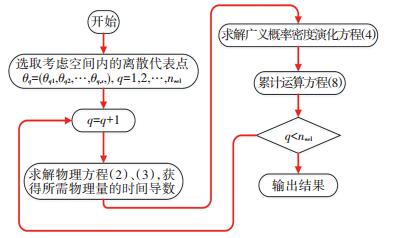
1.2 广义概率密度演化方程的求解广义概率密度演化方程求解流程如图 1所示, 主要步骤如下:1)概率空间选点.在基本随机向量θ的分布空间Ω中选取一系列代表性的离散点,记为θq= (θq, 1, θq, 2, …, θq, s), q=1, 2,…, nsel,这里nsel为所取离散点的数目,同时,确定每个代表点的赋得概率
|
图 1 广义概率密度演化方程求解流程 Fig. 1 Flow chart for the solution of the generalized probability density evolution equation (GDEE) |
| $ {P_z}\left( {\mathit{\boldsymbol{z}},t} \right) = \sum\limits_{q = 1}^{{n_{{\rm{sel }}}}} {{P_{z\theta }}} \left( {\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\theta }}_q},t} \right). $ | (8) |
本文基于结构有限元模型,进行多模态颤振耦合分析[15].桥梁结构进行颤振分析时,自激力作用下的结构运动方程一般形式[16]可表示为
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{F}}_{{\rm{se}}}} = {\mathit{\boldsymbol{F}}_{{\rm{se}}C}} + {\mathit{\boldsymbol{F}}_{{\rm{se}}K}} = {\mathit{\boldsymbol{C}}_{{\rm{se}}}}\mathit{\boldsymbol{\dot X}} + {\mathit{\boldsymbol{K}}_{{\rm{se}}}}\mathit{\boldsymbol{X}}. $ | (9) |
式中:M、K、C分别为结构质量、刚度和阻尼比矩阵;X、
| $ \mathit{\boldsymbol{M\ddot X}} + \left( {\mathit{\boldsymbol{C}} - {\mathit{\boldsymbol{C}}_{{\rm{se}}}}} \right)\mathit{\boldsymbol{\dot X}} + \left( {\mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{K}}_{{\rm{se}}}}} \right)\mathit{\boldsymbol{X}} = {\bf{0}}. $ | (10) |
假设结构的特征运动形式可描述为
| $ \mathit{\boldsymbol{X}} = \varphi {{\rm{e}}^{\lambda t}}. $ | (11) |
式中:φ为结构复模态振动响应,ξ为振动的对数衰减率,ω为振动圆频率,i=
| $ \lambda \mathit{\boldsymbol{\tilde C}}\varphi + \mathit{\boldsymbol{\tilde K}}\varphi = - {\lambda ^2}\mathit{\boldsymbol{M}}\varphi . $ | (12) |
由此,颤振分析问题即转化为求解如下方程的广义特征值问题.式中
按照式(10),物理方程可建立为
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot X}}}\\ \mathit{\boldsymbol{X}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&\mathit{\boldsymbol{I}}\\ { - \left( {\mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{K}}_{{\rm{se}}}}} \right)/\mathit{\boldsymbol{M}}}&{ - \left( {\mathit{\boldsymbol{C}} - {\mathit{\boldsymbol{C}}_{{\rm{se}}}}} \right)/\mathit{\boldsymbol{M}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot X}}}\\ \mathit{\boldsymbol{X}} \end{array}} \right]. $ | (13) |
令
| $ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{X}}&{\mathit{\boldsymbol{\dot X}}} \end{array}} \right]}^{\rm{T}}} = \mathit{\boldsymbol{Y}},}\\ {\left[ {\begin{array}{*{20}{c}} {\bf{0}}&\mathit{\boldsymbol{I}}\\ { - \left( {\mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{K}}_{{\rm{se}}}}} \right)/\mathit{\boldsymbol{M}}}&{ - \left( {\mathit{\boldsymbol{C}} - {\mathit{\boldsymbol{C}}_{{\rm{se}}}}} \right)/\mathit{\boldsymbol{M}}} \end{array}} \right] = \mathit{\boldsymbol{G}},} \end{array} $ |
则有
| $ \mathit{\boldsymbol{\dot Y}} = \mathit{\boldsymbol{GY}}. $ | (14) |
至此,通过求解G的特征值,即可求得各参与模态在不同风速下的特征频率及阻尼比,方程(2)的物理方程变为
| $ \text{eig}\left( {\mathit{\boldsymbol{G}}\left( {U,\mathit{\boldsymbol{\theta }}} \right)} \right). $ | (15) |
方程中U代表风速.从上述分析可以看出,桥梁颤振临界风速的概率密度演化计算过程只需将对应的物理方程换成方程(15),将风速看成广义的时间变量,即可求解,求解流程如图 1所示.
2 桥梁基本参数 2.1 结构参数本文选取江阴长江大桥作为本次计算的实例.大桥主桥跨径布置为336.5 m+1 385 m+309.34 m.主梁采用扁平状闭口钢箱梁,主梁宽36.9 m,主梁高3.0 m.主缆横桥向中心间距为32.5 m,主缆矢跨比为1/10.5,吊杆纵桥向间距为16 m.桥塔为门式框架结构,南北桥塔高分别为187、184 m.桥梁总体立面布置图及主梁断面布置图参见图 2、3.

|
图 2 桥梁总体立面布置(m) Fig. 2 Main elevation of the bridge (m) |

|
图 3 桥梁主梁断面(m) Fig. 3 Cross-section of the bridge deck (m) |
结构的主要振型、频率及等效质量列于表 1,结构一阶正对称竖弯频率为0.133 706 Hz,结构一阶正对称扭转频率为0.272 963 Hz.
| 表 1 结构主要振型及等效质量 Tab. 1 Main mode and equivalent mass of the bridge |
气动导数按照文献[17]取值,A1*~A4*及H1*~H4*的取值参见表 2.零攻角下模型的静力系数及对应的导数分别为:CD=0.069 7,dCD/dα=0,CL=-0.128,CM=-0.007 4,与横向振动相关的气动导数按拟静力理论采用,桥梁固有模态的结构阻尼比取为0.005.
| 表 2 结构气动导数 Tab. 2 Aerodynamic derivatives of the bridge |
参照文献[4, 18-19]的研究成果,选取桥梁结构的质量M、刚度K、阻尼比ζ和气动导数作为影响颤振临界风速的随机变量.记竖向运动相关的气动导数H1*, H4*, A1*, A4*, P5*, P6*, 为V*,记扭转运动相关的气动导数H2*, H3*, A2*, A3*, P2*, P3*, 为T*,记侧向运动相关的气动导数H5*, H6*, A5*, A6*, P1*, P4*, 为L*.结构质量服从正态分布,变异系数取为0.05,结构刚度服从对数正态分布,变异系数取为0.05,结构阻尼比采用瑞雷阻尼比,服从对数正态分布[19],变异系数取为0.2,气动导数V*、T*、L*均服从对数正态分布[19],变异系数取为0.05.各随机变量分布相互独立.
3 桥梁颤振的概率密度演化分析 3.1 代表点的选取及检验代表点选取采用基于概率空间剖分的两步选点法[10, 20],主要步骤如下:1)获得一个在Ωe分布空间均匀散布的点集; 2)根据Ωe概率分布特性对此点集进行变换,获得F-偏差及一阶和二阶偏差均较小的点集作为最终的离散代表点集.本文选取离散代表点2 000个,对应的各随机变量的分布及相关系数如图 4所示,各随机变量的分布和初始假定分布一致,且各随机变量之间的相关系数均小于3%,选点符合要求. 图 5、6为初始风速下结构频率及阻尼比与各随机变量的分布及相关性.

|
图 4 各随机变量分布及相互之间的相关性 Fig. 4 Random variables distribution and correlations |
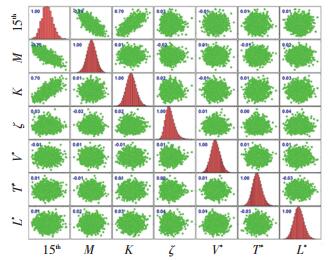
|
图 5 第15阶频率分布及其与其他随机变量相关性 Fig. 5 Fifteenth modal frequency distribution and its correlation with other random variables |

|
图 6 第15阶阻尼比分布及其与其他随机变量相关性 Fig. 6 Fifteenth modal damping ratio distribution and its correlation with other random variables |
从图 5可以看出,结构频率和结构质量、结构刚度的相关系数为0.7,符合1/
概率演化过程的计算参见第1节的介绍,本文颤振分析采用多模态耦合颤振分析方法进行计算,选取结构前30阶模态参与颤振分析及概率密度演化分析,给出各个模态频率及阻尼比的概率密度演化过程.为方便叙述,本文仅选取具有代表性的模态对其计算结果进行阐述.
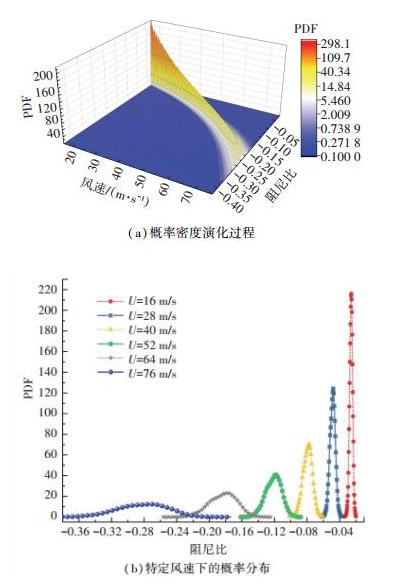
3.2.1 阻尼比图 7为结构一阶对称竖弯阻尼比概率演化过程. 7(a)对应的概率密度随风速的演进过程,7(b)对应的是特定风速下的概率密度分布.在低风速下,一阶对称竖弯阻尼比的概率密度分布可近似认为服从正态或对数正态分布,但方差或者变异系数会随着风速的加大而不断增大,且变异度不断加剧,而在高风速下(v=64 m/s), 阻尼比的概率分布已经无法用单一的概率分布来描述,概率分布会出现双峰甚至多峰的情况.
|
图 7 一阶对称竖弯对应的阻尼比概率密度演化过程 Fig. 7 Probability density evolution of modal damping ratio for the 1st-S-V mode |
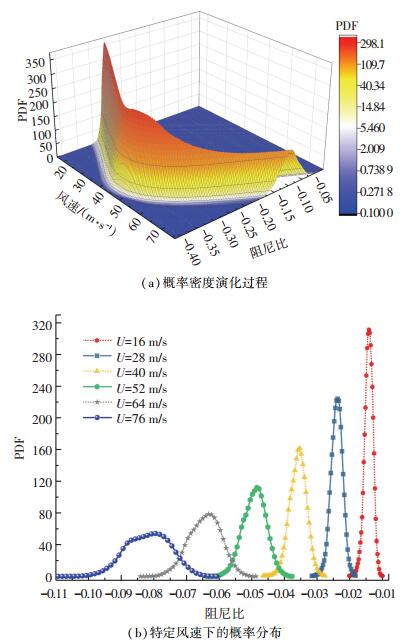
图 8为结构一阶对称扭转阻尼比概率演化过程. 8(a)对应的概率密度随风速的演进过程,8(b)对应的是特定风速下的概率密度分布.低风速下,一阶对称扭转阻尼比的概率密度分布可近似认为服从正态或对数正态分布,方差或者变异系数会随着风速的加大而不断增大,且变异度不断加剧,其阻尼比均值则呈现先减小后增大的趋势,这与按照确定性方法得到阻尼比随风速的变化曲线一致(在3.3节中论述).高风速下的概率密度则无法用单一的概率分布来描述,概率分布会出现双峰甚至多峰的情况.
|
图 8 一阶对称扭转对应的阻尼比概率密度演化过程 Fig. 8 Probability density evolution of modal damping ratio for the 1st-S-T mode |
图 9为结构一阶对称竖弯频率概率演化过程. 9(a)对应的是概率密度随风速的演进过程,9(b)对应的是特定风速下的概率密度分布.低风速下,一阶对称竖弯频率的概率密度分布可近似认为服从正态或对数正态分布,但方差或者变异系数会随着风速的加大而增大,但增大率较小.而在高风速下, 频率的概率分布已经无法用单一的概率分布来描述,概率分布会出现双峰甚至多峰的情况.竖弯频率均值随着风速加大而加大,与按照确定性方法得到竖弯频率随风速的变化曲线一致(在3.3中论述).

|
图 9 一阶对称竖弯对应的频率概率密度演化过程 Fig. 9 Probability density evolution of modal frequency for the 1st-S-V mode |
图 10为结构一阶对称扭转频率概率演化过程. 10(a)对应的是概率密度随风速的演进过程,10(b)对应的是特定风速下的概率密度分布.一阶对称扭转频率的概率密度分布可近似认为服从正态或对数正态分布,但方差或者变异系数会随着风速的加大而增大.频率均值随风速的增大而减小,这与按照确定性方法得到频率随风速的变化曲线一致(在3.3中论述).

|
图 10 一阶对称扭转对应的频率概率密度演化过程 Fig. 10 Probability density evolution of modal frequency for the 1st-S-T mode |
确定性方法采用多模态耦合分析方法确定颤振临界风速,选取结构前30阶模态参与颤振临界风速多模态计算.判别颤振临界风速标准为任一参与多模态计算的模态阻尼比大于零,模态初始阻尼比均取为0.005.计算方法参见第2节中的论述.结构主要模态频率及阻尼比随风速的变化曲线如图 11所示,以阻尼比大于零作为颤振临界风速的判别标准,得到颤振临界风速vcr=68.7 m/s.与文献[17]中的vcr=67.69 m/s较为一致,故下文采用vcr=68.7 m/s.

|
图 11 结构频率及阻尼比随风速的变化 Fig. 11 Variation of modal damping ratio and frequency with wind speed |
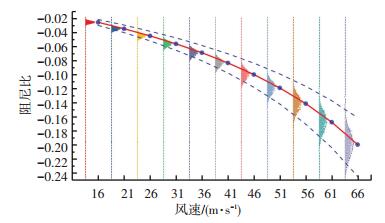
为了采用概率密度演化方法对颤振临界风速进行评价,需要首先确定阻尼比在不同风速下的概率分布情况,进而确定标准差及置信区间. 图 12~14为结构主要模态阻尼比不同风速下的均值、概率分布及置信线.
|
图 12 结构一阶对称竖弯阻尼比不同风速下的均值、概率分布及置信线 Fig. 12 Mean, probability density function(PDF), and confidence curves of modal damping ratio for the 1st-S-V mode at different wind speeds |
|
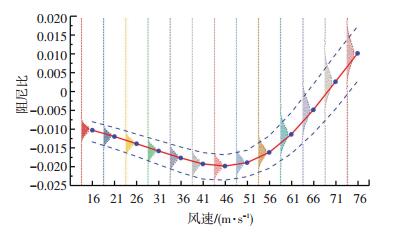
图 13 结构一阶对称扭转阻尼比不同风速下的均值、概率分布及置信线 Fig. 13 Mean, PDFs, and confidence curves of modal damping ratio for the 1st-S-T mode at different wind speeds |
|
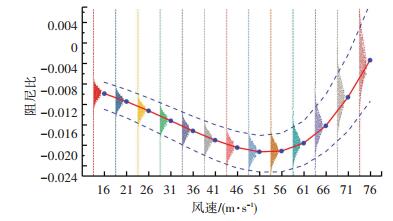
图 14 结构一阶反对称扭转阻尼比不同风速下的均值、概率分布及置信线 Fig. 14 Mean, PDFs, and confidence curves of modal damping ratio for the 1st-A-T mode at different wind speeds |
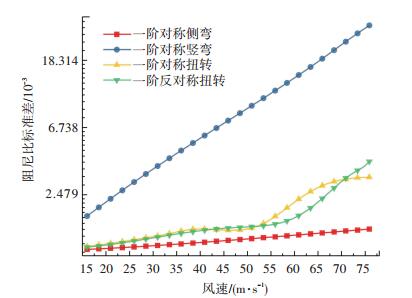
通过对比可以发现,低风速下各主要模态阻尼比在不同风速下的概率分布可近似认为服从正态分布或对数正态分布.标准差随风速的增大有所增大,近似服从指数分布,其中一阶正对称竖弯对应的标准差增幅最为明显,一阶侧弯增幅较小,而扭转模态对应的阻尼比在低风速下增幅较小,在高风速下增幅较大(参见图 15).
|
图 15 结构阻尼比标准差随风速的变化曲线 Fig. 15 Variation of standard deviation of modal damping ratio with wind speed |
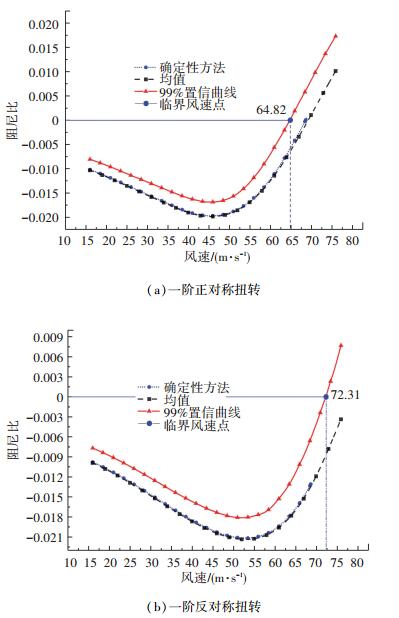
基于概率密度演化方法的颤振临界风速确定如下:采用99%置信曲线确定各模态阻尼比零点对应的风速,以最小的风速作为颤振临界风速.根据3.2节的研究,本部分仅列出一阶对称扭转以及一阶反对称扭转求得的对应风速点.如图 16所示,一阶正对称扭转及一阶反对称扭转阻尼比概率均值变化曲线与按照确定性方法得到曲线基本重合,说明概率密度演化方法可靠性较好.基于概率密度演化方法,按照一阶正对称扭转得到的颤振临界风速为vcr=64.82 m/s,按照一阶反对称扭转得到的颤振临界风速为vcr=72.31 m/s,故最终颤振临界风速为vcr=64.82 m/s.
|
图 16 结构阻尼比标准差、置信曲线随风速的变化曲线 Fig. 16 Variation of standard deviation of modal damping ratio and confidence curve with wind speed |
与按确定性方法到的颤振临界风速相比,颤振临界风速降低了68.7 m/s-64.82 m/s=3.88 m/s.因此,采用传统的确定性方法得到的颤振临界风速会较高地估计结构的安全度,应该采用概率评价的方法,进行颤振临界风速估算.
4 结论1) 将概率密度演化方法与桥梁颤振多模态耦合分析方法相结合,以江阴长江大桥作为实例, 通过考虑桥梁自身结构的不确定性以及气动导数的不确定性,给出不同模态的阻尼比及频率的概率密度演化过程.按照99%保证率曲线,给出该桥的颤振临界风速,与按确定性方法到的颤振临界风速相比,颤振临界风速降低了3.88 m/s.
2) 结构阻尼比和结构质量、结构刚度的相关系数为0.2左右,与初始阻尼的相关系数为0.91.而结构阻尼比主要与对应的运动形态一致的气动导数相关度较大,而与其他气动导数相关度较小.
3) 结构模态阻尼比及频率在低风速情况下的概率密度分布可近似认为服从正态或对数正态分布,高风速下的概率密度则无法用单一的概率分布来描述,概率分布会出现双峰甚至多峰的情况.
4) 结构模态阻尼比的标准差随风速的增大有所增大,近似服从指数增大.其中一阶正对称竖弯对应的标准差增幅最为明显,一阶侧弯增幅较小,而扭转模态对应的阻尼比在低风速下增幅较小,在高风速下增幅较大.
| [1] |
XIANG Haifan, GE Yaojun. Refinements on aerodynamic stability analysis of super long-span bridges[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2002, 90(12): 1493. |
| [2] |
GE Yaojun, XIANG Haifan. Recent development of bridge aerodynamics in China[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(6): 736. |
| [3] |
MANNINI C, BARTOLI G. Aerodynamic uncertainty propagation in bridge flutter analysis[J]. Structural Safety, 2015, 52: 29. DOI:10.1016/j.strusafe.2014.07.005 |
| [4] |
GE Yaojun, XIANG Haifan, TANAKA H. Application of a reliability analysis model to bridge flutter under extreme winds[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2000, 86(2): 155. |
| [5] |
CHENG Jin, CAI C S, XIAO Rucheng, et al. Flutter reliability analysis of suspension bridges[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2005, 93(10): 757. |
| [6] |
葛耀君, 项海帆. 桥梁结构颤振稳定的概率性评价[J]. 同济大学学报(自然科学版), 2001, 29(1): 70. GE Yaojun, XIANG Haifan. Probabilistic assessment study of flutter instability of bridge structures[J]. Journal of Tongji University, 2001, 29(1): 70. DOI:10.3321/j.issn:0253-374X.2001.01.015 |
| [7] |
周峥, 葛耀君, 杜柏松. 桥梁颤振概率性评价的随机有限元法[J]. 工程力学, 2007, 24(2): 98. ZHOU Zheng, GE Yaojun, DU Baisong. Probabilistic assessment of bridge flutter based on stochastic finite element method[J]. Engineering Mechanics, 2007, 24(2): 98. DOI:10.3969/j.issn.1000-4750.2007.02.017 |
| [8] |
LUTES L D, SARKANI S. Random vibrations: analysis of structural and mechanical systems[M]. Oxford, UK: Butterworth Heinemann, 2004.
|
| [9] |
NAESS A, MOE V. Efficient path integration methods for nonlinear dynamic systems[J]. Probabilistic Engineering Mechanics, 2000, 15(2): 221. DOI:10.1016/S0266-8920(99)00031-4 |
| [10] |
CHEN Jianbing, GHANEM R, LI Jie. Partition of the probability-assigned space in probability density evolution analysis of nonlinear stochastic structures[J]. Probabilistic Engineering Mechanics, 2009, 24(1): 27. DOI:10.1016/j.probengmech.2007.12.017 |
| [11] |
GHANEM ROGER G, SPANOS P D. Stochastic finite elements: a spectral approach[M]. New York, NY: Springer, 1991.
|
| [12] |
李杰, 陈建兵. 概率密度演化理论的若干研究进展[J]. 应用数学和力学, 2017, 38(1): 32. LI Jie, CHEN Jianbing. Some new advances in the probability density evolution method[J]. Applied Mathematics and Mechanics, 2017, 38(1): 32. |
| [13] |
MAO Jianfeng, YU Zhiwu, XIAO Yuanjie, et al. Random dynamic analysis of a train-bridge coupled system involving random system parameters based on probability density evolution method[J]. Probabilistic Engineering Mechanics, 2016, 46: 48. DOI:10.1016/j.probengmech.2016.08.003 |
| [14] |
PAPADOPOULOS V, KALOGERIS I. A Galerkin-based formulation of the probability density evolution method for general stochastic finite element systems[J]. Computational Mechanics, 2016, 57(5): 701. DOI:10.1007/s00466-015-1256-9 |
| [15] |
GE Yaojun, TANAKA H. Aerodynamic flutter analysis of cable-supported bridges by multi-mode and full-mode approaches[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2000, 86(2): 123. |
| [16] |
GE Yaojun, XIANG Haifan. Computational models and methods for aerodynamic flutter of long-span bridges[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(10): 1912. |
| [17] |
DING Quanshun, CHEN Airong, XIANG Haifan. Coupled flutter analysis of long-span bridges by multimode and full-order approaches[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2002, 90(12): 1981. |
| [18] |
BRUNO L, FRANSOS D. Probabilistic evaluation of the aerodynamic properties of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(6/7): 718. |
| [19] |
BALDOMIR A, KUSANO I, HERNANDEZ S, et al. A reliability study for the Messina Bridge with respect to flutter phenomena considering uncertainties in experimental and numerical data[J]. Computers and Structures, 2013, 128: 91. DOI:10.1016/j.compstruc.2013.07.004 |
| [20] |
LI Jie, CHEN Jianbing, SUN Weiling, et al. Advances of the probability density evolution method for nonlinear stochastic systems[J]. Probabilistic Engineering Mechanics, 2012, 28: 132. DOI:10.1016/j.probengmech.2011.08.019 |
 2020, Vol. 52
2020, Vol. 52


