概率地震需求模型(probabilistic seismic demand model, PSDM)作为基于性能的地震工程研究框架中的重要一环,建立了不同构件的峰值响应与地震动强度指标(intensity measures, IM)间的关系,而地震动强度指标的选择决定了概率地震需求模型的离散程度.过去数十年来,研究人员从峰值、持续时间、频谱特性和能量的角度提出了许多地震动强度指标,包括常用的峰值加速度(peak ground acceleration, PGA)、峰值速度(peak ground velocity, PGV)、峰值位移(peak ground displacement, PGD)、谱加速度(Sa)等,以及一些新兴的IM:如文献[1]提出了分数阶IM,文献[2]提出的两参数自适应IM.这些IM大体可以分为3类:加速度相关型,速度相关型和位移相关型.必须注意的是,这些IM必须针对特定的场地条件和结构类型才适用. Riddell指出加速度相关IM更适用于短周期结构,位移相关IM更适用于长周期结构,速度相关IM更适用于中等周期结构[3].文献[4]以IM的高效性、实用性、充分性以及灾害的可计算性为评价指标, 对10个IM进行了比较分析,提出对于多跨简支钢梁桥PGA是最优的IM.文献[5]指出对于超高层建筑结构,以结构前几阶周期对应的加速度反应谱的几何平均值Sa为IM能够减小结构响应的变异系数.文献[6]分析了液化场地的桩基础桥梁,结果表明相比加速度相关的IM和位移相关的IM,速度相关的IM更加适用. Baker等在标量地震动强度指标的基础上进一步提出了矢量地震动强度指标[7],并指出在分析近场地震动时由Sa(T1)和反应谱形状相关的参数ε组成的矢量地震动强度指标表现优异[8].可以发现当前主要通过人工比较的方式选取单个IM来建立PSDM,过程较为繁琐,且标量IM只能反映地震动幅值、频谱特性、持时的一部分信息.
本文旨在不显著增加计算量的前提下,简化地震动强度指标的选取流程,减小概率地震需求模型的变异性.为此在已有IM的基础上,通过方差扩大因子法剔除能被其他IM线性表示的IM,消除IM间的多重共线性;对线性无关的IM进行所有子集回归,按偏决定系数选取高效的矢量地震动强度指标分量;并以无速度脉冲地震动作用下的三跨连续梁桥为例,证明了该方法的有效性.
1 标量地震动强度指标及地震动时程文献[9]假定工程需求参数(engineering demand parameter, EDP,对混凝土连续梁桥一般为墩顶漂移率和支座位移)的均值与IM之间满足对数线性关系:
| $ \ln (\mathrm{EDP})=\beta_{0}+\beta_{1} \ln (\mathrm{IM})+\tau. $ | (1) |
式中:β0、β1均为回归系数,τ为均值为0方差恒定的随机误差.
文献[7]把式(1)推广到了矢量IM(多个IM)的情况,即
| $ \begin{aligned} \ln (\mathrm{EDP})=& \beta_{0}+\beta_{1} \ln \left(\mathrm{IM}_{1}\right)+\beta_{2} \ln \left(\mathrm{IM}_{2}\right)+\cdots+\\ & \beta_{p} \ln \left(\mathrm{IM}_{p}\right)+\tau. \end{aligned} $ | (2) |
为表述方便,将矢量IM表示为VIM,VIM具有多个分量,即[IM1, IM2, …];将只有一个分量的标量地震动强度指标表示为IM.本文从以往的研究中获取了20个IM[3, 6, 10],见表 1.旨在从中挑选出合适的分量组成VIM.由于许多其他的IM都与表 1中所列的IM成完全的对数线性关系, 故没有考虑在内,如:V/A=PGV/PGA、Ia=PGA×td
| 表 1 标量地震动强度指标 Tab. 1 Scalar-valued intensity measures |
参考文献[6]的地震波选取原则,采用文献[11]为加利福尼亚州土质场地选取的80条水平地震动分量,为了得到更大的非线性地震响应范围,将这些波乘以放大系数2得到另外的80条水平地震波.为了能够反映结构从弹性到完全破坏的全过程,本文还从Baker等选取的50 a超越概率2%的40条地震波中选择了20条经过放缩后PGA均在1.0g左右的水平地震动分量.这180条地震波均无速度脉冲,图 1给出了加速度反应谱和均值谱,图 2给出了这些波的震级和震源距分布直方图.将180条地震波打乱顺序后分为6组,每次取其中5组作为训练数据集,1组作为测试数据集,进行交叉验证.

|
图 1 地震波的加速度反应谱(阻尼比5%) Fig. 1 Acceleration response spectra of seismic wave(damping ratio of 5%) |

|
图 2 震级和震源距分布直方图 Fig. 2 Statistics of magnitude and source distance |
已有研究发现IM之间存在强相关性[3, 7, 12-13],但这些研究只关注IM两两之间的相关性,而采用VIM得到模型(2)时必须关注多个IM间的多重共线性[7],即存在一组不全为0的数α1, α2, …, αp,使得
| $ \alpha_{1} \ln \left(\mathrm{IM}_{1}\right)+\alpha_{2} \ln \left(\mathrm{IM}_{2}\right)+\cdots+\alpha_{p} \ln \left(\mathrm{IM}_{p}\right)+\tau=0. $ | (3) |
其中E(τ) =0,V(τ) < ∞.
多重共线性的存在将会使回归系数β0、β1、…、βp的估计值很不稳定,回归模型(2)失去预测功能,因此多重共线性的诊断和处理是多元线性回归中讨论的重点.本文通过方差扩大因子法剔除不重要的IM,方差扩大因子的定义式为
| $ \mathrm{VIF}_{i}=1 /\left(1-R_{i}^{2}\right). $ | (4) |
式中Ri2为以IMi为因变量对其余IM进行多元线性回归得到的决定系数.
根据经验,VIFi≥10则表明IMi与其余IM间存在严重的多重共线性[14]. IM筛选的具体步骤如下:
步骤1 计算n条地震波的p个地震动强度指标得到矩阵Xn×p(对于本文的训练数据集n=150,p=20),对矩阵Xn×p的每一列作中心标准化处理得到Xn×p*.
步骤2 求自变量相关矩阵的逆矩阵(cij)=r-1=(n-1)(X*T X*)-1,则IMi的方差扩大因子VIFi=cii.
步骤3 VIFmax=max {VIFi|i∈[1, p], i∈Z},若VIFk=VIFmax≥10,则剔除IMk,重新回到步骤2.
步骤4 将被剔除的IMq逐一加入到自变量中,若重新计算VIFmax≤10,则重新选入IMq,反之则剔除IMq.
经过上述筛选,最终留下6个IM,分别为PGD、Tpre、Tm、SD、Sa(0.2)、Sa(1.0),6组训练数据集得到6个IM的方差扩大因子见表 2.若以这6个IM为自变量拟合其他IM,决定系数R2的最小值为0.853,平均值为0.917,也就是说这6个IM已经包含了其他IM的绝大部分信息.
| 表 2 6个IM的方差扩大因子 Tab. 2 Variance inflation factors of 6 IMs |
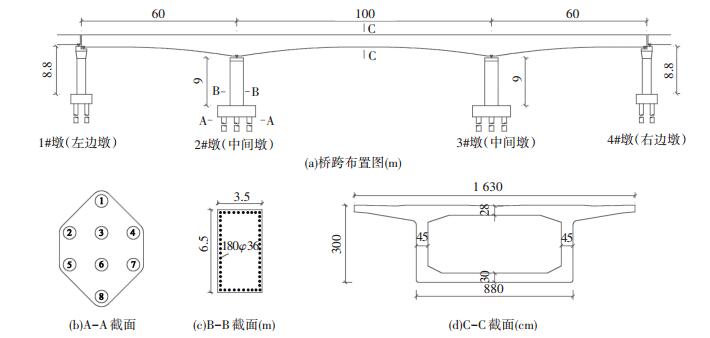
本文的工程原型为邯郸市南环路东延的一座跨度60 m+100 m+60 m的典型预应力混凝土连续梁桥,主梁为变截面混凝土箱梁,采用C50混凝土,中间墩处最大梁高为6.67 m,跨中和边墩处最小梁高为3 m,梁底按二次抛物线变化.中墩墩高为9 m,边墩高为8.8 m,均采用C40混凝土,矩形截面,中墩截面高宽分别为6.5 m和3.5 m,边墩截面较小,截面为5 m×2.5 m.在连续梁桥两端各建了一跨30 m的预应力混凝土简支梁桥作为引桥,梁高为3 m,墩高为8.8 m.采用梅花形布置的直径为2 m钻孔灌注桩作为桥梁基础,混凝土抗压强度等级为C30.全桥总体布置及主要构件的尺寸如图 3所示.支座采用曲率半径为5 m,摩擦系数为0.02的双曲面摩擦摆支座,均为双向滑动.使用OpenSees有限元分析软件建立全桥三维模型,如图 4所示.
|
图 3 桥梁结构总体布置 Fig. 3 Layout of bridge configuration |

|
图 4 有限元模型示意图 Fig. 4 Numerical model of the prototype bridge |
主梁采用elasticBeamColumn单元模拟,单元长度在1~2 m之间,变截面处单元截面特性近似采用原单元一侧的截面特性,将主梁节点建在相应截面的形心处,并将Midas civil软件计算出的等效节点质量赋予节点的3个平动方向.支座采用等效双线性本构,屈服位移取2 mm[15],屈后刚度比为0.022.桥墩采用考虑弹塑性行为的nonlinerBeamColumn单元模拟,每1 m取一个单元,混凝土本构采用Kent-Park-Scott模型[16],钢筋采用考虑强化的双线性本构,纵向钢筋配筋率为0.8%,体积配箍率为1%.为了模拟地震动作用下的桩土效应,利用m法计算出群桩6个自由度的刚度并赋给弹簧单元相应的方向,通过弹簧单元将承台底节点和地基土壤连接起来.支座和土弹簧均采用zeroLength单元模拟,碰撞单元采用Muthukumar提出的本构模型[17],根据伸缩缝宽将初始间隙取为10 cm,其余参数均按文献[17]的推荐取值,以impactMaterial材料的truss单元模拟.通过有限元分析得出180条地震动纵桥向输入下连续梁桥的支座位移δb和墩顶漂移率Dr.
4 矢量地震动强度指标选取在IM的选取中,部分学者将决定系数(R2)作为评判IM优劣的指标[2, 10],由于R2反映了IM的高效性和实用性,即式(1)的回归残差平方和与直线斜率β1,表征了ln(IM)与ln(EDP)的相关程度.而对于VIM情况,单个IM变化的同时其他IM一般也在变化,这就需要在固定其他IM的前提下探讨单个IM与结构峰值响应的相关性.本文在选取对结构响应影响显著的IM时,采用偏决定系数[18](Ra2)作为衡量IM优劣的标准.偏决定系数Raq2定义为多元回归模型中已经包含有若干个IM时,再引入IMq后,残差平方和(SSE)的相对减少量,即
| $ R_{a q}^{2}=\frac{\operatorname{SSE}\left(\operatorname{IM}_{1}, \mathrm{IM}_{2}, \cdots\right)-\operatorname{SSE}\left(\operatorname{IM}_{q}, \mathrm{IM}_{1}, \mathrm{IM}_{2}, \cdots\right)}{\operatorname{SSE}\left(\mathrm{IM}_{1}, \mathrm{IM}_{2}, \cdots\right)}, $ | (5) |
则偏相关系数绝对值为|ra|=

|
图 5 VIM和IM回归结果对比 Fig. 5 Comparison of regression results of VIM and IM |
由图 5可知,无论是在训练数据集上还是在测试数据集上,采用VIM建立的回归模型的离散性都要明显小于以IM建立的回归模型.采用6折交叉验证得到的R2平均值进行比较见表 3,当以支座位移作为EDP时,VIM相比IM在训练数据集和测试数据集上的性能分别提升13.76%和16.67%;当以墩顶漂移率作为EDP时,性能分别提升13.58%和17.47%.同时,数据表明VIM在训练数据集和测试数据集上的表现没有明显差异,也就是说不存在过拟合问题.
| 表 3 交叉验证结果(R2平均值) Tab. 3 Cross-validation results (average of R2) |
当前一些地震动强度指标的灾害曲线还没有建立,因此这部分地震动强度指标的灾害可计算性还有赖于地震工程工作者的进一步研究.对于已经建立起灾害曲线的常用IM,如PGA、PGV、Sa(0.2)、Sa(1.0),虽然它们可能与第1步筛选出的6个IM存在多重共线性,但如果某个常用IM的回归结果能够满足PSDM建立的基本要求(如本例中以PGV为IM,以支座位移和墩顶漂移率为EDP,6折交叉验证得到测试数据集上的R2平均值分别为0.846、0.788),当前应优先考虑采用该标量地震动强度指标.
5 结论1) 提出了针对特定场地条件和结构类型的矢量地震动强度指标选取方法,能够在不显著增加计算量的前提下,简化地震动强度指标的选取流程,减小概率地震需求模型的变异性,并通过算例验证了其应用于无脉冲地震动作用下典型连续梁桥的有效性.
2) 针对现有标量地震动强度指标间的多重共线问题,提出了诊断和处理方法,筛选出了没有共线性的6个地震动强度指标PGD、Tpre、Tm、SD、Sa(0.2)、Sa(1.0),通过验证说明了20个现有地震动强度指标的信息都能包含在其中.
3) 提出了以偏决定系数选取矢量地震动强度指标分量的方法,交叉验证结果表明,采用两步筛选后得到的矢量地震动强度指标VIM[Sa(0.2), Sa(1.0), Tm]建立回归模型,在训练数据集和测试数据集上的离散性较采用标量地震动强度指标IM[Sa(1.0)]建立的回归模型分别减小13.67%和17.07%.
| [1] |
SHAFIEEZADEH A, RAMANATHAN K, PADGETT J E, et al. Fractional order intensity measures for probabilistic seismic demand modeling applied to highway bridges[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(3): 391. |
| [2] |
DU Ao, PADGETT J E, SHAFIEEZADEH A. A posteriori optimal intensity measures for probabilistic seismic demand modeling[J]. Bulletin of Earthquake Engineering, 2019, 17(2): 681. DOI:10.1007/s10518-018-0484-8 |
| [3] |
RIDDELL R. On ground motion intensity indices[J]. Earthquake Spectra, 2007, 23(1): 147. DOI:10.1193/1.2424748 |
| [4] |
PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake Engineering & Structural Dynamics, 2008, 37(5): 711. |
| [5] |
卢啸, 陆新征, 叶列平, 等. 适用于超高层建筑的改进地震动强度指标[J]. 建筑结构学报, 2014, 35(2): 15. LU Xiao, LU Xinzheng, YE Lieping, et al. Development of animproved ground motion intensity measure for super high-rise buildings[J]. Journal of Building Structures, 2014, 35(2): 15. |
| [6] |
WANG Xiaowei, SHAFIEEZADEH A, YE Aijun. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground[J]. Bulletin of Earthquake Engineering, 2018, 16(1): 229. DOI:10.1007/s10518-017-0199-2 |
| [7] |
BAKER J W. Probabilistic structural response assessment using vector-valued intensity measures[J]. Earthquake Engineering & Structural Dynamics, 2007, 36(13): 1861. |
| [8] |
BAKER J W, CORNELL C A. Vector-valued intensity measures for pulse-like near-fault ground motions[J]. Engineering Structures, 2008, 30(4): 1048. DOI:10.1016/j.engstruct.2007.07.009 |
| [9] |
CORNELL C A, JALAYER F, HAMBURGER RONALD O, et al. Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526. |
| [10] |
MACKIE K R, STOJADINOVIĆ B. Fragility basis for California highway overpass bridge seismic decision making[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2005
|
| [11] |
BAKER J W, LIN T, SHAHI S K, et al. New ground motion selection procedures and selected motions for the PEER transportation research program[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2011
|
| [12] |
KOSTINAKIS K, ATHANATOPOULOU A, MORFIDIS K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings[J]. Engineering Structures, 2015, 82: 151. DOI:10.1016/j.engstruct.2014.10.035 |
| [13] |
YAKUT A, YILMAZ H. Correlation of deformation demands with ground motion intensity[J]. Journal of Structural Engineering, 2008, 134(12): 1818. DOI:10.1061/(ASCE)0733-9445(2008)134:12(1818) |
| [14] |
何晓群. 应用回归分析(R语言版)[M]. 北京: 电子工业出版社, 2007: 154. HE Xiaoqun. Applied regression analysis (R language edition)[M]. Beijing: Publishing House of Electronics Industey, 2007: 154. |
| [15] |
毛玉东, 李建中. 大跨连续梁桥纵向减震机理和减震效果分析[J]. 同济大学学报(自然科学版), 2016, 44(2): 185. MAO Yudong, LI Jianzhong. Analysis of seismic mitigation mechanism and effect on longitudinal direction of long-span continuous bridges[J]. Journal of Tongji University (Natural Science), 2016, 44(2): 185. |
| [16] |
SCOTT B, PARK R, PRIESTLEY M. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain ratio rates[D]. Lulea, Sweden: Lulea University of Technology, 1989
|
| [17] |
MUTHUKUMAR S. A contact element approach with hysteresis damping for the analysis and design of pounding in bridges[D]. Atlanta: Georgia Institute of Technology, 2003
|
| [18] |
JOHNSON R A, WICHERN D W. Applied multivariate statistical analysis[M]. 6th ed. Upper Saddle River, New Jersey: Prentice Hall, 1998: 409.
|
 2020, Vol. 52
2020, Vol. 52


